
An Efficient Dual Dimensionality Reduction Scheme of Features for
Image Classification
Hai-Xia Long, Li Zhuo, Qiang Zhang, Jing Zhang and Xiao-Guang Li
Signal & Information Processing Laboratory, Beijing University of Technology, Chaoyang District, Beijing, China
Keywords: Dual Dimensionality Reduction, Locality Preserving Projections, Sparse Coding, Image Classification.
Abstract: The statistical property of Bag of Word (BoW) model and spatial property of Spatial Pyramid Matching
(SPM) are usually used to improve distinguishing ability of features by adding redundant information for
image classification. But the increasing of the image feature dimension will cause “curse of dimensionality”
problem. To address this issue, a dual dimensionality reduction scheme that combines Locality Preserving
Projection (LPP) with the Principal Component Analysis (PCA) has been proposed in the paper. Firstly,
LPP has been used to reduce the feature dimensions of each SPM and each dimensionality reduced feature
vector is cascaded into a global vector. After that, the dimension of the global vector is reduced by PCA.
The experimental results on four standard image classification databases show that, compared with the
benchmark ScSPM( Sparse coding based Spatial Pyramid Matching), when the dimension of image features
is reduced to only 5% of that of the baseline scheme, the classification performance of the dual
dimensionality reduction scheme proposed in this paper still can be improved about 5%.
1 INTRODUCTION
Image classification is the basic research problem in
the field of computer vision, artificial intelligence
and machine learning (Xie et al., 2014). With the
rapidly increasing number of images, however, the
traditional classification scheme has not been
applicable any more. Various image classification
schemes have been proposed. The representative
scheme is the Bag of Word (BoW) model based on
sparse representation proposed by Yang et al.,
(2009). In the scheme, the local feature is firstly
extracts from the image; next the over-complete base
(dictionary) is obtained by dictionary learning
method; then the linear combination of a few
dictionary atoms are used to represent the image;
finally, SVM (Support Vector Machine) classifier is
adopted for classification and recognition. The
greater the dictionary atom number is, the sparser
the image representation is, and the stronger the
characterization ability is.
The BoW model mainly uses statistics
information of local features of image, tends to
ignore the spatial information of image. Therefore,
Spatial Pyramid Matching (SPM) has been
introduced by Lazebnik et al., (2006). For a three
layers of SPM (1 + 4 + 16 = 21), if the dictionary
number is 1024, then the final feature dimension of
each image is 1024×21. With the increasing
number of images, the matrix size is more and more
big, and the calculation is more complicated, leading
to huge computation and memory pressure for
subsequent analysis, so-called the “curse of
dimensionality” problem (Bellman, 1961).
Dimensionality reduction technique can
effectively overcome the problem of “curse of
dimensionality". The DPL (Projective Dictionary
Pair Learning) algorithm was proposed by Gu et al.,
(2014), in which the advantages of analysis
dictionary and synthesis dictionary were combined,
and used in the objective function. The algorithm
improved the distinguishing performance of features
by increasing the type of dictionary. Object Bank
algorithm was proposed Li et al., (2010), in which
177 object filters were used to extract high-level
semantic feature for each image by the sliding
window method, and SPM and max pooling to
representation feature, with each image being
represented as a 44604-D vector. PCA technique
was been reduced dimensionality Literature (Gu et
al., 2014; Li et al., 2010), in which centralized
dimensionality reduction scheme was used, with the
672
Long, H-X., Zhou, L., Zhang, Q., Zhang, J. and Li, X-G.
An Efficient Dual Dimensionality Reduction Scheme of Features for Image Classification.
DOI: 10.5220/0005787506720678
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 672-678
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

spatial information of features being ignored, did not
highlight the advantages of SPM.
A dual dimensionality reduction scheme in
which feature dimension is reduced on the premise
of reserving image spatial information has been
proposed in this paper. Different from the
centralized dimensionality reduction scheme in
Literature (Gu et al., 2014; Li et al., 2010), the
scheme adopts the Spatial Pyramid Matching (SPM)
and Locality Preserving Projection technique
(Niyogi, 2004) to reduce feature dimension in each
subspace, which is called subspace dimensionality
reduction scheme, in order to reserve spatial
information of the image. Each subspace vector is
cascaded into a global vector; after that, the
dimension of the global vector is reduced by the
Principal Component Analysis, in order to reserve
the principle component of the vector and obtain
more compact image representation vector.
Experimental results show that, when the feature
dimension is reduced to 5% of the ScSPM (Yang et
al., 2009) by the dimensionality reduction scheme
proposed in this paper, the accuracy of image
classification is still slightly increased, which proves
the effectiveness of the scheme.
2 DUAL DIMENSIONALITY
REDUCTION SCHEME
In the field of image classification, the suitable
combination of BoW model and SPM (
Zhang et al.,
2014; Zhang et al., 2014; Lei et al., 2015; Wang et
al., 2014; Yan et al., 2015; Yang et al., 2015) is
used to improve distinguishing ability of image
representation by adding redundant information.
However, it leads to the image representation
dimension being increased dramatically, and brings
huge calculation and memory pressure of subsequent
image classification. Therefore, many researchers
adopt dimensionality reduction technique to solve
the “curse of dimensionality” problem. With both of
speed and efficiency being taken into considered, the
Dual Dimensionality Reduction Scheme (DDRS)
has been proposed in this paper, on the basis of
which an image classification scheme has been also
proposed. The block diagram is shown in figure 1.
2.1 Image Representation
Dense SIFT feature (Lazebnik et al., 2006) has been
extracted for each image in this paper. The sample
region is 16×16 pixel patches and the step size is 6
pixels (Yang et al., 2009).
Suppose that X is the set of M column-wise D-
dimension feature vectors from an image,
12
,,
D
M
M
Xxx x
. In a visual
dictionary
DN
V
, each element is called visual
word; N is the number of visual word.
12
,,,
N
M
M
Uuu u
is the reconstitu-tion
sparse coefficients. The goal of sparse coding is to
approximate the input vector X by a linear
combination of the dictionary:
2
,
1
1
2
min -
. . 1, 1, 2,...,
M
UV m m
m
m
n
x
Vu
s
tv n N
u
(1)
This is a non-convex problem. If a variable can be
fixed, it becomes a convex optimization problem. So
method of fixing a variable is used to attain the
visual dictionary and sparse coefficients. Firstly,
sparse coefficients are fixed and Eq. (2) is obtained.
2
,
1
min
M
UV
m
m
UV
x
(2)
This optimization can be solved efficiently by the
Lagrange dual as used in Yang et al., (2009) to get
the visual dictionary. Then, the visual dictionary is
fixed and Eq. (3) is obtained.
2
,
1
1
min
M
UV
m
mm m
V
x
uu
(3)
In order to solve this optimization, sparse
coefficients can be obtained by feature-sign search
algorithm. The visual dictionary with smallest
reconstruction error is gotten by multiple iterations.
At last, the visual histogram is generated with by
combining SPM and the max pooling algorithm.
2.2 Dual Dimensionality Reduction
Scheme
In this paper, the dual dimensionality reduction
scheme diagram is shown in figure 2. This scheme is
divided into two layers: in the first layer, LPP is
adopted to reduce dimension of corresponding
feature in each subspace of SPM, respectively; then,
each subspace vector is cascaded into a global vector;
in the second layer PCA is used to reduce
dimensionality, to further remove redundancy
between feature vectors and obtain the final image
representation vector in the lower dimension.
Two important parameters have been involved in
LPP: Maximum dimension (dmax) and Principal
An Efficient Dual Dimensionality Reduction Scheme of Features for Image Classification
673

0 10 20 30 40 50
0
0.5
1
1.5
2
2.5
0 10 20 30 40 50
0
0.5
1
1.5
2
2.5
0 10 20 30 40 50
0
0.5
1
1.5
2
2.5
0 5 10 15 20 25
0
0.5
1
1.5
0 5 10 15 20 25
0
0.5
1
1.5
0 5 10 15 20 25
0
0.5
1
1.5
0 50 100 150 200
0
0.5
1
1.5
2
2.5
0 10 20 30 40 50
0
0.5
1
1.5
2
2.5
Figure 1: A typical example and the flowchart of the proposed dual dimensionality reduction based image classification
method.
Component Analysis ratio (PCAratio), the number
of K-Nearest Neighbour (KNN) is fixed as 20. The
Maximum dimension indicates how many dimension
vectors have been retained to be, while the Principal
Component Analysis ratio refers to the proportion of
the proposed principal component accounted in the
total of contracted dimension in a vector. These two
parameters are related. When the parameter dmax is
larger than the value of the PCAratio, the PCAratio
becomes the priority, vice versa.
3 EXPERIMENT RESULTS AND
ANALYSIS
The comparison of classification accuracies has been
made between the ScSPM scheme and the dual
dimensionality reductions scheme on Butterfly (Li et
al., 2004), Scene-15 (Lazebnik et al., 2006), Caltech-
101 (Lazebnik et al., 2004) and Caltech-256 (Griffin
et al., 2007) dataset.
The Butterfly-7 dataset contains 619 images of
7different species of butterflies. In these species, the
minimum number of images is 42 while the
maximum number is 134. This dataset is character-
ized with variety in resolutions, small difference
between species and large difference in species.30
images per category have been selected and used as
training set, and others as testing set.
The Scene-15 dataset contains15 scenes: thirteen
scenes are provided by Li et al., (2004) and two
scenes (industrial and store) are added, which totally
is composed of 4485 images. Each category has 200
to 400 images, Where 100 images per category are
selected randomly for training and others or testing.
The Caltech-101 dataset contains 9144images of
101 categories and one kind of background. Each
category has 31 to 800 images. Image categories
include animal, plant, face, etc. The objects in the
same category are in large difference. 30 images per
category are randomly picked up for training, and
the rest for testing.
The Caltech-256 dataset contains 29,780 images
of 256 categories and one kind of background with
much higher object location variability and higher
intra-class variability compares with Caltech-101
(Yang et al., 2009). Each category has at least 80
images. In our experiments, we take 60 images for
training and use the rest for testing.
3.1 Influence of Different Parameters
Two important parameters have been involved in
LPP: Maximum dimension (dmax) and Principal
Component Analysis (PCAratio). We analyse the
influence of these two parameters by image
classification accuracy on three datasets of
Butterfly-7, Scene-15, Caltech-101, experimental
results are shown in figure 3~5. Figure (a) indicates
that how dmax affects the classification accuracy on
three datasets when PCAratio is fixed, while Figure
(b) indicates, how PCAratio affects the classification
accuracy when dmaxis fixed. It can be known from
figure3~5 that, with the increase of image
dimension, the classification accuracy on three
datasets increase first, and then decline, which
indicates that not the higher the image representation
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
674
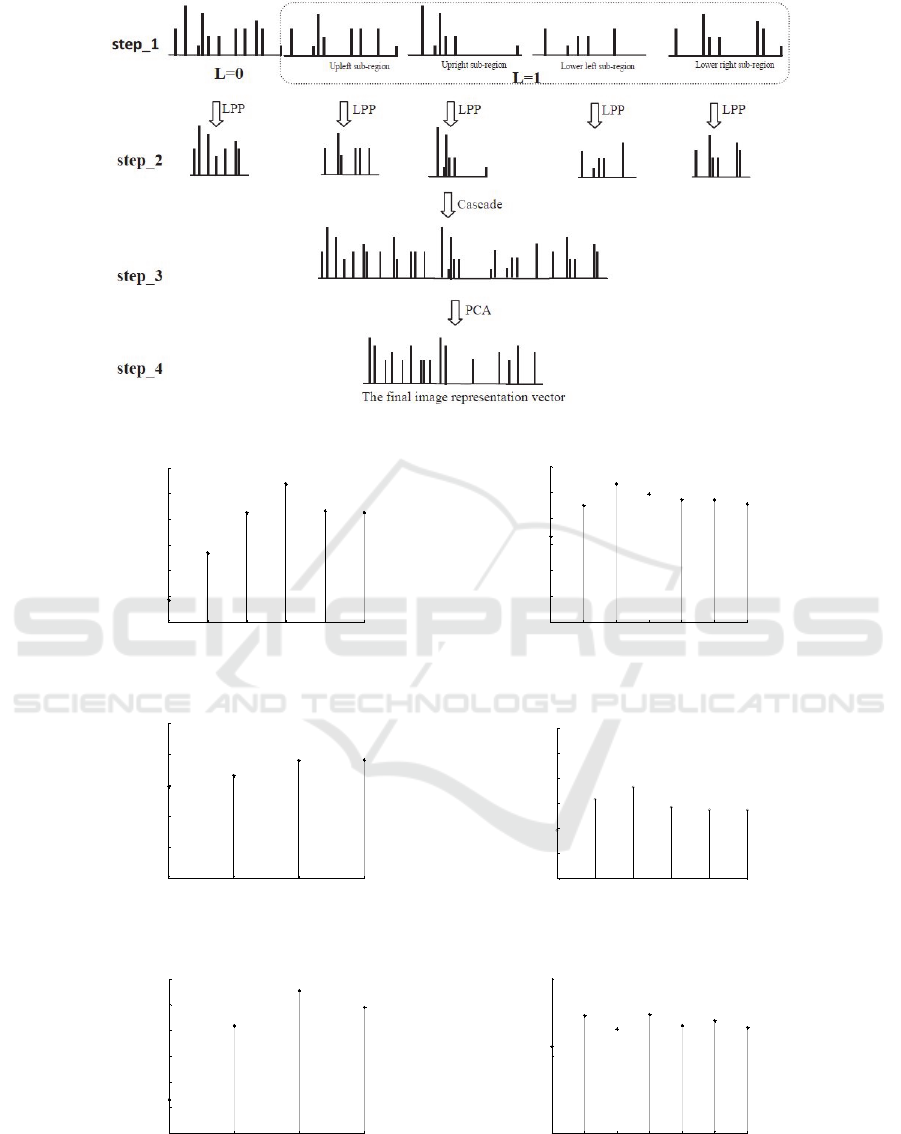
Figure 2: The diagram of Dual dimension reduction scheme.
(a) (b)
Figure 3: The dmax and PCAratio parameters effect on image classification accuracy in Butterfly-7 dataset.
(a) (b)
Figure 4: The dmax and PCAratio parameters effect on image classification accuracy in Scene-15 dataset.
(a) (b)
Figure 5: The dmax and PCAratio parameters effect on image classification accuracy in Caltech-101 dataset.
8 16 32 64 128 256
72
74
76
78
80
82
84
Max dimension
Classification accuarcy
0.2 0.3 0.4 0.5 0.6 0.7 0.8
80
81
82
83
84
85
86
PCAratio
Claasification accuracy
64 128 256 512
75
76
77
78
79
80
Max dimension
Classification accuracy
0.2 0.3 0.4 0.5 0.6 0.7
79
79.5
80
80.5
81
81.5
82
PCAratio
Classification accuracy
64 128 256 512
65
66
67
68
69
70
71
Max dimension
Classification accuracy
0.2 0.3 0.4 0.5 0.6 0.7 0.8
65
70
75
PCAratio
Classification accuracy
An Efficient Dual Dimensionality Reduction Scheme of Features for Image Classification
675
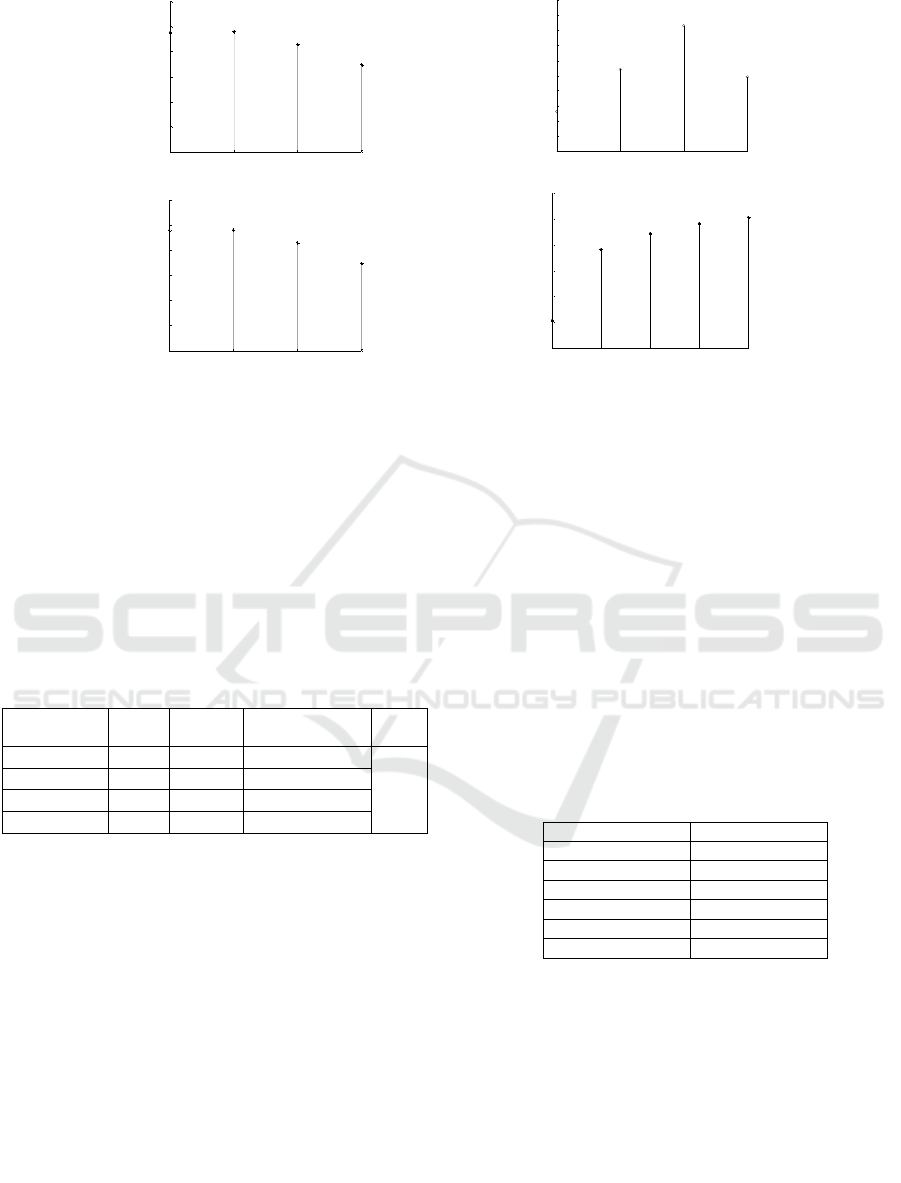
(a) Butterfly-7 dataset (b) Scene-15 dataset
(c) Caltech-101 dataset (d) Caltech-256 dataset
Figure 6: The Dim parameters effect on image classification accuracy in four datasets.
dimension is, the better the classification accuracy
is. Similarly, the principal component analysis ratios
begin to decline after reaching peak. The parameter
combinations of four databases are shown in table 1.
The parameter of PCA is mainly dimension
(Dim); this parameter also has direct impact on the
classification accuracy. The following is analysis
influence of different Dim values for classification
accuracy; the specific results are shown in figure 6.
Table 1: Combination of parameters in four datasets.
dataset dmax PCAratio
Image
representation
KNN
Butterfly-7 64 0.4
1344×619
20
Scene-15 256 0.4
2794×4485
Caltech-101 256 0.3
2876×9144
Caltech-256 256 0.3
2876×30607
According to the change trend of figure 6, it can
be seen that with the increase of the dimension, the
classification accuracy does not increase accordingly.
When it reaches a certain value, it begin to drop; this
shows that the high dimension do not improving the
characterization ability of feature. In this paper, final
dimensions of image representation are determined
on Buterfly-7, Scene-15, Caltech-101 and Caltech-
256 datasets to 256, 512, 1024, and 2048,
respectively.
3.2 Comparison of Image Classification
Scheme
3.2.1 Caltech-101 Dataset
Image representation dimension is set as 1024 in
Caltech-101 dataset, 1/21(1024/(21 × 1024)) of
ScSPM. Table 2 shows the classification accuracy of
different image classification schemes on Caltech -
101 dataset. It can be seen that the classification
accuracy of the proposed scheme has drastically
improved, increasing nearly 10%, compared with the
kernel Spatial Pyramid Matching (KSPM) (Lazebnik,
2006) and kernel Codebook Spatial Pyramid
Matching (KCSPM) (Van Gemert et al., 2008).
Compared with ScSPM, locality-constrained coding
(LLC) (Wang et al., 2010) and IMFSC (Luo et al.,
2014) based on Combing Multi-feature and Sparse
Coding scheme, it has different degrees of increase.
Table 2: The classification accuracy on Caltech-101
dataset.
Scheme Acc.
KSPM 64.4±0.80
KCSPM 64.14±1.18
ScSPM 73.2±0.54
LLC 73.44
IMFSC 73.55
DDSR 74.10
3.2.2 Caltech-256 Dataset
In this paper, the feature dimension of the Caltech -
256 dataset is set as 2048, 2/21 of benchmark
scheme. Table 3 shows the classification accuracy
the different classification schemes on the dataset. It
can be seen that the proposed scheme is slightly
higher than the Laplace sparse coding LScSPM (Gao
et al., 2010) and benchmark scheme. Dictionary
number of locality-constrained coding algorithm
LLC (Wang et al., 2010) is 4096, image vector
dimension is 21×4096, data quantity is 42 times
128 256 512 1024
84
84.5
85
85.5
86
86.5
87
dimension
classification accuracy
128 256 512 1024
80
80.1
80.2
80.3
80.4
80.5
80.6
80.7
80.8
80.9
81
dimension
claasification accuracy
128 256 512 1024
84
84.5
85
85.5
86
86.5
87
dimension
classification accuracy
128 256 512 1024 2048
35
36
37
38
39
40
41
dimension
claasification accuracy
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
676

over ours, if the dictionary number is set as 1024, its
classification accuracy is 37.79±0.42% (Gao et al.,
2013), classification accuracy of our proposed
scheme is 3.18% higher than LLC algorithm.
Table 3: The classification accuracy on Caltech-256
dataset.
Scheme Acc.
ScSPM 40.14
LLC 47.68
LScSPM 40.43
DDSR 40.97
3.2.3 Butterfly-7 Dataset
In this paper, the image representation dimension of
the Butterfly-7 dataset is set as 256, 1/84 of ScSPM.
Butterfly dataset is different from Caltech dataset, it
belongs to fine-grained recognition. The inter-class
difference among sample data is small, the inner-
class difference is big, and so its classification is
more difficult. Table 4 shows the classification
accuracy of different classification methods on
Butterfly-7 dataset. It can be seen from the table
that, the classification accuracy of the scheme
provided in this paper is higher than that of ScSPM
and LLC.
Table 4: The classification accuracy on Butterfly- 7
dataset.
Scheme Acc.
ScSPM 81.30±1.57
LLC 87.54
DDSR 89.92
3.2.4 Secne-15 Dataset
The image representation dimension of Secne-15
dataset is set as 512, 1/42 of benchmark scheme. The
classification accuracy of different algorithms on
Secne-15 dataset is given in table 5, of which OB (Li
et al., 2010) scheme based on object bank, WSR-EC
(Zhang et al., 2013) based on weak attributes of
object combining template classifier. As can be seen
from the table, the classification accuracy of the
proposed scheme is 4.91% higher than KCSPM
scheme, and slightly higher than the other scheme.
Table 5: The classification accuracy on Scene-15 dataset.
Scheme Acc.
KSPM 81.40±0.50
KCSPM 76.67±0.39
WSR-EC 81.54±0.59
OB 80.9
ScSPM 80.28±0.93
DDSR 81.58
4 CONCLUSIONS
In order to solve the problem that image represent-
tation dimension is over high, the dual dimensiona-
lity reduction scheme has been proposed in this
paper, being designed to reduce image
representation dimension, and reverse the
distinguishing ability of image representation at the
same time. In four standard dataset of Butterfly - 7,
Scene - 15, Caltech - 101 and Caltech-256,
compared with the benchmark scheme, experimental
results show that, on condition that the image
representation dimension is reduced to 5% of the
original dimension, the image classification
accuracy of the dual dimensionality reduction
scheme is still improved more than 3% average.
ACKNOWLEDGEMENTS
The work in this paper is supported by the National
Natural Science Foundation of China (No.61372149,
No.61370189, No.61471013), the Importation and
Development of High-Caliber Talents Project of
Beijing Municipal Institutions (No.CIT&TCD2015
0311,No.CIT&TCD201304036, CIT& TCD201404
043), the Program for New Century Excellent
Talents in University(No.NCET-11-0892) , the
Specialized Research Fund for the Doctoral Program
of Higher Education(No.20121103110017), the
Natural Science Foundation of Beijing (No.414200
9), the Science and Technology Development
Program of Beijing Education Committee(No.KM20
1410005002.
REFERENCES
Xie L, Tian Q, Wang M, et al. Spatial pooling of
heterogeneous features for image classification. IEEE
Transactions on Image Processing, 2014 (23): 1994-
2008.
Yang J, Yu K, Gong Y, et al. Linear spatial pyramid
matching using sparse coding for image classification.
Computer Vision and Pattern Recognition, 2009:
1794-1801.
Lazebnik S, Schmid C, Ponce J. Beyond bags of features:
Spatial pyramid matching for recognizing natural
scene categories. Computer Vision and Pattern
Recognition, 2006 IEEE Computer Society
Conference on. 2006, 2: 2169-2178.
R Bellman. Adaptive Control Processes:A Guided Tour
1961.
S. Gu, L. Zhang, W. Zuo, and X. Feng. Projective
Dictionary Pair Learning for Pattern Classification.
An Efficient Dual Dimensionality Reduction Scheme of Features for Image Classification
677

In NIPS 2014.
Li L J, Su H, Fei-Fei L, et al. Object bank: A high-level
image representation for scene classifica-tion &
semantic feature sparsification. Advances in neural
information processing systems. 2010: 1378-1386.
Niyogi X. Locality preserving projections. Neural
information processing systems. MIT, 2004, 16: 153.
Zhang C, Xiao X, Pang J, et al. Beyond visual word
ambiguity: Weighted local feature encoding with
governing region. Journal of Visual Communication
and Image Representation, 2014, 25(6): 1387-1398.
Zhang C, Liang C, Pang J, et al. Undoing the codebook
bias by linear transformation with sparsity and F-norm
constraints for image classification. Pattern
Recognition Letters, 2014, 45: 197-204.
Lei B, Tan E L, Chen S, et al. Saliency-driven image
classification method based on histogram mining and
image score. Pattern Recognition, 2015, 48(8): 2567-
2580.
Wang X, Ma J, Xu M. Image Classification Using Sparse
Coding and Spatial Pyramid Matching. 2014
International Conference on e-Education, e-Business
and Information Management. Atlantis Press, 2014.
Yan S, Xu X, Xu D, et al. Image classification with
densely sampled image windows and generalized
adaptive multiple kernel learning. Cybernetics, IEEE
Transactions on, 2015, 45(3): 395-404.
Yang Y B, Zhu Q H, Mao X J, et al. Visual feature coding
for image classification integrating dictionary
structure. Pattern Recognition, 2015.
Fei-Fei L, Fergus R, Perona P. Learning generative visual
models from few training examples: An incremental
bayesian approach tested on 101 object categories.
Computer Vision and Image Understanding, 2007,
106(1): 59-70.
Lazebnik S, Schmid C, Ponce J. Semi-local affine parts for
object recognition. British Machine Vision Conference
(BMVC'04). 2004: 779-788.
Griffin G, Holub A, Perona P. Caltech-256 object category
dataset. California Institute of Technology (2007).
Supplied as additional material tr. 5(6).
Van Gemert J C, Geusebroek J M, Veenman C J, et al.
Kernel codebooks for scene categorization. Computer
Vision–ECCV 2008. Springer Berlin Heidelberg, 2008:
696-709.
Wang J, Yang J, Yu K, et al. Locality-constrained linear
coding for image classification. Computer Vision and
Pattern Recognition (CVPR), 2010: 3360-3367.
Luo Hui-lan, Guo Min-Jie, Kong Fan-Sheng. Image
Classification Method by Combing Multi-feature and
Sparse Coding. Pattern Recognition and Artificial
Intelligence, 2014,27 (4): 345-355.
Gao S, Tsang I W, Chia L T, et al. Local features are not
lonely–Laplacian sparse coding for image
classification. Computer Vision and Pattern
Recognition (CVPR), 2010: 3555-3561.
Gao S, Tsang I W, Chia L T. Sparse representation with
kernel. Image Processing, IEEE Transactions on,
2013, 22(2): 423-434.
Zhang C, Liu J, Tian Q, et al. Beyond visual features: A
weak semantic image representation using exemplar
classifiers for classification. Neuro-computing, 2013,
120: 318-324.
Li L J, Su H, Fei-Fei L, et al. Object bank: A high-level
image representation for scene classification &
semantic feature sparsification. Advances in neural
information processing systems. 2010: 1378-1386.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
678
