
Programming for the Humanities
Logic and Adaptable Languages
Jerzy Karczmarczuk
Dept. of Computer Science, University of Caen, Caen, France
Keywords:
Logic, Prolog, Abstraction, Constraint programming, Non-determinism.
Abstract:
We argue in favour of teaching modern programming to students of “non-scientific” undergraduate disciplines
(humanities), considering that computer-assisted learning should not be reduced to the usage of tools, but
provides some answers to the question: how the knowledge is built. The computer science should be treated as
an inherent part of their culture. We advocate the teaching of Logic Programming languages: Prolog, and of the
Constraint Programming languages, such as CHR. Logic programming permits to formulate the computational
problems and their solutions in a form more close to human reasoning than several other languages, and
adaptable to the domains of interest of the learners.
1 INTRODUCTION
The necessity to use computing techniques in Hu-
manities (Human and Social Sciences) is visible since
the beginning of the fifties, and the related teach-
ing progresses steadily. The plethora of applications:
databases for historians, visual recognition for archae-
ologists, analytic tools for linguists, etc., need no ad-
vertising, see (Schreibman et al., 2004; Arthur and
Bode, 2014). The Association for Computers and Hu-
manities has 38 years. Stanford and the University
of Geneva offer such combined specialization to their
students, the King’s College has a PhD program in
digital Humanities, etc. But, the integration of these
two worlds, analogous to the “strong coupling” be-
tween computer specialists and physicists, is less easy
than in a formalized discipline, operating on numeri-
cal data which are “naturally” processed by comput-
ing devices.
But in our opinion, the major difference between
the humanities and the “hard” sciences, in relation
with the information technologies, is that in the lat-
ter case, for the last 60 years students learn how to
develop and modify their specific tools, while in the
former – just how to use them. The word “program-
ming” became almost a taboo. . . The Digital Human-
ities Quarterly (Quarterly, 2015) had no title including
this word for almost ten years. In the section Q&A of
the ACH site, the number of questions in the cate-
gory “Programming” is of 3%: 13/392. There are 166
questions about tools and formats. . .
Christian Koch (Koch, 1991) underlines that to
survive, the domain cannot remain a loose amalga-
mation of the two fields. Teachers in human sci-
ences should develop their understanding of com-
puter science, and the computing specialists should
acquire some feeling for more cultural, less techni-
cal approaches to their work in contact with the other
side. We believe that we should teach more pro-
gramming for the first, and adapt ourselves to their
methodologic needs. This is not a question of pro-
filing the taught topics: to teach formalized music to
musicologists, computer grammars to linguists, etc.
The idea that programming is a universal cultural tool,
is more important. The reasoning with abstractions
is fundamental, and often better adapted to students
in human sciences, than to “technologists”. There is
nothing wrong with using simple arithmetic, or ba-
sic data processing examples in teaching computing
to humanities.
20 years after the article of Koch, in “Program or
be Programmed” (Rushkoff, 2010), the author draws
the picture of the society, where we still teach how to
become the consumer of tools made and controlled
by somebody else. Shall humanities’ teachers and
students remain eternal consumers?
1
1
This reminds the allegory of Asimov: “Profession”,
about a society where all knowledge is registered directly
into the brain, only a tiny minority of “ retarded” learn ev-
erything the hard way, by reading, calculating. . . We dis-
cover that these “handicapped” are the true intellectual elite,
only they are able to create new knowledge.
298
Karczmarczuk, J.
Programming for the Humanities - Logic and Adaptable Languages.
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 1, pages 298-305
ISBN: 978-989-758-179-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 SOME DIFFICULTIES
In 2015 the Soci
´
et
´
e Informatique de France organized
a panel session on the teaching of computing in hu-
man sciences. The participants concentrated on the
universality of the ‘informatized’ culture, on the data
search, etc. The coding, and the construction of tools
used to analyze and structure the information were
barely mentioned. The tools were considered given.
We tried to analyze why.
• The Humanities people need not accept the affirma-
tion that in order to use computers efficiently, they
should know how they function, as a harpsichordist
doesn’t need to know how his instrument works,
and researchers, also in physics, will not waste their
time on technicalities
2
. Bread, airplanes, and com-
puters, including the software, are made by special-
ists. It is too easy to disperse the effort on technical
details, and neglect the essence.
• Computer science: algorithmics, optimization, etc.,
are formal, mathematically oriented, and the word
“numerics” influence negatively the interest of stu-
dents. They would agree that some elements of the
theory of coding and data structuring, etc., are parts
of the human culture, useful in general, but it is a
different culture, in Humanities the researchers are
reluctant to code.
But Steve Jobs said that “everybody should learn how
to program a computer, because it teaches you how
to think. Computer science is a liberal art”. Writing
in a disciplined way about anything, conditions the
mind, and it should be taught early. Musical compo-
sition and choreography are programming. The world
needs new specialists, and it is a historian, and not an
engineer, who will design a new schema establishing
the chain of events leading to some historical context
(Cameron and Richardson, 2005).
The words such as numeric or digital lost their
immediate meaning, the bulk of the information pro-
cessed by computers is symbolic in its essence. This
“different culture” might not be easy to accept by
teachers formed 40 years ago, but it is natural for
children, not knowing any mathematics. If instead
of providing a modern education to the Humanities
students, we train them how to use some obsolescent
software products, we fail.
The question of teaching to code in High Schools,
has an old tradition, and is constantly rekindled.
There were successes and failures, and thousands of
errors. Some statistics says that a serious percentage
2
This is manifestly false, both for musicians and for No-
bel prize winners in physics; M. Veltman built a universal
computer algebra package with his hands.
of students simply cannot learn to program. Then, we
read that the authors began with such programming
languages as Java. . . In our opinion, the most harm-
ful teaching errors comes from such myths as : “learn
to reason as the computers do”, or “learn to think as
a computer scientist”. We should adapt the program-
ming paradigms to human reasoning.
3 LOGIC PROGRAMMING
3.1 Language Choice Criteria
Stephen Ramsay (Ramsay, 2012), admitting that the
choice of programming language is arbitrary and con-
tentious, enumerates his choice criteria, whose first
is: low entrance barrier – simple, consistent syntax,
no low-level manipulations in typical programs, but
a reasonably large base of third-party librairies, and
decent interfacing (APIs). Also, that the language
should support multiple programming paradigms /
styles. We complete this with the following:
• Extensibility. The language should provide a gen-
eral basis for the DSL extensions (Domain-Specific
Languages), permitting to operate with concepts
and entities which are relevant to the domain of
interest of the user: linguistical analysis, real-time
communication, game-making, design of circuits,
etc. This requirement cannot be universally satis-
fied, e.g., the number-crunching needs are too far
from symbolic communication. We assume that
here the speed of the language processors is not the
first criterion, but the possibility to operate within
the problem space of immediate interest – is, and
the facility of operating with symbolic data is pri-
mordial.
• Interactivity. The language implementation should
be conversational, permitting to add incrementally,
and test small pieces, to debug interactively a faulty
program, and in general, to see what is the context,
when the program fails. This is relevant to teaching
of programming in general.
• “Web awareness”. Taking into account that the
bulk of data is stored in shared databases (linguis-
tical corpora, maps, etc.), the access to the Web re-
sources should be easy and natural. It should be
easy, see: (Karczmarczuk, 2015), not only to oper-
ate a browser, but also to install a small applicative
server, which might facilitate the pedagogical com-
munication.
We think that more attention should be given to the
language Prolog and its descendants, and to the logic
paradigms in programming in general. This is not
Programming for the Humanities - Logic and Adaptable Languages
299

new, Prolog was invented in 1972, see (Kowalski,
2014). It was a project meant as a tool for processing
natural languages (French), a noble pedigree for the
Humanities. . . It has already been extensively used
for teaching, and has been designed as the program-
ming basis for the Japanese 5-th generation project,
1982 – 1992. The teaching didn’t “fail”, but it lost
the popularity war with such languages as Java or
Python, for different reasons. One of them was the
“academic essence” of this domain, while the over-
whelming trend was to have the computing for the
“masses”. Another one was the spreading of the opin-
ion that the entry barrier was too high, since average
users don’t care about formal logic. Finally, the evolu-
tion of Constraint Programming helped to spread the
opinion that Prolog became obsolete, a “dead” lan-
guage, which should not be taught (it was similar to
the abandon of Pascal in favour of “C”).
Such arguments are discutable, but the teaching
modes, are living, evolving entities, which kill weaker
species. Thus, the popular and prestigious (almost
100 countries participate, UNESCO and IFIP patron-
age) International Olympiad in Informatics (Informat-
ics, 2015) for secondary school pupils, permits to use
Pascal, C, C++ and Java only, which contributes to
this deplorable polarization
3
. The ACM International
Collegiate Programming Contest is no more tolerant.
This seems analogous to the organization of universal
musical competitions, and forbidding all but two or
three instruments.
As mentioned, linguists use Prolog intensely, but
they teach it rarely. H. Christiansen (Christiansen,
2002) shares his experience with teaching Prolog used
as a meta-language permitting to understand better
other languages. (He advocates Logic Programming
as a second language, after, say, Java, but this has
some sense mainly for computer science students).
We return to this teaching vehicle, because in view
of its potentialities, it simply hasn’t been adequately
exploited in the discussed context. We taught Prolog
in Engineering Schools and at the University: com-
puter science, and formerly some courses for physi-
cists, and for philosophers (mostly humanists), and
we have some experience with teaching Prolog to sec-
ondary school pupils, where the imposed constraint
was: no serious mathematics. Remarkably, we could
use similar
4
presentation strategies in all those cases,
because of the universality of the language.
Recently we used the popular implementation
SWI-Prolog of Jan Wielemaker, see (Wielemaker,
3
Paradoxically, many contests problems in IOI and sev-
eral national Olympiads are logical puzzles, well adapted to
relational or functional programming.
4
Not identical ; examples were chosen specifically.
2012), and their Web site. While installing the sys-
tem is easy, in order to start programming, the stu-
dents don’t need to, it suffices to connect their Web
browser to the Prolog server (SWI, 2015), remote, or
installed locally, write or load some definitions, and
launch some query in another frame, open in the same
browser window. The first contact is established in
one minute.
The usage of the Web interface to teach program-
ming is progressing slowly, but steadily. This is par-
ticularly easy for languages implemented through vir-
tual machines with internal compilers: Java, Ruby,
Scheme/Racket, Python, and of course Prolog. The
authors of (Stutterheim et al., 2012) installed their
own “nano-Prolog” server, and taught how to make
it, as an example of the transmitted techniques. We
used a micro-server to test on line some students’ DC
Grammars in Prolog.
3.2 A Way to Program in Prolog
We assume that the Reader can read Prolog, and can
understand its basic structures. We sketch here the
presentation strategy during some of the first hours of
the course. We wanted at the beginning to underline
the specific nature of the language, although we did
not discourage the students of searching some paral-
lels with the techniques they knew.
The basic syntax can be exposed in less than 20
minutes, and there is some time to warn the students
that the language is infinitely extensible through user-
defined operators. A program rule P:-Q1,Q2;Q3.
says that P is true, if both Q1 and Q2 are true, or
if Q3 is true. It may be also an elementary fact,
e.g.: rains(today). Essentially, all program is
a sequence of combinations of such elements. The
passage of parameters, atomic and composite is in-
tuitive. From the procedural point of view, what
is a function of N parameters in other languages:
f (X
1
, X
2
, . . . , X
N
), becomes a predicate with N + 1 pa-
rameters, one (or more) of them is the answer, e.g.,
f(X1,X2,...,XN,R).
We often worked the concrete details by showing
first a small (but complete) example, and then elab-
orating the sense of its components and their rela-
tionships. When the students knew already about the
AND/OR syntax and the lists patterns, they grasped
the idea of non-instantiated variables, and they mas-
tered the primitive arithmetic (X is 7+2*X, etc.), we
surprised them with the following single query pro-
gram:
length(L,4),member(a,L),member(b,L),
member(c,L),member(d,L).
CSEDU 2016 - 8th International Conference on Computer Supported Education
300

which generates incrementally all the 24 permutations
of 4 symbols.
L = [a,b,c,d] ;
L = [a,b,d,c] ;
...
L = [d,c,b,a]
The program trying to establish the truth value of
some statements about the properties of the processed
data (the list must contain a, etc.), is able to gener-
ate some complex answers. It happens when some
parts of input data are unknown/arbitrary, they are
responses, not input, like the list L above, and the
program provided a model which “made dream come
true”. It was far from the the (still. . . ) standard
teacher’s reproach: “come on, what is L, do you think
that computer will invent it itself?”. . .
We had to explain the concept of backtracking, of
the automatic search for alternative solutions, which
was not difficult to accept. Among students with sim-
ilar background, we had more problems with those
having some former experience with other languages
(Basic, Pascal, Fortran. . . ), since they wanted to know
how it could be done in languages they knew. Some
of our students knew the concept of Ariadne’s thread,
but it was initially easier to work with the youngest,
who accepted the code without being surprised. The
introduction to the logical non-determinism in pro-
gramming demands a certain discipline, it is possible
to confound it with the trial-and-error strategy, and
all had to be explained. But this example shows that
the the claim that computers “need” from the user de-
tailed algorithms showing how to solve a problem, is
na
¨
ıve. The declarative features of Prolog are practical
concepts. We could then unveil the internal proce-
dures driving the process, namely
member(X,[A|Q]):-X=A ; member(X,Q).
length([],0).
length([X|R],N):-
length(R,N1),N is N1+1.
. . . which suggested a way to generalize the strategy
to any number of elements, with a easy layer of arith-
metic. We talked about recursion (linear), which we
tried to present as the most fundamental way in the
world to repeat actions: a snail building its shell, ap-
plies recursion; a 14-month child learning to walk, is
tail-recursive; they don’t know how to “iterate”, they
have no counters, nor the built-in mechanisms to con-
trol the loop. They make one step, and proceed with
the same action. They stop, because something “goes
wrong”, and the procedure breaks. Here, the head pat-
tern recognition cannot be fulfilled (an empty list is
not compatible with a list possessing at least one ele-
ment), and we choose an alternative clause. (The tod-
dler sits down. . . ) Simultaneously, the students recog-
nized that they had already two answers to the ques-
tion: “how to make a loop, to write all elements of
the sequence at once, without having to demand them
one by one”, one using the forgetting backtracking,
and another, progressive/recursive:
bkloop(L):-member(X,L),writeln(X),fail.
rcloop([X|Q]):-writeln(X),rcloop(Q).
The first one shows that the “failure”, the negative an-
swer to a logical query may be used as a generating,
constructive control structure. The backtrack-driven
loops were easier to assimilate by freshmen than by
the engineering students. The failure-driven loops
could be used to iterate some imperative side-effects,
e.g., to generate graphical elements, which could not
be forgotten; a picture could not be “undrawn”.
A Prolog course introduces at the beginning
the notion of predicate, the yes/no function of
any parameters (some of which may be unknown,
they are instantiated answers). They may be facts,
which state some relations between the arguments,
or rules, which permit to assemble a deductive
database. The standard examples include often
the “family” collection, which begins with facts
(plain truths), such as father(adam,abel).
father(adam,cain). father(cain,enoch).
father(enoch,irad)., etc., if one likes biblical
references. . . This permits to deduce:
brother(X,Y):-
father(Z,X),father(Z,Y),X\=Y.
ancestor(X,Y):-father(X,Y) ;
ancestor(X,Z),father(Z,Y).
and, with some generalization, to play with
real, complex hierarchical links. Here the stu-
dents were already able to launch two-way
queries, such as ancestor(Who,enoch)., or
ancestor(cain,Who).. One important conceptual
point here, is the existential binding of the variable
Z. The facility to generate auxiliary data in Prolog:
“something unknown, but which helps to continue
the search” is incomparable with other languages. A
good percentage of our exercises led to errors, not to
trivial bugs, but to inspiring failures, which exposed
important misunderstanding of the problem or of its
solution strategies, or the incoherence of data, which
had to be localized and corrected (e.g., two different
“family members” porting the same name).
The second point, was related to the ultimate crash
of the program ancestor above, triggered by the
infinite left recursion (ancestor may invoke ancestor,
which invokes ancestor. . . but doesn’t change the rel-
evant argument. The reasonable impression that the
order of clauses in a logical conjunction is irrelevant,
like in elementary propositional calculus, is danger-
ous. The logic may exist without time sequencing, but
Programming for the Humanities - Logic and Adaptable Languages
301

human minds don’t. Logic programs have their log-
ical, declarative, often “timeless” meaning, but also
some operational sense, like programs in other lan-
guages. The students have to grasp the difference
between: “father of ancestor” and “ancestor of fa-
ther”. . . From the pedagogical perspective this in-
troduces some additional conceptual problems, takes
time to explain, and potential teaching difficulties are
serious, but inspiring.
When one works with graphs more elaborate than
simple trees, including graphs with cycles (e.g., the
collections of linked references in Web pages; social
exchanges in groups of people, etc.), and the prob-
lem needs to find paths between nodes, or to construct
closures, it is necessary to avoid dead loops, which
could crash the algorithm. This is taught everywhere
in computer science, and in this context all program-
ming languages are equal, but Prolog is nice, because
of its facility to construct auxiliary data structures for
tracing the possible paths.
A functional term: the construction “father(A,B)”
or similar, is more rich in properties than one may
think. First examples in Prolog usually have a some-
what procedural sense, such construct (predicate) is
a “function” from two objects to a Boolean (im-
plicit: success or failure), which provides answers
to an appropriate question, here: is A father of B?.
But at the same time, this is a composite data struc-
ture, and the program can analyse the data item:
...,somePred(father(seth,X),...),.... We
have specified a deductive database!
The concept of databases is related to composite
data structures, historians need them often (Thaller,
1993), but M. Thaller argues that standard DB are
of limited use, because of the non-determinism, and
fuzziness of data, pertinent to historical thinking.
The users should know how to analyse abstract func-
tional relations, e.g., to operate logically on symbolic
constructions such as brother(ancestor(noah)),
without precising who exactly is (are) this person(s).
A Logic Programming system can be used as
an abstraction builder. It facilitates e.g., the hypo-
static abstraction, the passage from brother(X,Y)
to relative(X,Y,brother) where we speak about
generic properties, relations between concepts, not
only between individuals. In general, the term “ab-
straction” means different concepts for a philosopher,
for an artist, and for a computer scientist. But one
property in common is the information hiding, op-
erating only with properties and entities which are
meaningful in a given context. This information hid-
ing and generality is a known good feature of Logic
Programming.
4 ABSTRACTIONS AND
EXTENSIONS
We used logical programming to teach language pro-
cessing and to create some non-trivial graphics. We
didn’t want to present just tools, applications for lan-
guages/arts students, and of restricted interest for the
others, but to show how this abstraction layer can be
easily and intuitively implemented.
4.1 DCG Grammars
Prolog was created with linguistic objectives in mind,
and its facility to process symbolic data is good (com-
pact, readable, and functionally rich) by design. The
Direct Clause Grammar formalism (Pereira and War-
ren, 1980) addresses this field, despite the warning
that this subject is for advanced students, already
knowing Prolog, we taught it in second-year (a course
on automatic treatment of languages), where knowl-
edge of programming was weak. It was easier and
more instructive than using such pre-cooked tools as
parsers in the Python NLTK package. As a bonus,
we could speak about the ways to extend/adapt a pro-
gramming language for the specific domain-oriented
needs.
Below is an executable program which recog-
nizes simple English phrases, such as [a, mouse,
scares, the, cat, which, loves, the,
mouse].
phrase --> noun_phr,verb_phr.
noun_phr --> det,noun.
verb_phr --> verb,noun_phr,
([which],verb_phr | []).
det --> [the]|[a].
noun --> [cat]|[mouse].
verb --> [scares]|[loves].
It has the traditional form of a context-free grammar,
known to all who learn linguistics or compilation, of-
ten shown as one of the first examples, whose aim is
to show the recognition decision: correct/bad. The
words in brackets are literals (constants), and others
are non-terminals (variables). The context-free gram-
mars are too weak for natural languages, but they are
the initial examples.
A query phrase([a,mouse,loves,...],R),
accepts the phrase or not, and yields the tail of the
parsed list, which may undergo further treatment. The
definitions of phrase or noun, simple words, may
become “procedures” which take two parameters be-
cause of the power of abstraction-building extension.
The operator (-->) is a converter which turns a DCG
clause into a parameterized predicate, but this is in-
visible when designing a grammar, unless we want to
show the details.
CSEDU 2016 - 8th International Conference on Computer Supported Education
302
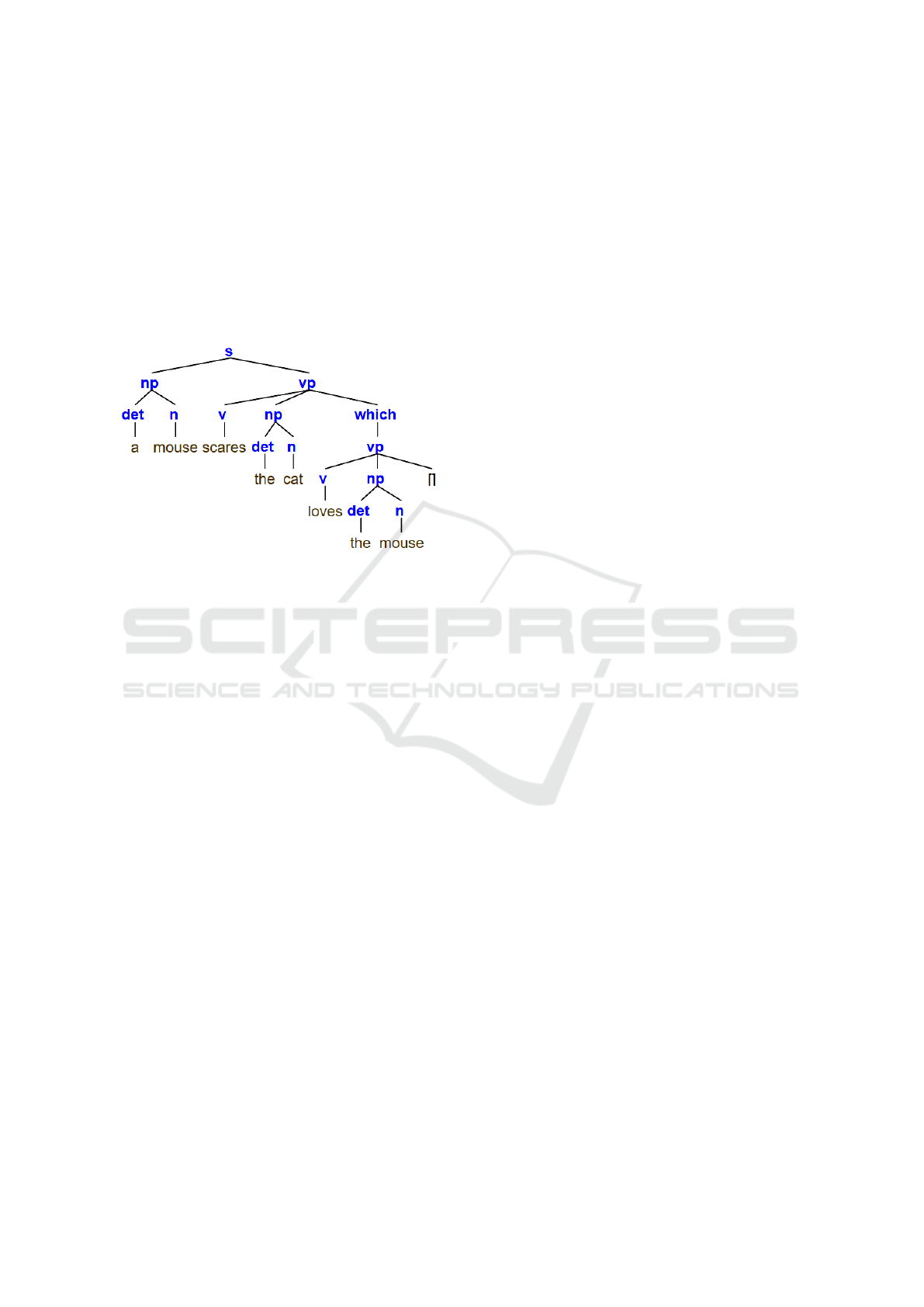
Such extensions may be built by the learners, and
if they need more, e.g., the construction of the syn-
tax tree corresponding to the phrase containing verbs
v(X), nouns n(X), etc., they need only to parametrise
the clauses with structures yielding the answers, e.g.:
verb(v(X)) --> [X],{X=scares; X=loves}.
A result, say s(np(det(a), n(mouse)),
vp(v(scares), ...) may be automatically
drawn in a suggestive form shown on Fig. 1.
Figure 1: Syntax Tree
We got all in one place: the abstract grammar,
which defines the phrase structure, the executable
parser, and plenty of tools to introduce meta-rules,
such as sequencing: a word is a letter followed by a
word, etc. The students could see directly the relation
between the abstraction and the implementation.
4.2 Higher-order Graphics
This topic has been presented to low grade students,
where we couldn’t rely on the knowledge of compli-
cated graphics. The high-level paradigm meant, as
always: abstraction, operating with opaque entities :
“pictures”, which could be added, rotated, embedded,
etc., and such actions may be implemented in any lan-
guage; Prolog offers simply intuitive, and very com-
pact meta-tools, accessible to beginners. If P, Q are
pictures, it suffices to operate with P+Q, where
show(P+Q,Frame):-
show(P,Frame),show(Q,Frame).
specifies the drawing composite, which remains ab-
stract, “+” is just a symbol. Frame is the coordi-
nate system, specifying the origin, and axes. The
students appreciated the “allegory”: the Frame is the
observer, and moving a picture is equivalent to mov-
ing its observer, so defining picture transformations
was remarkably easy, we needed just simple vector
operations, known to everybody; transforming the
frame permitted to transform any picture. The stu-
dents were able to implement easily such construc-
tions as: putting one picture above another one, iter-
ate scaling, rotating and translating recursively some
picture in order to generate some fractals, etc. It was
easier, and more powerful than the known Logo “tur-
tle” operations. The primitive pictures such as lines
and points were pre-defined.
In order to ensure the principle of data hiding,
while designing a picture, the Frame should be invisi-
ble. The user program introduces thus a new operator,
say, (=>>), and after having defined, say:
(P =>> Q,R):-assert(show(P,Fr):-
show(Q,Fr),show(R,Fr)).
the composition reduces to a surprisingly short spec-
ification A+B =>> A,B: a composite of two pictures
means that we draw both, no data manipulation us-
ing lists or arrays. The program size matters for stu-
dents without much experience not only for psycho-
logical reasons, but shorter programs offer less occa-
sions to make errors. Such abstract programming en-
courages the students to exploit their intuition, their
human reasoning, and this increases their coding effi-
ciency. Thus, although language extension is usually
an advanced issue, adapting the software to the user,
could have been introduced to beginners.
5 CONSTRAINT
PROGRAMMING
Here, the relation between data are expressed as con-
strains, e.g., “the painting X belongs to the ’XVII,
but is later than Y”. This is declarative, the user asks
the system to combine this constraint with some oth-
ers, and, eventually, to deduce the creator. Prolog it-
self contains several elements permitting to code in
this style, but some patterns are so frequent, e.g. be-
ing member of an ordered interval, that it was judi-
cious to augment the logic systems with specific li-
braries and comfortable syntax, and finally to man-
ufacture special languages. For us, two such pack-
ages were particularly interesting, the Finite Domain
constraint module CLP(FD) (Triska, 2012), and CHR
(Constraint Handling Rules). This approach liberates
the users, even more than Prolog, from the low level
chores. To solve some simple equations within inte-
ger intervals, we load the library clpfd included in
SWI, and we write
X#=3*(Y+1), Y+6#=X+1, (L+7)^2#=L*L+189,
L in 0 .. 447, X in -22 .. 44.
which yields: X = 6, Y = 1, L = 10, and the
students learn that there is no miraculous equa-
Programming for the Humanities - Logic and Adaptable Languages
303

tion solver inside, but the system seeing A#=B
equality, without knowing the values of the vari-
ables, stores this relation, which will be used when
needed. The program: X in 0 .. 12, X
in -2 .. 4, X#<3. produces a “fuzzy” an-
swer: X in 0..2. A relatively complex Sudoku
solver can be coded in about 10 lines, the puzzle
“SEND+MORE=MONEY”, even less. The students
learned how to deal with such concepts as redundancy
of information, contradictions, and conventions, not
always explicit, but current (here: the first digit of a
natural integer is non-zero). The specials operators,
such as #=<, enable the coexistence between standard
mathematical relations in Prolog (=<), and the set-
valued constraints. The students could invent them-
selves the CLP variant of the permutation program,
with arbitrary number N of integer constants:
length(L,N),L ins 1 .. N,
all_different(L),label(L).
where label assigns concrete values to members of
a constrained data set. The constraint systems are
used for scheduling, optimization and fault diagno-
sis, etc. Some graphical constraint applications as
the drawing package Asymptote permit to state such
commands as “put the box A in the middle of the line
B, and orient it orthogonally to it”, without specifing
the coordinates, and not even knowing where lies the
line B, given only as a “vertical line of length 10, end-
ing on the intersection ef curves C and D”. Constraint
(visual) tools are used to teach geometry in school.
But geometry is not just for mathematical problems,
historians of visual arts, and archaeologists need it ev-
ery day.
5.1 Just Logic. . .
There are many categories of constraints. Temporal
intervals are different from binary logic. While teach-
ing elements of Artificial Intelligence, we proposed
some logic puzzles published by R. Smullyan, e.g., in
(Smullyan, 1978). We didn’t ask to solve such prob-
lems using Prolog, but the constraint package CLP(B)
turned out to be excellent for formalizing problems,
and for testing the solution. Here are two easy prob-
lems, belonging to the world of Knights, who told
only the truth, and Knaves, constant liars. The first
problem is: two individuals approach, the first says,
“Neither of us is a knight.” What are they? The
boolean constraint solution is a one-liner:
sat(A =:= ~A * ~B),labeling([A,B]).
The form sat(...) takes an expression, and finds
its satisfiability, with * being the conjuction, +: dis-
junction, =:=: equality, and ~: negation. The form
labeling constructs a model of the represented uni-
verse, with the variables being assigned some values
from the allowed set. The argument of sat is a literal
translation of the verbal statement. The expression is
manifestly false, nobody can say that he is a Knave,
and the solution is here: A=Knave, B=Knight.
The second problem is more complicated. Three
people, Black, White and Red approach, Black says:
“all of us are Knaves”, and White: “exactly one of us
is a Knight.” Which is which? The solution [Knave,
Knight, Knave] is given by another one-liner:
L=[Black,White,Red],sat((Black # +L) *
(White=:=card([1],L))),labeling(L).
where # is the inequality, “+” computes the n-ary dis-
junction, and card finds the number of truths in a
list. This is not a domain specific strategy, but a pro-
gramming methodology. Already school pupils learn
how to transform equations and inequalities with un-
knowns, yet later some teachers and textbooks of-
fer them a restricted meaning of the concept of algo-
rithm, and convince them that computers may operate
only with concrete, known data, through sequences
of statements. Kuhn in “The Structure of Scientific
Revolutions” (Kuhn, 1962) observes that “a student
in the humanities has constantly before him a num-
ber of competing and incommensurable solutions to
his problems, solutions that he must ultimately exam-
ine for himself”. It is more natural for him to operate
with unknowns, while for an engineer, an unknown
often reduces to a placeholder awaiting the derivation
of its value from the data, and untouched before.
5.2 Constraint Handling Rules
The CHR formalism (Fr
¨
uhwirth, 2009), is an ad-
vanced topic, designed to assemble specific, domain-
oriented algorithms efficiently, and easy to embed
into existing languages. The basic implementation
platform remains Prolog. CHR is able to propagate
and simplify constraints, and eliminate the redundan-
cies. Its teaching helps to understand how the con-
straint systems work.
The example below is an arithmetic exercise. The
standard recursive formulation of maxl(L,X), which
computes X, the maximum of numbers in L, say,
maxl([2,9,7,1],X) is shown first:
maxl([X],X). % What else?...
maxl([Y|Q],X):-maxl(Q,Z),(Y>Z,X=Y;X=Z).
This reduces the set of eligible values by
rejecting those known to be smaller than
some other. The equivalent CHR program:
max(X) \ max(Y) <=> X>=Y | true., which
may be called: max(2), max(9), max(7),
CSEDU 2016 - 8th International Conference on Computer Supported Education
304

max(1)., is shorter. max(X) means that X is a
potential maximum of an unknown set of values,
which gets precised when we throw in new candi-
dates. If there is just one, it IS. But a rule: H1 \ H2
<=> Body, called “simpagation” (propagation and
simplification), verifies whether the constraint pool
contains relations compatible with both H1 and H2,
and if yes, then H2 is eliminated. At the end there can
be only one.
The user need not always to assemble her
items in a composite data structures. The
code ..., f(X,Y), ..., max(Y), g(Y,P,Q),
... max(P), ... does what the user wants, the
constraint store is built while processing other data,
and at the end the program yields also the informa-
tion about the maximum. The user has less code to
write, and there is no recursion.
Our “family” database can be also based on a con-
straint pool. It may then automatically propagate and
add new relationships: uncle, cousin, etc., if the ade-
quate rules are defined.
6 FINAL REMARKS
Our privileged audience are teachers in other domains
than Computer Science. Transmitting the basics of
logic programming to students without the “classical”
algorithmic background is inspiring. It shows how
the automated reasoning helps us to derive new in-
formation, permitting not only to confirm some hy-
potheses, but to formulate new ones. It unveils on
simple examples the power and the sense of com-
puting abstractions, and of such concepts as the non-
determinism, facilitating the work with intricate sets
of unknowns. They are modern tools, extensible and
non-mechanical, useful not only technically, but for
the development of the students’ culture.
This methodology has been thoroughly tested dur-
ing the last 40 years, it belongs already to the hard
core of computer science, but our pedagogical world
doesn’t profit from it as it should.
A. J.Perlis, the developer of Algol60, said (Perlis,
1982): “A language that doesn’t affect the way you
think about programming is not worth knowing”.
This might not be a plain truth, but a language which
does affect the thinking, is certainly worth teaching.
REFERENCES
Arthur, P. L. and Bode, K., editors (2014). Advancing Dig-
ital Humanities: Research, Methods, Theories. Pal-
grave Macmillan.
Cameron, S. and Richardson, S. (2005). Using Computers
in History. Palgrave Macmillan.
Christiansen, H. (2002). Using prolog as metalanguage
for teaching programming language concepts. In
Kacprzyk, J., Krawczak, M., and Zadro
˙
zny, S., edi-
tors, Issues in Inf. Technology. Warszawa.
Fr
¨
uhwirth, T. (2009). Welcome to constraint handling rules.
In Schrijvers, T. and Fr
¨
uhwirth, T., editors, Constraint
Handling Rules, Current Research Topics, Lecture
Notes in Artificial Intelligence 5388. Springer.
Informatics, Intl. Olympiad in (2015). URL:
www.ioinformatics.org/index.shtml.
Karczmarczuk, J. (2015). Teaching with dynamic docu-
ments – web applications and local resources. In Proc.
of the 7th Int. Conf. on Comp. Supported Education,
pages 315–322, Lisbon, Portugal.
Koch, C. (1991). On the benefits of interrelating computer
science and the humanities: The case of metaphor.
Computers and the Humanities, (25):289–295.
Kowalski, R. (2014). History of logic programming. In
Siekmann, J., editor, Computational Logic, Vol. 9,
pages 523–569. Elsevier.
Kuhn, T. (1962). The Structure of Scientific Revolutions.
University of Chicago Press.
Pereira, F. and Warren, D. (1980). Definite clause gram-
mars for language analysis – a survey of the formal-
ism and a comparison with atn. Artificial Intelligence,
13(3):231–278.
Perlis, A. J. (1982). Epigrams on programming. ACM SIG-
PLAN Notices, 17(9):7–13.
Quarterly, Digital Humanities (2015). URL:
www.digitalhumanities.org/dhq/.
Ramsay, S. (2012). Programming with humanists: Reflec-
tions on raising an army of hackers-scholars in the
digital humanities. In Digital Humanities Pedagogy:
Practices, Principles and Politics. OpenBook.
Rushkoff, D. (2010). Program or be Programmed Ten Com-
mands for a Digital Age. O/R Books, New York.
Schreibman, S., Siemens, R., and Unsworth, J., editors
(2004). A Companion to Digital Humanities. Wiley.
Smullyan, R. (1978). What is the Name of this Book?
Prentice-Hall.
Stutterheim, J., Swierstra, W., and Swierstra, D. (2012).
Forty hours of declarative programming: Teaching
prolog at the junior college utrecht. In Moraz
´
an,
M. and Achten, P., editors, Proc., Trends in Func-
tional Programming in Education, pages 50–62, St.
Andrews.
SWI (2015). URL: swish.swi-prolog.org/.
Thaller, M. (1993). Kleio. a database system. In Halbgraue
Reihe zur historischen Fachinformatik, volume B11.
St. Katharinen.
Triska, M. (2012). The finite domain constraint solver of
SWI-Prolog. volume 7294 of LNCS, pages 307–316.
Wielemaker, J. (2012). Swi prolog. Theory and Practice of
Logic Programming, (12):67–96.
Programming for the Humanities - Logic and Adaptable Languages
305
