
New Renewable Energy Allocation Algorithms based on Bin Packing
in a Smart Home
N. Benjamin Sendama
1
, Mehdi Laraki
1
, Aawatif Hayar
1
and Yassine Rifi
2
1
RTSE/ENSEM/GREENTIC, Hassan II University, Casablanca, Morocco
2
Department of electrical engineering, Polytech University, Nantes, France
Keywords: Energy Allocation Strategy, Best Fit/First Fist, Bin Packing, Smart Home, Smart Grid.
Abstract: More and more home owners fit their homes with renewable energy sources. Thus, to capitalize this, they are
willing to install intelligent energy management systems to try to reduce their energy bills, which requires
optimal use of energy. To deal with this, this paper presents two energy management algorithms, all based on
the principle of the bin packing problem. The proposed solutions are built on prioritizing the use of renewable
energy produced locally over energy provided by the main grid. A well detailed simulation was carried out to
highlight the contribution of the implementation of this solution in a smart home located in Casablanca,
Morocco, whose energy needs are from a daily approximation of the habits of the city residents. Moreover, a
comparison between the two algorithms was made to showcase the benefits of each, and their difference.
1 INTRODUCTION
Day after day, the traditional grid undergoes major
transformations which are observable at the
production sites, the consumption point, and of
course, along the whole network of
transmission/distribution lines. There is no point of
the grid that is untouched by the integration of the ICT
in the grid conversion into smart grid (Kempener,
Komor and Hock, 2013).
As power energy price has been both increasing
through years and requested by more consumers,
energy good management is of absolute necessity.
Therefore sustained works need to be done in this
direction: find new ways to optimize at the same time
the production, the transport and the consumption of
the power energy.
The incorporation of smart items such as smart
meters, actuators, middleware in the grid lead us to
two major interacting components: a smart grid and a
smart load. Hence the need to develop good strategies
of energy allocation either between the two
components, or only at the smart load. This because
the smart load has sometimes a production unit of
electric energy (solar, wind …), which makes him a
small smart grid apart (Considine and Cox, 2009).
This paper is all about these smart loads,
especially smart homes, because the third sector in
energy consumption, which includes households, is
the one that consumes the most electric energy,
especially in Morocco (Jaouhari, et al., 2013), as
elsewhere around the world. This prompted us to seek
a solution to maximize the use of renewable energy
produced on site. The renewable energy produced
will be called local energy for the rest of the paper.
Recent research topics point out some solutions
which have already been used in strategies of energy
allocation in smart homes. Guo, et al. (2012) and Wu,
et al. (2013) apprehend this problem as stochastic
optimisation by minimizing the energy cost based on
dynamic pricing. Samadi, Schober and Wong (2012)
propose the use of Vickrey-Clarke-Groves (VCG)
mechanism to maximize the social welfare where the
implemented solution of pricing can benefit both
users and utility companies. Mishra, et al. (2012)
introduce a way to minimize the electric bill with the
help of storage components (batteries) as controller of
energy consumption. Alamdar (2013) ushers us to a
solution based on strip packing. It consists in finding
a schedule that minimizes the peak load.
In this paper we focus on a different way to
optimize the use of energy, not by minimizing the
electric bill directly, but rather maximizing the use of
the local energy. Thence, the combination on an
optimum use of local energy and the battery ensures
a low dependence opposite the main grid, and
consequently a reduction of the electricity bill. The
Sendama, N., Laraki, M., Hayar, A. and Rifi, Y.
New Renewable Energy Allocation Algorithms based on Bin Packing in a Smart Home.
In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 309-315
ISBN: 978-989-758-184-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
309
proposed solution is based on the bin packing
algorithms.
The bin packing problem falls within the
operations research and combinatorial optimization.
It is about finding the most economical storage
possible for a set of items in boxes (Scribe, Watson
and Shuchi, 2007). These algorithms, applied to a
smart home, turns out to be an interesting solution in
energy management.
To address this issue, this paper is organized as
the following: In the next section we present a smart
home as a working environment. In section 3 we
formulate the energy allocation problem as a bin
packing problem. Then in section 4 we describe the
proposed algorithms that address our issue, and
present some results with a certain number of figures
computed with the Matlab software (Mathworks,
2015). We conclude in section 5.
2 SYSTEM MODEL
We consider a smart power environment with middle-
class residential house, consisting of four blocks: the
living room, two bedrooms, a bathroom and a kitchen,
as shown on Figure 3.
2.1 The Energy Production
Local energy comes from the exposure of solar panels
to the sun, during the day. We assume that our house
features two solar panels whose power peak is 1Kw
p
each, within standard conditions. So the energy
produced equals to 1 kWh in the same condition
(Lewis and Crabtree, 2005). For a real installation, the
energy produced is generally much less than what
would be produced under standard conditions. It
essentially depends on three factors: the daily global
radiation, the solar panels position and their
temperature (Duffie and Beckman, 1980).
To obtain an estimate of the daily production of
local energy we used a complete photovoltaic
simulating software (PVSyst, 2015), then chose the
geographical position of Casablanca (33°65'N
07°26'W).
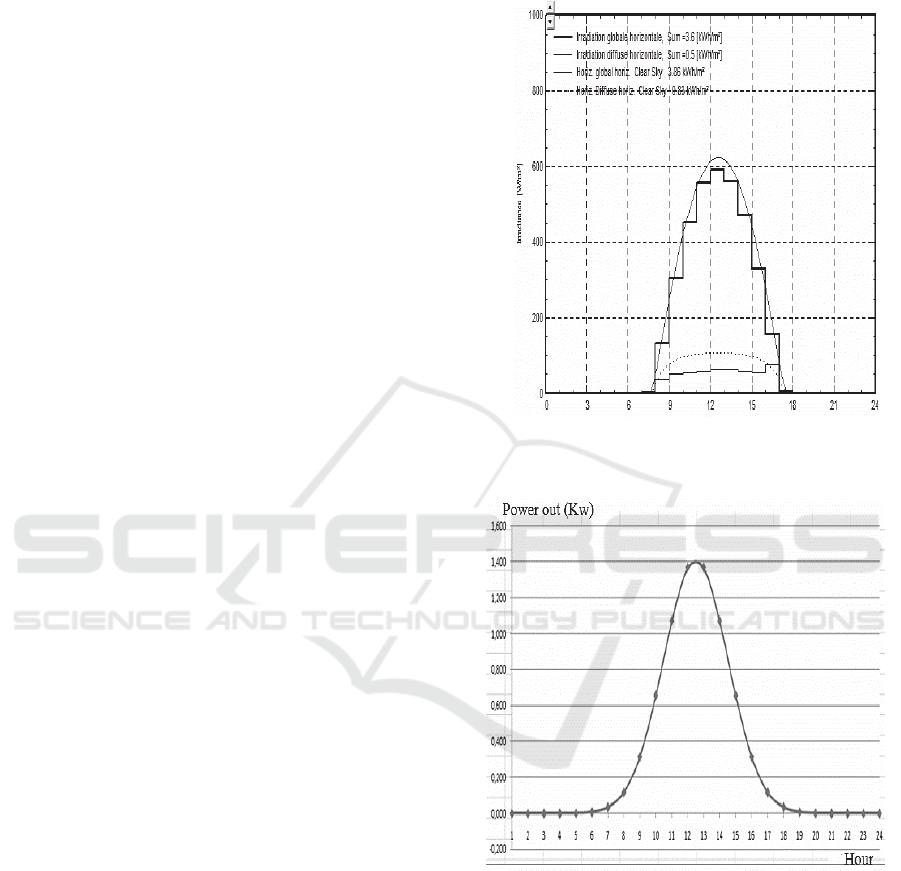
The solar irradiance on Figure 1, at that position
computed with PVsyst allow us to estimate the power
output of our house per hour.
The Figure 2 points out that the local energy
production follows a normal distribution of 3,57Kwh
as mean average and 25% as SD, per day; where
between 0am and 6am, 5pm and midnight the
contribution solar energy tends to zero.
The intended time cycle for the system’s operation
is divided in 24 time slots, regarding hours within a
full day (day and night).
Figure 1: PvSyst diurnal predicted hourly solar radiation for
Casablanca.
Figure 2: Electric power produced during a day.
2.2 The Energy Consumption
Our house is equipped with typical household
appliances (Laconde, 2015) gathered in table 1. It
must be recalled that this house is divided into four
blocks, which is an arbitrary choice but helps to
implement our solution based on bin packing; i.e., the
proposed energy allocation solution may, thereafter,
be either generalized (each block being an apartment
SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems
310

in a building) or refined (each block being a smart
plug in the house).
The consumption of each block takes the form of
a vector of 24 time slots, each slot corresponding to
an hour of a day. By adding the consumption of each
connected device during the same time slice, total
hourly energy consumption of the whole house is
obtained.
The calculation of different energy consumption
in different blocks has been done based on an
example of a middle class Moroccan family, living in
Casablanca. Data in Figure 4 do not represent all the
middle class Moroccan families. They are debatable
but not wrong at all. In any case, their approximation
does not alters the results of the solution proposed in
this paper, since it is an adaptable solution which
works in any scenario.
2.3 Hypothesis on Batteries
We assume that our smart home is equipped with a
12V, 150Ah battery; and has two operating modes:
The day mode is restricted from 7am to 6pm,
during which the battery is a receiver and loads up to
its maximum level; and the night mode, for the
remaining hours of the day, where there's a lack of
solar energy. The battery acts as a secondary voltage
source to local energy.
Figure 3: Smart home, divided into four blocks.
Table 1: List of appliances used in the home and their mean electric average power.
Appliances in the living
room
Number Average
power
Appliances in bedrooms Number Average
power
Lamp 3 10w lamp
2 20w
TV LCD 1 200w Computer
2 60w
Wi-Fi router 1 5w Alarm clock
2 20w
Heating 1 500w Smartphone
4 20w
Appliances in bathroom Number Average
power
Appliances in the
kitchen
Number Average
power
Lamp 1 10w lamp 2 20w
Hair dryer 1 600w Refrigerator 1 150w
Electric shaver 1 20w Microwave oven 1 800w
New Renewable Energy Allocation Algorithms based on Bin Packing in a Smart Home
311

3 PROBLEM FORMULATION
As the problem in this paper is to find an efficient way
to allocate energy in a smart home, the proposed
solution, based on the bin packing problem, appears
to be one of the best ways of solving this problem.
3.1 The Principle of Bin Packing
The bin packing problem can be described as follows:
having n items and n bins with:
w
j
= weight of item j
c = capacity of each bin
Must assign each item in a bin so the total weight of
the items in each bin does not exceed c and the
number of bins used is the minimum.
Mathematically this is written as follow:
Minimize
∑
Subjected to
∑
1, … ,
∑
1
Where
01
01,
3.2 Situation Scenario
We wish to apply the bin packing algorithms in
electrical engineering, specifically to our problem, in
order to optimize the power allocation. Our goal is to
reduce the use of the main grid energy to the benefit
of the use of local energy.
By analogy to the concepts of bin packing, the bins
correspond to both the local energy and the main grid
energy. The objects to be classified correspond to
different blocks of the house.
Among the bin packing algorithms, Next Fit, First Fit,
Best Fit, Next Fit Decreasing, First Fit Decreasing,
Best Fit Decreasing,… proposed in the literature
(Hayek, 2006) to solve the packing problem, we
selected two: the first fit decreasing for its low
execution time, and best fit because of its capacity of
using less bins for a maximum items (Lodi, 2000).
Figure 4: Energy Consumption of different blocks in a day.
SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems
312

Figure 5: Flowchart of the First Fit Decreasing energy allocation algorithm.
4 THE PROPOSED
ALGORITHMS, RESULTS &
ANALYSIS
Through the rest of the paper, following variables
represent respectively:
Ni = blocks’ energy needs, ∈
1, … , 4
S = a sum of a certain number of Ni
B = capacity of the battery
C = local energy remaining amount
P = main grid energy
4.1 First Fit Decreasing Algorithm
With this bin packing algorithm, the items are ordered
into their descending order, and then in this order the
next item is always placed into the first bin, where it
fits. For our problem, the proposed solution acts like
illustrated on Figure 6:
New Renewable Energy Allocation Algorithms based on Bin Packing in a Smart Home
313
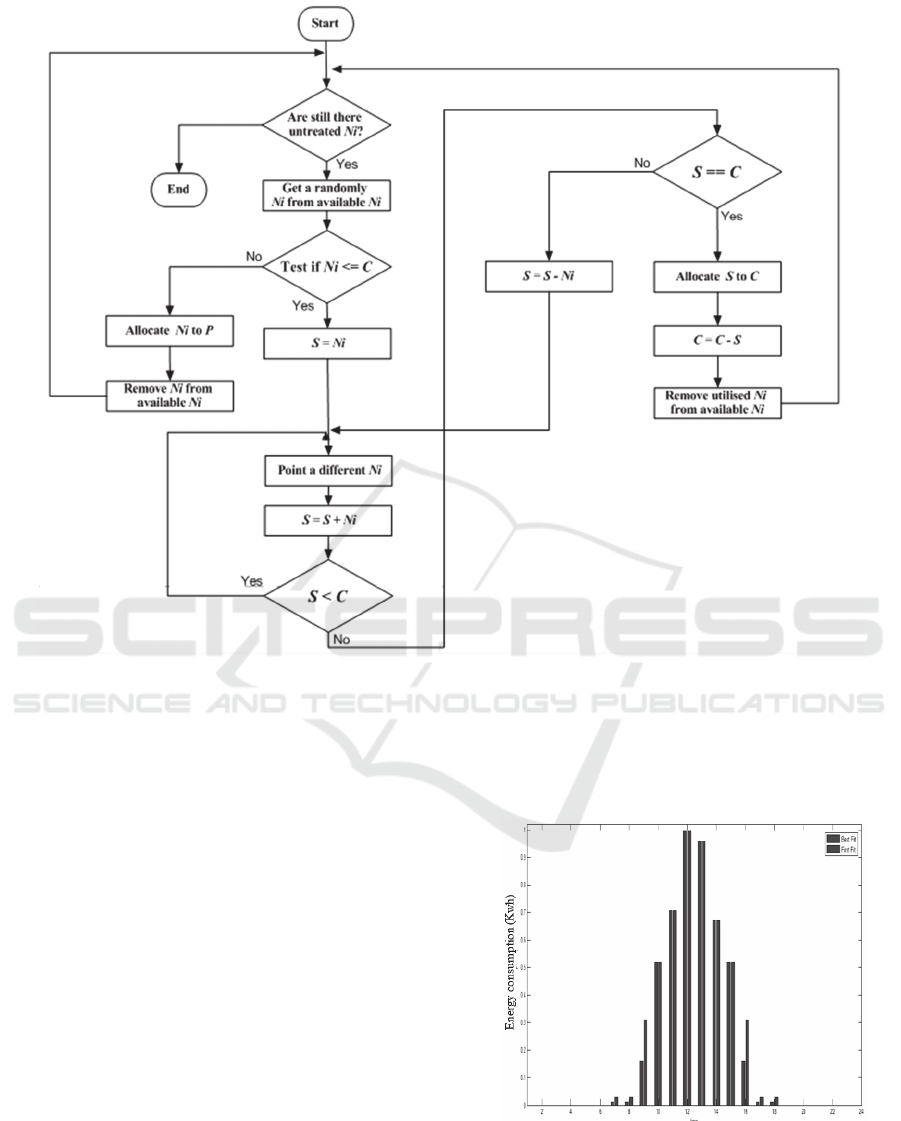
Figure 6: Flowchart of the Best Fit energy allocation algorithm.
4.2 Best Fit Algorithm
This algorithm scans all the boxes to find a best fit of
free available capacity for the requested item size.
The situation is more complicated, as the notion of the
“following bin” is not clear, in fact a careful choice is
needed. The proposed algorithm follows these steps
presented in Figure 6.
4.3 Results & Analysis
Local energy comes in from 7am to 6pm. The
interpretation of the Figure 7 shows us that there is a
very high contribution of energy around noon. This
would either reduce the peak load in case there is one,
or indicate that some household tasks could be
scheduled in case there is exceeding local energy.
Nevertheless, during the hours when there is not
much local energy (early morning and late afternoon),
we can see that the Best Fit (green) stands out from
the First Fist (brown) by allocating more efficiently
renewable energy to the consuming blocks (the
remanent local energy from First fit is stored in the
battery for to be used during the night). And this is
highlighted in the table 2, where BF stands for Best
Fit energy usage, and FFD for First Fit Decreasing
energy usage.
Figure 7: Comparison between the Best Fit and the First Fit
Decreasing energy allocation algorithm.
SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems
314

Table 2: Local energy gains.
hour Gain (%)= (BF/FFD)*100
6 am
0
7 am
66.6
8 am
66.6
9 am
48.38
10 am
0
11 am
0
12 am 0
1 pm
0
2 pm
0
3 pm
0
4 pm 48.3
5 pm 66.6
6 pm 66.6
5 CONCLUSIONS
Driven by a desire of finding a strategy to allocate
energy within a smart home, the work done in this
paper aimed to develop a solution that would
optimize the consumption of renewable energy
produced locally onsite.
We provided two algorithms, one based on the
First Fit Decreasing and the other on the Best Fit, all
based on the principle of the bin packing. Matlab
simulations of these algorithms have demonstrated a
clear fulfilment in their way to manage the energy, by
promoting the consumption of local energy over the
main grid energy. The first gives better satisfaction in
terms of execution time, the second gives more
satisfaction in terms of energy performance
allocation.
The only questionable problem is that the
consumption data we used is based on observation of
one middle class individual house in Casablanca, over
a period of a few days. A thorough study on the
consumption of households in Morocco to work with
real data would have been an asset to our work. That
is why in the work ahead, measurements made on
several houses are planned to establish a real energy
consumption profile of a typical Moroccan house.
REFERENCES
Alamdar, S., 2013. Smart grid electricity allocation via strip
packing with slicing, EuroCG2013.
Considine, T., Cox, W. T., 2009. Smart Loads and Smart
Grids: Creating the Smart Grid Business Case, Grid-
Interpol, The road to an interoperable grid, Denver.
Duffie, J. A., Beckman, W. A., 1980. Solar Engineering of
Thermal Processes, John Wiley & Sons, New York.
El Hayek, J., 2006. Le problème de bin-packing en deux-
dimensions, le cas non-orienté : résolution approchée et
bornes inférieures, Modeling and Simulation,
Université de Technologie de Compiègne.
Guo, Y., Pan, M., Fang, Y., Khargonekar, P. P., 2012.
Coordinated Energy Scheduling for Residential
Households in the Smart Grid, IEEE Smart grid
communication.
Jaouhari, S., Jelaidi, M., Nassir El Hak, R., 2013.
Tendances de l’éfficacité énergérique au Maroc,
IEEMOR.
Kempener, R., Komor, P. and Hoke, A., 2013. Smart grids
and renewables: A guide for effective deployment,
International Renewable Energy Agency.
Laconde, T., 2015. Puissance moyenne des appareils
électriques les plus courants, Energies&
Developpement blog [blog] 8 february, available at: <
http:/ /energie-developpement.blogspot.com/2011/ 09/
consommations-classiques-des-appareils.html>
[Accessed 10 November 2015).
Lewis, N. S., Crabtree, G., 2005. Basic research needs for
solar energy utilization, Report of the basic energy
sciences workshop on solar energy utilization.
Lodi, A., 2000. Algorithms for Two-Dimensional Bin
Packing and Assignment Problems, System
engineering, University of bologna.
Mathworks, 2015. Matlab (2015a beta), [computer
program] Mathworks Inc., available at <http://matlab-
r2015a-32-bit.software.informer.com/download/>,
(Accessed 25 October 2015).
Mishra, A., Irwin, D., Shenoy, P., Kurose, J., Zhu, T., 2012.
Smartcharge: cutting the electricity bill in smart homes
with energy storage, e-Energy, Madrid.
PVSyst photovoltaic software, 2015. PVSyst (6.4.0 beta)
[computer program] PVSyst Lab., available at
<http://www.pvsyst.com/en/download/>, [Accessed 18
November 2015].
Samadi, P., Schober, R., Wong, V.W.S., 2012. Advanced
demand side management for the future smart grid
using mechanism design, IEEE Trans. On Smart grid,
Vol. 3, no. 3, pp. 1170-1180.
Scribe, T., Watson, L., Shuchi, C., 2007. Bin packing and
Euclidian TSP, Lecture on approximations algorithms
at The College of information sciences and technology,
Pennsylvania.
Wu, H., Shahidehpour, M., Al-Abdulwahab A., 2013.
Hourly Demand Response in Day-ahead Scheduling for
Managing the Variability of Renewable Energy,
Generation, Transmission & Distribution IET, Vol. 7,
no. 3, pp. 226-234.
New Renewable Energy Allocation Algorithms based on Bin Packing in a Smart Home
315
