Correlation-Model-Based Reduction of Monitoring Data in Data Centers

Xuesong Peng and Barbara Pernici

Politecnico di Milano, Dipartimento di Elettronica Informazione e Bioingegneria,

Piazza Leonardo da Vinci, 32, 20133 Milano, Italy

Keywords:

Monitoring Data, Data Reduction, Time-series Prediction, Data Center.

Abstract:

Nowadays, in order to observe and control data centers in an optimized way, people collect a variety of

monitoring data continuously. Along with the rapid growth of data centers, the increasing size of monitoring

data will become an inevitable problem in the future. This paper proposes a correlation-based reduction

method for streaming data that derives quantitative formulas between correlated indicators, and reduces the

sampling rate of some indicators by replacing them with formulas predictions. This approach also revises

formulas through iterations of reduction process to ﬁnd an adaptive solution in dynamic environments of

data centers. One highlight of this work is the ability to work on upstream side, i.e., it can reduce volume

requirements for data collection of monitoring systems. This work also carried out simulated experiments,

showing that our approach is capable of data reduction under typical workload patterns and in complex data

centers.

1 INTRODUCTION

As data centers need to handle large amounts of ser-

vice requests, in order to optimize efﬁciency of re-

source usage, energy consumption and CO

emis-

sions, data centers exploit various monitoring sys-

tems currently available in industry and as open-

source components to understand the dynamic op-

erating conditions. These monitoring systems pro-

vide sensing services both on the physical environ-

ment and on computing resources, monitoring vari-

ables like CPU usage, memory usage, and power con-

sumption as indicators to measure working conditions

of virtual machines and host servers.

Even though monitoring systems aim to improve

efﬁciency, the workload for data collection and data

utilization can become a heavy burden because the

number of virtual machines and hosts in a data cen-

ter is always large and values of indicators are con-

tinuously changing. Furthermore, in the era of Big

Data, the size and energy consumption of data center

are also increasing owing to expansion of the Internet.

Future growth of data centers will doubtlessly raise

several challenges to the monitoring systems, such as

efﬁciency and cost of data acquisition, data transmis-

sion, data storage and so on. In short, the increasing

size of data is becoming a key problem.

As a proposal in the direction of reducing this

problem, we explore data reduction technologies to

reduce data quantity and keep abundant informative

values. This work focuses on monitoring data of

data centers, and most data are numerical time-series

data, namely, the representation of a collection of

values obtained from sequential measurements over

time (Esling and Agon, 2012). While other reduction

techniques try to bring down costs of data storage or

data transmission, this paper looks at the data reduc-

tion problem from a different point of view: indicators

of data center are not standalone, their correlations

reﬂect characteristics of system behaviors somehow.

We consider the common data correlations between

indicators as important clues to large amount of data

redundancy, which can be reduced at low cost, so re-

ducing only correlated data could avoid much aimless

computation and achieve reduction result at a good

level. Thus, we introduce a novel approach to exploit

correlations between indicators and predict values of

some indicators with regression formulas, aiming to

decreasing workloads of data collection in monitor-

ing systems. Compared to other reduction techniques,

this prediction method could work on the upstream

side (namely, data collection) of data streams. Fur-

thermore, for monitoring systems and other informa-

tion systems driven by massive data, reducing the up-

stream means reducing workloads, including data ac-

quisition, data transmission, data storage and so on.

The paper is organized as follows. In Section 2,

we introduce related work of time series data reduc-

Peng, X. and Pernici, B.

Correlation-Model-Based Reduction of Monitoring Data in Data Centers.

In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 395-405

ISBN: 978-989-758-184-7

395

tion. In Section 3, we introduce the concept of cor-

relation model and structure of our framework, and

details on the predictor and regression models. We

analyze the prediction power of regression formulas

in simple controlled conditions in Section 4, involv-

ing several typical workload patterns. In Section 5,

we study the predictor performance in a complex sim-

ulated data center under daily workloads.

2 RELATED WORK

Time series data are collected in various domains,

and how to reduce the massive data size has be-

come a main line of research. Dimension reduction

techniques have been proposed in past few decades,

such as PCA (Principal Component Analysis) (Jol-

liffe, 2002), PAA (Piecewise Aggregate Approxi-

mation) (Keogh et al., 2001), and many projects

also used signal transformations like DFT (Discrete

Fourier Transform), DWT (Discrete Wavelet Trans-

form), etc.

Some projects also used common statistical meth-

ods. In (Ding et al., 2015), a clustering method for

large-scale time series data called YADING exploits

random sampling and PAA to simultaneously reduce

multivariate data in both time and dimension direc-

tions. The Cypress framework (Reeves et al., 2009)

substitutes the single raw data stream with several

sub-streams which can support for archival and sim-

ple statistical query of massive time series data.

Even though those techniques give solutions to

the reduction problem of time series data in infor-

mation theory, they still have very limited usage in

real projects of many domains, because their lack

of semantic information cause much aimless compu-

tation. Furthermore, in the WSN (Wireless Sensor

Network) domain, some projects exploit correlation-

based methods to reduce data trafﬁc in networks, the

work of (Carvalho et al., 2011) improves prediction

accuracy of sensing data based on multivariate spa-

tial and temporal correlation, and (Zhou et al., 2015)

presents an adaptation scheme using sensors of differ-

ent types to enhance the system fault tolerance. How-

ever, those two methods assumes that the correlations

between variables are static, while the reality is not.

CloudSense (Kung et al., 2011) propose a switch

design on the data center network topology, which ex-

ploits compressive sensing to lower monitoring data

transmission. CloudSense aggregates status informa-

tion in each switch level and ﬁnally provides a general

status report of the whole data center, allowing early

detection of relative anomaly. However, this work is

not able to reduce data collection volume, and only

the applications of relative anomaly detection can use

the compressed outputs, ruling out other possibilities.

An initial version of Correlation-Model Based

Data Reduction (CMBDR) framework was proposed

in (Peng, 2015), to reduce data by building piecewise

regression models for correlated data on the basis of

priori knowledge. Based on that proposal, this work

elaborates CMBDR further and develops techniques

to enable the application of this approach in data cen-

ters. Aimed to reduce upcoming data streams, we

exploit indicators relation networks of data center to

adapt CMBDR to the speciﬁc scenario, and design

an online predictor based on CMBDR for dynamic

streams.

3 DATA REDUCTION METHOD

This section illustrates the correlation-based approach

of data reduction, which uses regression formulas be-

tween correlated indicators, to reduce sampling rate

of some indicators, and to reconstruct monitoring

data stream with formulas and other indicators. Sec-

tion 3.1 introduces the data center indicator network

proposed in the literature (Vitali et al., 2015), based

on which we build our initial correlation model to pro-

vide guidance to reduction process. In Section 3.2,

the correlation model based data reduction method is

presented. Then Sections 3.3 and 3.4 give details on

the stream predictor design and regression techniques

respectively.

3.1 Data Center Indicators Relation

Network

Figure 1: The indicators relation network (Vitali et al.,

2015).

In (Vitali et al., 2015), an indicator network is pro-

posed to understand the behavior of monitoring vari-

ables in data centers. The indicator network model

aims to illustrate relations among indicators and pro-

vide adaptation actions that lead data center to a bet-

ter state. The model consists of two layers: goal

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

396

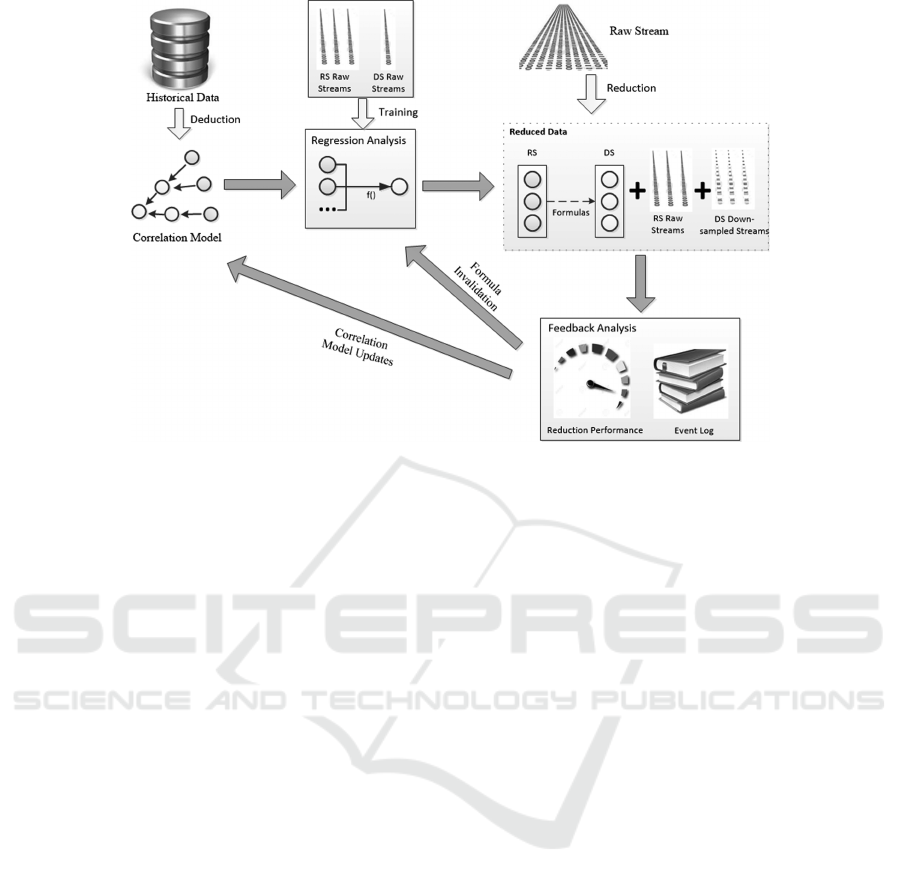
Figure 2: CMBDR prediction framework.

layer and treatment layer, but this paper only intro-

duces the goal layer as depicted in Figure 1, because

it indicates the knowledge of data correlations. In-

stead of using a human expertise, the indicators net-

work automatically learns from historical data. First,

possible relations between indicators are learned by

putting a threshold over their Pearson correlation co-

efﬁcients; then a MMHC-like algorithm (Tsamardi-

nos et al., 2006) is applied to orient all network edges;

ﬁnally a Bayesian Network is derived from monitored

data, depicting relations among indicators. Thus, as

the starting point of this paper, this Bayesian Network

model (a DAG) provides correlations between indica-

tors learned from historical data and it gives an initial

input to the data reduction.This paper only takes ad-

vantage of the DAG to serve as a model illustrating

correlations, called correlation model, and a directed

edge from indicator A to indicator B in the model im-

plies that values of B are conditionally dependent on

A, thus we could make predictions of B based on the

value of A.

3.2 CMBDR Framework

Data centers monitor a variety of variables continu-

ously, so values of each variable are in time-series,

among which most are numerical values. In this pa-

per, we refer those numerical variables as indicators,

and we consider the reduction problem of multiple in-

dicators streams. Denoting the set of all indicators as

S, this reduction method proposes to use a subset of

S, referred as Regressor Indicators Set (RS), to predict

values of other indicators, denoted as Dependent In-

dicators Set (DS). We try to ﬁnd a function F to quan-

tify the relation between DS and RS as Equations 1, 2

show, so that data of dependent indicators can be re-

duced. Namely on the micro level, each dependent

indicator di

∈ DS requires a formula f to reproduce

itself based on values of several regressor indicators

∈ RS, called Correlated Regressor Set (CRS), as

Equations 3, 4 show. This work achieves two goals:

• Identify appropriate RS/DS and CRS, derive accu-

rate prediction formulas for dependent indicators;

• Reduce data volume of dependent indicators in

data collection.

DS = S − RS (1)

DS = F(RS) (2)

= f (ri

,ri

,·· · , r i

) (3)

CRS[di

] = {ri

,ri

,·· · , r i

} (4)

With known correlations provided by the corre-

lation model and RS/DS conﬁguration, CMBDR re-

curses correlations in the DAG to identify CRS, and

performs regression analyses on values of correlated

indicators in a short period (called training window),

to ﬁnd a formula ﬁtting the quantitative relations of

these variables. Thus values of the dependent indi-

cator di

can be reproduced by the formula and cor-

related indicators CRS[di

], achieving data reduction.

This framework conducts model-based reduction in

an online manner, which adjusts the correlation model

and the reduction process based on performance feed-

back. Depicted in Figure 2, CMBDR separates reduc-

tion process into several iterations of the following

four main steps.

Correlation-Model-Based Reduction of Monitoring Data in Data Centers

397

• correlation Model Deduction: Derive the indica-

tors correlation model for the data center as Sec-

tion 3.1 illustrated, assign RS/DS and select the

correlated regressor indicators CRS[di

] for each

dependent indicators di

;

• Regression Formula Learning: Train a formula

for each dependent indicator to quantify their re-

lations with regressor indicators.

• Dependent Indicators Reduction: Reduce sam-

pling rate of dependent indicators, and adopt pre-

dictions of the formulas to replace lost samples.

• Feedback Analysis: Evaluate the performance of

the reduction process, and try to ﬁnd possible

problems and solutions to improve it.

The correlation model deduction is based on the

indicator relation network illustrated in Section 3.1,

which speciﬁes highly-correlated indicators. We gen-

erate this indicators network under a variable work-

load, in order to ﬁnd workload independent correla-

tions. We consider the correlations as a consequence

of interconnections of data center modules, for in-

stance, the CPU usage of a virtual machine is always

correlated to the CPU usage of its host. So we ex-

tract the DAG of the relation network as correlation

model, and with help of this model, we can identify

several indicators capable of predicting dependent in-

dicators. Then we assign the nodes of DAG to RS/DS,

and select correlated regressor indicators CRS[di

] of

by algorithm 1. This algorithm selects regressor

indicators ri ∈ RS to predict the dependent indicator

di ∈ DS if ri has a directed path p to di in the DAG,

and no other regressor indicators exist on the path p.

The selection of RS/DS and CRS has obvious impacts

on reduction performance, so in order to minimize the

size of RS, we select root nodes of the DAG as regres-

sor indicators of the ﬁrst loop, and select other nodes

as dependent indicators. And if the reduction perfor-

mance is poor under current RS/DS conﬁguration, we

update the RS/DS in the following loops according to

feedback analysis results. In addition, the correlation

model is not static in the framework, we need to re-

compute it if some indicators are added or removed in

the monitoring system.

In the regression formula learning step, in order to

quantify relations between indicators, we exploit re-

gression techniques on correlated indicators. A train-

ing window of streaming data is fetched for each

group of indicators as selected in the ﬁrst step, then

linear regression analysis is carried out, deriving a

prediction formula f that can reproduce values of the

dependent indicator.

Then in the dependent indicators reduction step,

formulas make predictions to replace raw samples of

Algorithm 1: Select regressor set for each dependent indica-

tor di

Require: RS, DS, DAG(V,E)

Ensure: CRS {the set of correlated regressor indica-

tors of each di

}

Function SelectCRS

Stack stack :=

for ri in RS do

stack.push( neighbors(ri) ) {ﬁnd neighbors that

are linked by an edge from current node v}

while stack 6=

0 do

v := stack.pop;

if v is in DS then

CRS[v].add(ri)

stack.push( neighbors(v) )

else

continue

end if

end while

end for

return CRS

End Function

the dependent indicators partially. As Figure 2 de-

picts, sampling rates of dependent indicators are re-

duced to a lower level, and the lost samples are re-

placed by the formula predictions, which are derived

out of the values of regressor indicators. Further-

more, we compare samples of the dependent indica-

tors to prediction results, providing a glimpse of ac-

curacy performance. Therefore, the ﬁnal reduced data

is composed of several parts, namely, all raw samples

of regressor indicators, training samples and check-

ing samples of dependent indicators, and formulas pa-

rameters.

Finally, the framework performs feedback analy-

ses, in which reduction performance and the event log

of the data center are analyzed to generate feedbacks,

helping to improve the next loop. Reduction per-

formance is evaluated with combined-criteria, cover-

ing compression ratio, execution time and informa-

tive value. By spotting the indicators and formulas

with poor performance, we identify problems in each

loop iteration, so we can update the corresponding re-

gression formula and correlation model to improve

performance. In addition, events in the log can also

guide reduction process to adapt to the changes of the

data center environment. For instance, in the feed-

back analysis, if we found a virtual machine is added

to or removed from a host server in feedback analysis,

then we need to recompute the correlation model be-

fore running the next loop. Details will be discussed

in Section 5.

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

398

Figure 3: Predictor workﬂow.

3.3 Indicators Stream Predictor

This section explains the design of the indicators

stream predictor in detail, which is a ﬁrst implemen-

tation of the CMBDR framework. Based on the cor-

relation model, the predictor tries to ﬁgure out for-

mulas of indicators by regression analysis on train-

ing dataset, and reduces their sampling rate to a low

level to serve as check items. Its working procedures

mainly include two phases: training phase and predic-

tion phase, the predictor always trains the formulas in

training phase, and then veriﬁes the formulas in pre-

diction phase. If a prediction result does not match the

sample result, then a prediction failure is generated as

feedback and the corresponding formula needs to be

recomputed in the next training phase. The predic-

tor workﬂow is depicted in Figure 3. Before predic-

tor running, the correlation model is initialized and

some parameters are conﬁgured. Afterwards train-

ing phase starts, predictor carries out regression anal-

ysis for each formula which involves the dependent

indicator di

and also correlated regressor indicators

ri ∈ CRS[di

]. Subsequently, we cut down sampling

rate of dependent indicators in the prediction phase.

Then we compare each sample with prediction re-

sults, and if their difference (residual) exceeds prede-

ﬁned tolerance, the prediction will be considered as a

failure and the prediction phase of this formula will be

terminated. Finally, a new training phase starts unless

the predictor has reached the end of the stream. In

order to control efﬁciency and accuracy of the reduc-

tion process, we introduce three important parameters

to the predictor:

• Length of Training Data Set: the number of sam-

ples required to train a formula, denoted as LT;

• Prediction Tolerance: the range for prediction er-

rors (or residuals) within which the prediction will

not be considered as a failure, denoted as PT ;

• Prediction Sampling Rate: sampling rate for de-

pendent indicators in prediction phase, denoted as

SR, which should be generally smaller than the

original sampling rate.

3.4 Linear Regression Method

To achieve our goal, the adopted reduction methods

should have the competence to derive quickly the

quantitative relationship between indicators in a time

slot, and to predict future values of some indicators.

In this approach, we explore methods of regression

analysis to discover formulas quantifying the relation-

ships and predicting values of dependent indicators

based on regressor indicators. Considering the time

to ﬁnd ﬁtting regression models of streaming indica-

tors, the computation complexity of regression anal-

ysis must be limited. Thus, CMBDR should give

preference to the regression model with the least time

complexity, namely, the linear regression model.

Generally, linear regression is an approach mod-

eling linear formulas between scalar dependent vari-

ables and independent variables. While multiple lin-

ear regression attempts to model the relationship be-

tween two or more independent variables and a re-

sponse variable by ﬁtting a linear equation to ob-

served data (see Equation 5), simple linear regression

is a special case of multiple linear regression having

only one independent variable (see Equation 6). In

the two equations, suppose data consists of n obser-

vations {y

, ··· ,x

}

i=1

, then x

i j

means the j

in-

dependent variable measured for the i

observation,

means the response variable measured for the i

observation, α is called intercept, β

are called slopes

or coefﬁcients, ε

are an unobserved random variable

that adds noise to the linear relationship.

Correlation-Model-Based Reduction of Monitoring Data in Data Centers

399

Figure 4: CPU ratios in four patterns (VM

- dotted lines, V M

- dashed lines, S - solid lines, Prediction of S - dash-dot lines).

= α + β

+ ·· · + β

+ ε

(5)

= α + β

+ ε

(6)

If X (the matrix of x

i j

) is full column rank,

CMBDR uses OLS (Ordinary Least Squares) regres-

sion method to estimate parameters of the formula

minimizing SSR (sum of squared residuals) over all

possible values of the intercept and slopes, as shown

in Equation 7. Details of OLS method can be found

in (Hayashi, 2000). If X is not full column rank, then

some column vectors must be linearly dependent, thus

CMBDR applies Gaussian Elimination to get the full

column rank matrix and then applies the OLS method.

SSR =

∑

− α − β

− ·· · − β

)

(7)

4 PREDICTION FORMULA

VALIDATION

Regression analysis derives the prediction formula

that best ﬁts training datasets. Therefore, this for-

mula could maintain a high prediction rate on follow-

ing testing data until the quantitative relation changes

and prediction rate dramatically decreases. So under-

standing when the relation will change is quite im-

portant for predictor performance. In this section, in

order to get insights into behaviors of the predictor,

we study prediction failures of the regression formu-

las under certain controlled conditions, by designing

several particular patterns to model typical situations

in data centers and validating prediction formulas in

each situation.

Experiments are conducted in MATLAB with a

data center simulation framework (Vitali et al., 2013).

With proper settings of the simulated data center, we

are able to control the framework to generate monitor-

ing data under speciﬁc workload, thus we can evaluate

performance of the predictor on various conditions.

We prepare a simple data center environment with

2 virtual machines (VM) deployed on 1 host server

(S), and CPU usages of VMs are and S are all 3 indi-

cators, in which CPU(V M

) and CPU(V M

) are re-

gressor indicators and CPU (S) is dependent indicator.

Furthermore, 4 slots of monitoring data are generated

under different workload patterns of VMs, as Fig-

ure 4 illustrates, to simulate possible workload con-

ditions of the data center. In the ﬁrst slot, workload

of V M

increases while V M

remains the same, but

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

400

Table 1: Indicators conﬁgurations in the ﬁrst loop.

Indicator Description Unit Indicator set Regressor Indicators

CPU(V M

i j

) CPU ratio of j

VM deployed on S

R(V M

i j

) Response time of j

VM deployed

on S

ms DS CPU(V M

i j

)

P(V M

i j

) Instant power consumption of j

VM deployed on S

watt DS CPU(V M

i j

)

CPU(S

) CPU ratio of S

DS CPU(V M

)··· CPU(V M

)

P(S

) Instant power consumption of S

watt DS CPU(V M

)···CPU(V M

)

Figure 5: Prediction results in four patterns.

due to the resource limits, the indicators CPU(V M

)

and CPU(S) stop increasing when CPU ratios reach

100%, which means the workload requests have ex-

ceeded the processing power. In the second slot, two

VMs workloads remain unchanged, so all indicators

remain stable. In the third slot, both VMs increase

their workloads at almost same speed; in the last slot,

V M

increases workload while V M

decreases, and

the CPU usage of the host CPU(S) grows slowly.

Each slot consists of 100 samples, and the start-

ing 20 samples are used to train a prediction formula,

which will be tested by all samples left. Applying the

threshold (Prediction Tolerance) to the residual be-

tween sample and prediction, a boolean result is gen-

erated, as Figure 5 depicts. In the beginning, all pre-

diction formulas perform well since most predictions

are accurate. Nevertheless, in pattern 1, 3, 4, the pre-

diction accuracy decreases suddenly afterwards and

it reveals a signiﬁcant change of indicators relation.

This happens when CPU ratio of a VM reach 100%

so it has to stop the previous trend.

These sudden relation changes can be explained

by overload conditions of VMs and the server. When

a VM get overloaded, the real CPU consumption of

the VM is still increasing even if monitored indica-

tor C PU(V M) remains at 100%, because VM can ac-

quire additional resource from the host server. Thus,

the previous prediction formula cannot explain cur-

Correlation-Model-Based Reduction of Monitoring Data in Data Centers

401

rent overload situations, for instance, from the mid-

dle part of the ﬁrst slot, the prediction remains stable

since CPU(V M

) and CPU(V M

) remain unchanged,

but the indicator CPU (S) is still increasing because

the real workload request of V M

does not stop in-

creasing.

This experiment demonstrates two outcomes.

First and most importantly, the regression formula of

correlated indicators is capable of making accurate

predictions in certain conditions. Secondly, the quan-

titative relations between indicators are not static, and

they evolve with dynamic data center environment.

Considering these two outcomes, in CMBDR frame-

work, we exploit regression formula to capture tem-

porary quantitative relation between correlated indi-

cators, and model feedback loops to adapt to dynamic

changes of formulas and correlations.

5 EXPERIMENTAL STUDY

In this section, we discuss experimental results

of the described approach to assess the performance

of CMBDR framework. We conduct experiments in

the same simulation tool of data center, which cre-

ates a virtualized data center environment and allows

the collection of simulation data at different work-

load rates. This tool emulates VMs resource alloca-

tion on servers and generates monitoring data such as

resource usage and power consumption under certain

workload rates. It also estimate power consumption

of a VM based on the amount of CPU it consumes.

5.1 Experiment Setting

To reveal the performance of CMBDR predictor, we

test it in a larger data center. This data center consists

of 100 servers with 6 VMs deployed on each server.

Monitoring data stream includes 2000 indicators that

cover CPU usage, response time and power consump-

tion of both VMs and servers. As Table 1 depicts, in

the initial reduction loop of CMBDR framework, we

select root nodes (namely, CPU(VM

i j

)) of the corre-

lation model as regressor indicators, and take other

nodes as dependent indicators. Testing data are gen-

erated by the simulation tool under simulated daily

workloads, with sampling rate of 1 per minute (1440

samples in one day).

As an important parameter of the predictor, pre-

diction tolerance PT deﬁnes the threshold for pre-

diction errors and has a great inﬂuence on reduction

results. In this work, the value of PT is directly

based on the measurement error of raw monitoring

data. We ﬁrst put the data center in a stable work-

load conditions, and collect values of indicators for a

period. Therefore, the multiple samples are repeated

measurements on the same state of the data center,

they should follow normal distribution around the true

value µ and variance is σ

, as Equation 8 depicts.

Therefore, we exploit the 95% conﬁdence interval

(approximately 1.96×σ) as a criteria for error behav-

ior of raw samples, and assign it to PT as Equation 9

shows. We consider the raw sample and the corre-

sponding prediction as two observations on the same

indicator, and if the difference between these two ob-

servations is within the 95% conﬁdence interval, this

prediction could be viewed as an accurate measure-

ment, namely, a true prediction.

measurement ∼ N(µ,σ

) (8)

PT = 1.96 × σ (9)

5.2 Evaluation Criteria

In order to evaluate the indicator stream predictor

comprehensively, this work proposes combined eval-

uation criteria covering operation speed, reduction

volume and informative values of reduced data. In-

formation value is a general term describing the abil-

ity of reduced data for supporting target applications;

it could be distinct for wide varieties of applications.

Thus, we exploit multiple metrics instead of a single

criterion to measure informative values. Details of the

combined evaluation metrics are as follows.

• Execution Time: processing time for the predictor

to reduce prepared data stream.

• Reduction Volume: the difference between raw

data size and reduced data size.

• Hit Rate: Consider the prediction within the error

range of raw data as a hit, thus the hit rate is the

percentage of accurate predictions, which reﬂects

informative values of reduced data.

• Relative Error: this metric measures information

loss of data reduction process, as shown in equa-

tion 10, for each indicator, η is relative error, ε is

absolute error and v is the interval of the values in

the test dataset.

η =

(10)

• Weighted mean of R

: R

is often used to measure

total goodness of ﬁt of linear regression models,

as equation 11 depicts, y

is raw value and f

prediction value. and R

= 1 indicates that the re-

gression line perfectly ﬁts raw data. In this work,

is used to measure accuracy in each predic-

tion phase, and length-based weighted average of

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

402

Table 2: Prediction performance of formulas in the same category.

R(V M) P(V M) CPU(S) P(S) P(S)revision

Relative error 3.45E-03 1.97E-03 4.82E-02 4.86E-02 1.19E-04

Average R

0.889 0.917 0.220 0.208 1.000

Hit rate 95.96% 98.57% 82.01% 81.85% 100.00%

Reduction volume 1241.46 1304.32 900.37 893.20 1339.25

Execution time sec. 0.144 s 0.070 s 0.680 s 0.690 s 0.029 s

those R

on data stream will be used as a metric

to evaluate how well predictions ﬁt raw data.

= 1 −

∑

i=1

− f

)

∑

i=1

− y)

(11)

5.3 Formulas Revisions

In the experiment, we monitor the reduction process,

and measure performance of each formula using the

aforementioned criteria. One interesting point we

found is that the variability of prediction ability is sig-

niﬁcant between formulas. Some formulas can make

very accurate predictions in a short execution time

while some formulas fail frequently and cost more

time to train new formulas. The reason for this dis-

crepancy lies in the correlation model. In the reduc-

tion process, if a prediction formula does not meet ac-

curacy requirements, then the predictor needs to learn

a new regression formula to replace t, thus the for-

mula could be always up-to-date. However, some de-

pendent indicators may be hard to predict by selected

regressor indicators, if their correlations are not high

enough. Thus, the framework would take much time

to update those formulas frequently, even though the

general performance increases very little.

Therefore, in order to solve the problem, the pre-

dictor need to revise those inefﬁcient formulas in the

next reduction loop. We denote dependent indicators

of those foot-dragging formulas as slowDS, and we

need to expand RS to include a subset of slowDS to

enhance prediction ability, since results have proved

current RS is not capable of making accurate predic-

tions on those indicators. Among all possible solu-

tions, adding the complete set of slowDS to RS can

solve the issue all at once, but obviously it can only

achieve minimal data reduction. This work recon-

siders correlations between indicators of slowDS in

the correlation model, it obtains several disconnected

subgraphs of the DAG containing only the slowDS

nodes, and add the root nodes of subgraphs to RS.

For instance, if any indicators of slowDS are corre-

lated, they must exist in the same subgraph, thus the

corresponding root node would serve as the regressor

indicator for other nodes in the next loop; otherwise

all slowDS will serve as regressor indicators. By this

gradual means of expanding RS, appropriate RS/DS

could be identiﬁed in iterations of reduction loops.

In this experiment, CMBDR framework selects

the root nodes of correlation model as RS in the ﬁrst

loop. Individual performance of indicators in the ﬁrst

loop are evaluated in the ﬁrst 4 columns of Table 2,

each column representing the average performance

of indicators in the same category. Under initial

RS/DS conﬁguration, the indicators of R(V M

i j

) and

P(V M

i j

) outperform evidently CPU (S

) and P(S

with higher reduction volume, better prediction ac-

curacy and much less execution time. To acquire

better performance in the second loop iteration, we

need to update RS/DS. By querying in the correlation

model, we ﬁnd CPU(S

) and P(S

) are highly corre-

lated. Then we just move one indicator CPU(S

) from

DS to RS, and then call Algorithm 1 to update regres-

sor set CRS for P(S

), thus CPU(S

) would be used to

predict P(S

) in the second loop. The performance are

also measured, as the ﬁfth column in Table 2 shows,

both accuracy and execution speed are improved dra-

matically and the relative error is at the same level

with P(V M

i j

We also measure overall reduction performance

of monitoring data in reduction process, to verify the

validity of this predictor and to assess the improve-

ment offered by RS/DS updates. As Figure 6 depicts,

in both ﬁrst and second loops, the predictor reduces

the raw monitoring data to slightly above one-third of

original volume, and reduction of 2 loops are nearly

the same although the predictor involves more regres-

sor indicators in the second loop. However, these new

regressor indicators improve processing speed and ac-

curacy performance of the predictor dramatically. As

Figure 7 and Figure 8 show, the second loop doubles

processing speed of the ﬁrst loop, and increases aver-

age prediction accuracy by almost an order of mag-

nitude. Results of the second loop in Figures 7, 8

also illustrate that, for a data center of 2000 indica-

tors, this predictor is able to reduce daily monitoring

data within 100 seconds, ensuring the average relative

error at 10

−3

Above all, this predictor could cut down the vol-

ume of data collection in monitoring systems, while

Correlation-Model-Based Reduction of Monitoring Data in Data Centers

403

still maintaining fast speed and a good quality of in-

formative values.

Figure 6: Data volume before and after reduction.

Figure 7: Execution time of CMBDR loops.

Figure 8: Average relative error of the predictor.

6 CONCLUSIONS

In this work, we developed and implemented a data

reduction framework for a data center monitoring sys-

tem. We derived the correlation model of indicators,

and based on correlations, we built a stream predictor

to decrease sampling of raw data by deducing quan-

titative relations between indicators. We have also

designed the feedback loop in the reduction process,

which evaluates and optimizes reduction performance

in iterations, enhancing adaptability of the correlation

model and formulas in a dynamic environment. Vali-

dation results show that regression formulas can pre-

dict indicators under typical workload patterns, and

predictor test results demonstrate that this approach

is capable of reduction in a simulated data center.

This mechanism could provide an extension to other

solutions in terms of upstream data reduction, and

it serves as a practical solution for monitoring data

streams in which variables are commonly correlated.

Future work may be carried on data center anomaly

detection, or fault-tolerant mechanisms of monitoring

data, which also exploits data correlations to establish

standby channels in monitoring systems, as in (Zhou

et al., 2015).

ACKNOWLEDGEMENTS

This work has been partially funded by the Italian

Project ITS Italy 2020 under the Technological Na-

tional Clusters program.

REFERENCES

Carvalho, C., Gomes, D. G., Agoulmine, N., and De Souza,

J. N. (2011). Improving prediction accuracy for

wsn data reduction by applying multivariate spatio-

temporal correlation. Sensors, 11(11):10010–10037.

Ding, R., Wang, Q., Dang, Y., Fu, Q., Zhang, H., and

Zhang, D. (2015). Yading: fast clustering of large-

scale time series data. Proceedings of the VLDB En-

dowment, 8(5):473–484.

Esling, P. and Agon, C. (2012). Time-series data mining.

ACM Computing Surveys (CSUR), 45(1):12.

Hayashi, F. (2000). Econometrics. Princeton Univ. Press,

Princeton, NJ [u.a.].

Jolliffe, I. (2002). Principal component analysis. Wiley

Online Library.

Keogh, E., Chakrabarti, K., Pazzani, M., and Mehrotra, S.

(2001). Dimensionality reduction for fast similarity

search in large time series databases. Knowledge and

information Systems, 3(3):263–286.

Kung, H., Lin, C.-K., and Vlah, D. (2011). Cloudsense:

Continuous ﬁne-grain cloud monitoring with com-

pressive sensing. In HotCloud.

Peng, X. (2015). Data reduction in monitored data. In

Loucopoulos, P., Nurcan, S., and Weigand, H., editors,

Proceedings of the CAiSE’2015 Doctoral Consortium

at the 27th International Conference on Advanced In-

formation Systems Engineering (CAiSE 2015), Stock-

holm, Sweden, June 11-12, 2015., volume 1415 of

CEUR Workshop Proceedings, pages 39–46. CEUR-

WS.org.

Reeves, G., Liu, J., Nath, S., and Zhao, F. (2009). Manag-

ing massive time series streams with multi-scale com-

pressed trickles. Proceedings of the VLDB Endow-

ment, 2(1):97–108.

Tsamardinos, I., Brown, L. E., and Aliferis, C. F. (2006).

The max-min hill-climbing bayesian network struc-

ture learning algorithm. Machine learning, 65(1):31–

78.

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

404

Vitali, M., O’Reilly, U.-M., and Veeramachaneni, K.

(2013). Modeling service execution on data centers

for energy efﬁciency and quality of service monitor-

ing. In Systems, Man, and Cybernetics (SMC), 2013

IEEE International Conference on, pages 103–108.

IEEE.

Vitali, M., Pernici, B., and OReilly, U.-M. (2015). Learn-

ing a goal-oriented model for energy efﬁcient adap-

tive applications in data centers. Information Sciences,

319:152–170.

Zhou, S., Lin, K.-J., Na, J., Chuang, C.-C., and Shih, C.-S.

(2015). Supporting service adaptation in fault toler-

ant internet of things. In Service-Oriented Comput-

ing and Applications (SOCA), 2015 IEEE 8th Inter-

national Conference on, pages 65–72.

Correlation-Model-Based Reduction of Monitoring Data in Data Centers

405