Analysis and Simulation of Fault Tolerance of a Grid-connected PV

Inverter by Z-source Impedance

Diego P. Chacón-Troya

, Christian Jara Alvarez

, Enrique Galarza Pablo

and José Manuel Aller

1,2

Universidad Politécnica Salesiana, Cuenca, Ecuador

Universidad Simón Bolívar, Caracas, Venezuela

Keywords: Fault Tolerant Circuits, Z-source Inverter, MPPT, PV Panels.

Abstract: This paper proposes the design of a monophasic inverter connected to a residential network by applying Z-

Source topology. The proposed models were verified in normal operation “STC” and under short circuit

conditions “SC”. The system is presented as coupled to a network without a transformer and with minimum

electrical components. The tolerance of the overcurrent or short-circuit current is also analyzed on this

topology. The signal’s power is conditioned to find the MPP of the PV panels. Its architecture will be outlined,

described and simulated in Matlab’s Simulink®. In order to verify that the design is working properly.

1 INTRODUCTION

The failure analysis in power conversion equipment

has become a critical focus of study in different types

of industrial applications (Cordeiro et al, 2011; Tajfar

and Mazumder, 2012). Current developments for

photovoltaic installations connected to the grid, due

to factors such as declining costs of solar panels and

decentralized power generation, offer a greater

market potential, making them competitive with

conventional energy sources. Guaranteeing the

continual operation of the system is of vital

importance, therefore making the fault tolerance

analysis for this type of systems of vital importance

as well (Tajfar and Mazumder, 2012; Chavan and

Chavan, 2014).

Among the faults that can be found in power

converters are the electrolytic capacitors which are

very susceptible to fault in the systems. In order to

continue the order of importance, we have the

switching devices which groups the semiconductors,

the control circuit, the ceramic capacitors, the diodes

and the inductors (Chan-Puc et al, 2009).

These devices perform the photovoltaic energy

conversion using only electrical components which

increases operational longevity when functioning

correctly. The power converters being the most

vulnerable to faults according to reliability studies

(Petrone et al, 2008; Dhople et al, 2012), its capacity

for fault tolerance reduces unit degradation and

increases performance. However, its cost, weight, and

size make its operation increasing complex because

the system requires more components, making future

improvements to overall system performance a

challenge for the future, including aspects of lifetime

performance of the integrated components in order to

reduce losses and increase reliability (Cordeiro et al,

2011; Petrone et al, 2008; Tuan et al, 2012)

Connecting to the grid without the use of a

transformer is an increasingly popular alternative

where new topologies are studied in order to develop

solid state architecture, mitigate problems associated

with the galvanic connection between the grid and the

PV generator, and reduce size and wear (Tuan et al,

2012; Patrao et al, 2011).

As new power conditioning strategies are

proposed ZSource topology is of special note because

studies have shown that it increases conversion

efficiency by 1% compared with existing systems and

the inverter system by 1% to 15% in comparison to

conventional PWM inverters depending on their use

(Patrao et al, 2011; Meinhardt and Mutschler, 1995).

This article proposes a study of photovoltaic

generation connected to a residential grid, using a

simple fault tolerant topological system in order to

increase reliability in the VSI. As a method for

conditioning solar power, an innovative design is

attached to the inverter which is used to adjust the

voltage levels at the inverter input to maximize the

energy extracted from the solar panels, allowing a

connection to the grid without a transformer

324

Chacón-Troya, D., Alvarez, C., Pablo, E. and Aller, J.

Analysis and Simulation of Fault Tolerance of a Grid-connected PV Inverter by Z-source Impedance.

In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 324-329

ISBN: 978-989-758-184-7

(Cordeiro et al, 2011). This design is known in

academic literature as ”Z inverter”. Its two inductors

connected in series between the DC source and

inverter allow the limitation of the di/dt variance of

the device, giving the system time to disconnect and

avoid damage or destruction of the system (Peng,

2003; Milady et al, 2009).

2 DEVELOPING

2.1 Z-source Topology

Figure 1: General configuration of a Z Source Inverter

(Hanif, Basu &Gaughan, 2011).

Its topology (Figure 1), allows the coupling between

the AC/DC inverter and the primary DC power source

through an LC filter forming an ”X” between two

inductors and two capacitors, usually with a smaller

capacity than those used in an equivalent

conventional converter, a diode then directs the DC

source current to flow only towards the load. With

this configuration, a short-circuit will not destroy the

system, compared with other types of power

converters, with Buck– Boost functioning stages in

the same device allowing the application of voltage

and current source inverters without needing to

change the system topology (Peng, 2003; Zope et al,

2010; Hanif et al, 2011).

2.2 Z- source Function

A conventional single-phase inverter has 4 operating

states, the Z inverter, allowing an additional

operational state called Short Through or ”ST”, the Z

Source Inverter has 5 operational states ”ZSI” are

classified by 3 operational modes, as detailed in

Figure 2 (Peng, 2003; Hanif et al, 2011):

1) Mode 1: The inverter is operating within normal

operational states, the current circulates through the

load, this mode is represented by an equivalent

circuit, represented by a current source as shown in

Figure 2 (1). The DC voltage source appears across

the Z-network inductor and capacitor. The capacitor

charges (kept in a charged steady state), the inductor

is discharged and energy flows through this to the

load (Zope et al, 2010; Hanif et al, 2011).

2) Mode 2: The Bridge AC / DC operates in zero

states, the higher or lower switches short-circuit the

charge through the device, leaving the load in open

circuit. Its equivalent circuit is a source of zero

amplitude current ”open circuit” as shown in Figure

2 (2). The DC source voltage appears across the

inductor and capacitor (Bost stage), no current flows

to the load (Zope et al, 2010; Hanif et al, 2011).

3) Mode 3: Running on ST inverter the switches short

the Z network, as shown in Figure 2 (3). The load

voltage is zero, the capacitor charge time (



) of the

ST required. This interval is inserted in the states zero

of mode 2, allowing the voltage boost whenever the

photovoltaic panel is unable to provide the required

voltage for any voltage drop due to changes in

temperature or insulation. It should be taken into

account that 











2



, at this moment

the voltage in capacitors charges the inductors (Zope

et al, 2010; Hanif et al, 2011).

Figure 2: Equivalent circuits of Z Source Inverter

(Rajakaruna and Jayawickrama, 2010). (1) Mode 1, (2)

Mode 2 and (3) Mode 3.

2.3 Simple Boost Control (SBC)

MATH

The SBC method proposed by Peng (Peng, 2003), is

a control method for the ZSI based on traditional

PWM modulation where two horizontal reference

lines called 



and 



are added to the carrier signal

and modulation. These two reference lines are

compared with the carrier to generate the ST time of

the Z converter. These levels must be higher than the

amplitude modulation index, so that the ST mode

does not interfere with conventional single-phase

modulation PWM inverter. Limiting the ST value of

the modulation index and meets the condition 









Analysis and Simulation of Fault Tolerance of a Grid-connected PV Inverter by Z-source Impedance

325

Figure 3: Switching time with “SBC” control method

(Zope, 2012).

2.4 Maximum Power Point Tracking

Strategy

The nonlinear characteristic of the photovoltaic

modules means that its maximum power point cannot

be reached by connecting directly to the load. For the

proposed system the P&O algorithm was been

chosen, a commonly used method, effective and easy

to apply.

Figure 4: MPPT P&O Algorithm (Rajakaruna and

Jayawickrama, 2010).

If the reference voltage 



, in the PV array is

disturbed in one direction and the power produced by

the same increases, it means that the operating point

has moved to the MPP, therefore the operating

voltage must be moved in the same direction,

otherwise if the power extracted from the PV array

decreases, the operating point is moved in the

direction opposite the MPP location, therefore the

operating voltage must be moved in the opposite

direction, allowing the system to have a built-in signal

conditioning and connecting directly to the residential

grid, achieving maximum continuous power transfer

from the PV panel to the grid or to the load (Hanif et

al, 2011).

2.5 Modelling Z-Source

Assuming inductors 1  2 and capacitors 1 

2, the mathematical equations that describe the

converter operating parameters for SBC Control Z are

(Hanif et al, 2011; Zope, 2012):





M BV

, (1)

B-1

*T,

(2)

VC=

B+1

(3)

1) Design of Inductor: In normal operation of the

inverter mode 1, the inductor current decreases

linearly and its voltage is the difference between the

input voltage PV and the capacitor voltage. At this

point the input voltage appears in capacitors and a

small DC current flows through the inductors.

During mode 2 when operating in Buck – Boost

mode the function of the inductor is to limit ripple

current, and finally in the ST mode, or operating

mode 3, the current inductor increases linearly and the

voltage across the inductor is equal to the voltage

across the capacitor (Peng, 2003; Hanif et al, 2011;

Zope, 2012). According to these considerations the

inductance is calculated:

V*T

∆L

(4)







is the maximum current in the inductor, 





is the

minimum current in the Inductor

Where, ∆  











and 



is the time to ST

2) Capacitor Design: The function of the condenser is

to absorb the ripple current and to be able to stabilize

the voltage giving a quality sinusoidal wave to the

inverter output. The capacitor is charged during the

ST period, also as explained above in mode 3 the

current through the capacitor and inductor are equal









(Rajakaruna and Jayawickrama, 2010; Zope,

2012). In order to define the specifications of the

voltage ripple in the capacitor ∆, we must consider

a tolerance about 3% of the peak voltage according to

the specifications given in many applications where Z

converters have been designed (Rajakaruna and

Jayawickrama, 2010; Hanif et al, 2011). In this

manner, the condenser value could be estimated as:









∗



∆



(5)

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

326

Where 



is the ST period, 





is the average current

through the inductor, and 4VC is considered 3% of

VC.

2.6 Modelling and Simulation

1) Characteristic PV Panel Curve: Considering the

standard operating conditions “STC”   25°;

  1000







, the values of the photovoltaic panel

MPP are: Voltage   220,  

40A Power   8800, as shown in Figure 5:

Figure 5: Characteristic curve PV Panel in "STC.

From the characteristic values of the PV panel the

maximum current through the Z inductor is obtained,

which corresponds to 30% of the average current 





2.7 Modeling Z-source

To know the maximum boost factor B, it is necessary

to know the peak output voltage





  294,

the



  208, and the modulation factor  

0,6, 



 230, using the equation (1):





2 ∗ 294

220 ∗ 0,6

=4,45

For a frequency modulation of 10, the time 



of ST according to the equation (2) is:







1

2

∗



4,45  1

2 ∗ 4,45

∗



1∗10





39,76μs,

It should be noted that the maximum



can be

inserted in mode 2 without any problem. The

maximum voltage the Z capacitor using equation (3)

is:

VC

B1



4,711

*230

599,5V.

The capacitor voltage provides the maximum values

supporting the DC bus and the switches of the inverter

bridge when in open circuit. With equation (4), the

value of the Z network inductance is calculated.

VC*T

∆L

599,5





*39,76





≅1 mH,

To calculate the Z-source capacitor, use the Equation

(5).

C =



∆V





*39,76





0,03*599,5

≅88,4 uF

The equations used for the analysis are

approximations of the Z converter and do not

consider factors such as transience due to switching,

resonant transience, or component resistances, so that

resonances not predicted in the design are occurring.

According to information obtained in literature (Zope

et al, 2010; Das et al, 2008; Shen et al, 2006

), the

converter stability output voltage can be increased by

a capacitor of1000.

Figure 6: Characteristic Curves of VZI in “STC”.

The AC output voltages connected to the network

shown in Figure 6 are very close to those calculated.

Analysis and Simulation of Fault Tolerance of a Grid-connected PV Inverter by Z-source Impedance

327

1) Fault Tolerance Test: When a short circuit occurs

in a conventional inverter “VSI” without Z network,

it produces a sudden change in current over time

/, as shown in Figure 7. A high current short-

circuit is generated in a short time putting the system

at risk, due to a delayed protection response which in

the best of cases produces strain on the components

or total destruction of the system.

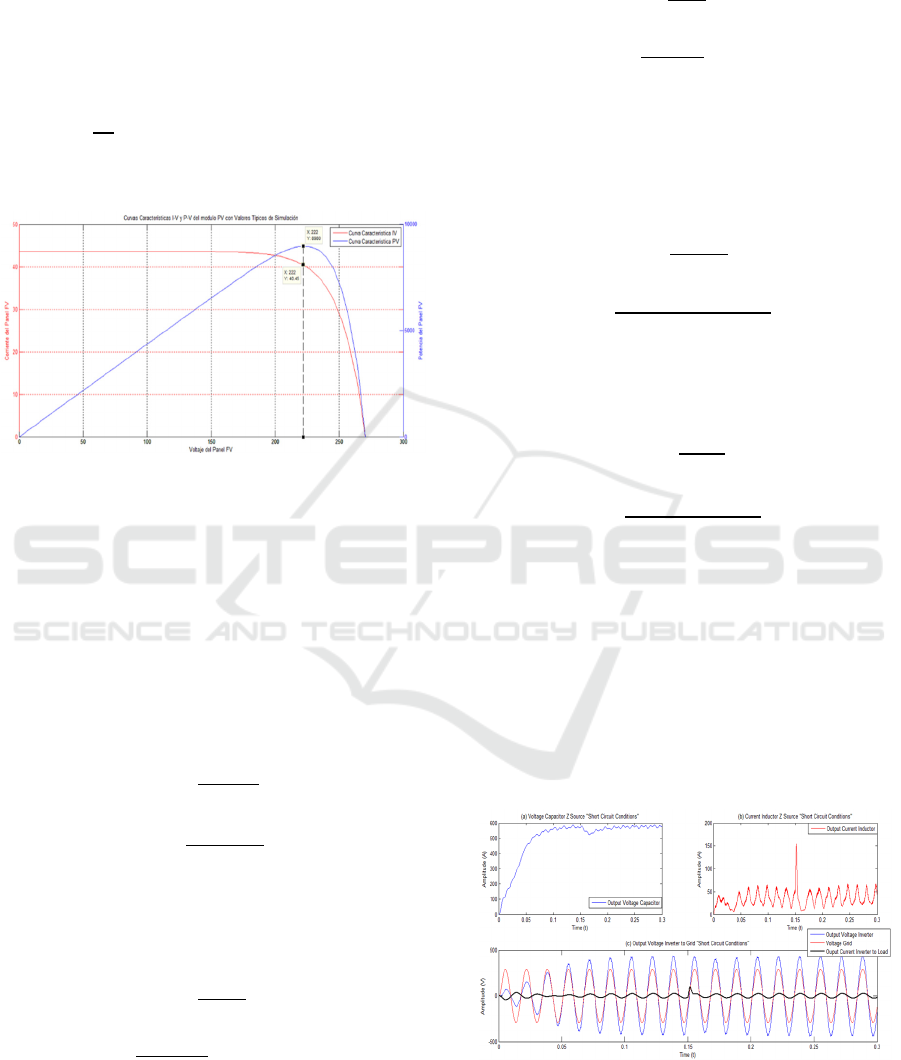
Figure 7: Output of “VSI” in Short Circuit Conditions.

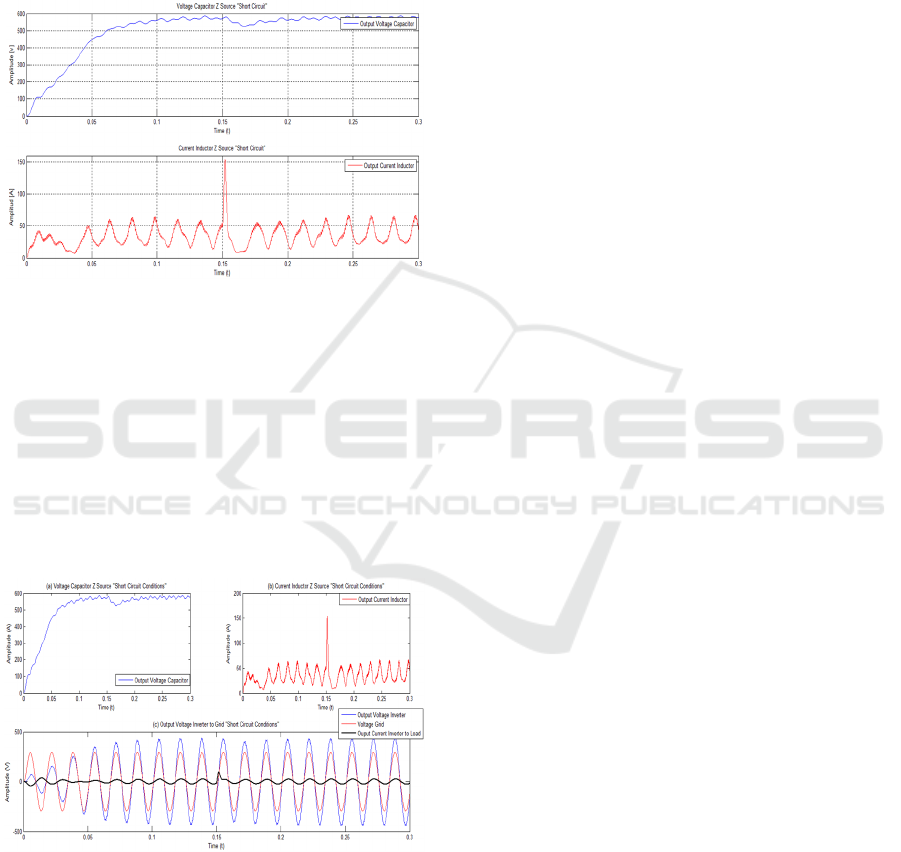
Upon the contingency of a short-circuit in the

proposed VZI system, as shown in Figure 8, the Z

network responds as we expected, attenuating the

variation /. This helps to allow the system

Protection the time needed to react without destroying

the enabled devices. In addition, if the failure is

dissipated before the protection activates, the inverter

can continue to operate normally as the Z network

does not allow the current to instantly rise to

destructive levels.

Figure 8: Ouput Waveforms from VZI “Short Circuit

Conditions”.

3 CONCLUSIONS

This paper proposes and analyzes a photovoltaic

system connected to the grid with a new fault-tolerant

topology.

The proposal combines an efficient topology fault

coverage, reduces stress on the components, and

increases the availability of power compared to

conventional photovoltaic inverter systems.

System behavior is analyzed via simulations in

STC and short circuit conditions, which reveals the

characteristic advantages offered by the Z Source

inverter. The results revealed that the Z network can

provide effective protection against short circuit,

decreasing the variation / in the system,

allowing enough time for the system protection to

intervene. With this feature, the system can withstand

short circuits without harming the operation or

performance of electronic devices.

This architecture is a good alternative for

applications in PV systems, for improving reliability

of these systems without increasing the number of

components and reducing the associated costs, and

improving the conversion efficiency of the inverter

compared to classical topologies.

REFERENCES

A. Cordeiro; J. Palma, J. Maia and M. Resende, 2011. Fault

tolerant design of a classical voltage-source inverter

using Z-source and standby redundancy, Electrical

Power Quality and Utilization (EPQU), 11th

International Conference,201, IEEE, pp. 1–6.

A. Tajfar, S. Mazumder 2012. A1 fault-tolerant switching

scheme for a high-power high-frequency-link inverter,

IECON 2012 - 38th Annual Conference on IEEE

Industrial Electronics Society, Oct 2012, pp. 5898–

5903.

F. Chan-Puc; H. Calleja, V. Sánchez, R. Acosta, and E.

Torres, 2009. Tendencias Actuales en el Diseño de

Convertidores de Potencia para Aplicaciones en

Fuentes de Energía Renovables, Revista de ingeniería

eléctrica, electrónica y computación, Diciembre 2009,

Vol. 7 No. 2.

S. B.Chavan and M. S. Chavan, 2014. Power switch faults,

diagnosis and tolerant schemes in converters of

photovoltaic systems a review, Department of

Electronic & Communication Technology, September

2014, vol. 3, Issue.

G. Petrone; G. Spagnuolo, R. Teodorescu, M. Veerachary,

and M. Vitelli, 2008. Reliability issues in photovoltaic

power processing systems, IEEE Trans Ind Electron,

July 2008, vol. 55, no. 7.

S. Dhople; A. Davoudi, A. D. Garcia, and P. Chapman,

2012. A unified approach to reliability assessment of

multiphase dc–dc converters in photovoltaic energy

conversion systems, Power Electronics, IEEE

Transactions, vol. 27, no. 2, pp.739–751.

M. Tuan; T. Wijnhoven, and J. Driesen, 2012. Fault-

tolerant topology of a grid-connected PV inverter

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

328

coupled by a scott transformer, Conference on Power

and Energy, IPEC 2012, IEEE, pp. 428–433.

I. Patrao, E. Garcia, and F. González, 2011.

Transformerless topologies for gridconnected single-

phase photovoltaic inverters, Renewable and

Sustainable Energy Reviews, vol. 15, no. 7, pp. 3423–

3431.

M. Meinhardt and P. Mutschler, 1995. Inverters without

transformer in photovoltaic applications, http://www,

srt. tu-darmstadt, de/fileadmin/general/publicat/

meinepe.

F. Z. Peng, 2003. Z-source inverter, Industry Applications,

IEEE Transactions, vol. 39, no. 2, pp. 504–510,.

S. Rajakaruna and L. Jayawickrama, 2010. Steady-state

analysis and designing impedance network of z-source

inverters, Industrial Electronics, IEEE Transactions,

vol. 57, no. 7, pp. 2483–2491.

P. Zope; A. Patil, and A. Somkuwar, 2010. Performance

and simulation analysis of single-phase grid connected

pv system based on z-source inverter, Power

Electronics, Drives and Energy Systems (PEDES) &

2010 Power India, 2010 Joint International

Conference, pp. 1–6.

S. Milady; D. Silber, F. Pfirsch, and F. Niedernostheide,

2009. Simulation studies and modeling of short circuit

current oscillations in igbts, Power Semiconductor

Devices & IC’s, 2009. ISPSD 2009. 21st International

Symposium on IEEE, pp.37–40.

M. Hanif; M. Basu, and K. Gaughan, 2011. Understanding

the operation of a z-source inverter for photovoltaic

application with a design example, IET Power

Electronics, 2011,vol. 4, no. 3, pp. 278–287.

P. Zope 2012. Modeling and simulation of z-source inverter

design and control strategies, Ph.d., thesis, Electronics

and telecommunication engineering under the faculty

of engineering and technology, no. 3, pp. 22–28.

A. Das; D. Lahiri, and A. Dhakar, 2008. Residential solar

power systems using z-source inverter, TENCON 2008-

2008 IEEE Region 10 Conference.

M. Shen; A. Joseph, Y. Huang, F. Peng, and Z. Qian, 2006.

Design and development of a 50kw z-source inverter

for fuel cell vehicles, vol. 2, pp. 1–5.

Analysis and Simulation of Fault Tolerance of a Grid-connected PV Inverter by Z-source Impedance

329