Memory Efﬁcient de novo Assembly Algorithm using Disk Streaming of

K-mers

Yuki Endo

, Fubito Toyama

, Chikafumi Chiba

, Hiroshi Mori

and Kenji Shoji

Collaboration Center for Research and Development, Utsunomiya University, Yoto 7-1-2,

Utsunomiya, Tochigi, 321-8585, Japan

Graduate School of Engineering, Utsunomiya University, Yoto 7-1-2, Utsunomiya, Tochigi, 321-8585, Japan

Faculty of Life and Environmental Sciences, University of Tsukuba, Tennoudai 1-1-1, Tsukuba, Ibaraki 305-8572, Japan

Keywords:

Bioinfomatics, Next Generation Sequencing, de novo Assembly.

Abstract:

Sequencing the whole genome of various species has many applications, not only in understanding biological

systems, but also in medicine, pharmacy, and agriculture. In recent years, the emergence of high-throughput

next generation sequencing technologies has dramatically reduced the time and costs for whole genome se-

quencing. These new technologies provide ultrahigh throughput with a lower per-unit data cost. However, the

data are generated from very short fragments of DNA. Thus, it is very important to develop algorithms for

merging these fragments. One method of merging these fragments without using a reference dataset is called

de novo assembly. Many algorithms for de novo assembly have been proposed in recent years. Velvet and

SOAPdenovo2 are well-known assembly algorithms, which have good performance in terms of memory and

time consumption. However, memory consumption increases dramatically when the size of input fragments is

larger. Therefore, it is necessary to develop an alternative algorithm with low memory usage. In this paper, we

propose an algorithm for de novo assembly with lower memory. In the proposed method, memory-efﬁcient

DSK (disk streaming of k-mers) to count k-mers is adopted. Moreover, the amount of memory usage for

constructing de bruijn graph is reduced by not keeping edge information in the graph. In our experiment using

human chromosome 14, the average maximum memory consumption of the proposed method was approxi-

mately 7.5–8.8% of that of the popular assemblers.

1 INTRODUCTION

Determining whole genome sequences of various

species has many applications not only in understand-

ing biological systems, but also in medicine, phar-

macy, and agriculture. In recent years, the emer-

gence of high-throughput next-generation sequenc-

ing (NGS) technologies has dramatically reduced the

time and cost for whole genome sequencing. These

new technologies provide ultrahigh throughput with a

lower per-unit data cost. However, these technologies

generate sequence data from many very small frag-

ments (sometimes fewer than 100 base pairs) of DNA.

These fragments are typically called reads. The pre-

cision of NGS is not perfect, and reads might include

sequencing errors. Thus, developing algorithms for

merging these reads is very important. Merging reads

without reference data is called de novo assembly.

The de novo assembly algorithms can be classi-

ﬁed into two approaches based on their features :

overlap-layout-consensus(OLC) and de Bruijn graph.

OLC relies on an overlap graph. Edena (Hernandez

et al., 2008), MIRA (Chevreux et al., 2004), Celera

(Miller et al., 2008), SSAKE (Warren et al., 2007),

and VCAKE (Jeck et al., 2007) assemblers are based

on the OLC approach. In the OLC strategy, over-

laps are found by all-against-all pair-wise compari-

son. Overlap graphs are constructed from pair-wise

overlaps. In the overlap graphs, a vertex represents

a read and an edge denotes an overlap between two

connected vertices (reads). Consensus sequences are

determined by tracing paths in the graph. On the other

hand, Velvet (Zerbino and Birney, 2008), ABySS

(Simpson et al., 2009), ALLPATHS (Butler et al.,

2008), and SOAPdenovo (Li et al., 2010) assemblers

are based on de Bruijn graph approach. In the de

Bruijn graph, a vertexrepresentsa sequence of k bases

(k-mer), where k is any positive integer. An edge rep-

resents an overlap of k-1 bases. Thus, two connected

vertices are denoted by a k-1 overlap between their

vertices (k-mers). After the de Bruijn graph is con-

structed from reads obtained by NGS, contigs are de-

266

Endo, Y., Toyama, F., Chiba, C., Mori, H. and Shoji, K.

Memory Efﬁcient de novo Assembly Algorithm using Disk Streaming of K -mers.

DOI: 10.5220/0005798302660271

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 266-271

ISBN: 978-989-758-170-0

termined by tracing paths in the graph. The de Bruijn

graph approach is most widely applied to the short

reads from Solexa and SOLiD platforms. In this ap-

proach, ﬁxed-length (k-1) overlaps are found and re-

dundant k-mers (subsequences) are compressed, mak-

ing it suitable for assembling vast quantities of short

reads. However, memory consumption increases dra-

matically when the size of input reads is extremely

large (more than several gigabytes) and it is hard to

use them for large-scale assemblies.

To overcome this problem, several algorithms

(Conway and Bromage, 2011; Bowe et al., 2012;

Chikhi and Rizk, 2012; Chikhi et al., 2014) have

been proposed in recent years. These algorithms are

also based on de Bruijn graph approach. In these

algorithms, the data structures for representing the

de Bruijn graphs are designed with small size. To

realize the compact de Bruijn graph, succinct data

structures (Conway and Bromage, 2011; Bowe et al.,

2012), Bloom ﬁlter(Chikhi and Rizk, 2012) and FM-

index(Chikhi et al., 2014) are used. However, the

overall costs, including the costs for constructing the

compact graph, are not discussed in detail because

these papers focused on how to represent the com-

pact de Bruijn graph. In general, the processes of

constructing de Bruijn graph (such as k-mer count-

ing) consume much memory and time. Therefore,

developing an algorithm in consideration of overall

costs is very important. On the other hand, an al-

gorithm called DSK (disk streaming of k-mers) for

k-mer counting with low memory usage (Rizk et al.,

2013) has been proposed. In this algorithm, the disk

storage (such as HDD and SSD) is used during pro-

cessing of k-mer counting. Thus, the amount of main

memory usage for k-mer counting can be greatly re-

duced in DSK.

In this paper, we propose an algorithm for large

scale de novo assembly with low memory usage. In

our method, k-mers are extracted using DSK. Al-

though our algorithm is based on de Bruijn graph ap-

proach in the same way as Velvet, edge information

is not kept in the main memory. Thus, the amount of

memory usage can be greatly reduced by our method.

The maximum memory usage in overall assembly

processes is evaluated and compared in our experi-

ments. Therefore, in the proposed method, the overall

costs for de novo assembly are taken into account. In

addition, the data structure for representing de Bruijn

graph is simple. In our experiments using the human

chromosome 14, the average maximum memory con-

sumption of the proposed method was approximately

7.5–8.8% of that of the popular assemblers.

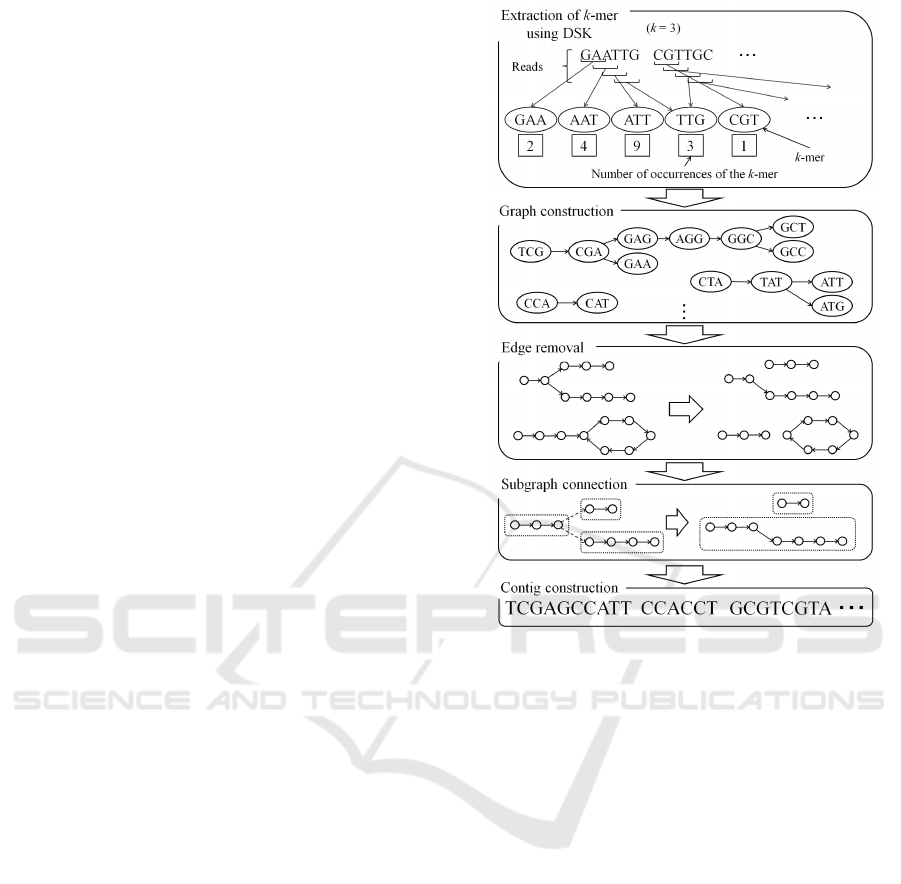
Figure 1: Outline of the proposed method.

2 ASSEMBLY ALGORITHMS

WITH LOW MEMORY

CONSUMPTION

In this paper, we propose an algorithm for large scale

de novo assembly with low memory usage. The pro-

posed method uses a memory-efﬁcient de novo as-

sembly algorithm (Endo et al., 2014), and k-mers are

extracted using DSK (Rizk et al., 2013). For more

detail on these algorithms refer to the each papers.

Figure 1 shows the outline of our algorithm. First,

from all reads, k-mers are extracted using DSK. At

the same time, the number of occurrences of each k-

mer is also counted. Second, all k-mers and number of

occurrences obtained by DSK are loaded. Third, the

de Bruijn graph is constructed using k-mers. Then,

the graph is partitioned into subgraphs such that the

subgraph has a simple path or a simple cycle. The

simple path does not have repeating vertices or edges

in the graph. Then subgraphs are connected to make a

larger simple path. The data about the number of oc-

currences of a k-mer are used to make an informed

selection of path connections. Finally, contigs are

Memory Efﬁcient de novo Assembly Algorithm using Disk Streaming of K-mers

267

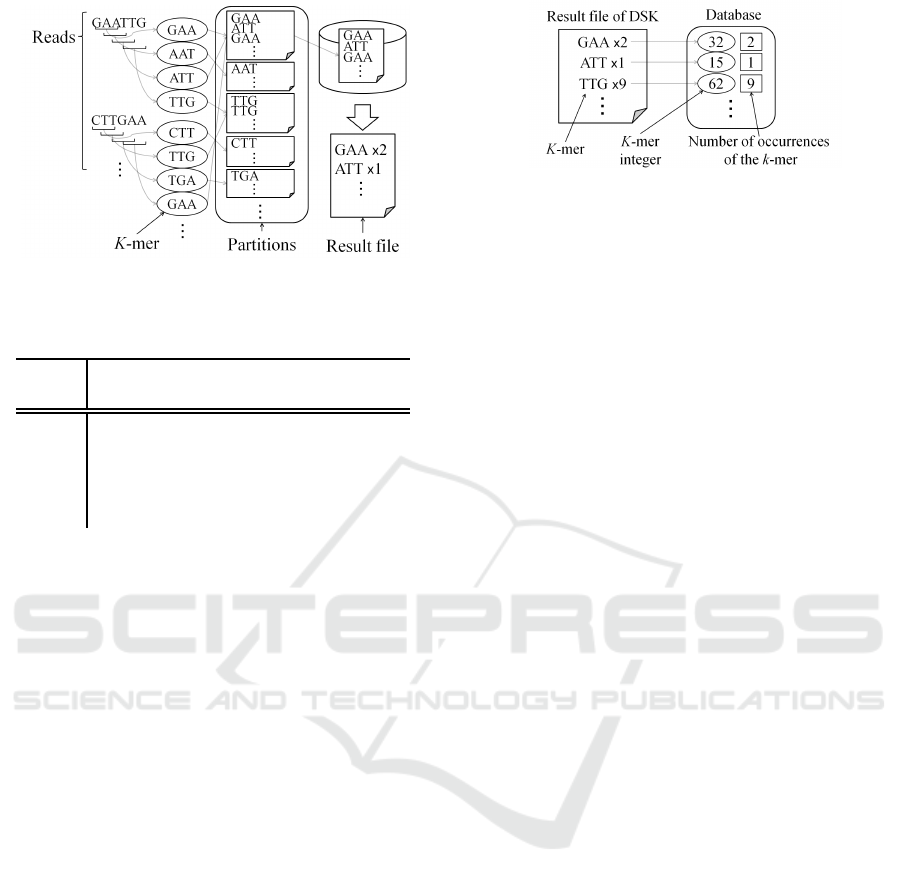
Figure 2: Outline of the DSK.

Table 1: k-mer sequence corresponding to k-mer integer

(in case of 3-mer).

k-mer Quaternary Binary

k-mer integer

(decimal)

AAA 0 0 0

AAC

1 1 1

AAG 2 10 2

AAT

3 11 3

ACA 10 100 4

ACC

11 101 5

generated by tracing vertices in each of the connected

graphs.

2.1 Counting K-mers using DSK

From all reads, k-mers and the number of occurrences

of each k-mers are extracted using DSK in the pro-

posed method. DSK is an algorithm for k-mer count-

ing, and can output k-mers and the number of occur-

rences of each k-mers. In this algorithm, the disk stor-

age (such as HDD and SSD) is used during processing

of k-mer counting. Although this approach requires

relatively large capacity disk, the amount of memory

usage can be greatly reduced.

Figure 2 shows the outline of DSK. First, the

multi-set of all k-mers present in the reads is parti-

tioned, and partitions are saved to disk. Next, the each

partition is separately loaded in main memory. The

size of each partition is comparatively small. Thus,

the required memory consumption can be reduced.

All k-mers are counted by traversing each partition.

As a result, all k-mers and the number of occurrences

of each k-mer are counted, these results are written to

a ﬁle.

2.2 Loading K-mers

All k-mers and the number of occurrences obtained

by DSK are loaded. They are kept in a database in

the memory as “k-mer integers”. As shown in Table

Figure 3: Collection of k-mer and the contents of database

in the proposed method (in case of 3-mer).

1, a k-mer integer is a one-to-one numeric represen-

tation of each k-mer. Using the k-mer integer repre-

sentation, the amount of memory for k-mer sequences

can be reduced. In this work, k-mer integers and the

number of occurrences of the k-mers corresponding

to the k-mer integer are kept in the main memory. In

order to lower memory usage, other data are not kept

in the main memory. The k-mer sequences in which

the number of occurrences is small (less than a thresh-

old) are not used in the graph construction because it

is likely that such k-mer sequences contain sequenc-

ing errors. In our experiments, the threshold was set

to 2. Figure 3 shows the collection of k-mers and the

contents of the database in the proposed method.

2.3 Graph Construction

The de Bruijn graph is constructed using loaded k-

mers. In the de Bruijn graph, each vertex represents

a k-mer. An edge represents an overlap of k-1 bases.

Thus, two connected vertices denote a k-1 overlap be-

tween their vertices (k-mers).

In conventional algorithms using de Bruijn

graphs, when the graph is constructed, edge informa-

tion about which vertices are connected to each other

is also kept in main memory. Since there are many

edges in the graph, keeping all the edge information

consumes a huge amount of memory. In our method,

the edge information is not kept in main memory. The

existence of the edge is calculated only when it is re-

quired. Speciﬁcally, the vertices that are connected

by a directed edge from a vertex have only 4 types of

k-mers because the k-mers, which are represented by

the connected vertices, overlap by k-1 bases. Thus,

the connected vertices (k-mer sequences) can be ob-

tained by checking for four values of k-mer integers in

the database. Only the data representing the vertices

are kept in the database. Construction of the graph is

ﬁnished by registering the k-mer integers from all k-

mer sequences and the number of occurrences of each

in our database.

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

268

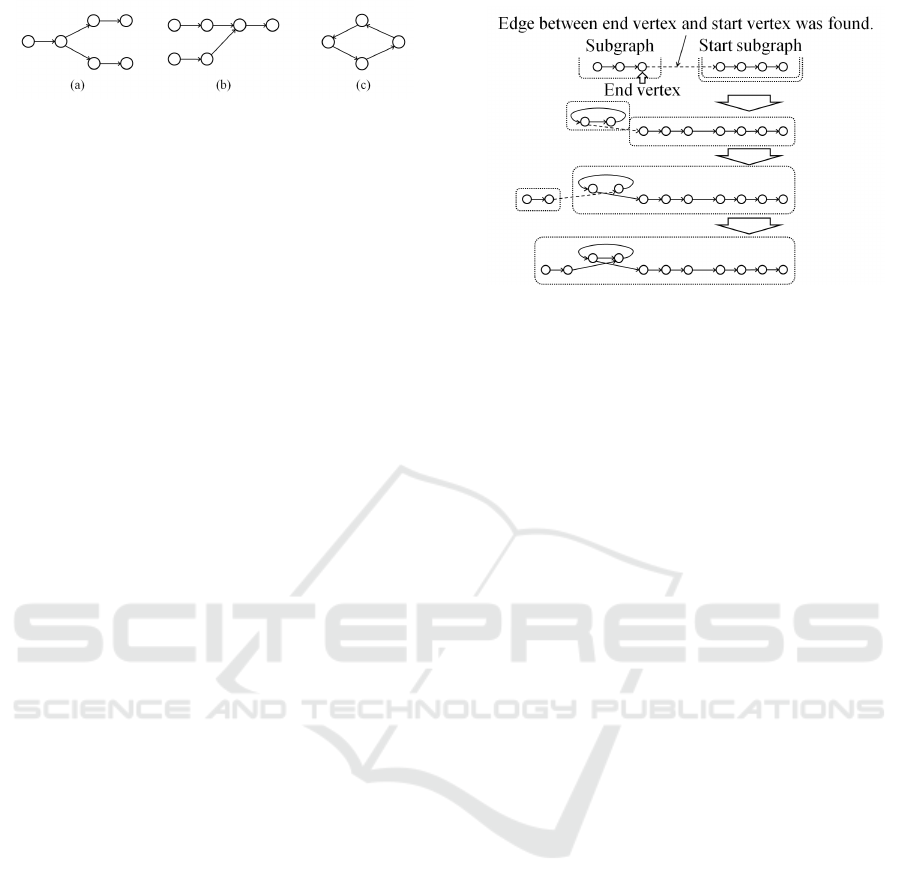
Figure 4: Examples of branches and cycle.

2.4 Edge Removal

The constructed graph has numerous branches and

cycles. Consequently, it is important to select the

connections in the path from which a contig is con-

structed. Figure 4 shows examples of branches and

cycle. A vertex with multiple edges connecting to

other vertices is illustrated in Fig. 4 (a) and 4 (b).

Figure 4 (c) shows an example of a cycle. In order to

solve these probrems, The edge removal process we

have used is as follows.

1. A start vertex (k-mer) that has the largest number

of occurrences is selected.

2. The start vertex is set to the current vertex.

3. Check for vertices that are connected to the cur-

rent vertex.

(a) If one connected vertex is found, the vertex is

set to the current vertex. Go to 3.

(b) If multiple connected vertices are found, one of

them is set to the current vertex. (The details

are described in later in this section.) Go to 3.

vertex is regarded as the end vertex. Go to 4.

4. Check for additional vertices that have not been

selected yet.

(a) If there are additional vertices that have not

been selected, a newstart vertex with the largest

number of occurrences is selected from the ver-

tices that have not been checked yet. Go to 2.

(b) If all vertices have been checked, the process is

ﬁnished.

In this process, the vertices that are put together in

a path are assigned the same label. A path from the

start vertex to the end vertex represents a subgraph.

Multiple subgraphs are created in this process.

The inclusion of branches and cycles in vertex se-

lection is as follow: when there are multiple outgoing

(incoming) edges from the current vertex as shown

Fig. 4 (a) and 4 (b), the edge connected to the vertex

in which the number of occurrences is the largest is

selected, and the other outgoing (incoming) edges are

removed. The current vertex is also regarded as the

end vertex when the label of the selected vertex is the

same as that of the current vertex as shown in Fig. 4

Figure 5: Example of subgraphs connection.

2.5 Subgraph Connection and Contig

Construction

To construct a longer path, subgraphs obtained by the

process described in previous section are connected.

The outline of the subgraph connection process is as

follows. First, a subgraph with simple path is se-

lected. The subgraph with the longest path is selected

from those subgraphs that have not previously been

selected. This subgraph is set as the start subgraph.

Next, the subgraphs in which the start vertex or the

end vertex are connected to the start or end vertex of

the selected subgraph are searched. If a connecting

subgraph is found, the start (end) vertex is connected

to the end (start) vertex, and the two subgraphs are

merged into a single subgraph. This graph expanding

process is repeated until no more merges can be made.

If there are multiple subgraphs that can be connected,

the subgraph with longer simple path is selected. Fig-

ure 5 shows an example of connecting subgraphs. The

connection in this example is on the left side. The

same process is also performed on the right side.

After the subgraphs are connected, a list of the

vertices is obtained by tracing all the paths that are

included in the subgraphs. A contig is generated

by merging the various k-mers that are referenced

from the vertices to eliminate the overlapping bases

as shown in Fig. 6. The ﬁnal contigs are obtained by

repeating this process for all subgraphs. Any contigs

that are longer than a given threshold are output. The

threshold was set to 200bp.

3 EXPERIMENTS AND RESULTS

To evaluate the performance of the proposed method,

we compare the performance of our method with that

of Velvet(Ver. 1.2.08) and SOAPdenovo2 (Ver. 2.04).

Velvet (Zerbino and Birney, 2008) is one of the most

popular de novo assembly algorithms based on the de

Memory Efﬁcient de novo Assembly Algorithm using Disk Streaming of K-mers

269

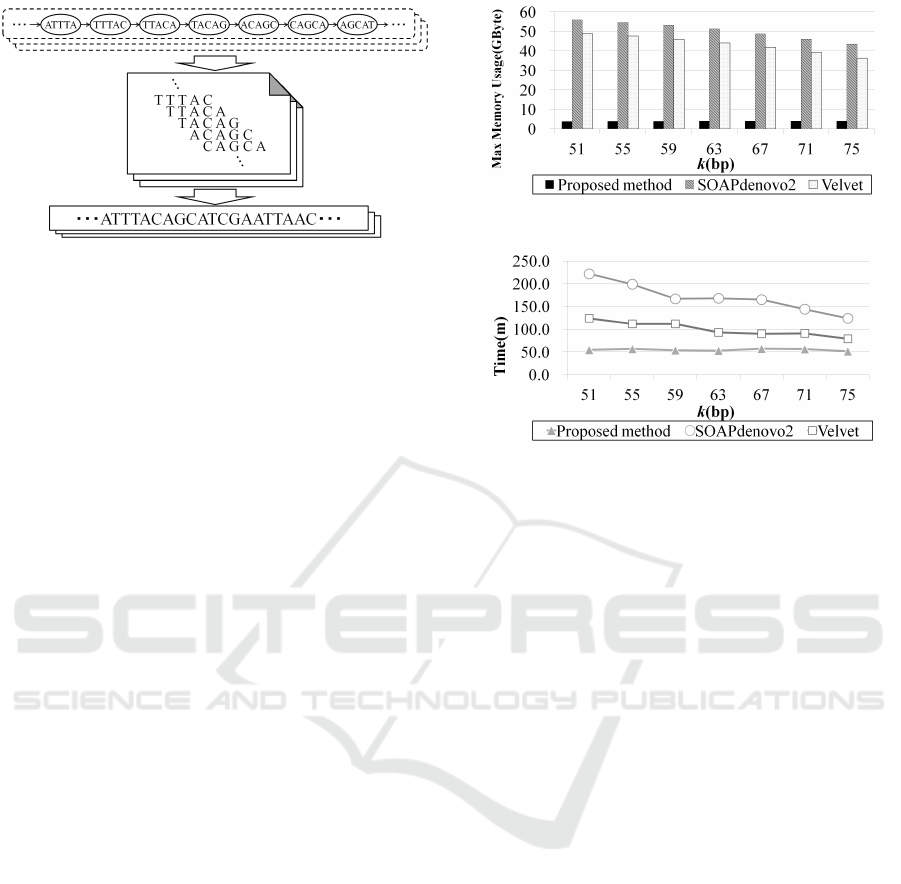
Figure 6: Generation of contigs.

Bruijn graph. In many papers on de novo genome as-

sembly, Velvet is used as a comparison to assess the

assembly performance. SOAPdenovo (Li et al., 2010)

is also a popular de novo assembler based on the de

Bruijn graph, which is designed to assemble large

genomes. SOAPdenovo has been successfully used

to assemble many published genomes. SOAPdenovo2

is the successor of SOAPdenovo. In SOAPdenovo2,

assembly performance in memory consumption, ac-

curacy, and coverage is improved. In the proposed

method, we used Ver. 2.0.7 of DSK. In our exper-

iment, the complete DNA sequence for human chro-

mosome 14 was used. The sequence length is approx-

imately 107Mbp, the ungapped sequence is approx-

imately 88Mbp. Assemblies were performed using

the reads form GAGE (Salzberg et al., 2012) datasets.

The GAGE (Genome Assembly Gold-standardEvalu-

ations) is one of the performance comparison datasets

used for de novo assembly algorithms. GAGE has

focused on the quality of the assembly, but not on

memory requirements. We used the dataset as a single

end and FASTA format, converted from the reads in

GAGE datasets, which are paired end and FASTQ for-

mat. The dataset is approximately 61 million reads,

and the size of read is 101bp. The assemblers were

run with k-mer sizes of 51, 55, 59, 63, 67, 71, and

75. We assessed the maximum memory consump-

tion, the running time, the contig length, and the accu-

racy of contigs from these programs in comparison to

ours. The experimental assemblies using these three

programs were all carried out on the same machine.

(CPU: Intel Xeon E5-2660 2.2GHz 8-core, Memory:

189GByte)

Figures 7 and 8 show the maximum memory us-

age and the running time of each assembly algorithm

for each tested k-mer. As shown in Fig. 7, The aver-

age maximum memory consumption of the proposed

method was approximately 7.5% of SOAPdenovo2,

and approximately 8.8% of Velvet. Therefore, we met

our goal of reducing memory usage. The amount of

memory usage was reduced for increased k-mer size

in both SOAPdenovo2 and Velvet. In the proposed

Figure 7: Comparison of maximum memory consumption.

Figure 8: Comparison of running time.

method, a relationship between k-mer size and maxi-

mum memory usage was not consistent for the human

assembly. Moreover, as shown in Fig. 8, the average

running time of the proposed method was faster than

both of the other methods. Table 2 shows the results

of the assemblies. The N50 length is deﬁned as the

length of the shortest contig where the sum of contigs

of an equal length or longer is at least 50% of the total

length of all contigs. The best k-mer size was the size

providing the largest N50. As shown in Table 2, the

N50 length of the proposed method was shorter than

that of the others, and the error rate was higher than

that of the others. In addition, the number of contigs

is more than that of the others. This is likely due to

the simplicity of the path-tracingalgorithm of the pro-

posed method. Thus, these results could be improved

with a more complicated path-tracing algorithm. On

the other hand, there were not large differences in the

genome coverage.

4 CONCLUSION

In this paper, we propose an algorithm for large-

scale de novo assembly with low memory usage. In

our experiments using the human chromosome 14,

the average amount of memory used in the proposed

method was approximately 7.5–8.8% of SOAPden-

ovo2 and Velvet. These results showed that the pro-

posed method outperformed SOAPdenovo2 and Vel-

vet for memory consumption. On the other hand, the

N50 and error rate of contigs obtained by the pro-

posed method were worse than that of the other as-

BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms

270

Table 2: Comparison of assemblies.

Assembler

Best k-mer

size (bp)

N50

(bp)

# of

contigs

Total

(kbp)

Genome

covered (%)

Genome covered

without gaps (%)

Error rate

(%)

Proposed method 55 2,801 127,326 91,796 76.733 93.298 7.764

SOAPdenovo2 63 4,005 43,032 85,648 78.695 95.684 0.128

Velvet

63 5,166 29,179 84,335 77.075 93.714 1.350

semblers. Further investigation is needed to improve

the N50 and error rate of contigs in our method by

modifying the path-tracing algorithm.

REFERENCES

Bowe, A., Onodera, T., Sadakane, K., and Shibuya, T.

(2012). Succinct de bruijn graphs. In WABI, volume

7534 of Lecture Notes in Computer Science, pages

225–235. Springer.

Butler, J., MacCallum, I., Kleber, M., Shlyakhter, I. A.,

Belmonte, M. K., Lander, E. S., Nusbaum, C., and

Jaffe, D. B. (2008). ALLPATHS: de novo assembly

of whole-genome shotgun microreads. Genome Res.,

18(5):810–820.

Chevreux, B., Pﬁsterer, T., Drescher, B., Driesel, A. J.,

Muller, W. E., Wetter, T., and Suhai, S. (2004). Using

the miraEST Assembler for Reliable and Automated

mRNA Transcript Assembly and SNP Detection in

Sequenced ESTs. Genome Res., 14(6):1147–1159.

Chikhi, R., Limasset, A., Jackman, S., Simpson, J., and

Medvedev, P. (2014). On the representation of de

bruijn graphs. In RECOMB, volume 8394 of Lecture

Notes in Computer Science, pages 35–55. Springer.

Chikhi, R. and Rizk, G. (2012). Space-efﬁcient and exact

de bruijn graph representation based on a bloom ﬁlter.

In WABI, volume 7534 of Lecture Notes in Computer

Science, pages 236–248. Springer.

Conway, T. C. and Bromage, A. J. (2011). Succinct data

structures for assembling large genomes. Bioinfor-

matics, 27(4):479–486.

Endo, Y., Toyama, F., Chiba, C., Mori, H., and Shoji, K.

(2014). De Novo Short Read Assembly Algorithm

with Low Memory Usage. In Proceedings of Inter-

national Conference on Bioinformatics Models, Meth-

ods and Algorithms (BIOINFORMATICS2014), pages

215–200.

Hernandez, D., Francois, P., Farinelli, L., Osteras, M., and

Schrenzel, J. (2008). De novo bacterial genome se-

quencing: millions of very short reads assembled on a

desktop computer. Genome Res., 18(5):802–809.

Jeck, W. R., Reinhardt, J. A., Baltrus, D. A., Hicken-

botham, M. T., Magrini, V., Mardis, E. R., Dangl,

J. L., and Jones, C. D. (2007). Extending assembly

of short DNA sequences to handle error. Bioinformat-

ics, 23(21):2942–2944.

Li, R., Zhu, H., Ruan, J., Qian, W., Fang, X., Shi, Z., Li,

Y., Li, S., Shan, G., Kristiansen, K., Li, S., Yang, H.,

Wang, J., and Wang, J. (2010). De novo assembly

of human genomes with massively parallel short read

sequencing. Genome Res., 20(2):265–272.

Miller, J. R., Delcher, A. L., Koren, S., Venter, E., Walenz,

B. P., Brownley, A., Johnson, J., Li, K., Mobarry,

C., and Sutton, G. (2008). Aggressive assembly of

pyrosequencing reads with mates. Bioinformatics,

24(24):2818–2824.

Rizk, G., Lavenier, D., and Chikhi, R. (2013). Dsk: k-mer

counting with very low memory usage. Bioinformat-

ics, 29(5):652–653.

Salzberg, S. L., Phillippy, A. M., Zimin, A., Puiu, D.,

Magoc, T., Koren, S., Treangen, T. J., Schatz, M. C.,

Delcher, A. L., Roberts, M., et al. (2012). GAGE: A

critical evaluation of genome assemblies and assem-

bly algorithms. Genome Res., 22(3):557–567.

Simpson, J. T., Wong, K., Jackman, S. D., Schein, J. E.,

Jones, S. J., and Birol, I. (2009). ABySS: a parallel

assembler for short read sequence data. Genome Res.,

19(6):1117–1123.

Warren, R. L., Sutton, G. G., Jones, S. J., and Holt, R. A.

(2007). Assembling millions of short DNA sequences

using SSAKE. Bioinformatics, 23(4):500–501.

Zerbino, D. R. and Birney, E. (2008). Velvet: algorithms for

de novo short read assembly using de Bruijn graphs.

Genome Res., 18(5):821–829.

Memory Efﬁcient de novo Assembly Algorithm using Disk Streaming of K-mers

271