Document Clustering Games

Rocco Tripodi

1,2

and Marcello Pelillo

1,2

ECLT, Ca’ Focsari University, Ca’ Munich, Venice, Italy

DAIS, Ca’ Foscari University, Via Torino, Venice, Italy

Keywords:

Document Clustering, Dominant Set, Game Theory.

Abstract:

In this article we propose a new model for document clustering, based on game theoretic principles. Each doc-

ument to be clustered is represented as a player, in the game theoretic sense, and each cluster as a strategy that

the players have to choose in order to maximize their payoff. The geometry of the data is modeled as a graph,

which encodes the pairwise similarity among each document and the games are played among similar players.

In each game the players update their strategies, according to what strategy has been effective in previous

games. The Dominant Set clustering algorithm is used to ﬁnd the prototypical elements of each cluster. This

information is used in order to divide the players in two disjoint sets, one collecting labeled players, which

always play a deﬁnite strategy and the other one collecting unlabeled players, which update their strategy at

each iteration of the games. The evaluation of the system was conducted on 13 document datasets and shows

that the proposed method performs well compared to different document clustering algorithms.

1 INTRODUCTION

Document clustering is a particular kind of cluster-

ing which involves textual data. The objects to be

clustered can have different characteristics, varying

in length and content. Popular applications of doc-

ument clustering aims at organizing tweets (Sankara-

narayanan et al., 2009), news (Bharat et al., 2009),

novels (Ardanuy and Sporleder, 2014) and medical

documents (Dhillon, 2001). It is a fundamental task in

text mining, with different applications that span from

document organization to language modeling (Man-

ning et al., 2008).

Clustering algorithms tailored for this task are

based on generative models (Zhong and Ghosh,

2005), graph models (Zhao et al., 2005; Tagarelli and

Karypis, 2013) and matrix factorization techniques

(Xu et al., 2003; Pompili et al., 2014). Generative

models and topic models (Blei et al., 2003) try to

ﬁnd the underlying distribution that created the set

of data objects. One problem with these approaches

is the conditional-independence assumption, which

does not hold for textual data, since they are intrinsi-

cally relational. A popular graph-based algorithm for

document clustering is CLUTO (Zhao and Karypis,

2004), which uses different criterion functions to par-

tition the graph into a predeﬁned number of clus-

ters. The problem with partitional approaches is that

it is necessary to give as input the number of clus-

ters to extract. The underlying assumption behind

models based on matrix factorization, such as Non-

negative Matrix Factorization (NMF) (Lee and Seung,

1999; Ding et al., 2006) is that words which occur

together are associated with similar clusters. (Ding

et al., 2006) demonstrated the equivalence between

NMF and Probabilistic Latent Semantic Indexing, a

popular technique for document clustering. A general

problem, common to all the approaches described, in-

volves the temporal dimension. In fact, for these ap-

proaches is difﬁcult to deal with datasets which evolve

over time and in many real world applications docu-

ments are streamed continuously.

With our approach we try to overcome this prob-

lem, simulating the presence of some clusters into

a dataset and classifying new instances according to

this information. We also try to deal with situations in

which the number of clusters is not given as input to

our algorithm. The problem of clustering new objects

is deﬁned as a game, in which we have labeled play-

ers (clustered objects), which always play the strat-

egy associated to their cluster and unlabeled players

which try to learn their strategy according to the strat-

egy that their co-players are choosing. In this way the

geometry of the data is modeled as a similarity graph,

whose nodes are players (documents), and the games

are played only between similar players.

Tripodi, R. and Pelillo, M.

Document Clustering Games.

DOI: 10.5220/0005798601090118

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 109-118

ISBN: 978-989-758-173-1

109

2 GAME THEORY

Game theory provides predictive power in interac-

tive decision situations. It was introduced by Von

Neumann and Morgenstern (Von Neumann and Mor-

genstern, 1944) in order to develop a mathematical

framework able to model the essentials of decision

making in interactive situations. In its normal-form

representation, it consists of a ﬁnite set of players I =

{1,..,n}, a set of pure strategies for each player S

,..., s

}, and a utility function u

: S

×...×S

→ R,

which associates strategies to payoffs. Each player

can adopt a strategy in order to play a game and the

utility function depends on the combination of strate-

gies played at the same time by the players involved

in the game, not just on the strategy chosen by a sin-

gle player. An important assumption in game theory

is that the players are rational and try to maximize the

value of u

. Furthermore, in non-cooperative games

the players choose their strategies independently, con-

sidering what the other players can play and try to ﬁnd

the best strategy proﬁle to employ in a game.

A strategy s

∗

is said to be dominant if and only if:

∗

−i

) > u

−i

),∀s

−i

∈ S

−i

where s

−i

denotes the strategy chosen by the other

player(s).

Nash equilibria represent the key concept of game

theory and can be deﬁned as those strategy proﬁles

in which each strategy is a best response to the strat-

egy of the co-player and no player has the incentive to

unilaterally deviate from his decision, because there

is no way to do better. The players can also play

mixed strategies, which are probability distributions

over pure strategies. Within this setting, the players

choose a strategy with a certain pre-assigned proba-

bility. A mixed strategy proﬁle can be deﬁned as a

vector x = (x

,. .. ,x

), where m is the number of pure

strategies and each component x

denotes the prob-

ability that the player chooses its hth pure strategy.

Each player has a strategy proﬁle which is deﬁned as

a standard simplex,

∆ =

x ∈ R :

∑

h=1

= 1, and x

≥ 0 for all h

(1)

Each mixed strategy corresponds to a point on the

simplex and its corners correspond to pure strategies.

In a two-player game, a strategy proﬁle can be de-

ﬁned as a pair (p,q) where p ∈ ∆

and q ∈ ∆

. The

expected payoff for this strategy proﬁle is computed

as:

(p,q) = p · A

q , u

(p,q) = q · A

p (2)

where A

and A

are the payoff matrices of player i and

j respectively. The Nash equilibrium is computed in

mixed strategies in the same way of pure strategies. It

is represented by a pair of strategies such that each is

a best response to the other.

Evolutionary game theory was introduced by John

Maynard Smith and George Price (Smith and Price,

1973), overcoming some limitations of traditional

game theory, such as the hyper-rationality imposed

on the players. In fact, in real life situations the play-

ers choose a strategy according to heuristics or so-

cial norms (Szab

o and Fath, 2007). It was introduced

in biology to explain the ritualized behaviors which

emerge in animal conﬂicts (Smith and Price, 1973).

In this context, strategies correspond to pheno-

types (traits or behaviors), payoffs correspond to off-

spring, allowing players with a high actual payoff (ob-

tained thanks to its phenotype) to be more prevalent in

the population. This formulation explains natural se-

lection choices between alternative phenotypes based

on their utility function. This aspect can be linked to

rational choice theory, in which players make a choice

that maximizes its utility, balancing cost against ben-

eﬁts (Okasha and Binmore, 2012).

This intuition introduces an inductive learning

process, in which we have a population of agents

which play games repeatedly with their neighbors.

The players, at each iteration, update their beliefs on

the state of the game and choose their strategy accord-

ing to what has been effective and what has not in pre-

vious games. The strategy space of each player i is de-

ﬁned as a mixed strategy proﬁle x

, as deﬁned above.

It lives in the mixed strategy space of the game, which

is given by the Cartesian product:

Θ = ×

i∈I

∆

. (3)

The expected payoff of a pure strategy e

in a single

game is calculated as in mixed strategies (see Equa-

tion 2). The difference in evolutionary game theory is

that a player can play the games with all other play-

ers, obtaining a ﬁnal payoff which is the sum of all

the partial payoffs obtained during the single games.

The payoff corresponding to a single strategy can be

computed as:

) =

∑

j=1

i j

)

(4)

and the average payoff is:

(x) =

∑

j=1

i j

(5)

where n is the number of players with whom the

games are played and A

i j

is the payoff matrix among

player i and j. Another important characteristic of

evolutionary game theory is that the games are played

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

110

repeatedly. In fact, at each iteration a player can up-

date his strategy space according to the payoffs gained

during the games, allowing the player to allocate more

probability on the strategies with high payoff, until an

equilibrium is reached, which means that the strategy

spaces of the players cannot be updated, because it is

not possible to obtain higher payoffs.

The replicator dynamic equation (Taylor and

Jonker, 1978) is used In order to ﬁnd those states,

which correspond to the Nash equilibria of the

games,:

˙x = [u(e

,x) −u(x,x)] ·x

∀h ∈ S (6)

This equation allows better than average strategies

(best replies) to grow at each iteration. It can be used

as a tool in dynamical systems to analyze frequency-

dependent selection (Nowak and Sigmund, 2004),

furthermore, the ﬁxed points of equation 6 corre-

sponds to Nash equilibria (Weibull, 1997). We used

the discrete time version of the replicator dynamic

equation for the experiments of this article:

(t + 1) = x

(t)

u(e

,x)

u(x,x)

∀h ∈ S (7)

where, at each time step t, the players update their

strategies according to the strategic environment, until

the system converges and the Nash equilibria are met.

In classical evolutionary game theory these dynamics

describe a stochastic evolutionary process in which

the agents adapt their behaviors to the environment.

3 DOMINANT SET CLUSTERING

Dominant set clustering generalizes the notion of

maximal clique from unweighted undirected to edge-

weighted graph (Pavan and Pelillo, 2007; Rota Bul

and Pelillo, 2013). Essentially, this generalization is

relevant because it enables to extraction of compact

structures from a graph in an efﬁcient way. Further-

more, it has no parameters and can be used on sym-

metric and asymmetric similarity graphs. It offers

measures of clusters cohesiveness and measures of

vertex participation to a cluster. It is able to model

the deﬁnition of a cluster, which states that a cluster

should have high internal homogeneity and that there

should be high inhomogeneity between the samples in

the cluster and those outside. (Jain and Dubes, 1988).

To model these notions we can use a graph G,

with no self loop, represented by its corresponding

weighted adjacency matrix A = (a

i j

) and consider a

cluster as a subset of vertices in it, C ⊆ V . The aver-

age weighted degree of node i ∈ C with regard to C is

deﬁned as,

awdeg

(i) =

|C|

∑

j∈C

i j

. (8)

We can also deﬁne the average similarity among a ver-

tex i ∈ C and a vertex j 6∈ C as,

φ(i, j) = a

i j

− awdeg

(i). (9)

The weight of node i with respect to C can be deﬁned

as,

(i) =

(

1, if |C| = 1

∑

j∈C\{i}

C\{i}

( j, i)W

C\{i}

( j), otherwise

(10)

and the total degree of C is,

W (C) =

∑

i∈C

(i). (11)

This measure gives us the relative similarity among

vertex i and the vertices in C\{i}, with respect to

the overall similarity between the vertices in cluster

C\{i}. W

(i) gives us the measure of vertex partici-

pation to a cluster, which should be homogeneous for

all i ∈ C. More formally, the conditions which en-

able the dominant set to realize the notion of cluster

described above are:

1. W

(i) > 0, for all i ∈ C

2. W

C∪{i}

(i) < 0, for all i 6∈ C

the ﬁrst refers to the internal homogeneity of the clus-

ter and the second refers to the external inhomogene-

ity.

A way to extract structures from graphs, which re-

ﬂects the two conditions described above, is given by

the following quadratic form:

f (x) = x

Ax. (12)

Within this interpretation, the clustering task is inter-

preted as that of ﬁnding a vector x, that maximize f .

The vector x is is a probability vector, whose compo-

nents express the participation of nodes in the cluster,

so we have the following program:

maximize f (x)

subject to x ∈ ∆.

(13)

A (local) solution of program 13 corresponds to a

maximally cohesive cluster (Jain and Dubes, 1988).

Furthermore we have,

Theorem 1. If S is a dominant subset of vertices, then

its weighted characteristic vector x

is a strict local

solution of program 13 (for the proof see (Pavan and

Pelillo, 2007)).

Document Clustering Games

111

By formulating the problem in this way, the solu-

tion of program 13 can be found using the replicator

dynamic equation,

x(t + 1) = x

(Ax)

. (14)

In the dominant set framework, the clusters are ex-

tracted sequentially from the graph and a peel-off

strategy is used to remove the data points belonging

to an determined cluster, until there are no points to

cluster or a certain number of clusters have been ex-

tracted.

4 CLUSTERING GAMES

This section describes how document clustering

games are formulated. The steps undertaken to re-

solve the task are as follows: document representa-

tion, data preparation, graph construction, clustering,

strategy space implementation and clustering games.

These steps are described in separate paragraphs be-

low.

4.1 Document Representation

We used the bag-of-words (BoW) model to represent

the documents in a text collection. With this model

each document is represented as a vector indexed ac-

cording to the vocabulary of the corpus. The vocabu-

lary of the corpus is represented as the set of unique

words, which appear in a text collection. It is con-

structed a D × T matrix C, where D is the number

of documents in the corpus and T the number of el-

ements in the vocabulary of the corpus. This kind

of representation is called document-term matrix, its

rows are indexed by the documents and its columns by

the vocabulary terms. Each cell of the matrix t f (d,t),

indicates the frequency of the term t in document d.

This representation can lead to a high dimensional

space, furthermore, the BoW model does not incorpo-

rate semantic information. These problems can result

in bad representations of the data. For this reason, dif-

ferent approaches to balance the importance of each

feature and to reduce the dimensionality of the fea-

ture space have been proposed. The importance of

a feature can be weighted using the term frequency

- inverse document frequency (tf-idf) method (Man-

ning et al., 2008). This technique takes as input a

document-term matrix C and update it with the fol-

lowing equation,

t f -id f (d,t) = t f (d,t) ·log

d f (d,t)

(15)

where d f (d,t) is the number of documents containing

the term t. Then the vectors are normalized so that no

bias can occur because of the length of the documents.

Latent Semantic Analysis (LSA) is used to derive

semantic information. (Landauer et al., 1998) and to

reduce the dimensionality of the data. The semantic

information is obtained projecting the documents into

a semantic space, where the relatedness of two terms

is computed considering the context in which they ap-

pear. This technique uses the Single Value Decompo-

sition (SVD) to create an approximation of the term

by documents matrix or tf-idf matrix. It decomposes

a matrix D in:

D = U ΣV

, (16)

where Σ is a diagonal matrix with the same dimen-

sions of D and U and V are two orthogonal matrices.

The dimensions of the feature space is reduced to k,

taking into account the ﬁrst k of the matrices in Equa-

tion (16).

4.2 Data Preparation

Each document i in a corpus D is represented with

a BoW approach. From this data representation it is

possible to adopt different dimension reductions tech-

niques, such as LSA (see Section 1), to achieve a more

compact representation of the data. The new vectors

will be used to compute the pairwise similarity among

documents and to construct, with this information, the

proximity matrix W. As measure for this task, it was

used the cosine distance,

cosθ

· v

||v

||||v

(17)

where the nominator is the intersection of the words

in the two vectors and ||v|| is the norm of the vectors,

which is calculated as:

∑

i=1

4.3 Graph Construction

The proximity matrix obtained, in the previous step,

can be used to represent the corpus D as a graph G,

whose nodes are the documents in D and whose edges

are weighted according to the similarity information

stored in W . Since, the cosine distance acts as a lin-

ear kernel, considering only similarity between vec-

tors under the same dimension, it is common to use a

kernel function to smooth the data and transform the

proximity matrix W into an afﬁnity matrix S (Shawe-

Taylor and Cristianini, 2004). This operation is also

useful because it allows to transform a set of complex

and nonlinearly separable patterns into patterns lin-

early separable (Haykin and Network, 2004). For this

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

112

task we used the classical Gaussian kernel,

ˆs(i, j) = exp

(

−

i j

)

(18)

where s

i j

is the dissimilarity among pattern i and j

computed with the cosine distance and σ is a is a pos-

itive real number which determines the kernel width,

and affects the decreasing rate of ˆs. This parame-

ter is calculated experimentally, since the nature of

the data and the clustering separability indices of the

clusters is not known (Peterson, 2011). The cluster-

ing process can also be helped using graph Lapla-

cian techniques. In fact, these techniques are able

to decrease the weights of the edges between differ-

ent groups of nodes. We use the normalized graph

Laplacian, in some of our experiments, which is com-

puted as L = D

−1/2

, where D is the degree

matrix of

S. Once we have matrix L we can reduce

the number of nodes in it, so that document games

are played only among high similar nodes, this re-

ﬁnement is aimed at modeling the local neighborhood

relationships among nodes and can be done with two

different methods, the ε-neighborhood graph, which

maintains only the edges which have a value higher

than a predetermined threshold, ε; and the k-nearest

neighbor graphs, which orders the edges weights in

decreasing order and maintains only the ﬁrst k.

The effect of these processes is shown in Figure

1. On the main diagonal of the matrix it is possible

to recognize some blocks which represent the clus-

ters of the dataset. The values of those points is low

in the cosine matrix, since it encodes the proximity

of the points. Then the matrix is transformed into a

similarity matrix by the Gaussian kernel, in fact, the

points on the main diagonal in this representation are

high. In the Laplacian matrix, it is possible to note

that some noise was removed from the matrix, the el-

ements far from the diagonal appear now clearer and

the blocks near the diagonal now are more uniform.

Finally the k-nn matrix remove many nodes from the

representation, giving a clear picture of the clusters.

We used the Laplacian matrix for the experiments

with the dominant set, since this framework requires

that the similarity values among the elements of a

cluster are very close to each other. The k-nn graph

was used to run the clustering games, since this

framework does not need many data to classify the

points of the graph.

4.4 Clustering

The clustering phase was conducted using the Domi-

nant Set algorithm to extract the prototypical elements

Figure 1: Different data representations for a dataset with 5

classes of different sizes.

of each cluster. We have developed different imple-

mentations, giving as input the number of clusters to

extract and also without this information, which is not

common in many clustering approaches. It is possible

to think at this situation as the case in which there are

some labeled points in the data and we want to clas-

sify new points according to this evidence.

4.5 Strategy Space Implementation

In the previous step it has been shown that with the

proposed approach, the Dominant Set clustering does

not cluster all the nodes in the graph but only some

of them. These points are used to supply information

to the nodes which have not been clustered. Within

this formulation, it is possible to adopt evolutionary

dynamics to cluster the unlabeled points

The strategy space of each player can be initial-

ized as follows,

i j

(

−1

, if node i is unlabeled.

1, if node i has label j,

(19)

where K is the number of clusters to extract and K

−1

ensures that the constraints required by a game theo-

retic framework are met (see equation (1).

4.6 Clustering Games

Once the graph that models the pairwise similarity

among the players and the strategy space of the games

has been created, it is possible to describe more in de-

tail how the games are formulated.

It is assumed that each player i ∈ I, which partic-

ipates in the games is a document in the corpus and

that each strategy, s ∈ S

is a particular cluster. The

players can choose a determined strategy among the

Document Clustering Games

113

set of strategies, each expressing a certain hypothe-

sis about its membership in a cluster and K being the

total number of clusters available. We consider S

the mixed strategy for player i as described in Sec-

tion 2. The games are played among two similar doc-

uments, i and j, imposing only pairwise interaction

among them. The payoff matrix Z

i j

is deﬁned as an

identity matrix of rank K. This choice is motivated

by the fact that, here all the players have the same

strategy space, we do not know in advance, what is

the range of classes to which the players can be as-

sociated, excluding the labeled points obtained in the

clustering phase. For this reason we have to assume

that a document can belong to all classes.

In this setting the best choice for two similar play-

ers is to be clustered in the same class, which is ex-

pressed by the entry Z

i j

= 1,i = j, of the identity

matrix. In these kinds of games, called imitation

games, the players try to learn their strategy by osmo-

sis, learning by their co-players. Within this formula-

tion, the payoff function for each player is additively

separable and is computed as described in Section 2.

Speciﬁcally, in the case of clustering games there are

labeled and unlabeled players, which, as proposed in

(Erdem and Pelillo, 2012), can be divided in two dis-

joint sets, I

and I

, denoting labeled and unlabeled

players, respectively. These players can be divided

further, taking into account the strategy that they play

without hesitation. In formal terms, we will have K

disjoint subsets, I

= {I

l|1

,..., I

l|K

}, where each sub-

set denotes the players that always play their kth pure

strategy.

The labeled players always play the strategy asso-

ciated to their cluster, because they lay on a corner of

the simplex, which is always a rest point (Hofbauer

and Sigmund, 2003). We can say that the labeled

players do not play the game to maximize their pay-

offs, because they have already a determined strategy.

Only unlabeled players play the games, because they

have to decide their cluster membership (strategy).

A strategy which can be suggested by labeled play-

ers, in fact, they act as bias over the choices of unla-

beled players. We recall that the games, formulated in

these terms, always have a Nash equilibrium in mixed

strategies (Nash, 1951) and that the adaptation of the

players to the proposed strategic environment is a nat-

ural consequence in game dynamics, given the fact

that each player gradually adjusts his choices accord-

ing to what other players do (Sandholm, 2010). Once

the equilibrium is reached, the cluster of each player i,

corresponds to the strategy s

i j

, with the highest prob-

ability.

The payoffs of the games are calculated equations

4 and 5, which in this case, with labeled and unlabeled

players, are deﬁned as,

) =

∑

j∈I

i j

)

∑

k=1

∑

j∈I

l|k

i j

(h,k) (20)

and,

(x) =

∑

j∈I

i j

∑

k=1

∑

j∈I

l|k

i j

)

. (21)

5 EXPERIMENTAL SETUP

We measured the performances of the systems using

the accuracy measure (AC) and the normalized mu-

tual information (NMI). AC is calculated with the fol-

lowing equation,

AC =

∑

i=1

δ(α

,map(l

))

(22)

where n denotes the total number of documents in the

test, δ(x,y) equals to 1, if x and y are clustered in the

same class; map(L

) maps each cluster label l

to the

equivalent label in the benchmark. The best mapping

is computed using the Kuhn-Munkres algorithm (Lo-

vasz, 1986). The NMI measure was introduced by

Strehl and Ghosh (Strehl and Ghosh, 2003) and in-

dicates the level of agreement between the clustering

C provided by the ground truth and the clustering C

produced by a clustering algorithm. The mutual infor-

mation (MI) between the two clusterings is computed

with the following equation,

MI(C,C

) =

∑

∈C,c

∈C

p(c

) · log

p(c

)

p(c

) · p(c

)

(23)

where p(c

) and p(c

) are the probabilities that a doc-

ument of the corpus belongs to cluster c

and c

, re-

spectively, and p(c

) is the probability that the se-

lected document belongs to c

as well as c

at the same

time. The MI information is then normalized with the

following equation,

NMI(C,C

) =

MI(C,C

)

max(H(C), H(C

))

(24)

where H(C) and H(C

) are the entropies of C and C

respectively, This measure ranges from 0 to 1. When

NMI is 1 the two clustering are identical, when it is

0, the two sets are independent. Each experiment was

run 50 times and is presented with standard deviation

(±).

For the evaluation of our approach, we used the

same datasets used in (Zhong and Ghosh, 2005),

where has been conducted an extensive comparison

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

114

of different document clustering algorithms

. The test

set is composed of 13 datasets, whose characteristics

are illustrated in Table 1. The datasets have differ-

ent sizes (n

), from 204 documents (tr23) to 8580

(sports). The number of classes (K) is different and

ranges from 3 to 10. Another important character-

istic of the datasets is the number of words (n

) in

the vocabulary of each dataset, which ranges from

5832 (tr23) to 41681 (classic) and is conditioned by

the number of documents on the dataset and on the

number of different topics in it. The last two features

which describe the datasets are n

and Balance. n

represents the average number of documents per class

and Balance is the ratio among the number of docu-

ments in the smallest class and in the largest class.

Table 1: Datasets description.

Data n

K n

Balance

NG17-19 2998 15810 3 999 0.998

classic 7094 41681 4 1774 0.323

k1b 2340 21819 6 390 0.043

hitech 2301 10800 6 384 0.192

reviews 4069 18483 5 814 0.098

sports 8580 14870 7 1226 0.036

la1 3204 31472 6 534 0.290

la12 6279 31472 6 1047 0.282

la2 3075 31472 6 513 0.274

tr11 414 6424 9 46 0.046

tr23 204 5831 6 34 0.066

tr41 878 7453 10 88 0.037

tr45 690 8261 10 69 0.088

5.1 Basic Experiments

In this section we tested our approach with the entire

feature space of each dataset. The graphs for our ex-

periments are prepared as described in Section 4.

The results of these experiments are shown in Ta-

ble 2 and Table 3 and will be used as point of compar-

ison for the next experiments. The results do not show

a stable pattern, in fact they range from NMI .27 on

the hitech dataset, to NMI .67 on k1b. The reason of

this incongruence is the representation of the datasets,

which in some cases has no good discriminators for

the described objects.

An example of the graphical representation of the

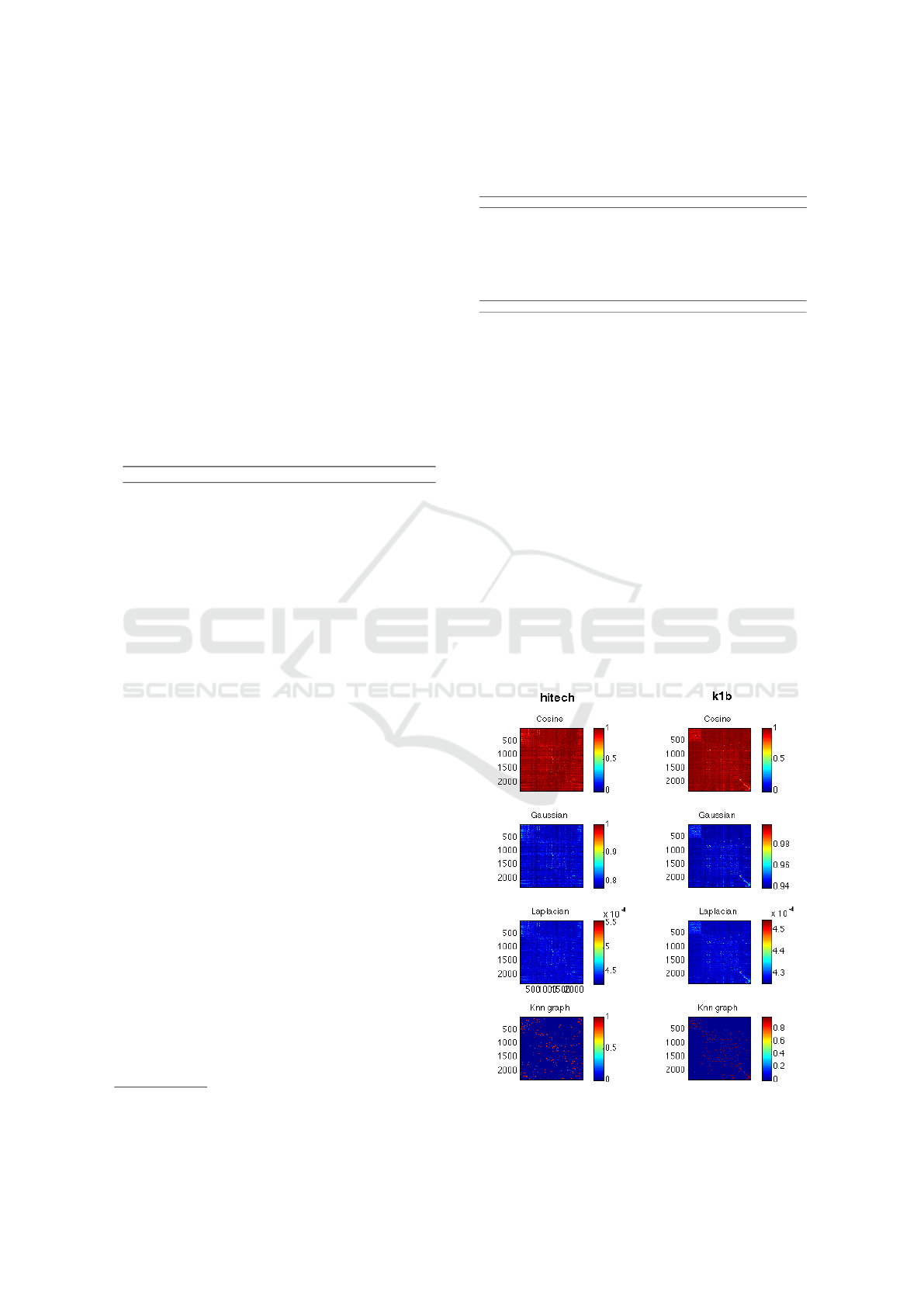
two datasets mentioned above is presented in Fig-

ure 2, where we can see that the similarity matrices

and the corresponding graphs constructed for hitech

do not show a clear structure on the main diagonal.

To the contrary, it is possible to recognize the cluster

structures clearly in the graphs representing k1b.

The datasets have been downloaded from,

http://www.shi-zhong.com/software/docdata.zip .

Table 2: Results as AC and NMI, with the entire feature

space.

NG17-19 classic k1b hitech review sports la1

AC .56± 0 .66 ± .07 .82 ± 0 .44 ± 0 .81 ± 0 .69 ± 0 .49 ± .04

NMI .42 ± 0 .56 ± .22 .66 ± 0 .27 ± 0 .59 ± 0 .62 ± 0 .45 ± .04

Table 3: Results as AC and NMI, with the entire feature

space.

la12 la2 tr11 tr23 tr41 tr45

AC .57 ± .02 .54 ± 0 .68 ± .02 .44 ± .01 .64 ± .07 .64 ± .02

NMI .46 ± .01 .46 ± .01 .63 ± .02 .38 ± 0 .53 ± .06 .59 ± .01

5.2 Experiments with Feature Selection

Each dataset described in (Zhong and Ghosh, 2005),

represents a corpus as BoW feature vectors, where

each vector represents a document and each column

indicates the number of occurrences of a particular

word in the corresponding text. This representation

leads to high dimensional space. It gives to each fea-

ture the same importance and does not take into ac-

count the problems of homonymy and synonymy. To

overcome these limitations, we decided to apply to the

corpora a basic frequency selection heuristic, which

eliminates the features which occur more often than

a determined thresholds. In this study only the words

occurring more than once were kept.

This basic reduction leads to a more compact fea-

ture space, which is easier to handle. Words that ap-

Figure 2: Different representations for the datasets hitech

and k1b.

Document Clustering Games

115

Table 4: Number of features for each dataset before and

after feature selection.

classic k1b la1 la12 la2

pre 41681 21819 31472 31472 31472

post 7616 10411 13195 17741 12432

% 0.82 0.52 0.58 0.44 0.6

Table 5: Mean results as AC and NMI, with frequency se-

lection.

classic k1b la1 la12 la2

AC .67 ± 0 .79 ± 0 .56 ± .11 .56 ± .03 .57 ± 0

NMI .57 ± 0 .67 ± 0 .47 ± .12 .44 ± .01 .47 ± 0

pear very few times in the corpus can be special char-

acters or miss-spelled words and for this reason can

be eliminated. The number of features of the new

dataset, after the frequency selection, are shown in Ta-

ble 4. From the table, we can see that the reduction

is signiﬁcant for ﬁve of the datasets used, arriving at

82% of reduction for classic, the other datasets have

not been affected by this process.

In Table 5 we show the results obtained employing

the same algorithm used to test the datasets with all

the features. This reduction can be considered a good

choice to reduce the size of the datasets and the com-

putational, but do not have a big impact on the per-

formances of the algorithm. In fact, the results show

that the improvements, in the performance of the al-

gorithm, are not substantial. We have an improve-

ment of 1%, in terms of NMI, in four datasets over

ﬁve. In one dataset we obtained lower results. This

could be due to the fact that we do not know exactly

what words have been removed from the datasets, be-

cause they are not provided with the datasets. In fact,

it is possible that the reduction has removed some im-

portant (discriminative) word from the feature space,

compromising the representation of the documents.

5.3 Experiments with LSA

In this section is presented the evaluation of the pro-

posed approach, using LSA to construct a semantic

space which reduces the dimensions of the feature

space. The evaluation was conducted using different

numbers of features to describe each dataset, ranging

from 10 to 400. This is due to the fact that there is no

agreement on the correct number of features to extract

for a determined dataset. For this reason this value has

to be calculate experimentally.

The results of this evaluation are shown in two dif-

ferent tables, Table 6 indicates the results as NMI and

Table 7 indicates the results as accuracy. The perfor-

mances of the algorithm measured as NMI are sim-

ilar on average (excluding the case of 10 features),

but there is no agreement on different datasets. In

fact, different data representations affect heavily the

performances on datasets such as NG17-19, where

the performances ranges from .27 to .46. This phe-

nomenon is due to the fact that each dataset has dif-

ferent characteristics, as shown in Table 1.

The results with this new representation of the

data shows that the use of LSA is beneﬁcial. In fact,

it is possible to achieve results higher than with the

entire feature space or with the frequency reduction.

The improvements are substantial and in many cases

are 10% higher.

Table 6: Results as NMI for all the datasets. Each column

indicates the results obtained with a reduced version of the

feature space using LSA.

Data 10 50 100 150 200 250 300 350 400

NG17-19 .27 .37 .46 .26 .35 .37 .36 .37 .37

classic .53 .63 .71 .73 .76 .74 .72 .72 .69

k1b .68 .61 .58 .62 .63 .63 .62 .61 .62

hitech .29 .28 .25 .26 .28 .27 .27 .26 .26

reviews .60 .59 .59 .59 .59 .59 .58 .58 .58

sports .62 .63 .69 .67 .66 .66 .66 .64 .62

la1 .49 .53 .58 .58 .58 .57 .59 .57 .59

la12 .48 .52 .52 .52 .53 .56 .54 .55 .54

la2 .53 .56 .58 .58 .58 .58 .59 .58 .58

tr11 .69 .65 .67 .68 .71 .70 .70 .69 .70

tr23 .42 .48 .41 .39 .41 .40 .41 .40 .41

tr41 .65 .75 .72 .69 .71 .74 .76 .69 .75

tr45 .65 .70 .67 .69 .69 .68 .68 .67 .69

avg. .53 .56 .57 .56 .57 .57 .57 .56 .57

Table 7: Results as AC for all the datasets. Each column

indicates the results obtained with a reduced version of the

feature space using LSA.

Data 10 50 100 150 200 250 300 350 400

NG17-19 .61 .63 .56 .57 .51 .51 .51 .51 .51

classic .64 .76 .87 .88 .91 .88 .85 .84 .80

k1b .72 .55 .58 .73 .75 .75 .73 .70 .73

hitech .48 .36 .42 .41 .47 .46 .41 .43 .42

reviews .73 .72 .69 .69 .69 .71 .71 .71 .71

sports .62 .61 .71 .69 .68 .68 .68 .68 .61

la1 .59 .64 .72 .70 .73 .72 .73 .72 .73

la12 .63 .63 .62 .62 .63 .67 .64 .67 .65

la2 .69 .66 .60 .60 .61 .60 .65 .60 .60

tr11 .69 .66 .69 .70 .72 .71 .71 .71 .71

tr23 .44 .51 .43 .42 .43 .43 .43 .43 .43

tr41 .60 .76 .68 .68 .65 .75 .77 .67 .77

tr45 .57 .69 .66 .68 .67 .67 .67 .67 .67

avg. .62 .63 .63 .64 .65 .66 .65 .64 .64

5.4 Evaluation of Document Clustering

Games

The results of the evaluation of the Document Cluster-

ing Games are shown in Table 8 and 9 (third column,

DCG), where, for each dataset, are compared the best

results obtained with the document clustering games

approach and the best results indicated in (Zhong and

Ghosh, 2005) and in (Pompili et al., 2014). In the ﬁrst

article was conducted an extensive evaluation of dif-

ferent generative and discriminative models, speciﬁ-

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

116

cally tailored for document clustering and two graph-

based approaches, CLUTO and a bipartite spectral

co-clustering method, which obtained better perfor-

mances than the other algorithms. The results in this

article are reported as NMI. In the second article there

is an evaluation on different NMF approaches to doc-

ument clustering, on the same datasets that we used

and the results are reported as AC.

From Table 8 it is possible to see that the results of

the document clustering games are higher than those

of state-of-the-art algorithms on ten datasets out of

thirteen. On the remaining three datasets we obtained

the same results on two datasets and a lower result in

one. On classic, tr23 and tr26 the improvement of our

approach is substantial, with results higher than 5%.

Form Table 9 we can see that our approach performs

substantially better that NMF on all the datasets.

Table 8: Results as NMI of generative models and graph

partitioning algorithm (Best) compared to our approach

with and without the number of clusters to extract.

Data DCG

noK

DCG Best

NG17-19 .39 ± 0 .46 ± 0 .46 ± .01

classic .71 ± 0 .76 ± 0 .71 ± .06

k1b .73 ± .02 .68 ± .02 .67 ± .04

hitech .35 ± .01 .29 ± .02 .33 ± .01

reviews .57 ± .01 .60 ± .01 .56 ± .09

sports .67 ± 0 .69 ± 0 .67 ± .01

la1 .53 ± 0 .59 ± 0 .58 ± .02

la12 .52 ± 0 .56 ± 0 .56 ± .01

la2 .53 ± 0 .59 ± 0 .56 ± .01

tr11 .72 ± 0 .71 ± 0 .68 ± .02

tr23 .57 ± .02 .48 ± .03 .43 ± .02

tr41 .70 ± .01 .76 ± .06 .69 ± .02

tr45 .70 ± .02 .70 ± .03 .68 ± .05

Table 9: Results as AC of NMF models (Best) compared

to our approach with and without the number of clusters to

extract.

Data DCG

noK

DCG Best

NG17-19 .59 ± 0 .63 ± 0 -

classic .80 ± 0 .91 ± 0 .59 ± .07

k1b .86 ± .02 .75 ± .03 .79 ± 0

hitech .52 ± .01 .48 ± .02 .48 ± .04

reviews .64 ± .01 .73 ± .01 .69 ± .07

sports .78 ± 0 .71 ± 0 .50 ± .07

la1 .63 ± 0 .73 ± 0 .66 ± 0

la12 .59 ± 0 .67 ± 0 -

la2 .55 ± 0 .69 ± 0 .53 ± 0

tr11 .74 ± 0 .72 ± 0 .53 ± .05

tr23 .52 ± .02 .51 ± .05 .43 ± .06

tr41 .75 ± .01 .76 ± .08 .53 ± .06

tr45 .71 ± .01 .69 ± .04 .54 ± .06

5.5 Experiments with no Cluster

Number

The last experiment was conducted without using the

number of clusters to extract. It has been tested the

ability of dominant set to ﬁnd natural clusters and the

performances that can be obtained in this context by

the document clustering games. In this way, we ﬁrst

run dominant set to discover many small clusters, set-

ting the parameter of the gaussian kernel with a small

value (0.1). Then we re-clusters the obtained clusters

using as similarity matrix the similarities shared be-

tween the nodes of two different clusters.

The results of this evaluation are shown in Table

8 and 9 (second column, DCG

noK

). The results show

that this new formulation of the clustering games per-

forms well in many datasets. In fact, in datasets such

as k1b, hitech, tr11 and tr23 has results higher than

the clustering games performed in the previous sec-

tions. This can be explained by the fact that with this

formulation the number of clustered points is higher

that in the previous version. This can improve the per-

formances of the system when dominant set is able

to ﬁnd the exact number of natural clusters from the

graph. To the contrary, when it not able to predict

this number, the performances as NMI decrease dras-

tically. This phenomenon can explain why in some

datasets it does not perform well. In fact, in datasets

such as, NG18-19, la1, la12 and l2 the performances

of the system are very low.

6 CONCLUSIONS

In this article we explored new methods for document

clustering based on game theory. We have conducted

an extensive series of experiments to test the approach

on different scenarios. We have also evaluated the

system with different implementations and compared

the results with state-of-the-art algorithms.

Our method can be considered as a continuation

of graph based approaches but it combines together

the partition of the graph and the propagation of the

information across the network. With this method we

used the structural information about the graph and

then we employed evolutionary dynamics to ﬁnd the

best labeling of the data points. The application of a

game theoretic framework is able to exploit relational

and contextual information and guarantees that the ﬁ-

nal labeling is consistent.

The system has demonstrated to perform well

compared with state-of-the-art system and to be ex-

tremely ﬂexible. In fact, it is possible to implement

Document Clustering Games

117

new graph similarity measure or new dynamics to im-

prove the results or to adapt it to different contexts.

REFERENCES

Ardanuy, M. C. and Sporleder, C. (2014). Structure-based

clustering of novels. EACL 2014, pages 31–39.

Bharat, K., Curtiss, M., and Schmitt, M. (2009). Methods

and apparatus for clustering news content. US Patent

7,568,148.

Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). La-

tent dirichlet allocation. J. Mach. Learn. Res., 3:993–

1022.

Dhillon, I. S. (2001). Co-clustering documents and words

using bipartite spectral graph partitioning. In Pro-

ceedings of the seventh ACM SIGKDD international

conference on Knowledge discovery and data mining,

pages 269–274. ACM.

Ding, C., Li, T., and Peng, W. (2006). Nonnegative ma-

trix factorization and probabilistic latent semantic in-

dexing: Equivalence chi-square statistic, and a hybrid

method. In Proceedings of the national conference

on artiﬁcial intelligence, volume 21, page 342. Menlo

Park, CA; Cambridge, MA; London; AAAI Press;

MIT Press; 1999.

Erdem, A. and Pelillo, M. (2012). Graph transduction

as a noncooperative game. Neural Computation,

24(3):700-723.

Haykin, S. and Network, N. (2004). A comprehensive foun-

dation. Neural Networks, 2(2004).

Hofbauer, J. and Sigmund, K. (2003). Evolutionary game

dynamics. Bulletin of the American Mathematical So-

ciety, 40(4):479–519.

Jain, A. K. and Dubes, R. C. (1988). Algorithms for clus-

tering data. Prentice-Hall, Inc.

Landauer, T. K., Foltz, P. W., and Laham, D. (1998). An in-

troduction to latent semantic analysis. Discourse pro-

cesses, 25(2-3):259–284.

Lee, D. D. and Seung, H. S. (1999). Learning the parts of

objects by non-negative matrix factorization. Nature,

401(6755):788–791.

Lovasz, L. (1986). Matching theory (north-holland mathe-

matics studies).

Manning, C. D., Raghavan, P., Sch

utze, H., et al. (2008).

Introduction to information retrieval, volume 1. Cam-

bridge university press Cambridge.

Nash, J. (1951). Non-cooperative games. Annals of mathe-

matics, pages 286-295.

Nowak, M. A. and Sigmund, K. (2004). Evolutionary dy-

namics of biological games. science, 303(5659):793–

799.

Okasha, S. and Binmore, K. (2012). Evolution and rational-

ity: decisions, co-operation and strategic behaviour.

Cambridge University Press.

Pavan, M. and Pelillo, M. (2007). Dominant sets and pair-

wise clustering. Pattern Analysis and Machine Intel-

ligence, IEEE Transactions on, 29(1):167–172.

Peterson, A. D. (2011). A separability index for clustering

and classiﬁcation problems with applications to clus-

ter merging and systematic evaluation of clustering al-

gorithms.

Pompili, F., Gillis, N., Absil, P.-A., and Glineur, F. (2014).

Two algorithms for orthogonal nonnegative matrix

factorization with application to clustering. Neuro-

computing, 141:15–25.

Rota Bul

o, S. and Pelillo, M. (2013). A game-theoretic

approach to hypergraph clustering. IEEE transac-

tions on pattern analysis and machine intelligence,

35(6):1312–1327.

Sandholm, W. H. (2010). Population games and evolution-

ary dynamics. MIT press.

Sankaranarayanan, J., Samet, H., Teitler, B. E., Lieberman,

M. D., and Sperling, J. (2009). Twitterstand: news

in tweets. In Proceedings of the 17th acm sigspatial

international conference on advances in geographic

information systems, pages 42–51. ACM.

Shawe-Taylor, J. and Cristianini, N. (2004). Kernel methods

for pattern analysis. Cambridge university press.

Smith, J. M. and Price, G. (1973). The logic of animal con-

ﬂict. Nature, 246:15.

Strehl, A. and Ghosh, J. (2003). Cluster ensembles—

a knowledge reuse framework for combining multi-

ple partitions. The Journal of Machine Learning Re-

search, 3:583–617.

Szab

o, G. and Fath, G. (2007). Evolutionary games on

graphs. Physics Reports, 446(4):97-216.

Tagarelli, A. and Karypis, G. (2013). Document clustering:

The next frontier. Data Clustering: Algorithms and

Applications, page 305.

Taylor, P. D. and Jonker, L. B. (1978). Evolutionary sta-

ble strategies and game dynamics. Mathematical bio-

sciences, 40(1):145–156.

Von Neumann, J. and Morgenstern, O. (1944). Theory

of Games and Economic Behavior (60th Anniversary

Commemorative Edition). Princeton University Press.

Weibull, J. W. (1997). Evolutionary game theory. MIT

press.

Xu, W., Liu, X., and Gong, Y. (2003). Document clustering

based on non-negative matrix factorization. In Pro-

ceedings of the 26th annual international ACM SI-

GIR conference on Research and development in in-

formaion retrieval, pages 267–273. ACM.

Zhao, Y. and Karypis, G. (2004). Empirical and theoretical

comparisons of selected criterion functions for docu-

ment clustering. Machine Learning, 55(3):311–331.

Zhao, Y., Karypis, G., and Fayyad, U. (2005). Hierarchi-

cal clustering algorithms for document datasets. Data

mining and knowledge discovery, 10(2):141–168.

Zhong, S. and Ghosh, J. (2005). Generative model-based

document clustering: a comparative study. Knowledge

and Information Systems, 8(3):374–384.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

118