
Earth Rotation: An Example to Teach Rigid Body Motion
and Environmental Monitoring
A Fallout of the Exploitation of LARES Satellite Data
Antonio Paolozzi
1,3
, Erricos Pavlis
2
, Claudio Paris
3,1
, Giampiero Sindoni
1
and Ignazio Ciufolini
4,3
1
Scuola di Ingegneria Aerospaziale, Sapienza University of Rome, Via Salaria 851-881, 00138 Rome, Italy
2
Joint Center for Earth Systems Technology, (JCET/UMBC), University of Maryland,
1000 Hilltop Circle, Baltimore, Maryland, 21250, U.S.A.
3
Museo Storico della Fisica e Centro Studi e Ricerce Enrico Fermi, Via Panisperna, 89, 00184, Rome, Italy
4
Dipartimento di Ingegneria dell’Innovazione Università del Salento, Via per Monteroni, 73100, Lecce, Italy
Keywords: Earth Rotation, Gravitation, Environmental Changes, Satellite Laser Ranging.
Abstract: The use of satellite laser ranging in combination with other space geodetic techniques allows us to determine
Earth’s motion with unprecedented accuracy, which is not as simple as usually described in basic textbooks.
Besides rotation and revolution there is a wobble of the rotation axis that can be derived by the torque free
case in rigid body dynamics. The presence of gravitational perturbations complicates the motion and
considering Earth as non-rigid introduces even more variations in the basic Earth motion theory. What is
interesting is that also the mass redistribution of air and water on the planet can affect the motion of Earth’s
rotational axis. Thanks to the millimetre accuracy achievable today, it is possible to correlate very small
anomalous rotational axis displacements with global environmental changes such the change in ice melting.
The paper will show the experimental motion of the Earth rotation axis and interpret it with the use of the
Euler rigid body equations of motion, outlining also the effects of the gravitational perturbations of other
bodies in the solar system and of the global climate changes on the Earth rotational axis.
1 INTRODUCTION
The Earth rotation is more complicated than what
non-specialists could think, although the main
components of the motion are sufficiently intuitive.
Before the advent of space age it was not possible to
test appropriately freely rotating bodies, so the
planetary motion was the best paradigm available.
In the paper it will be first considered the Earth
as a rigid body so that part of the wobble of the
rotation axis will be explained using rigid body
motion equations: the Euler equations. Incidentally
we recall that the solution provided by Euler is still
valid in the limit case of the rigid Earth. The new
techniques available today can position the Earth
rotation axis with accuracies at the level of one
millimetre. Among those, laser ranging to LARES-
type satellites gives a fundamental contribution.
LARES is an Italian Space Agency (ASI) funded
program with the aim to improve the measurement of
frame dragging or Lense-Thirring effect (Ciufolini et
al., 2012a) from about 10% obtained in (Ciufolini and
Pavlis, 2004) down at the level of 1% (Ciufolini et al.
2012b). The measurement of this effect is of great
interest among scientists. Under development is the
GINGER (Gyroscopes IN GEneral Relativity)
experiment (Bosi, 2011, di Virgilio, 2014). The
apparatus will exploit the Sagnac effect in the ring-
lasers to measure frame-dragging.
Contrary to the above missions, LARES is instead
a completely passive satellite so it is intrinsically
simpler and more reliable. It is covered with Cube
Corner Reflectors (CCRs) that have the property of
reflecting laser pulses sent from the ground stations
of the International Laser Ranging Service (Pearlman
et al., 2002). Counting the return time of the pulses
one determines the satellite position with few
millimetres accuracy.
The accurate reconstruction of the orbit not only
is useful for fundamental physics but also for the
accurate determination of the position of the centre of
mass and rotation axis of the Earth (in one word of
the Earth reference frame). The feasibility of
Paolozzi, A., Pavlis, E., Paris, C., Sindoni, G. and Ciufolini, I.
Earth Rotation: An Example to Teach Rigid Body Motion and Environmental Monitoring - A Fallout of the Exploitation of LARES Satellite Data.
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 2, pages 339-346
ISBN: 978-989-758-179-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
339

verifying the General Relativity effect but also the
possibility of determining accurately the rotation axis
of the Earth rely not only to the high accuracy of the
orbit determination reachable with the laser ranging
technique. Other factors such as the reduction of the
effects on the non-gravitational perturbation achieved
with a special design of LARES satellite and its
estimation is mandatory, as shown in the Monte Carlo
simulations of the experiment reported in (Ciufolini
et al., 2013a).
The special design of LARES provides accurate
data that integrated with data of other satellites and
techniques allow us determine an accurate Earth
reference frame (Pavlis et al., 2015a). In particular to
reduce the non-gravitational perturbations a very high
density material (Paolozzi et al., 2009) have been
chosen for the satellite. To further reduce unmodeled
effects on the satellite orbit, radiation pressure
uncertainties have been limited by avoiding painting
the surface of the satellite. Also thermal thrust
perturbation have been minimized (Ciufolini et al.,
2014) using a different approach with respect to what
originally proposed in (Bosco et al., 2007) i.e.
reducing the main origin of this perturbation: the
CCRs. The surface of the CCRs as compared to the
metallic surface of the satellite is the lowest with
respect to what obtained in all other laser-ranged
satellites (Ciufolini et al., 2013b; Paolozzi et al.,
2015).
February 13, 2012 LARES was successfully put
in orbit with the VEGA launcher (Paolozzi et al.,
2013; Paolozzi et al., 2012b) and data analysis for
testing General Relativity is now in progress
(Ciufolini et al., 2015).
In this paper we will concentrate on Earth’s
rotation axis showing that most of its motion can be
explained by rigid body dynamics. Relation with
climate change is also pointed out and indeed the
combination of mechanics and environmental
monitoring is believed to be an excellent driver to
raise students’ interest in both fields.
2 PLANETARY MOTION
In basic textbooks it is reported that planets, and in
particular the Earth, have two main motions:
revolution, which follows the second Kepler law
(equal areas are swept out in equal time) and rotation
characterized by a spin axis and angular velocity
(considered both constant at first approximation). It is
interesting to observe that those two motions are
easily predictable under two simplified assumptions:
• Rigid body Earth
• External actions limited to conservative
central forces.
If one neglects the non-gravitational perturbations
and the gravitational actions of all the other bodies
with the exclusion of the Sun, that is the source of the
conservative central force, the second hypothesis
applies to all planets in the solar system. In this
simplified scenario the conservation law of angular
momentum provides an endless motion of the planets
according to the second Kepler law i.e. the well-
known revolution motion.
Concerning the rotation being constant in
magnitude and direction, the additional hypothesis of
the Earth being infinitely rigid is required. In fact for
a non-rigid Earth it could happen that the rotational
speed would increase as a result of a reduction of the
diameter, exactly in the same way as it would happen
to a spinning ice skater when she/he brings the arms
closer to the body. Also the direction of the rotational
axis could change if the symmetry is broken by mass
redistribution on the Earth. In the analogy of the
skater also the rotational axis would change if only
one arm is retracted. However this hypothesis is not
sufficient to guarantee that the spin axis remains
constant in inertial space. This aspect will be analyzed
in detail later in the paper.
It is customary in rigid body motion analysis to
use a reference frame fixed with the body, and this
approach is maintained here for the case of the Earth.
The Earth reference frame is defined by the
International Earth Rotation and Reference Systems
Service (IERS) and is called International Terrestrial
Reference Frame or ITRF in short. The geographic
position of the North and South poles are defined with
a complex procedure that uses several techniques
including satellite laser ranging on LARES-like
satellites. The addition of LARES by the way will
improve the accuracy of such a reference frame by
about 20% as shown in (Pavlis et al., 2015a; Sindoni
et al., 2015). The geographic location of North and
South will define a geometric axis that does not
coincide with the rotational axis of the Earth. One
could think this rotation axis of the Earth is fixed in
inertial space and consequently could be considered a
realization of an inertial reference frame. But that in
general would be a mistake even if the Earth would
be an ideal perfect gyroscope as will be shown later
in the paper.
In summary there are several reasons why the
rotation axis of the Earth cannot be fixed in inertial
space, and with respect to the ITRF:
CSEDU 2016 - 8th International Conference on Computer Supported Education
340
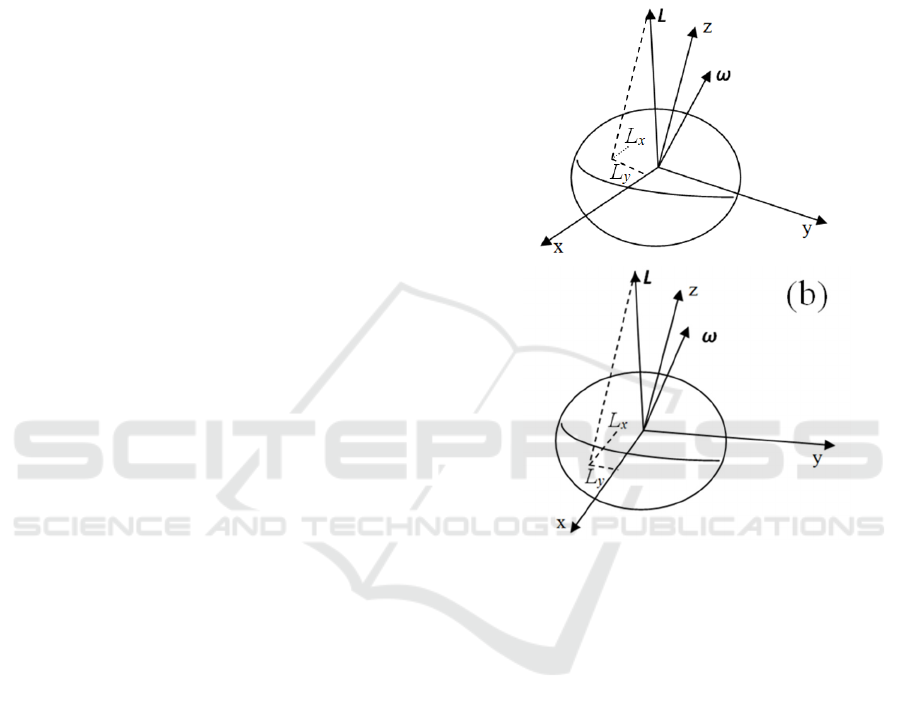
1) Even if the Earth would be an ideal gyroscope,
the rotation axis, in general, is not fixed in
inertial space. In fact what remains fixed in
inertial space is the angular momentum vector
(see details later in the paper). In short,
Newton’s second law, written in an inertial
reference frame, will imply the conservation of
angular momentum vector L that only under
very special situations is parallel to the angular
velocity vector ω.
2) The Earth is not a rigid body.
3) There are gravitational actions acting on the
Earth other than the solar attraction.
4) There are non-gravitational perturbations
acting on the Earth.
In the following section we recall some
fundamentals of rigid body dynamics preferring,
whenever possible under the limited space available
here, a graphical approach and pointing out some
pitfalls that usually arise in this area.
3 ANGULAR MOMENTUM
AND ANGULAR VELOCITY
First we recall that the angular momentum vector L is
a quantity that depends on the rotation speed of the
body, and on the mass distribution of the body itself
with respect to three arbitrary axes. The angular
velocity vector of the body ω is measured in a chosen
reference frame (usually an inertial frame, but not
necessarily). The mass distribution is summarized by
six independent numbers that are collected in a
symmetric matrix called the matrix of inertia I also
defined in an arbitrary reference frame (usually the
body fixed reference frame). In compact form the
rigorous definition of angular momentum in a
reference frame where the body is “seen” to rotate
with an angular velocity ω is:
L=Iω
(1)
If the reference frame, where ω is measured, is an
inertial reference frame and there are no torques
applied to the body, the vector L does not change
(conservation of angular momentum) so that in
general if ω changes in direction and/or magnitude
also I need to change to maintain L constant in time.
The change of I is difficult to deal with so one can
considerer at each instant an inertial reference frame
that is aligned with the body reference frame and
centred in the centre of mass of the body. In this series
of inertial reference frames the above equation holds,
meaning the L is constant although its components
change in time because the reference frame is
changing. If, in addition, we take the axes of those
inertial reference frames parallel to the principal axes
of inertia of the body (in general for regular shaped
object those coincide with the symmetry axes), then
the matrix I becomes diagonal. In Figure 1 the
situation is depicted.
Figure 1: (a) Inertial reference frame at instant t=t
1
; (b)
Inertial reference frame, rotated with respect to (a), at
instant t=t
2
. Vector L is the same as in (a) (conservation of
angular momentum) but its components have changed.
For the sake of clarity only x and y components of L
have been represented. Note that L has not changed
(conservation of angular momentum) from Figures 1a
to Figure 1b, while its components on the rotated
reference frame have changed. Also ω from time t
1
(Figure 1a) and time t
2
(Figure 1b) has changed. Also
note that in general L and ω are not parallel in this
series of inertial reference frames.
There are however special cases in which the two
vectors L and ω are parallel:
a) All three components of moments of inertia are
equal, i.e.
=
00
0
0
00
(2)
with I
xx
=I
yy
=I
zz
=I.
(a)
Earth Rotation: An Example to Teach Rigid Body Motion and Environmental Monitoring - A Fallout of the Exploitation of LARES Satellite
Data
341
In this case Eq. 1 reduces to L=Iω, i.e. the two
vectors differ in magnitude by the factor given
by the moment of inertia I.
b) Only one component of vector ω is different
from zero, with the exclusion of the component
corresponding to the direction of the
intermediate moment of inertia (because of
instability of rotation around the intermediate
axis) i.e. suppose I
xx
<I
yy
<I
zz
then it can be
ω
y
=ω
z
=0 or ω
x
=ω
y
=0. In this last case one has:
L
x
=L
y
=0 and L
z
=I
zz
ω
z
.
In both cases ω is conserved and this fact let
erroneously think that this is a general law, which is
not, since what is conserved in torque free motion and
in an inertial reference frame is the angular
momentum vector and not the angular velocity
vector.
As an example of the fact that the two vectors are
not parallel let us consider the Earth. Using updated
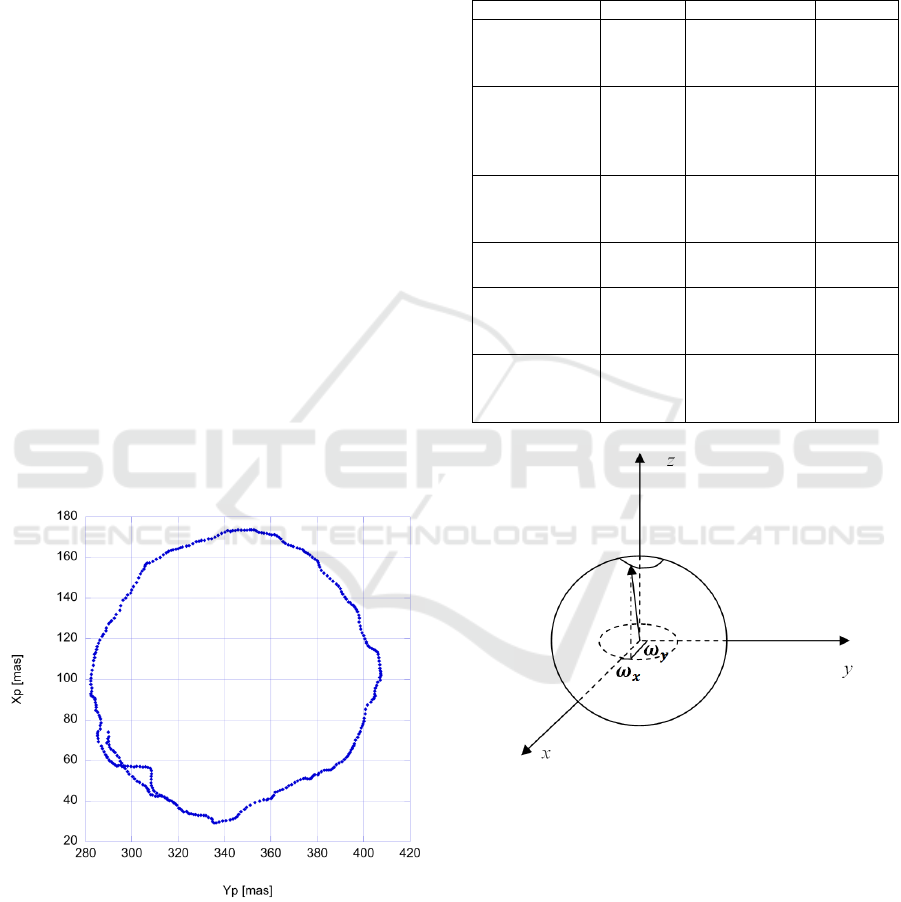
data from LARES satellite, in Figure 2 is reported the
actual motion of the Earth axis in year 2013 as seen
from the ITRF. The motion shown in Figure 2 proves
that L and ω are not parallel. In fact the Earth is not
perfectly spherical as shown by the values reported in
Table 1 (thus point (a) above does not apply) and ω
has components, though extremely small, also along
the two horizontal axes of the ITRF (thus point (b)
above does not apply).
Figure 2: Track of the Earth rotation axis with the Earth
surface as seen from an observer over the North pole and
fixed in the ITRF. The figure refers to year 2013 and has
been obtained including LARES data. 1 milliarcsecond
(mas) corresponds approximately to 3 cm on the Earth’s
surface.
In Figure 3 is reported a sketch where the diameter of
the trajectory of Figure 2 has been magnified by a
factor of about 10
5
.
Table 1: Earth’s moments of inertia. Uncertainty on last
digit in parenthesis. (from http://hpiers.obspm.fr/eop-
pc/models/constants.html#chenshen).
Constant Symbol Value Unit
First equatorial
moment of
inertia
I
xx
8.0101 (2)
10
37
kg m
2
Second
equatorial
moment of
inertia
I
yy
8.0103 (2)
10
37
kg m
2
Mean equatorial
moment of
inertia
I
mean
=
(I
xx
+I
yy
)/2
8.010171 (84)
10
37
kg m
2
Axial moment
of inertia
I
zz
8.0365 (2)
10
37
kg m
2
Mean angular
velocity of the
Earth
Ω 7.2921150 (1) 10
-5
rad/s
First equatorial
moment of
inertia
I
xx
8.0101 (2)
10
37
kg m
2
Figure 3: Trajectory (out of scale) of ω vector in the body
fixed reference frame.
4 EQUATIONS OF RIGID
BODY MOTION
What is causing the wobble reported in Figure 2 and
Figure 3? At the beginning of the paper we listed four
possible causes of the movement of the rotation axis
of the Earth. It is reasonable to expect all of them
contributing to this unexpected movement. Referring
to point 2 for instance one can refer to (Creveling J.R.
CSEDU 2016 - 8th International Conference on Computer Supported Education
342

et al., 2012). But what is the major contributor for the
Earth axis rotation? We will see, in the relatively
straightforward derivations below, that this wobble is
mainly due to the most basic law of mechanics: F=ma
(with F=0) applied as a total moment to a rigid body.
Euler calculated this effect, with a period of about 305
days, back in 1765. The actual experimental value
was observed by Chandler as being of about 439 days.
The discrepancy was later explained by Newcomb by
the fact that the Earth is not rigid (point 2 at beginning
of paper). But there are also other effects contributing
to this motion as will be mentioned at the end of the
paper.
Euler second law in an inertial reference frame
states that the rate of change of angular momentum
equates the applied torque T:
=
(3)
But as mentioned earlier it is convenient to use a body
fixed reference frame. So how the previous law will
change? To make the graphical representation more
understandable let us consider t=0 so that angular
momentum conservation applies and L is therefore
constant. in the body fixed reference frame an
observer would see the vector L changing direction
(Figure 4). It is easy to see that the rate of change of
L is given by Ω L sinθ, or using the vector product
notation, -Ω×L where Ω is the angular velocity vector
of the body fixed reference frame with respect to an
inertial reference frame and ω is the angular velocity
magnitude. What described is a transformation valid
for calculating the rate of change of any vector in two
rotating reference frames. So the rate of change of a
vector, and in particular of L, as seen from a body
fixed reference frame is:
=
−×
(4)
Note: it is useful to observe something that is obvious
but that sometimes is confusing. Vector Ω is
measured in the inertial reference frame. Instead the
angular velocity as measured from the body fixed
reference frame, i.e. the one of the inertial frame with
respect to the body frame, is Ω
from_body
= - Ω. It is also
useful to note that those two angular velocities do
exist in their respective reference frames. Although
the angular velocity Ω of the relative rotation of the
two reference frames equals the angular velocity of
the body ω, the two quantities are conceptually
different. In fact ω would be zero as measured from
the body fixed reference frame while in this frame the
angular velocity of the inertial frame with respect to
the body frame Ω
from_body
is equal to – Ω.
Figure 4a: Vector L as seen from the inertial reference
frame (solid line). The body fixed reference frame rotates
with angular velocity Ω. At time t
2
it is in the position
shown by the dashed lines. Subscripts correspond to the
time t
1
and t
2
.
Figure 4b: Vector L as seen from the body fixed reference
frame (dashed line). An observer on the moving frame would
see the inertial frame rotate in opposite direction so that at t
2
it will be as shown by the solid lines. The rate of change of L
is due to the rotation of the axes and is -Ω×L
1
or to
Ω
from_body
×L
1
. Subscripts correspond to the time t
1
and t
2
.
Rewriting Equation 4 in the general case of torque T
different from zero we have:
=
+×
=
(5)
Recalling that the inertia matrix I, in the body fixed
reference frame, does not change, the definition of L
from Equation 1 and that Ω=ω (remembering the note
reported above) we obtain the Euler equation for rigid
body motion in vector form:
∙
+×
∙
=0
(6)
Earth Rotation: An Example to Teach Rigid Body Motion and Environmental Monitoring - A Fallout of the Exploitation of LARES Satellite
Data
343

Having chosen the body axis aligned with the inertia
principal axis, the above equation becomes:
00
0
0
00
+
×
00
0
0
00
=
(7)
By performing the simple calculations one obtains the
Euler equations:
−
−
=
−
−
=
−
−
=
(8)
Now in the case of the Earth, if we neglect the
external actions and the very small differences
between I
xx
and I
yy
, the above equations simplifies to:
=
−
=−
−
=0
(9)
with the third equation providing ω
z
=constant.
Furthermore by posing:
Ω
=
−
(10)
and substituting the values reported in Table 1 one
obtains:
Ω
=
8.0365−8.0102
8.0102
7.2921∙10
=2.3942∙10
=3.294∙10
(11)
This angular frequency corresponds to a period of
303.6 days and the above equations reduce to:
=−Ω
=Ω
(12)
The solution to this system of linear differential
equations can be easily verified to be:
=
cosΩ
=
sinΩ
(13)
In the x-y plane of the body reference frame the
projection of the vector ω will trace in a period of
303.6 days a circle similar to that depicted with
dashed line in Figure 3.
So we have shown that a rotating body with no
external torques does not have, in general, a rotation
axis fixed in inertial space and with respect to the
body fixed reference frames. This last motion is
referred to as polar motion. Incidentally we observe
that it is still not clear what maintains the wobble
against the viscoelastic damping of the interior of the
Earth (Jenkins, 2015).
5 OTHER EFFECTS
AND ENVIRONMENTAL
MONITORING.
In this section we will briefly assess the effects of
points 2 and 3 mentioned at the beginning of the
paper.
We have mentioned that the polar motion is a
combination of several effects. The main one has
been described in the previous section and is due to
the law of mechanics applied to a torque free rigid
body. If we add the non-rigid Earth component, the
resulting wobble period would change from 303.6
days to about 439 days which is approximately the
value measured by Chandler. A more accurate
inspection of the motion over a longer period of time
will reveal that the radii of the circles (one is shown
in Figure 2), varies from about 3 meters to about 15
meters over a 6.5 year period. This variation cannot
be simply explained with the torque free motion and
the non-rigidity of the Earth because it is due to some
external seasonal forcing action that has a period of
one year.
But besides the wobbles just described there are
other components on the motion of the rotation axis
of the Earth. The effects of the gravitational torques
mainly of the Moon and the Sun, on the equatorial
bulge of the Earth causes the rotational axis of the
Earth to precess with a period of 25700 years. This
phenomenon is analogous to the precession of a
spinning top. Furthermore since the positions of the
Moon and the Sun change with time this effect
produces a nutation i.e. an oscillation of the Earth spin
axis with main period of 18.6 years (lunisolar
precession). Also the gravitational perturbations of
the planets induce a change of inclination of the Earth
axis in the range 22.2 – 24.3 degrees with a mean
period of 41.000 years (Berger A.L., 1976).
Possible indications on climate change can be
inferred by additional Earth rotation axis shift (Roy
and Peltier, 2011; Pavlis et al., 2015b). In fact mass
CSEDU 2016 - 8th International Conference on Computer Supported Education
344
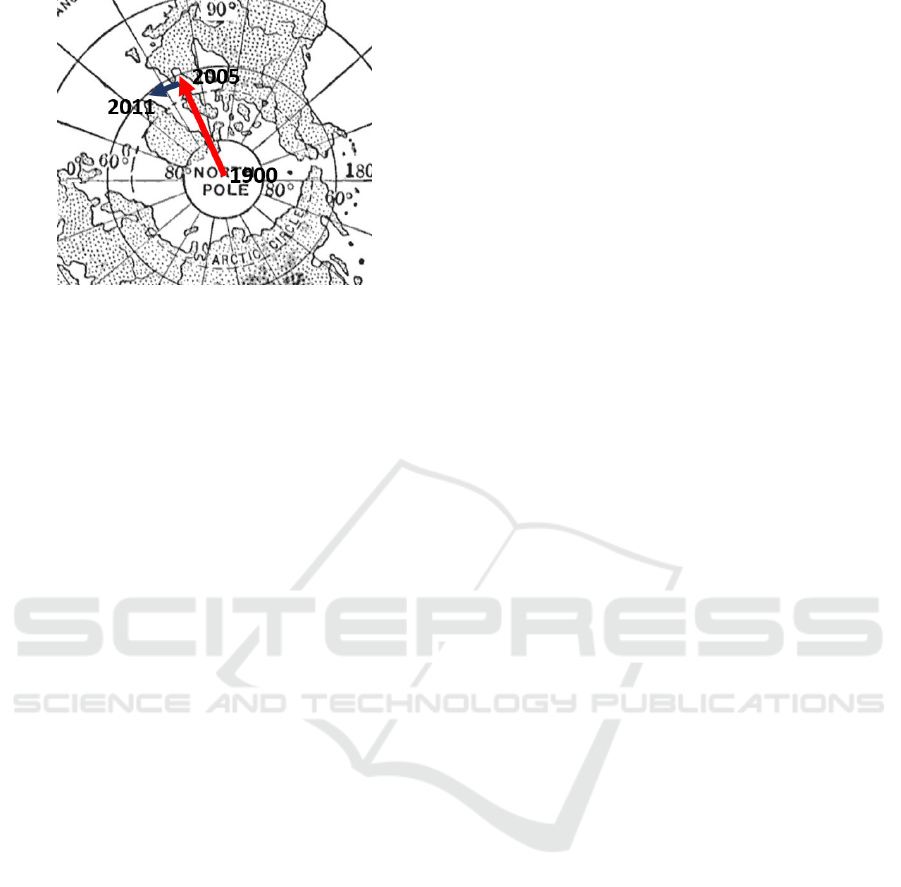
Figure 5: The long arrow (from year 1900 to 2005)
corresponds to 12.6m, the short arrow (from 2005 to 2011)
is of 1.6 m.
redistribution inside or on the surface of the planet
will affect the Length of the Day (LOD) and the
rotation axis direction (in one sentence, the angular
velocity vector) similarly to what would happen to the
skater mentioned above when he/she moves the arms.
The mass redistribution on the surface of the planet
concerns the atmosphere, the glaciers (Cazenave, A.,
and Chen J.L. 2010), the oceans, etc… We just would
like to mention another small motion of the rotation
axis of the Earth that is a secular drift towards East
which is partly due to post-glacial rebound i.e. the
slow ground rise due to the recovery of the original
position of the ground after the melting, and
consequently the release of weight, of the enormous
quantity of glaciers produced during the ice age. In
2005 it was observed a sudden change of the direction
of this secular drift that is attributed to a rapid melting
of Greenland glaciers and polar caps (Figure 5) (Chen
et al., 2013). Also the El Niño, due to thermal
expansion of the Pacific ocean (about 20 cm sea level
rise for an extension of thousands of kilometers)
produces variation on the Earth Orientation
Parameters (EOP) i.e. LOD and rotation axis
direction. The variations are very small but the
accuracy reached with the laser ranging technique on
LARES and other geodetic satellites and other
methods such as GNSS and Very Long Baseline
Interferometry (VLBI) allow to monitor the axis
position with an error of the order of 0.03
milliarcsecond i.e. about 1 mm on the Earth surface.
6 CONCLUSIONS
Taking the planet Earth as an example for a rotating
body, the paper describes first the case in which the
Earth is considered infinitely rigid. In this limit case
the rigid body Euler equations of motion predict a
counterintuitive oscillation of the Earth rotation axis,
that is the main contributor to the so called Chandler
wobble. This oscillation is a remarkable case because
it is not due to external torques but simply to the laws
of mechanics for a freely rotating body. The
discrepancy of the period of the wobble obtained
experimentally by Chandler with what obtained by
the Euler equations is explained with the non-rigid
Earth. Other motions of the axis are due to external
gravitational actions of the planets and particularly of
the Moon and the Sun. Finally the correlation
between the variation on the angular velocity vector
or if you like on the Earth Orientation Parameters
(EOP) and global climate changes is outlined. In
particular it has been observed that rapid Greenland
and polar ice melting may be the cause of the sudden
change in the polar motion secular drift. Also the
Pacific Ocean thermal expansion of El Niño
frequently leaves a signature on the EOP. Besides
being important for research in the field of global
climate change monitoring, Earth rotation studies
have recently gained considerable interest with the
public, mainly thanks to the proliferation of the web
and the increased outreach efforts of all scientists.
The combination of two fields, climatology and
mechanics, that appear to be so far apart seems to
attract very much the interest probably due to the
increasing concern on environmental issues. We plan
to apply this approach of combining mechanics, Earth
rotation and global environmental monitoring in an
educational and public outreach context to verify its
validity.
ACKNOWLEDGEMENTS
Research on the LARES mission is supported by the
Italian Space Agency under contracts I/034/12/0,
I/034/12/1, and 2015-021-R.0. E. C. Pavlis
acknowledges the support of NASA Grants
NNX09AU86G and NNX14AN50G. The authors
thank the International Laser Ranging Service for
tracking LARES and providing the laser ranging data.
REFERENCES
Berger A. L., 1976. Obliquity and Precession for the Last
5.000.000 Years. Astron. & Astrophys., 51, 127-135.
Bosi F., et al., 2011. Measuring gravito-magnetic effects by
multi ring-laser gyroscope. Phys. Rev. D. vol. 84, p.
122002-1-23.
Earth Rotation: An Example to Teach Rigid Body Motion and Environmental Monitoring - A Fallout of the Exploitation of LARES Satellite
Data
345

Bosco, A., Cantone, C., Dell'Agnello, S., Delle Monache,
G. O., Franceschi, M. A., Garattini, M., et al., 2007.
Probing gravity in NEO with high-accuracy laser-
ranged test masses. International Journal of Modern
Physics D, vol. 16, p. 2271-2285.
Cazenave, A., and Chen J. L., 2010, Time-variable gravity
from space and present-day mass redistribution in the
Earth system, Earth and Planetary Science Letters,
298, 263–274.
Chen, J. L., Wilson, C. R., Ries, J. C., Tapley, B. D., 2013.
Rapid ice melting drives Earth’s pole to the east,
Geophysics Research Letters, 40, 2625–2630.
Ciufolini, I. and Pavlis E. C., 2004. A confirmation of the
general relativistic prediction of the Lense-Thirring
effect. Nature 431, 958–960.
Ciufolini, I., Pavlis, E. C., Paolozzi, A., Ries, J., Koenig, R.,
Matzner, R., Sindoni, G., Neumayer H., 2012a.
Phenomenology of the Lense-Thirring effect in the
Solar System: Measurement of frame-dragging with
laser ranged satellites. New Astronomy, 17(3), 341-346.
Ciufolini, I., Paolozzi, A., Paris, C., 2012b. Overview of the
LARES Mission: orbit, error analysis and technological
aspects. Journal of Physics, Conference Series, vol.
354, p. 1-9.
Ciufolini, I., Moreno Monge, B., Paolozzi, A., Koenig, R.,
Sindoni, G., Michalak G., Pavlis, E. C., 2013a. Monte
Carlo simulations of the LARES space experiment to
test General Relativity and fundamental physics.
Classical and Quantum Gravity, 30, 235009.
Ciufolini, I., Paolozzi, A., Koenig, R., Pavlis, E. C., Ries,
J., Matzner, R., Gurzadyan, V., Penrose, R., Sindoni,
G., Paris, C., 2013b. Fundamental Physics and General
Relativity with the LARES and LAGEOS satellites.
Nuclear Physics B-Proceedings Supplements, vol. 243-
244, p. 180-193.
Ciufolini, I., Paolozzi, A., Paris, C., Sindoni, G., 2014. The
LARES satellite and its minimization of the thermal
forces. In: IEEE International Workshop on Metrology
for Aerospace. Conference Proceedings, pp. 299-303.
IEEE.
Ciufolini, I., Paolozzi, A., Pavlis, E. C., Koenig, R., Ries,
J., Gurzadyan, V., Matzner, R., Penrose, R., Sindoni,
G., Paris, C., 2015. Preliminary orbital analysis of the
LARES space experiment. The European Physical
Journal Plus, vol. 130.
Creveling, J. R., J. X. Mitrovica, N.-H. Chan, K. Latychev,
and I. Matsuyama (2012), Mechanisms for oscillatory
true polar wander, Nature, 491, 244–248.
Di Virgilio, A., Allegrini, A., Beghi, M., Belfi, A., et al.,
2014. A ring lasers array for fundamental physics.
Comptes Rendus Physique, vol. 15, p. 866-874.
Jenkins, A., 2015. On the maintenance of the Chandler
wobble. arXiv:1506.02810v1 [physics.geo-ph], 9 Jun,
2015.
Paolozzi, A., Ciufolini, I., Felli, F., Brotzu, A., Pilone, D.,
2009. Issues on lares satellite material. In: Proceedings
of International Astronautical Congress IAC 2009,
Daejeon, Republic of Korea.
Paolozzi, A., Ciufolini, I., Flamini, E., Gabrielli, A.,
Pirrotta, S., Mangraviti, E., Bursi, A., 2012. LARES in
orbit: some aspects of the mission. Proceedings of
Inter, Astronautical Congress IAC 2012
, Naples, Italy.
Paolozzi, A., Ciufolini, I., 2013. LARES successfully
launched in orbit: satellite and mission description.
Acta Astronautica, vol. 91, pp. 313-321.
Paolozzi, A., Ciufolini, I., Paris, C., Sindoni, G., 2015.
LARES a new satellite specifically designed for testing
general relativity. International Journal of Aerospace
Engineering, vol. 2015, p. 1-10.
Pavlis, E. C., Ciufolini, I., Paolozzi, A., Paris, C., Sindoni,
G., 2015a. Quality assessment of LARES satellite
ranging data. LARES contribution for improving the
terrestrial reference frame. In: 2nd IEEE International
Workshop on Metrology for Aerospace. Conference
Proceedings. vol. 1, p. 33-37. IEEE.
Pavlis, E. C., Sindoni, G., Paolozzi, A., Ciufolini, I., 2015b.
Contribution of LARES and Geodetic Satellites on
Environmental Monitoring. Proc. of 15th IEEE
International Conference on Environment and
Electrical Engineering - IEEE EEEIC 2015. IEEE.
Pearlman, M. R., Degnan, J. J. and Bosworth, J. M., 2002.
The International Laser Ranging Service. Advances in
Space Research, 30, pp. 135-143.
Roy, K., and Peltier W. R., 2011. GRACE era secular trends
in Earth rotation parameters: A global scale impact of
the global warming process?. Geophysics Research
Letters, 38, L10306, pp.1-5.
Sindoni, G., Paris, C., Vendittozzi, C., Pavlis, E. C.,
Ciufolini, I., Paolozzi A., 2015. The contribution of
LARES to global climate change studies with geodetic
satellites. Proc. of the ASME 2015 Conference on Smart
Materials, Adaptive Structures and Intelligent Systems
SMASIS 2015. ASME.
CSEDU 2016 - 8th International Conference on Computer Supported Education
346
