A Demonstration of Compilability for UML Template Instances

José Farinha

ISTAR, ISCTE-IUL, Av. Forças Armadas, Lisbon, Portugal

Keywords: UML, Templates, Verification, Compilability, Activities.

Abstract: Because of the thin set of well-formedness rules associated to Templates in UML, ill-formed elements may

result from bindings to templates. Although such ill-formedness is generally detected by some UML

validation rule, the problem is poorly reported because it is not normally imputed to the binding. Typically,

such problems are detected as non-compilable code in the template instances. A set of well-formedness rules,

additional to those of the standard UML, was proposed as a way to ensure the compilability of instances and

prevent this problem from occurring. Such set of constraints was proposed in a previous paper and named

Functional Conformance, but a demonstration of its effectiveness was not yet provided. Such a demonstration

is outlined in the current paper. Carrying out the demonstration revealed the need for two more rules than

those previously envisioned for Functional Conformance.

1 INTRODUCTION

An UML template is a model element embodying a

patterned solution that can be instantiated to solve a

recurring problem. A template is instantiated in a

model by binding an element of that model to the

template. In order to have a template instance

contextualized to the target model, templates are

defined as parameterised elements. A template

parameter marks an element participating in the

template’s definition to tell that it must be substituted

by an element of the target model. Only when all of

the template’s parameters are substituted, it becomes

an actual, fully integrated solution in the target model.

Aiming at ensuring that elements bound to

templates are well-formed, UML enforces a set of

constraints to parameter substitutions. One such

constraint imposes that a substitute element must be

of the same kind (Class, Attribute, Operation, etc.) as

the parametered element. Another constraint enforces

that if a parameter marks a typed element, this

element and its substitute have conforming types.

Yet, the set of validations falls short in

guaranteeing the well-formedness of template

instances. For instance, UML allows an operation

Op1 be substituted by an operation Op2 whose

signature is not compatible with the former’s. If so,

every call to Op1 in the template’s code will be

reproduced in the bound element as a call to Op2 with

an unaligned set of arguments, an ill-formed call.

Even though the problem was caused by a bad

substitution, it is reported on the operation call,

without any back tracking to the source of the

problem being recommended by UML (as of version

2.5 (OMG, 2015)). There are far more other such

scenarios of inadequate substitutions going unnoticed

by UML templates and causing incidental errors

inside template instances, mainly in the body of the

operations. This causes bad error reporting and is a

consequence of the scarce set of the validation rules

for UML templates.

In (Farinha and Ramos, 2015) a set of additional

rules was proposed for UML template as a way to

overcome the aforementioned problem. Such rules

implemented a concept named Functional

Conformance (FC). With FC enforcement, improper

substitutions of template parameters would be

immediately signalled and reported, providing

accurate error reporting. Since (Farinha and Ramos,

2015) provides only an intuitive perspective on the

solution, a formal proof of the effectiveness of it is

required.

This paper outlines how such a proof is achieved.

One that demonstrates that the enforcement of FC

ensures that operations’ code resulting from a

template binding will compile successfully, if the

corresponding code in the template also compiles.

E.g., the ill-formed operation call mentioned above

would not be allowed by FC. Due to space

restrictions, the actual demonstration could not be

Farinha, J.

A Demonstration of Compilability for UML Template Instances.

DOI: 10.5220/0005808503970404

In Proceedings of the 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2016), pages 397-404

ISBN: 978-989-758-168-7

397

provided in this paper. The interested reader may

refer to (Farinha, 2015). In such demonstration, the

well-formedness of methods is verified assuming that

these are represented as UML Activity Diagrams. It

is also assumed that methods are purely built with

UML constructs that also exist in the most common

OOP languages, i.e., Java, C# and C++.

The process of building the proof was useful to

uncover the need for two more well-formedness

constraints than those suggested by the empirical

experimentation that lead to (Farinha and Ramos,

2015). This reinforced the importance of developing

formal demonstrations. The two additional

constraints are related to the preservation of

subtyping relationships and of the abstract/non-

abstract nature of classifiers (i.e., classes,

associations, use cases, etc.) when mapping from a

template to its instances.

The structure of the paper is as follows: §2

presents some core concepts of UML templates and

introduces the terminology and symbology used in

this paper; §3 briefly presents FC; §4 outlines the

demonstration strategy; §5 presents related work; and

§6 draws some conclusions and foresees further steps

towards FC as a sound concept.

2 CONCEPTS, TERMINOLOGY

AND SYMBOLOGY

This paper uses the term “space of an element” to

refer to the model fragment that is composed of that

element and all the elements directly used by it. The

set of model elements composed of a template and all

of the elements directly used (referenced) by it is

called that template’s space. The term “template

space” is used for a general, non-specific template.

Similarly, the term “target space” is used to denote

the model fragment composed of an instance of a

template and all the elements used by that instance.

Some of the elements in a template’s space will

be marked as parameters of the template. Others will

be used ordinarily by the template, without been

specified as parameters.

When binding to the template – i.e., instantiating

the template – the elements marked as parameters will

be replaced by elements in the target space. This

means that the instance of the template – termed the

bound element – will use those elements of the target

space instead of the ones of the template space. The

concept in UML representing this replacements in the

context of a binding is termed Substitution. It is said

that an element in the target space substitutes an

element in the template space.

In a binding, the Projection of an element E of the

template space is the element of the target space that

corresponds to E in the context of that binding. I.e.,

the projection of E is one of the following:

 the actual substitute of E – if E is substituted;

 a replica (or reproduction) of E, if E is a

member of the template that is not substituted;

 E itself, if E is not substituted nor a template’s

member (E is simply used by the template and,

therefore, will be used by the bound element as

well).

In this paper, an identifier with a ‘

’, e.g. E

represents an element in a template space. An

identifier with a ‘



’, e.g. E



, represents an element in

a target space. E



is the projection of E

3 FUNCTIONAL

CONFORMANCE

Functional Conformance (FC) is a term that was

introduced in (Farinha and Ramos, 2015) aiming to

denote the equivalence between two model elements,

from a third-party, client perspective. It is a directed

relationship between two elements e

and e

, herein

represented in formulas as ‘FC (e

, e

)’, meaning that

the first element may be replaced by the second in a

model without compromising the consistency of that

model. In (Farinha and Ramos, 2015) and in the

current paper, the concept is applied to the

instantiation of UML templates, being proposed as a

set of well-formedness constraints that should rule

every template parameter substitution. FC is defined

as a set of criteria, presented next.

Type Conformance

Type Conformance states that if an element e

in the

template space has type T

, then the projection of e

must have the projection of T

as type. This criterion

should hold for all the types of e

, i.e., for e

’s direct

and indirect types (ascendants of the direct type). It

can be announced two-fold:

(1) If a type T of an element e

is not substituted,

then e



must have T as type;

(2) If the type T of an element e

is substituted,

then e



must have T’s substitute as type.

UML only enforces (1) (OMG 2015, sec.7.8.18.5).

MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development

398

Subtyping Conformance

Subtyping Conformance is intended to preserve every

is-a relationship from the template to the target

spaces, in case any classifier substitution occurs on a

generalisation hierarchy. The definition is: if T

is a

subtype of T

super

, then T



must be a subtype of T

super



or T

super



itself.

Multiplicity Conformance

Two elements conform regarding multiplicity if they

are both single-valued (multiplicities’ upper bound =

1) or both multivalued (multiplicities’ upper bound >

1) and, in the latter case, if they are both ordered or

both not-ordered.

Contents Conformance

Contents Conformance applies only to model

elements that are namespaces. In the context of a

certain bind, the namespace ns



conforms in contents

with ns

if every member of the ns

being used by the

template is substituted by a member of ns



. If the

namespace is a type, its members are properties,

operations, or inner types. If it is package, members

are packages or classifiers.

Contents Conformance has a corollary, named

Membership Conformance, which enforces that, if A

is substituted by B, members of A must be substituted

by members of B.

Signature Conformance

Signature Conformance is Contents Conformance as

applied to operations. It is the criteria that ensures that

a substituting operation has a set of parameters

compatible with that of the substituted.

Staticity Conformance

A static feature may only be substituted by another

that is also static, and a non-static by a non-static.

Abstraction Conformance

This criterion applies only to parametered elements

that are classifiers and is already supported by UML

2.5. It states that a classifier that is not abstract must

substituted by another that is also not abstract

Visibility Requirement

This requirement states that an element may

substitute a template parameter only if that element is

visible from the bound element.

4 DEMONSTRATION STRATEGY

4.1 Representing Code by UML

Activities

The goal of this demonstration is to show that the

code of operations in a class template remains

compilable once reproduced in instances of that

template. For instance, a class template that keeps a

list of items ordered by name would have an operation

insert (Item) with the following Java definition:

AlphabeticList::insert (Item itm) {

int k = 1;

while (itm.name < self.items[k].name)

k++;

self.items.insertAt (itm, k);

}

If a class CustomerList is bound to such template

and substitutes class Item by Customer and itm by

cust, the following method is generated:

CustomerList::insert (Customer cust) {

int k = 1;

while (cust.name < self.items[k].name)

k++;

self.items.insertAt (cust, k);

}

It must be proved that if method

AlphabeticList::insert (Item) compiles successfully

and FC is enforced on substitutions, then

CustomerList::insert (Customer) compiles as well. In

a Java setting, such a proof would use the syntax rules

of that language to check compilability.

Alternatively, our demonstration assumes that all

code is represented by UML Activities and, therefore,

compilability will be checked using the UML’s well-

formedness rules for Activities. E.g., the previous

method is represented by the activity in Figure 1.

Figure 1: A method represented as an activity with an

expression.

It could be noted however that the compilability

of the method in Figure 1 cannot yet be fully assessed

by UML Activity well-formedness rules. That is

because of the guard of one of the flows branching

A Demonstration of Compilability for UML Template Instances

399

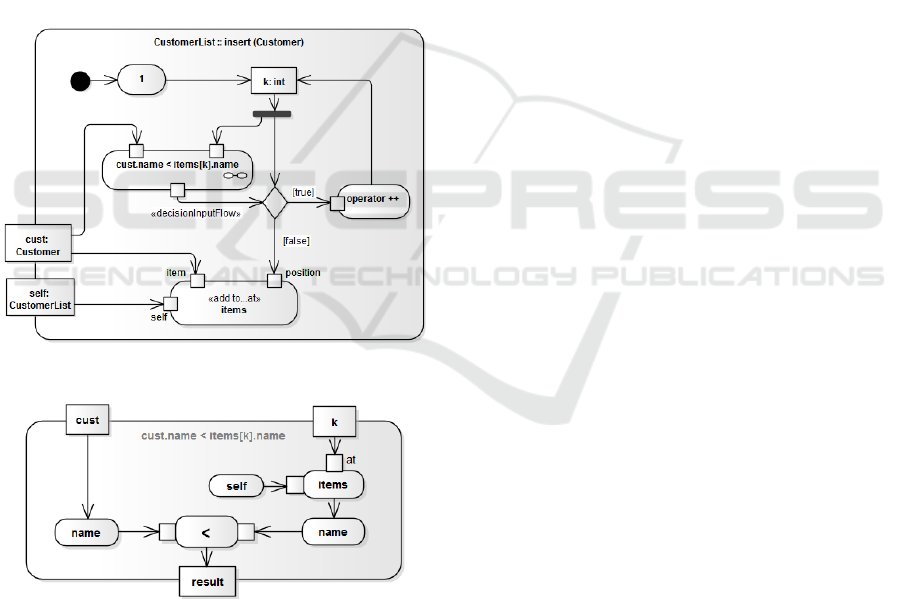
out of the decision node, which is represented by an

expression. The assessment of that guard would

require UML’s well-formedness rules for expressions

as robust as those of programing languages, which is

not the case: the UML metamodel stores expressions

as simple tree structures, without establishing

validation rules for the compatibility between those

trees’ nodes. E.g., UML considers 3 * “potato” a

valid expression. Hence, to achieve our goals,

expressions must be represented by activities. E.g.,

the guard expression in Figure 1 must be replaced by

the composite activity “cust.name < items[k].name”

shown in Figure 2, which internally should be as in

Figure 3. Since this expression-activity feeds the

«decisionInputFlow» of the decision node, its result

will steer execution as desired. Once every expression

is formally represented by an activity, the

compilability of a method may be fully verified

through UML well-formedness rules.

Figure 2: A method fully represented as an activity.

Figure 3: The internals of an expression-activity.

Although activity’s well-formedness rules do not

verify the compilability of constructs of the target

language that have no equivalent in UML, it provides

a compilability check strategy that is valid for

multiple languages in what is common between the

UML Activity model and those languages.

For the sake of a clear scope definition, it is

considered that what is common to the most usual

structured programing languages with object

orientation – such as Java, C# and C++ – may be

translated to UML activity diagrams exclusively built

with the following concepts of the UML Activity

formalism: Object Action, Structural Feature Action,

Call Action, Object Node, Control Flow, Object

Flow, and Decision Node. Every construct of such

languages that is not subsumed by those concepts is,

therefore, out of the scope of this paper. Limited to

such a scope, the problem of compilability

assessment may be further reduced to the assessment

of the well-formedness of a general, archetypal

action, as shown in §4.3.

4.2 UML Activities

This section overviews UML Activity concepts with

the goal of explaining how PL code is represented in

the demonstration.

Paraphrasing (OMG, 2015, sec.15.1): “An

Activity is a kind of behaviour that is specified as a

graph of nodes interconnected by flows. A subset of

the nodes are executable nodes that embody lower-

level steps in the overall activity.” Such executable

nodes are called Actions and correspond to statements

in programing languages. UML defines several kinds

of action. “Object Nodes hold data that is input to and

output from executable nodes”, and may represent

variables, operation parameters and their arguments.

The data in object nodes moves across Object Flows.

The sequencing of actions is specified through

Control Flows, and these may be controlled by if-

then-else, switch, loop, fork and join nodes, globally

designated Control Nodes.

In this paper, it is considered that the operations’

code under consideration is purely represented using

the UML concepts described below.

The UML kinds of action that are relevant to this

demonstration are: Object Actions, Structural

Feature Actions and Call Actions. Object Actions

operate on objects as a whole, representing statements

that create objects, destroy them, check their

classification (

myObj instanceof MyClass) or their

identities (

obj1 == obj2). See Figure 4.

Object actions also include Value Specification

Actions. These are actions that yield a value after

evaluating a textual expression. In this paper, only

actions evaluating a single literal are considered (such

as the ‘1’ action in Figure 2). Other value

specification actions are represented as composite

activities (see §4.1).

MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development

400



o = new Order



delete o

Figure 4: Object actions.

Structural Feature Actions read or write on

properties of objects (Figure 5).



o.totalCost



o.customer = c



o.customer = null

Figure 5: Structural Feature actions.

A Call Action invokes a behaviour (Figure 6) or

an operation on an object (Figure 7).



processOrders (

rders,

currentUser)

Figure 6: ‘Call Behaviour’ action.



o.add (p, qty)

Figure 7: ‘Call Operation’ action.

Object Nodes are used to store data that is used

and/or produced by actions. Those may represent

variables (e.g., ‘o: Order’ in the examples above) or,

through the concept of Pin – a specialization of

Object Node – may represent behaviour’s or

operation’s parameters (e.g., quantity, in Figure 7).

A Decision Node chooses one between multiple

outgoing flows: the first one whose guard is true.

Figure 8 shows two possible configurations for a

decision node. Decision nodes may also be used to

implement loops, as shown in Figure 9. Even though

UML provides a construct specific for looping

(LoopNode), representing loops as in Figure 9

narrows down the set of UML constructs required for

compilability assessment.



if (guard1)

...

elseif (guard2)

...



switch (getSomething){

case guard1: ...

case guard2: ...

}

Figure 8: Decision nodes.



while (guard1)

doSomething

Figure 9: A loop in an activity.

4.3 Demonstrating Compilability

through an Archetypal Action

This section shows that the verification of the

compilability of the bound element may be reduced

to the verification of a general, archetypal action.

Taking into account the semantics of UML

template binding – recalling: the bound element is a

replica of the template with superimposed

substitutions – and that the compilability of the

template is a premise, it may be deduced that only

those elements being impacted by substitutions may

spoil the compilability of the bound element. This

narrows down the set of elements to consider to those

whose validation rules reference parameterable

(therefore, substitutable) elements. Since neither the

source nor the target of an activity flow are

parameterable, flows’ connecting points are never

changed by template substitutions. This means that

the topology of an activity is preserved from the

template to the bound element. Consequently, it is

possible to consider individually each element kind

presented in the previous section.

Control Flow’s well-formedness constraints

mostly deal with topology. The only exceptions are

the flow’s weight and guard. Since the concept of

weight doesn’t exist in programing languages, only

the guard expression may jeopardize compilability.

As seen in §4.2, every expression that is not a plain

literal is represented as a composite activity. Hence,

the compilability of control flow may be ultimately

A Demonstration of Compilability for UML Template Instances

401

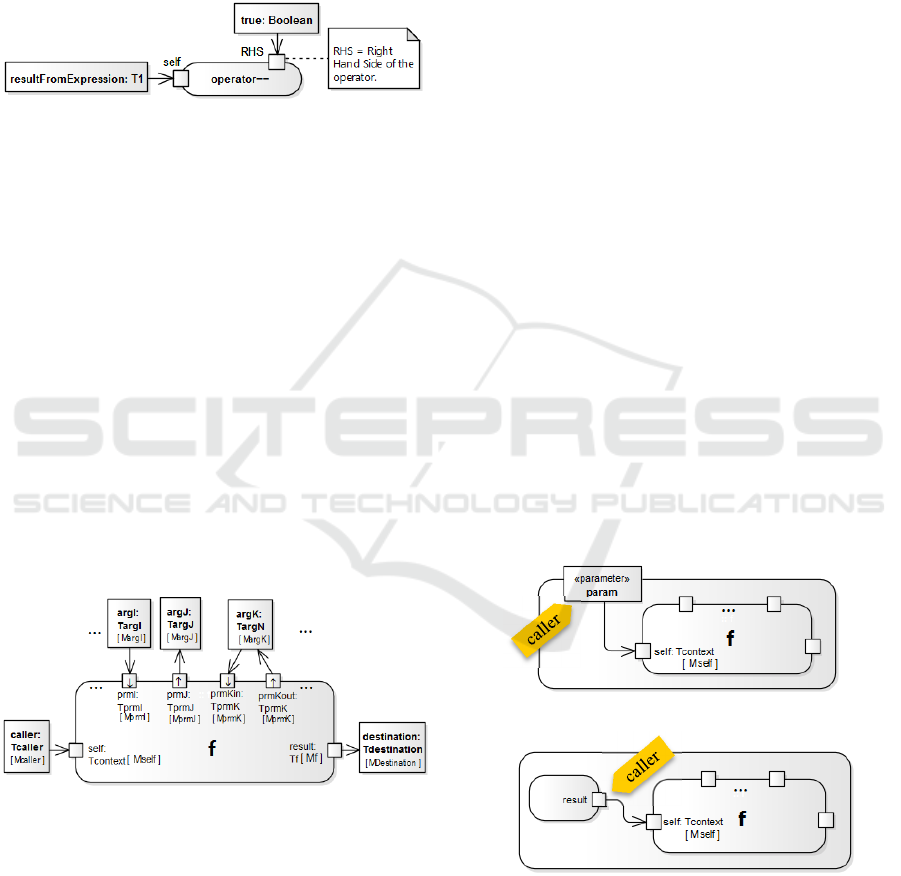
determined by the joint compilability of an activity

without guards and an action such as the one in Figure

10, which happens to be a call action, already elicited

in §4.2. The same is also valid for Decision Nodes, if

in Figure 10 “true: Boolean” is replaced by “aLiteral:

Any” or “aVariable: Any” (Farinha, 2015). This

filters out guards, control flows and decision nodes

from consideration.

Figure 10: Fragment of the semantics of a guard.

Hence, the compilability assessment of a bound

activity becomes reduced to the verification of the

action kinds designated in §4.2 and of the object

nodes and object flows connecting to those actions.

This allows further simplifying our demonstration

because all those action kinds may be subsumed by

the generic, archetypal action in Figure 11. Such

action aims at representing a feature call in the broad

sense: a call to a feature of an object, of a class (a call

to a static feature), or of the run-time system (e.g., a

call to the new operator). The demonstration strategy

from this point on is somewhat straightforward:

assuming that well-formedness rules hold for the

archetypal action in a template, it must be shown that

they hold as well for the corresponding bound action

if FC is enforced in the binding. I.e., representing the

archetypal action by a, it is shown that:

WellFormed

)  FC (a

, a



) 

WellFormed



)

Figure 11: An action in the template.

Since the archetypal action is included in a

template it will be reproduced in every element bound

to that template. The archetypal action within the

template will be referred as templated action and

represented as in Figure 11. Its reproduction in a

bound element will be referred as bound action and

represented as in Figure 14.

The Templated Action

The feature being called by the templated action in

Figure 11 is represented by the meta-variable f. For

Create Object actions f is a class, not a feature. For

Value Specification actions f is an expression;

specifically to this demonstration, it is a literal. For

Destroy Object actions f doesn’t exist.

Self is a pin that represents the usual variable

self/this: a reference to the object that executes the

feature, from the perspective of the code of that

feature. Self doesn’t exist in Create Object, Value

Specification, and Call Behaviour actions.

As imposed by UML’s constraints (OMG, 2015,

sec.16.14.54.6 and 16.14.10.6), self’s type is the type

that owns – i.e., declares and provides context to – the

feature being called. The type of self is represented by

Tcontext.

The multiplicity of the self pin is represented by

Mself. Mself’s upper bound must be 1 if f is a

property. If f is an operation, self may be multivalued

(Mself’s > 1), to represent calls to collection

operations (size(), includes(…), etc.).

The caller object node represents the instance that

embodies self in an execution of the action. In a

statement ‘anObject.feature’, anObject is represented

in Figure 11 by caller. Depending on the topology of

the activity containing the action, caller may

represent a variable, a parameter of the activity that

contains the action (Figure 12) – including that

activity’s self – or the

result pin of a preceding action

(Figure 13). Caller’s type and multiplicity are

represented by Tcaller and Mcaller, respectively.

Figure 12: Caller is a parameter of the owning activity.

Figure 13: Caller is a previous result.

Prm

, for i from 1 to N, only exists for call actions

and it is a parameter of f with direction other than

return. Prm

’s type and multiplicity are represented

by Tprm

and Mprm

, respectively. Prm

also

represents the pin that passes values to or from the

MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development

402

prm

parameter, depending on that parameter’s

direction being in or out, respectively. If prm

is a

bidirectional parameter (inout), values may be passed

to and from it. Since UML pins may not be

bidirectional, two pins are required to every inout

parameter: these will be called prm

_in

and prm

_out

That’s the case of prm

in Figure 11.

Arg

, for i from 1 to N, is the argument passed to

prm

. Arg

’s type and multiplicity are represented by

Targ

and Marg

, respectively. Similarly to caller,

arg

may represent a variable, a parameter of the

activity, or the result pin of an upstream action.

Result is the pin that yields the value returned by

the action. If f is a property, result yields the value of

that property in the instance provided by caller. If f is

an operation, result yields the value returned by the

operation. Result´s type and multiplicity are

represented by Tf and Mf, respectively.

Destination represents the element that receives

the result of the action. Also depending on the

topology of the activity containing the action, it might

be a variable, an output (out, inout or return)

parameter of the activity, or a pin of a downstream

action (a subsequent self or prm

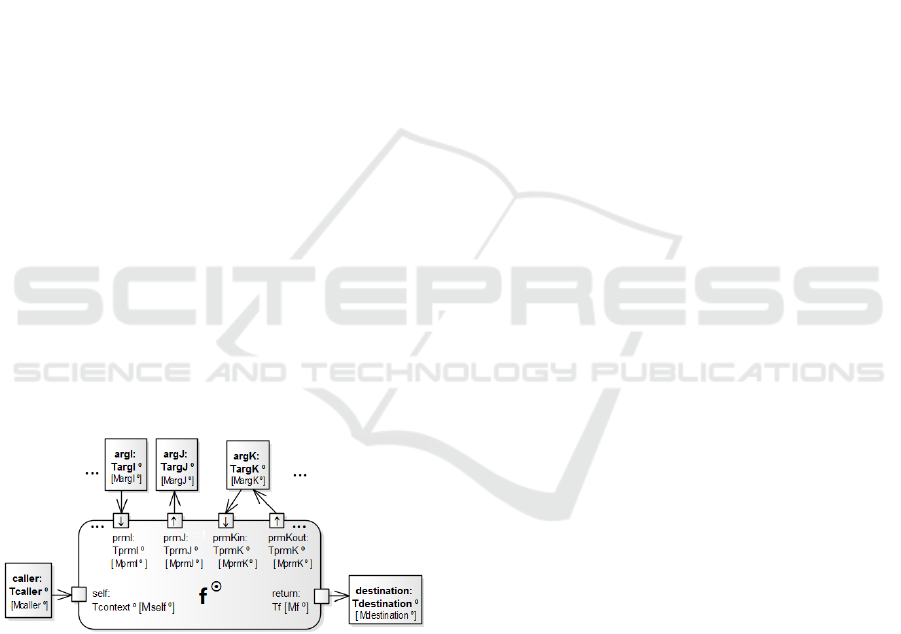
The Bound Action

The reproduction of the templated action within the

bound element will be termed bound action and

represented as in Figure 14. In that figure, the

elements that may differ from their original

counterparts are marked with ‘



’ (in some cases

reduced to a ‘’, due to typewriting constraints).

Figure 14: The bound action.

4.4 Compilability Criteria

This section states how compilability assessment

rules are elicited out of the whole set of UML

Activity’s well-formedness constraints. It must be

noted that such criteria will be applied to the bound

action. Only constraints belonging to both the

following sets are relevant:

 Those being defined for the constructs that

build up the archetypal action; i.e., well-

formedness constraints of: Object Node, Pin,

Object Flow, Structural Feature Action, Call

Action and Object Action;

 Those referencing elements that UML defines

as parameterable in a template (therefore,

substitutable in a binding).

(Farinha, 2015) lists those constraints and

formulates them in terms of the archetypal action. The

holding of those constraints in the templated action

are stated as premises and the holding in the bound

action are the hypotheses, which are proved on the

basis of the premises and that FC holds. I.e., it is

shown that, being a the archetypal action:

 rule  {Compilability rules},

rule (a

), FC (a

, a



) ⊢ rule (a



5 RELATED WORK

For classifier template parameters only, UML allows

the specification of constraining classifiers, which

will act as required contracts that substituting

classifiers must fulfil. This provides compatibility

assurance between the substituted and the substituting

classifiers, but limits the applicability of templates,

because these classifiers must inherit some common

supertype and/or implement common interfaces.

(Cuccuru et al., 2009) presents a way to contour the

need for such common supertype/interface, but

imposes the need for a common template. Although

that solution actually increases the applicability of

templates, applicability is even greater using FC,

because there is no need of any kind of common

ancestor as long as every member of the substituted

classifier is substituted by a member of the

substituting classifier (Cts

Cnf

). Furthermore,

constraining classifiers only provide compatibility for

classifier parameters, while FC works for any kind of

parameterable element.

(Caron and Carré, 2004) also proposes a set of

rules, additional to that of UML, to ensure that

template instances are well-formed. However, the

proposed rules overlook several aspects, such as

multiplicity, staticity, and visibility. FC takes such

aspects under consideration.

(Vanwormhoudt et al., 2015) proposes an

extension to the UML Template concept called

Aspectual Template (AT). Instead of having multiple

parameters, ATs have a single parameter, which

exposes a model as a whole. Associated to ATs, a set

of constraints ensures that the target model fragment

is conformant with the AT parameter. However, AT’s

constraints overlook multiplicities and the static

A Demonstration of Compilability for UML Template Instances

403

nature of features. AT’s rules also overlook subtyping

in some circumstances and that makes templates less

flexible. FC doesn’t have such limitations.

None of the aforementioned outline a formal

proof for their contributions.

In the Generic Programing field, the concept of

Concept was introduced to impose requirements on

template arguments (Dehnert and Stepanov, 1998).

Since in C++, template parameters are … In Java

Generics and in C# Templates, Concepts are specified

through interfaces, the same approach as that of

UML’s constraining classifiers, having the same

limitations. (Siek et al., 2005) and (Gregor et al.,

2006) are proposals for introducing Concepts in C++,

and are the approaches to Concepts that most

resemble UML Templates with FC. A concept

definition in a C++ template plays the same role as an

element that is exposed as a parameter of an UML

template, if FC is enforced. The advantage of

UML+FC lies in the fact that no additional constructs

are required: concepts are modelled by ordinary

classes, packages, operations, etc.

6 CONCLUSIONS AND FUTURE

WORK

Building a proof was useful because it confirmed the

theory put forth and because it uncovered issues that

otherwise might become unnoticed. These were

mostly related with the substitution of classifiers and

revealed the need for the Subtyping and Abstraction

Conformance criteria. The former was not initially

apparent because Type conformance seemed to

suffice for the purpose under consideration.

Abstraction Conformance was not detected

previously because none of the empirically tested

templates included a new statement that could be

substituted by an abstract class. It looks like a formal

proof is worth a thousand tests.

The demonstration strategy use only proves that

FC is sufficient to ensure compilability. As a next

step, a demonstration that shows that FC’s rules are

the necessary ones must be done.

REFERENCES

Caron, O. & Carré, B., 2004. An OCL formulation of

UML2 template binding. UML’ 2004 — The Unified

Modeling Language. Modeling Languages and

Applications, 3273, pp.27–40.

Cuccuru, A. et al., 2009. Constraining Type Parameters of

UML 2 Templates with Substitutable Classifiers. Model

Driven Engineering Languages and Systems, 12th Int.

Conf., MODELS 2009, Denver, CO, USA, 2009.

Proceedings, 5795, pp.644–649.

Dehnert, J. C. & Stepanov, A. A., 1998. Fundamentals of

Generic Programming. Generic Programming, Int.

Seminar on Generic Programming, Dagstuhl Castle,

Germany, 1998, Selected Papers, 1766, pp.1–11.

Farinha, J., 2015. A Demonstration of Compilability for

UML Template Instances with Activities, Lisbon,

Portugal. Available at: https://repositorio.iscte-

iul.pt/browse?type=author&value=Farinha%2C+Jos%

C3%A9.

Farinha, J. & Ramos, P., 2015. Extending UML Templates

towards Computability. In MODELSWARD 2015, 3rd

Int. Conf. on Model-Driven Engineering and Software

Development. ScitePress.

Gregor, D. et al., 2006. Concepts: Linguistic Support for

Generic Programming in C++. In Procs. 21st ACM

SIGPLAN Conference on Object-Oriented

Programming, Systems, Languages, and Applications,

OOPSLA 2006, October 22-26, 2006, Portland,

Oregon, USA. ACM, pp. 291–310.

OMG, 2015. OMG Unified Modeling Language, version

2.5, Available at: http://www.omg.org/spec/UML/2.5.

Siek, J.G. et al., 2005. Concepts for C++0x. Technical

Report N1758=05-0018, ISO/IEC SC22/JTC1/WG21,

Available at: https://www.academia.edu/16888725/

Concepts_for_C_0x.

Vanwormhoudt, G., Caron, O. & Carré, B., 2015. Aspectual

templates in UML. Software & Systems Modeling.

MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development

404