Using Sum-Frequency Generation (SFG) to Probe Electric-Fields

within Organic Field-Effect Transistors

Douglas J. C. Gomes

, Silvia G. Motti

and Paulo B. Miranda

São Carlos Institute of Physics, University of São Paulo,

C.P. 369, São Carlos – SP, 13560-970, Brazil

Center for Nano Science and Technology @PoliMi, Istituto Italiano di Tecnologia,

Via Pascoli 70/3, 20133 Milano, Italy

Keywords: Sum-Frequency Generation, Organic Transistors, Electric-Field Poling.

Abstract: Organic Field-Effect Transistors (OFETs) have attracted much research interest due to their potential for

unique applications, such as flexible electronics. The operation of OFETs depends on the charge

accumulation at the interface between an organic semiconductor and a dielectric material, induced by the

voltage applied at the gate electrode. Direct measurements of the electric-field distribution in an operating

device are useful for proposing and validating theoretical models for OFET operation. Here we propose

using the second-order nonlinear optical process of Sum-Frequency Generation vibrational spectroscopy

(SFG spectroscopy) to probe the presence of an electric-field in the dielectric layer of OFETs, in a non-

invasive, non-destructive and remote fashion. The OFETs were fabricated with a dielectric layer consisting

of poly(methyl-methacrylate) – PMMA, and an active layer based on poly(3-hexyl thiophene) – P3HT, and

SFG spectra were acquired from the channel region of operating OFETs. It was observed the appearance of

vibrational bands due to carbonyl groups (~ 1720 cm

-1

) of the PMMA layer, whose χ

(2)

were induced by the

electric-field within the dielectric, similarly to a reversible poling of polymers. This phenomenon opens up

the possibility of mapping the spatial charge distribution in the conducting channel using SFG microscopy

in operating devices.

1 INTRODUCTION

Semiconductor devices based on organic materials,

such as transistors or solar cells, have attracted much

research interest due to their potential for unique

applications, such as flexible and/or low-cost

electronics. The operation of organic ﬁeld-eect

transistors (OFETs) depends on the modulation of

charge accumulation at the interface between an

organic semiconductor and a dielectric material,

induced by the voltage applied at the gate electrode.

The accumulated charge carriers form a conducting

channel and are driven along this interface by

application of an electric field parallel to the

interface, between drain and source electrodes (Sze

and Kwok, 2007). Although the basic physics of

OFETs is well known, there is currently no single

model that can explain its operation both in the

linear regime and in saturation, after the pinch-off of

the conduction channel (Stallinga and Gomes,

2006). Therefore, direct measurements of the

electric field distribution in an operating device are

useful for proposing and validating theoretical

models.

Several methods have been used to probe the

potential, field or charge distribution in operating

OFETs, including Kelvin probe microscopy (Hallam

et al., 2009), microwave conductivity microscopy

(Babajanyan et al., 2011), charge modulation

spectroscopy (Sciascia et al., 2011), Raman

microscopy (Furukawa et al., 2012), and second-

order nonlinear optical processes, such as second-

harmonic generation (SHG) (Manaka et al., 2007a)

and vibrational spectroscopy by sum-frequency

generation (SFG) (Nakai et al., 2009). The optical

methods have the advantage of being non-invasive,

that is, they do not affect the charge distribution that

is being probed. Among them, SHG and SFG are

very versatile, since they allow probing the field

distribution (Manaka et al., 2007a; Nakai et al.,

2009) and dynamics (Manaka et al., 2007b) within

the organic semiconductor. In this work, we further

194

Gomes, D., Motti, S. and Miranda, P.

Using Sum-Frequency Generation (SFG) to Probe Electric-Fields within Organic Field-Effect Transistors.

DOI: 10.5220/0005812801920196

In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 194-198

ISBN: 978-989-758-174-8

extend these methods by showing that SFG

vibrational spectroscopy can be used to selectively

probe the electric-field inside the dielectric layer of

OFETs, which is directly related to the charge

distribution in the OFET channel.

2 MATERIALS AND METHODS

2.1 Materials and Sample Preparation

The bottom-gate/top-electrode OFETs have been

fabricated by sequential spin-coating of a dielectric

layer consisting of poly(methyl-methacrylate) –

PMMA, and an active layer based on poly(3-hexyl

thiphene) – P3HT, using solutions made with

orthogonal solvents. The PMMA layer was ~ 400

nm thick and was spin-coated from a methy-ethyl

ketone solution, while the P3HT film was spin-

coated over the PMMA film from a tetralin solution.

The thickness of this P3HT film was only ~ 30 nm

to minimize the absorption of the SFG light

(wavelength ~ 480 nm) generated at the PMMA

film, while exiting through the P3HT layer.

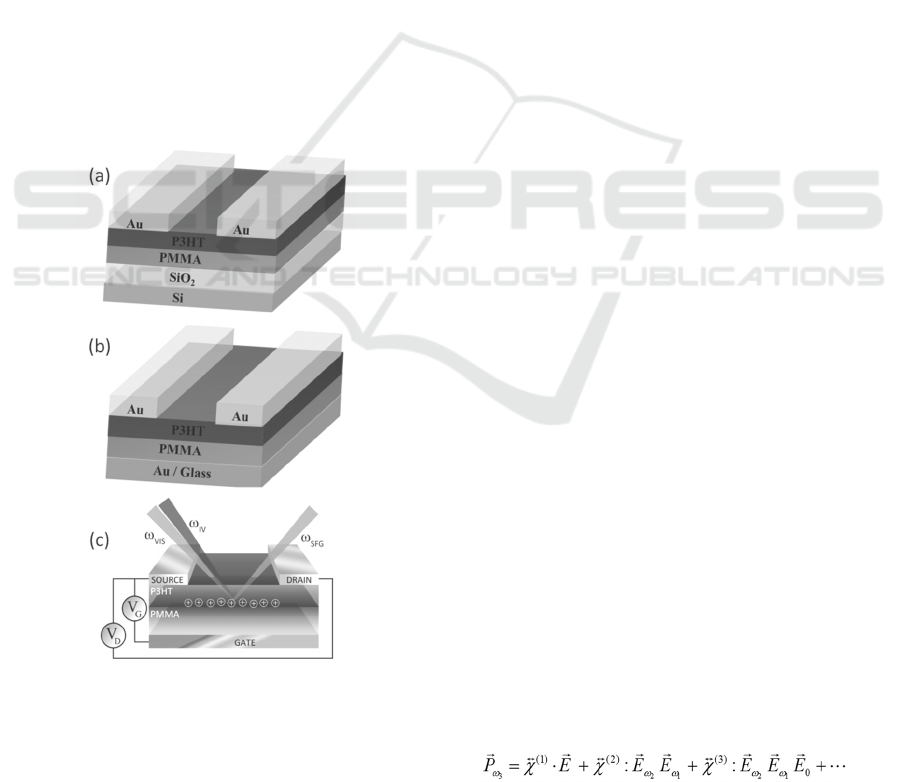
Figure 1: Scheme of the device structures: (a)

Si/SiO

/PMMA/P3HT/Au and (b) Glass/Au/PMMA/P3HT

/Au. (c) Schematic view of the SFG spectroscopy

experiment in the channel of the polarized device.

Two types of substrates were used: for the

measurements of SFG spectra as a function of

applied potential, we used n-doped Si wafers with a

300 nm thermal oxide layer as a gate electrode,

while the temperature dependence was measured on

a device fabricated on glass substrates, with the gate

electrode produced by thermal evaporation of Au.

The top electrodes were also evaporated Au films,

with channel dimmensions L = 100 μm and W = 2

mm. The structure of the devices is shown in Figure

1, together with a scheme of the SFG experiment on

a polarized device.

2.2 SFG Spectroscopy

The second-order nonlinear optical process of sum-

frequency generation (SFG) is forbidden in media

with inversion symmetry, so that it has been widely

used to selectively probe the interfacial region

between two materials, where the inversion

symmetry is usually broken (Shen, 1996). In its

conventional implementation for surface studies,

two high intensity laser pulses (one usually in the

visible and another tunable in the mid-infrared) is

incident at the sample interface, and a sum-

frequency beam is generated in the reflected

direction due to the second-order polarization

generated at the interface (see Equation (1)). The

SFG intensity is proportional to the product of the

input beam intensities and the square of the effective

second-order susceptibility of the interface, 



()

and it is measured with a photomultiplier, after

spectral and spatial filtering. However, if a strong

DC electric field E

is present in the bulk of a

centrosymmetric material, it breaks the inversion

symmetry and leads to a significant increase of the

SFG signal. As shown in Equations (1) and (2), this

increase of 



()

has two contributions (Hayes,

2010): (i) a field-induced orientation of the dipoles

in the material that leads to a non-vanishing



()

(



), and (ii) a third-order contribution that

mixes two laser fields E

, E

and the DC field E

They can be lumped together as an effective third-

order contribution, which is proportional to the

amplitude of the DC field, 



()





. Therefore, if in

the zero-field limit 



()

is negligible, the SFG

intensity is proportional to the square of the DC field

in the material.

(1)

Using Sum-Frequency Generation (SFG) to Probe Electric-Fields within Organic Field-Effect Transistors

195

(2)

Our SFG experiments were performed with a

commercial SFG spectrometer (Ekspla, Lithuania),

which is based on a picosecond high energy

:YAG laser (30 mJ, 20 Hz repetition rate, 1064

nm) and an OPG/OPA/DFG unit pumped by the

third harmonic of the laser (355 nm), to generate

tunable mid-IR beam from 1000 cm

-1

to 4000 cm

-1

with pulse energies at the sample attenuated to ~150

μJ. The visible beam pumping the sample was a

portion (~10 μJ) of the second-harmonic of the laser

(532 nm). The incidence angles were 51° and 60° for

the mid-IR and visible beams, respectively. The SFG

output beam direction was determined by

phasematching along the surface plane, being ~

59.2° for an IR frequency of 1700 cm

-1

. In these

conditions, the coherence length (L

= 1/Δk) for the

SFG process in the reflection direction was ~ 76 nm.

This sets the maximum PMMA film thickness from

which the SFG signal is coherently generated (being

proportional to the square of the film thickness).

However, since both types of OFET samples had

reflective gate electrodes, we may also have

collected simultaneously the SFG signal generated

in the PMMA layer in the transmission direction,

which was then reflected by the gate electrode. For

the transmission geometry, the coherence length is

much longer (~ 65 μm), so that in this case the

whole PMMA film is contributing to the detected

SFG signal.

3 RESULTS AND DISCUSSION

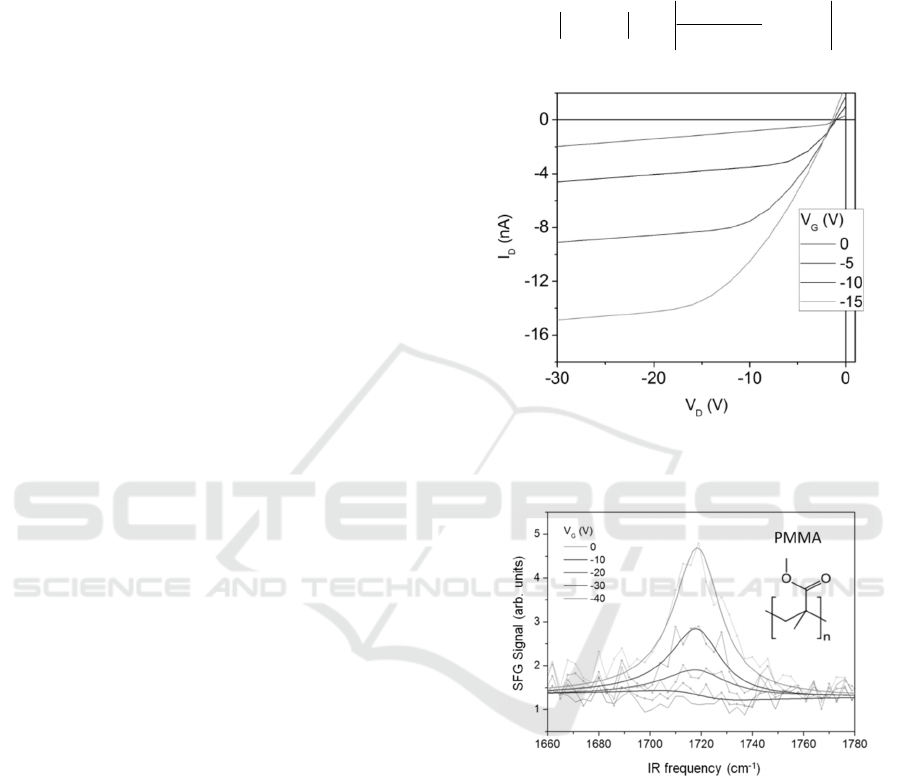
Figure 2 displays the electrical characteristics of the

OFET on the Si substrate (Si/SiO

/PMMA/

P3HT/Au). These output curves show a nice

saturation and typical p-type OFET performance.

However, it can be seen that they do not cross the

origin, indicating that the gate leakage current is

considerable, since the top contact pads had an area

of ~16 mm

, and the whole substrate is conductive.

Figure 3 shows the SFG spectra obtained in the

channel region of the OFET on the Si substrate, for

several gate voltages (keeping V

= 0). It can be

seen that upon polarizing the device, a vibrational

resonance arises at ~1720 cm

-1

, which is assigned to

the C=O stretch of the PMMA monomer (its

chemical structure is shown in the inset of Figure 3).

We have checked this assignment by repeating the

experiment on an OFET without the PMMA layer

(only SiO

as dielectric), when the SFG peak

disappeared. The solid line is a fit to Equation (3),

which represents the superposition of a vibrational

resonance at

with amplitude A and width Γ, plus

a weak nonresonant background, 



()

(3)

Figure 2: Output curves for the OFET with the structure:

Si/SiO

/PMMA/P3HT/Au.

Figure 3: SFG spectra for the OFET on Si substrate, with

several gate voltages, keeping V

= 0. The solid lines are

fits to Equation (3). The inset shows the chemical structure

of the PMMA monomer.

From the fits, we can see that the amplitude A of

the resonance increases nearly proportional to the

applied gate voltage, as expected from Equation (2).

Therefore, the amplitude of this peak can be used to

probe the magnitude of the electric field within the

organic dielectric layer (PMMA). The carriers

accumulated at the semiconductor-dielectric

interface could in principle give rise to an increase

of the nonresonant contribution, 



()

, but this is not

very significant, as can be seen from the fits and

() ()

()

() ()

22 3 3

000eff eff

EEE

χχ χ χ

=+=

()

(2)

()

eff IR

SFG NR

χω

ωω

∝= +

−+Γ

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

196

from the SFG signal far off resonance (Figure 3).

However, due to interference with the weak

nonresonat background, we can see that the peak

lineshape is a bit asymmetric. It is possible to exploit

this interference to get not only the magnitude, but

also the relative sign of the DC field within the

PMMA layer. For that, we need a stronger 



()

comparable to the resonant peak nonlinearity (A/Γ).

With this purpose, we then fabricated the OFETs on

glass substrates with Au films as gate electrodes.

Gold has a high 



()

at the wavelengths used, so that

it provides a reference signal with which the

resonant peak from PMMA interferes. Figure 4

shows the SFG spectra obtained for the device with

the glass substrate (Glass/Au/PMMA/P3HT/Au),

with both positive and negative gate voltages (and

not polarized, as a reference). With V

= 0, we

detect only the nonresonant contribution from the

Au electrode (gate). For negative gate voltages, we

see that the vibrational peak from the C=O stretch of

PMMA interferes destructively with the nonresonant

background from Au, producing a dip in the

spectrum. For positive voltages, the orientation of

the C=O dipoles is inverted, changing the sign of the

peak amplitude A and yielding a constructive

interference with 



()

and giving rise to a

pronounced peak at the molecular resonance.

We could estimate the sensitivity of the method

to detect electric fields in the dielectric layer (at least

for these non-optimized conditions) by considering

that the minimum detectable change in the spectra

shown in Figure 3 occurs for V

~ - 10V. This

corresponds to an E-field of about 2.5⋅10

V/cm.

Figure 4: SFG spectra for the OFET with a Gold gate

electrode (Glass/Au/PMMA/P3HT/Au), without and with

both positive and negative gate voltages, keeping V

= 0.

Finally, we tried to address the origin of the

effective second-order nonlinearity that we have

been measuring in our devices. Is 



()

mostly due to

the field-induced reorientation of the molecular

dipoles (as in a fully reversible electric field poling

of polymers (Bauer, 1996)), or is it a higher order





()





contribution, that does not require any

molecular reorientation in the solid polymer film and

may happen in perfectly isotropic materials? In the

first case, we should expect a strong temperature

dependence of the resonant contribution 



()

, as

shown by Equation (4) (μ is the molecular dipole

moment), provided that the DC field is not strong

enough to reach dielectric saturation. If 

()

dominates, its temperature dependence should be

rather weak, because it would not depend as strongly

as 

()

on the average molecular orientation.

(4)

Figure 5 shows the temperature dependence of

the peak intensity of the spectrum in Figure 4, with

= +60 V. It can be seen that there is a significant

decrease of the SFG intensity while heating the

sample, which is reversible upon cooling, within the

uncertainty of the measurement. The solid line

represents a signal decrease as predicted by Equation

(4). Therefore, these data support the conclusion that

even for our samples, which are solid and should

have a relatively low molecular mobility, the 

()

contribution due to DC field poling of the PMMA

layer is the dominant contribution to the effective

second-order nonlinearity. Any 

()

contribution

appears to be negligible.

Figure 5: SFG signal for the OFET with a Gold gate

electrode, biased with V

= +60 V and V

= 0, upon a

heating and cooling cycle (heating/cooling rate ~ 2

°C/min). The solid line is the temperature dependence

predicted by Equation (4).

()

∝

Using Sum-Frequency Generation (SFG) to Probe Electric-Fields within Organic Field-Effect Transistors

197

4 CONCLUSIONS

Direct measurements of the electric-field distribution

in an operating organic transistor are useful for

proposing and validating theoretical models for their

electrical behavior. Here we showed that Sum-

Frequency Generation vibrational spectroscopy

(SFG spectroscopy) is a valuable tool to probe the

electric field within the (organic) dielectric layer of

the transistor. The SFG spectra from polar groups of

the dielectric (PMMA) show a marked resonance,

whose amplitude is proportional to the applied gate

voltage, which in turn is proportional to the field

within the dielectric, when V

= 0. Using the

interference of this resonant contribution with a

large nonresonant background from the gate

electrode, it is possible to determine not only the

relative magnitude of the field within the dielectric,

but also its sign. We further demonstrated that even

for solid samples, where the dipoles are less mobile

than in the case of organic molecules in solution, the



()

contribution due to DC field reorientation of the

dielectric layer is the dominant contribution to the

effective second-order nonlinearity, and any 

()

contribution appears to be negligible. This

phenomenon allows probing the electric field in the

dielectric, which is directly related to the charge

distribution in the OFET channel, and opens up the

possibility of mapping the spatial field distribution

in the conducting channel by SFG microscopy of

OFETs (Nakai et al., 2009).

ACKNOWLEDGEMENTS

DJCG gratefully acknowledges a PhD scholarship

from FAPESP and SGM thanks CAPES for a MSc

scholarship. This work has been supported by the

Brazilian agencies FAPESP and CNPq.

REFERENCES

Babajanyan, A., Melikyan, H., Kim, J., Lee, K., Iwamoto,

M., Friedman, B., 2011. Direct imaging of

conductivity in pentacene field-effect transistors by a

near-field scanning microwave microprobe. Org.

Electron. 12, 263–268.

Bauer, S., 1996. Poled polymers for sensors and photonic

applications. J. Appl. Phys. 80, 5531–5558.

Furukawa, Y., Seto, K., Nakajima, K., Itoh, Y., Eguchi, J.,

Sugiyama, T., Fujimura, H., 2012. Infrared and Raman

spectroscopy of organic thin films used for electronic

devices. Vibr. Spectrosc. 60, 5–9.

Hallam, T., Lee, M., Zhao, N., Nandhakumar, I.,

Kemerink, M., Heeney, M., McCulloch, I.,

Sirringhaus,H., 2009. Local charge trapping in

conjugated polymers resolved by scanning Kelvin

probe microscopy. Phys. Rev. Lett. 103, 256803.

Hayes, P. L., Malin, J. N., Jordan, D. S., Geiger F. M.,

2010. Get charged up: Nonlinear optical voltammetry

for quantifying the thermodynamics and electrostatics

of metal cations at aqueous/oxide interfaces. Chem.

Phys. Lett. 499, 183–192.

Manaka, T., Nakao, M., Yamada, D., Lim E., Iwamoto M.,

2007 a. Optical second harmonic generation imaging

for visualizing in-plane electric field distribution.

Optics Express 15, 15964-15971.

Manaka, T., Lim E., Tamura, R., Iwamoto M., 2007 b.

Direct imaging of carrier motion in organic transistors

by optical second harmonic generation. Nat. Photonics

1, 581-584.

Nakai, I. F. et al., 2009. Molecular structure and carrier

distributions at semiconductor/dielectric interfaces in

organic field-effect transistors studied with sum-

frequency generation microscopy. Appl. Phys. Lett. 95,

243304.

Sciascia, C. et al., 2011. Sub-micrometer charge

modulation microscopy of a high mobility polymeric

n-channel field-effect transistor. Adv. Mater. 23,

5086–5090.

Shen, Y. R., 1996. A few selected applications of surface

nonlinear optical spectroscopy. Proc. Natl. Acad. Sci.

USA 93, 12104.

Stallinga, P., Gomes, H., 2006. Modeling electrical

characteristics of thin-ﬁlm ﬁeld-effect transistors I:

trap-free materials. Synth. Met. 156, 1305–1315.

Sze, S. M., Kwok, K. Ng., 2007. Physics of Semiconductor

Devices, Wiley, New Jersey.

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

198