Numerical Experiments with a Primal-Dual Algorithm for Solving

Quadratic Problems

Derkaoui Orkia and Lehireche Ahmed

University Djillali Liabes of Sidi Bel Abbes, Computer Science Department, BP 89 City Sidi Bel Abbes 22000, Algeria

Keywords: Interior-point Methods, SemiDefinite Programming, Linear Research, Primal-Dual Interior-Point Method,

Predictor-corrector Procedure, HRVM/KSH/M Search Direction.

Abstract: This paper provides a new variant of primal-dual interior-point method for solving a SemiDefinite Program

(SDP). We use the PDIPA (primal-dual interior-point algorithm) solver entitled SDPA (SemiDefinite

Programming Algorithm). This last uses a classical Newton descent method to compute the predictor-

corrector search direction. The difficulty is in the computation of this line-search, it induces high

computational costs. Here, instead we adopt a new procedure to implement another way to determine the

step-size along the direction which is more efficient than classical line searches. This procedure consists in

the computation of the step size in order to give a significant decrease along the descent line direction with a

minimum cost. With this procedure we obtain à new variant of SDPA. The comparison of the results

obtained with the classic SDPA and our new variant is promising.

1 INTRODUCTION

We consider the standard primal form of

semidefinite program (1), and its dual (2) in block

diagonal form:



∗

:





.. 















, ≻0

(1)



∗

:



•

..



•







1,2,…,



,≻0,

(2)

Where 



, belong to the space 



of 



real symmetric matrices, c



,…,







∈



the cost vector and x



,…,







∈



 is the

variables vector. The operator • denotes the standard

inner product in 



, i.e., 



•













∑

















, and ≻0 means that  is positive

semidefinite (∈





, see for example Figure 1.1.

The values 

∗

and 

∗

are the optimal value of the

primal objective function and the optimal value of

the dual objective function respectively.

Semidefinite Program is an extension of LP

(Linear Program) in the Euclidean space to the space

of symmetric matrices. These problems are linear.

Their feasible sets involving the cone of positive

semidefinite matrices, a non polyhedral convex cone

and they are called linear semidefinite programs.

Such problems are the object of a particular attention

since the papers by Alizadeh (Alizadeh, 1995) and

(Alizadeh at al., 1994), as well on a theoretical or an

algorithmical aspect, see for instance the following

references (Alizadeh and Haberly, 1998; Benterki et

al., 2003; Jarre, 1993; and Nesterov and

Nemirovskii, 1990.

Figure 1.1: Boundary of the set of semidefinite matrices

in



SDP is not only an extension of LP but also

includes convex quadratic optimization problems

and some other convex optimization problems. It has

a lot of applications in various fields such as

combinatorial optimization (Goemans and

Williamson, 1995), control theory (Boyd et al.,

1994), robust optimization (Ben-Tal and

Nemirovskii, 2001) and (Wolkowicz et al., 2000)

and quantum chemistry (Nakata at al., 2001) and

204

Orkia, D. and Ahmed, L.

Numerical Experiments with a Primal-Dual Algorithm for Solving Quadratic Problems.

DOI: 10.5220/0005813802040209

In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 204-209

ISBN: 978-989-758-171-7

(Nakata et al., 2002). See (Todd, 2001),

(Vandenberghe and Boyd, 1994), (Vandenberghe

and Boyd, 1995) and (Wolkowicz et al., 2000) for a

survey on SDPs and the papers in their references.

The duality theory for semidefinite programming

is similar to its linear programming counterpart, but

more subtle (see for example (Alizadeh, 1995),

(Alizadeh et al., 1994), (Alizadeh and Haberly,

1998)). The programs 





and 





satisfy the weak

duality condition: 

∗



∗

, at the optimum, the

primal objective



is equal to the dual

objective



•.

Our objective is to solve the SDP in optimal time

following our work (Derkaoui and Lehireche, 2014).

The SDP problem is solved with interior point

methods. These last use a classical Newton descent

method to compute the search direction. The

difficulty is in the line-search, it induces high

computational costs in classical exact or

approximate line-searches. Here, instead we use the

procedure of (Crouzeix and Merikhi, 2008). This last

proposes another ways to determine the step-size

along the direction which are more efficient than

classical line searches.

This paper is organized as follows. In Section 2,

we present some useful notions and results about

semidefinite programming. In Section 3, an

overview of the interior point methods used for the

resolution of SDP is considered. In Section 4, the

primal-dual and the step size procedure algorithms,

bases of the new variant, are described. In Section 5,

the computational experience is described. A brief

description of the used tools is given and the

obtained results with the new versions and the

classical method are compared.

2 BACKGROUND FOR

SEMIDEFINITE

PROGRAMMING

Semidefinite Programming is currently the most

sophisticated area of Conic Programming that is

polynomially solvable. More precisely, SDP is the

optimization over the cone of positive semidefinite

matrices of a linear objective function subject to

linear equality constraints. It can also be viewed as a

generalization of Linear Programming where the

nonnegativity constraints on vector variables are

replaced by positive semidefinite constraints on

symmetric matrix variables.

The past few decades have witnessed an

enormous interest for SDP due to the identification

of many theoretical and practical applications, e.g.,

combinatorial optimization (graph theory), spectral

optimization, polynomial optimization, engineering

(systems and control), probability and statistics,

financial mathematics, etc... In parallel, the

development of efficient SDP solvers, based on

interior point algorithms, also contributed to the

success of this method.

Although many solvers have been developed in

the last twenty years to handle semidefinite

programming, this area, unlike LP, is still in its

infancy, and most codes are offered by researcher to

the community for free use and can handle moderate

sized problems. The Table 2.1 identifies the different

software and their associated programming

language. Another simple possibility for comparing

several solvers is to use the standard file format

SDPA (Fujisawa and Kojima, 1995), where several

LMI (Linear Matrix Inequality) constraints are

possible. This format is accepted by most of the SDP

solvers.

Table 2.1: The different SDP solvers.

Software Algorithm Interface

CSDP

IPM (Primal-Dual path)

DSDP

Potential reduction

C, Matlab

SeDuMi Self-dual method Matlab

SB Bundle method C/C++

SDPA

IPM (Primal-Dual path)

C++

SDPLR

Augmented Lagrangian

C, Matlab

For more details about these solvers see

respectively (Borchers. 1999), (Benson et al., 2000),

(Sturm, 1998), (Helmberg and Rendl, 2000),

(Yamashita et al., 2010) and (Burer and Monteiro,

2003).

The PDIPA (primal-dual interior-point

algorithm) (Jarre, 1993), (Nesterov and Todd, 1995),

(Helmberg et al., 1996) and (Monteiro, 1997) is

known as the most powerful and practical numerical

method for solving general SDPs. The method is an

extension of the PDIPA (Wolkowicz et al., 2000)

and (Tanabe, 1988) developed for LPs. The SDPA

presented in this paper is a PDIPA software package

for general SDPs based on the paper (Fujisawa et al.,

1997) and (Jarre, 1993).

3 RESOLUTION OF SDP

Interior-points methods (IPM) for SDP have

sprouted from the seminal work of Nesteror &

Nemirovksi (Nesterov and Nemirovskii, 1994) and

Numerical Experiments with a Primal-Dual Algorithm for Solving Quadratic Problems

205

(Nesterov and Nemirovskii, 1993). Indeed, in 1988,

a major breakthrough was achieved by them

(Alizadeh, 1995), (Alizadeh et al., 1994) and

(Alizadeh and Haberly, 1998).

They stated the theoretical basis for an extension

of interior-methods to conic programming and

proposed three extensions of IPM to SDP : the

Karmarkar’s algorithm, a projective method and

Ye’s potential reduction method. In parallel, in

1991, Alizadeh (Alizadeh, 1995) also proposed a

potential reduction projective method for SDP. Then

in 1994, Boyd and Vandenberghe presented an

extension of Gonzaga & Todd algorithm for LP that

uses approximated search direction and able to

exploit the structure of the matrix. These methods

conserve the polynomiality under relevant

conditions. For this reason, these methods are crucial

for convex optimization. To explain the basic idea of

interior point method we need two ingredients:

Newton’s method for equality constrained

minimization and barrier functions.

Interior-point methods can be classified into

three major categories depending on the type of

algorithm:

 Affine-scaling algorithms ;

 Projective methods with a potential function ;

 Path-following algorithms.

However, in extending primal-dual interior-point

methods from LP to SDP, certain choices have to be

made and the resulting search direction depends on

these

choices. As a result, there can be

several search directions for SDP corresponding to

a single search direction for LP. We can cite the

following four search directions:

 HRVW/KSH/M direction (proposed by

Helmberg, Rendl, Vanderbei and Wolkowicz

(Helmberg et al., 1996)),

 MT direction (proposed by Monteiro and

Tsuchiya (Monteiro and Tsuchiya, 1996)),

 AHO direction (proposed by Alizadeh,

Haeberly, and Overton (Alizadeh et al.,

1994)),

 NT direction (proposed by Nesterov and

Todd (Nesterov and Todd, 1995)). 

The convergence property of the interior-point

methods algorithm varies depending on the choice of

direction.

To compute the search direction, the SDPA

employs Mehrotra type predictor-corrector

procedure (Mehrotra, 1992) with use of the

HRVW/KSH/M search direction (Helmberg et al.,

1996), (Vandenberghe and Boyd, 1994) and (Kojima

et al., 1989).

With this work, we intend to obtain a predictor-

corrector primal-dual interior point algorithm with

better performance and more precise than the other

algorithms of the same type already known.

We present a new variant of the algorithm used

in the SDPA solver with the procedure proposed in

(Crouzeix and Merikhi, 2008) in order to determine

the step-size along the direction which is more

efficient than classical line searches.

4 PRIMAL-DUAL PATH

FOLLOWING ALGORITHM

FOR SDPA WITH

PREDICTOR -CORRECTOR

TECHNIQUE

In this paragraph, we report the algorithm proposed

in (Helmberg et al., 1996) and implemented in the

solver SDPA (Fujisawa and Kojima, 1995). This

primal-dual path following method uses the

predictor-corrector technique of Mehrotra and has

the advantage of not requiring any specific structure

of the problem matrices.

Roughly speaking, the SDPA starts from a given

initial point ,, satisfying ≻0, ≻0and

numerically traces the central path 









,







,







:0 that forms a smooth

curve converging to an optimal solution ,,

which corresponds to an optimal solution of (1) and

(2), as →0. Letting , it chooses a target point









,







,







on the central path to move from

the current point . Then the SDPA compute a search

direction to approximate the point, and updates the

current point ,,.Then the SDPA computes a

search direction,, to approximate the

point



,,



←



dx,



dX, 





dY, where 



and 



are primal and dual step

lengths to keep 



dX and 



dY positive

definite. The SDPA repeats this procedure until it

Figure 4.1: The graphical representation of the interior

points algorithm.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

206

attains an approximate solution





∗

,

∗

,

∗



problems (1) and (2), see Figure 4.1.

In our work, we propose a new variant of SDPA

with another computation of the step sizes. We use

the procedure in (Crouzeix and Merikhi, 2008) that

gives an alternative ways to determine the step-size

along the direction which are more efficient than

classical line searches.

4.1 The Step-Size Procedure

In (Crouzeix and Merikhi, 2008), the problem (1) is

approximated by a barrier problem. This problem is

solved via a classical Newton descent method. The

difficulty is in the line-search: the presence of a

determinant in the definition of the barrier problem

induces high computational costs in classical exact

or approximate line-searches. Here, instead of

minimizing the barrier problem along the descent

direction at the current point , we minimize a

function  with its upper-approximaty

functions. This last reduce the computational cost of

the algorithm compared with classical methods. This

function needs to be appropriately chosen so that the

optimal step length is easily obtained and to be close

enough to in order to give a significant decrease of

the barrier problem in the iteration step. In

(Crouzeix and Merikhi, 2008), they propose

functions θ for which the step-size optimal solution

is explicitly obtained. For more details about this

procedure see (Chouzenoux et al., 2009), (Crouzeix

and Merikhi, 2008), (Benterki and Merikhi, 2001)

and (Benterki at al., 2003). In this paper we apply

this procedure to compute the step length in the

Primal-Dual Interior-Point Algorithm of SDPA.

4.2 Description of the Algorithm

SDPA has the highest version number 6.0 among all

generic SDP codes, due to its longest history which

goes back to December of 1995. We use the version

6.0 of SDPA.

The Primal-Dual Interior-Point Algorithm

(PDIPM) of SDPA

Step 0 (Initialization): Choose an initial point





,



,



satisfying 



≻0

and





≻0

Let k = 0.

Step 1 (Checking Feasibility): If 



,



,



is an

-approximate optimal solution of the (1) and (2),

stop the iteration.

Step 2 (Computing a search direction): As

described in (Mehrotra, 1992), apply Mehrotra type

predictor-corrector procedure to generate a search

direction,,.

Step 3 (Generating a new iterate): We use the

procedure (Crouzeix and Merikhi, 2008) to compute





and 



as primal and dual step lengths so that













 and 













remain positive semidefinite.

We set the next iterate 



,



,













, 







,







.

Let ←1. Go to Step 1.

5 COMPUTATIONAL

EXPERIENCE

Now, we will describe the computational experience

that we have done to compare the new version of

our predictor-corrector variant and the classical

predictor-corrector method, described in the

previous sections.

5.1 Brief Description of the Used Tools

The computational tests were performed in Intel(R)

Core™ i5 2.50 GHz with 4Go memory under Linux

11. To implement the new predictor-corrector

variant we used the 6.0 version of the source code of

the package SDPA by Makoto Yamashita, Katsuki

Fujisawa and Masakazu Kojima (Fujisawa and

Kojima, 1995). The code was modified to achieve

two main purposes: it was adapted to be possible to

implement the different version of the predictor-

corrector variant and it was optimized to become

faster and more robust.

To compare the performance of the algorithms,

we generated automatically particular quadratic

programs. These results are preliminaries.

5.2 Results

We present the results corresponding to the new

predictor-corrector variant described earlier and

compare those results with the ones obtained with

the classical predictor-corrector algorithm. To test

our procedure, we generated particular quadratic

programs automatically for which we know the

primal objective value. We thus allow to validate our

procedure in experiments with comparison. We

solved the semidefinite relaxation of the problem

considered with the two variants of SDPA and then

we compare the results.

The motivation to consider this example is to

show the effectiveness and the realizability of our

procedure and to generate big instances.

We use the graphic with information about some

instances of the problem and the CPU time (in

Numerical Experiments with a Primal-Dual Algorithm for Solving Quadratic Problems

207

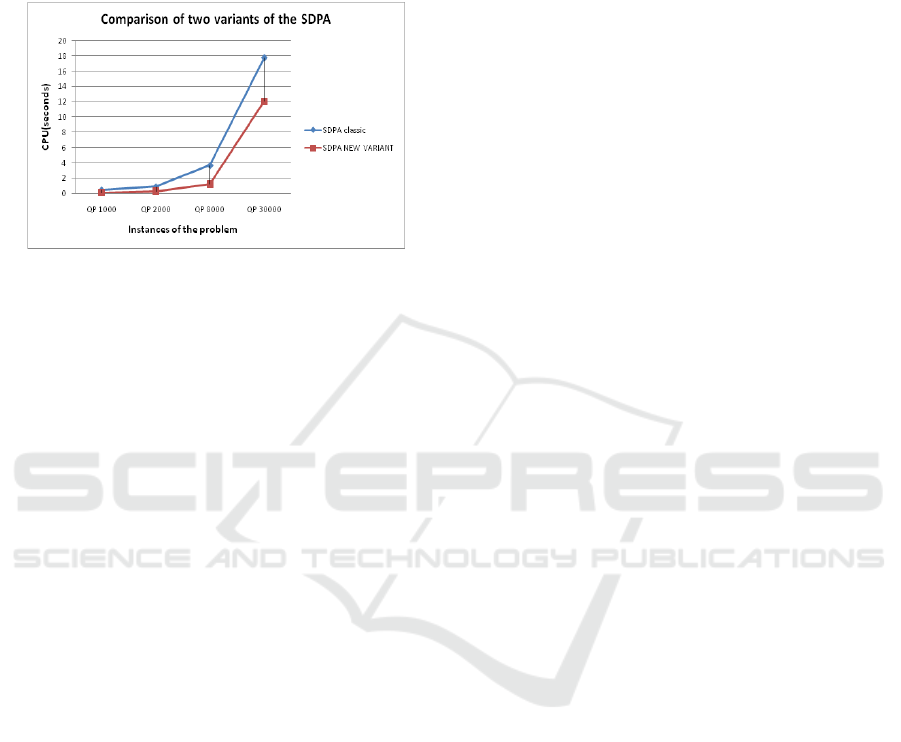
seconds), see Figure 5.1.

We consider the quadratic program:



 







..





2,



1..



(3)

Figure 5.1: Comparison of the CPU with SDPA classic

and SDPA new variant.

6 CONCLUSION AND FUTURE

WORKS

In this paper, we have applied a new procedure to

solve the SDP in optimal time. The logarithmic

barrier approach with the technique of upper-

approximaty functions reduce the computational cost

of the algorithm compared with classical methods.

The preliminaries numerical results show the

performance of this procedure. This work opens

perspectives for exploring the potentiality of

semidefinite programming to provide tight

relaxations of NP-hard, combinatorial and quadratic

problems. Our future work is to program another

line-searches and another barrier functions. We will

test the performance of the algorithms with the

SDPLIB collection of SDP test problems (Borchers,

1999) .

REFERENCES

Alizadeh, F., 1995. Interior point methods in semidefinite

programming with application to combinatorial

optimization, SIAM journal on Optimization, 5:13–51.

Alizadeh, F., Haberly, J.-P., and Overton, M.-L.. 1998.

Primal-dual interior-point methods for semidefinite

programming, convergence rates, stability and

numerical. SIAM J. Optim.8 746–768.

Benterki, D., Crouzeix, J.-P., and Merikhi., B., 2003. A

numerical implementation of an interior point method

for semi-definite programming. Pesquisa Operacional

23–1, 49–59.

Fujisawa, K. and Kojima, M., 1995. SDPA(Semidefinite

Programming Algorithm) Users Manual. Technical

Report b-308, Tokyo Institute of Technology.

Jarre. F., 1993. An interior-point method for Programming

minimizing the maximum eigenvalue of a linear

combination of matrices. SIAM Journal on Control

and Optimization, 31:1360–1377.

Nesterov Y. E., and Nemirovskii. A. S., 1990.

Optimization over positive semidefinite matrices:

Mathematical background and user’s manual.

Technical report, Central Economic & Mathematical

Institute, USSR Acad. Sci. Moscow, USSR.

Nesterov Y. E., and Nemirovskii. A. S., 1993. Interior

Point Polynomial Methods in Convex Programming :

Theory and Algorithms. SIAM Publications,

Philadelphia.

Vandenberghe, L. and Boyd. S., 1995. Primal-dual

potential reduction method for problems involving

matrix inequalities. Mathematical Programming,

69:205-236.

Nesterov, Y.E., and Nemirovskii, A.S., 1994. Interior-

Point Polynomial Algorithms in Convex

Programming. SIAM Studies in Applied Mathematics

13. SIAM, Philadelphia, PA, USA. 185, 461, 564, 584,

602.

Nesterov, Y. E., and Todd, M. J., 1995. Primal-dual

interior-point methods for self-scaled cones. Technical

Report 1125, School of Operations Research and

Industrial Engineering, Cornell University, Ithaca,

New York, 14853-3801.

Crouzeix, J.P. Merikhi, B., 2008, A logarithm barrier

method for semidefinite programming, R.A.I.R.O-

Oper. Res. 42, pp. 123-139.

Benterki, D., Merikhi, B., 2001. A modified algorithm for

the strict feasibility problem, RAIRO Oper. Res. 35,

pp. 395-399.

Monteiro, R.D.C., 1997. Primal-dual path- following

algorithms for semidefinite programming. SIAM

Journal on Optimization, 7, pp. 663-678.

Derkaoui, O., Lehireche, A, 2014. Safe bounds in

Semidefinite programming by using interval

arithmetic. American Journal of Operations Research,

Vol. 4 No. 5, septembre, PP. 293-300. DOI:

10.4236/ajor.2014.45029.

Helmberg, C., Rendl, F., Vanderbei, R.J., and

Wolkowicz, H., 1996. An interior point method for

semidefinite programming. SIAM Journal on

Optimization, 6:342–361.

Monteiro, R. D. C., and Tsuchiya, T., 1996. Polynomial

convergence of a new family of primal-dual

algorithms for semidefinite programming.Technical

report, Georgia Institute of Technology,Atlanta,

Georgia, USA.

Mehrotra, S., 1992. On the implementation of a primal-

dual interior point method, SIAM Journal on

Optimization 2 575-601.

Monteiro, R. D. C., 1997. Primal-dual path following

algorithms for semidefinite programming, SIAM

Journal on Optimization 7 663-678.

Nakata, M., Nakatsuji, H., Ehara, M., Fukuda, M.,

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

208

Nakata, K. and Fujisawa, K., 2001. Variational

calculations of fermion second-order deduced density

matrices by semidefinite programming algorithm,

Journal of Chemical Physics 114 8282-8292.

Nakata, M., Ehara, M., and Nakatsuji, H., 2002. Density

matrix variational theory: Application to the potential

energy surfaces and strongly correlated systems,

Journal of Chemical Physics 116 5432-5439.

Ben-Tal, A., and Nemirovskii, A., 2001. Lectures on

Moden Convex Optimizatin Analysis, Algorithms, and

Engineering Applications, (SIAM, Philadelphia).

Boyd, S., Ghaoui, L. E., Feron, E., and Balakrishnan, V.,

1994. Linear matrix inequalities in system and control

theory, Society for Industrial and Applied

Mathematics Philadelphia, PA, ISBN 0-89871-334-X.

Goemans, M. X., and Williamson, D. P., 1995. Improved

approximation alogrithoms for maxmum cut and

satisfiability problems using semidefinite

programming, Journal of Association for Computing

Machinery 42(6) 1115-1145.

Todd, M. J., 2001. Semidefinite optimization, Acta

Numerica 10 515-560.

Vandenberghe, L., Boyd, S., 1994. Positive-Definite

Programming, Mathematical Programming: State of

the Art J. R. Birge and K. G. Murty ed.s, U. of

Michigan.

Wolkowicz, H., Saigal, R., and Vandenberghe, L., 2000.

Handbook of Semidefinite Programming, Theory,

Algorithms, and Applications, (Kluwer Academic

Publishers, Massachusetts.

Kojima, M., Mizuno, S. and Yoshise, A., 1989. A Primal-

Dual Interior Point Algorithm for Linear

Programming, in: N. Megiddo, ed., Progress in

Mathematical Programming: Interior Point and

Related Methods (Springer-Verlag, New York) 29-47.

Tanabe, K., 1988. Centered Newton Method for

Mathematical Programming, in: M. Iri and K. Yajima,

eds., System Modeling and Optimization (Springer,

New York) 197-206.

Borchers. B., 1999. CSDP, a C library for semidefinite

programming. Optimization Methods and Software,

11.

Benson, S. J., Ye, Y., and Zhang, X., 2000. Solving

large-scale sparse semidefinite programs for

combinatorial optimization. SIAM Journal on

Optimization, 10(2):443–461.

Sturm, J. F., 1998. Using SeDuMi 1.02, a MATLAB

toolbox for optimization over symmetric cones.

Yamashita, M., Fujisawa, K., Nakata, K., Nakata, M.,

Fukuda, M., Kobayashi, K., and Goto, K.., 2010. A

high-performance software package for semidefinite

programs: SDPA 7. Technical report, Dept. of

Mathematical and Computing Science, Tokyo Institute

of Technology.

Burer, S., and Monteiro, R. D. C., 2003. A nonlinear

programming algorithm for solving semidefinite

programs via low-rank factorization. Math. Program.,

95(2):329–357.

Helmberg, C., and Rendl. F., 2000. A spectral bundle

method for semidefinite programming. SIAM Journal

on Optimization, 10:673–696.

Borchers, B., 1999. SDPLIB 1.2, a library of semidefinte

programming test problems, Optimization Methods

and Software 11 & 12 683-690.

Chouzenoux, E., Moussaoui, S., Idier, J., 2009. A

Majorize-Minimize line search algorithm for barrier

function optimization. EURASIP European Signal and

Image Processing Conference, Aug, Glasgow, United

Kingdom. pp.1379-1383, 2009. <hal-00456013>.

Numerical Experiments with a Primal-Dual Algorithm for Solving Quadratic Problems

209