Energy Minimization during Transcutaneous Electrical Stimulation by
Charge Efficient Stimulation Pulses
Benefits of using Short Duration and High Amplitude Stimulation Pulses
Jan C. Loitz, Aljoscha Reinert, Nils Remer, Dietmar Schroeder and Wolfgang H. Krautschneider
Institute of Nano- and Medical Electronics, Hamburg University of Technology, Eißendorfer Str. 38, Hamburg, Germany
Keywords:
Transcutaneous Electrical Stimulation, Stimulation Device, Energy, Charge, Minimization Problem, Simula-
tion, Pulse Shape.
Abstract:
In transcutaneous electrical stimulation motor axons are activated by externally applied electrical pulses. More
efficient stimulation pulses could lead to less stress for the patient and to prolonged battery lifetime of the stim-
ulation device. In this study a minimization problem was solved to find charge efficient stimulation pulses,
which could potentially reduce the necessary energy provided by the stimulator. The findings of the minimiza-
tion problem as well as simulations with an active axon model lead to the conclusion that short duration, high
amplitude pulses are favorable and that the choice of the correct stimulation amplitude and pulse duration is
more important than using the most efficient pulse shape.
1 INTRODUCTION
Transcutaneous electrical stimulation (TES) of mus-
cles and motor neurons as a rehabilitation technique
can be used to treat patients suffering from stroke
or spinal cord injury (Knutson et al., 2007; Man-
gold et al., 2005). Stimulation parameters that can
be controlled by the physician or patient are stimula-
tion amplitude (mA), pulse duration (µs) and stimu-
lation frequency (Hz) (Hunter Peckham, 1999; Gre-
gory et al., 2007). In most cases biphasic rectangular
pulses with a short interphase are used. The question
whether pulses different to rectangular ones could
lead to better stimulation outcomes has been dis-
cussed several times (Jezernik and Morari, 2005; Jez-
ernik et al., 2010; Wongsarnpigoon and Grill, 2010;
Meza-Cuevas et al., 2012; Krouchev et al., 2014). Es-
pecially the question whether energy could be saved
by using more efficient pulse shapes has been of great
interest.
It is necessary to differentiate between the energy
applied to the patient, which depends on the voltage
drop over the attached electrodes, or the total energy
the stimulation device consumes. Most stimulation
devices are supplied from with a constant high voltage
source and therefore the energy consumed depends
solely on pulse current amplitude and duration. The
product of both these parameters is equivalent to the
electric charge of the stimulation pulse.
In previous studies different pulse shapes were of-
ten compared for fixed pulse durations here we would
like to use a different approach and regard the pulse
duration as a part of the pulse shape. Consequently
the pulses will be compared for fixed stimulation am-
plitudes.
The goal of this study is to elaborate possible ad-
vantages by using pulse shapes other than rectangular
ones in regards of delivered electrical charge and to
give some advice on performing efficient stimulations
which can benefit the patient as well as the battery
lifetime of the used device.
2 METHODS
2.1 3D Finite Element Simulation
A 3D finite element model described in (Loitz et al.,
2015) was used to calculate the response of a mo-
tor neuron to TES (figure 1). The forearm model
consisted of several layers including skin, fat, mus-
cle bone and electrodes. All of these had a specific
conductivity and permittivity associated to them. To
reduce computation time and to perform an optimiza-
tion the response to a 1 mA, 1 µs stimulation pulse
I
pulse
along a line was simulated. The electric poten-
tial along this line was used as the external electric po-
Loitz, J., Reinert, A., Remer, N., Schroeder, D. and Krautschneider, W.
Energy Minimization during Transcutaneous Electrical Stimulation by Charge Efficient Stimulation Pulses - Benefits of using Short Duration and High Amplitude Stimulation Pulses.
DOI: 10.5220/0005814202510255
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 1: BIODEVICES, pages 251-255
ISBN: 978-989-758-170-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
251

tential around a motor axon lying parallel to the skin
surface at a specific depth of 8 mm.
Figure 1: Simple 3D model of the human forearm after
I
pulse
. The red lines represent the current flow between the
two multicolored electrodes.
2.2 Minimization Problem
The first step was to investigate what kind of wave-
form was suited best to increase the membrane poten-
tial, using a passive axon model. Therefore the ex-
ternal potential V
e
caused by I
pulse
was used to calcu-
late the membrane potential V
m
according to (McNeal,
1976):
dV
m,n
dt
=
1
C
m
[G
a
(V
m,n−1
− 2V
m,n
+V
m,n+1
+V
e,n−1
−2V
e,n
+V
e,n+1
) − G
m
V
m,n
]
(1)
Thereby C
m
represents the membrane capacitance,
G
a
the conductance along the axon and G
m
the mem-
brane conductance.
The membrane potential V
m,n
constitutes the unit
impulse response of the arm and axon system. V
m
at
a single node of Ranvier n was then used as the basis
for the minimization problem. The goal of the mini-
mization problem was to find the pulse shape which
needs the least amount of charge to exceed a thresh-
old potential. The final membrane potential elicited
by an arbitrary stimulation pulse was computed as a
discrete convolution of a vector ~x
stim
and a matrix K
containing the response of V
m
as follows:
~
V
m,stim
= K ~x
stim
(2)
with K =




V
m
(t
0
) 0 .. . 0
V
m
(t
1
) V
m
(0) .. . 0
.
.
.
.
.
.
.
.
.
.
.
.
V
m
(t
end
) V
m
(t
end−1
) .. . V
m
(t
0
)




The vector ~x
stim
defines the stimulation pulse
shape as its amplitude in mA in 1 µs steps.
During the optimization of the stimulation pulse,
some boundary conditions were set: The pulse was
not allowed to be longer than 500 µs, the pulse was
not allowed to exceed a preset maximum amplitude
(a
max
), the minimum amplitude of the pulse had to be
larger than zero and the evoked change in membrane
potential had to be smaller or equal to the threshold
potential until t = t
end
= 500 µs was reached. For the
optimization a starting solution ~x
start
with a duration
of 500 µs and an amplitude of a
start
was defined that
satisfied the boundary conditions. The difference be-
tween the electrical charge of the starting solution and
the optimized pulse was used as the optimization ob-
jective. This task constitutes a linear programming
problem, and therefore the Matlab function ’linprog’
(equation 3) was used to find the solution.
min
~x
~
f
T
~x such that
(
A ~x ≤
~
b,
lb(t) ≤ x(t) ≤ ub(t).
(3)
with~x =~x
start
−~x
stim
, lb(t) = x
start
(t)− a
max
, ub(t) =
x
start
(t),
~
f = [−1,−1, ...,−1]
T
,
~
b = [0,0, ...,0]
T
and
A =




−V
m
(t
0
) 0 .. . 0
−V
m
(t
1
) −V
m
(0) .. . 0
.
.
.
.
.
.
.
.
.
.
.
.
+V
m
(t
end
) +V
m
(t
end−1
) .. . +V
m
(t
0
)




2.3 Active Axon Model Simulation
To check whether an active model containing ion
channels supports the results of the minimization
problem the charge necessary to elicit a propagating
action potential by a rectangular pulse with fixed max-
imal amplitudes was compared to a linear increas-
ing and a sinusoidal pulse (figure 2). Previous stud-
ies have claimed that linear increasing and/or sinu-
soidal pulses are more energy efficient compared to
rectangular ones (Wongsarnpigoon and Grill, 2010;
Meza-Cuevas et al., 2012). The active model used the
same equivalent circuit as described in equation 1 but
with ionic currents described by (Hodgkin and Hux-
ley, 1952) like equations from (McIntyre et al., 2002).
Divergent from other studies, in this study com-
parisons of energy efficiency were performed for
fixed pulse amplitudes with the pulse duration al-
lowed to vary, since the pulse duration was regarded
as a part of the pulse shape.
BIODEVICES 2016 - 9th International Conference on Biomedical Electronics and Devices
252

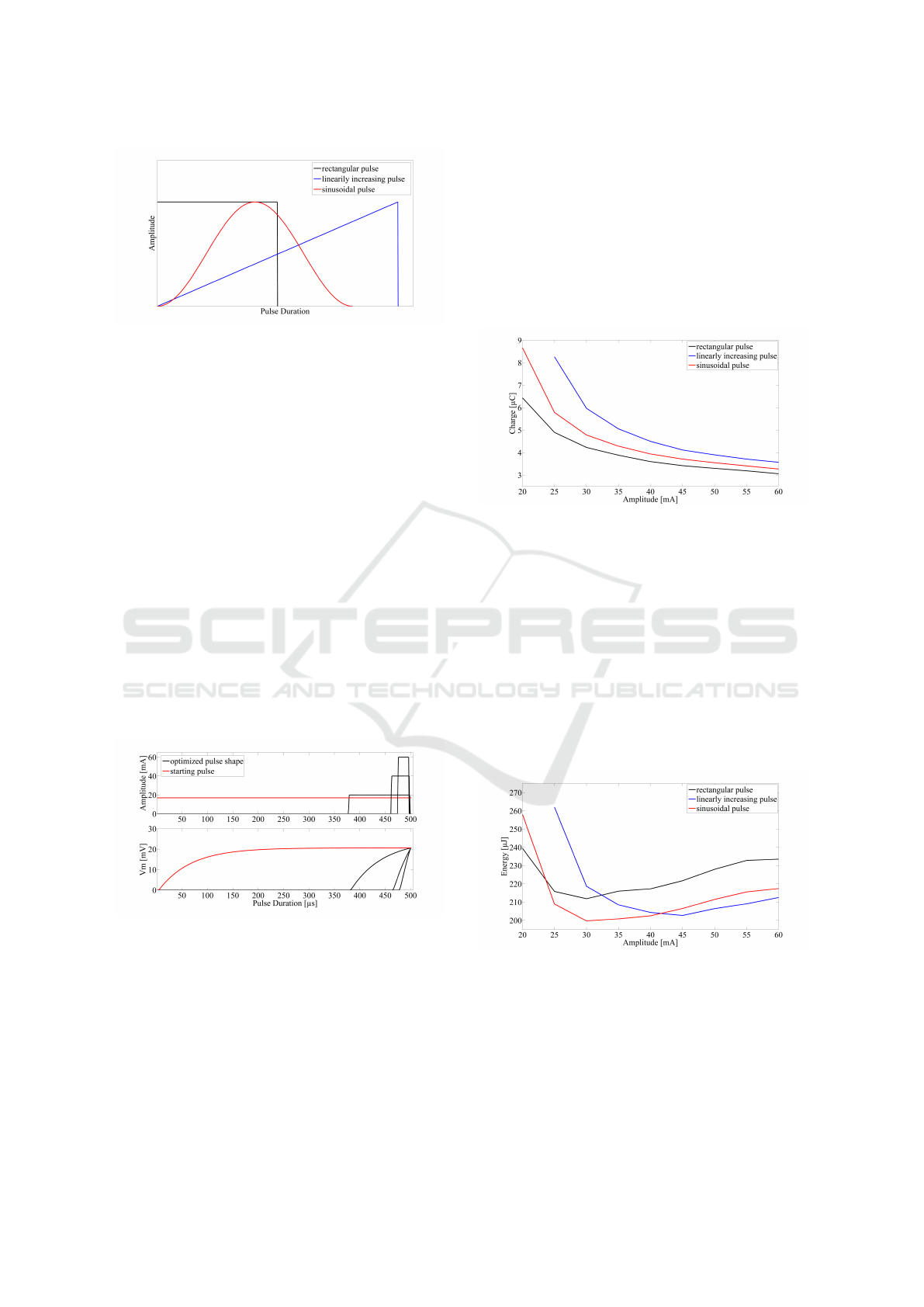
Figure 2: The three pulses used for the active axon model
simulation. The amplitude was always the same for all
pulses, but the pulse duration was adjusted to elicit an action
potential.
3 RESULTS
The result of the minimization problem described in
section 2.2 can be seen in figure 3. Three different
maximum amplitudes were used in this example: 20,
40 and 60 mA. The optimized solution always used
the maximum available amplitude to reach the prede-
fined threshold potential and had a rectangular shape.
No limitation of the maximum amplitude would re-
sult in a Dirac impulse as the optimal solution. In or-
der to achieve a charge optimal stimulation apparently
the necessary electrical charge should be applied as
fast as possible which results in a rectangular shape.
However, increasing the maximum amplitude after a
certain value did not reduce the required charge by a
lot.
Figure 3: The upper figure shows the starting pulse in red
and three optimized solutions for maximal amplitudes of
20, 40 and 60 mA. The figure below shows the elicited
change in V
m
. Thereby all pulses reach the same poten-
tial at the end of the stimulation.
Since the minimization problem just used a sim-
ple passive axon model, a comparison to other pulse
shapes was performed with an active axon model to
see whether the observed results are valid. Figure 4
shows the necessary charge for different stimulation
amplitudes. As predicted by the minimization prob-
lem, the necessary charge reduces when the stimula-
tion amplitude is increased. This behavior can be ob-
served for all three pulse shapes. However, both of
the other pulses require more charge for all amplitude
levels. For higher amplitudes saturation appears and
the charge requirement of the different pulses comes
closer to each other. It can be assumed that at some
point the amplitude will be so high that the pulse
shape has no impact.
Figure 4: Required charge plotted over the stimulation am-
plitude.
Since using high stimulation amplitudes will re-
sult in a high voltage drop over the patient, an addi-
tional computation of the energy dissipation between
the electrodes was performed (figure 5). For each
pulse shape a minimum in the energy dissipation can
be observed at one specific amplitude level. Opposed
to the charge, the energy dissipation does increase for
higher amplitudes, although the rate is not very high.
The linearly increasing pulse as well as the sinusoidal
pulse dissipates less energy compared to the rectan-
gular pulse at higher amplitudes.
Figure 5: Dissipated energy plotted over the stimulation
amplitude.
4 CONCLUSION
The minimization problem showed that using stim-
ulation pulses with high amplitudes does reduce the
required charge to cause a desired change in V
m
. This
Energy Minimization during Transcutaneous Electrical Stimulation by Charge Efficient Stimulation Pulses - Benefits of using Short
Duration and High Amplitude Stimulation Pulses
253

finding was supported by the active model simulation.
Nevertheless increasing stimulation amplitudes over
a certain point will not decrease the required charge
in an efficient way, especially if the increased en-
ergy dissipation over the patient is taken into account.
The linearly increasing pulse and the sinusoidal pulse
were both showing a higher charge requirement than
the rectangular pulse for fixed amplitudes. However,
the sinusoidal pulse dissipated the least amount of en-
ergy over the patient whereas the rectangular one dis-
sipated the most.
Figure 6: Required charge plotted over the stimulation
amplitude. Experimental data from (Meza-Cuevas et al.,
2012).
Figure 7: Dissipated energy plotted over the stimulation
amplitude. Experimental data from (Meza-Cuevas et al.,
2012).
Comparing the simulation results from this study
(figure 4 and figure 5) to older experimental data
of our institute (figure 6 and figure 7) from (Meza-
Cuevas et al., 2012) a very similar behavior could
be observed. The rectangular pulse showed the least
amount of required charge whereby the sinusoidal
pulse dissipated the least amount of energy. Only the
slow increase in dissipated energy for higher stimula-
tion amplitudes of figure 5 was not visible in figure 7.
One possible reason is the low number of data points.
Moreover in (Meza-Cuevas et al., 2012) symmet-
ric biphasic pulses without an interphase were used,
whereas this study focused on monophasic pulses.
The low energy dissipation of sinusoidal pulses
described in this present study and by (Meza-Cuevas
et al., 2012) are comparable to the findings of
(Wongsarnpigoon and Grill, 2010) who identified a
Gaussian function as the most efficient stimulation
pulse in their study.
It was stated by (Jezernik et al., 2010) that a Dirac
impulse will provide the most charge efficient stimu-
lation, which is supported by our study.
Even though differences in efficiency across the
pulse shapes could be observed, it should be stated
that choosing an efficient stimulation amplitude and
duration has a much larger effect than just changing
one pulse shape to another. Before investing in find-
ing a different pulse shape it is important to know
what should be achieved with the new pulse shape and
also to investigate whether the available pulse shapes
have already been used accordingly.
One suggestion that could be extracted from our
findings is that there is no need to worry about short
duration and high amplitude stimulation pulses. This
does not mean that in every case the stimulation am-
plitude should be set to the available maximum value.
We would rather advice to start with a relatively high
amplitude and short pulse duration and from there on
start to increase the duration step wise. Pulse dura-
tions between 50 and 150 µs for rectangular pulses
showed good results in this simulation study.
At this point it has to be noted that the presented
graphs and the containing numbers are very specific to
the simulation environment used. Usage of different
axon properties will change the results. Nevertheless,
we are convinced that the shown trends are valid and
will be supported by experimental evidence and fur-
ther simulations in the future. In a future study the
impact of a charge balance pulse and its time delay
after the actual stimulation pulse should be investi-
gated. A new device able to deliver programmable
stimulation pulse shapes could be used to support our
results and would help us to design efficient charge
balanced stimulation pulses to improve the treatment
of patients with TES.
ACKNOWLEDGEMENTS
This work was supported by a grant from the Fed-
eral Ministry of Education and Research (BMBF, ES-
iMED [16M3201]).
REFERENCES
Gregory, C. M., Dixon, W., and Bickel, C. S. (2007). Im-
pact of varying pulse frequency and duration on mus-
cle torque production and fatigue. Muscle & nerve,
35(4):504–509.
BIODEVICES 2016 - 9th International Conference on Biomedical Electronics and Devices
254

Hodgkin, A. L. and Huxley, A. F. (1952). A quantitative
description of membrane current and its application to
conduction and excitation in nerve. The Journal of
Physiology, 117(4):500–544.
Hunter Peckham, P. (1999). Principles of electrical stim-
ulation. Topics in Spinal Cord Injury Rehabilitation,
5(1):1–5.
Jezernik, S. and Morari, M. (2005). Energy-optimal elec-
trical excitation of nerve fibers. Biomedical Engineer-
ing, IEEE Transactions on, 52(4):740–743.
Jezernik, S., Sinkjaer, T., and Morari, M. (2010). Charge
and energy minimization in electrical/magnetic stim-
ulation of nervous tissue. Journal of Neural Engineer-
ing, 7(4):046004.
Knutson, J. S., Harley, M. Y., Hisel, T. Z., and Chae, J.
(2007). Improving hand function in stroke survivors:
a pilot study of contralaterally controlled functional
electric stimulation in chronic hemiplegia. Archives
of Physical Medicine and Rehabilitation, 88(4):513–
520.
Krouchev, N. I., Danner, S. M., Vinet, A., Rattay, F.,
and Sawan, M. (2014). Energy-optimal electrical-
stimulation pulses shaped by the least-action princi-
ple. PloS one, 9(3).
Loitz, J. C., Reinert, A., Schroeder, D., and Krautschnei-
der, W. H. (2015). Impact of electrode geometry on
force generation during functional electrical stimula-
tion. Current Directions in Biomedical Engineering,
1(1):458–461.
Mangold, S., Keller, T., Curt, A., and Dietz, V. (2005).
Transcutaneous functional electrical stimulation for
grasping in subjects with cervical spinal cord injury.
Spinal Cord, 43(1):1–13.
McIntyre, C. C., Richardson, A. G., and Grill, W. M.
(2002). Modeling the excitability of mammalian nerve
fibers: influence of afterpotentials on the recovery cy-
cle. Journal of Neurophysiology, 87(2):995–1006.
McNeal, D. R. (1976). Analysis of a model for excitation
of myelinated nerve. Biomedical Engineering, IEEE
Transactions on, (4):329–337.
Meza-Cuevas, M., Schroeder, D., Krautschneider, W. H.,
et al. (2012). Neuromuscular electrical stimulation
using different waveforms: Properties comparison by
applying single pulses. In Biomedical Engineering
and Informatics (BMEI), 2012 5th International Con-
ference on, pages 840–845. IEEE.
Wongsarnpigoon, A. and Grill, W. M. (2010). Energy-
efficient waveform shapes for neural stimulation re-
vealed with a genetic algorithm. Journal of Neural
Engineering, 7(4):046009.
Energy Minimization during Transcutaneous Electrical Stimulation by Charge Efficient Stimulation Pulses - Benefits of using Short
Duration and High Amplitude Stimulation Pulses
255