From Arguments and Reviewers to their Simulation

Reproducing a Case-Study

Simone Gabbriellini

and Francesco Santini

Dipartimento di Economia e Management, Universit

a di Brescia, Brescia, Italy

Dipartimento di Matematica e Informatica, Universtit

a di Perugia, Perugia, Italy

Keywords:

Argumentation, Social Simulation, Review-based Systems.

Abstract:

We propose an exploratory study on arguments in Amazon.com reviews. Firstly, we extract positive (in favour

of purchase) and negative (against it) arguments from each review concerning a selected product. We ac-

complish this information extraction manually, scanning all the related reviews. Secondly, we link extracted

arguments to the rating score, to the length, and to the date of reviews, in order to undertand how they are

connected. As a result, we show that negative arguments are quite sparse in the beginning of such social

review-process, while positive arguments are more equally distributed along the timeline. As a ﬁnal step, we

replicate the behaviour of reviewers as agents, by simulating how they assemble reviews in the form of argu-

ments. In such a way, we show we are able to mirror the measured experiment through a simulation that takes

into account both positive and negative arguments.

1 INTRODUCTION

Recent surveys have reported that 50% of on-line

shoppers spend at least ten minutes reading reviews

before making a decision about a purchase, and 26%

of on-line shoppers read reviews on Amazon prior to

making a purchase.

This paper reports an exploratory study of how

customers use arguments in writing such reviews. We

start from a well acknowledged result in the literature

on on-line reviews: the more reviews a product gets,

the more the rating tends to decrease (Rogers, 2003).

Such rating is, in many case, a simple scale from 1

to 5, where 1 is a low rating and 5 is the maximum

possible rating.

This fact can be explained easily considering that

ﬁrst customers are more likely to be enthusiast of the

product, then as the product gets momentum, more

people have a chance to review it and inevitably the

average rating tends to stabilise on some values lower

than 5. Such process, with a few enthusiast early

adopters then followed by a majority of innovators,

ultimately followed by late adopters that end the hype

of an innovation, is a typical pattern in diffusion stud-

ies (Rogers, 2003). In on-line reviews however, when

http://www.forbes.com/sites/jeffbercovici/2013/01/25/how-

amazon-should-ﬁx-its-reviews-problem/.

more people get involved in reviewing a product, we

observe a lower level of satisfaction among them.

More data is needed to assess the shape of diffusion

of products through on-line reviews, but our initial in-

vestigation points in this direction.

However, the level of disagreement in product re-

views remains a challenge: does it inﬂuence what

other customers will do? In particular, what does it

happen, on a micro level, that justiﬁes such diminish-

ing trend in ratings? Since reviewing a product is a

communication process, and since we use arguments

to communicate our opinions to others, and possibly

convince them (Mercier and Sperger, 2011), it is evi-

dent that late reviews should contain enough negative

arguments to explain such a negative trend in ratings -

or that we are more susceptible to negative arguments.

The presence of extreme opinions on-line is a

well-known issue grounded on the reporting bias and

the purchasing bias of online customers - we will

deepen this argument in the next section.

We limited the horizon of our study to a “micro”

dimension (Gabbriellini and Santini, 2015) due to

the constraint imposed by the argument-mining ﬁeld,

which is still at its ﬁrst steps: no well-established tool

seems already to exist to handle this task in our ap-

plication, except for some emerging approach (Lippi

and Torroni, 2015).

Gabbriellini, S. and Santini, F.

From Arguments and Reviewers to their Simulation - Reproducing a Case-Study.

DOI: 10.5220/0005816200740083

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 1, pages 74-83

ISBN: 978-989-758-172-4

Our present study can be considered as “micro”

because we focus on a single product only, even if

with a quite large number of reviews (i.e., 253). Un-

fortunately, due to the lack of well-established tools

for the automated extraction of arguments and attacks,

we cannot extend our study “in the large” and draw

more general considerations.

We extracted by hand, for each review about the

selected product, both positive and negative argu-

ments expressed, the associated rating (from one to

ﬁve stars), and the time when the review has been

posted. Afterwords, we analyse our data in terms of:

• how positive/negative arguments are posted

through time.

• how many positive/negative arguments a review

has (through time).

In particular, we argue that the reason why aver-

age ratings tend to decrease as a function of time de-

pends not only on the fact that the number of negative

reviews increases, but also on the fact that negative

arguments tend to permeate positive reviews, decreas-

ing de facto the average rating of these reviews.

Finally, we propose three different core mecha-

nisms to understand the two main stylised facts ob-

served in the data: a) the tendency for average re-

view rating to decrease with time, and b the pres-

ence of negative arguments in reviews with positive

ratings. The goal of this step is to evaluate the sim-

ilarity between empirical and simulated data as per

the correlations and distribution outlined in Section 4.

In addition, reviews, reviewers and products could be

mapped as in (Bal

azs, 2014):

• reviewers and products are represented as two sets

of nodes in a bipartite network;

• reviews are represented as links that connect con-

sumers and products, where the weight of the link

represents the rating of the review.

Different strategies are thus possible to check how

much empirical and simulated networks share a com-

mon topology and to validate the realism of the mech-

anisms proposed. An interesting approach is to use as

more statistics as possible, coupling for example de-

scriptive statistics and GOF statistics (Manzo, 2013;

Gabbriellini, 2014).

To run our simulation on all such three mech-

anisms we use NetLogo, which is a programmable

modelling environment for simulating natural and so-

cial phenomena.

The rest of the paper is structured as follows. Sec-

tion 2 sets the scene where we settle our work: we in-

troduce related proposals that aggregate Amazon.com

reviews in order to produce an easy-to-understand

summary of them. Afterwards, in Sec. 3 we de-

scribe the Amazon.com dataset from where we se-

lect our case-study. Section 4 plots how both positive

and negative arguments dynamically change through

time, zooming inside reviews with a more granular

approach. Section 5 reproduce the observed phe-

nomenon through a simulation of different mecha-

nisms. Finally, Sec. 6 wraps up the paper and hints

direction for future work.

2 LITERATURE REVIEW

Electronic Word-of-Mouth (e-WoM) is the passing of

information from person to person, mediated through

any electronic means. Over the years it has gained

growing attention from scholars, as more and more

customers started sharing their experience online

(Anderson, 1998; Stokes and Lomax, 2002; Zhu

and Zhang, 2006; Goldenberg et al., 2001; Chat-

terjee, 2001). Since e-WoM somewhat inﬂuences

consumers’ decision-making processes, many review

systems have been implemented on a number of

popular Web 2.0-based e-commerce websites (e.g.,

Amazon.com

and eBay.com

), product comparison

websites (e.g., BizRate.com

and Epinions.com

and news websites (e.g., MSNBC.com

and Slash-

Dot.org

Unlike recommendation systems, which seek to

personalise each user’s Web experience by exploit-

ing item-to-item and user-to-user correlations, review

systems give access to others’ opinions as well as an

average rating for an item based on the reviews re-

ceived so far. Two key facts have been assessed so

far:

• Reporting Bias: customers with more extreme

opinions have a higher than normal likelihood of

reporting their opinion (Anderson, 1998);

• Purchasing Bias: customers who like a product

have a greater chance to buy it and leave a review

on the positive side of the spectrum (Chevalier and

Mayzlin, 2006).

These conditions produce a J-shaped curve of rat-

ings, with extreme ratings and positive ratings being

more present. Thus a customer who wants to buy

a product is not exposed to a fair and unbiased set

http://www.amazon.com.

http://www.ebay.com.

http://www.bizrate.com.

http://www.epinions.com.

http://www.msnbc.com.

http://slashdot.org.

From Arguments and Reviewers to their Simulation - Reproducing a Case-Study

of opinions. Scholars have started investigating the

relation between reviews, ratings, and disagreement

among customers (Moe and Schweidel, 2012; Del-

larocas, 2003). In particular, one challenging question

is: does the disagreement about the quality of a prod-

uct in previous reviews inﬂuence what new reviewers

will post?

A common approach to measure disagreement in

reviews is to compute the standard deviation of rat-

ings per product, but more reﬁned indexes are pos-

sible (Nagle and Riedl, 2014). The next step is to

detect correlations among disagreement as a function

of time (Dellarocas, 2003; Nagle and Riedl, 2014).

We aim, however, at modelling a lower level, micro-

founded mechanism that could account for how cus-

tomers’ reviewing behaviour evolves over time. We

want to analyse reviews not only in terms of rating and

length, but also in terms of what really constitutes the

review itself, i.e., the arguments used by customers.

We aim at explaining disagreement as a consequence

of customers’ behaviour, not only at describing it as a

correlation among variables; an analytical and micro-

founded modelling of social phenomena is well de-

tailed in some works (Manzo, 2013; Hedstrom, 2005;

Squazzoni, 2012), and applied to on-line contexts as

well (Gabbriellini, 2014).

However, before automatically reasoning on ar-

guments, we have ﬁrst to extract them from a text

corpora of on-line reviews. On this side, research

is still dawning, even if already promising (Villalba

and Saint-Dizier, 2012; Wyner et al., 2012). In ad-

dition, we would like to mention other approaches

that can be used to summarise the bulk of unstruc-

tured information (in natural language) provided by

customer reviews. Some authors (Hu and Liu, 2004)

summarise reviews by i) mining product features that

have been commented on by customers, ii) identify-

ing opinion sentences in each review and deciding

whether each opinion sentence is positive or nega-

tive, and, ﬁnally, iii) summarising the results. Sev-

eral different techniques have been advanced to this,

e.g., sentiment classiﬁcation, frequent and infrequent

features identiﬁcation, or predicting the orientation of

opinions (positive or negative).

3 DATASET

Amazon.com allows users to submit their reviews to

the web page of each product, and the reviews can be

accessed by all users. Each review consists of the re-

viewer’s name (either the real name or a nickname),

several lines of comments, a rating score (ranging

from one to ﬁve stars), and the time-stamp of the re-

view. All reviews are archived in the system, and

the aggregated result, derived by averaging all the re-

ceived ratings, is reported on the Web-page of each

product. It has been shown that such reviews pro-

vide basic ideas about the popularity and dependabil-

ity of corresponding items; hence, they have a sub-

stantial impact on cyber-shoppers’ behaviour (Cheva-

lier and Mayzlin, 2006). It is well known that the

current Amazon.com reviewing system has some no-

ticeable limits (Wang et al., 2008). For instance, i)

the review results have the tendency to be skewed to-

ward high scores, ii) the ageing issue of reviews is not

considered, and iii) it has no means to assess reviews’

helpfulness if the reviews are not evaluated by a suf-

ﬁciently large number of users.

For our purposes, we retrieved the “Clothing,

Shoes and Jeweller” products section of Amazon

The dataset contains approximately 110k products

and spans from 1999 to July 2014, for a total of more

than one million reviews. The whole dataset contains

143.7 millions reviews.

We summarise here a quick description of such

dataset:

• the distribution of reviews per product is highly

heterogeneous;

• the disagreement in ratings tends to rise with the

number of reviews until a point after which it

starts to decay. Interestingly, for some highly re-

viewed products, the disagreement remains high:

this means that only for speciﬁc products opin-

ions polarise while, on average, reviewers tend to

agree;

• more recent reviews tend to get shorter, irrespec-

tively of the number of reviews received, which

is pretty much expectable: new reviewers might

realise that some of what they wanted to say has

already been stated in previous reviews;

• more recent ratings tend to be lower, irrespec-

tively of the number of reviews received.

To sum up, it seems that the disagreement in pre-

vious reviews does not affect much latest ratings -

except for some cases which might correspond to

products with polarised opinions. This result has al-

ready been found in the literature (Moe and Schwei-

Courtesy of Julian McAuley and SNAP project (source:

http://snap.stanford.edu/data/web-Amazon.html and https:

//snap.stanford.edu).

Space constraints prevented us to show more detailed re-

sults here, but additional plots are available in the form of

research notes at http://tinyurl.com/pv5owct.

Polarisation only on speciﬁc issues has already been ob-

served in many off-line contexts, see (Baldassarri and

Bearman, 2007).

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

del, 2012). However, it has also already been chal-

lenged by Nagle and Riedl (Nagle and Riedl, 2014),

who found that a higher disagreement among prior

reviews does lead to lower ratings. They ascribe their

new ﬁnding to their more accurate way of measuring

the disagreement in such J-shaped distributions of rat-

ings.

One of the main aims of this work is to under-

stand how it is that new reviews tend to get lower rat-

ings. Our hypothesis is that this phenomenon can be

explained if we look at the level of arguments, i.e., if

we consider the dynamics of the arguments used by

customers, more than aggregate ratings.

Since techniques to mine arguments from a text

corpora are yet in an early development stage, we

focus on a single product and extract arguments by

hand. We randomly select a product, which happens

to be a ballet tutu for kids, and we examine all the 253

reviews that this product received between 2009 and

July 2014. From the reviews, we collect a total of 24

positive arguments and 20 negative arguments, whose

absolute frequencies are reported in Tab. 1.

There are of course many issues that arise when

such a process is done by hand. First of all, an ar-

gument might seem positive to a reader and nega-

tive to another. For the purpose of this small exam-

ple, we coded arguments together and, for each argu-

ment, tried to achieve the highest possible agreement

on its polarity. A better routine, for larger studies,

would be to have many coders operate autonomously

and then check the consistency of their results. How-

ever, we didn’t ﬁnd case where an argument could be

considered both positive and negative, maybe because

the product itself didn’t allow for complex reasoning.

When we encountered a review with both positive and

negative arguments, like ”the kid loved it, but it is

not sewed properly”, we split the review counting one

positive argument and one negative argument. The

most interesting thing emerging from this study is the

fact that, as reviews accumulate, they tend to contain

more negative bits, even if the ratings remain high.

4 ANALYSIS

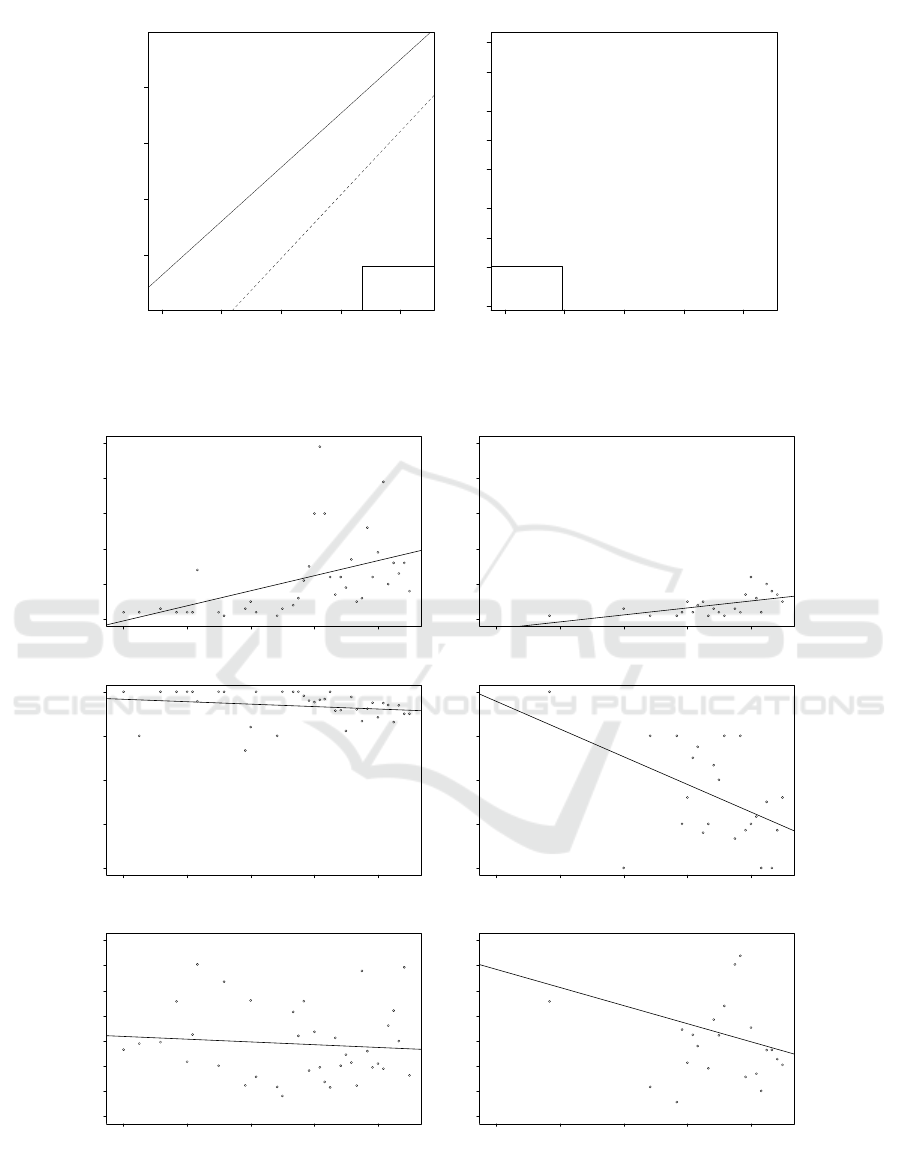
In Fig. 2, the ﬁrst plot on the left shows the monthly

absolute frequencies of positive arguments in the

speciﬁed time range. As it is easy to see, the num-

ber of positive arguments increases as time goes by,

which can be a consequence of a success in sales:

more happy consumers are reviewing the product. At

the same time, the ﬁrst plot on the right shows a sim-

ilar trend for negative arguments, which is a signal

that, as more customers purchase the product, some

Table 1: Positive and negative arguments, with their number

of appearances in reviews between 2009 and July 2014.

ID Positive arguments #App.

A the kid loved it 78

B it ﬁts well 65

C it has a good quality/price ratio 52

D it has a good quality 44

E it is durable 31

F it is shipped fast 25

G the kid looks adorable 23

H it has a good price 21

I it has great colors 21

J it is full 18

K it did its job 11

L it is good for playing 11

M it is as advertised 9

N it can be used in real dance classes 7

O it is aesthetically appealing 7

P it has a good envelope 2

Q it is a great ﬁrst tutu 2

R it is easier than build your own 2

S it is sewed properly 2

T it has a good customer service 1

U it is secure 1

V it is simple but elegant 1

W you can customize it 1

X you cannot see through it 1

ID Negative arguments #App.

a it has a bad quality 18

b it is not sewed properly 17

c it does not ﬁt 12

d it is not full 11

e it is not as advertised 8

f it is not durable 7

g it has a bad customer service 4

h it is shipped slow 3

i it smells chemically 3

j you can see through it 3

k it cannot be used in real dance class 2

l it has a bad quality/price ratio 2

m it has a bad envelope 1

n it has a bad waistband 1

o it has bad colours 1

p it has high shipping rates 1

q it has no cleaning instructions 1

r it is not lined 1

s it never arrived 1

t it was damaged 1

of them are not satisﬁed with it. According to what

we expect from the literature (see Sec. 2), the higher

volume of positive arguments is a consequence of the

J-shaped curve in ratings, i.e., a consequence of re-

porting and selection biases. What is interesting to

note though, is that the average review rating tends to

decrease with time, as shown by the second row of

plots in Fig. 2. This holds both for reviews contain-

ing positive arguments as well as for those containing

negative arguments. In particular, the second plot on

the right shows that, starting from 2012, negative ar-

guments start to inﬁltrate “positive” reviews, that is

reviews with a rating of 3 and above. Finally, the last

row of plots in Fig. 2 shows that the average length of

From Arguments and Reviewers to their Simulation - Reproducing a Case-Study

reviews decreases as time passes; this happens both

for reviews with positive arguments and for reviews

with negative arguments. However, such a decrease is

much more steep for negative ones than for positive

ones.

In Fig. 3 we can observe the distribution of posi-

tive and negative arguments.

Regarding positive ar-

guments, we cannot exclude a power-law model for

the distribution tail with x-min = 18 and α = 2.56

(pvalue = 0.54)

. We also tested a log-normal model

with x-min = 9, µ = 3.01 and σ = 0.81 (pvalue =

0.68). We then searched a common x-min value to

compare the two ﬁtted distributions: for x − min =

4, both the log-normal (µ = 3.03 and σ = 0.78) and

the power-law (α = 1.55) models still cannot be ruled

out, with p − value = 0.57 and pvalue = 0.54 re-

spectively. However, a comparison between the two

leads to a two-sided pvalue = 0.001, which implies

that one model is closer to the true distribution - in

this case, the log-normal model performs better. For

negative arguments, we replicated the distribution ﬁt-

ting: for xmin = 2, a power law model cannot be

ruled out (α = 1.78 and p-value = 0.22) as well as

a log-normal model (µ = 1.48 and σ = 0.96, pvalue =

0.32). Again, after comparing the ﬁtted distributions,

we cannot drop the hypotheses that both the distribu-

tions are equally far from the true distribution (two-

sided pvalue = 0.49). In this case, too few data are

present to make a wise choice.

Among the positive arguments (plot on the left),

there are four arguments that represent, taken to-

gether, almost 44% of customers’ opinions. These ar-

guments are: i) good because the kid loved it, ii) good

because it ﬁts well, iii) good because it has a good

quality/price ratio, iv) good because it has a good

quality. Negative arguments represent, all together,

less than 20% of opinions.

We have a clear view where the pros and cons of

this product are stated as arguments: not surprisingly,

the overall quality is the main reason why customers

consider the product as a good or bad deal. Even

among detractors, this product is not considered ex-

pensive, but quality still is an issue for most of them.

The plots in Fig. 1 show the cumulative frequen-

cies and the rate at which new arguments are added

as a function of time. In the left plot, it is interesting

to note that, despite the difference in volume (positive

arguments are more cited than negative ones), the cu-

mulative frequencies at which positive and negative

arguments are added are almost identical. Positive ar-

We used the R poweRlaw package for heavy tailed distri-

butions (developed by Colin Gillespie (Gillespie, 2015)).

We used the relatively conservative choice that the power

law is ruled out if pvalue 0.1 (Clauset et al., 2009).

guments start being posted earlier than negative ones,

consistently with the fact that enthusiast customers

are the ﬁrst that review the product. Moreover, it is

interesting to note that no new positive argument is

added in the 2011-2013 interval, while some negative

ones arise in the reviews. Since 2013, positive and

negative arguments follow a similar trajectory. How-

ever, as can be noted in the second plot on the right,

new arguments are not added at the same pace. If we

consider the total amount of added arguments, posi-

tive ones are repeated more often than negatives, and

the rate at which a new positive argument is added is

considerably lower than its counterpart. This infor-

mation sheds a light on customers’ behaviour: dissat-

isﬁed customers tend to post new reasons why they

dislike the product, more than just repeating what

other dissatisﬁed customers have already said.

5 SIMULATION

In this section we propose an agent-based simulation

to replicate empirical data about customers, reviews,

and arguments as described in Section 4. The aim of

this step is to translate the theoretical mechanism used

to write reviews into its computational counterpart.

Following J. Moody (Moody, 2008), our aim is to

specify a substance-speciﬁc model that can shed light

on how customers behave when they have to review

a product, thus to identify properties that make real-

world data and simulated data differ, without quanti-

fying these differences with a statistical signiﬁcance.

We opt for the Agent-Based Modelling (ABM)

computational approach (Macy and Willer, 2002) to

simulate arguments networks of online reviews from

user behaviour. There is a growing literature that uses

ABM in network studies (Macy and Skvoretz, 1998;

Flache and Macy, 2011). ABMs are a straightfor-

ward way to detail and implement substance-speciﬁc

mechanisms in the form of computational models,

i.e., software that generates entities with attributes and

decision-making rules, and that is goal-oriented.

Despite the speciﬁc solution implemented, the

main logic would be to test different speciﬁcations

of the mechanism against empirical data and to re-

ﬁne such implementations until a satisfactory match is

found or, alternatively, to get back to the blackboard

and think again about the hypotheses - agent-based

modelling is, ultimately, a tool to aid theory building.

An interesting analytical strategy to understand

the robustness of an ABM is to compare its results

against empirical data (Manzo, 2007) in order to as-

sess how realistic the model behaves - thus how sound

is the theory behind it. We will also compare the re-

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

2010 2011 2012 2013 2014

5 10 15 20

FREQUENCIES OF NEW ARGUMENTS

TIME

CUMULATIVE FREQUENCIES

positive

negative

2010 2011 2012 2013 2014

0.002 0.005 0.020 0.050 0.200 0.500

RATES OF NEW ARGUMENTS

TIME

RATE

positive

negative

Figure 1: Left plot: cumulative frequencies of new positive and negative arguments per month. Right plot: rate of new positive

and negative arguments over total arguments per month.

2010 2011 2012 2013 2014

0 10 20 30 40 50

POSITIVE ARGUMENTS

YEARS

NUMBER OF ARGUMENTS PER MONTH

2010 2011 2012 2013 2014

0 10 20 30 40 50

NEGATIVE ARGUMENTS

YEARS

NUMBER OF ARGUMENTS PER MONTH

2010 2011 2012 2013 2014

1 2 3 4 5

RATING (Positive Arguments)

YEARS

AVERAGE RATING

2010 2011 2012 2013 2014

1 2 3 4 5

RATING (Negative Arguments)

YEARS

AVERAGE RATING

2010 2011 2012 2013 2014

50 100 150 200 250 300 350 400

REVIEW LENGTH (Positive Arguments)

YEARS

AVERAGE NUMBER OF CHARACTERS

2010 2011 2012 2013 2014

50 100 150 200 250 300 350 400

REVIEW LENGTH (Negative Arguments)

YEARS

AVERAGE NUMBER OF CHARACTERS

Figure 2: Argument trends: (row1) absolute frequency of arguments per month, (row2) average rating of reviews per month,

(row3) average review-length per month.

From Arguments and Reviewers to their Simulation - Reproducing a Case-Study

1 2 5 10 20 50

0.05 0.10 0.20 0.50 1.00

POSITIVE ARGUMENTS

REPETITIONS

FREQUENCY

logn

plaw

1 2 5 10 20 50

0.05 0.10 0.20 0.50 1.00

NEGATIVE ARGUMENTS

REPETITIONS

FREQUENCY

logn

powl

Figure 3: Arguments distribution: probability of observing an argument repeated x times.

sults of our ABM against a random baseline in order

to assess whether a simpler model can sufﬁce to deal

with the complexity of what we observed empirically.

The idea is that our ABM should outperform the base-

line model in approximating empirical data.

We adopt NetLogo

, a programmable modelling

environment in Scala for simulating natural and so-

cial phenomena, to implement our model. NetLogo

is particularly well suited for modelling complex sys-

tems developing over time. Modellers can give in-

structions to hundreds or thousands of agents all oper-

ating independently. This makes it possible to explore

the connection between the micro-level behaviour of

individuals and the macro-level patterns that emerge

from their interaction. Figure 4 shows our simulation

running in NetLogo.

Our simulation model assumes a few constraints

from empirical data:

1. the size of simulated and empirical populations

coincide and it is equal to 198;

2. reviewers decide to review with a probability pro-

portional to observing a review in empirical data:

the frequency of reviews is thus mimicked real-

istically, but each time reviewers are chosen ran-

domly to avoid artefacts (i.e. reproducing the

same order in which physical reviewers reviewed

the product);

3. the percentages of happy and unhappy reviewers

coincide in real and simulated scenarios (around

80% are happy about the product);

4. the average number of arguments per review is 2,

with a minimum of 1 argument and a max of 4;

5. the number and distribution of both positive and

negative arguments is held constant (24 positive

https://ccl.northwestern.edu/netlogo/

arguments and 20 negative arguments) and possi-

bly similar to the empirical one (we use a Poisson

generator to assign to every reviewers positive and

negative arguments among the 44 possible argu-

ments).

We then propose three different core mechanisms

to understand the two main stylized facts observed in

the data: (a) the tendency for average review rating

to decrease with time; (b) the presence of negative

arguments in reviews with positive ratings.

The ﬁrst mechanism, Mechanism 1, is used as a

random baseline where arguments and ratings are not

related: we start assigning to reviewers a rating for

their reviews (a value between 1 and 5) and then we

randomly assign positive or negative arguments, irre-

spective of the rating value.

With Mechanism 2, we assume that a strict corre-

lation is in place between ratings and arguments, thus

reviews with positive ratings contain only positive ar-

guments and vice versa.

With Mechanism 3 we relax Mechanism 2 a bit,

assuming that positive reviews can contain also neg-

ative arguments. In this case, for a certain positive

rating (3, 4 or 5) the probability to contain a positive

arguments is given by:

1/1 + exp(α − β ∗ x)

As in Mechanism 2, however, negative reviews

contain only negative arguments.

We have a very simple scheduling: at each time

step, reviewers examine their probability to review

the product. If this is the case, then they “write” a

review with their rating and all the arguments they

know. Each reviewer can review just once. The result

of this process is simply a list of lists, where every

inner list represents an agent’s review.

We simulate each of the three mechanisms 100

times and we record, for each outcome, the distribu-

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

Figure 4: Our simulation running in NetLogo.

tion of positive and negative arguments, as well as the

corresponding ratings. We then compare each simu-

lated result against empirical data using the euclidean

distance between the two curves, and report the dis-

tributions of distances as box-plots in Figure 5.

Figure 5 (a) shows, for each mechanism, the dis-

tribution of distances from the cumulative frequency

curve of positive arguments. It is evident that all

mechanisms can produce equally distant curves from

the empirical one. When it comes to negative argu-

ments, however, things are different. Figure 5 (b)

shows the distribution of distances from the cumula-

tive frequency curve of negative arguments: it is ev-

ident that Mechanisms 2 and 3 do a statistically bet-

ter job. Figure 5 (c) shows, for positive arguments,

the distribution of distances from the curve of ratings

over time. While it looks like Mechanism 3 is per-

forming slightly better than the others, we can say

that the three mechanisms are doing pretty much the

same job. When it comes to the same measure, but for

negative arguments, Figure 5 (d) shows clearly that

Mechanism 3 performs better than the others, produc-

ing curves of ratings versus time that are statistically

more close to the empirical one w.r.t. the other two

mechanisms.

6 CONCLUSIONS

In this paper we have proposed a ﬁrst exploratory

study on how to use Abstract Argumentation to under-

stand how it can improve our knowledge about social

trends in product reviews.

More in particular, we “enter” into an Ama-

zon.com review and we achieve a more granular view

of it by considering the different arguments expressed

in each of the 253 reviews about the randomly se-

lected product (a ballerina tutu). What we observe is

that the frequency of negative arguments (against pur-

chasing the tutu) increases after some time, while the

distribution of positive arguments (in favour of pur-

chasing the tutu) is more balanced between the con-

sidered period. Moreover, while positive arguments

are always associated with high ratings (i.e., 4 or 5),

negative arguments are associated with low (as ex-

pected) but also high ratings. In addition, negative ar-

guments are more frequently associated with shorter

reviews, while enthusiasts tend to be less concise. To

summarise, the aim is to “explode” reviews into argu-

ments and then try to understand how the behaviour

of reviewers changes through time, from the point of

view of arguments.

In the second part of the paper (Sec. 5) we ded-

icate ourselves to the replication of the social phe-

nomenon measured in the ﬁrst sections: we propose

three different core mechanisms to understand the two

main stylised facts observed in the data: a) the ten-

dency for average review rating to decrease with time,

and b the presence of negative arguments in reviews

with positive ratings. By modelling both positive and

negative arguments in reviews rather than either pos-

itive or negative ones, it is possible to get closer to

the experimented empirical curves concerning the ﬁ-

nal rating (from 1 to 5 stars).

Our aim is to detail a work ﬂow to model cus-

tomers’ behaviour when it comes to review prod-

ucts. Our idea is that, by understanding arguments,

we could better understand why people do things in

a particular context, in this case buy or not a product.

We are full aware of the little explanatory power of

our study due to our limited empirical investigation

conducted by hand. We nevertheless think that pro-

gresses in argument mining will help us to overcome

this constraint. One of the most interesting outcome

From Arguments and Reviewers to their Simulation - Reproducing a Case-Study

Figure 5: Simulation results: each of the plots shows the distribution of euclidean distances between simulated curves and

empirical ones over 100 replications. For Mechanism 3, α = 4.8 and β = 1.8.. From left to right in each ﬁgure, Mechanisms

from 1 to 3.

of our approach is to being able to couple our analy-

sis with products selling data: this would open a new

research approach for correlating what customers say

and what customers do in on-line marketing.

In the future, we will widen our investigation by

taking advantage of mining-techniques, e.g., (Wyner

et al., 2012; Villalba and Saint-Dizier, 2012). In ad-

dition, we plan to consider computational approaches

based on Abstract Argumentation; for instance, if tol-

erating a given low amount of inconsistency (i.e., at-

tacks) in extensions (Bistarelli and Santini, 2010) can

help softening the impact of weak arguments (i.e.,

rarely repeated ones). Due to the possible partitioning

of arguments into clusters related to different aspects

of a product (e.g., either its quality or appearance),

we also intend to apply coalition-oriented semantics,

as proposed in (Bistarelli and Santini, 2013).

Following (Gabbriellini and Torroni, 2014), we

also plan to implement an Agent-Based Model with

Argumentative Agents to explore the possible mech-

anisms, from a user’s perspective, that give raise to

such trends and correlations among positive and neg-

ative arguments.

With our model are in the position to offer a pos-

sible explanation of reviewers’ behaviour, but we still

do not know much about why some opinions are in

place among reviewers nor how they engage in dis-

cussions when they disagree. In other words, we still

know nothing about the arguments used by review-

ers. Much research is at stake in computational ar-

gumentation and some frameworks for agent-based

modelling with argumentative agents have been pro-

posed. It would be interesting to mine the dataset for

arguments and then model how argumentative frame-

works evolve when disagreement is strong: a closer

examinations of such exchanges should lead to more

insightful conclusions.

REFERENCES

Anderson, E. W. (1998). Customer satisfaction and word of

mouth. Journal of Service Research, 1(1):517.

Bal

azs, K. (2014). The duality of organizations and audi-

ences, pages 397–418. John Wiley & Sons, Ltd.

Baldassarri, D. and Bearman, P. (2007). Dynamics of po-

litical polarization. American Sociological Review,

72:784811.

Bistarelli, S. and Santini, F. (2010). A common compu-

tational framework for semiring-based argumentation

systems. In ECAI 2010 - 19th European Conference

on Artiﬁcial Intelligence, volume 215 of FAIA, pages

131–136. IOS Press.

Bistarelli, S. and Santini, F. (2013). Coalitions of argu-

ments: An approach with constraint programming.

Fundam. Inform., 124(4):383–401.

Chatterjee, P. (2001). Online reviews do consumers use

them? In Gilly, M. C. and Myers-Levy, J., editors,

ACR 2001 Proceedings, pages 129–134. Association

for Consumer Research.

Chevalier, J. and Mayzlin, D. (2006). The effect of word

of mouth on sales: Online book reviews. Journal of

Marketing, 43(3):345354.

Clauset, A., Shalizi, C., and Newman, M. (2009). Power-

law distributions in empirical data. SIAM Review,

51(4):661–703.

Dellarocas, C. (2003). The digitization of word of mouth:

promise and challenges of online feedback mecha-

nisms. Management Science, 49(10):14071424.

Flache, A. and Macy, M. W. (2011). Local convergence and

global diversity: From interpersonal to social inﬂu-

ence. Journal of Conﬂict Resolution, 55(6):970–995.

Gabbriellini, S. (2014). The evolution of online forums as

communication networks: An agent-based model. Re-

vue Francaise de Sociologie, 4(55):805–826.

Gabbriellini, S. and Santini, F. (2015). A micro study on

the evolution of arguments in amazon.com’s reviews.

In PRIMA 2015: Principles and Practice of Multi-

Agent Systems - 18th International Conference, vol-

ume 9387, pages 284–300. Springer.

Gabbriellini, S. and Torroni, P. (2014). A new frame-

work for abms based on argumentative reasoning.

In Kaminski and Koloch, editors, Advances in So-

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

cial Simulation, volume 229 of LNCS, pages 25–36.

Springer Berlin Heidelberg.

Gillespie, C. (2015). Fitting heavy tailed distributions: the

powerlaw package. Journal of Statistical Software,

64(2).

Goldenberg, J., Libai, B., and Muller, E. (2001). Talk of

the network: a complex systems look at the under-

lying process of word-of-mouth. Marketing Letters,

12(3):211223.

Hedstrom, P. (2005). Dissectin the Social: on the Principles

of Analytical Sociology. Cambridge University Press,

1st edition.

Hu, M. and Liu, B. (2004). Mining and summariz-

ing customer reviews. In Proceedings of the Tenth

ACM SIGKDD International Conference on Knowl-

edge Discovery and Data Mining, KDD ’04, pages

168–177. ACM.

Lippi, M. and Torroni, P. (2015). Context-independent

claim detection for argument mining. In Proceedings

of the Twenty-Fourth International Joint Conference

on Artiﬁcial Intelligence, IJCAI 2015, pages 185–191.

AAAI Press.

Macy, M. W. and Skvoretz, J. (1998). The evolution of trust

and cooperation between strangers: A computational

model. American Sociological Review, 63(5):638–

660.

Macy, M. W. and Willer, R. (2002). From factors to actors:

Computational sociology and agent-based modeling.

Annual Review of Sociology, 28:143–166.

Manzo, G. (2007). Variables, mechanisms, and simulations

: Can the three methods be synthesized ? Revue

franaise de sociologie, 48:156.

Manzo, G. (2013). Educational choices and social interac-

tions: A formal model and a computational test. Com-

parative Social Research, 30:47–100.

Mercier, H. and Sperger, D. (2011). Why do humans rea-

son? Arguments for an argumentative theory. Behav-

ioral and Brain Sciences, 34(2):57–74.

Moe, W. W. and Schweidel, D. A. (2012). Online product

opinions: Incidence, evaluation, and evolution. Mar-

keting Science, 31(3):372386.

Moody, J. (2008). Network Dynamics, pages 447–474. Pe-

ter Hedstrom and Peter S. Bearman.

Nagle, F. and Riedl, C. (2014). Online word of mouth

and product quality disagreement. In ACAD MAN-

AGE PROC, Meeting Abstract Supplement. Academy

of Management.

Rogers, E. (2003). Diffusion of Innovations. Simone &

Schuster, 5st edition.

Squazzoni, F. (2012). Agent-Based Computational Sociol-

ogy. Wiley, 1st edition.

Stokes, D. and Lomax, W. (2002). Taking control of word of

mouth marketing: the case of an entrepreneurial hote-

lier. Journal of Small Business and Enterprise Devel-

opment, 9(4):349357.

Villalba, M. P. G. and Saint-Dizier, P. (2012). A framework

to extract arguments in opinion texts. IJCINI, 6(3):62–

87.

Wang, B.-C., Zhu, W.-Y., and Chen, L.-J. (2008). Im-

proving the amazon review system by exploiting the

credibility and time-decay of public reviews. In Pro-

ceedings of the 2008 IEEE/WIC/ACM International

Conference on Web Intelligence and Intelligent Agent

Technology - Volume 03, WI-IAT ’08, pages 123–126.

IEEE Computer Society.

Wyner, A., Schneider, J., Atkinson, K., and Bench-Capon,

T. J. M. (2012). Semi-automated argumentative analy-

sis of online product reviews. In Computational Mod-

els of Argument - Proceedings of COMMA 2012, vol-

ume 245 of FAIA, pages 43–50. IOS Press.

Zhu, F. and Zhang, X. (2006). The inﬂuence of online con-

sumer reviews on the demand for experience goods:

The case of video games. In Proceedings of the In-

ternational Conference on Information Systems, ICIS,

page 25. Association for Information Systems.

From Arguments and Reviewers to their Simulation - Reproducing a Case-Study