3D Gaze Estimation using Eye Vergence

Esteban Gutierrez Mlot

, Hamed Bahmani

, Siegfried Wahl

and Enkelejda Kasneci

Perception Engineering Group, Computer Science Department, University of T

ubingen,

Sand 14, 72076 T

ubingen, Germany

ZEISS Vision Science Lab, Institute for Ophthalmic Research, University of T

ubingen,

ontgenweg 11, 72076 T

ubingen, Germany

Keywords:

3D Calibration, Eye Tracking, Eye Vergence, Gaze Localization, Depth Perception.

Abstract:

We propose a fast and robust method to estimate the 3D gaze position based on the eye vergence information

extracted from eye-tracking data. This method is specially designed for Point-of-Regard (PoR) estimation in

non-virtual environments with the aim to make it applicable to the study of human visual attention deployment

in natural scenarios. Our approach starts with a calibration step at different depth distances in order to achieve

the best depth approximation. In addition, we investigate the distance range, for which state-of-the-art eye-

tracking technology allows 3D gaze estimation based on eye vergence. Our method provides a mean accuracy

of 1.2

◦

at a working distance between 200 mm and 400 mm from the user without requiring calibrated lights

or cameras.

1 INTRODUCTION

Determining the 3D gaze position in natural settings

is of great interest for different ﬁelds of research and

applications, e.g., investigation human attention de-

ployment when buying products (Gidl

of et al., 2013)

or analysis of visual behavior for driver assistance

in the automotive industry (Braunagel et al., 2015;

Fletcher et al., 2005; Kasneci et al., 2014; Kasneci

et al., 2015). Moreover, in virtual environments,

depth estimation could help to improve the sensa-

tion of immersion into the virtual world optimizing

the level of detail (Duchowski, 2007) or adjusting the

sharpness (Hillaire et al., 2008), where the user’s at-

tention is focused. In this paper, we address a cen-

tral question for video-based 3D gaze estimation, i.e.,

how much focus depth information can be derived

solely from images of the user’s eyes.

3D gaze estimation in video-based eye tracking

consists of mapping the pupil’s center estimate ex-

tracted from the eye image to an actual 3D position

in the scene. For this purpose, depth perception has to

be extracted from the visual system. The human brain

uses several sources of information for 3D vision and

reconstruction including monocular cues, such as oc-

clusion, as well as binocular disparity (Kandel et al.,

2000). Furthermore, it receives information from

three oculomotor systems to perceive depth (Reichelt

et al., 2010): accommodation, miosis, and vergence.

The sense of depth is delivered to the viewer by any

of these depth cues. Accommodation is the process

by which the vertebrate eye changes optical power

to maintain focus on an object as its distance varies

(Davson, 2012). Miosis is the constriction of the

pupil relative to the amount of light the pupil receives

(Rogers, 1988). Finally, vergence is the simultaneous

movement of both eyes in opposite directions to ob-

tain or maintain single binocular vision (Cassin et al.,

1984). For the purpose of designing a 3D eye-tracking

system, measuring accommodation needs perfectly

controlled conditions and complex devices (e.g., Pow-

errefractor™(Schaeffel et al., 1993)), or ultrasound

biomicroscopy (Kasthurirangan, 2014); and it is not

recommended for continuous long exposure. Miosis

is easily measurable, but is very sensitive to ambient

light (Cheng et al., 2006). Thus, among the three in-

formation sources from the oculomotor system, we

are left with the vergence information to estimate the

gaze position or Point of Regard (PoR). In video-

based 3D eye-tracking systems, the vergence infor-

mation is the only signal that is robust and easy to

measure.

Existing 3D gaze estimation techniques can be di-

vided in two main categories: (i) methods based on a

geometrical models of the eye, and (ii) methods based

on interpolation, i.e., the direct mapping of eye posi-

tion and PoR.

Common ground in the model-based approach

Mlot, E., Bahmani, H., Wahl, S. and Kasneci, E.

3D Gaze Estimation using Eye Vergence.

DOI: 10.5220/0005821201250131

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 5: HEALTHINF, pages 125-131

ISBN: 978-989-758-170-0

125

is the use of multiple light sources to calculate

the corneal center (Shih and Liu, 2004). Addi-

tional improvements allow restricted head movements

(Craig Hennessey, 2009). Gaze estimation techniques

in this category have a good accuracy but rely on mul-

tiple infrared lights pointing to the eye, which can be

impractical in outdoor environments or unhealthy un-

der certain conditions (Mulvey et al., 2008), (Kourk-

oumelis and Tzaphlidou, 2011). Furthermore, other

algorithms do not require calibrated lighting features

(

Swirski and Dodgson, 2013), but there is no evidence

for their application to non-virtual environments.

Approaches based on interpolation originate from

2D PoR estimation methods and are extended

for binocular gaze vector estimation in 3D PoR

(Duchowski et al., 2001). Other variations use neural

networks instead of polynomial functions for a better

accuracy (Essig et al., 2006) but are designed speciﬁ-

cally for 3D displays. Neural networks are compared

with a geometry-based algorithm, which provides bet-

ter results for real-time execution (Wang et al., 2014).

However, both methods have been only tested in vir-

tual environments.

In summary, all previously mentioned methods

lack the applicability in real-time, non-virtual, and

non-laboratory scenarios. In this paper, we propose

an online 3D gaze estimation method based on inter-

polation that is suitable for 3D eye-tracking in real-

world scenarios. How the theoretical vergence angle

varies with the observation distance to a target object

is analyzed in Section 2.1. Based on this theoretical

analysis we derive the range in which an eye tracker

can determine the vergence angle with sufﬁcient accu-

racy. The proposed 3D PoR estimation is presented in

Section 2.2 with details regarding pupil position cal-

culation explained in Section 2.2.1. The experimental

validation of the method is described in Section 3.1

and results are presented in Section 3.2. Section 4

concludes this work.

2 METHOD

Our method determines a 3D gaze point from images

of both eyes of the observer. After a calibration phase,

the gaze position can be estimated. For the initial cal-

ibration step, several points on different depth planes

are presented to the observer and looked at sequen-

tially. While the observer is looking at a given point,

the corresponding pupil center position is recorded.

Pupil center and point position are then used to calcu-

late the gaze vector from both eyes and then estimate

the vergence angle. At the end of this step, infor-

mation about the relationship between the vergence

angle and distance is calculated and stored for later

use. For the ﬁnal estimation step, the vergence angle

is calculated from the pupil centers and a 3D PoR is

calculated as described below.

2.1 Relationship between Vergence and

Observation Distance

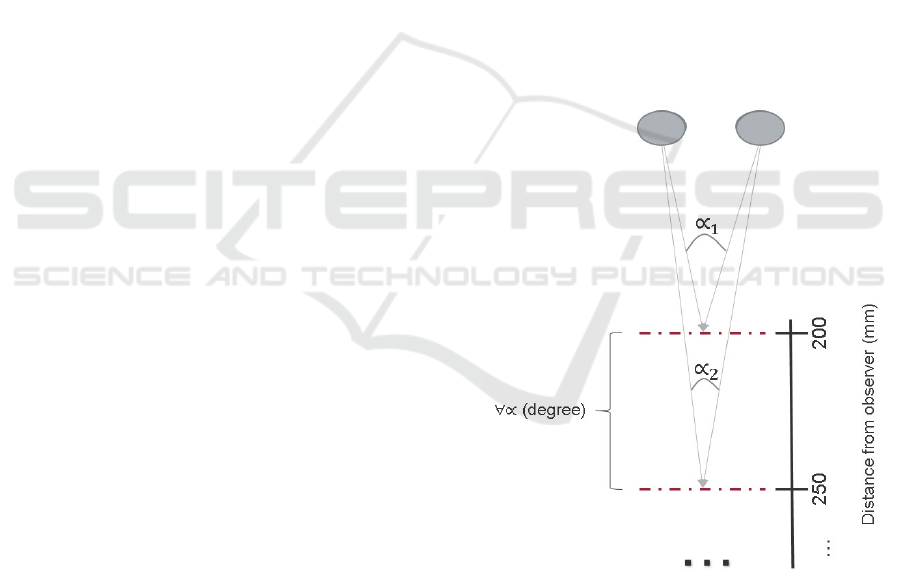
The vergence angle change is the difference between

the vergence angles resulting when moving a target

at given distance from the observer (see Figure 1)

(Healy and Proctor, 2003). This change will be higher

the closer the ﬁxated object is to the observer. Within

the range of 2 meters, the change in vergence an-

gle decreases exponentially with distance (Howard,

2012) (see Figure 2), implying thus, the existence of

a certain distance range in which the vergence an-

gle change is measurable within an acceptable ex-

perimental error. Therefore, before applying the pro-

posed 3D PoR estimation method, it is essential to ﬁnd

out within which range the eye-tracking signal can be

used to extract useful information on vergence.

Figure 1: Calculation of the vergence angle difference.

To approach this, we ﬁrst calculate the theoretical

variation of the vergence angle with the distance. The

relevant parameters are the positions of the eyes and

the attended point in front of them. A ray is traced

from each eye towards this point. For our theoretical

considerations we assume that the ﬁxated at point is

positioned straight ahead of the eyes (from the center

point between both eyes). Since the vergence angle

depends on the distance to the eyes, other points on a

HEALTHINF 2016 - 9th International Conference on Health Informatics

126

sphere around the eyes would yield a similar result.

We sampled the vergence angle difference be-

tween planes positioned in steps of 50 mm. The dif-

ference was calculated by subtracting the vergence

angle value in a plane to the previous one, start-

ing at the plane located further away from the ob-

server. We can therefore infer the maximum distance

at which the vergence difference between two sequen-

tial planes is still larger than our assumed eye-tracker

accuracy. In consequence, planes with less vergence

difference among them will be indistinguishable. For

these calculations, we considered an interpupillary

distance of 64 mm, which correspond to the popula-

tion mean (Dodgson, 2004).

Figure 2 shows the vergence angle for distances

ranging from 20 mm to 1200 mm from the user. Mea-

suring differences of less than 50 mm from 400 mm

distance to the user requires a maximum error of 1°.

This is the maximum distance limit we have chosen

for the experiments, since the required accuracy is

feasible. We use a minimum distance of 200 mm be-

cause looking at closer objects is very uncomfortable

and these objects are hard to ﬁxate. Moreover, this

theoretical calculation has been corroborated by the

empirical results obtained in our experiments.

Figure 2: Theoretical angle difference of vergence and com-

parison with empirical values in setup range.

2.2 Estimation of 3D Gaze Position

The core idea of the proposed method is to cross the

gaze rays of both eyes and thereby determine the 3D

gaze position. Two steps have to be solved ﬁrst: we

have to determine the gaze ray of each eye and we

have to ﬁnd a solution to non-intersecting rays (which

in 3D space will be more common than actually inter-

secting rays).

To solve the ﬁrst issue we employ an

interpolation-based approach as described in Section

2.2.2. To address the second problem, we estimate

the intersection as the middle of the perpendicular

line between the two rays, or the point where the

interlinear distance is minimal.

Figure 3: Ray trace from eyes to PoR.

Two different algorithms have been tested for PoR

estimation using the line of sight. The ﬁrst one was

proposed by (Wang et al., 2014), while the second ap-

proach is a pure geometrical procedure based on the

Dan Sunday algorithm (Sunday, 2012). Despite be-

ing based on the same principles, the two methods

perform differently. Best results have been achieved

with the method proposed by (Wang et al., 2014).

Based on (Wang et al., 2014), we propose an al-

gorithm that follows a two-step approach to estimate

an accurate 3D gaze position in non-virtual environ-

ments. In a ﬁrst step, a coarse depth approximation is

done. The second step reﬁnes the 3D PoR in order to

get the most accurate result possible. Both steps use

triangulation mappings based on (Wang et al., 2014).

However, the method presented in this paper differs at

several steps:

• Our method is able to use calibration points from

different depth layers. Therefore, we are able to

calibrate not only in one plane but also the depth

layer and to include subject-speciﬁc effects.

• We apply the method to an experimental dataset

in a real-world environment, outside of a virtual

reality and without stereoscopic displays.

• The polynomial mapping function as well as the

pupil center detection of the ﬁrst algorithm step is

included in our procedure and not provided by a

commercial eye-tracking software. Therefore, we

can apply a custom mapping function and have

full control over the estimation process.

• We do not rely on smoothing ﬁlters and can there-

fore shorten the execution time of the algorithm.

Since experimental measurements have shown

that using only one plane for getting the interpolated

3D Gaze Estimation using Eye Vergence

127

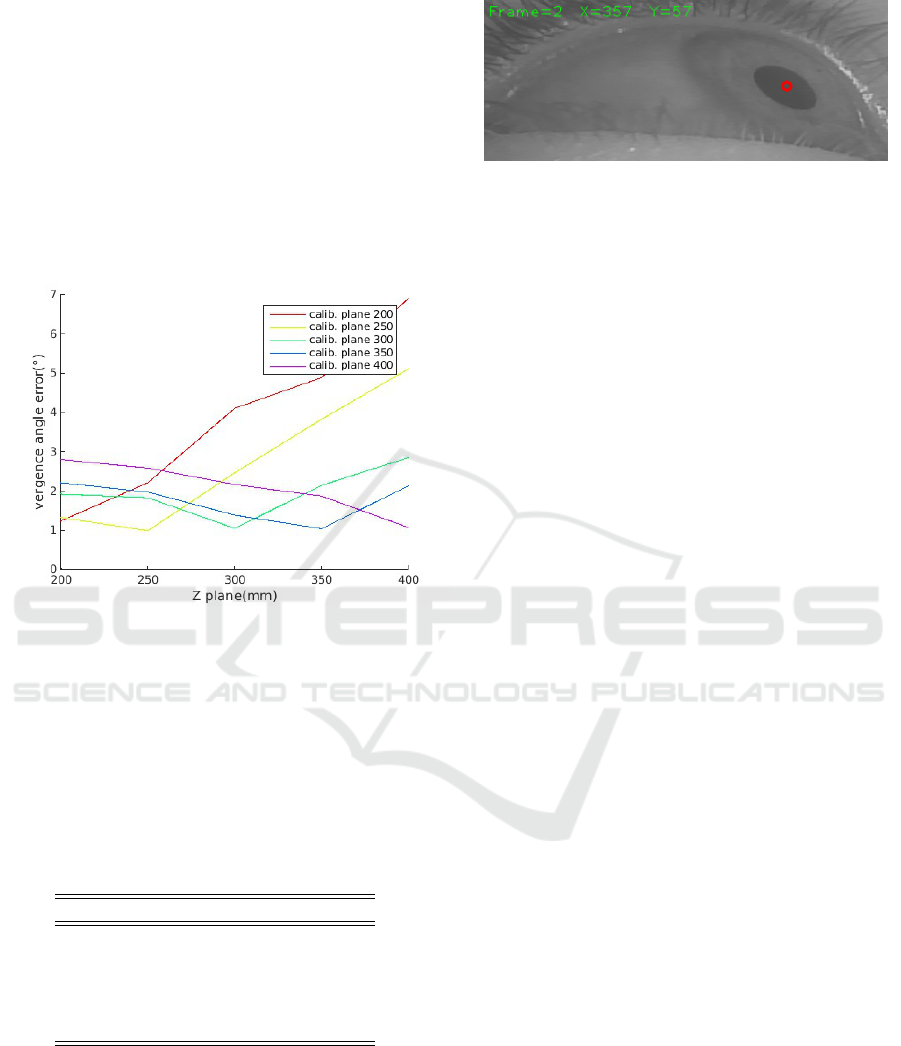
points to calculate the line of sight (LoS) is not accu-

rate enough, we have used different base planes for

interpolation. Additionally, error rises accordingly as

the PoR lies further away from the interpolation plane

(see Figure 4). This problem is solved by selecting

the closest interpolation plane for calculating PoR. In

the ﬁrst step, we used the ﬁrst interpolation plane to

get an approximate vergence angle. This vergence an-

gle is used with a pre-calculated table (see Table 1) to

select the closest interpolation plane to the PoR. Then

the selected interpolation plane is used to calculate an

accurate PoR position in 3D.

Figure 4: Vergence angle error using different calibration

planes.

Table 1 is determined in a calibration procedure.

This procedure consists of calculating the median ver-

gence angle of 16 calibration points for each depth

plane. All the points are on the selected plane (see

Figure 7) and the vergence angles are calculated for

each point using the eye positions and the target point.

Table 1: Relationship between eye vergence and viewing

distance.

Distance (mm) Vergence Angle (°)

200 14.4

250 11.6

300 9.3

350 7.4

400 6.1

2.2.1 Pupil Position Calculation

In order to test the accuracy of the calibration method

and to reduce other error sources, pupil center posi-

tions were determined by the ExCuSe algorithm (Fuhl

et al., 2015a) ﬁrst and checked manually afterwards

(see Figure 5).

Figure 5: Pupil position detected by the custom developed

program.

2.2.2 Interpolation Function

Interpolation is one of the fundamental steps used

in feature-based gaze estimation (Chennamma and

Yuan, 2013). The basis of this method is to obtain

a polynomial function that relates the pupil position

in the eye image to a position on a screen or a plane in

space. The polynomial coefﬁcients are approximated

using a regression analysis. We tested different poly-

nomial mapping functions. A 2

order polynomial

function (see Equation 1) showed best results and is

therefore used in this work. This is consistent with a

study by (Cerrolaza et al., 2012) that concludes that

higher order polynomials do not improve the system

behavior.



PoR



eye

= C

eye













(1)

where PoR

and PoR

are the interpolated points in the

plane of one eye, ϑ

and ϑ

are the pupil center posi-

tion of an eye in the image and C

eye

is the coefﬁcients

matrix for this eye.

3 EXPERIMENTAL EVALUATION

3.1 Setup

To corroborate our method for gaze estimation, an

experimental setup has been developed. The aim of

this setup is to provide empirical validation of PoR

estimation in a real environment only by using the

vergence angle information. The test setup com-

prises a chin rest for ﬁxing the subject’s head posi-

tion, a moving actuator for changing depth plane (Z

plane) and a head-mounted camera device (see Fig-

HEALTHINF 2016 - 9th International Conference on Health Informatics

128

Figure 6: Experimental setup for calibration and evaluation. The complete setup is transportable and consists of a camera and

a motorized linear rail system for moving the target.

ure 6). The moving actuator supports a transparent

Plexiglas

panel with 25 marker points (see Figure 7).

The test procedure consisted of asking the subject

to look at speciﬁc points on the panel (numbered 1

to 25) at different depths. The points were separated

3 cm from each other covering an area of 20 × 20

. The central point was located in the middle be-

tween the subject’s eyes. The Plexiglas

plane was

presented at 20, 25, 30, 35 and 40 cm distance from

the subject. The full workspace covered volume of 20

× 20 × 20 cm

. Later on, 16 points of the panel were

used for calibration and all 25 points were used for

evaluation of the algorithm (see Figure 7).

Figure 7: Grid pattern presented to the subjects. The red

colored circles are used for calibration. Additionally the

blue circles are used for evaluation.

During the experiment, images of the subject’s

eyes were taken in the exact time when the subject

ﬁxated a speciﬁc point. These images of 720 × 480

pixels resolution were used to calculate the pupil po-

sition.

Six subjects took part in the experiment. The age

of participants varied between 22 and 34 years, re-

cruited on a voluntary basis. All subjects have nor-

mal vision except for one, who was wearing correc-

tive contact lenses, which did not affect the test.

3.2 Results

Table 2 represents the error between the estimated and

the real position for all the points. Error for each

axis, Euclidean distance and angular difference (see

Equation 2) are shown for each Z plane. Furthermore,

overall average and standard deviation from all planes

are presented.

Dist. =

−X

)

+ (Y

−Y

)

+ (Z

−Z

)

dot p = X

∗X

∗Y

+ Z

∗Z

lenSq

= X

+ Z

lenSq

= X

+ Z

Angle = arccos(

dot p

√

lenSq

∗lenSq

)

(2)

where r is real position and e is estimated position.

The results show an average error of 1.2°, which

lies within our expectations. As shown previously in

Figure 2, this accuracy allows us to estimate PoR in a

distance below 400 mm.

The accuracy of the proposed algorithm can be

compared with a model-based method such as the

one proposed by Hennessey (Craig Hennessey, 2009).

Both algorithms estimate PoR in non-virtual scenarios

for planes positioned at 200 - 400 mm from the sub-

ject. The comparison is made only in terms of the

distance error for each axis and Euclidean distance.

The method proposed by Wang (Wang et al., 2014)

employs 5 planes positioned at 380 - 620 mm from

the subject, separated 6 cm from each other. It is dif-

ﬁcult to infer precise values from the data shown in

(Wang et al., 2014), therefore, we made a rough esti-

mation of their results using the histogram bars pro-

vided. Table 3 presents a comparison of these three

methods. As shown in Table 3, our method achieves

signiﬁcantly better accuracy, especially with respect

to the Z axis. It is noticeable, that this level of accu-

racy is achieved without using additional infrared il-

lumination and the experiments have been carried out

3D Gaze Estimation using Eye Vergence

129

Table 2: Average accuracy and standard deviation of 3D PoR estimation over the workspace for all subjects.

Z Depth Average Accuracy (mm) Average Accuracy Standard Deviation

(mm) X Y Z Euc. (°) (mm) (°)

200 3.5 4.3 9.1 10.8 1.2 8.6 0.6

250 2.7 3.6 8.6 10.5 0.8 9.4 0.8

300 2.3 3.1 10.4 13.3 1.2 7.4 0.8

350 3.8 4.4 18.7 20.8 1.5 8.9 0.6

400 2.4 3.7 14.5 15.9 1.2 8.5 0.5

Overall 2.9 3.8 12.3 14.3 1.2 8.6 0.7

in a natural setting, in contrast to related approaches

that use 3D displays.

Table 3: Average results for the ﬁve depth positions for

the proposed method and state-of-the art as presented in

(Craig Hennessey, 2009) and (Wang et al., 2014).

Method Avg. accuracy (mm) Std.dev.

(mm) X Y Z Euc. (mm)

Ours 2.9 3.8 12.3 14.3 8.6

Hennessey 12.7 12.0 32.3 39.3 28.3

Wang ≈ 25 ≈ 20 ≈ 42 ≈ 53.2 -

The proposed method enables a robust calculation

of the gaze point in 3D as required in several applica-

tion ﬁelds, e.g., in the context of assistive technology

(especially where gesture and gaze is coupled for in-

teraction (Lukic et al., 2014)) or for gaze-based inter-

action with multimedia in the car. In our future work,

we will integrate the proposed method in operation

microscopes in order to enable gaze-based autofocus.

Thus, instead of manual focusing, the ﬁxations loca-

tions of the surgeon will be analyzed in an online fash-

ion (e.g., as in (Tafaj et al., 2012)) and coupled with

the vergence information to determine the focus depth

in an automated way. Despite the above use cases,

the proposed method could improve current develop-

ments based on 2D eye tracking (Lopes et al., 2012)

with detailed 3D gaze point selection.

4 CONCLUSIONS

We presented an accurate method for gaze point esti-

mation in 3D based on the eye vergence calculated

from eye-tracking data. Our evaluation in a natu-

ral setting with 6 subjects, 5 different depth planes,

and a total number of 125 calibration points showed

that our method achieves a high average accuracy of

1.2°. According to our experimental measurements,

the upper limit for the viewing distance when less

than 1°accuracy is required, is 400 mm from the ob-

server. Future work will include incorporating dif-

ferent pupil detection algorithms, e.g. (Fuhl et al.,

2015b), and ﬁnding the optimum number of interpo-

lation planes within the range 200 - 400 mm.

ACKNOWLEDGEMENTS

This project has been founded by the Inter-University

Center for Medical Technologies Stuttgart - T

ubingen

(IZST) and Carl Zeiss Meditec AG.

REFERENCES

Braunagel, C., Stolzmann, W., Kasneci, E., and Rosenstiel,

W. (2015). Driver-activity recognition in the context

of conditionally autonomous driving. In 2015 IEEE

18th International Conference on Intelligent Trans-

portation Systems (ITSC), pages 1652–1657.

Cassin, B., Rubin, M. L., and Solomon, S. (1984). Dictio-

nary of eye terminology. Triad Publishing Company.

Cerrolaza, J. J., Villanueva, A., and Cabeza, R. (2012).

Study of Polynomial Mapping Functions in Video-

Oculography Eye Trackers. ACM Transactions on

Computer-Human Interaction, 19(2):1–25.

Cheng, A. C., Rao, S. K., Cheng, L. L., and Lam, D. S.

(2006). Assessment of pupil size under different light

intensities using the procyon pupillometer. Journal of

Cataract & Refractive Surgery, 32(6):1015–1017.

Chennamma, H. and Yuan, X. (2013). A Survey on

Eye-Gaze Tracking Techniques. arXiv preprint

arXiv:1312.6410, 4(5):388–393.

Craig Hennessey, P. L. (2009). Noncontact binocular eye-

gaze tracking for point-of-gaze estimation in three di-

mensions. IEEE Transactions on Biomedical Engi-

neering, 56(3):790–799.

Davson, H. (2012). Physiology of the Eye. Elsevier.

Dodgson, N. A. (2004). Variation and extrema of human

interpupillary distance,” in stereoscopic displays and

virtual reality systems. In Proc. SPIE 5291, pages 36–

46.

Duchowski, A. T. (2007). Foveated Gaze-Contingent Dis-

plays for Peripheral LOD Management , 3D Visual-

ization , and Stereo Imaging. 3(4).

Duchowski, A. T., Medlin, E., Gramopadhye, A., Melloy,

B., and Nair, S. (2001). Binocular eye tracking in VR

HEALTHINF 2016 - 9th International Conference on Health Informatics

130

for visual inspection training. Proceedings of the ACM

symposium on Virtual reality software and technology

- VRST ’01, page 1.

Essig, K., Pomplun, M., and Ritter, H. (2006). A neural net-

work for 3D gaze recording with binocular eye track-

ers. International Journal of Parallel, Emergent and

Distributed Systems, 21(February 2015):79–95.

Fletcher, L., Loy, G., Barnes, N., and Zelinsky, A. (2005).

Correlating driver gaze with the road scene for driver

assistance systems. Robotics and Autonomous Sys-

tems, 52(1):71–84.

Fuhl, W., K

ubler, T. C., Sippel, K., Rosenstiel, W., and

Kasneci, E. (2015a). Excuse: Robust pupil detec-

tion in real-world scenarios. In Azzopardi, G. and

Petkov, N., editors, Computer Analysis of Images and

Patterns - 16th International Conference, CAIP 2015,

Valletta, Malta, September 2-4, 2015 Proceedings,

Part I, volume 9256 of Lecture Notes in Computer Sci-

ence, pages 39–51. Springer.

Fuhl, W., Santini, T. C., Kuebler, T., and Kasneci,

E. (2015b). ElSe: Ellipse Selection for Ro-

bust Pupil Detection in Real-World Environments.

arxiv:1511.06575.

Gidl

of, K., Wallin, A., Dewhurst, R., and Holmqvist, K.

(2013). Using eye tracking to trace a cognitive pro-

cess: Gaze behaviour during decision making in a nat-

ural environment. Journal of Eye Movement Research,

6(1):1–14.

Healy, A. F. and Proctor, R. W. (2003). Handbook of psy-

chology: Experimental psychology.

Hillaire, S., Lecuyer, A., Cozot, R., and Casiez, G. (2008).

Using an eye-tracking system to improve camera mo-

tions and depth-of-ﬁeld blur effects in virtual environ-

ments. In Virtual Reality Conference, 2008. VR ’08.

IEEE, pages 47–50.

Howard, I. P. (2012). Depth from accommodation and ver-

gence. In Perceiving in DepthVolume 3 Other Mech-

anisms of Depth Perception, pages 1–14. Oxford Uni-

versity Press (OUP).

Kandel, E. R., Schwartz, J. H., and Jessell, T. M. (2000).

Principles of neural science. McGraw-Hill, New

York.

Kasneci, E., Kasneci, G., K

ubler, T. C., and Rosenstiel, W.

(2015). Online Recognition of Fixations, Saccades,

and Smooth Pursuits for Automated Analysis of Traf-

ﬁc Hazard Perception. In Artiﬁcial Neural Networks,

volume 4 of Springer Series in Bio-/Neuroinformatics,

pages 411–434. Springer International Publishing.

Kasneci, E., Sippel, K., Heister, M., Aehling, K., Rosen-

stiel, W., Schiefer, U., and Papageorgiou, E. (2014).

Homonymous visual ﬁeld loss and its impact on vi-

sual exploration: A supermarket study. TVST, 3(6).

Kasthurirangan, S. (2014). Current methods for objectively

measuring accommodation. Presented as AAO Work-

shop on Developing Novel Endpoints for Premium In-

traocular Lenses.

Kourkoumelis, N. and Tzaphlidou, M. (2011). Eye safety

related to near infrared radiation exposure to biometric

devices. The Scientiﬁc World Journal, 11:520–528.

Lopes, P., Lavoie, R., Faldu, R., Aquino, N., Barron, J.,

Kante, M., and (advisor, W. M. (2012). Icraft eye-

controlled robotic feeding arm technology members.

Lukic, L., Santos-Victor, J., and Billard, A. (2014). Learn-

ing robotic eye—arm—hand coordination from hu-

man demonstration: A coupled dynamical systems ap-

proach. Biol. Cybern., 108(2):223–248.

Mulvey, F., Villanueva, A., Sliney, D., Lange, R., Cotmore,

S., and Donegan, M. (2008). Exploration of safety

issues in eyetracking. Technical Report IST-2003-

511598, COGAIN EU Network of Excellence.

Reichelt, S., Haussler, R., F

utterer, G., and Leister, N.

(2010). Depth cues in human visual perception

and their realization in 3D displays. In Three Di-

mensional Imaging, Visualization, and Display 2010,

pages 76900B–76900B–12.

Rogers, A. (1988). Mosby’s guide to physical examination.

Journal of anatomy, 157:235.

Schaeffel, F., Wilhelm, H., and Zrenner, E. (1993). Inter-

individual variability in the dynamics of natural ac-

commodation in humans: relation to age and refrac-

tive errors. The Journal of Physiology, 461(1):301–

320.

Shih, S.-W. and Liu, J. (2004). A novel approach to 3-d gaze

tracking using stereo cameras. IEEE Transactions on

Syst. Man and Cybern., part B, 34:234–245.

Sunday, D. (2012). Distance between 3d lines & segments.

Swirski, L. and Dodgson, N. (2013). A fully-automatic,

temporal approach to single camera, glint-free 3D eye

model ﬁtting. Proc. PETMEI.

Tafaj, E., Kasneci, G., Rosenstiel, W., and Bogdan, M.

(2012). Bayesian online clustering of eye movement

data. In Proceedings of the Symposium on Eye Track-

ing Research and Applications, ETRA ’12, pages

285–288. ACM.

Wang, R. I., Pelfrey, B., Duchowski, A. T., and House, D. H.

(2014). Online 3D Gaze Localization on Stereoscopic

Displays. ACM Transactions on Applied Perception,

11(1):1–21.

3D Gaze Estimation using Eye Vergence

131