Exploiting Ambiguities in the Analysis of Cumulative Matching Curves

for Person Re-identiﬁcation

Vito Ren

, Angelo Cardellicchio

, Tiziano Politi

, Cataldo Guaragnella

and Tiziana D’Orazio

Institute of Intelligent Systems for Automation, Italian National Research Council, via Amendola 122 D/O,

70126 Bari, Italy

Dipartimento di Ingegneria Elettrica e dell’Informazione, Politecnico di Bari, via Orabona 4, 70126 Bari, Italy

Keywords:

Person Re-Identiﬁcation, Computer Vision, Video Surveillance.

Abstract:

In this paper, a method to ﬁnd, exploit and classify ambiguities in the results of a person re-identiﬁcation

(PRID) algorithm is presented. We start from the assumption that ambiguity is implicit in the classical for-

mulation of the re-identiﬁcation problem, as a speciﬁc individual may resemble one or more subjects by the

color of dresses or the shape of the body. Therefore, we propose the introduction of the AMbiguity rAte in RE-

identiﬁcation (AMARE) approach, which relates the results of a classical PRID pipeline on a speciﬁc dataset

with their effectiveness in re-identiﬁcation terms, exploiting the ambiguity rate (AR). As a consequence, the

cumulative matching curves (CMC) used to show the results of a PRID algorithm will be ﬁltered according to

the AR. The proposed method gives a different interpretation of the output of PRID algorithms, because the

CMC curves are processed, split and studied separately. Real experiments demonstrate that the separation of

the results is really helpful in order to better understand the capabilities of a PRID algorithm.

1 INTRODUCTION

One of the most interesting topics regarding the im-

provement of video surveillance systems is person re-

identiﬁcation (PRID), i.e. the re-identiﬁcation of the

same individual given two (or more) different views

acquired by a set of non-overlapping cameras cover-

ing the same environment.

This task has become a crucial topic in the last few

years, when the increased need for security originated

from events like the September 11th has led to the

deployment of a great number of video surveillance

cameras over crowded areas like airports or train sta-

tions. As these cameras produce a large, and often

hardly manageable, amount of raw video data, a way

to properly analyze and classify them without the in-

tervention of an human operator is needed.

The PRID task is complicated by a certain num-

ber of related problems, which can be divided in two

categories (Saghaﬁ et al., 2014):

• Intra-camera Issues: these issues are essentially

related to the internal conﬁguration of each cam-

era, and may reguard the low resolution of the sen-

sor, occlusion phenomena or different acquisition

conditions;

• Inter-camera Issues: these issues are essentially

related to the conﬁguration of the camera set, in

which each camera is subject to different lighting

conditions and may have different hardware fea-

tures.

The PRID methods proposed in literature try to

deal with these issues, extracting relevant information

from each view to properly characterize each individ-

ual. In order to do this, PRID methods use two kinds

of feature:

• Appearance: these features are related to the ap-

pearance of the individual, and include texture,

color and shape (Farenzena et al., 2010) (Gheis-

sari et al., 2006) (Roy et al., 2012) (D’Orazio and

Guaragnella, 2012);

• Non-appearance: these include features not re-

lated to the appearance of the individual, likegait

(Bauml and Stiefelhagen, 2011).

Various datasets have been acquired in order to

test the effectiveness of PRID methods (Bedagkar-

Gala and Shah, 2014), each one differing from the

others for the acquisition settings. Intuitively, not all

datasets are well suited to test every PRID algorithm,

as one dataset may present speciﬁc issues and advan-

tage the use of certain features; thus, the application

of the same algorithm to different datasets may give

484

Renò, V., Cardellicchio, A., Politi, T., Guaragnella, C. and D’Orazio, T.

Exploiting Ambiguities in the Analysis of Cumulative Matching Curves for Person Re-identiﬁcation.

DOI: 10.5220/0005822104840494

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 484-494

ISBN: 978-989-758-173-1

inconsistent results.

In this work, we address this problem introduc-

ing the Ambiguity Rate, an index that relies the results

given by a PRID algorithm with the speciﬁc dataset

against which this algorithm is being tested. The main

idea is to evaluate the statistical properties of the re-

sults given by the application of the PRID algorithm

of the results of the PRID method: informally speak-

ing, if an high variance is associated with these re-

sults, it may be reasonable to assume that the algo-

rithm is not well suited to operate on that speciﬁc

dataset; on the other side, if we obtain a low vari-

ance, the dataset is very ambiguous for these features,

so the algorithm works properly.

The rest of this paper is structured as follows. In

the second section, we formalize the basilar concept

of the PRID task. In the third section, we expose

our methodology, and we expose some results in the

fourth section. In the ﬁfth section, the conclusion and

some perspectives on the future works are given.

2 MATHEMATICAL

FORMULATION OF THE PRID

TASK

2.1 PRID Task

Given a generic image dataset D which can be parti-

tioned into a gallery set G and a probe set P, asso-

ciate to each image of G the subset of the images of P

which minimize a certain distance metric d.

Given c cameras, we hypothesize that each one

of them acquire exactly one frame for each of the n

individuals who pass through the video surveillance

system, so:

= n ∗ c

As a consequence, in the most generic case:

D = G ∪ P

= n = N

= n ∗ (c − 1) = N

Informally speaking, G contains exactly one view

per individual, while P may contain one or more

views per individual, according to the number of cam-

eras.

The PRID task is generically ascribable to what

we deﬁne as PRID pipeline, which is usually struc-

tured in three different steps. We hypothize that D

has already been splitted in G and P.

Image Segmentation. In this phase each frame is

subject to a pre-processing step, which includes

background subtraction ((Stauffer and Grimson,

1999), (Zivkovic, 2004), (Jojic et al., 2009),

(Ren

o et al., 2014),(Spagnolo et al., 2004)), hu-

man detection ((Dalal and Triggs, 2005), (Corvee

et al., 2012)) and shadow suppression ((Lu and

Zhang, 2007)), in order to discard noisy informa-

tion reguarding background and shadows.

Descriptor Extraction. In this phase a robust and

discriminative descriptor is computed per each

frame combining both texture and chromatic fea-

tures.

Descriptor Matching. In this phase the descriptor

of the each image belonging to G is compared

with the descriptors of the images belonging to P,

searching for the best match (i.e. the one which

minimize the distance metric d).

Over the years, various approaches to the different

phases of the PRID pipeline have been proposed. The

proposed methods can be classiﬁed in three ways.

2.1.1 Appearance vs. Non-appearance Methods

We can discriminate the PRID algorithm basing on

the kind of features used to extract the frame descrip-

tor, as stated in the ﬁrst section.

2.1.2 Single-shot vs. Multiple-shot Methods

We can discriminate the single-shot case from the

multiple-shot case evaluating both the cardinality of

G and P and the number of frames used to extract a

descriptor for the appearance of each individual.

In the single-shot case, the descriptor S

of the i-th

individual is computed as:

∀i ∈ D :



= g( f

)

= g( f

)

More informally, the cardinality of both the

gallery set and the probe set is equal to n, as there

are only two cameras which acquire exactly one view

per individual. As a consequence, for each individual

in G the signature S

is a generic function g(·) of the

unique frame f

related to the individual i, and this is

true also for the corresponding signature S

extracted

from the frame f

which depicts the individual in the

probe set.

The multiple-shot case is slightly different:

∀i ∈ D :



= g( f

)

= h( f

1,i

, ..., f

c,i

)

We note that the cardinality of G is strictly less

than the cardinality of P. It means that the function

Exploiting Ambiguities in the Analysis of Cumulative Matching Curves for Person Re-identiﬁcation

485

g(·) used to extract S

cannot be used to compute

, as it has to be modiﬁed to take in account c pa-

rameters, i.e. the f

frames related to the i-th individ-

ual, with j = 1, ..., c. We denote the modiﬁed function

used to extract S

with h(·).

Obviously, multiple-shot methods may provide a

richer and more discriminative descriptor than single-

shot methods, meaning that the PRID task is easier

in the multiple-shot case. A review about single-shot

and multiple-shot methods is given in (D’Orazio and

Cicirelli, 2012).

2.1.3 Contextual vs. Non-contextual Methods

Contextual PRID methods are strictly dependent on

the context of the video surveillance system. There

are two types of contextual PRID methods:

• Camera Geometry Methods: these methods ex-

ploit the spatial and temporal relationships be-

tween cameras in the dataset (Javed et al., 2008);

• Camera Calibration: these methods exploit cam-

era calibration or homography tecniques to ex-

tract discriminative descriptor for PRID purposes

(Lantagne et al., 2003).

Non-Contextual methods do not use context infor-

mation, and may be distinguished into passive meth-

ods, which do not rely on learning techniques for de-

scriptor matching, and active methods, which employ

supervised or unsupervised learning algorithms for

descriptor extraction or matching (Bedagkar-Gala and

Shah, 2014). Active methods can be further classiﬁed

into:

• Color Calibration Methods: these methods ex-

ploit color calibration techniques to model chro-

matic relationships between cameras in a given

camera set. Usually, a brightness transfer func-

tion (BTF) (D’Orazio et al., 2009) is learned be-

tween each pair of cameras in a training stage and

used to improve PRID robustness;

• Descriptor Learning Methods: these methods

evaluate the various features used to compute

the descriptor of each frame and choose the

most meaningful ones or at least a discriminative

weighting scheme to apply to a raw feature vector

in order to extract a robust descriptor (Zheng et al.,

2009; Wang et al., 2007; Gray and Tao, 2008);

• Distance Metric Learning Methods: these meth-

ods attempt to maximize the matching accuracy

between frame descriptors, employing a training

stage where a distance metric is learned throught

the resolution of a convex programming problem

which allows to evaluate a symmetric positive-

semideﬁnite matrix D that will be used in a

quadratic distance framework. A comprehensive

survey on these approaches is given in (Yang and

Jin, 2006).

Finally, the results are displayed on the Cumula-

tive Matching Characteristic (CMC) curve, that rep-

resents the expectation of ﬁnding the correct match

in the top n matches of the chosen algorithm ((Faren-

zena et al., 2010)). More speciﬁcally, the x axis of

such curve represents the rank and the y one the per-

centage of recognition (or the number of images rec-

ognized). For example, a CMC value of 50% for a

rank r means that the 50% of the images taken from

the gallery set can be found in a range of ranks be-

tween 1 and r, because of the cumulative nature of

the curve. An example of CMC is shown in Figure

2(a) and 2(b).

3 METHODOLOGY

3.1 Algorithm Description

The proposed algorithm, named AMARE, is divided

in three main steps, as it is shown in ﬁgure 1:

1. Ambiguity Descriptor calculation (in blue);

2. Ambiguity evaluation (in red);

3. CMC separation (in green).

The ﬁrst step takes place in a preprocessing phase,

while the other two need to be executed in a postpro-

cessing stage. This means that the PRID pipeline is

enriched by two modules that aim to quantify the ac-

curacy of a generic re-identiﬁcation algorithm. At-

tention will also be focused on the computational

complexity of the whole approach, as it is pointed out

in the corresponding subsection.

3.1.1 Ambiguity Descriptor Calculation

Given a generic dataset D, an Ambiguity Descrip-

tor (ad) is calculated for each frame. The ad is an

arbitrary-rank tensor that embeds information about

the kind of scene that is being observed, allowing het-

erogeneous features to be exploited in order to deﬁne

this kind of descriptor.

Nevertheless, we start from the assumption that an

operator who is manually supervising a surveillance

system will probably try to estimate the accuracy of

the results with respect to the color of the images re-

turned by the algorithm.

We follow the framework deﬁned in (Cardellic-

chio et al., 2015), using an ambiguity descriptor

which takes in account the tint of an image preserving

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

486

spatial information about the location of the speciﬁc

colour. Therefore, we divide the i-th frame of D in six

horizontal stripes and then calculate the trend value of

the Hue coordinate for each stripe, assuming that the

images are in the HSV format. Hence, the ad is a six

elements vector of natural numbers:













∈ N

(1)

∀i ∈ D

3.1.2 Ambiguity Evaluation

Given a set of q PRID algorithms to test

ALG = {α

, α

, . . ., α

} (2)

the best M results of each algorithm α

are stored in

a matrix R

while the respective ranks are stored in a

column vector K













∈ N

(3)







. . . r







∈ N

×M)

(4)

In the matrix there is one row for each image taken

from the gallery set G and the results are ordered by

descendant score of the speciﬁc algorithm within each

row. Since an r

i j

element is an image taken by the

probe set P with an ambiguity descriptor ad

i j

asso-

ciated to it, also these descriptors can be stored in an

Ambiguity Descriptor Matrix ADM

∈ N

×M)

that

has the same structure of the previous one. Conse-

quently, each element must be replaced by the de-

scriptor chosen in the preprocessing stage and ex-

ploited in order to obtain the Ambiguity Rate (AR).

In this work, the z-th row of ADM

is a matrix

ADM



, ad

, . . . , ad









. . . τ













τS







(5)

where τS

is the row vector that contains the trend

values of the M best frames with respect to the i-th

stripe. Such rows are used to calculate the percentage

deviation (%

) of the trend values while preserving

the spacial information about the Hue value using the

following formula:







max(τS

)−min(τS

)

256

max(τS

)−min(τS

)

256







(6)

Finally, the AR value is calculated as the average

value of the percentage deviations

= 1 −

∑

s=1

(s) (7)

so that an high variation of the percentual dis-

placement returns no ambiguity. This index is ready

to be used to correct the results of the CMC curve.

This task is described in the next subsection.

3.1.3 CMC Separation

The CMC curve is calculated as described in the pre-

vious paragraph using only the information about the

ranks (equation 3). The aim of this work is to split

this curve evaluating its building blocks, and this op-

eration can be achieved with the fuzziﬁcation of the

ranks according to the AR value in the following way:

[0, 0.4] ⇒ LOW

(0.4, 0.9] ⇒ MEDIUM

(0.9, 1] ⇒ HIGH

Therefore, the CMC curves can be calculated

again considering three different contributions that re-

ﬂect the three levels of the ambiguity rate.

3.2 Computational Complexity

The computational complexity of this approach is

strictly dependent on the parameters used to model

the ambiguities. The number of operations may sig-

niﬁcantly vary according to the descriptor chosen,

as it can be any n-dimensional tensor. Let N

+ N

) be the cardinality of the dataset that is be-

ing processed, N

the number of pixels and f (·) the

number of operations required by the task, the com-

putational complexities are the following:

1. Ambiguity Descriptor Calculation requires

O(k · N

· N

) operations to be processed, where

k =

∑

i=1

f (i)

is the sum of the number of operations needed

to calculate each element of the descriptor and K

represents the dimensionality of the descriptor.

Exploiting Ambiguities in the Analysis of Cumulative Matching Curves for Person Re-identiﬁcation

487

Figure 1: Algorithm high level ﬂowchart.

2. Ambiguity Evaluation has a complexity of O(q ·

M · N

)

Finally, the computational complexity of the am-

biguity rate process computation depends on N

while the one of the whole process depends on the

computational complexity of the most expensive al-

gorithm.

4 EXPERIMENTS AND RESULTS

The methodology described in this paper has been

tested on the PRID algorithms proposed in (Farenzena

et al., 2010) and (Cardellicchio et al., 2015), in order

to better understand the performances obtained on the

dataset VIPeR (Gray et al., 2007). This dataset con-

tains 632 images taken from non overlapping cameras

with arbitrary viewpoints. All the images have been

taken under varying illumination conditions and each

one is scaled to 128 × 48 pixels. In (Farenzena et al.,

2010), the authors use both color (MSCR and wHSV)

and texture (RHSP) features to recognize the subjects,

while in (Cardellicchio et al., 2015) only the color is

exploited (HSV and log RG). However, the approach

presented in this paper is focused on the interpretation

of the results with respect to the CMCs.

5 10 15 20 25 30 35 40 45 50

100

Cumulative Matching Characteristic

Rank

Recognition percentage

(a) Overall CMC - Algorithm (Farenzena et al., 2010)

5 10 15 20 25 30 35 40 45 50

100

Cumulative Matching Characteristic

Rank

Recognition percentage

(b) Overall CMC - Algorithm (Cardellicchio et al., 2015)

Figure 2.

Figures 2(a) and 2(b) report the overall CMC that

represent the state of art method used to measure

the performances of the algorithms on the chosen

dataset. Looking at the curves, algorithm (Farenzena

et al., 2010) works better than the other because the

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

488

Figure 3: Results given by the traditional PRID pipeline. Visual matching for algorithm (Cardellicchio et al., 2015). The ﬁrst

column GS represents the query images taken from the Gallery Set, the second one contains the Foreground Masks, while the

other columns are the responses taken from the Probe Set, ordered by the rank. The red box indicates the Ground Truth.

CMC starts from a higher value at the ﬁrst rank and

the values of the other ranks are always higher than

the ones of algorithm (Cardellicchio et al., 2015).

However, this curves present some drawbacks be-

cause they effectively embed information about the

re-identiﬁcation rank, but we actually don’t know if

the results for a speciﬁc rank have been obtained in

ambiguous situations or not. For example, given the

ﬁrst rank, it is not possible to determine if the re-

identiﬁcation percentage has been achieved in easy or

hard conﬁgurations. In fact, one would suppose that

in cases of low ambiguity, the correct result should be

returned at the ﬁrst iteration. On the contrary, worst

responses should be expected when the algorithm has

to choose among ambiguous observations. Further-

more, ﬁgure 3 gives a graphical overview of a certain

number of results. In this example, the ﬁrst six images

are correctly recognized by the algorithm because the

ﬁrst response is the one surrounded by the red box

that represents the ground truth, i.e. the right image

taken from the probe set that depicts the same subject

of the query image. Rows from 7 to 10 show that the

algorithm is giving a rank 2 response, while the last

two represent a failure because there is no recogni-

tion in the ﬁrst 20 responses. Looking at the images,

it is possible to notice that there is no regularity in the

responses with respect to the ambiguity. For exam-

ple, in the second row there is a person with a green

sweater, but the other images returned by the algo-

rithm are really different one from the other. For this

reason, the experiments presented in this section will

exploit the AR value to understand how a speciﬁc al-

gorithm is working given a speciﬁc ambiguity range.

First, the ambiguity descriptor is calculated ac-

cording to equation 1 for each image of the collection.

Then, the rest of the PRID pipeline is executed for

both algorithms and ﬁnally the results are processed

in order to calculate the ambiguity rate as described

in equation 7. In order to obtain a visual compari-

son of the least ambiguous result and the most am-

biguous one, an example of boxplot enriched by the

corresponding frames is provided in ﬁgure 5 and 6.

Each box refers to one of the stripes used to divide the

images, as noticeable in the ﬁgure, so it is represen-

tative of one row of the ADM described in equation

5. Moreover, there is a blue circle that indicates the

value of the ambiguity descriptor of the gallery set

image, i.e. the one that is being re-identiﬁed by the

algorithm. If the image taken from the gallery set is

re-identiﬁed correctly, the blue circle should lie inside

the box. Otherwise, the distance of the circle from the

box can be exploited to understand how far the im-

Exploiting Ambiguities in the Analysis of Cumulative Matching Curves for Person Re-identiﬁcation

489

Table 1: Dataset separation for different values of the ambiguity rate.

Ambiguity rate (Farenzena et al., 2010) (Cardellicchio et al., 2015)

LOW 46 img 7.28 % 18 img 2.85 %

MEDIUM 559 img 88.45 % 581 img 91.93 %

HIGH 27 img 4.27 % 33 img 5.22 %

age is from the results, and so quantify how much an

algorithm is doing wrong in a speciﬁc situation. In

the ﬁrst case (ﬁgures 5(a) and 5(b)) the situation is

so ambiguous that each person can easily be misin-

terpreted even by an expert human operator because

everyone wears similar clothes. In the second case

(ﬁgures 6(a) and 6(b)), the images of the probe set are

not so ambiguous, in fact the ﬁrst 5 returned values

are different one from the other: different colours of

the shirt/dress (red, black, white and yellow) and dif-

ferent colours of the trousers/skirt (pink, black, red,

jeans). Hence, a boxplot with large boxes will refer

to a non ambiguous response, that should basically

imply that the algorithm is operating in an easy con-

dition, so the correct response should be given at the

ﬁrst rank. On the contrary, small boxes are related to

ambiguous responses that are likely to be mistaken.

In this situation, a good PRID algorithm answers with

the correct image in one of the ﬁrst ranks, but not al-

ways at rank 1.

Figure 4 shows the ambiguity rate histogram for

each response of the two algorithms. It is immediate

to notice that a small number of responses has a corre-

sponding LOW ambiguity rate (< 0.4) or a HIGH one

(> 0.9), according to the fuzziﬁcation rule presented

in section 3.1.3.

Looking at Table 1, both algorithms are isolating

about 10% of the images in the tails of the distribu-

tion, namely the 5% of the results of the algorithms

has low ambiguity and similarly another 5% has high

ambiguity. Looking at the peak of the distribution

we observe that it is located around 0.6 for algorithm

(Farenzena et al., 2010), that means that a medium

level of ambiguity is produced most of the time. For

algorithm (Cardellicchio et al., 2015), the peak is lo-

cated around 0.7, that means that the responses are

more similar one to the other. The corresponding

CMC curves for LOW, MEDIUM and HIGH ambi-

guity rate values are reported in ﬁgure 7, 8 and 9 and

are called split CMC. For each curve, the x axis re-

ports the ﬁrst 100 ranks and the y axis shows the per-

centage of images that have been recognized at the

speciﬁc rank. Due to the cumulative nature of the

curve, if there is a step, it means that there are no

matches at the corresponding rank. For example, the

CMC in ﬁgure 7(b) illustrates that algorithm (Cardel-

licchio et al., 2015) does not have any match at ranks

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

AR histogram

AR 5

Images

(a) Ambiguity rate distribution for algorithm (Farenzena et al.,

2010). The peak is located around AR = 0.6.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

AR histogram

AR 5

Images

(b) Ambiguity rate distribution for algorithm (Cardellicchio et al.,

2015). The peak is located around AR = 0.7.

Figure 4: Ambiguity rate histogram on VIPeR results.

2, 3, 5 − 7, 9 − 19, 21 − 70 . . . , while the one in ﬁgure

7(a) is more similar to a curve, even if in some points

it is ﬂat (e.g. ranks 4, 5, 10 − 15. . . ). Here, algorithm

(Cardellicchio et al., 2015) shows a high percentage

than the other approach at rank 1. Such situation

should be the easiest for an algorithm, so the expected

result would be a really high percentage at rank 1.

The CMCs in ﬁgure 8(a) and 8(b) are similar to

the ones already known in literature because they are

representative of about 90% of the dataset. The last

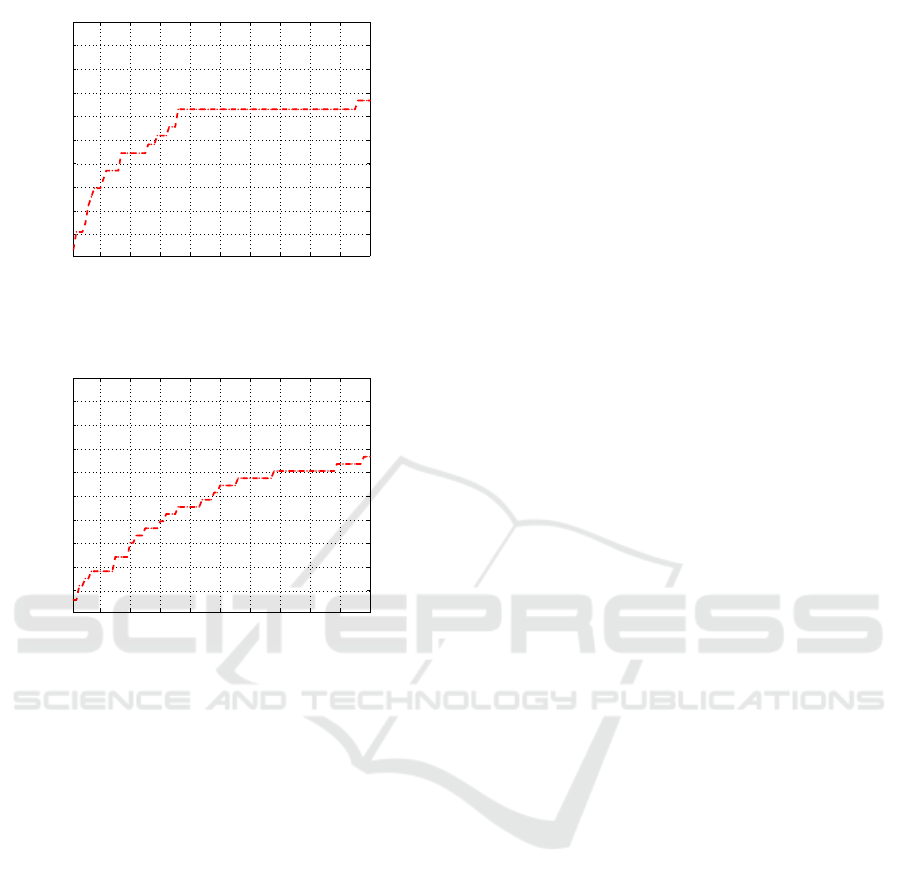
two curves indicate the response in HIGH ambigu-

ity cases. In both cases (ﬁgure 9(a) and 9(b)) there

is an increment of the correct answers starting from

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

490

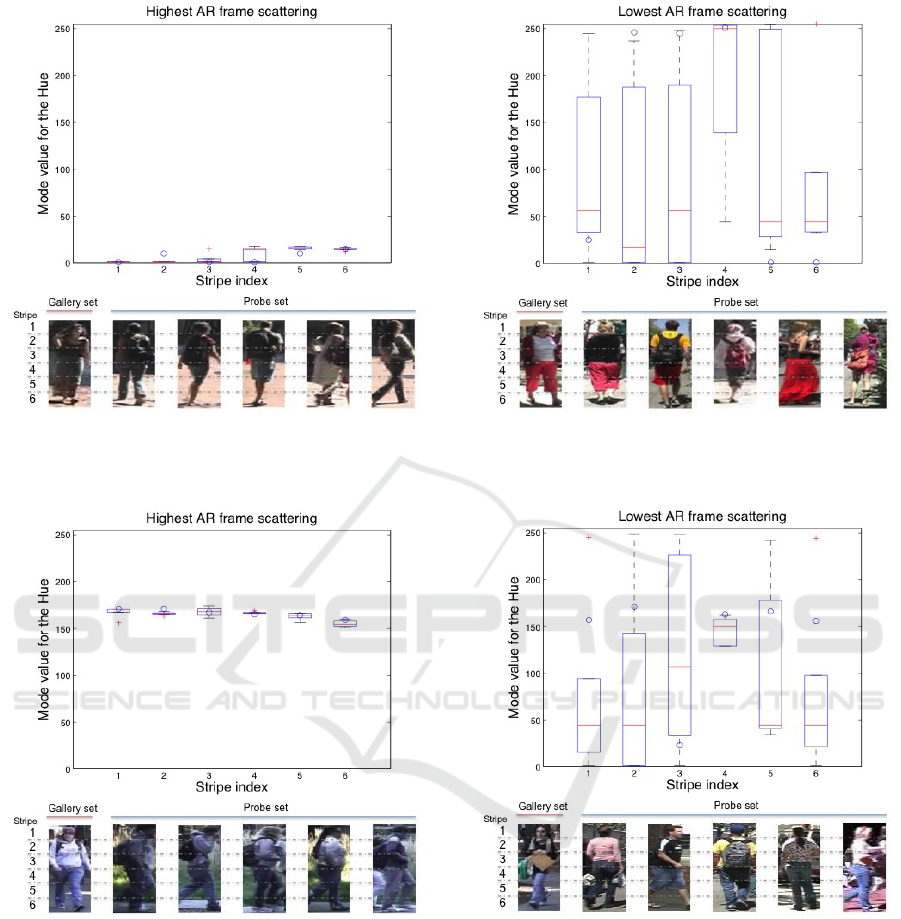
(a) Highest AR obtained with algorithm (Farenzena et al., 2010).

The visual matching represents the query image (gallery set) and

the ﬁrst 5 responses. The boxes are referred to the probe set, while

the circle represents the query.

(b) Highest AR obtained with algorithm (Cardellicchio et al.,

2015). The visual matching represents the query image (gallery set)

and the ﬁrst 5 responses. The boxes are referred to the probe set,

while the circle represents the query.

Figure 5: Boxplot comparison for the highest AR and visual

matching of the result.

rank 5. This is an interesting result because it means

that both approaches do not give meaningful answers

in the ﬁrst iterations when operating in challenging

situations. Focusing on low ranks, we notice that

the algorithms give similar results for both LOW and

MEDIUM ambiguity values. However, we expected

that the majority of the low rank responses occurred

in the condition AR < 0.4, thus obtaining the best re-

(a) Lowest AR obtained with algorithm (Farenzena et al., 2010).

The visual matching represents the query image (gallery set) and

the ﬁrst 5 responses. The boxes are referred to the probe set, while

the circle represents the query.

(b) Lowest AR obtained with algorithm (Cardellicchio et al., 2015).

The visual matching represents the query image (gallery set) and the

ﬁrst 5 responses. The boxes are referred to the probe set, while the

circle represents the query.

Figure 6: Boxplot comparison for the lowest AR and visual

matching of the result.

sults in easy conﬁgurations, i.e. when the images re-

turned are really different one from the other. Finally,

an algorithm should be able to increase the number

of images that lie in LOW or HIGH ambiguity val-

ues. In the ﬁrst case the recognition percentage at

rank 1 should be the highest, while in the second one

the correct response is expected within the ﬁrst ranks.

These quite uniform results for each ambiguity value

Exploiting Ambiguities in the Analysis of Cumulative Matching Curves for Person Re-identiﬁcation

491

10 20 30 40 50 60 70 80 90 100

100

CMC for results with AR below 0.4

Image rank

Percentage of images

(a) CMC referred to the low ambiguity results obtained with

algorithm (Farenzena et al., 2010). The cardinality of this set

is 46 images.

10 20 30 40 50 60 70 80 90 100

100

CMC for results with AR below 0.4

Image rank

Percentage of images

(b) CMC referred to the low ambiguity results obtained with

algorithm (Cardellicchio et al., 2015). The cardinality of this

set is 18 images.

Figure 7: CMC split comparison, LOW ambiguity values.

show how the features used by the algorithms can not

isolate easy recognizable situations for a human eye.

This is probably due to the representation of the col-

ors in different visual systems: the human one and

the digital one. For the ﬁrst, peaks on different color

tones can be immediately distinguishable, while in a

digital color space the same peaks can generate values

that are likely to be classiﬁed as similar colors even if

they are different.

5 CONCLUSION

In this paper, a method to quantify the accuracy of

a re-identiﬁcation algorithm exploiting the ambiguity

of its responses has been presented. This method en-

riches the PRID pipeline deﬁning an ambiguity de-

scriptor and taking advantage of it to calculate the AR

of each response of the algorithm. This ambiguity

can be seen as a relative one, because its formulation

is dependent on the results of the chosen algorithm,

10 20 30 40 50 60 70 80 90 100

100

CMC for results with AR between 0.4 and 0.9

Image rank

Percentage of images

(a) CMC referred to the medium ambiguity results obtained

with algorithm (Farenzena et al., 2010). The cardinality of this

set is 559 images.

10 20 30 40 50 60 70 80 90 100

100

CMC for results with AR between 0.4 and 0.9

Image rank

Percentage of images

(b) CMC referred to the medium ambiguity results obtained

with algorithm (Cardellicchio et al., 2015). The cardinality of

this set is 581 images.

Figure 8: CMC split comparison, MEDIUM ambiguity val-

ues.

as stated in equation 7 and it can be used to under-

stand the operative conditions in which the algorithm

works. Looking at the results presented in section 4,

the performances of a generic algorithm can be stud-

ied exploiting its behaviour in ambiguous and non

ambiguous situations. Moreover, the AR histogram

(ﬁgure 4) gives an immediate graphical description of

the ambiguity distribution among the images of a spe-

ciﬁc dataset. Finally, the split CMC curves can be

studied separately using this information to measure

the performance of different algorithms that run on

the same dataset. In conclusion, the work presented in

this paper can be seen as the ﬁrst step in the exploita-

tion of ambiguities in order to understand the results

of a PRID pipeline. Future research trends will re-

gard the extension of this approach in order to model

an absolute ambiguity value associated to a dataset.

Exploiting both relative and absolute ambiguities, a

generic rank of a CMC can be promoted or penal-

ized starting from the assumption that if an algorithm

gives for example a rank 3 output in an ambiguous

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

492

10 20 30 40 50 60 70 80 90 100

100

CMC for results with AR above 0.9

Image rank

Percentage of images

(a) CMC referred to the high ambiguity results obtained with

algorithm (Farenzena et al., 2010). The cardinality of this set

is 27 images.

10 20 30 40 50 60 70 80 90 100

100

CMC for results with AR above 0.9

Image rank

Percentage of images

(b) CMC referred to the high ambiguity results obtained with

algorithm (Cardellicchio et al., 2015). The cardinality of this

set is 33 images.

Figure 9: CMC split comparison, HIGH ambiguity values.

situation, then it can be promoted. Moreover, if an

algorithm does not give a rank 1 output in unambigu-

ous situations (e.g. the re-identiﬁcation of the only

one person dressed with dark clothes in a controlled

environment), then it can be penalized. Finally, the

research on the absolute ambiguity value should give

to an operator the possibility to compare different al-

gorithms that run on different datasets.

ACKNOWLEDGEMENTS

The authors would like to thank Mr. Michele Attolico

for his technical support.

REFERENCES

Bauml, M. and Stiefelhagen, R. (2011). Evaluation of lo-

cal features for person re-identiﬁcation in image se-

quences. In Adv. Video and Signal-Based Surveill.

(AVSS), 2011 8th IEEE Int. Conf. on, pages 291–296.

IEEE.

Bedagkar-Gala, A. and Shah, S. K. (2014). A survey of ap-

proaches and trends in person re-identiﬁcation. Image

and Vis. Comput., 32(4):270–286.

Cardellicchio, A., D’Orazio, T., Politi, T., and Ren

o, V.

(2015). An human perceptive model for person re-

identiﬁcation. In VISAPP-Int. Conf. on Comput. Vis.

Theory and Appl.-2015.

Corvee, E., Bak, S., Bremond, F., et al. (2012). People

detection and re-identiﬁcation for multi surveillance

cameras. In VISAPP-Int. Conf. on Comput. Vis. The-

ory and Appl.-2012.

Dalal, N. and Triggs, B. (2005). Histograms of oriented

gradients for human detection. In Comput. Vis. and

Pattern Recognit., 2005. CVPR 2005. IEEE Comput.

Soc. Conf. on, volume 1, pages 886–893. IEEE.

D’Orazio, T. and Cicirelli, G. (2012). People re-

identiﬁcation and tracking from multiple cameras: A

review. In Image Process. (ICIP), 2012 19th IEEE Int.

Conf. on, pages 1601–1604.

D’Orazio, T. and Guaragnella, C. (2012). A graph-based

signature generation for people re-identiﬁcation in a

multi-camera surveillance system. In VISAPP, vol-

ume 1, pages 414–417.

D’Orazio, T., Mazzeo, P., and Spagnolo, P. (2009). Color

brightness transfer function evaluation for non over-

lapping multi camera tracking. In Distrib. Smart Cam-

eras, 2009. ICDSC 2009. Third ACM/IEEE Int. Conf.

on, pages 1–6. IEEE.

Farenzena, M., Bazzani, L., Perina, A., Murino, V., and

Cristani, M. (2010). Person re-identiﬁcation by

symmetry-driven accumulation of local features. In

Comput. Vis. and Pattern Recognit. (CVPR), 2010

IEEE Conf. on, pages 2360–2367. IEEE.

Gheissari, N., Sebastian, T. B., and Hartley, R. (2006). Per-

son reidentiﬁcation using spatiotemporal appearance.

In Comput. Vis. and Pattern Recognit., 2006 IEEE

Comput. Soc. Conf. on, volume 2, pages 1528–1535.

IEEE.

Gray, D., Brennan, S., and Tao, H. (2007). Evaluating ap-

pearance models for recognition, reacquisition, and

tracking. In Proc. IEEE Int. Workshop on Perform.

Eval. for Track. and Surveill. (PETS), volume 3. Cite-

seer.

Gray, D. and Tao, H. (2008). Viewpoint invariant pedestrian

recognition with an ensemble of localized features. In

Comput. Vis.–ECCV 2008, pages 262–275. Springer.

Javed, O., Shaﬁque, K., Rasheed, Z., and Shah, M. (2008).

Modeling inter-camera space–time and appearance re-

lationships for tracking across non-overlapping views.

Comput. Vis. and Image Understanding, 109(2):146–

162.

Jojic, N., Perina, A., Cristani, M., Murino, V., and Frey,

B. (2009). Stel component analysis: Modeling spatial

correlations in image class structure. In Comput. Vis.

and Pattern Recognit., 2009. CVPR 2009. IEEE Conf.

on, pages 2044–2051. IEEE.

Lantagne, M., Parizeau, M., and Bergevin, R. (2003). Vip:

Exploiting Ambiguities in the Analysis of Cumulative Matching Curves for Person Re-identiﬁcation

493

Vision tool for comparing images of people. In Vis.

Interface, volume 2.

Lu, J. and Zhang, E. (2007). Gait recognition for

human identiﬁcation based on ica and fuzzy svm

through multiple views fusion. Pattern Recognit. Lett.,

28(16):2401–2411.

Ren

o, V., Marani, R., D’Orazio, T., Stella, E., and Nitti, M.

(2014). An adaptive parallel background model for

high-throughput video appl. and smart cameras em-

bedding. In Proc. of the Int. Conf. on Distrib. Smart

Cameras, ICDSC ’14, pages 30:1–30:6, New York,

NY, USA. ACM.

Roy, A., Sural, S., and Mukherjee, J. (2012). A hierarchical

method combining gait and phase of motion with spa-

tiotemporal model for person re-identiﬁcation. Pat-

tern Recognit. Lett., 33(14):1891–1901.

Saghaﬁ, M. A., Hussain, A., Zaman, H. B., and Saad, M.

H. M. (2014). Review of person re-identiﬁcation tech-

niques. IET Comput. Vis., 8(6):455–474.

Spagnolo, P., Leo, M., D’Orazio, T., and Distante, A.

(2004). Robust moving objects segmentation by back-

ground subtraction. In The International Workshop

on Image Analysis for Multimedia Interactive Services

(WIAMIS).

Stauffer, C. and Grimson, W. E. L. (1999). Adaptive back-

ground mixture models for real-time tracking. In

Comput. Vis. and Pattern Recognit., 1999. IEEE Com-

put. Soc. Conf. on., volume 2. IEEE.

Wang, X., Doretto, G., Sebastian, T., Rittscher, J., and Tu,

P. (2007). Shape and appearance context modeling. In

Comput. Vis., 2007. ICCV 2007. IEEE 11th Int. Conf.

on, pages 1–8. IEEE.

Yang, L. and Jin, R. (2006). Distance metric learning: A

comprehensive survey. Michigan State Universiy, 2.

Zheng, W.-S., Gong, S., and Xiang, T. (2009). Asso-

ciating groups of people. In Proc. of the British

Machine Vis. Conf., pages 23.1–23.11. BMVA Press.

doi:10.5244/C.23.23.

Zivkovic, Z. (2004). Improved adaptive gaussian mixture

model for background subtraction. In Pattern Recog-

nit., 2004. ICPR 2004. Proc. of the 17th Int. Conf. on,

volume 2, pages 28–31 Vol.2.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

494