
Is It Reasonable to Employ Agents in Automated Theorem Proving?
∗
Max Wisniewski and Christoph Benzm
¨
uller
Dept. of Mathematics and Computer Science, Freie Universit
¨
at Berlin, Berlin, Germany
Keywords:
ATP, Multi-Agent Systems, Blackboard Architecture, Concurrent Reasoning.
Abstract:
Agent architectures and parallelization are, with a few exceptions, rarely to encounter in traditional automated
theorem proving systems. This situation is motivating our ongoing work in the higher-order theorem prover
Leo-III . In contrast to its predecessor – the well established prover LEO-II – and most other modern provers,
Leo-III is designed from the very beginning for concurrent proof search. The prover features a multiagent
blackboard architecture for reasoning agents to cooperate and to parallelize proof construction on the term,
clause and search level.
1 INTRODUCTION
Leo-III (Wisniewski et al., 2014) – the successor
of LEO-I (Benzm
¨
uller and Kohlhase, 1998) and
LEO-II (Benzm
¨
uller et al., 2008) Leo-III – is a
higher-order automated theorem prover currently un-
der development at FU Berlin. It is supporting a poly-
morphically typed λ-calculus with nameless spine no-
tation, explicit substitutions and perfect term sharing.
On top of that it uses a multiagent blackboard archi-
tecture to parallelize the proof search.
The development of an automated theorem prover
(ATP) often follows a common pattern. Significant
time is spend on developing a new and more sophis-
ticated calculus. The automated theorem prover is
then designed as a sequential loop in which clause
creating inference steps of the calculus, and normal-
ization steps are performed alternately, just as in the
famous Otter loop (McCune, 1990). The theorem
prover may be augmented by means to collect and
employ additional information. For example, in order
to support its proof splitting technique, the AVATAR
(Voronkov, 2014) prover maintains and uses informa-
tion on models constructed by a SAT solver. Sim-
ilarly, LEO-II incorporates a first-order logic auto-
mated theorem prover.
Although parallelization is heavily used and re-
searched in computer science, there has not been
much impact on the automated theorem proving com-
munity. A possible explanation is that parallelization
introduces a range of additional challenges, whereas
∗
This work has been supported by the DFG under grant BE
2501/11-1 (Leo-III ).
the implementation of a state of the art sequential
prover is already challenging enough (and pays off
easier). Even though various architectures have been
proposed and studied (Bonacina, 2000), there are
not many provers experimenting with parallelization
(e.g. SETHEO derivatives SPTHEO (Suttner, 1997),
PARTHEO (Schumann and Letz, 1990), or ROO
(Lusk et al., 1992)). And, most of the existing im-
plementations are only subsequent parallelizations of
previously existing sequential theorem provers.
In Leo-III we are from the beginning developing
the prover for parallel execution. Just as its prede-
cessors, Leo-III aims at automating classical higher-
order logic (Benzm
¨
uller and Miller, 2014). In com-
parison to the state of the art in first-order auto-
mated theorem proving, higher-order automated the-
orem provers are still much less sophisticated. In par-
ticular, there exists no single calculus yet which is em-
pirically superior to all other calculi and the search
space can be much bushier e.g. due to instantiations
of propositional quantified variables.
Leo-III ’s design is influenced by the
Ω-ANTS system (Benzmller et al., 2008), an
agent-based command suggestion mechanism sup-
porting the user in an interactive theorem proving
environment. Each agent Ω-ANTS encompasses
one calculus rule. Leo-III exploits this idea and
eliminates the user from the system by letting the
agents compete for the execution of their solutions.
The underlying architecture used in Leo-III has
been made available as LEOPARD
2
(Wisniewski
et al., 2015). This reusable system platform serves
2
https://github.com/cbenzmueller/LeoPARD
Wisniewski, M. and Benzmüller, C.
Is It Reasonable to Employ Agents in Automated Theorem Proving?.
DOI: 10.5220/0005824702810286
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 1, pages 281-286
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
281

as a starting point to implement parallel, higher-order
theorem provers. In particular, it aims at lowering the
entry level for new developers in the area.
In the remainder of this position paper we address
the following question: How reasonable is it to em-
ploy agents in automated theorem proving? Our focus
is on higher-order logic and we outline a first imple-
mentation of a respective reasoner in LEOPARD.
2 HIGHER-ORDER LOGIC
Classical Higher-Order Logic is based on the simply
typed λ-calculus
3
by Alonzo Church.
The syntax of the simply typed λ-calculus is de-
fined in two layers – types τ, ν and terms s,t– over a
set of constants Σ, variables V and base types T .
τ,ν ::= t ∈T (Base type)
| τ → ν (Abstraction type)
s,t ::= X
τ
∈ V |c
τ
∈ Σ (Variable/Constant)
| (λX
τ
s
ν
)
τ→ν
|(s
τ→ν
t
τ
)
ν
(Term abstr./appl.)
Defining a logic in this syntax requires Σ to con-
tain a complete logical signature. In this case we
choose the signature {∨
o→o→o
,¬
o→o
,∀
(α→o)→o
} ⊆ Σ
for all α ∈ T and {o,i}⊆T to be the type of booleans
and individuals respectively. The remaining symbols
can be defined as usual. A term s
o
is called formula.
An example formula of this language is
∀(λA
i→o
.∃(λB
i→o
.∀(λX
i
.¬(AX) ∨(BX)))) (1)
Here, ∃(λX .ϕ) stands for ¬∀(λX . ¬ϕ). Interpreting
A,B as characteristic predicates for sets this formula
postulates, that each set has a superset. Note that by
exploiting λ abstraction, there is no need to introduce
an additional binding mechanism for quantifiers, pro-
vided the constants ∀ and ∃ are appropriately inter-
preted (see below).
To evaluate the truth value of a formula a model
M = ({D
α
}
α∈T
,I ) is introduced, where D
α
6=
/
0 is the
domain of objects for type α and I is an interpretation
assigning each symbol c
α
∈ Σ an object in D
α
.
Given a substitution σ for variables we can define
the valuation [.]
σ
M
:
[X
α
]
σ
M
= σ(X
α
)
[c
α
]
σ
M
= I (c
α
)
s
α→β
t
α
σ
M
=
s
α→β
σ
M
[t
α
]
σ
M
λX
α
.s
β
σ
M
= f
α→β
∈ D
α→β
s.t. for each z ∈ D
α
holds f z = [s]
σ◦[z/X
α
]
M
3
Although Leo-III actually supports a polymorphic typed
λ-calculus we will stick here to the simply typed λ-
calculus for a better understanding.
[A[T
γ
]]
α
∨C [L
γ
= R
γ
]
T
∨D
para
[A[R]]
α
∨C ∨D ∨[T = L]
F
C ∨[A
γ→β
C
γ
= B
γ→β
D
γ
]
F
dec
C ∨[A = B]
F
∨[C = D]
F
C ∨[A ∨B]
T
∨
T
C ∨[A]
T
∨[B]
T
C ∨[A ∨B]
F
∨
F
C ∨[A]
F
C ∨[B]
F
Figure 1: Selection of the rules of E P .
A formula s
o
is called valid, iff [s
o
]
σ
M
evaluates
to true under every substitution σ and every consid-
ered model M . We will only consider Henkin mod-
els (where the function domains do not necessarily
have to be full); for Henkin semantics sound and
complete calculi exist (Benzm
¨
uller and Miller, 2014).
For all the fixed signature {∨
o→o→o
,¬
o→o
,∀
(α→o)→o
}
we assume that I is fixed to the intended seman-
tics and D
o
only contains true and false. The
choice of I (∨
o→o→o
) and I (¬
o→o
) is obvious, and
I (∀
(α→o)→o
) is chosen to be a function, that applies
the first argument to ∀ to every element of the domain
D
α
; true is returned if the result of this application
leads to true in every case. With this interpretation of
∀
(α→o)→o
, it is easy to see that proposition is valid.
3 ATP
First- and higher-order ATPs cannot simply “com-
pute” the truth value of a formula. Instead, ATPs
“search” for proofs by employing sound and (ideally)
complete proof calculi. One of the earliest proof cal-
culi considered for automation is the resolution cal-
culus (Robinson, 1965). As most other proof calculi
for ATPs, the resolution calculus proves a formula by
contradiction. Resolution based provers first trans-
form the negated input problem into conjunctive nor-
mal form (cnf) and then they search for a proof us-
ing resolution and factorization rules. For first-order
ATPs the resolution approach, explicitly one of its en-
hanced versions the superposition calculus (Bachmair
and Ganzinger, 1994), seems to outperforms all other
calculi. In higher-order ATPs the race for a “best” ap-
proach is much less settled.
We here take a closer look at a higher-order calcu-
lus – the paramodulation calculus EP (Benzm
¨
uller,
1999), which is a derivative of the resolution approach
in the higher-order setting.
In Figure 1 a selection of rules of the calculus is
displayed. The last two rules ∨
T
and ∨
F
are part of
the clausification of the input problem. In an ATP
they can be exhaustively applied before all other rules
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
282

or be interleaved with the rest. The paramodulation
rule combines two clauses. It operates by replacing
a subterm T in a literal of the first clause with the
right-hand side of a positive equality literal [L = R]
T
in the second clause. This operation can of course
only be performed, if L and T can be made equal,
which is encoded in the literal [T = L]
F
and which
can be understood as a unification constraint for the
remaining clause.
Solving this unification constraint can be at-
tempted eagerly. Generally, however, we allow to
postpone its solution, since higher-order unification
is not decidable. Instead unification constraints are
handled in our approach by (unification) rules such
as dec, which now become explicit calculus rules.
dec decomposes an application and asserts equality
of function and argument individually.
A sequential theorem prover based on such a cal-
culus can be roughly implemented as follows:
wh ile ([ ] /∈ ac t i v e _ c l au s e s )
c < - a c t i v e _ c l a u s e s
new = cnf (c )
fo r e a ch ( c1 in new )
un ify ( c1 )
new += pa r m od ( c , a c t i v e _ c l a u s e s )
passiv _ c l a u s e s += c
active _ c l a u s e s += n ew
We focus here on E P for two reasons: First the
calculus of Leo-III , which is currently in develop-
ment, will be an adaptation of the superposition cal-
culus of first-order to higher-order. This calculus is
closely related to the paramodulation calculus by re-
stricting the newly created clauses by using ordering
constraints.
The second reason is, that in this special calcu-
lus most of the steps are local or have at least very
few dependencies outside of the inference. Hence,
there exist many points to parallelize this loop, with-
out introducing much overhead. Unifying the new
clauses is a task completely mutually independent and
hence, it can easily be parallelized. Same holds for
the paramodulation step with all active clauses. With
a bit more effort even the whole loop body can be par-
allelized, with a trick developed in ROO. This allows
to select multiple clauses at once and to perform the
loop body in parallel to itself.
Employing agents in other calculi is nonetheless
possible, but there exist more constraints on the in-
teractions. In a tableaux calculus, closing of a branch
(i.e. unification) is a highly dependent operation since
the implicit quantified variables are globally bound.
On the other hand, expanding and exploring the proof
tree is still possible to be performed in parallel by
agents.
4 MULTIAGENT BLACKBOARD
ARCHITECTURE
One important property of a multiagent system is, that
no single agent can solve a given problem by itself
(Weiss, 2013). This can be either achieved by a par-
tial view on the available information for each agent
or by limited capabilities of each agent. The idea of
the architecture of Leo-III is to maintain all informa-
tion on the current proof state globally available in a
blackboard. The general principle of a blackboard ar-
chitecture (Weiss, 2013) is that no expert (i.e. agent)
hides information.
Just as in Ω-ANTS, the agents in Leo-III are au-
tonomous implementations of inference or compound
rules. No single agent in Leo-III will (usually) be
able to solve an arbitrary given proof problem on its
own.
Even though these agents are in the main focus
implementing a multi-agent theorem prover, there are
additional agents one could add to the system. First,
we can incorporate external provers, just as done in
LEO-II with first-order provers. Leo-III can even let
higher-order provers compete and return the solution
of the first prover to finish in order to find a result.
Second, we can gather extra information from SAT
solvers or model finders as AVATAR does or simply
run different calculi in the same proof context. Lastly,
the system allows to analyze itself during the run and
adapt, for example the selection algorithm, to the cur-
rent demand. Most importantly, all these task are in-
herently executed in parallel.
The main problem in designing a blackboard ar-
chitecture is the access coordination of the agents
to the blackboard. Two agents may read the same
data. But the resulting state would be inconsistent,
if two agents write to the same position at the same
time. To solve this problem the action of an agent in
Leo-III is designed as a transaction. As known from
database systems, which suffer from the same prob-
lem, transactions are a common and elegant way to
deal with updating inconsistencies. In the context of
Leo-III these transactions are called tasks.
Leo-III operates in the following scheme (cf. Fig-
ure 2): Each agent perceives the proof state of the
blackboard. Upon change of the proof state the agent
decides on all actions he wants to execute and com-
mits them to a scheduler as a task. The scheduler se-
lects a non-conflicting set of tasks from all commit-
ted tasks and distributes them between the available
processes. Finally the result of the transaction are in-
serted into the blackboard and a new iteration of this
scheme is triggered.
Information distribution is performed through
Is It Reasonable to Employ Agents in Automated Theorem Proving?
283
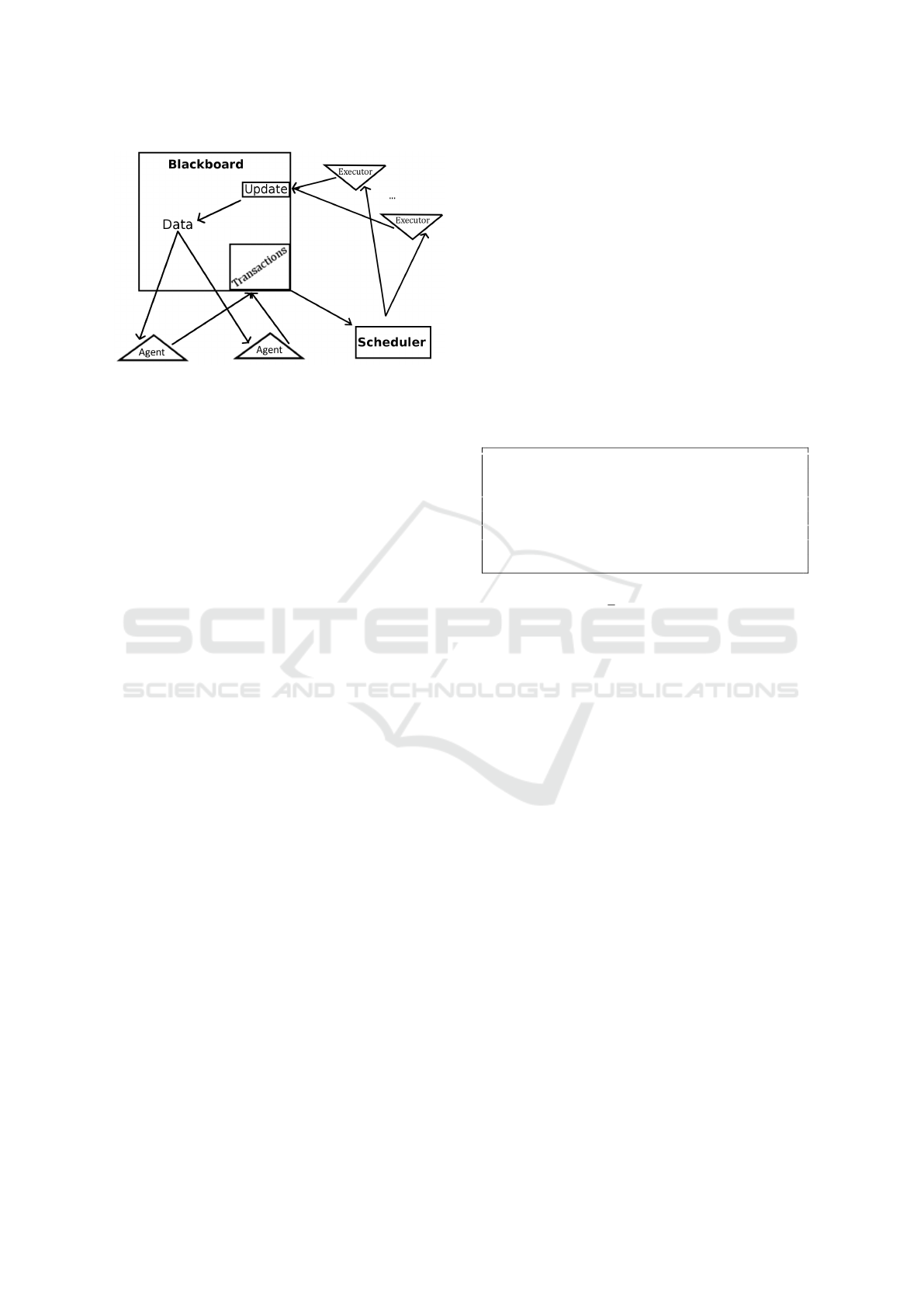
Figure 2: Parallelized Operation Loop of Leo-III .
messages to the agents. Although inspired by LINDA
(Gelernter et al., 1982) and JADE (Bellifemine et al.,
2001), the messaging will not actively interact with
the current execution of an agent. Agents handle a
message by creating a new task, based on the content
of the message. Just as in JADE the messages have
a structure, to define a message type and its contents.
Besides this there is no bigger protocol defined, since
most messages are information messages of updated
data in the blackboard.
The selection of non-conflicting tasks is a cru-
cial part in the development of the prover. A
wrong or one-sided selection of tasks could yield a
non-complete implementation of the calculus, which
might not only be unable to proof all valid formulas,
but find no proofs at all.
An interesting side-effect of implementing agents
through tasks is the inherent self-parallelization.
Since each agent can commit several tasks at once, it
is able to execute all of these tasks concurrently. An-
other feature of this agent implementation of a prover
is we can play more loosely with the completeness of
the system. As long as we can guarantee one com-
plete calculus can execute eventually, we can adorn
the system with incomplete, special purpose rules to
enhance the proof search.
5 TASK SELECTION
The idea of the selection is to let the agents com-
pete with each other which task should be executed.
Each agent supports for its own tasks a ranking in
which order it wants to execute the tasks. The rank-
ing should reflect the benefit of a task to the proof
search. The scheduler has then to select a set of non
conflicting tasks to maximize the benefit to the proof
search. This approach is similar to prominent heuris-
tics as Shortest-Job-Next or Highest-Response-Ratio-
Next for process schedulers with the addition, that se-
lecting one task can kill others.
This problem is a generalization of the combina-
torical auction (Nisan et al., 2007). In a combinator-
ical auction a bidder tries to achieve a set of items.
He wants either all of the items in the set or non of
them. The auctioneer has to assign the items to the
bidders, such that no item is shared by two bidders
and the revenue is maximal. The task auction we play
in our scheduler allows two kinds of items in the bid-
ders set: sharable items that are only read, and private
items that are also written. It is easy to see, that com-
binatorical auctions can be reduced to task auctions.
As in many scheduling problems the combinator-
ical auction is NP-complete. Luckily there exists a
fast approximation algorithm for combinatorical auc-
tions, that can be easily adapted for the task auction.
au c t i on ( t : 2
Task
):
ta ke =
/
0
wh ile ( t 6=
/
0):
i = argmax
x∈t
|
x.writeSet ∪x.readSet
|
ta ke = i :: tak e
t = {x ∈t |¬conflict(x,i)}
t = {y |x ∈t,y.r = x.r \i.r}
re t urn ta ke
For n bidders and k distinct items in t the algo-
rithm auction is a
√
k-approximation of the task auc-
tion and runs in O(k
2
n
2
) (Wisniewski, 2014).
The system runs by iterating this scheduling algo-
rithm. The runtime suggest to restrain the amount of
committed tasks per agent. In Leo-III each agent can
make its own preselection of tasks to keep the burden
on the scheduler to a minimum. To ensure that each
agent will eventually be able to execute, a natural ag-
ing is implemented: Each round an agent is granted
an income, which he can spend on its tasks. Hence
an agent that has been idle for a long time will have a
better chance to acquire one of its tasks.
One open problem for this approach is priority in-
version. Since we create a task only if it is possible
to execute, we are not able to track any dependen-
cies that might block a task. This problem can be
solved as soon as the ranking of the tasks is supervised
by the blackboard. As mentioned earlier we want to
build agents controlling the selection mechanism and
adapting it to the current situation. This mechanism
can be exploited by the agents to boost the importance
of their counterparts to push the importance of their
tasks. One could even think about a donation system
between the agents to model this behavior in the auc-
tion game.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
284
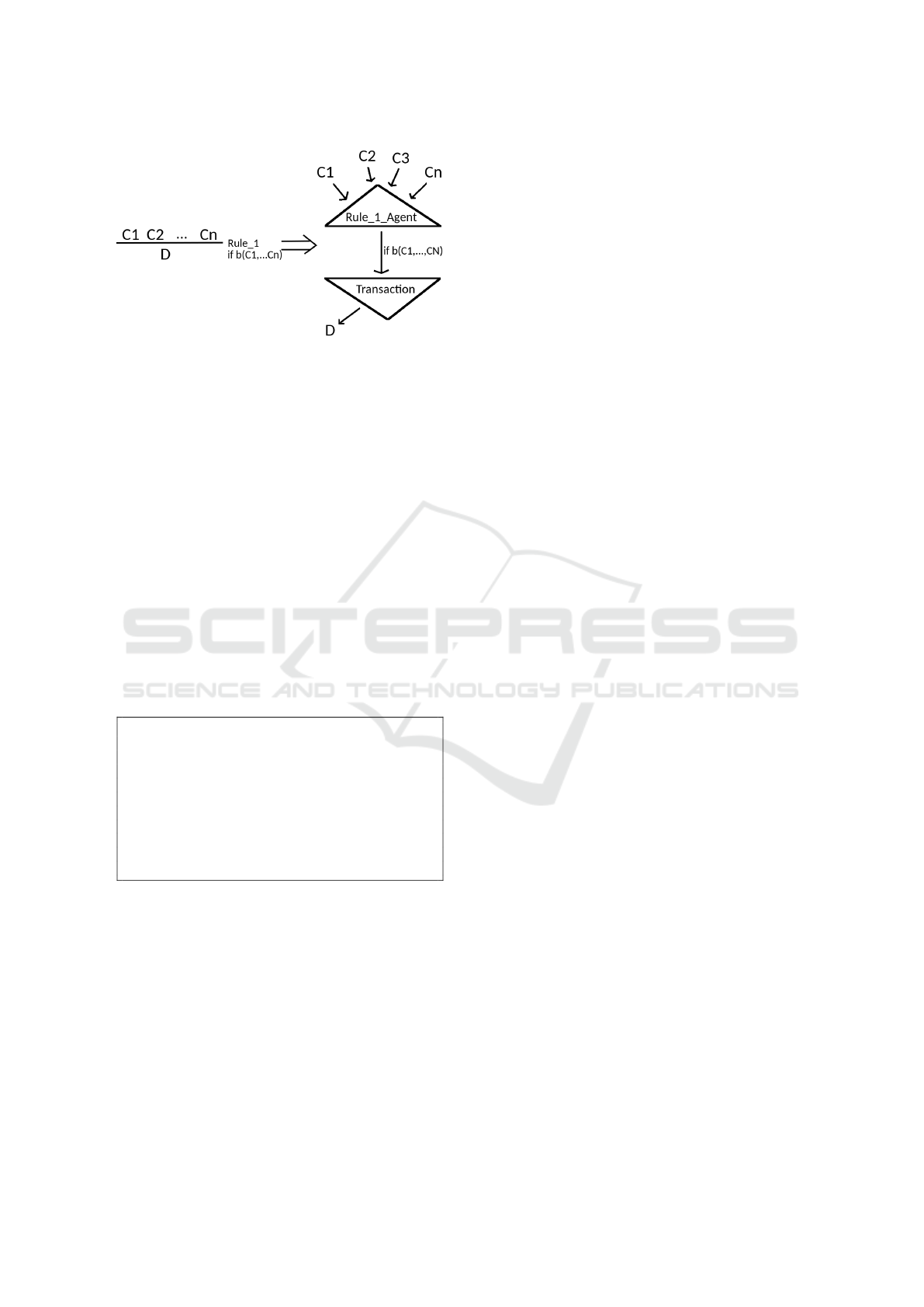
Figure 3: Transforming a rule into an agent.
6 RULE-BASED AGENTS
For a first test of the agent approach for theorem
proving we implemented the paramodulation calcu-
lus from Section 3 with the described agent archi-
tecture. As described in Figure 3 for each agent
we created an agent. This agents look at the black-
board and upon insertion of a new clause C
1
search
for compatible clauses. In this first, simple test the
blackboard only offered a set of clauses. Hence the
agent has to search all existing clauses for a part-
ners C
2
,...,C
n
. With these partners the inference con-
straints b(C
1
,...,C
n
) is tested. The calculation of the
result D is delayed as a transaction and send to the
scheduler.
Applying this structure to the inference rules of
E P we obtain agents of the following form:
Or F _ A g e n t {
On I n s e r t ( C ) if ( co n t a i n s O r F ( C )) - >
C ’ , A , B < - d e c o m p o s e O r F ( C )
Or F T a sk (C ’ , A , B )
}
Or F T a sk (C ’ , A , B ) {
ex e c u te ->
in s ert ( [ A ]ˆ F :: C ’ )
in s ert ( [ B ]ˆ F :: C ’ )
}
The agents can react on insertion triggers to look
at every inserted data, in this case a clause. In simple
rules as this clausification no further cooperation with
the blackboard is needed.
As already mentioned in this first implementation
this happened by iterating over all existing, active
clauses. But the blackboard allows it easily to add
specialized search data structures for each agent to
improve on the time for searching partners. To still
model part of the sequential loop behavior we intro-
duced the passive/active status by adding a selection
timer to all clauses considered for paramodulation.
The bid assigned to each task favored a small
amount of literals. The bid for a task is the wealth of
the agent divided by the amount of literals in the task.
Although there is not yet a completeness result for this
implementation, the idea to increasingly augment the
proof state beginning with the smallest clauses is one
of the promising options. Since this process enumer-
ates all valid clauses implied by the initial clauses, the
proof will eventually be found.
Astonishingly, this implementation yields an al-
ready powerful prover. For example, we were able
to proof some of the Boolean properties of sets from
the TPTP (SET014ˆ5, SET027ˆ5, SET067ˆ1, etc.)
including the distributivity law of union and intersec-
tion, and even the surjective cantor theorem. The later
one states that there cannot exist a surjective function
from a set to its superset or, in other words, a super-
set is strictly greater then the underlying set. Inter-
estingly, most of these theorems are very difficult for
first-order provers to solve. Anyhow, our initial exper-
iments indicate that a multiagent based proof search
approach is pragmatically feasible. More experiments
are clearly needed to assess the benefits and limits of
the approach.
7 FURTHER WORK
As soon as the general calculus for Leo-III is fixed
we will start experimenting on the granularity of the
rules. For the test implementation of EP we choose
to implement every inference rule as a single agent.
Commonly in the implementation we can identify rea-
sonable sequential workflow, e.g. a clause inferred in
a unification should be immediately simplified. The
first approach of agentifying the inference rules will
hence be extended to agentifying a tactic level of com-
pound rules.
Orthogonal to experimenting on the Leo-III cal-
culus applying agents to other calculi is possible. As
mentioned other calculi as tableaux calculus or nat-
ural deduction are more globally depended, but one
could look into a parallel approach to these calculi.
Even more interesting is the combination of differ-
ent calculi. This scenario is interesting, if the calculi
share the same search space, and hence can cooperate.
LEO-II uses first-order ATPs as subprovers. Peri-
odically, after conducting some higher-order specific
inferences, (part of) the proof context is translated
into a first-order representation and send to an exter-
nal prover. This is a direction, we again want to de-
velop Leo-III into. The agent architecture allows us
to run multiple instances of the subprovers in paral-
lel. Either with different proof modi (flag settings) or
varying proof obligations.
Is It Reasonable to Employ Agents in Automated Theorem Proving?
285

Concerning the auction scheduler we still have to
deal with priority inversion. As presented we can aug-
ment the auction scheduler with a donation system al-
lowing high priority agents to donate to low priority,
dependent agents. This augmentation should be tested
for performance and practicality.
8 CONCLUSION
We initially posed the question whether employing
agents in higher-order automated theorem proving is
reasonable. We have then provided some first evi-
dence that applying an agent architecture to higher-
order automated theorem proving is not only pos-
sible, but that even straightforward implementations
may yield promising systems in practice. First ex-
periments were successful, and for the open problems
multiple directions for further developments exist.
Besides the parallelization of a calculus, the
agent-based approach benefits from a high flexibil-
ity. It is easily possible to add and remove agents
from an inference, to a tactic up to a complete the-
orem prover layer. The high amount of parameters
in ATPs and the vast amount of small single tactics
in interactive provers indicate a great potential in the
agent technology. In traditional systems different set-
tings are tested sequentially and many shared tasks
(e.g. normalization) are duplicated and executed nu-
merous times. Running in a shared setting can reduce
this number significantly.
ACKNOWLEDGEMENTS
We would like to thank all members of the
Leo-III project.
REFERENCES
Bachmair, L. and Ganzinger, H. (1994). Rewrite-based
equational theorem proving with selection and simpli-
fication. J. Log. Comp., 4(3):217–247.
Bellifemine, Fabio and Rimassa, Giovanni (2001), De-
veloping Multi-agent Systems with a FIPA-compliant
Agent Framework. J. Softw. Pract. Exper., 31, pages
103–128, John Wiley & Sons.
Benzm
¨
uller, C. (1999). Extensional higher-order paramod-
ulation and RUE-resolution. In CADE, number 1632
in LNCS, pages 399–413. Springer.
Benzm
¨
uller, C. and Kohlhase, M. (1998). LEO – a higher-
order theorem prover. In CADE, number 1421 in
LNCS, pages 139–143. Springer.
Benzm
¨
uller, C. and Miller, D. (2014). Automation of
higher-order logic. In Siekmann, J., Gabbay, D., and
Woods, J., eds., Handbook of the History of Logic, Vol.
9 – Logic and Computation. Elsevier.
Benzm
¨
uller, C., Theiss, F., Paulson, L., and Fietzke, A.
(2008). LEO-II - a cooperative automatic theorem
prover for higher-order logic. In IJCAR, volume 5195
of LNCS, pages 162–170. Springer.
Benzmller, C., Sorge, V., Jamnik, M., and Kerber, M.
(2008). Combined reasoning by automated cooper-
ation. J. Appl. Log., 6(3):318 – 342.
Bonacina, M. (2000). A taxonomy of parallel strategies for
deduction. Annals of Mathematics and Artificial Intel-
ligence, 29(1–4):223–257.
Gelernter, David and Bernstein, Arthur J./1982) Distributed
Communication via Global Buffer. Proceedings of the
First ACM SIGACT-SIGOPS, PODC ’82, pages 10–
18. ACM.
Lusk, E. L., McCune, W., and Slaney, J. K. (1992). Roo:
A parallel theorem prover. In CADE, volume 607 of
LNCS, pages 731–734. Springer.
McCune, W. (1990). OTTER 2.0. In CADE, pages 663–
664.
Nisan, N., Roughgarden, T., Tardos, E., and Vazirani, V. V.
(2007). Algorithmic Game Theory. Cambridge Uni-
versity Press, New York, NY, USA.
Robinson, J. A. (1965). A machine-oriented logic based on
the resolution principle. J. ACM, 12(1):23–41.
Schumann, J. and Letz, R. (1990). Partheo: A high-
performance parallel theorem prover. In CADE, vol-
ume 449 of LNCS, pages 40–56. Springer.
Suttner, C. B. (1997). Sptheo - a parallel theorem prover. J.
Autom. Reason., 18(2):253–258.
Voronkov, A. (2014). AVATAR: the architecture for first-
order theorem provers. In CAV, volume 8559 in
LNCS, pages 696–710. Springer.
Weiss, G., editor (2013). Multiagent Systems. MIT Press.
Wisniewski, M. (2014). Agent-based blackboard architec-
ture for a higher-order theorem prover. Master’s the-
sis, Freie Universit
¨
at Berlin.
Wisniewski, M., Steen, A., and Benzm
¨
uller, C. (2014). The
Leo-III project. In Bolotov, A. and Kerber, M., editors,
Joint Automated Reasoning Workshop and Deduktion-
streffen, page 38.
Wisniewski, M., Steen, A., and Benzm
¨
uller, C. (2015).
Leopard - A generic platform for the implementation
of higher-order reasoners. In Kerber, M., et al., ed-
itors, CICM, volume 9150 of LNCS, pages 325–330.
Springer.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
286
