The Role of the Complex Extended Textural Microstructure

Co-occurrence Matrix in the Unsupervised Detection of the HCC

Evolution Phases, based on Ultrasound Images

Delia Mitrea

, Sergiu Nedevschi

and Radu Badea

Technical Unniversity of Cluj-Napoca, Department of Computer Science, Cluj-Napoca, Romania

Iuliu Hatieganu University of Medicine and Pharmacy of Cluj-Napoca,

Department of Medical Imaging, Cluj-Napoca, Romania

Keywords: Complex Extended Textural Microstructure Co-occurrence Matrix (CETMCM), Hepatocellular Carcinoma

(HCC), Evolution Phases, Unsupervised Classification, Ultrasound Images.

Abstract: The hepatocellular carcinoma (HCC) is a frequent malignant liver tumour and one of the main causes of death.

Detecting the HCC evolution phases is an important issue, aiming the early diagnosis of this tumour and

patient monitoring with maximum accuracy. Our objective is to discover the evolution stages of HCC, through

unsupervised classification techniques, using advanced texture analysis methods. In this work, we assessed

the role that the Haralick features derived from the Complex Extended Textural Microstructure Co-occurrence

Matrices (CETMCM) have in the unsupervised detection of the HCC evolution stages. A textural model for

these phases was also generated. The obtained results were validated by supervised classifiers, well known

for their performance, such as the Multilayer Perceptron (MLP), Support Vector Machines (SVM),

respectively decision trees and they were also compared with the previously obtained results in this domain.

The final classification accuracy was about 90%.

1 INTRODUCTION

The hepatocellular carcinoma (HCC) is the most

frequent malignant liver tumour, present in 75% of

the liver cancer cases. It evolves from cirrhosis, after

a liver parenchyma restructuring phase, towards the

end of which dysplastic nodules that can turn into

HCC result. Detecting HCC in early evolution stages

presents a major importance. Also, accurately

identifying the evolution stage is essential, in order to

adopt the appropriate treatment (Sherman, 2005).

Ultrasonography (US) is a safe method for patient

examination, non-invasive, inexpensive, easy to

apply and, thus, repeatable. Other medical imaging

based examination methods, such as the computer

tomography (CT), the magnetic resonance imaging

(MRI), or the contrast enhanced ultrasonography

(CEUS) are irradiating or expensive. In ultrasound

images, HCC appears, in incipient phases, as a small

lesion, having 3-4 cm in size. In more advanced

stages, the most relevant characteristic of HCC is the

heterogeneity, due to the co-existence of fibrosis,

regeneration nodules, hepatocitar necrosis and fat

cells. Advanced HCC is also featured by a very

complex structure of vessels. Thus, HCC is usually

hypoechogenic and homogeneous in the incipient

phase and during its evolution, it usually becomes

inhomogeneous and hyperechogenic. The most

frequent form of HCC is the focal, encephalic form.

There are, however, multiple variants observed for

the encephalic form of HCC, within the ultrasound

images, most of them being associated to a certain

evolution phase (American Liver Foundation, 2015).

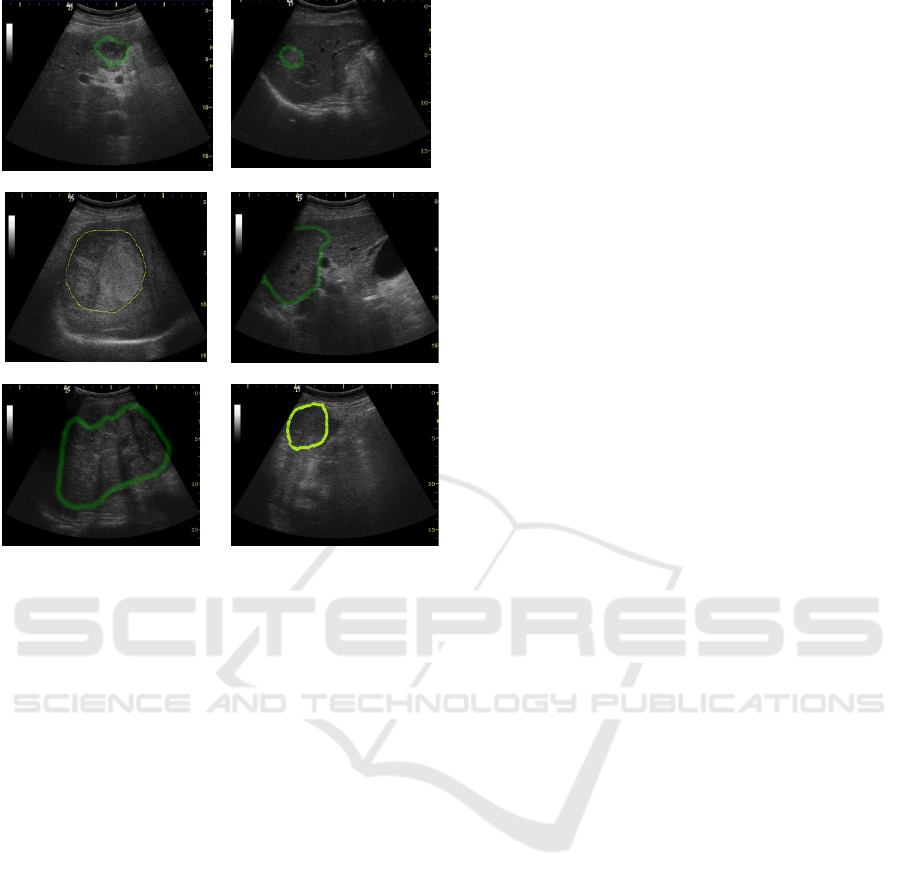
These forms are depicted in the figure below (Figure

1). The Edmondson and Steiner staging system stated

the existence of four evolution stages for the HCC

tumour (Atupelage, 2013). In our research, we aim to

perform the detection of the HCC evolution phases

based on textural features determined from

ultrasound images. Thus, we analyse the capability

that the ultrasound images have in order to reveal the

HCC evolution phases and we study the properties of

each phase through textural parameters. In order to

derive new, subtle information, concerning the HCC

evolution phases, we applied unsupervised

classification techniques for the automatic staging of

HCC, based on ultrasound images.

698

Mitrea, D., Nedevschi, S. and Badea, R.

The Role of the Complex Extended Textural Microstructure Co-occurrence Matrix in the Unsupervised Detection of the HCC Evolution Phases, based on Ultrasound Images.

DOI: 10.5220/0005825506980705

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 698-705

ISBN: 978-989-758-173-1

(a.) (b.)

(c.) (d.)

(e.) (f.)

Figure 1: Visual forms of the HCC tumor, in US images:

(a.) Incipient form, hypoechogenic aspect; (b.) Incipient

form, hyperechogenic aspect; (c.) Encephalic form,

hyperechogenic, inhomogeneous aspect; (d.) Encephalic

form, isoechogenic, homogeneous aspect; (e.) Encephalic

form, hyperechogenic, fibrolamelar aspect; (f.) Encephalic

form, hypoechogenic aspect.

Concerning the computerized detection of the

HCC evolution phases, several approaches exist,

involving texture-based features and supervised

classification methods (Atupelage, 2013),

respectively histological features and a combination

between supervised and unsupervised classification

techniques (Ciocchetta, 2000), but no significant

research exists regarding the automatic grading of the

HCC severity, based on ultrasound images, in an

unsupervised manner. Thus, in (Atupelage, 2013), the

authors determined the evolution stages of HCC, in

supervised manner, from histological images, using

newly defined textural features, derived through

multifractal analysis. A bag-of-features based

supervised classifier was employed in order to

identify one of the five evolution stages of HCC (four

that conformed to the Edmondson and Steiner grading

system, together with an additional stage, which

preceded the malignity). The final resulted accuracy

was 95%. Another approach combined the supervised

and unsupervised classification techniques, in order

to detect the HCC tumour in incipient phase, using

histological features (Ciocchetta, 2000). For

performing supervised classification, a combination

scheme based on the sum of the basic classifier

outputs was implemented, while for unsupervised

classification, a fuzzy-k-means clustering method

was employed. Regarding the unsupervised

classification of the malignant diseases, the authors

assessed the role of the dimensionality reduction

methods, in the context of the differentiation among

the glioma brain tumour evolution phases, based on

spectroscopic image (Resmi, 2010). Two techniques,

the Laplacian Eigenmaps, respectively the

Independent Component Analysis (ICA) were

compared, the first method resulting as superior. A

hierarchical classifier that performed agglomerative

clustering was also implemented, the final accuracy

being 91%. In our work, we discovered the evolution

phases of HCC from ultrasound images, through

computerized methods, in unsupervised manner, by

using textural features and clustering techniques. We

previously employed, for this purpose, existing,

classical methods for texture analysis, as well as

advanced, newly defined techniques, based on

generalized, superior order co-occurrence matrices

(Mitrea D., 2015). The Complex Extended Textural

Microstructure Co-occurrence Matrix (CETMCM),

based on Laws’ and gradient features, was firstly

defined in (Mitrea, D., 2014) and assessed in the

context of the supervised classification of some

abdominal tumours within ultrasound images. In this

work, we highlighted the role that the CETMCM

matrix had in the unsupervised detection of the HCC

evolution phases. For the validation of the

unsupervised classification results, appropriate

supervised classification techniques were adopted

(Witten, 2005). The results obtained in this work, due

to the CETMCM parameters, were also compared

with the previously obtained performances. The

content of this paper is structured in the following

manner: after the introduction, the state of the art is

presented. Then, the proposed methods are described

in details, followed by experiments and discussions.

At the end, the conclusions are stated and some

bibliographic references are proposed.

2 THE PROPOSED SOLUTION

The textural model of the HCC evolution stages

consists of: (a) the relevant textural features for the

differentiation among these stages and (b) the specific

values associated to each relevant textural feature:

arithmetic mean, standard deviation, and probability

distribution. In order to build the textural model of the

The Role of the Complex Extended Textural Microstructure Co-occurrence Matrix in the Unsupervised Detection of the HCC Evolution

Phases, based on Ultrasound Images

699

HCC evolution stages a methodology consisting of

the following steps was implemented: 1.) A

preliminary step, when the appropriate images were

gathered and regions of interest were marked inside

the HCC tissue. 2.) The image analysis phase was

performed then, consisting of feature computation, by

applying specific methods for texture analysis. 3.)

The learning phase, in order to discover the existing

classes, to derive the set of the relevant textural

features and their specific values. 4.) The validation

phase, the purpose being to assess the model obtained

during the previous phases, through supervised

classification methods. The techniques corresponding

to each step will be described in the next sections.

2.1 The Image Analysis Phase

The textural features were computed using both

classical and newly defined texture analysis methods.

Concerning the classical methods for texture analysis,

we considered first order statistics of the grey levels,

second order statistics of the grey levels such as the

GLCM matrix and the autocorrelation index, edge-

based statistics and gradient based features, statistics

of the textural microstructures obtained after the

application of the Laws’ convolution filters, as well

as the Shannon entropy computed after applying the

wavelet transform recursively, twice (Meyer-Base,

2009). Also, more advanced texture analysis

methods, described in our previous works, (Mitrea D.,

2012) and (Mitrea D., 2015) were implemented, such

as the following types of generalized co-occurrence

matrices: the Grey Level Co-occurrence Matrix

(GLCM), the Edge Orientation Co-occurrence Matrix

(EOCM), the Complex Textural Microstructure Co-

occurrence Matrix (CTMCM) based on Laws’

features. In this work, we analysed the role that the

Complex Extended Textural Microstructure Co-

occurrence Matrix (CETMCM) had in the detection

and characterization of the HCC evolution phases.

The CETMCM matrix was defined as follows:

)}sgn()))(sgn((,

),..sgn()))(sgn((

|,||||,..,||||,|||

|,||||,..,|||,|||

,),(,..,),(,),(

:)),(),..,,(),,(),,{((#),..,,(

1111

111212

11213112

222111

33221121

−−

−

⋅=−−

=−=−=−

===

nnnn

nnn

nnnD

ydxdyyxx

ydyyydyyydyy

xdxxxdxxxdxx

tyxAtyxAtyxA

yxyxyxyxtttC





(1)

In (1), #S is the number of elements of the set S,

while n is the matrix dimension. Thus, each element

of this matrix, C

, t

,..., t

), is equal with the

number of n-tuples of pixels, with the spatial

coordinates (x

, y

), having the values t

for the

attribute A(x

, y

). „A” stands for the attribute

associated to each pixel, corresponding to the textons

(cluster labels) resulted after the application of the

improved k-means clustering algorithm, while t

,..., t

are the values of these attributes. The

improved k-means clustering algorithm was applied

upon the combined feature vectors resulted after the

convolution with the Laws’ filters, respectively with

some representative edge detection techniques. In the

case of the Laws’ convolution filters, the 5x5 kernels

(Laws’, 1980) were taken into account: L

, E

, W

, R

, together with the combined

kernels, S

, R

, which provided good results in

our experiments (Mitrea D., 2012). Concerning the

edge detection techniques, we considered the Sobel

filters for detecting horizontal and vertical edges, the

Kirsch Compass filters in order to detect edges with

different orientations (multiples of 45

), as well as the

Laplacian convolution filter (Meyer-Base, 2009). In

practice, the probability matrix was employed (Davis,

1981). The spatial relation between the pixels (x

, y

)

was defined by the set of the displacement vectors

provided in (2)

(2)

We computed the second and third order

CETMCM matrix (for n=2 and n=3) and we

determined the Haralick features, as in (Mitrea D.,

2012). We also considered some features referring to

the n-dimensional spatial representation of the

CETMCM matrix which were not experimented

before in our research: cluster shade (equivalent to the

skewness of the histogram associated to the co-

occurrence matrix); cluster prominence (equivalent to

the histogram kurtosis); the maximum area for the

intersection of the co-occurrence matrix with a

horizontal plan in the 3D case and the corresponding

extension to the n-dimensional case. The

mathematical expressions of these features are

provided in (3), (4) and (5).

),..,,(

*}......{...

2121

xxxpCETMCM

xxxClShade

 

−

−−−−+++=

μμμ

(3)

),..,,(

*}......{...Pr

2121

xxxpCETMCM

xxxomCl

 

−

−−−−+++=

μμμ

(4)

}),...,,(|,),...,,({|

2121

NxxxCETMCMxxxMaxMaxAreaH

nnN

)

In the case of the second order CETMCM

computation, the following directions were

considered: 0°, 90°, 180°, and 270°. For the third

)),(),..,,(),,((

112211 −−

ydxdydxdydxdd





ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

700

order CETMCM, the current pixel was considered in

the central position and together with the other two

pixels, they were either collinear, or formed a right

angle triangle, the current pixel being situated in the

position of the right angle. The following

combinations of orientations were taken into account

for the two displacement vectors: (0°, 180°), (90°,

270°), (45°, 225°), (135°, 315°) in the case of the

collinear pixels; (0°, 90°), (90°, 180°), (180°, 270°),

(0°, 270°), (45°, 135°), (135°, 225°), (225°, 315°),

(45°, 315°), in the case of the right angle triangle. The

displacement vectors had the absolute value 2, in both

cases. We determined the CETMCM and the

pCETMCM matrices for all the considered direction

combinations, the final Haralick feature values

resulting as an arithmetic mean between the values of

the Haralick features of the individual matrices.

2.2 The Learning Phase

Each of the clustering methods described below was

applied and assessed individually, before and after

relevant feature selection. Then the number of the

clusters in the data was decided, based on the

combination of the results provided by the three

methods (a majority voting procedure). The results

were validated through supervised classification.

2.2.1 Clustering Methods

The method of Expectation Maximization (EM) is a

powerful technique that iteratively estimates the

desired parameters, by maximizing the log-likelihood

of the model (Witten, 2005). The parameters

estimated in our work through this technique were the

number of clusters and the sample distributions

within the clusters. The X-means clustering method

was employed as well, being an improved version of

k-means clustering (Pelleg, 2000). The method of X-

means clustering expects a maximum and a minimum

value for the k parameter and performs the following

steps: (1.) Run conventional k-means (Witten, 2005)

to convergence, for a certain value of k. (2.) Decide

whether new cluster centroids should appear or not,

by splitting the old centroids into two. (3.) If k>k

max

then stop and report the best model identified during

the algorithm, according to the Bayesian Information

Criterion – BIC (XMeans). The BIC criterion is used

both for deciding which centroids to split,

respectively in order to identify the best model. The

overall algorithm performance is estimated by the

distortion, computed as the average squared distance

from the points to their centroids, for the best model.

The method of Particle Swarm Optimization (PSO)

aims to optimize the solution of a problem by

simulating the movement of a particle swarm and by

determining the best position for each particle (Das,

2008). Each particle has associated a position and a

velocity. The velocity of a particle k increases from

an iteration to another. The speed is influenced by a

cognitive component, which refers to the distance

from the personal best position, as well as by a social

component, referring to the distance from the best

global position. The optimal particle positions are

determined through an evaluation function, defined

according to the specific of each problem.

Considering our problem, of unsupervised

classification through clustering (grouping), a particle

is represented by a certain cluster configuration,

respectively by the way the cluster labels are

associated to the input data, for a given number of

clusters. We combined the PSO technique with the k-

means clustering method. The initial configuration of

the swarm resulted after the application of the k-

means method upon the initial data. We defined the

evaluation function using the specific metrics for

assessing the unsupervised classification

performance, in the case of the k-means clustering

method, meaning, the Within Cluster Sum of Squares

(WCSS). The maximum difference between the

cluster proportions, as well as the number of

insignificant clusters (having a proportion less than

10%), were also taken into account. Thus, the

evaluation function, in our case, was a weighted

mean, as described in (6). All the terms of this

weighted mean were normalized between 0 and 1.

Eval = 0.5*WCSS + 0.2*max_dif_clust_prop +

0.3*no_insignifiant_clust

(6)

2.2.2 Relevant Textural Feature Selection

Our method for relevant feature selection aims to

achieve best class separation, in the context of the

unsupervised classification. Thus, the overlapping

area between two neighbouring clusters must be as

small as possible. For each textural feature f, a

relevance score was defined, as described below:



−=

sizereggOverlappinflevance

)

__1()(Re

(7)

In (7), i and j are neighbouring clusters. The relevance

of f depends on the sizes of the overlapping regions

that exist between each pair of Gaussian distributions

of f corresponding to each pair of neighbouring

clusters. The overlapping region size was computed

as in (Mitrea D., 2015).

The Role of the Complex Extended Textural Microstructure Co-occurrence Matrix in the Unsupervised Detection of the HCC Evolution

Phases, based on Ultrasound Images

701

2.2.3 The Specific Values of the Relevant

Features

The arithmetic mean of the relevant textural features,

corresponding to the cluster centres were computed

for each cluster. The Graphical representation of

these arithmetic means, for all the detected clusters,

was performed, in order to analyse the correlation of

the feature values with the evolution of HCC. The

specific variation intervals per class, for each relevant

feature, were also determined, using the probability

density tables obtained after applying the Bayesian

Belief Networks method (Witten, 2005).

2.3 The Validation Phase

In order to evaluate the model resulted during the

learning phase, the relevant textural features were

provided at the inputs of some supervised classifiers,

well known for their performance. The following

supervised classification techniques, which provided

the best results in our experiments, were adopted:

Multilayer Perceptron (MLP), Support Vector

Machines (SVM), the C4.5 algorithm of decision

trees, and also a specific multiclass meta-classifier, in

combination with these basic learners. The multiclass

meta-classifier reduced the classification process to a

combination of binary classifications and was used in

conjunction with the Exhaustive Correction Code

strategy (Weka, 2015). For classification

performance evaluation, we used the recognition rate

(accuracy), the average sensitivity (average TP rate)

and the area under the ROC curve (Witten, 2011).

3 EXPERIMENTS

AND DISCUSSIONS

The experimental dataset consisted of 200 HCC

cases, three B-mode ultrasound images being taken

into account for each case (patient). All the patients

underwent biopsy, for diagnostic confirmation. The

images were acquired with an ultrasound machine of

type Logiq 7, under the same settings: 5.5 MHz

frequency, gain of 78, depth of 16 cm. A region of

interest (ROI), having 50x50 pixels in size, was

selected on each image, inside HCC. The textural

features were determined for each ROI,

independently on orientation, illumination and ROI

size. The texture analysis methods were applied using

our own modules, implemented in Visual C++. The

clustering methods, the supervised classifiers and the

Bayesian Belief Networks were implemented using

the Weka 3.6 library (Weka, 2015). The PSO method

was implemented in Matlab using a specific

framework (Biswas, 2013).

3.1 The Learning Phase

3.1.1 Discovering Clusters in the Data

First, the individual clustering techniques:

Expectation Maximization (EM), X-means clustering

(XMeans), respectively Particle Swarm Optimization

(PSO) combined with k-means clustering were

applied, before and after feature selection. The

unsupervised classification performances obtained

after performing feature selection, using the

algorithm described within the 2.2.2 section, was

usually better than the performance obtained before

feature selection. Then, the estimation concerning

the number of clusters within the data was

performed, by combining the individual results of the

adopted methods. For the XMeans method, the

Euclidean distance was considered. For each

unsupervised classification method, the parameters

representing the number of clusters (for EM and PSO

combined with k-means), respectively the minimum

and maximum number of clusters (in the case of

XMeans), were set to consecutive, integer values

ranging for 2 to 6, in order to identify the best cluster

configuration.

Table 1: The performance of EM.

No. Clusters Log likelihood Score

2 -139.87

0.41

3 -131.95 0.51

4 -117.87 0.74

5 -112.42 0.94

6 -109.027 0.5

In the case of the EM method, the log likelihood was

estimated and a score was computed, as well, using

the following formula: Score= 0.5*log_likelihood

+0.3*(1-n)+ 0.2*(1-dif), where n is the number of

small clusters, while dif is the maximum difference

between the cluster propor-tions. When computing

this score, the values for log_likelihood, n and dif

were normalized between 0 and 1. As we notice from

Table 1, the maximum score was obtained in the case

of 5 clusters, so, according to the EM method, there

are 5 clusters within the data.

In the case of the X-means clustering technique,

the distortion measure was estimated and an index

was computed as follows: Index= 0.5*distortion

+0.3*n+0.2*dif, where n is the number of small

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

702

clusters, while dif is the maximum difference between

the cluster proportions. All the terms (distortion, n

and dif) were normalized between 0 and 1. Thus, the

smallest index value indicated the best solution in this

situation. This index had a minimum value for 5

clusters, so there exist 5 clusters within the data,

according to the X-means clustering technique.

Table 2: The performance of PSO+k-means clustering.

No.

Clusters

WCSS Index

2 1.256e+012 0.27

3 7.392e+011 0.62

4 5.312e+011 0.34

5 4.172e+011 0.23

6 1.333e+011 0.32

In the case of PSO combined with k-means

clustering, the WCSS measure, specific for the

evaluation of the k-means technique, was considered,

and also an index was computed, corresponding to the

best values of the evaluation function, as described in

(6). Thus, also in this situation, both the WCSS

parameter and the index must take minimum values

in the best case. According to Table 2, the index took

the smallest value in the case of 5 clusters.

Considering the results provided by each of the three

adopted clustering methods, we can conclude that

there are, most likely, 5 distinct clusters within the

data, corresponding to the HCC evolution phases.

3.1.2 The Relevant Textural Features

The relevant textural features were detected by the

algorithm described in 2.2.2, for each clustering

method. Only the features that had a relevance index

above the threshold (0.6) were taken into account.

The three resulting relevant feature sets were

intersected, yielding the final set, depicted in (8).

Relevant_features = {Max_grey_level,

EOCM_Homogeneity, EOCM_Energy,

EOCM_Coreelation, GLCM3_Energy,

GLCM5_Variance, Directional_grad_variance,

Mean_level, Mean_Laws_edges, Spot_Frequency,

CETMCM_Max_AreaH,

CETMCM_Cluster_Shade, CETMCM_Cluster

_Promminence, CETMCM3_Energy,

CETMCM3_Homogeneity}

(8)

Besides the classical textural features, we notice

the presence of the CETMCM based features: the

homogeneity and the energy, derived from the third

order CETMCM, stood for the homogeneity

decrease, respectively for the echogenicity increase,

towards the advanced HCC evolution phases; the

second order CETMCM cluster shade and cluster

promminence, respectively the maximum area for the

interesection with a horizontal plan, revealed a sparse

distribution of the complex extended textural

microstructures during the initial evolution phases,

respectively an increased density of these

microstructures towards the advanced HCC evolution

phases. We also remarked the increased values for the

mean relevance index associated to the parameters

CETMCM_Cluster_Shade and

CETMCM_Max_AreaH, of 0.97, respectively 0.85.

The homogeneity, energy and variance, derived from

the EOCM matrix, as well as from the third and fifth

order GLCM, were also included in the relevant

feature set, expressing again the heterogeneous,

complex structure of the HCC tissue that

corresponded to the advanced HCC evolution phases.

We also remark the presence of the first order

statistics concerning the gradient based features and

the textural Laws’ microstructures, standing for the

variations in the tissue structure complexity, as well

as of the correlation computed from the EOCM

matrix, emphasizing differences in granularity

between various HCC evolution phases.

3.1.3 The Specific Values of the Relevant

Textural Features

In Figure 2, the values of the arithmetic means that

corresponded to some of the relevant textural

features, considered for each cluster, were graphically

represented. According to the a-priori existing

knowledge concerning the decrease in homogeneity,

respectively the increase in echogenicity during the

evolution of HCC, the second cluster, c

corresponded to the incipient phase, having the most

decreased value for the grey levels, respectively the

maximum GLCM homogeneity, while cluster c

corresponded to the most advanced evolution phase

for the HCC tumor, presenting the most increased

value of the gray levels, respectively the minimum

value of the GLCM homogeneity. The other clusters,

, c

and c

corresponded to intermediary evolution

phases: c

was closer to the incipient evolution phase,

while c

and c

were closer to the advanced evolution

phases. The arithmetic mean values of other features,

such as the energy of the third order CETMCM and

the cluster promminence derived from the second

order CETMCM, were also analyzed.

We notice, from Figure 2, that the third order

CETMCM energy had low values for the incipient

phases and high values for more advanced phases,

The Role of the Complex Extended Textural Microstructure Co-occurrence Matrix in the Unsupervised Detection of the HCC Evolution

Phases, based on Ultrasound Images

703

Figure 2: The mean values of the relevant textural features

for each HCC evolution phase.

denoting an increase in the density of the complex

extended textural microstructures during the HCC

evolution. The cluster promminence of the CETMCM

matrix, corresponding to the 3D histogram kurtosis,

had maximum values during the incipient evolution

phase and small values during the advanced evolution

phases, due to the fact that, during the incipient phase,

umany small values of the complex extended textural

microstructures and few increased values of these

microstructures occur. The probability distributions

generated by Bayesian Belief Networks confirmed

these results.

3.2 The Validation Phase

During this phase, the values of the relevant textural

features were provided at the inputs of some

powerfull supervised classifiers and meta-classifiers,

as described before. The SMO method, standing for

the SVM classifier, with a 3

degree polynomial

kernel was considered; the MLP classifier was also

adopted, with a learning rate of 0.2, a momentum (α)

of 0.8, and the number of nodes from the single

hidden layer equal with a = (nr_input_features +

nr_classes)/2; the J48 method, the Weka equivalent

of C4.5, was employed as well. Also, we adopted the

multiclass meta-classifier of Weka 3.6 (Weka, 2015).

The instances were labeled according to the results

provided by PSO combined with k-means clustering.

The following situations were compared: the case of

using only the previous textural features; the case of

using the former textural features, combined with the

recently defined Haralick features, derived from the

CTMCM matrix, based on Laws’ features (Mitrea D.,

2015); the case of using the former textural features

combined with the newly defined CETMCM features.

For the last case, both situations of 5 and 6 clusters

were considered, as, for 6 clusters, increased values

of the usual unsupervised classification performance

parameters were obtained, but, however the size of

some resulted clusters was very small. The

comparison of the recognition rates is depicted in

Figure 3.

It results that the CETMCM features led to the

best recognition accuracy, in most of the situations.

The values obtained for 5 clusters were superior to

those obtained in the case of 6 clusters. The average

recognition rate obtained in the first case was 88.95%,

while the average accuracy obtained in the second

case was 78.63%. This confirms the results obtained

in the previous subsection, so there exist 5 clusters in

the data. When considering the combination between

the former textural features and the CETMCM

features, the maximum recognition rate, of 93.35%,

together with the maximum sensitivity (average TP

rate), of 93.14%, respectively the maximum value of

the AUC, of 98.3%, resulted in the case of the MLP

classifier.

The obtained results, indicating a 90% accuracy,

were comparable with the already obtained accuracy

for the supervised and unsupervised classification of

the HCC evolution phases (Atupelage, 2013),

(Ciocchetta, 2000). In addition, in our research, five

evolution stages of HCC were discovered,

noninvasively, through unsupervised classification

methods, from ultrasound images.

Figure 3: Evaluation of the CETMCM textural features through supervised classification methods.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

704

4 CONCLUSIONS AND FUTURE

WORK

The textural features, based on the CETMCM matrix,

provided satisfying results in our study, leading to the

discovery of 5 HCC evolution phases and to an

increase in accuracy in comparison with our

previously obtained results in this domain (Mitrea D,

2015). The newly considered textural features,

associated to the spatial representation of the

CETMCM, were selected as relevant and indicated

differences concerning the complexity of the tissue

structure during the evolution of HCC. The obtained

results were validated through supervised

classification, achieving classification accuracies

around 90%. In our future work, the newly defined

features will be compared with other existing textural

features, such as the Local Binary Pattern (LBP). We

also aim to further increase the accuracy of the texture

analysis methods by employing more multiresolution

features. Larger datasets will be considered as well

and data representation techniques, such as Self

Organizing Maps (SOM) will be also employed. (Yin,

2008).

REFERENCES

Sherman, M., 2005. Approaches to the Diagnosis of

Hepatocellular Carcinoma. In Current

Gastroenterological Reports, vol. 7, no. 1, 2005, pp.11-

18.

American liver foundation, 2015. Online: http://www.

liverfoundation.org/abouttheliver/info/

Atupelage, C., Nagahashi, H., 2013. Computational grading

of hepatocellular carcinoma using multifractal feature

description. In Computers in Medical Images and

Graphics, vol. 37, 2013, pp. 61-71.

Ciocchetta, F., et al., 2000. Combining Supervised and

Unsupervised Methods to Support Early Diagnosis of

Hepatocellular Carcinoma. In Artificial Intelligence in

Medicine, vol. 2780, 2000, pp 239-243.

Resmi, A., 2010. Texture description of low grade and high

grade glioma using statistical features in brain MRIs. In

International J. of Recent Trends in Eng. and

Technology, vol. 4, no. 3, 2010, pp. 27-33.

Mitrea, D., Nedevschi, S., Abrudean, M., Badea, R., 2015.

Detecting the evolution phases of the hepatocellular

carcinoma from ultrasound images, using generalized

co-occurrence matrices. In Acta Electrotehnica, Vol.

56, No. 1-2, 2015, pp.46-54.

Mitrea D., Nedevschi S., Abrudean M., Badea, R., 2014.

Abdominal tumor recognition from ultrasound images

using Complex Extended Textural Microstructure Co-

occurrence Matrices. In Automation, Computers and

Applied Mathematics, Vol. 23, No.1, 2014, pp. 9-17.

Witten, I., Frank, E., 2005. Data Mining. Practical Machine

Learning Tools and Techniques (3rd edition), Morgan

Kaufmann.

Meyer-Base, A., 2009. Pattern recognition for medical

imaging, Elsevier.

Mitrea, D., Mitrea, P., Nedevschi, S., et al., 2012.

Abdominal tumor characterization and recognition

using superior order cooccurrence matrices, based on

ultrasound image. In, Computational and Mathematical

Methods in Medicine. Online: http://www.

hindawi.com/ journals/cmmm/2012/34813/

Laws, K.I., 1980. Rapid texture identification. In SPIE, vol.

238, 1980, pp.76-380.

Davis, L.S., 1981. Image Texture Analysis Techniques – A

Survey. In Digital Image Processing, Simon and R. M.

Haralick (eds.), pp. 189-201, 1981.

Pelleg, A., Moore, W., 2000. X-means: Extending K-

means with Efficient Estimation of the Number of

Clusters. In International Conference on Machine

Learning (ICML), pp. 727-734.

Das, S., 2008. Particle Swarm Optimization and Differen-

tial Evolution Algorithms: Technical Analysis, Appli-

cations and Hybridization Perspectives. In Studies in

Computational Intelligence, no.116, 2008, pp. 1–38.

Weka 3, Data Mining Software in Java, 2015. Online:

http://www.cs.waikato.ac.nz/ml/weka.

Biswas, P., 2013. Particle Swarm Optimization for Matlab,

Online: http://www.mathworks.com/matlabcentral/file

exchange/43541-particle-swarm-optimization--pso.

Yin, H., 2008. The Self-Organizing Maps: Background,

Theories, Extensions and Applications. In

Compu-

tational Intelligence, no. 115, 2008, pp. 715–762.

The Role of the Complex Extended Textural Microstructure Co-occurrence Matrix in the Unsupervised Detection of the HCC Evolution

Phases, based on Ultrasound Images

705