
A Trust-based Decision-making Approach Applied to Agents in
Collaborative Environments
Lucile Callebert, Domitile Lourdeaux and Jean-Paul Barth
`
es
Sorbonne Universit
´
es, Universit
´
e de Technologie de Compi
`
egne, CNRS,
Heudiasyc UMR 7253, CS 60 319, 60 203 Compi
`
egne, France
Keywords:
Cognitive Agents, Trust-based Decision-making, Activity Description, Multi-agent Systems.
Abstract:
In Virtual Environments for Training, the agents playing the trainee’s teammates must display human-like
behaviors. We propose in this paper a preliminary approach to a new trust-based decision-making system that
allow agents to reason on collective activities. The agents’ integrity, benevolence and abilities dimensions
and their trust beliefs in their teammates’ integrity, benevolence and abilities allow them to reason on the
importance the give to their goals and then to select the task that best serves their goals.
1 INTRODUCTION
In Collaborative Virtual Environments for Training
(CVET), virtual characters and the trainee have to
work together on a collective activity to achieve team
goals. Examples of such CVET include the SecuReVi
application for firefighters training (Querrec et al.,
2003), or the 3D Virtual Operating Room for medical
staff training (Sanselone et al., 2014). In those CVET,
agents must display a human-like behavior and peo-
ple must monitor their teammate activities to make the
best decisions.
To train people to work in teams, we must con-
front them with all types of teammates: ’good team-
mates’ (i.e. working hard to achieve the team goals
and doing their best to help other team members, etc.),
or on the opposite, ’bad teammates’ (i.e. favoring
to their own goals, not helping team members, etc.)
Team members will then have to address questions
like: Is my teammate able to do that or should I do
it myself?, Is my coworker committed enough to the
team to help? or Would my teammate be kind enough
with me to help me?. Such questions rely on the con-
cept of trust (i.e. Do I trust my coworker’s commit-
ment to the team? , Do I trust my teammate’s benev-
olence toward me?, Do I trust my teammate’s capac-
ities?).
We propose in this paper a preliminary approach
to a trust-based decision-making mechanism enabling
agents in CVET to reason on collective activities. We
first introduce some major works on activity descrip-
tion models and on trust models in Section 2. We
present in Section 3 a general overview of our system.
In Section 4 we present the activity model used to de-
scribe the team activity, and in Section 5 we present
the activity instances on which agents reason. In Sec-
tion 6 we introduce the agent model. We detail in
Section 7 the decision-making mechanisms a=that we
then illustrate by an example in Section 8, before con-
cluding in Section 9. The coupling with a virtual en-
vironment and the integration of the trainee will not
be discussed in this paper.
2 RELATED WORK
2.1 Activity Models in CVET
In the SecuriVi project (Chevaillier et al., 2012) and
the 3D Virtual Operating Room project (Sanselone
et al., 2014) the activities that the agent and the trainee
can perform are described respectively thanks to
the HAVE activity meta-model and Business Process
Model Notation diagrams. In both projects, agents
are assigned to a role and have specific tasks to do for
which they must be synchronized. Yet we want the
trainee to adapt her behavior to her teammates on ac-
tivities where no roles are pre-attributed to team mem-
bers. The scenario language LORA (Language for
Object-Relation Application) (Gerbaud et al., 2007)
supports the description of collective activity: roles
can be associated with actions and domain experts can
specify collective actions that several agents have to
Callebert, L., Lourdeaux, D. and Barthès, J-P.
A Trust-based Decision-making Approach Applied to Agents in Collaborative Environments.
DOI: 10.5220/0005825902870295
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 1, pages 287-295
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
287

do simultaneously. However in LORA only the pre-
scribed procedure is represented, which does not al-
low agents to deviate from this procedure. The activ-
ity meta-model ACTIVITY-DL (Barot et al., 2013) is
used both for monitoring the trainee’s behavior and
for generating virtual-characters’ behavior. Task de-
scription in ACTIVITY-DL corresponds to a cogni-
tive representation of the task, which is well suited to
our human-like behavior-generation objective: agents
will be able to reason on the task description in a way
that imitates human cognitive processes. ACTIVITY-
DL supports the description of procedure deviations:
it is representative of the activity observed in the field.
2.2 Dyadic Trust Models
A dyadic trust model will allow agents to take into
account individual characteristics of their teammates
to make a decision about the collective activity. In the
following, we call ’trustor’ the subject of the trust-
relationship (i.e. the person who trusts). The trustee
is the object of the trust-relationship (i.e. the person
who is trusted).
(Mayer et al., 1995) propose a model of organi-
zational trust including factors often cited in the trust
literature. They identify three dimensions to trust: in-
tegrity, benevolence and ability. One trusts someone
else’s integrity if one believes the other will stick to
its word and fulfill her promises. The trustor trusts the
trustee’s benevolence toward her if she ascribes good
intentions to the trustee toward her. The trustor’s trust
in the trustee’s abilities depends on how she evaluates
the trustee’s capacity to deal with an identified task.
(Marsh and Briggs, 2009) propose a computa-
tional model of trust for agent collaboration. To de-
cide over cooperation, the trustor compares the situ-
ational trust, which represents how much she trusts
the trustee in an identified situation with a coopera-
tion threshold, which represents how much she needs
to trust the trustee in this situation to cooperate with
her. In this model, there is no notion of team, yet we
believe that the team concept itself plays a role in the
team member behavior.
(Castelfranchi and Falcone, 2010) propose a com-
putational model of social trust. In this model the
trustor’s beliefs about the trustee’s motivation, capac-
ity and opportunity to do a task, are used to decide
over delegation. In this model the motivation belief
is very difficult to compute without a context: for
example it is deduced from the trustee’s profession
(e.g. a doctor is believed to be motivated to help her
patients), or from the trustee’s relationship with the
trustor (e.g. friends are supposed to be willing to help
one another). Without this context, motivation is diffi-
cult to explain, yet agent behavior needs to be explain-
able to the trainee. The integrity and benevolence di-
mensions in the model of (Mayer et al., 1995) provide
such an explanation.
The model of organizational trust of (Mayer et al.,
1995) is the most appropriate in our context: it takes
into account a dimension specific to the team, and the
benevolence relationships provide a basis for helping
behaviors without having to add specific models of
interpersonal relationships.
3 GENERAL FUNCTIONING
The general functioning of the trust-based task-
selection system for agent x in the team of agents
A = {x, y, z} is presented in Figure 1. We propose
augmenting the activity meta-model ACTIVITY-DL
to support collective-activity description. The collec-
tive activity model is described by ergonomists as a
tree of tasks, in which leaf tasks correspond to ac-
tions. At the beginning of the simulation, the activity-
treatment module uses the activity model to generate
an activity instance representative of agents’ progress
on the activity and on which agents will reason dur-
ing the whole simulation. This corresponds to Step ¬
of Figure 1. Agent x reasons on the activity instances
that correspond to its goals for selecting a task that
corresponds to an action. Its personal integrity, benev-
olence and ability dimensions influence its choices
as well as the other agents that it takes into account
thanks to its trust beliefs about them. This corre-
sponds to Step of Figure 1. In Step ® of Figure 1
x’s action is treated by the virtual-environment mod-
ule, which then informs the activity-treatment module
in Step ¯ of Figure 1. Those two stages are not fur-
ther discussed in this paper since not directly related
to the agents decision-making system for collective
activities. Finally the activity-treatment module up-
dates the activity instances in Step ° of Figure 1.
4 ACTIVITY MODEL
We first briefly present ACTIVITY-DL before propos-
ing our augmentation of ACTIVITY-DL for collective
activities.
4.1 ACTIVITY-DL
ACTIVITY-DL is a meta-model for describing human
activities inspired from studies in ergonomics: the ac-
tivity is represented as a set of tasks hierarchically de-
composed into subtasks in a way that reflects human
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
288
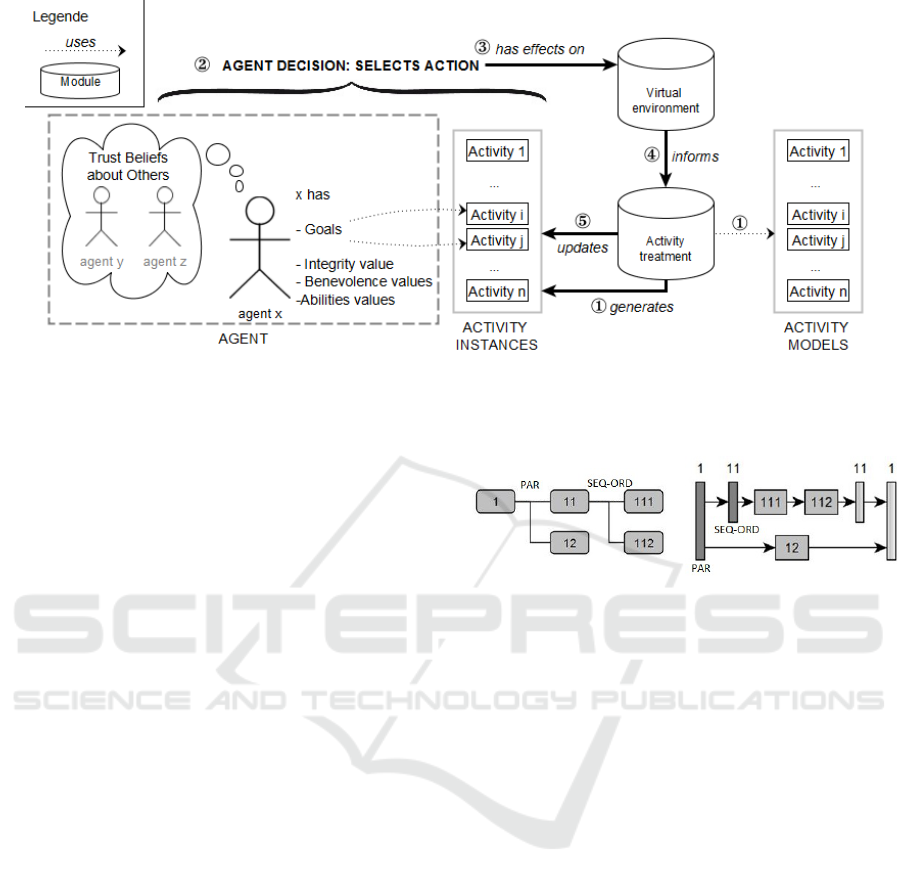
Figure 1: General functioning of the agent decision-making system and its effects on the simulation.
cognitive representations. Task hierarchical decom-
position takes the form of tree of tasks, with leaf tasks
τ
l
representing concrete actions to be executed in the
virtual environment. Non-leaf tasks τ
k
are abstract
tasks and are decomposed into subtasks: let T
k
be
the set of τ
k
’s subtasks. Those substasks are logically
organized thanks to satisfaction conditions and tem-
porally organized through ordering constraints. For
more details, see (Barot et al., 2013).
We give an example of activity description in
ACTIVITY-DL that we will use to illustrate agent rea-
soning. If we consider the utterance: ’For the lab to
be set up, the floors have to be cleaned and the desk
has to be assembled. To clean the floors, vacuum-
ing should be done first and then mopping. Assem-
bling the desk and cleaning the floors can be done at
the same time.’ This example can be represented in
ACTIVITY-DL through the tree of tasks:
• τ
111
= vacuum floors (corresponds to an action).
• τ
112
= mop floors. (corresponds to an action).
• τ
11
= clean floors. τ
111
and τ
112
are τ
11
’s sub-
tasks: T
11
= {τ
111
, τ
112
}. τ
111
and τ
112
have
to both be done sequentially so a SEQ-ORD
ordering-constraint and an AND satisfaction con-
dition are attached to τ
11
.
• τ
12
= assemble desk. (corresponds to an action).
• τ
1
= set up lab. τ
11
and τ
12
are τ
1
’s subtasks:
T
1
= {τ
11
, τ
12
}. A PAR ordering-constraint and
an AND satisfaction condition are attached to τ
1
since τ
11
and τ
12
can be done at the same time.
We provide two graphical representations of a task
tree described in ACTIVITY-DL: as a tree in Fig-
ure 2(a), and as a work flow in Figure 2(b). In this
latter representation, dark-gray bars indicate the be-
ginning of the task, and light-gray bars indicate the
end. Rectangular boxes represent concrete actions.
Figure 2: Set-up-lab example of an ACTIVITY-DL tasks-
tree represented as a task tree on the left(a) and a work-flow
on the right (b).
4.2 Augmenting ACTIVITY-DL to
Support Collective-activity
Until now, ACTIVITY-DL was used for describing in-
dividual activity. In order to describe collective ac-
tivities, we added some requirements that have to be
specified by ergonomists only on leaf tasks τ
l
(i.e.
tasks corresponding to actions). Such requirements
are the followings:
Number-of-agent Requirement: We consider col-
lective activities with collective actions on which
several agents can or have to do at the same time.
For a leaf task τ
l
representing such a collective ac-
tion, it is necessary to specify n
min
(τ
l
) a minimum
of persons that are needed to do τ
l
and n
max
(τ
l
) a
maximum of persons that can work together on τ
l
.
For example ergonomists can specify that two to
four persons can work on τ
12
= assemble desk:
n
min
(τ
12
) = 2 and n
max
(τ
12
) = 4.
Skill Requirement: An action may require some
particular skills that are attached to the action. We
define Σ = {σ
1
, σ
2
, ...} the set of skills and Σ
l
⊆ Σ
the set of skills attached to τ
l
. For example er-
gonomists can specify that skills σ
1
= know how
A Trust-based Decision-making Approach Applied to Agents in Collaborative Environments
289

to use a screwdriver and σ
2
= know haw to read
instructions are necessary to do τ
12
.
5 ACTIVITY INSTANCE
To enable agents to reason on the abstract tasks of
the activity tree, the leaf task requirements have to
be propagated to all abstract tasks, which is done by
the activity-treatment module when generating an ac-
tivity instance (i.e. Step ¬ of Figure 1). An ac-
tivity instance is different from an activity model in
that it directly supports agent reasoning thanks to ab-
stract task constraints that are representative of the
agent progress in the activity tree. Also because those
constraints are representative of the agent progress in
the activity, the activity instances are updated by the
activity-treatment module each time progress is made
(i.e. Step ° of Figure 1), namely each time agents do
an action.
For an abstract task τ
k
, two types of conditions are
generated by the activity-treatment:
The Feasibility Condition is static and must be ver-
ified so that τ
k
can be done. This condition
relies on the satisfaction condition attached to
τ
k
: there must be enough agents and all to-
gether agents must have all the required abili-
ties to achieve either all of τ
k
’s subtasks (AND
satisfaction-condition) or one of τ
k
’s subtasks
(OR satisfaction-condition).
The Progress-representative Condition is dynamic
and is representative of agents’ process in the col-
lective activity, thus this condition is updated each
time agents do an action. This condition relies
on the ordering constraint attached to τ
k
: if a
PAR ordering constraint is attached to τ
k
at time
t their must be enough agents to do one of τ
k
’s
subtasks that is not done yet. If a SEQ-ORD or-
dering constraint is attached to τ
k
, the progress-
representative condition is representative of τ
k
’s
next subtask to be achieved.
We do not further detail the constraint propagation
rules in this paper due to space limitations. Consider-
ing the activity model described in Section 4, at the
activity instance generation, the constraint propaga-
tion gives:
• for τ
11
that has a SEQ-ORD ordering constraint
and an AND satisfaction condition attached:
– The feasibility condition expresses that one
agent is enough to realize both τ
111
and τ
112
,
and no skills are required.
– The progress-representative condition is ini-
tially representative of τ
111
: one agent is
enough and no skill is required.
• for τ
1
that has a PAR ordering constraint and an
AND satisfaction-condition attached:
– The feasibility condition expresses that two
agents are necessary to execute τ
1
since τ
12
re-
quires two persons, and those agents must have
the skills σ
1
and σ
2
required by τ
12
.
– The progress-representative condition is ini-
tially representative of both τ
11
and τ
12
. The
minimum of agents is then one, since only one
agent is required for τ
11
. Agents with no skill
can participate to τ
1
by doing τ
11
.
6 AGENT MODEL
We propose an agent model that will allow agents to
reason on their goals and on the activity instances that
correspond to their goals while taking others into ac-
count. We first present the goals and dimensions of
our agents and then the beliefs agents have about other
agents.
6.1 Agent Goals and Dimensions
Agents have goals and personal dimensions based
the model of organizational trust proposed by (Mayer
et al., 1995) that we formally define in the following
paragraphs.
Agent Goals. We make a distinction between agent
personal goals and goals that the agent shares with
the rest of the team. We define γ
x,sel f
, the personal
goal of agent x, and γ
x,team
the goal that x shares with
the team. Each goal corresponds to a task tree which
describes the tasks that should be done to achieve the
goal.
Agent Dimensions. For agent x in the team of
agents A =
{
x, y
1
, y
2
, ...
}
, we describe x’s personal di-
mensions as follows:
• Integrity. i
x
∈]0, 1[ is x’s integrity value toward the
team.
• Benevolence. As the benevolence is directed to-
ward other agents, x has a set of benevolence val-
ues {b
x,y
1
, b
x,y
2
, ...}. For all agents y
i
∈ A , y
i
6= x,
x’s benevolence value toward y
i
is such that b
x,y
i
∈
]0, 1[.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
290

• Ability. Similarly to x’s benevolence, x’s abilities
are related to specific skills: for all skills σ
j
∈ Σ,
x has an ability value a
x, j
∈ [0, 1[. Thus x’s set of
abilities is {a
x,1
, a
x,2
, ...}. A high ability value on
skill σ
j
indicates that x tends to master the skill,
as a low ability value indicates that x is not very
competent on that skill.
The integrity, benevolence and ability values de-
fine x’s state of mind, and will influence x’s decision.
6.2 Agent Beliefs
When making a decision, people tend to imagine how
others would react to their choice. This theory-of-
mind capability (Carruthers and Smith, 1996) allows
people to take others into account in their decision-
making. To reason on what others would like, agents
use the beliefs they have about others’ goals and oth-
ers’ state of mind.
Others’ Goals. Agents have beliefs about their
teammates’ goals. For all agents x, y
i
∈ A , x 6= y
i
, we
define γ
x
y
i
,sel f
that is what x thinks is y
i
’s personal goal,
and γ
x
y
i
,team
that is what x believes is y
i
’s goal shared
with the team.
Others’ Personal Dimensions. Following the
model of organizational trust if (Mayer et al., 1995),
we define the trust beliefs of x ∈ A about agent
y
i
∈ A , x 6= y
i
:
• Integrity trust-belief. i
x
y
i
∈]0, 1[ is what x thinks of
y
i
’s integrity.
• Benevolence trust-belief. x’s trust in y
i
’s benevo-
lence is
b
x
y
i
,x
, b
x
y
i
,y
1
, ...
, where b
x
y
i
,y
j
∈]0, 1[. For
agent y
j
6= y
i
, b
x
y
i
,y
j
is what x thinks of y
i
’s benev-
olence toward y
j
.
• Ability trust-belief.
n
a
x
y
i
,1
, a
x
y
i
,2
, ...
o
is what x be-
lieves of y
i
’s abilities, with a
x
y
i
, j
∈ [0, 1[ what x
thinks of y
i
’s ability on skill σ
j
∈ Σ.
7 DECISION-MAKING PROCESS
Agents’ decision-making process allow them to rea-
son on their goals to decide which one is the most
important, and then to reason on the collective activ-
ity instances to select a task that serves their preferred
goal. Both when reasoning on goal importance and
when selecting a task, agents take others into account
thanks to their trust beliefs. We develop in the fol-
lowing sections processes of goal importance compu-
tation and task selection.
7.1 Goal Importance
Agent x has to compute the importance it gives to its
personal goal and to its team goal in order to decide
which one to favor. In order to do so, x computes the
initial importance value it gives to its goals and then
takes others into account to compute the final impor-
tance value of its goals.
Initial Goal Importance. Let iImp
x
(γ) ∈ [0, 1[ be
the initial importance value of the goal γ for agent
x. Since x’s integrity represents x’s tendency to
fulfill its promises, x’s initial importance value for
the team goal corresponds to x’s integrity value:
iImp
x
(γ
x,team
) = i
x
, while x’s initial importance value
for its personal goal is iImp
x
(γ
x,sel f
) = 1 − i
x
.
x then uses its theory-of-mind capability to com-
pute how much much importance it thinks its team-
mates initially give to their goals. We define iImp
x
y
i
(γ)
what x thinks of the initial importance of γ for agent
y
i
. For all agents y
i
∈ A , y
i
6= x, x uses its theory-
of-mind capability and reasons on i
x
y
i
to compute
iImp
x
y
i
(γ
y
i
,team
) and iImp
x
y
i
(γ
y
i
,sel f
).
Final Goal Importance. Let f Imp
x
(γ) ∈ [0, 1[ be
the final importance value of the goal γ for agent x,
which designates the importance x gives to γ after tak-
ing into account its teammates.
x first computes with Equation 1 its desirability
d
x,y
i
(γ) ∈] − 1, 1[ to realize the goal γ for agent y
i
.
d
x,y
i
(γ) is proportional to both iImp
x
y
i
(γ) and to x’s
benevolence toward y
i
. The formula used in Equa-
tion 1 allows d
x,y
i
(γ) to be positive if x is benevolent
toward y
i
(i.e. wants to help) and negative if x is not
benevolent toward y
i
(i.e. does not want to help).
d
x,y
i
(γ) = iImp
x
y
i
(γ) × 2(b
x,y
i
− 0.5) (1)
Then in Equation 2 if x also has γ as a goal, x com-
putes the mean of its own initial importance value for
γ and the desirability values d
x,y
i
(γ) for all of the n
agents y
i
that also have γ as a goal. Since this value
might be negative, the final importance of γ for x is
the maximum between this mean and zero.
f Imp
x
(γ) = max
iImp
x
(γ) +
∑
n
i=1
d
x,y
i
(γ)
n + 1
, 0
(2)
A very process (except that no initial importance
value is taken into account) is used if x does not ini-
tially have γ as a goal. This process is defined in Equa-
tion 3.
f Imp
x
(γ) = max
∑
n
i=1
d
x,y
i
(γ)
n
, 0
(3)
A Trust-based Decision-making Approach Applied to Agents in Collaborative Environments
291

7.2 Task Selection
Based on how much importance agent x gives to its
goals and how much importance it thinks its team-
mates give to their goals, x has to choose the task it
wants to do. In order to do so, x recursively reasons
on task trees and computes task utilities. Finally x
generates task distributions among agents to choose
the one that best serves its interests.
7.2.1 Recursive Process
We explain in the following paragraphs the function-
ing of the recursive task-selection process for agent x.
We provide in Figure 3 a diagram that represents the
set of agents on which x reasons at steps n and n + 1
of the recursive process, and Figure 3 illustrates those
sets.
Set of Tasks on which x Reasons. We define T
x,n
⊂
T the set of tasks on which x reasons during Step n of
its recursive process of task selection. If Tr ⊂ T is
the set of the task-tree roots, then x reasons at the first
step of the recursive process on T
x,1
= Tr. If τ
k
is the
task that x selects at Step n of the recursive process,
then at Step n + 1, x reasons on T
x,n+1
= T
k
, where
T
k
is the set of τ
k
’s subtasks. Of course, x chooses
one of τ
k
’s subtasks only if τ
k
has a PAR ordering-
constraint attached. If a SEQ-ORD ordering-onstraint
is attached to τ
k
x has to do the first subtask of τ
k
that
is not done yet.
Set of Agents on which x Reasons. When making
a choice, people tend to anticipate how their choice
would impact others. They use their theory-of-mind
capability to make a decision that takes others into ac-
count. At the first step of the recursive task-selection
process, x takes into account all its teammates. But
then in the following steps of the recursive process,
x only takes into account the relevant agents, namely
those that x thinks will choose the same task τ
k
as
itself in the previous step of its recursive decision-
making process. Similarly to T
x,n
, we define A
x,n
⊆ A
the set of agents on which x reasons during Step n
of the recursive task-selection process. At the first
step of the recursion, A
x,1
= A . If τ
k
is the task
that x selects at Step n, the agents y
i
∈ A
x,n
that x
thinks will also choose τ
k
compose the set of agents
A
x,n+1
⊆ A
x,n
on which x reasons at Step n + 1.
7.2.2 Task Utility
Let o
+
k
be a state of the world that corresponds to a
success outcome for the task τ
k
and let U
x
(o
+
k
) ∈ [0, 1[
Figure 3: Step n and Step n + 1 of the recursive task-
selection process of agent x.
be the utility for agent x to achieve o
+
k
. At the step
n of the recursive task-selection process, x computes
U
x
(o
+
k
) for every task τ
k
such that τ
k
∈ T
x,n
. To com-
pute U
x
(o
+
k
), x has to consider if it can, if it wants,
and if it should do the task.
Can x do the Task? x first checks that the task is
doable by the team of agents by reasoning on the fea-
sibility condition. Then x checks if it can participate
to τ
k
by reasoning on the progress-representative con-
dition. When doing so, x reasons on its abilities and
on what it thinks of the abilities of its teammates.
Does x Want to do the Task? By reasoning on the
task trees, x checks if τ
k
contributes to any of its goals,
according to the contributes relationship defined by
(Lochbaum et al., 1990). If it is not the case, then x
has no interest to do τ
k
and U
x
(o
+
k
) is set to 0. Other-
wise x considers how much it is skilled to do τ
k
.
Should x do the Task? x’s abilities influence x’s
choice to do the task: x has to compute a
x,τ
a general
ability value on the task. If the task is a leaf task τ
l
,
then x takes into account its ability values on the skills
that are attached to τ
l
, if any. If the task is an abstract
task τ
k
, x reasons on the progress-representative con-
dition attached to τ
k
to compute a
x,τ
k
. Due to space
limitations, we do not further develop the calculation
process of a
x,τ
k
.
Task Utility Value. Finally, if τ
k
contributes to one
of x’s goals, x computes U
x
(o
+
k
) with Equation 4,
which formula allows U
x
(o
+
k
) to stay in the interval
[0, 1[. U
x
(o
+
k
) is proportional to f Imp
x
(γ) and if x is
skilled on the skills attached to τ
k
, U
x
(o
+
k
) is increased
proportionally to a
x,τ
k
.
U
x
(o
+
k
) = f Imp
x
(γ) ×(1 + a
x,τ
k
(1 − f Imp
x
(γ))) (4)
Task Utility for Others. x also computes the utili-
ties it thinks its teammates have for the task outcomes.
We define U
x
y
i
(o
+
k
) what x thinks of the utility for y
i
to
achieve o
+
k
. At Step n of the recursive task-selection
process, x has to compute U
x
y
i
(o
+
k
) for all agents y
i
such that y
i
∈ A
x,n
, y
i
6= x and for all tasks τ
k
such that
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
292

τ
k
∈ T
x,n
. To compute U
x
y
i
(o
+
k
), x uses the same pro-
cess than for itself but reasons on a
x
y
i
, j
its ability trust-
beliefs about y
i
what it thinks of y
i
’s goals γ
x
y
i
,team
and
γ
x
y
i
,sel f
.
7.2.3 Task Distribution
Once utility values are computed, x generates task dis-
tributions among agents and computes their utilities to
select the task that best serves its interests.
Task Distribution Generation. At the step n of
the recursive task-selection process, x generates task
distributions with all tasks τ
k
such that τ
k
∈ T
x,n
and with all agents y
i
such that y
i
∈ A
y
i
,n
. At this
point x takes into account the number-of-agent con-
straints that were propagate through the progress-
representative condition on the tasks: if a task τ
k
ne-
cessitates a minimal number of agents n
min
(τ
k
) and a
maximal number of agents n
max
(τ
k
), then x only gen-
erates arrangements where m(τ
k
) agents are assigned
to τ
k
such that m(τ
k
) = 0 (i.e. in this case, τ
k
is not
executed) or n
min
(τ
k
) ≤ m(τ
k
) ≤ n
max
(τ
k
).
Task Distribution Utility. Agent x then selects the
action that corresponds to what it thinks is the best
task distribution. In order to do so, x computes the
utility of a task distribution as the average of all util-
ities that x thinks agents have for the outcomes of the
tasks they are assigned to in the distribution.
Task Selection. x finally selects the task τ
k
for
which the utility of the task distribution is maxi-
mized. If this task is a leaf-task, then the recursive
task-selection process ends and x does the action cor-
responding to τ
k
. Otherwise x continues the recur-
sive task-selection process, and as explained in Sec-
tion 7.2.1, at step n + 1, T
x,n+1
= T
k
and A
x,n+1
is
the set of agents that were assigned to τ
k
in the task
distribution (i.e. x and maybe others). We underline
that x does not make a decision for its teammates: x
selects a task that it thinks corresponds to the best
task distribution. When doing so, x does not distribute
tasks to other agents. When making a decision, other
agents may or may not choose the task x projected
they would choose.
8 EXAMPLE
We develop in this section a small example of the
functioning of our system. Let A = {xenia, yuyu, zoe}
a team of agents who have one team goal γ
1
= lab
set up. xenia has a personal goal, γ
2
= paper writ-
ten. In formulas we designate the agents by their
initial letter (e.g. b
x,y
is xenia’s benevolence toward
yuyu). In this scenario yuyu and zoe are rather up-
right: i
y
= i
z
= 0.75, unlike xenia: i
x
= 0.25. They all
are rather highly benevolent toward their teammates
(i.e. all benevolence values are 0.75). For simplicity
reasons, we consider that agents have the true models
of their teammates.
Goal Importance Computation. We develop
yuyu’s process of goal-importance-value computa-
tion:
• She computes her initial importance value for
γ
1
as described in Section 7.1. She obtains
iImp
y
(γ
1
) = 0.75.
• She uses her theory-of-mind capability and com-
putes iImp
y
x
(γ
1
) = 0.25, iImp
y
x
(γ
2
) = 0.75 and
iImp
y
z
(γ
1
) = 0.75: she thinks that xenia will fa-
vor her personal goal and that zoe gives a high
importance to the team goal.
• Then she uses Equation 1 and computes d
y,x
(γ
1
) =
0.125, d
y,x
(γ
2
) = 0.375 and d
y,z
(γ
1
) = 0.375: she
rather likes xenia and zoe and so she wants them
to have the goals they value achieved.
• Using Equation 2 and Equation 3 she finally ob-
tains f Imp
x
(γ
1
) ' 0.417 and f Imp
x
(γ
2
) = 0.375:
she is benevolent toward xenia so she adopts her
goal, but it is still more important to her to achieve
the team goal.
Influence of Integrity and Benevolence. Agent in-
tegrity plays a crucial role in computing the goal-
importance value computation: although her team-
mates give importance to the team goal and even tak-
ing into account their teammates preferences, her per-
sonal goal is more important to xenia: from xenia’s
point of view, we obtain: f Imp
x
(γ
1
) ' 0.333 and
f Imp
x
(γ
2
) = 0.75. Agent benevolence also plays a
crucial role: if in the same example, yuyu is not
benevolent toward xenia (i.e. b
y,x
< 0.5) then she
will have a negative desirability to see xenia’s goal
achieved. Hence yuyu would compute f Imp
y
(γ
2
) = 0
and would not help xenia.
Task Selection. We consider that all agents have the
same ability value on σ
1
(∀i ∈ A , a
i,1
= 0.5), but dif-
ferent abilities values on σ
2
(a
x,2
= 0.75, a
y,2
= 0.25
and a
z,2
= 0.25). yuyu will reason here on the set up
lab activity instance described in Section 4. We con-
sider the task τ
2
as the root of the activity-instance
tree write paper.
A Trust-based Decision-making Approach Applied to Agents in Collaborative Environments
293

As explained in Section 7.2.1, at the first step of
her recursive decision-making process for task se-
lection, yuyu reasons on the set of agents A
y,1
=
{xenia, yuyu, zoe} and on the set of tasks T
y,1
=
{τ
1
, τ
2
}. yuyu computes the success-outcome utili-
ties of the tasks in T
y,1
. She goes through the task
utility computation process to compute U
y
(o
+
1
) as de-
scribed in Section 7.2.2: she can do τ
1
since she has
the required abilities. She wants to do τ
1
since τ
1
con-
tributes to her goal γ
1
. She computes her general abil-
ity value for τ
1
and obtains a
y,τ
1
= 0.5. She finally
computes U
y
(o
+
1
) as described in Equation 4 and ob-
tains U
y
(o
+
1
) ' 0.54. She applies the same process
with o
+
2
and obtains U
y
(o
+
2
) = f Imp
y
(γ
2
) = 0.375.
She then uses her theory-of-mind capability to com-
pute what she thinks of xenia’s utilities, applying the
same process than for herself. She obtains U
y
x
(o
+
1
) =
0.375 and U
y
x
(o
+
2
) = 0.75. She does the same for zoe
and obtains U
z
x
(o
+
1
) ' 0.82 and U
z
x
(o
+
2
) = 0.
yuyu then generates task distributions as explained
in Section 7.2.3, which we do not list here, but it is
obvious here that the maximal task-distribution utility
is obtained when yuyu and zoe are assigned to τ
1
and
xenia is assigned to τ
2
. Hence yuyu selects the task τ
1
.
Because τ
1
is an abstract task, she recursively starts
again the task-selection process as described in Sec-
tion 7.2.1 to choose one of τ
1
’s subtasks: it is the step
2 of her recursive task-selection process. At this step,
she reasons on the set of tasks T
y,2
= T
1
= {τ
11
, τ
12
}
and on the set of agents A
y,2
= {yuyu, zoe} since she
thinks zoe will also choose τ
1
. This second step of re-
cursive decision-making is similar to the first one and
we will not develop it here. At the end of this step,
yuyu chooses the task τ
12
(because both τ
11
and τ
12
contribute to her goal γ
1
, she is skilled on τ
12
and she
thinks zoe will also choose τ
1
2). This task is a leaf
task that corresponds to an action, hence the recur-
sion stops here, and yuyu will try execute the action
that corresponds to τ
12
.
9 CONCLUSIONS
We proposed in this paper mechanisms of decision-
making for generating agent behavior in collective ac-
tivities. We proposed an augmentation on ACTIVITY-
DL that supports collective activity description. We
defined activity instances that are representative of
agents progress on the collective activity and on
which agents can directly reason to select their ac-
tions. We proposed an agent model based on the
trust model of (Mayer et al., 1995) and a trust-based
decision-making system that allow agents to reason
on activity instances and to take their teammates into
account to select an action. We gave an example of
the functioning of the activity-treatment module and
of the decision-making system. Further work per-
spectives include testing the decision-making system
when agents have false beliefs about others, and eval-
uating the credibility of the produced behaviors. The
model could also be extended so that agents could to
act purposely to harm the team or their teammates,
which is not currently possible since agents can only
decide not to help the team.
ACKNOWLEDGEMENTS
This work was carried out in the framework of the
VICTEAMS project (ANR-14-CE24-0027, funded
by the National Agency for Research) and funded by
both the Direction G
´
en
´
erale de l’Armement (DGA)
and the Labex MS2T, which is supported by the
French Government, through the program ”Invest-
ments for the future” managed by the National
Agency for Research (Reference ANR-11-IDEX-
0004-02).
REFERENCES
Barot, C., Lourdeaux, D., Burkhardt, J.-M., Amokrane,
K., and Lenne, D. (2013). V3s: A Virtual En-
vironment for Risk-Management Training Based on
Human-Activity Models. Presence: Teleoperators
and Virtual Environments, 22(1):1–19.
Carruthers, P. and Smith, P. K. (1996). Theories of Theories
of Mind. Cambrige University Press, Cambrige.
Castelfranchi, C. and Falcone, R. (2010). Trust theory: A
socio-cognitive and computational model, volume 18
of John Wiley & Sons.
Chevaillier, P., Trinh, T.-H., Barange, M., De Loor, P.,
Devillers, F., Soler, J., and Querrec, R. (2012). Se-
mantic modeling of Virtual Environments using MAS-
CARET. pages 1–8. IEEE.
Gerbaud, S., Mollet, N., and Arnaldi, B. (2007). Virtual
environments for training: from individual learning to
collaboration with humanoids. In Technologies for E-
Learning and Digital Entertainment, pages 116–127.
Springer.
Lochbaum, K. E., Grosz, B. J., and Sidner, C. L. (1990).
Models of Plans to Support Communication: an Initial
Report.
Marsh, S. and Briggs, P. (2009). Examining trust, forgive-
ness and regret as computational concepts. In Com-
puting with social trust, pages 9–43. Springer.
Mayer, R. C., Davis, J. H., and Schoorman, F. D. (1995).
An Integrative Model of Organizational Trust. The
Academy of Management Review, 20(3):709.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
294

Querrec, R., Buche, C., Maffre, E., and Chevaillier, P.
(2003). ScuRVi: virtual environments for fire-fighting
training. In 5th virtual reality international conference
(VRIC03), pages 169–175.
Sanselone, M., Sanchez, S., Sanza, C., Panzoli, D., and
Duthen, Y. (2014). Constrained control of non-playing
characters using Monte Carlo Tree Search. In Com-
putational Intelligence and Games (CIG), 2014 IEEE
Conference on, pages 1–8. IEEE.
A Trust-based Decision-making Approach Applied to Agents in Collaborative Environments
295
