Towards a Synthetic Data Generator for Matching Decision Trees

Taoxin Peng and Florian Hanke

School of Computing, Edinburgh Napier University, 10 Colinton Road, Edinburgh, EH10 5DT, U.K.

Keywords: Synthetic, Data Generator, Data Mining, Decision Trees, Classification, Pattern.

Abstract: It is popular to use real-world data to evaluate or teach data mining techniques. However, there are some

disadvantages to use real-world data for such purposes. Firstly, real-world data in most domains is difficult to

obtain for several reasons, such as budget, technical or ethical. Secondly, the use of many of the real-world

data is restricted or in the case of data mining, those data sets do either not contain specific patterns that are

easy to mine for teaching purposes or the data needs special preparation and the algorithm needs very specific

settings in order to find patterns in it. The solution to this could be the generation of synthetic, “meaningful

data” (data with intrinsic patterns). This paper presents a framework for such a data generator, which is able

to generate datasets with intrinsic patterns, such as decision trees. A preliminary run of the prototype proves

that the generation of such “meaningful data” is possible. Also the proposed approach could be extended to a

further development for generating synthetic data with other intrinsic patterns.

1 INTRODUCTION

In our modern society in the internet age, collections

of data and even more important making use of

existing available data gain more and more importance.

Especially in the domain of teaching data mining or

data mining research, investigators often come across

some main problems. Firstly, in order to research or

teach a certain problem, most of the techniques and

methods in this domain rely on having relevant, big

collections of data. It is very common to use real-world

data for such purposes. However, real-world data in

most domains is difficult to obtain for several reasons,

such as budget, technical or ethical (Rachkovskij and

Kussul, 1998). Secondly, the use of many of the real-

world data is restricted or in the case of data mining,

those data sets do either not contain specific patterns

that are easy to mine for teaching purposes or the data

needs special preparation and the algorithm needs very

specific settings in order to find patterns in it. For

example, it is also very likely that real data may contain

sensible data (be it personal or confidential) which

makes it necessary to hide or obscure those parts,

resulting in a huge effort to carry out this task because

of the sheer size of these data collections. The third

problem is that in case of teaching data mining

techniques, learners may encounter the same “standard

datasets” (e.g. the IRIS dataset or the Cleveland Heart

Disease dataset) multiple times during their studies and

mining them becomes “less exciting” . This can lower

their motivation and as a consequence their learning

success.

A solution to these problems could be using

synthetic generated data with intrinsic patterns. There

are a number of approaches and techniques that have

been developed for generating synthetic data (Coyle

et al., 2013, Frasch et al., 2011, van der Walt and

Bernard, 2007, Sanchez-Monedero et al., 2013, Jeske

et al., 2005, Lin et al., 2006, and Pei and Zaiane,

2006). However, since each of the previous research

was either focused on a particular category, such as

clustering, or using some special techniques, there are

still spaces for further research. There is also a survey

paper that provides current development about

general test data generation tools (Galler and

Aichernig, 2014).

This paper presents a novel approach to a

synthetic data generator for matching data mining

patterns, such as decision trees, by developing a novel

decision tree pattern generating algorithm. A

preliminary run of the prototype proves that the

generation of such big size of “meaningful data” is

possible. Also the proposed approach could be

extended to a further development for generating

synthetic data with other intrinsic patterns.

The rest of this paper is structured as follows.

Related works are described in next section. The main

contribution of this paper is presented in section 3,

Peng, T. and Hanke, F.

Towards a Synthetic Data Generator for Matching Decision Trees.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 1, pages 135-141

ISBN: 978-989-758-187-8

135

which introduces the novel approach, the

architecture, the algorithm, the design and

implementation of the generator. The testing and

evaluation are discussed in section 4. Finally, this

paper is concluded and future work pointed out in

section 5.

2 RELATED WORK

Sanchez-Monedero et al (2013) proposed a

framework for synthetic data generation, by adopting

a n-spheres based approach. The method allows

variables such as position, width and overlapping of

data distributions in the n–dimensional space can be

controlled by considering their n-spheres. However,

this approach only focuses on cases dealing with

topics specially in the context of ordinal

classifications.

Coyle et al (2014) presented a method for

estimating data clusters at operating conditions where

data has been collected to estimate data at other

operating conditions, enabling classification. This

can be used in machine learning algorithms when real

data cannot be collected. This method uses the earlier

mean interpolation along with a method of

interpolating all of the matrices comprising the

singular value decomposition (SVD) of the

covariance matrix to perform data cluster

interpolation, based on a methodology termed as

Singular Value Decomposition Interpolation (SVDI).

It is claimed that the method can be used to yield

intuitive data cluster estimates with acceptable

distribution, orientation and location in the feature

space. However, as authors admitted the method

“assumes a uni-model distribution, which may or may

not true for classification and regression problems”.

Motivated by research work on data

characteristics (van der Wlat and Bernard, 2007,

Wolpert snd Macready, 1997), Frasch et al (2011)

proposed a method for generating synthetic data with

controlled statistical data characteristics, like means,

covariance, intrinsic dimensionality and the Bayes

errors. It is claimed that synthetic data generator

which can control the statistic properties are

important tools for experimental inquiries performed

in context of machine learning and pattern

recognition. The proposed data generator is suitable

for modelling simple problems with fully known

statistical characteristics.

Pei and Zaiane (2006) developed a distribution-

based and transformation-based approach to synthetic

data generation for clustering and outlier analysis.

There are a set of parameters that are considered as

user’s requirements, such as the number of points, the

number of clusters, the size, shapes and locations, and

the density level of either cluster data or noise/outliers

in a dataset. The generator can handle two-

dimensional data. However, it was claimed that based

on the heuristic devised, the system could be extended

to handle three or higher dimensional data.

Jeske et al. (2005) proposed an architecture for an

information discovery analysis system data and

scenario generator that generates synthetic datasets

on a to-be-decided semantic graph. Based on this

architecture, Lin et al. (2006) developed a prototype

of this system, which is capable of generating

synthetic data for a particular scenario, such as credit

card transactions.

The work probably most closely related to the one

proposed in this paper is the one by Eno and Thompson

(2008). The authors proposed an approach toward

determining whether patters found by data mining

models could be used and reverse map them back into

synthetic data sets of any size that would exhibit the

same patterns, by developing an algorithm to map and

reverse a decision tree. Their approach was based on

two technologies: Predictive Model Markup Language

(PMML) and Synthetic Data Definition Language

(SDDL). The algorithm would scan a decision tree

stored as PMML to create an SDDL file that described

the data to be generated. It was claimed that their

method confirmed the viability of using data mining

models and inverse mapping to inject realistic patterns

into synthetic data sets. However, their work is limited

to the two techniques used.

3 THE APPROACH

This section describes the proposed framework,

including the architecture, the pattern generating

algorithm, the design and implementation of the

approach.

3.1 Architecture

Figure 1 illustrates the relationship of all modules in

the framework. These modules can be implemented

to run in separate threads or even on separate systems

to create a distributed system which would optimise

the performance of the whole application. The

architecture is a modified version of the one proposed

by Houkjær et al. (2006).

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

136

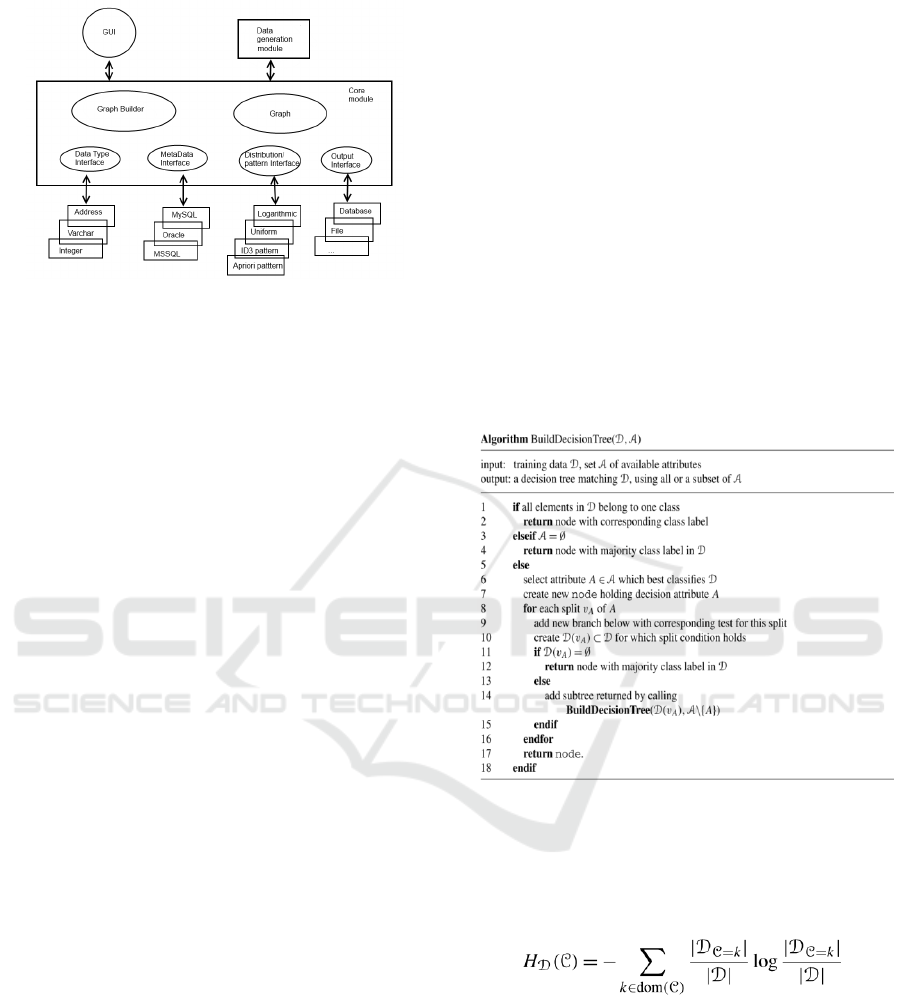
Figure 1: The Architecture.

Main components in this architecture are described as

below:

 GUI: This package contains all the classes

necessary for the graphical user interface. The

GUI classes enable the user

- to set parameters and inputs;

- to choose and set up the connection to the

database;

- to view the meta data connected to the tables in

the database;

- to choose from a list of available data generation

algorithms/methods;

- to set the desired output formats.

 Data Generation Module: This package contains

the classes needed to generate data, e.g. different

number generators (such as zero bitmap number

generators, shuffle number generators or

specialised number generators), classes that can

produce addresses or names and so on;

 The Core Module: This package contains three

sub packages:

- Graph Builder: This sub package contains all

classes necessary to generate a directed graph

which represents the database/table structures

retrieved from the database through the Metadata

Interface;

- Graph: The graph sub package holds a

representation of the database in memory. This is

necessary in order to generate consistent data that

fulfils constraints as well as intra- and inter-table

relations;

- Interfaces: This sub package contains the

interfaces and their class implementations which

are used by the graph, graph builder and data

generation module classes and provide the

different ways of input (different DBMS, e.g.

MySQL, Oracle, etc.; inputs for name/address

generation), output (e.g. into flat files) and the

interfaces used for the different data generation

algorithms or number distributions. One of the

most important interfaces in this design is the

pattern interface. This interface can be used

together with the new approach to pattern

generation in data to form a really unique data

generator.

3.2 A Decision Tree Algorithm: ID3

This new approach employs the idea of “Backwards

Engineering”: an existing well established

classification algorithm (in this case ID3) is used as

the basis to discover the patterns; then an algorithm is

developed that produces data in way such that this

basis algorithm is able to discover a structure in the

data.

In this framework, the well-known ID3 algorithm,

originated by Quinlan (1979, 1986) was used

following the description of Berthold et al (2010):

Figure 2: The ID3 algorithm as described by Berthold et al.

(Berthold et al., 2010, p. 211).

Figure 2 shows a general algorithm to build

decision trees. ID3 in particular uses a concept called

the Shannon Entropy H:

Here,

indicates the training data set,

the target

(class) attribute, i.e. the attribute towards which the

entropy is calculated, and

the set of attributes. The

entropy ranges from 0 to 1 and reaches the maximal

value of 1 for the case of two classes and an even

50:50 distribution of patterns of those classes. On the

other hand, an entropy value of 0 would tell us that

only one of these classes would exist in the given

subset of data. The entropy H therefor provides us

with a measure of the diversity of a given data set.

Towards a Synthetic Data Generator for Matching Decision Trees

137

The ID3 algorithm tries to reach the leaves of a

decision tree (i.e. nodes that only hold a single class

of attributes) as fast as possible, meaning that the

entropy of each subset of data after the split of the

values should have the least possible entropy.

Therefore, another measurement is needed, called the

“Information Gain”:

Where

and

A=a

indicates the subset of

for which attribute

A has value a. H

(C, A) denotes the entropy that is left

in the subsets of the original data after they have been

split according to their values of A.

This Information Gain makes it possible to split

the classes in

into subsets with each having the least

possible remaining entropy within. Using this

Information Gain as measurement in the split

condition for the Class attribute of the algorithm

outlined in figure 2, the ID3 algorithm is complete.

3.3 The Algorithm

With the ID3 algorithm and its underlying concepts

defined, the pattern generating algorithm can be

described.

The requirements for this algorithm are a

classification decision tree with a table in a database

having at least columns for each of the attributes that

are present in the nodes of the tree and the Class

attribute. In contrast to the ID3 algorithm that will

later be used to find the same tree again, the proposed

pattern generating algorithm does not start from the

root of the tree, working its way “downwards” over

nodes with the highest Information Gain to the leave

nodes, but it starts from the leave nodes in an

“upward” way.

The basic idea of the algorithm can be described

as follows. The leave nodes L have to be the nodes

with the least Information Gain of the whole data set.

This can be ensured by maximally distributing the

values of the Class attribute C on this level (this will

of course result in a very inaccurate classification

tree; in the implementation different distribution

levels can be used to make it more accurate). To do

this, a minimum number of entries in the database

table has to be specified; according to this number,

the table is then populated with maximal distribution

in C (which means all possible value c in C appears

with the same frequency), leaving all other columns

blank with the exception of the values in L (noted as

l in future). These are then chosen such that each

combination of l and c appears equally.

Now, when c is maximally distributed among l,

the entropy of L in respect to C is 1 and since the

Information Gain can never be negative and the range

of entropy is between 0 and 1, the Information Gain

for L is 0 and ID3 will use L as the leave nodes when

the other attributes have a higher Information Gain.

For the next level of nodes N

in the given

classification tree, all that has to be done is to make

sure the entropy for this level is a little lower than the

previous one, the easiest way to ensure this is to add

one more combination of a specific value of c and a

specific value n

of N

; the rest of the combinations

should stay maximally distributed (again, in the

implementation this “step width” can be set to

different values). To achieve this, a number of rows

depending on the number of different values of c rows

have to be added. Only the distribution among the

combinations of n

and c must be altered, not the

distribution of combinations of l and c. This will

result in an entropy value slightly lower than 1 for the

attribute N

in respect to C thus this attribute N

will

be used in the node level just above the leaves.

For the next node level N

(again having the

different values n

) in the classification tree, not only

one specific combination of n

and c has to be added

but two, therefore two times the number of values c

of rows have to be added to keep the combinations of

c and l maximally distributed and the combinations of

c and n

slightly less distributed.

This means again the entropy H(N

|C) < H(N

|C)

< H(L|C) and in that way, L will be found as leaves

by ID3, N

as the node level above the leaves, N

the node level above N

and if this procedure is

repeated until the root of the classification tree. The

database table will grow with each step. But the

entropy of each attribute higher to the top of the input

classification tree will be lower than the entropy to

the attributes closer to the leave nodes, which means

their Information Gain is higher. Thus ID3 will place

them into the right position.

3.4 Implementation

This section describes the implementation of the

algorithm outlined above.

3.4.1 Overview of the Implementation

Figure 3 shows the complete class diagram of the

prototype. The implementation of the pattern

generating algorithm is split among three main classes:

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

138

 the “Tree” class provides the framework for the

classification tree data structure required for

the algorithm;

 the “Node” class provides all the methods and

functions necessary to traverse the tree, get

certain nodes and update the entropy values

accordingly;

 the “TestMain” class makes the use of this data

structure, sets the entropy values of the

different Node levels and finally also deals with

the data generation;

In addition to the three main classes, there are two

helper classes, “BSGTree” and “BSGTreeBean”:

 “BSGTree” class defines and builds the tree

data structure utilising the “Tree” and “Node”

classes;

 the “BSGTreeBean” class is a simple Java

Bean with private members and Getters and

Setters for them. It is used by the “TestMain”

class in order to generate the data.

Figure 3: Class diagram.

3.4.2 The Implementation

The prototype only includes the implementation of

the pattern generating algorithm, which can be

described as the following steps:

 first of all, conclusion lists containing the

values of the class attribute are generated with

different entropy values;

 then, each of these lists is used to set the

conclusion lists of the nodes in one level.

Hence, these lists define the starting entropy for

level 0 and the “step width” as described in the

“description of the algorithm” section;

 the next step is the generation of the predefined

tree data structure followed by getting node

lists for the different types and levels. With

these node lists, each level can be populated

with conclusion lists with increasing entropy

values;

 further, after the above are all done, each row

of data has to be generated. As stated before,

each entry in the conclusion lists of the leaf

nodes represents a complete data set to be

generated. Consequently in order to generate

the data rows, all of the leaf nodes can be

retrieved by the tree and then their conclusion

lists can be looped through; the parent nodes of

the leaf nodes recursively contain the values of

other attributes. Of course, some attributes

might be missing in the chain from a leaf node

to the root node. These missing values are

replaced by a placeholder value and handled

later. All of these row data is collected in a list

of beans of the corresponding tree.

 finally, the placeholder values have to be

replaced with real attribute values. It is of high

importance that the entropy values for the

different attributes are not altered in this step.

This could happen easily if the placeholder

vales are not replaced carefully.

The generated data then can be exported after

optionally shuffling the resulting rows.

4 TESTING AND EVALUATION

4.1 Testing

The proposed pattern generator was tested by

arbitrarily generating three datasets with three

different types of classification trees constructed in,

and then finding the patterns in each of the dataset by

the J48 classification algorithm of WEKA.

Testing results are shown in figures 4, 5 and 6.

Figure 4: Left: Test tree 1. Right: Tree found by WEKA

J48.

Towards a Synthetic Data Generator for Matching Decision Trees

139

Figure 5: Left: Test tree 2. Right: Tree found by WEKA

J48.

Figure 6: Left: Test tree 3. Right: Tree found by WEKA

J48.

Figure 4 shows a simple tree with only 6 notes

constructed in a generated dataset at the left hand side

and the tree found by the J48 algorithm in Weka at

the right hand side. Figure 5 and 6 shows the similar

practice with a little bit more complicated tree

structures in generated datasets. In all of the testing

cases, the designed tree structures were found

successfully in the generated datasets, respectively.

4.2 Evaluation

The test cases show that it is definitely possible to

generate data that matches a data mining pattern. In

some cases, the entropy step width had to be altered

or additional “hidden nodes” had to be introduced to

the tree in order to make some splits. But this is most

likely due to the fact that the pattern generator

algorithm’s implementation is not technically mature

yet and can be improved in further versions.

Furthermore, a module should be developed that

reads trees as XML files (or similar) and generates the

tree structure necessary to generate the data

automatically. This would greatly increase the

versatility of the synthetic data generator.

In summary, the testing results prove that the

proposed synthetic data generator is able to generate

datasets with intrinsic patterns, such as decision trees.

Additionally, the performance of the data generator

was surprisingly good. It was possible to create

almost a million rows in a few seconds with a laptop

with basic specifications.

5 CONCLUSIONS AND FUTURE

WORK

In this paper, a novel approach for developing a

synthetic data generator for matching decision trees

has been proposed. A prototype of such a generator

has been implemented. The results of the test run

prove that a large dataset with patterns like decision

trees can be generated automatically within seconds.

While the prototype meets all requirements set out

within the aims of the project, the work introduces a

number of further investigations, including: a) to add

more classification algorithms into the generator; b)

to add more algorithms into the generator, which

allow patterns of association rules, clustering and

repression to be created; c) to develop a

comprehensive, user-friendly interface, which allows

users to select algorithms from different categories,

define the number of attributes, and other parameters.

The successful outcome of such future work would

result in a comprehensive synthetic data generator,

which is able to generate big datasets with patterns for

data mining research and training.

REFERENCES

Berthold, M., Borgelt, C., Höppner, F., & Klawonn, F.

2010. Guide to intelligent data analysis: How to

intelligently make sense of real data. Springer-Verlag

London.

Coyle, E., Roberts, R., Collins, E., and Barbu, A. 2014.

Synthetic Data Generation for Classification via Uni-

Modal Cluster Interpolation. Auto Robot 37:27 - 45.

Eno, J. and Thompson, C., 2008. Generating Synthetic Data

to Match Data Mining Patterns. IEEE Intenet

Computing, Vol. 12, No. 3 pp. 78 – 82.

Frasch, J. V., Lodwich, A., Shafait, F. and M. Breuel, T. M.,

2011. A Bayes-true data generator for evaluation of

supervised and unsupervised learning Methods. Pattern

Recognition Letters 32.11, pp. 1523–1531.

Galler, S. J. and Aichernig, B. K. 2014. An Evalaution of

White- and Grey-box Testing Tools for C#, C++, Eiffel,

and Java, Int J Softw Tools Technol Transfer 16: pp. 727

-751.

Houkjær, K., Torp, K., and Wind, R. 2006. Simple and

Realistic Data Generation. Proceedings of the 32

international conference on very large data bases

(VLDB ’06), pp. 1243-1246

Jeske, D. R., Samadi, B., Lin, P. J., Ye, L., Cox, S., Xiao,

R., Younglove, T., Ly, M., Holt, D., and Rich, R., 2005.

Generation of Synthetic Data Sets for Evaluating the

Accuracy of Knowledge Discovery Systems. In

Proceedings of the Eleventh ACM SIGKDD

International Conference on Knowledge Discovery in

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

140

Data Mining. ACM, New York, NY, USA. pp. 756 –

762.

Lin, P., Samadi, B., Cipolone, A., Jeske, D., Cox, S.,

Rendon, C., Holt, D. and Xiao, R., 2006. Development

of a Synthetic Data Set Generator for Building and

Testing Information Discovery Systems. In

Proceedings of the Third International Conference on

Information Technology: New Generations. IEEE, pp.

707 - 712

Pei, Y. and Zaiane, O., 2006. A Synthetic Data Generator

for Clustering and Outlier Analysis. Technical Report,

University of Alberta, Canada.

Quinlan, J. R. 1979. Discovering Rules by Induction from

Large Collections of Examples. In D. Michie (Ed.),

Expert Systems in the Micro Electronic Age. Edinburgh

University Press.

Quinlan, J. R. 1986. Induction of Decision Trees, Machine

Learning 1: 81-106.

Rachkovskij, D. A. and Kussul, E. M., 1998. Datagen: A

Generator of Datasets for Evaluation of Classification

Algorithms. Pattern Recognition Letters 19 (7), 537-

544.

Sánchez-Monedero, J., Gutiérrez, P. A., Pérez-Ortiz, M.

and Hervás- Martínez, C. 2013. An n-Spheres Based

Synthetic Data Generator for Supervised Classification.

Advances in Computational Intelligence. Ed. by Rojas,

I., Joya, G. and Gabestany, J. Lecture Notes in

Computer Science 7902. Springer Berlin Heidelberg,

pp. 613–621.

van der Walt, C. and Barnard, E. 2007. Data Characteristics

That Determine Classifier Performance. SAIEE Africa

Research Journal, Vol 98(3), pp 87-93.

Towards a Synthetic Data Generator for Matching Decision Trees

141