
Agile-similar Approach in Traditional Project Management
A Generalisation of the Crashing Model
Dorota Kuchta
1
, Pierrick L`Ebraly
2
and Ewa Ptaszyńska
1
1
University of Technology, Wrocław, Poland
2
Ecole Nationale des Ponts et Chaussees, Paris, France
Keywords: Time-cost Trade-off, Project Crashing, Linear Programming, Agile Development, Decision-making Tools.
Abstract: In numerous industries such as software development there has been increasing pressure on the supplier to
provide early results. In this study we propose a method to adapt traditional project scheduling in order to
meet early expectations of the client while limiting costs. First we present the philosophy of the agile
methodologies in which meetings with stakeholders play an important role. Therefore it is valuable to take
them into account in order to develop new models. Based on it we present a proposal of Linear Programing
(LP) model which goal is to minimize the crashing cost and maximize customer satisfaction. In our model we
distinguish activities that are rewarded (can increase customer satisfaction) if they are completed before
certain meetings. What is more, we assume that project’s budget can be modified during meetings. At the end
we present an example of using the proposed model.
1 INTRODUCTION
Recently we have been dealing with two types of
project management approaches (Wysocki, 2014) -
traditional approaches and agile approaches.
Simplifying, it can be said that the main difference
between them is that in the traditional approach the
project scope, deadline and budget are essentially
known at the beginning and the project management
methods aim at realizing this scope while in the agile
approach, the scope, and even the goal tend to change
during the project realisation and the project
management methods are aimed at helping the project
team to adapt the project and its realisation to the
changing objective. However, the two approaches
cannot be isolated from each other. Recently,
researchers have noticed the need to compare and
combine the two approaches.
(Kosztyn, 2015) proposes a matrix-based
approach to project planning and describes a generic
algorithm that builds schedules for both agile and
traditional project management approaches.
(Spundak, 2014) compares both approaches and
suggests that a mixed approach may be needed in the
future as we have been facing a more and more varied
spectrum of project types and, to use his words,
methodology should be adapted to the project and not
vice versa. This paper continues this line of research,
as it allows introduction of agile elements into
traditional project management. In Figure 1 and
Figure 2 both approaches (traditional and agile) are
described; the upper part of triangle represents
objectives while the lower parts represent the chosen
set of constraints. These are widely inspired by a
similar representation found in (Kosztyn, 2015).
Figure 1 presents agile approach. A simple way to
understand agile approach is to see it in terms of
maximizing goals in a fixed time and cost
environment.
Figure 1: Short term approach, agile approach.
Figure 2 presents traditional approach. Traditional
planning focuses on reaching fixed goals while trying
to minimise time and cost; which implies solving
a time-cost trade-off problem.
g
oals
time
cost
318
Kuchta, D., L’Ebraly, P. and Ptaszy
´
nska, E.
Agile-similar Approach in Traditional Project Management - A Generalisation of the Crashing Model.
In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 1, pages 318-326
ISBN: 978-989-758-187-8
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 2: Long term approach, traditional approach.
In this paper we will present an approach to
introduce an agile element into traditional approach.
Figure 3: Mixing both approach.
The approach we propose here allows
modification in the project short-term objectives in
order to deal with another major aspect of project
planning - client satisfaction.
Our proposal is motivated by the fact that the
customer plays a growing role in project
management. In a competitive environment it is
important to keep in mind that a major criterion for
project success is customer satisfaction (Al-Tmeemy
et al., 2010). This aspect is made clear in the agile
approach to project management, where the customer
is allowed to change his expectancies between every
sprint as to the project expected outcome. Thus, the
aim of our proposal is to allow the customer to
influence the project realisation in the traditional
approach to a greater degree than it is usually done.
We blend in the traditional approach to project
management the idea taken from agile management
of regular meetings, where customers should be
”made as happy as possible” (Al-Taani et al., 2013).
In traditional project management minimizing
cost or time, or more often achieving an optimal cost-
time trade-off (Alba, 2007) is a common goal and has
been tackled by different methods, including neural
networks (Dohi et al., 1999) Linear programming
models have been used for a long time to model the
dependencies in the project network and their
consequences for the project schedule. The crashing
model is a well-known model in formal traditional
project management, i.e. (Abbasi et al., 2011).
Traditional project crashing is a method for
shortening project duration by reducing the duration
of project activities situated on the critical path. It
allows, in the scheduling phase, to decide which
project activities should be crashed shortened at
a cost in order to achieve a desired project completion
time while keeping the cost minimal (or to find the
earliest possible completion time given a global
budget for activities shortening, a problem that is
outside of the scope of this article). The desired
project completion is dictated by the customer.
We thus propose to complete the crashing model
with a measure of customer satisfaction, implemented
through regular meetings with the customer.
This paper proposes a LP model which should
help deciding which activities should be crashed to
ensure the client is satisfied throughout the project
realisation, and not only after project completion, to
the highest possible degree at the minimal cost in
a budget and time limited environment.
The proposed set of constraints provide time and
money limits trough-out the project evolution, as well
as a reward system to encourage early satisfaction of
client’s needs.
2 CLIENT INTERACTIONS IN
DIFFERENT CONTEXTS
We made frequent use of meetings with client to
define time-cost trade-off. The notion of clients and
meetings can be given a more general definition.
Definition 1. A client is the person or the
organization who/which is the addressee of the
project product, interested in the development of the
project for future work.
Note that there could be many stakeholders of the
project. Here we concentrate on the principle
stakeholder, as different stakeholders may have
conflicting interests (Freeman, 1984). Focusing on
handling the expectancies of different stakeholders
could be an object of future research.
Definition 2. A meeting is a point in time at which the
client has access to the state of the project, and thus
is able to measure the state of advancement of the
project according to its own criteria. Having taken
knowledge about the current project state, it is
possible that after the meeting the client changes its
priorities, induce more resources for the future of the
project or even redefines the project.
Meetings are important in that they are the tools
that allow clients to have insight and impact on the
time cos
t
goals
g
oals
time
cost
time cost
goals
Agile-similar Approach in Traditional Project Management - A Generalisation of the Crashing Model
319

project. In the planning stage we try to model the
customer ongoing satisfaction after each meeting
according to the information possessed in this
moment, but after each meeting the customer has the
right to change its mind, which implies the model
must be reapplied to the unaccomplished part of the
project with changed parameters each time the client
express a change in priorities.
Definition 3. The project end date is the furthest
possible date at which the project stops. Three
reasons may cause a project to stop: project
completion, when no further activities are to be
completed, the end of the current planning horizon for
the project, that is, a new planning phase needs to be
planned later before this point so the project can
carry on, or the decision to give up on the project
because it has taken too long to give expected results.
For some projects, end date considered as a hard
deadline is quite unsatisfactory, as the project
outcome is not clearly perceived at the beginning of
the project. In this case, the project end date should
be referred to as the planning horizon and the role of
the finish activity is modified as project success does
not require any given activity to be completed.
We will now discuss three project examples,
showing how different the role of the client and form
take by the meetings can be:
1. A Road-construction Project. In this type of
project, the client is the sponsor for the road-work,
has little interest for the project inner
development, and has strong expectations for the
project completion date. For this reasons, all
meetings are set after the would-be finishing date
of the project, at which point strong penalties will
be handed for not completing the project in time.
In this case, the project end date would represent
the latest possibly conceivable time for finishing
the project.
2. A Not-for-profit Open-source Software Project. In
this radically different project, the aims of the
team developing the software is to deliver
a software that meets their own expectations,
while trying to get other developers to join their
development team. For this reason, the client is
any hypothetical developer potentially interested
in giving time to the project, including but not
limited to those actually handing in code for the
project. Costs should be expressed in terms of
man-hours rather than any other unit, and bounties
represent further involvement from developers in
the next development run, either through current
project developers deciding to give in more time
for the project, or other developers joining the
project. Meetings here are public releases for the
software, which correspond to the time at which
each developer can benefit from the work done on
other parts of the project, while Tend is the date at
which the geometry of the development team is
anticipated to change.
3. A Commercial Software Project for an External
Customer. Here, the customer pays for the
development of the product, but he may stay very
imprecise during project planning and even
during the early stages of project realisation.
Though he is often unaware of this, the customer
is not sure about what he wants the product to
address. However, there are usually certain
functionalities and concerns that the customer
wants with certainty, and that would keep him
satisfied during early project development. If the
team can make his early satisfaction high enough,
then the customer will be more inclined to accept
future failures or constraints while carrying on
with the project. Thus, it is vital in this type of
project to ensure early satisfaction is reached by
presenting achievements straight away even
though some important aspects of the final
product are yet to be decided or even identified.
3 PROPOSED MODEL
3.1 Basic Definitions
A project P can be broken down in a number of
activities that can be either tasks or events, an event
being an activity of zero duration by opposition to
a task which has to be performed (Elkadi, 2013). In
the rest of this paper we will use the word activity.
For the purpose of this model, we suppose that each
task and event is performed at most once in the course
of the project. Two additional dummy events are
added to provide the beginning and the completion of
the project. Let V =
0, + 1
be the set of activities
(Freeman, 1984).
For each of these activities we define a base
duration and cost, using notations that are consistent
with those proposed. This is done by introducing
vectors D∈ℕ
and ∈ℝ
, where
and
are
respectively the duration and the cost of performing
activity i. Additionally each activity can be crashed
by devoting more resources to it. This increases the
total cost to perform the activity. We introduce
vectors
∈ℕ
and
∈ℝ
as, respectively, the
maximal crashing duration (i.e. by how many days we
can maximally shorten the activity) and the daily cost
of crashing activities (the cost of shortening a given
activity by one day).
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
320

Crashing cost is always positive, and we have
0 ≤
≤
for each activity. If
=
then we say
the activity can be externalized.
Another concern that has to be addressed is the
relationship between activities. For this purpose, we
introduce a graph A in which each arc indicates that
the predecessor activity must be completed before
starting the successor activity. Unlike (Brucker,
1999) we will not introduce waiting times between
two activities, as those can be modelled by adding
additional dummy activities with a fixed duration
between activities that need to be separated, which
means that the graph can be seen as a subset of V×V,
at the cost of over-dimensioning the set V.
Actual starting times are kept in a variable vector
∈ℕ
and actual crashing times are kept in
a variable vector ∈ℕ
.
3.2 The Linear Programming Model
proposed – A General Description
Three different objectives have to be taken in account
in order to plan a project: reaching goals, as perceived
by the client, the time needed to do so and the money
used to do so. However, these are all dependent on
each other and for this reason, as described above,
past approaches made some of them constraints and
other objectives. It is also important to take into
account, as mentioned above, the objective of
customer satisfaction which is absent in classical
crashing models.
On the one hand, our model focuses on two
resources: time (the project completion time), and
money (budget available for crashing activities and
carrying tasks), to reach a fixed goal. What is more,
we keep track of project’s achievement throughout
the duration of the project by introducing meetings
with the client to take into account client satisfaction
at different points during the project, because we
assume that the customer, though interested in the
development of the project, does not need to be aware
of every activity but rather has knowledge about the
state of a project at a number of given times
(meetings) during the project.
In order to address the three objectives: early
completion time, minimal cost and maximal ongoing
customer satisfaction, we decided:
- to make the time objective a constraint - a project
deadline will be imposed;
- to make the cost objective both a model objective
(the total cost of activities crashing should be
minimal) and a constraint: in each consecutive
period between two meetings with the customer
there is a budget available for carrying out
activities, including crashing;
- to make the customer satisfaction a model
objective. For this reason, the objective function
will focus on money.
Thus, our model will have two objectives: the
total cost of crashing the activities (minimised) and
the satisfaction of the customer throughout project
realisation (maximised). The latter objective is
difficult to express in a formal way and to measure,
as it is immaterial. We have decided to measure it in
monetary units - project planners will be asked to
express the customer satisfaction in terms of value.
This translation is crucial, as it will play an important
role when we combine the objectives, which will be
discussed later on. The problem of expressing
consumer satisfaction in monetary units will be
discussed further in the next subsection.
To account for time-wise gain in this objective
function, bounties are awarded for early activity
completion. These bounties are awarded for each
activity if the given activity is started before the j-th
meeting with the client. For this we introduce ⊂ℕ
the set of meetings and ∈ℕ
the vector of meeting
dates.
is the bounty awarded for activity i if it has
completed before meeting j. For the purpose of
calculation, we use a matrix
∈ℝ
×
where
=
−
. This comes in handy as we can
now attribute a bounty for meeting j without checking
whether or not we already gave a bounty for week
j − 1. However, it can be noted that activities that are
not valued by the client, or activities that need to be
completed in order to have a value for the client, must
be treated with caution. In the first case no bounty
should be awarded for the activity, and, in the second
case, bounties should be awarded for an event that
depends on and only on the completion of the activity.
Things such as finishing a user interface, or giving a
functional preview to the client, should be modelled
through events and awarded with big bounties, as
even if they have shallow meaning in terms of work-
involvement, they play a great role in client
satisfaction. It needs to be remembered that bounties
are not used to congratulate a team on its fast work,
but to represent the value-added of having the client
implied in the development. For this reason, bounties
should be calculated based on their capacity to get the
client further involved in the project.
We obtain a bi-criteria linear programming
problem, which can be solved in many ways. Here we
assume the weighting approach with equal weights
given to both objectives, but of course the approach
to solving the bi-criteria problem could be changed,
either by modifying the weights or by using a
different method to combine the criteria.
Agile-similar Approach in Traditional Project Management - A Generalisation of the Crashing Model
321
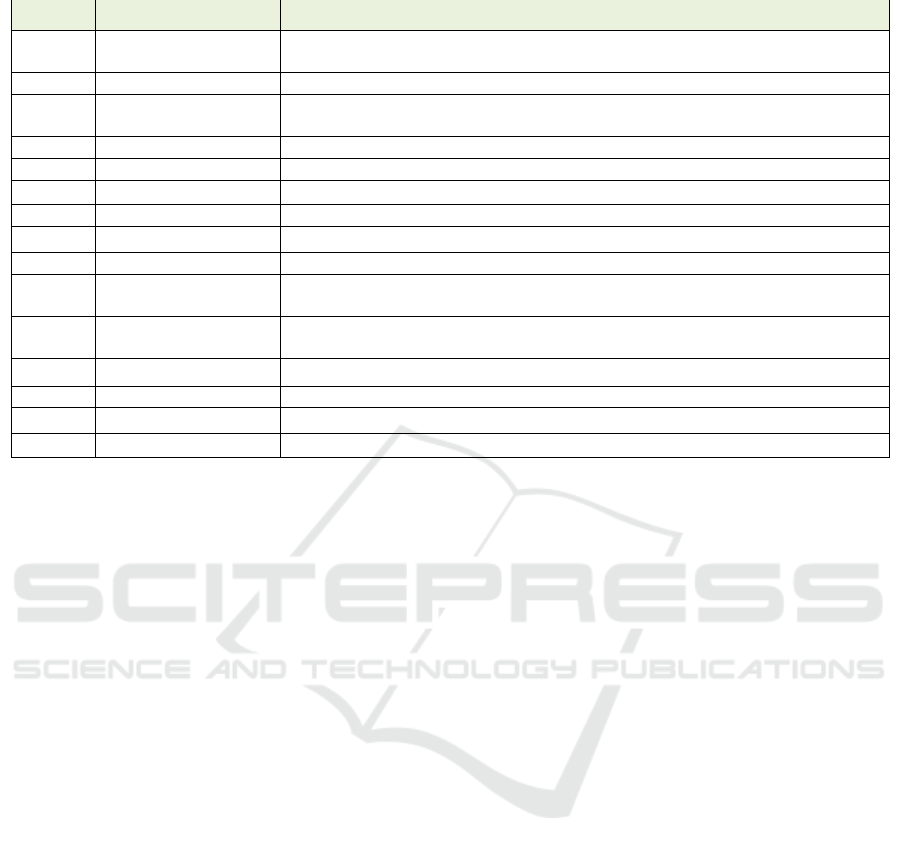
Table 1: Notations previously introduced.
Name Type Notes
N natural number The number of activities to be performed throughout the project, including
dummy activities
V
subset of ℕ
Project activities, including start and finish activities
A subset of V × V Activity dependency graph. If (a,b) is present in the graph then b depends on a to
start
W
subset of ℕ
Meetings
D
element in ℕ
V
Vector of the base durations in time unit for each activity
element in ℕ
V
Vector of the maximum crashing durations
C
element in ℝ
V
Vector of the base costs for each activity
element in ℝ
V
Vector of the crashing cost per time unit for each activity
MT
element in ℕ
W
Vector indicating the times on which meetings take place
Tend natural number Hard limit for project completion (note this can also denote the project planning
horizon)
B (B’)
element in ℝ
V ×
W
Matrix of the bounties handed out for completing a given activity before a given
meeting.
M (M
’
)
element in ℝ
W
Vector used to represent budget limits in the span between two meetings
y
variable in ℕ
V
Calculated starting time
x
variable in ℕ
V
Calculated crash duration
o variable in {0,1}
V ×
W
Binary indicating whether an activity is started before a given meeting
As mentioned above, resources availability for
activities crashing is limited in time which is
modelled using a fixed budget limit for each interval
between two meetings,
. We use a construction
similar to the one used for B’ to deduct a matrix M’
which can then be used to account for staying in the
budget during intervals [0..j].
A variable has to be introduced to denote whether
activity i has started before meeting j. This variable
matrix is noted (
) and calculated dynamically.
3.3 The Linear Programming Model
proposed – Mathematical
Formulation
In this subsection we will present the mathematical
formulation of the model described in the previous
section. Below we present a table summing up all
notations used to this point.
This leads us to introduce the following LP model:
Min cost :
∑
(
∙
−
∑
∙
)
(1)
∀
j
∈
W,
∑
∙ Ci ≤ Mj
(2)
∀
i
∈
V, x
i
≤
(3)
=0 and
≤
(4)
∀
(i,j)
∈
A,
−
+
≥
(5)
∀
,
10000 ∙
≥
−
(6)
∀
,
10000 ∙ (1 −
)≥−(
−
)
(7)
Equation (1) is the objective function and
equations (2) - (7) represent constraints. Constraint
(2) refers to budget limits in the timespan between
two meetings. Equation (2) is there to make sure the
project does not fail because of solvability limits. It is
important only for project that have a big monetary
impact on the firm. For those projects it is important
to keep in mind that a project could be profitable but
run through a phase in which is not solvable.
Constraint (3) refers to maximum crashing durations
of specific activities. Constraint (4) refers to starting
and finishing time of the project. Constraint (5) refers
to the order of activities. Constraints (6) and (7) are
used for indicating whether an activity is started
before a given meeting. The ‘10000’ is a more or less
arbitrary constant in order to be able to linearize ‘if’
tests. Note that in equation (1) two different
objectives were accounted for in an equation. The
sum here is used because matrix B can always be
normalized to be of the same order of magnitude as
the costs in the project, as it is used there and only
there. However, the decision of whether or not to
normalize the bounty matrix has to be taken when this
matrix is filled: in some situations the benefits of
showing early results to the client are not
commensurable to the crashing costs involved, and,
in these cases, no crashing should occur. On the other
hand, sometimes costs are not an issue if the client
can have early results, for example while handling a
project designed at resuming production for a much
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
322

larger manufacturing scheme, only early delivery
should be valued.
4 EXAMPLE
In this section we go through a few cases in which the
introduced model results in a different schedule
chosen for the project development than in a classical
approach. Due to the limited space in this article we
present only a brief example of a project. The
proposed linear programming model has been
implemented in a free editor GUSEK (GLPK Under
SciTE Extended Kit) and tested on a selected research
project performed by Wroclaw University of
Technology. The main goal of the analysed project is
to identify success and failure factors of research
projects with particular emphasis on projects
performed at universities, based on the example of
Poland and France.
Identifying success and failure factors of projects
is a popular problem in the scientific literature of
project management, i.a. (Blumer et al., 2013),
(Elkadi, 2013),, (Kosztyn, 2015), (Zou et al., 2014).
Research projects at universities represent very
specific type of project, i.a. (Luglio et al., 2010),
(Powers et al., 2009) therefore they require dedicated
research.
In the analysed project the following activities
were identified:
1. Preparing IT tools to support project realization.
2. Collecting contacts among stakeholders of
research projects in Poland.
Collecting contacts among stakeholders of research
projects in France.
3. Studying literature.
4. Conducting a survey among stakeholders of
research projects in Poland.
5. Performing interviews with specific stakeholders
of research projects in Poland.
6. Conducting a survey among stakeholders of
research projects in France.
7. Performing interviews with specific stakeholders
of research projects in France.
8. Organizing workshops with specific stakeholders
of research projects in Poland.
9. Organizing workshops with specific stakeholders
of research projects in France.
10. Preparing research results.
Network diagram (presented in Figure 4) explains
the sequencing of activities that needs to be applied
for the analysed project. In the diagram the red colour
represents the project critical path.
Figure 4: Project Network Diagram.
Gantt Chart for the analysed research project is
shown in Figure 5. Meetings (M1-M4) with different
stakeholders are also marked in this figure.
Figure 5: Initial Gantt Chart.
The first important meeting (M1) in our project
takes place in the second month. This is a scientific
seminar not only for the project team but also for
other scientists from the university. At the seminar the
concept of the project is presented. From the point of
view of scientists participating in the seminar the
important outcome of this meeting is building the
common understanding of its idea that definitely must
be supported by the analysis of the literature. That is
why we can state that we should crash activity 4. In
traditional project management approach activity
4 will never be crashed if its length is smaller than
activity 2 or 3. But in this case we get a greater reward
if we shorten activity 4.
= 500 (all bounties are
presented in Table 2) is the bounty rewarded for
completing activity 4 before starting the meeting M1,
specified by Project Manager. For scientists activity
4 is much more important than having a tool to
manage our project (activity 1) or how many contacts
Agile-similar Approach in Traditional Project Management - A Generalisation of the Crashing Model
323

Table 2: Input data.
V
Pred.
D C
0
∅
0 0 0 0 0 0 0 0
1 {0} 2 2000 1 1000 0 0 0 0
2 {0} 4 500 1 200 0 0 0 0
3 {0} 4 500 1 200 0 0 0 0
4 {0} 3 500 1 200 500 0 0 0
5 {2} 7 5000 1 1500 0 0 0 0
6 {2} 5 2000 2 1000 0 2000 0 0
7 {3} 7 5000 1 1500 0 0 0 0
8 {6} 3 3000 1 1000 0 0 2000 0
9 {5} 3 6000 1 0 0 0 0 7000
10 {7} 3 10000 1 0 0 0 0 0
11 {9, 10} 5 7000 0 0 0 0 0 0
12 {11} 0 0 0 0 0 0 0 0
W MT
1 2
2 7
3 11
4 13
among stakeholders of research projects we have
(activities 2, 3). Moreover if scientists are properly
understanding the subject of our project, they will
better support our research by answering questions in
interviews (activities 6, 8) or filling in survey
questionnaires (activities 5, 7). Based on this example
we can observe that in some cases it is worth crashing
a shorter activity before the meeting, while leaving
longer activity uncompleted after the meeting. Such
decisions are specific for agile approach. In the
example above, a completed activity 4 is shown to the
stakeholders (scientists) while other activities, which
are not important to the scientists, are not crashed
even though they are cheaper to crash than activity 4.
The second meeting (M2) in our project takes
place in the seventh month. After three months of
performing activities 5, 7 the survey team expects the
results from the interviews (activity 6) because they
can help to determine the final version of the
questionnaire for stakeholders in Poland and France.
Therefore the activity 6 should be shortened to 3
months. Project Manager defined that for completing
activity 6 before starting M2 the rewarded bounty is
= 2000 zl. Thanks to this operation of shortening
activity 6, we not only get a reward in the form of
better questionnaires but also the interview team is
able to start immediately the next interview with
French scientists (activity 8). As a consequence we
are then allowed to finish activity 8 before the third
meeting (M3) in 11th month. This is a meeting with
Rector of the Wroclaw University of Technology to
report progress in our project and may give us another
reward. Project Manager defined that for completing
activity 8 before starting M3 the rewarded bounty is
= 2000 zl. The fourth meeting (M4) in our project
takes place in the thirteenth month when we have to
report progress in our project to NCN (Narodowe
Centrum Nauki – National Science Centre).
This is the example of crashing activities in series.
Activity 9 cannot be performed until activity 5 is
completed. In traditional approach crashing the
project is done by crashing the cheapest-to-crash
activity situated on the critical path. However, when
5 and 9 have comparable crashing costs, crashing 5 to
meet the deadline is preferable, even when the
crashing cost for 5 is slightly higher than the crashing
cost for 9. Crashing early is important in time-
constrained projects as it gives room for the possible
last-minute crashing of final activities. That could not
be done in the case when these activities are already
crashed to their minimum length. In our case we crash
activity 9 before the fourth meeting with National
Science Centre because of the two reasons:
- activity 5 cannot be shortened any more,
- Project Manager defined that for completing activity
9 before starting meeting M4 the rewarded bounty is
=7000 zl. It is because of the fact that National
Science Centre is more interested in the results of
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
324

Polish workshops than in results of surveys.
Table 2 presents input data to the model in the
analysed case of research project. Based on the
project documentation the dependencies between the
activities, durations of activities (D) and their costs
(C) were determined. Furthermore Project Manager
defined: dates of meetings with specific stakeholder
of the project (MT), maximum crashing durations for
each activity (
), crashing cost per time unit for
each activity (
) and bounties for completing
specific activities before meetings planned with
different stakeholders (
,
,
,
). In this case
there were no budget limits in the span between
meetings (M).
According to the data of the project described
above, the following model can be built based on Eqs.
(1), (3)-(7) in Section 3:
Min cost :
∑
(
∙
−
∑
∙
)
s.t.
∑
∙
≤
, j = 1,2,3,4
x
i
≤
, i = 0,1,…,12
=0 and
≤20
−
+
≥
, i = 0,1,…,12, j = 1,2,3,4
10000 ∙
≥
−
, i=0,1,…,12, j=1,2,3,4
10000 ∙ (1 −
)≥−(
−
),
i=0,1,…,12, j=1,2,3,4
Table 3 presents results obtained by solving the
given model and Figure 6 shows the updated
schedule, including the changes described above. In
Figure 6 dashed stroke and light colour mean old
tasks and continuous stroke and saturated colour
mean updated tasks.
Table 3: Results.
V x
i
y
i
0 0 0 1 1 1 1
1 0 0 1 1 1 1
2 0 0 0 1 1 1
3 0 0 0 1 1 1
4 1 0 1 1 1 1
5 0 4 0 0 1 1
6 2 4 0 1 1 1
7 0 4 0 0 1 1
8 0 7 0 0 1 1
9 1 11 0 0 0 1
10 0 11 0 0 0 0
11 0 14 0 0 0 0
12 0 19 0 0 0 0
Figure 6: Uploaded Project Network Diagram.
We have seen in the analysed case that the model can
render in a systematic manner decisions that make
sense from the point of view of satisfying selected
project stakeholders during the project realisation but
are not the choice that would have been retained by
a traditional crashing. This allows for better project
planning in an environment where stakeholders stay
present throughout project execution and may
influence it and its perception. In the analysed case
the proposed approach would positively influence the
satisfaction of the following stakeholders:
1. Scientists – because of completing activity
4 before starting meeting M1.
2. The survey team – because of completing activity
6 before starting meeting M2.
3. Rector of the Wroclaw University of Technology
– because of completing activity 8 before starting
meeting M3.
4. National Science Centre – because of completing
activity 9 before starting meeting M4.
The proposed model has also its weaknesses. The
more input data we have, the more accurate model we
get. This can cause problems for the projects where
no input would be available. Our future work will
focus on the dependencies between the input dataset
size and the accuracy of the estimations. Another
future work is to examine more complicated
relationships between the parameters of our model
(e.g. non linear relationships between crashing cost
and crashing duration) as well as to investigate the
accuracy of our model on projects of different sizes
and number of available resources.
5 CONCLUSIONS
Recent years have shown a paradigm shift in project
Agile-similar Approach in Traditional Project Management - A Generalisation of the Crashing Model
325

management approaches. The most important change
can be observed in the increasing role of client and
other stakeholders in managing projects.
Traditionally the client input was important only
during planning phase and the acceptance. Nowadays
client feedback is important all along the project
execution. The changes can be particularly observed
in the industries where this feedback can lead to better
and more accurate products, such as software
development. It is always worth combining both agile
and traditional methods of project management. This
article presents such an approach. The example from
this article shows the project type where this
combined approach leads to better results. The
method presented in this article helps in managing
projects in fast changing environments where the
input of the client and stakeholders can shape the
initial scope of the project, but where the customer
satisfaction is maximized at each stage of project
execution.
REFERENCES
Abbasi, G. Y., Mukkatash, A. M., 2011. Crashing PERT
networks using mathematical programming,
International Journal of Project Management, Vol. 9.
Al-Taani R. H., Razali R., 2013. Prioritizing Requirements
in Agile Development: A Conceptual Framework,
Procedia Technology Vol. 11.
Al-Tmeemy S.H., Abdul-Rahman H., Harun Z., 2010.
Future criteria of success of building projects in
Malaysia, International Journal of Project.
Alba E., Software project management with gas, 2007.
Information Sciences 177 (11).
Blumer Y. B., Stauffacher M., Lang D. J., Hayashi K.,
Uchida S., 2013. Non-technical success factors for
bioenergy projects-Learning from a multiple case study
in Japan. Energy Policy.
Brucker M. N. P., 1999. Resource-constrained project
scheduling: Notation, classification, models, and
methods, European Journal of Operational Research
112 (1).
Dohi S. O. T., Nishio Y., 1999. Optimal software release
scheduling based on artificial neural networks, Annals
of Software Engineering.
Elkadi H., 2013. Success and failure factors for
e-government projects: A case from Egypt. Egyptian
Informatics Journal, 14(2).
Freeman R. E, 1984. Strategic Management: a stakeholder
approach, Pitman Series in Business and Public Policy,
Harpercollins, College Div.
Kosztyn Z. T., 2015. Exact algorithm for matrix-based
project planning problems, Expert Systems with
Applications 42 (9).
Luglio F., Bertazzoni N., 2010. Research management in
higher education institutions: A process management
experience in Italian Universities, CRIS 2010:
Connecting Science with Society - The Role of
Research Information in a Knowledge-Based Society -
10th International Conference on Current Research
Information Systems.
Powers L.C., Kerr G., 2009. Project Management and
Success in Academic Research. Realworld Systems.
Spundak M., 2014. Mixed agile/traditional project
management methodology reality or illusion?,
Procedia – Social and Behavioral Sciences, Vol. 119.
Wysocki R. K., 2014. Effective Project Management:
Traditional, Agile, Extreme. Wiley.
Zou W., Kumaraswamy M., Chung J., Wong J., 2014.
Identifying the critical success factors for relationship
management in PPP projects. International Journal of
Project Management, 32(2).
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
326
