A Hybrid Interaction Model for Multi-Agent

Reinforcement Learning

Douglas M. Guisi

, Richardson Ribeiro

, Marcelo Teixeira

, André P. Borges

, Eden R. Dosciatti

and Fabrício Enembreck

Federal University of Technology-Paraná, Pato Branco, Brazil

Federal University of Technology-Paraná, Ponta Grossa, Brazil

Pontificial Catholical University-Paraná, Curitiba, Brazil

Keywords: Multi-Agents Systems, Coordination Model, Reinforcement Learning, Hybrid Model.

Abstract: The main contribution of this paper is to implement a hybrid method of coordination from the combination

of interaction models developed previously. The interaction models are based on the sharing of rewards for

learning with multiple agents in order to discover interactively good quality policies. Exchange of rewards

among agents, when not occur properly, can cause delays in learning or even cause unexpected behavior,

making the cooperation inefficient and converging to a non-satisfactory policy. From these concepts, the

hybrid method uses the characteristics of each model, reducing possible conflicts between different policy

actions with rewards, improving the coordination of agents in reinforcement learning problems. Experi-

mental results show that the hybrid method can accelerate the convergence, rapidly gaining optimal policies

even in large spaces of states, exceeding the results of classical approaches to reinforcement learning.

1 INTRODUCTION

Multi-agent systems in general comprises of adap-

tive agents that interact with each other in order to

conduct a given task. In a multi-agent system, agents

need to interact and to coordinate themselves for

carrying out tasks (Stone and Veloso, 2000). Coor-

dination between agents can help to avoid problems

with redundant solutions, inconsistency of execution,

resources wasting and deadlock situations. In this

context, coordination models based on learning are

capable of solving complex problems involving social

and individual behaviors (Zhang and Lesser, 2013).

Besides learning how to coordinate itself, an

agent from a multi-agent system must also be able to

cooperate to other agents in the system, attempting

to solve problems that locally require unknown

knowledge or problems that compromise the agent

performance to be solved. In this way, sharing agent

expertise (usually in terms of action policies) be-

comes essential to converge to a global behavior that

satisfies a certain specification or that simply solves

a particular problem.

An alternative to share agent’s expertise among

multi-agents is using specific computational para-

digms that maximize performance based on rein-

forcement parameters (reward or punishment) ap-

plied to agents as they interact with the environment.

Such paradigms are called Reinforcement Learning

(RL) (Kaelbling et al., 1996) (Sutton and Barto,

1998).

RL algorithms, such as Q-learning (Watkins and

Dayan, 1992), can be used to discover the optimal

action policy for a single agent when it repeatedly

explores its state-space.

Formally, an action policy can be modeled by a

5-tuple b=

〈

A, S, s°, *,

〉

that maps states and ac-

tions in order to determine, among a set of actions A

and a set of states S, which an action a

∈ A should

be performed at a given state s ∈ S. An action policy

model has also an initial state s°

∈

S, an objective

state s*

∈

S, and a transition relation



that defines

the range of actions possible to be generated from a

state. The relation  is defined as memoryless, i.e.,

it defines actions taking into account uniquely the

current state, which qualifies the approach as a Mar-

kovian Decision Process (MDP).

A major concern that arises from this action-

policy-discovering approach is that it tends to suffer

with large state-spaces, due to state-space explosion

problems. In this case, RL involving multiple agents

has shown to be a promising strategy that modular-

Guisi, D., Ribeiro, R., Teixeira, M., Borges, A., Dosciatti, E. and Enembreck, F.

A Hybrid Interaction Model for Multi-Agent Reinforcement Learning.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 2, pages 54-61

ISBN: 978-989-758-187-8

izes the whole problem and locally implements ac-

tion policies (Ribeiro et al., 2008).

The whole idea behind the implementation of lo-

cal policies is discovering a global action plan gen-

erated by the proper combination of local knowledge

of agents. When this approach leads to the best global

action plan, the policy Q is said to be optimal (Q*)

and it maximizes the reward received by agents.

The approach investigated in this paper aims to

improve the way agents share information with each

other. In order to transmit and receive information,

agents are required to share a cooperative and coor-

dinated interaction model that eventually leads to

improved action policies. So, the kernel for estab-

lishing optimized information sharing strategies for

multiple agents is the interaction model.

In this paper we introduce a hybrid coordination

model for multi-agents using RL techniques. Our

approach collects “good” features from individual

approaches in the literature and integrates them into

a single framework, which can then be used to estab-

lish optimized information sharing strategies for

multiple agents. Preliminary results compare the

performance of the hybrid model with respect to the

each particular model that has been used to compose

our framework. In general, we have observed a con-

vergence rate among agents substantially better than

in the other cases.

The remainder of this paper is organized as fol-

lows. In the following section, the state of the art is

presented, in which: (i) describes some coordination

methods for learning in multi-agent systems; (ii)

reviews of the Q-learning algorithm; and (iii) sum-

marizes the interaction models. The details of the

proposed method, environmental assessment and

numerical results to demonstrate the performance of

the method are present in Section 3. Conclusions are

drawn in Section 4.

2 LEARNING IN MULTI-AGENT

SYSTEMS

Learning in multi-agent systems, unlike learning in

environment with a single agent, assumes that the

relevant knowledge is not locally available in a sin-

gle agent, although it is necessary to coordinate the

whole process (Chakraborty and Stone, 2014),

(Zhang and Lesser, 2010), (Xuan and Lesser, 2002).

One way for an agent to coordinate its actions is by

interacting with other agents, changing and evolving

their own coordination model.

Coordination by interaction provides the combi-

nation of efforts among a group of agents when

searching for solutions to global problems (DeLoach

and Valenzuela, 2007). A situation of interaction is a

set of behaviors resulting from a group of agents that

act to satisfy their goals and consider constraints

imposed by resources limitations and individual

skills. In the literature, learning from interactions

composes a preeminent research topic (Ribeiro et al.,

2013), (Xinhai and Lunhui, 2009), as well as collec-

tive or social learning (Ribeiro et al., 2013), (Ribeiro

and Enembreck, 2013).

Learning problems involving RL interaction

models depends basically on a structure that enables

communication among agents, so that they can share

their accumulated rewards, which immediately rein-

forces the transition system. With this propose,

Chapelle et al. (2002) propose an interaction model

that calculates rewards based on the individual satis-

faction of neighboring agents. In this learning pro-

cess, agents continuously emit a level of personal

satisfaction. Differently, Saito and Kobayashi (2016)

develop a learning strategy in which agents are able

to keep memory about information they have accu-

mulated, so they can reuse them in the future. This

method has been tested on colored mazes and re-

ports confirm that it positively impacts on jumpstarts

and reduces the total learning cost, compared to the

conventional Q-learning method.

Ribeiro and Enembreck (2013) combine theories

from different fields to build social structures for

state-space search, in terms of how interactions be-

tween states occur and how reinforcements are gen-

erated. Social measures are used as a heuristic to

guide exploration and approximation processes. Ex-

periments show that, identifying different social be-

havior within the social structure that incorporates

patterns of occurrence between explored states helps

to improve ant coordination and optimization process.

Usually, it is challenging to integrate different

methods into a single improved generic coordination

model, especially due to the diversity of the classes

of problems and the amount of knowledge necessary

from the problem domain. Furthermore, in a multi-

agent system, conflicting values for cumulative re-

wards can be generated, as each agent uses only lo-

cal learning values (DeLoach and Valenzuela,

2007). Thus, the collective learning assumes that the

relevant knowledge occurs when rewards are shared,

intensifying the relationship between agents.

2.1 Reinforcement Learning

RL tries to solve problems where an agent receives a

return from the environment (rewards or punish-

A Hybrid Interaction Model for Multi-Agent Reinforcement Learning

ments) for its actions. This type of learning has been

extensively investigated in the literature (Grze’s and

Hoey, 2011), (Devlin et al., 2014), (Efthymiadis and

Kudenko, 2015), (Tesauro, 1995), (Walsh et al.,

2010), (Zhang and Lesser, 2013) in order to approx-

imate solutions to NP-hard problems.

To properly formalize a RL problem, it is essen-

tial to first describe how a MDP structure is com-

posed. A MDP is a tuple

〈

S, A, T

s,s’

, R

s,s’

〉

such that

S is a finite set of environmental conditions, that

may be composed, for example, by a variable se-

quence of states

〈

, x

, …, x

〉

; A is a finite set of

actions, where an episode a

is a sequence of actions

a ∈ A which leads the agent from a state s

initial

to a

state s

objective

, T

s,s’

is a transition state relation T : S ×

A → [0,1], that indicates the probability of an agent

to reach a state s’ when an action is applied at the

state s. Similarly, R

s,s’

is a reward function R : S × A

→

ℜ

received whenever a transition T

s,s’

occurs.

The goal of a RL agent is to learn a policy π: S ×

A which maps the current state s into a desired ac-

tion to maximize the rewards accumulated over the

time, describing the agent’s behavior (Kaelbling et

al., 1996). To achieve optimal policies, the RL algo-

rithm must iteratively explore the state space S × A,

updating the accumulated rewards and storing re-

wards in Q(s, a) (Equation 1).

A well known method that can be used to solve

RL problems is called Q-learning (Watkins and Da-

yan, 1992). The basic idea of the method is that the

learning algorithm learns an optimal evaluation

function for all pair state-action in S × A. The Q

function provides a mapping Q: S × A → V, where V

is the value of expected utility when performing an

action a in state s. The function Q(s,a), of the ex-

pected reward when choosing the action, is learned

through a trial and error approach, as described by

Equation 1:

)]([),(),( VyRasQasQ ×++←

(1)

where α ∈ [0,1] is the learning rate, R is the reward,

or cost resulting from taking action a in state s, y is

the discount factor and V is obtained by using the

function Q learned by now. A detailed discussion

about Q-learning can be found in (Watkins and Da-

yan, 1992).

In this paper, Q-learning is used to generate and

evaluate partial and global action policies. By apply-

ing Q-learning it is possible to find a policy to an

agent. However, if similar agents interact into the

same environment, each agent has its own MDP, and

optimal global behavior can not be set by local anal-

ysis. Thus, in an environment formed by several

agents, the goal is to select the actions of each MDP

at time t, so that the total expected rewards for all

agents is maximized.

2.2 Reinforcement Learning with

Multiple Shared Rewards

In RL algorithms with multiple shared rewards,

agents can produce a refined set of behaviors ob-

tained from the executed actions. Some behaviors

(e.g., a global action policy) are shared by agents

through a partial policy action (Q

). Usually, such

policies contain partial information (learning values)

about the environment (E), but communicate with a

central structure to share rewards in an integrated

way in order to maximize the sum of the partial re-

wards obtained during the learning process. When

policies Q

,…,Q

are integrated, it is possible to

make a new policy ∂ = {Q

,....,Q

}, where ∂(s,a) is a

table that denotes the best rewards acquired by

agents during the learning process.

Figure 1: Learning with shared rewards (Ribeiro et al.,

2008).

Figure 1 shows how agents exchange infor-

mation during learning. When the agent A* receives

rewards from other agents Agent

, the following pro-

cess occurs: when Agent

reaches the goal state g

from a state s ≠ g with a lower-cost way, the agent

uses a model to share such rewards with other

agents. The learning values of a partial policy

can be used to upgrade the overall policy ∂(s,a), fur-

ther interfering in how other agents update their

knowledge and interact with the environment.

Figure 1 also shows the function that shares such

rewards. This task can be accomplished in three

ways (summarized in subsection 2.2.1), all internally

using Q-learning. The best rewards from each agent

are sent to ∂(s,a), forming a new policy with the best

rewards acquired by agents Agent

= {i

,...i

}, which

can be socialized with other agents. A cost function

(Equation 2) is used to estimate ∂(s,a), which calcu-

lates the cost of an episode (path from an initial state

s to the goal g) in a given policy.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

∑∑

∈∈

Sst.gsstoc )(10),(

(2)

The discovery of this path is performed with the

A* algorithm which produces a generative model for

managing policies that maximize the expected

amount of reward, i.e., optimal policies, according to

the methodology presented in (Ribeiro et al., 2006).

The cooperative RL algorithm, the other algo-

rithms, and the elements formalizing the RL models

are detailed in (Ribeiro et al., 2008). Figure 2 sum-

marizes the learning process with the models in an

activity diagram that uses the algorithms proposed in

(Ribeiro et al., 2008).

Figure 2: The learning process activity diagram with the

interaction models.

2.2.1 Interaction Models

In this subsection, we summarize the models pre-

sented in (Ribeiro et al., 2008).

Discrete Model: The agents share learning in a

predefined cycle interactions c. Cooperation in the

discrete model occurs as follows: the agent accumu-

lates rewards obtained from its actions during the

learning cycle. At the end of the cycle, each agent

sends the values of

to ∂(s,a). The agent share its

reward if and only if it improves the efficiency of

the other agents at the same state.

Continuous Model: The agents cooperate at

every transaction T

s,s’

. Cooperation in the continu-

ous model occurs as follows: if s ≠ g, then every

action performed by the agent generates a reward

value, which is the sum of the accumulated rein-

forcements for all players in action a in state s. The

goal is to accumulate the greatest rewards in

that

can be shared at each iteration.

Objective-driven Model: Unlike the discrete

model, cooperation occurs when the agent reaches

the goal state, i.e., s = g. In this case, the agent inter-

acts accumulating reward values. It is necessary be-

cause in this model the agent shares his rewards only

when the state goal is reached. When the agent

reaches the goal state, the rewards value is sent to

∂(s,a). If the state reward value improves the overall

efficiency, then the agents share such rewards. It

shows that even sharing unsatisfactory rewards (due

to of lack interaction), the agent is able to adapt his

behavior without damaging the global convergence.

3 HYBRID COOPERATION

MODEL

In RL based on shared rewards, is usual to discover

intermediate action policies that are not appropriate

to achieve a certain goal. In fact, the knowledge ex-

change among agents may lead to intermediate ac-

tion plans that do not immediately fit to the agent’s

convergence. As each agent constantly updates its

own learning, it becomes necessary that all agents

are aware of all updates happening and of the reward

from each agent.

Using the previously presented approaches for

agent’s coordination based on shared rewards, there

is no guarantees that the action plans will converge

sometime. It can happen that policies with initially

mistaken states and values are improved by rewards

informed by other intermediate policies, improving

the ∂(s,a) function. However, the opposite is also

possible, i.e., initially interesting policies, with high

level rewards, may become less interesting to be

chosen during a given policy, as states previously

producing successful hits and errors.

A. 400 states and 5 agents

B. 400 states and 10 agents

Figure 3: Coordination models (Ribeiro et al., 2008).

In order to overcome this inconvenience (local

A Hybrid Interaction Model for Multi-Agent Reinforcement Learning

maximum), we develop in this paper a hybrid meth-

od for multi-agents coordination. This approach

emerges from the discrete, continuous and objective-

driven models previously presented. By analyzing

results collected from those models, we claim that

the behavior of ∂(s,a) changes as a function of num-

ber of interactions of the algorithms, the quantity of

episodes involved in the problem and the cardinality

of the set of agents that have been used. Figure 3

supports our claim by comparing coordination mod-

els immerse in a 400-states environment.

The proposed hybrid method capture the best

features from each individual interaction model, at

every interaction of the coordination. The discovery

of new action policies is done without delaying the

learning process, reducing the probability of con-

flicts among actions from different policies.

Technically, the hybrid method can be summa-

rized as follows: at every interaction of Q-learning,

the agent’s performance is collected from each inter-

action model. This composes what we call a learn-

ing table named HM-∂(s,a) (Hybrid Method). When

the model update condition is reached, the agent

starts its learning process using the best performance

calculated from the learning tables in the interaction

models. The learning is then transferred to HM-

∂(s,a). Therefore, the function HM-∂(s,a) will al-

ways comprise the best rewards obtained from the

discrete, continuous and objective-driven models.

Algorithm for the Hybrid Method

M:discrete-D, continuous-C, objective-O

//models

: Q

, Q

//learning tables

For each instance of Q

∈ M do

If Q

*> Q

and

*> Q

then

HM-∂(s,a)  Q

else if

*> Q

and

*> Q

then

HM-∂(s,a)  Q

else

HM-∂(s,a)  Q

end if

end for

Return (HM-∂(s,a))

Algorithm 1: Hybrid Method Algorithm.

Algorithm 1 presents the integration of discrete,

continuous and objective-driven interaction models.

As it can be observed, for every learning cycle, the

agent performance is compared with respect to the

interaction models that have been used (by the oper-

ator ‘*>’ over the three learning tables). When a

given model returns a superior performance with

respect to the model that has been compared, this

learning is transferred to HM-∂(s,a), which repre-

sents the current action policy of the Hybrid Method.

The next section presents a simulation environment

to assess the efficiency of the proposed model.

3.1 Experimental Results

In order to assess the proposed approach, we present

a simulation environment composed by a state-space

representing a traffic structure over which agents

(drivers) try to find a route.

The structure has an initial state (s

init

), an objec-

tive state (g) and a set of actions A = {↑ (forward),

→ (right), ↓ (back), ← (left)}. A state s is a pair

(X,Y) in which the element define the position on the

axis X and Y, respectively. A status function st : S →

ST maps traffic situations (rewards) to states, such

that ST = {–0,1 (free route); –0,2 (a bit stuck); –0,3

(stuck or unknown); –0,4 (heavily stuck); –1

(blocked); 1,0 (g)}.

For this scenario, agents simulates available

routes for drivers. The global goal is elaborate an

action policy (combination that maps states and ac-

tions) that can determine the best route connecting

init

to g. The global action policy is defined by de-

termining step by step which action a

∈

A should be

performed at each state s

∈

S. After every moving of

the agent (transition/ interaction) from a state s to a

state s’, it knows whether or not its action has been

positive, as it recognizes the set of rewards shared

by the other models. The rewards for a given transi-

tion T

s,s’

is denoted by st(s’).

Figure 4: Simulated scenarios. The agents have a visual

field depth of 1.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

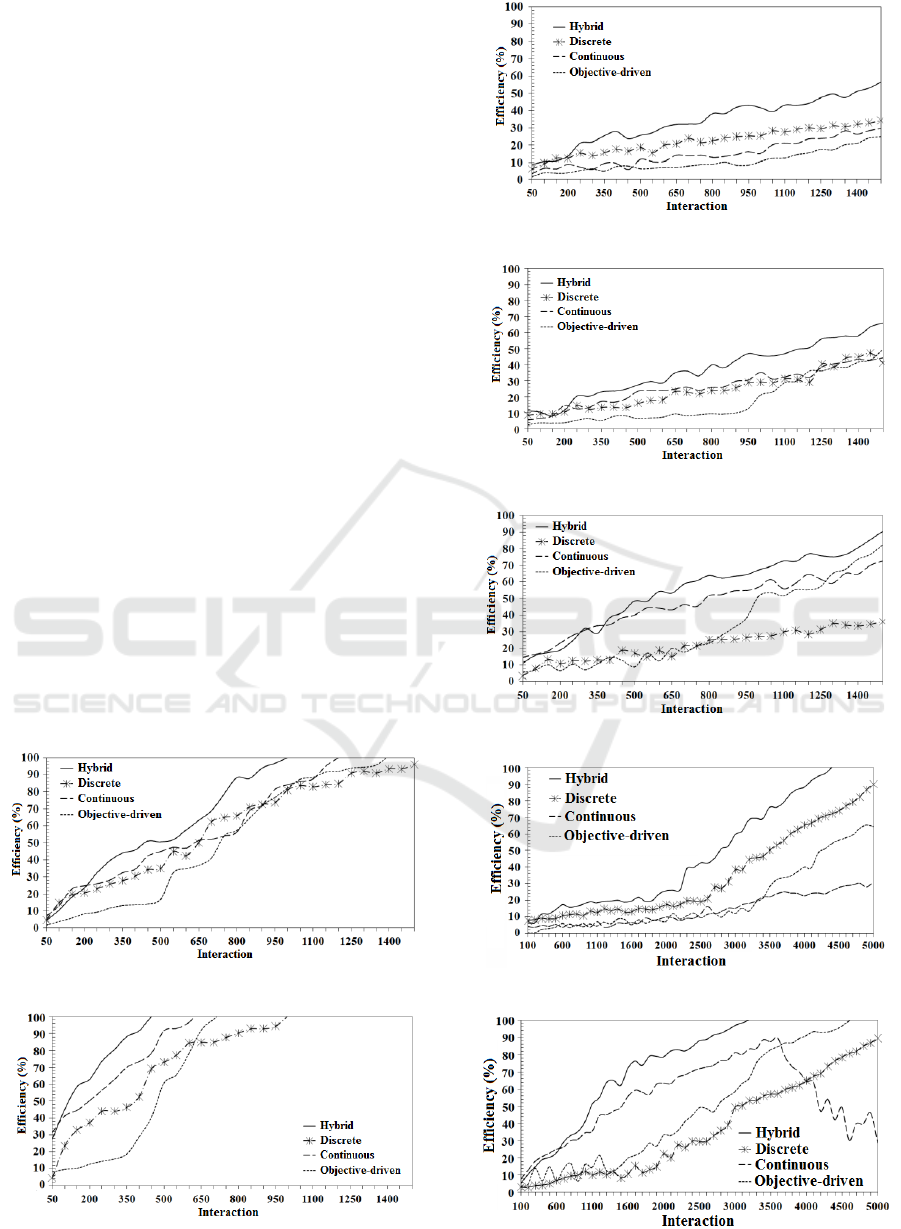
Figure 4 presents some scenarios that have been

used for simulations. They have been arbitrarily

generated, aiming to reproduce situations as closely

as possible to real world situations. The agents are

randomly positioned into the state-space. When an

agent reaches the goal state, this agent is randomly

positioned into others state s, until the stopping crite-

rion is satisfied (interactions numbers).

3.2 Comparative Analysis

The results illustrated in this section compares the

Hybrid Method to the individual performances ob-

tained as in the Discrete, Continuous and Objective-

driven interaction models.

The parameters that have been used in the Hy-

brid Method are the same as those used for the indi-

vidual models: discount fator (y) of 0.99 and learn-

ing rate (α) of 0.2 (Ribeiro et al., 2008).

Experiments have been conducted on environ-

ments ranging from 100 (10 × 10) to 400 (20 × 20)

states. For the sake of clarity, however, in this paper

we concentrate them on the largest state-space. The

results that follow compare the Hybrid Method to

the other methods using 3, 5 and 10 agents, in an

environment composed by 100, 250 and 400 states.

Observe that in Figures 5-11 the Hybrid Method

has shown to be more efficient with respect to the indi-

vidual performance achieved by the other models. In

general, it has shown to be superior at any interaction

phase, which substantially reduces the number of inter-

actions necessary to find out a proper action policy.

Figure 5: 100 states and 3 agents.

Figure 6: 100 states and 10 agents.

Figure 7: 250 states and 3 agents.

Figure 8: 250 states and 5 agents.

Figure 9: 250 states and 10 agents.

Figure 10: 400 states and 3 agents.

Figure 11: 400 states and 10 agents.

A Hybrid Interaction Model for Multi-Agent Reinforcement Learning

For experiments on environments with 100

states, the number of interactions has been reduced

in average 22.8% when using 3 agents; 26.7% with 5

agents; and 41.1% using 10 agents. For environ-

ments with 250 states, the method reduces the num-

ber of interactions in 21.1% with 3 agents; 21.9%

with 5 agents; and 32.7% for 10 agents. For envi-

ronments with 400 states, the number of interactions

has been reduced in 17,4% with 3 agents; 22,9%

with 5 agents; and 29,1% for 10 agents. Table 1

summarizes the improvements of the Hybrid Method

compared to the best method among the other mod-

els.

Table 1: Overall comparative analysis.

State-space

Number of agents

3 5 10

100

16.5% 68.7% 36.9%

250

49.4% 30.9% 32.6%

400

44.2% 41.1% 38.2%

The overall improvement achieved by the Hybrid

Method, considering all tested number of agents and

state-spaces, reaches the order of 40%.

4 CONCLUSIONS AND

DISCUSSIONS

This article designs a hybrid method to improve co-

ordination in multi-agent systems from the combina-

tion of interaction models presented in a previous

work. In sequential decision problems an agent in-

teracts repeatedly in the environment and tries to

optimize its performance based on the rewards re-

ceived. Thus, it is difficult to determine the best ac-

tions in each situation because a specific decision

may have a prolonged effect, due to the influence on

future actions. The proposed hybrid method is able

to take the agent to an acceleration in the conver-

gence of their action policy, overcoming the particu-

larities found in the interaction models presented in

(Ribeiro et al., 2008). The political of these models

may have different characteristics in environments

with different configurations, causing the agent fails

to converge at certain cycles of learning. Thus, the

hybrid method of coordination uses the best features

of interaction models (summarized in Subsection

2.3.1). The hybrid method policies outweigh the

policy of each model, assisting in the exchange of

best rewards to form a good overall action policy.

This is possible because the hybrid method can es-

timate the best rewards acquired through learning,

discovering an arrangement with the best ribs found

in partial action policies for each model.

Accumulate rewards generated by different ac-

tion policies is an alternative to support an adaptive

agent in search of good action policies. Experiments

with the hybrid method show that even with a higher

computational cost, the results are satisfactory, since

the approach improves convergence in terms of the

Q-learning algorithm standard. The complexity in-

troduced using n agents is around O(n × m), which is

equal to O(m) since n is a small constant and O(m) is

the complexity of the RL algorithm used as baseline.

Despite the satisfactory results, additional exper-

iments are needed to answer some open questions.

For example, the use of algorithms with different

paradigms could be used to explore the states with

the highest congestion regions? We observed that in

these regions the rewards of states are smaller. A

reinforcement learning algorithms system with dif-

ferent paradigms was proposed in (Ribeiro and En-

embreck, 2013), where the results seem to be en-

couraging. It is intended also use different methods

of learning to analyze situations such as: (i) explore

the most distant states the goal, where exploration is

less intense and; (ii) use a heuristic function, which a

priori could accelerate the convergence of algo-

rithms, where a heuristic policy indicate the choice

of the action taken and, therefore, limit the agent of

the search space. It is intended to further evaluate

the method in dynamic environments and with

greater variations states.

4.1 Real-world Applications

The hybrid model proposed in this paper has been

tested in scenarios in which it was possible to con-

trol all the environmental variables. In many real-

world problems, you cannot always control the fac-

tors that affect the system, such as external variables

to the environment. With the promising results of the

hybrid model presented in this article, we started to

adapt this model to a real case to support the daily

decisions of the poultry farmer. In this problem, the

agent of the system is used to generate action poli-

cies, in order to control the set of factors in the daily

activities, such as food-meat conversion, amount of

food to be consumed, time to rest, weight gain, com-

fort temperature, water and energy to be consumed,

etc. The main role of the agent is to perform a set of

actions to consider aspects such as productivity and

proﬁtability without compromising bird welfare.

Initial results show that, for the decision-taking pro-

cess in poultry farming, our model is sound, advan-

tageous and can substantially improve the agent ac-

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

tions in comparison with equivalent decision when

taken by a human specialist. In the moment, we are

evaluating the performance of the agent when han-

dling speciﬁc management situations; checking the

performance of the algorithm to process variations

of scenario; and changing the set of attributes used

to generate the rules, which can make them less sus-

ceptible to inﬂuence. Such statements are objects of

study for future research.

ACKNOWLEDGEMENTS

This research has been supported by Araucária

Foundation and National Council for Scientific and

Technological Development (CNPq), under grants

numbers 378/2014 and 484859/2013-7 respectively.

REFERENCES

Chakraborty, D. and Stone, P. (2014). Multiagent learning

in the presence of memory-bounded

agents. Autonomous Agents and Multi-Agent Systems,

28(2):182–213.

Chapelle, J., Simonin, O., and Ferber, J. (2002). How situ-

ated agents can learn to cooperate by monitoring their

neighbors’ satisfaction. ECAI, 2:68–78.

DeLoach, S. and Valenzuela, J. (2007). An agent envi-

ronment interaction model. In Padgham, L. and

Zambonelli, F., editors, Agent-Oriented Software En-

gineering VII, volume 4405 of Lecture Notes in Com-

puter Science, pages 1–18. Springer Berlin Heidel-

berg.

Devlin, S., Yliniemi, L., Kudenko, D., and Tumer, K.

(2014). Potential-based difference rewards for multia-

gent reinforcement learning. In Proceedings of

the 2014 International Conference on Autonomous

Agents and Multi-agent Systems, AAMAS ’14, pages

165–172, Richland, SC. International Foundation for

Autonomous Agents and Multiagent Systems.

Efthymiadis, K. and Kudenko, D. (2015). Knowledge

revision for reinforcement learning with abstract

mdps. In Proceedings of the 2015 International Con-

ference on Autonomous Agents and Multiagent Sys-

tems, AAMAS ’15, pages 763–770, Richland, SC. In-

ternational Foundation for Autonomous Agents and

Multiagent Systems.

Grze’s, M. and Hoey, J. (2011). Efficient planning in

rmax. In The 10th International Conference on Auton-

omous Agents and Multiagent Systems - Volume 3,

AAMAS ’11, pages 963–970, Richland, SC. Interna-

tional Foundation for Autonomous Agents and Multi-

agent Systems.

Kaelbling, L. P., Littman, M. L., and Moore, A. P. (1996).

Reinforcement learning: A survey. Journal of Artifi-

cial Intelligence Research, 4:237–285.

Ribeiro, R., Borges, A., and Enembreck, F. (2008). Inter-

action models for multiagent reinforcement learning.

In Computational Intelligence for Modelling Control

Automation, 2008 International Conference on, pages

464–469.

Ribeiro, R. and Enembreck, F. (2013). A sociologically

inspired heuristic for optimization algorithms: A case

study on ant systems. Expert Systems with Applica-

tions, 40(5):1814 – 1826.

Ribeiro, R., Enembreck, F., and Koerich, A. (2006). A

hybrid learning strategy for discovery of policies of

action. In Sichman, J., Coelho, H., and Rezende, S.,

editors, Advances in Artificial Intelligence -

IBERAMIASBIA 2006, volume 4140 of Lecture Notes

in Computer Science, pages 268–277. Springer Berlin

Heidelberg.

Ribeiro, R., Ronszcka, A. F., Barbosa, M. A. C., Favarim,

F., and Enembreck, F. (2013). Updating strategies

of policies for coordinating agent swarm in dynamic

environments. In Hammoudi, S., Maciaszek, L. A.,

Cordeiro, J., and Dietz, J. L. G., editors, ICEIS (1),

pages 345–356. SciTePress.

Saito, M. and Kobayashi, I. (2016). A study on efficient

transfer learning for reinforcement learning using

sparse coding.

Automation and Control Engineering,

4(4):324 – 330.

Stone, P. and Veloso, M. (2000). Multiagent systems: A

survey from a machine learning perspective. Autono-

mous

Robots, 8(3):345–383.

Sutton, R. S. and Barto, A. G. (1998). Reinforcement

Learning : An Introduction. MIT Press.

Tesauro, G. (1995). Temporal difference learning and

tdgammon. Commun. ACM, 38(3):58–68.

Walsh, T. J., Goschin, S., and Littman, M. L. (2010). Inte-

grating sample-based planning and model-based rein-

forcement learning. In Fox, M. and Poole, D., editors,

AAAI. AAAI Press.

Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning.

Machine Learning, 8(3):272–292.

Xinhai, X. and Lunhui, X. (2009). Traffic signal control

agent interaction model based on game theory

and reinforcement learning. In Computer Science-

Technology and Applications, 2009. IFCSTA ’09. In-

ternational Forum on, volume 1, pages 164–168.

Xuan, P. and Lesser, V. (2002). Multi-Agent Policies:

From Centralized Ones to Decentralized Ones. Pro-

ceedings of the 1st International Joint Conference

on Autonomous Agents and Multiagent Systems, Part

3:1098–1105.

Zhang, C. and Lesser, V. (2010). Multi-Agent Learning

with Policy Prediction. In Proceedings of the

24th AAAI Conference on Artificial Intelligence, pages

927–934, Atlanta.

Zhang, C. and Lesser, V. (2013). Coordinating Multi-

Agent Reinforcement Learning with Limited Commu-

nication. In Ito, J. and Gini, S., editors, Proceedings of

the 12th International Conference on Autonomous

Agents and Multiagent Systems, pages 1101–1108, St.

Paul, MN. IFAAMAS.

A Hybrid Interaction Model for Multi-Agent Reinforcement Learning