Faceted Queries in Ontology-based Data Integration
Tadeusz Pankowski
Institute of Control and Information Engineering, Pozna
´
n University of Technology, Pozna
´
n, Poland
Keywords:
Data Integration, Faceted Queries, Ontology, RDF Data.
Abstract:
The aim of using ontology-based data integration is to provide users with a unified view, in a form of a global
application domain ontology, over a multitude of data sources. The terminological component of this ontology
is then presented as the global schema of the system and is used as the reference model for formulating queries.
The extensional knowledge consists of RDF data sets (graphs) stored in local databases. In such scenario, a
faceted query interface is a desired solution for end-user data access. Then there is a need for effective query
answering utilizing both extensional and intentional knowledge representation. In this paper, we propose and
discuss a possible solution to this issue. We show how a class of deductive rules, in particular Datalog rules
and rules defining functionality, can be incorporated in the process of ontology-enhanced query answering in
ontology-based data integration systems.
1 INTRODUCTION
Data integration systems provide users with a uni-
form view over a multitude of heterogeneous data
sources. This uniform view has a form of a
global schema, which realize so called global-as-
view (GAV) paradigm (Lenzerini, 2002), (Ullman,
1997). The data is stored in data sources in their own
schemas. The global schema frees users from having
to locate the sources relevant to their queries. In or-
der to answer queries formulated against the global
schema, the system provides the semantic mappings
between the global schema and the local (source)
schemas (Halevy et al., 2006), (Cal
`
ı et al., 2004), (Fa-
gin et al., 2009), (Bernstein and Haas, 2008).
Currently, a broad class of data integration sys-
tems uses ontologies as global schemas, which led
to emergence of ontology-based data integration
(OBDI) and to ontology-based data access (OBDA)
(Cruz and Xiao, 2009), (Calvanese et al., 2010), (Das
et al., 2004), (Eklund et al., 2004), (Calvanese et al.,
2007a), (Skjæveland et al., 2015).
Now, the most popular means to specify and query
ontologies are OWL (OWL 2 Web Ontology Lan-
guage Profiles, 2009), RDF (Resource Description
Framework (RDF) Model and Syntax Specification,
1999) and SPARQL (SPARQL Query Language for
RDF, 2008). OWL provides a method to formalize
a domain by defining classes and properties of those
classes (by means of rules or axioms), and to de-
fine individuals and assert properties about them (by
means of facts or assertions). OWL is based on de-
scription logic (Baader et al., 2003). In practice, on-
tology rules are usually written in a form of first or-
der language (FOL) formulas, and facts are usually
defined by means of RDF graphs or FOL sentences.
A standard language to formulate queries over on-
tologies is SPARQL. SPARQL, however, is not suit-
able query language for end-users. Instead, so called
faceted search is used for end-user data access (Yee
et al., 2003), (Oren et al., 2006), (Hahn et al., 2010).
In OBDI systems, an ontology is divided into two
components: terminological component (TBox) con-
sisting of signature (a set of unary predicate names
(classes) and binary predicate names (properties)),
and rules (axioms); and assertional component con-
sisting of a set of facts (assertions). The terminolog-
ical component forms the global schema of OBDI,
and the assertional component consists of a set of
local databases. Any local database state is a set
of RDF data, which can be represented as an RDF
graph, so we call it a graph database. The set of RDF
graphs forms extensional knowledge. The set of rules
in global schema constitutes the intentional knowl-
edge about the application domain, and substantially
enrich the extensional knowledge. The challenging
issue in OBDI is to take into account both the ex-
tensional and intentional knowledge while answering
queries. Data in different local databases can comple-
ment each other and can overlap. However, we as-
150
Pankowski, T.
Faceted Queries in Ontology-based Data Integration.
In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 1, pages 150-157
ISBN: 978-989-758-187-8
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sume that they are consistent with the global schema
and do not contradict one another.
In this paper, we propose a method for query
answering in OBDI systems in the situation when
queries are formulated against the global schema as
faceted queries. To create the answer, the service uses
relevant data from all local databases as well as data
necessary in reasoning procedures implied by ontol-
ogy rules.
The main contribution of the paper, is the proposal
of an algorithm for extending the query graph (created
from a faceted query) with edges implied by relevant
deductive rules. The set of considered ontology rules
includes so called Datalog rules and rules specifying
functionality of binary predicates and their inversions
(key properties). We also show how the extended
query graph (a global query pattern) can be used to
merge local answers by means of a chase procedure.
The structure of the paper is as follows. Some
preliminaries concerning graph databases, ontologies
and queries, are reviewed in Section 2. Faceted
queries are defined in Section 3, and their formal se-
mantics, understood as first order open formulas, is
given. In Section 4 we characterize ontology-based
data integration, and describe architecture of an OBDI
system. Also the running example is introduced. The
process of answering faceted queries is described in
Section 5. We propose an algorithm for creating
global, ontology-enhanced query graph, and its usage
in merging local answers and obtaining the final re-
sult. Section 6 concludes the paper.
2 PRELIMINARIES
A graph database is a finite, edge-labeled and di-
rected graph (Barcel
´
o and Fontaine, 2015). Formally,
let the following sets be infinite and pairwise disjoint:
Const – a set of constants, LabNull – a set of labeled
nulls (treated as variables), UP – a set of unary pred-
icates, BP – set of binary predicates. Additionally,
we assume that type and ≈ are distinguished binary
predicates in BP. A signature Σ is a finite subset of
UP ∪ BP.
A graph database (or RDF graph) G = (V,E)
with signature Σ consists of a finite set V ⊆ Const ∪
LabNull ∪ UP of node identifiers (or nodes for short)
and a finite set of labeled edges (or facts) E ⊆ V ×Σ ×
V , such that:
• if (v
1
, p,v
2
) ∈ E and p ∈ BP\{type}, then v
1
,v
2
∈
Const ∪ LabNull,
• if (v
1
,type,v
2
) ∈ E then v
1
∈ Const ∪ LabNull,
and v
2
∈ UP.
In first order logic (FOL), we use the following
notation for edges:
• for (v,type,C), where C ∈ UP, we use C(v),
• for (v
1
,≈,v
2
) we use v
1
≈ v
2
,
• for (v
1
,P,v
2
, where P ∈ BP, we use P(v
1
,v
2
).
A rule is a FOL sentence (implication) of the form
∀x∀y(ϕ(x,y) → ∃zψ(x, z)), where x, y, z are tuples of
variables. Formulas ϕ (the body) and ψ (the head) are
conjunctions of atoms of the form C(v), P(v
1
,v
2
), and
v
1
≈ v
2
, where v,v
1
,v
2
ranges over Const ∪ LabNull.
If the tuple z of existentially quantified variables is
empty, the rule is Datalog rule. By G ∪ R we denote
all facts belonging to G and deduced from G using
rules in R.
An ontology (or a knowledge base) is a triple
O = (Σ,R,G), where Σ is a signature, R is a finite set
of rules, and G is a database graph (a set of facts). A
kind of ontology depends on the form of rules. For
example, OWL 2 defines three profiles with differ-
ent computational properties (OWL 2 Web Ontology
Language Profiles, 2009).
A query is a FOL open formula. If the formula
is constructed only with: (a) atoms of the form C(v),
P(v
1
,v
2
) and v ≈ a, where v,v
1
,v
2
are variables, and
a is a constant or labeled null; (b) symbols of con-
junction (∧), disjunction (∨), and existential quan-
tification (∃), then the query is a positive existential
query (PEQ). A PEQ is monadic if has exactly one
free variable, and is conjunctive query (CQ) if dis-
junction does not occur in this query.
A query Q(x), where x is a tuple of free variables,
is satisfiable in O = (Σ,R,G), denoted O |= Q(x) if
Q is built from predicates in Σ, and there is a tuple a
of elements from Const ∪ LabNull such that G ∪ R |=
Q(a). Then a is an answer to Q(x) with respect to O.
Set of answers will be denoted by Ans(Q).
3 FACETED QUERIES
There is an increasing number of data centered sys-
tems based on RDF and OWL 2. A standard query
languages in such systems is SPARQL. This lan-
guage, however, is not a convenient to end-users.
As a more suitable interface for end-user data access
have been developed approaches based on so-called
faceted search. Now, we will define faceted queries
for search over RDF graphs, and we will consider an-
swering such queries when a database is additionally
enhanced with an ontology. The considered system
is a data integration system, where the graph data
must be composed from data graphs stored in local
databases.
Faceted Queries in Ontology-based Data Integration
151

In (Arenas et al., 2014), a facet is defined as a pair:
F = (X, ∧Γ) (conjunctive facet), or F = (X, ∨Γ) (dis-
junctive facet), where:
• X ∈ BP is the facet name, denoted by F|
1
,
• Γ defines a set of facet values and is denoted F|
2
,
• if X = type, then Γ ⊆ UP,
• if X ∈ BP \ {type}, then Γ ⊆ Const ∪ {any} or
Γ ⊆ UP ∪ {any}.
Any faceted query can be represented by a user-
friendly graphical interface. A graphical form of
faceted query in Figure 1, searches for ACM authors
from NY university who have written a publication in
year 2014.
Figure 1: A graphical form of a faceted query.
Example 3.1. For the considered example, the fol-
lowing facets can be defined:
F
1
= (type, ∨{ACMAuthor,Paper}),
F
2
= (authorO f ,∨{any, p
1
,a
1
,a
2
}),
F
3
= (pyear, ∨{any,2013,2014}),
F
4
= (univ,∨{any, NY, LA}),
F
5
= (uinv,∧{NY,LA}).
Note, that F
5
is a conjunctive facet and denotes indi-
viduals which are simultaneously from two universi-
ties – NY and LA.
Definition 3.2. Let F = (X ,◦Γ), ◦ ∈ {∧,∨}, be a
facet. A basic faceted query determined by F is a pair
of the form Q = (X, S), where S ⊆ Γ. A basic faceted
query will be denoted by Q
t
, if X = type, and by Q
b
when X ∈ BP \ {type}. A faceted query (or query for
short) is an expression Q conforming to the following
grammar:
Q ::= q | (q ∧ q) | (q ∨ q)
q ::= Q
t
| Q
b
| (Q
b
/Q)
Example 3.3. The faceted query corresponding to
this in Figure 1 is:
Q = ((F
1
,{ACMAuthor}) ∧ (F
4
,{NY }))
∧((F
2
,{any})/(F
3
,{2014}))
(1)
In Definition 3.4, we define semantics for faceted
queries. The semantics JQ(x)K assigns to each query
Q and a given variable x, a monadic PEQ with one
free variable x.
Definition 3.4. Let Q
t
be a basic faceted query over
F
t
= (type,◦Γ), Q
b
be a basic faceted query over
F
P
= (P, ◦Γ), P ∈ BP \ {type}, and Q be an arbitrary
faceted query. Then semantics of faceted queries is
defined as follows:
1. Q
t
= (F
t
,S), S ⊆ UP:
JQ
t
(x)K = ◦
C∈S
C(x).
2. Q
b
= (F
P
,{any}):
JQ
b
(x)K = ∃y P(x,y),
J(Q
b
/Q)(x)K = ∃y P(x,y) ∧ JQ(y)K.
3. Q
b
= (F
P
,S), S ⊆ Const ∪ LabNull:
JQ
b
(x)K = ◦
a
i
∈S
∃y
i
P(x,y
i
) ∧ y
i
≈ a
i
,
J(Q
b
/Q)(x)K = ◦
a
i
∈S
∃y
i
P(x,y
i
)∧y
i
≈ a
i
∧JQ(y
i
)K.
4. Q
b
= (F
P
,S), S ⊆ UP:
JQ
b
(x)K = ◦
C
i
∈S
∃y
i
P(x,y
i
) ∧C
i
(y
i
),
J(Q
b
/Q)(x)K = ◦
C
i
∈S
∃y
i
P(x,y
i
)∧C
i
(y
i
)∧ JQ(y
i
)K.
5. Q
b
= (F
P
,{any} ∪ S), :
JQ
b
(x)K = J(F
P
,{any})(x)K ◦ J(F
P
,S)(x)K,
J(Q
b
/Q)(x)K = J((F
P
,{any})/Q)(x)K
◦J((F
P
,S)/Q)(x)K.
6. Let q
1
and q
2
be queries, then:
J(q
1
∧ q
2
)(x)K = Jq
1
(x)K ∧ Jq
2
(x)K,
J(q
1
∨ q
2
)(x)K = Jq
1
(x)K ∨ Jq
2
(x)K.

The semantics of basic type-faceted queries of the
form (F,S) is the conjunction (disjunction) of atoms
of the form C(x) over the same variable, where C ∈ S.
If the facet name is a binary predicate P, then the
query is translated to: (a) an atom whose second argu-
ment is existentially quantified (if any occurs); (b) a
conjunction (disjunction) of binary atoms whose sec-
ond argument must be equal to a constant or a labeled
null, or must satisfy an unary predicate. In the case
of nesting, a variable from the parent is shifted to the
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
152

child. Finally, conjunction (disjunction) of queries is
interpreted as the conjunction (disjunction) of the cor-
responding formulas.
The first order interpretation (the PEQ) of faceted
query (1) is given in (2).
JQ(x)K = ACMAuthor(x)
∧∃y(authorO f (x,y)
∧∃z(pyear(y,z) ∧ z ≈ 2014))
∧∃w(univ(x,w) ∧ w ≈ NY ).
(2)
4 ONTOLOGY-BASED DATA
INTEGRATION
Ontology Based Data Integration (OBDI), or Ontol-
ogy Based Data Access (OBDA) involves the use of
ontology to effectively combine data or information
from multiple heterogeneous sources (Wache et al.,
2001). In this paper we will follow so called single
ontology approach, i.e., an approach when a single
ontology is used as a global reference model in the
system. We assume that the data integration system
is based on a global schema (Ullman, 1997), (Halevy
et al., 2006), (Lenzerini, 2002) (another approaches
assume P2P data integration, see for example (Cal-
vanese et al., 2004)).
On the conceptual level, a user perceives contents
of the system as a large single ontology O = (Σ, R, G),
and formulates faceted queries against this ontology.
On the implementation level, we assume that (see Fig-
ure 2):
1. The (global) schema of the system consists of the
signature and the set of rules of the ontology, i.e.,
Sch = (Σ,R).
2. Facts, represented by means of RDF graphs, are
stored in local databases, DB
i
= (Σ
i
,G
i
), where
Σ
i
⊆ Σ consists of symbols, i.e., unary and binary
predicates, occurring in RDF graph G
i
.
3. Data in different local databases complement each
other and can overlap. We assume, however, that
databases are consistent and do not contradict one
another.
4. Local databases are created by local users and the
global schema is used as the reference in introduc-
ing new facts.
A user query is rewritten and sent to each database
in a form understandable and executable to this
database management system. Next, partial answers
are sent back, merged accordingly and finally re-
turned to the user.Answering queries requires some
data inferring processes implied by ontology deduc-
tive rules. The architecture of such a system is given
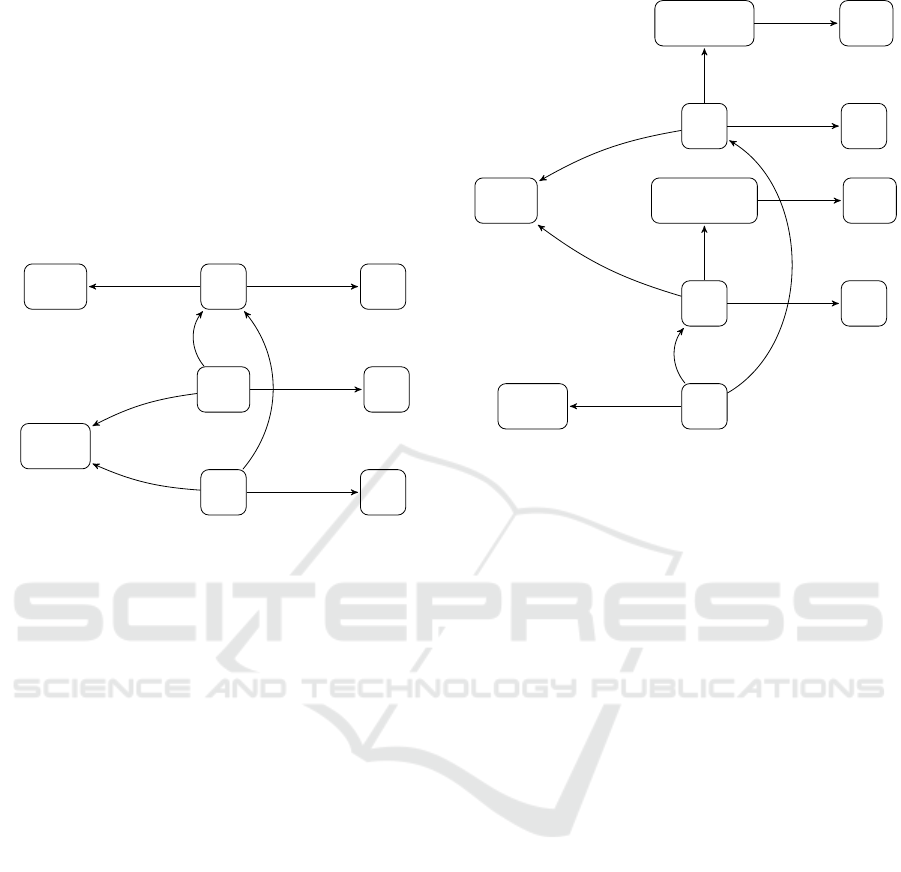
in Figure 2.
Figure 2: Architecture of an ontology-based data integra-
tion.
The system works as follows:
(1) The user formulates a faceted query Q.
(2) Q is translated to a FOL formula J(Qx)K and its
graph representation is created. This graph is ex-
tended to E with elements corresponding to rel-
evant deductive rules in the schema. Graph E is
sent to local database management systems.
(3) E is reduced to E
i
using information from signa-
ture Σ
i
.
(4) A set of edges is selected from G
i
, which are rel-
evant to query answering.
(5) Selected subgraphs are merged into graph G
0
.
(6) The user query Q is evaluated over G
0
, and the
answer A is obtained.
(7) A is returned to the user.
Example 4.1. The global schema, O = (Σ,R), rele-
vant to our example can contain the following set of
deductive rules:
(R1) atCon f (x, y) ∧ y ≈ ACMCon f
→ ACMPaper(x),
(R2) authorO f (x,y) ∧ ACMPaper(y)
→ ACMAuthor(x),
(R3) atCon f (x, y) ∧ cyear(y,z) → pyear(x,z),
(R4) univ(x,y
1
) ∧ univ(x, y
2
) → y
1
≈ y
2
,
(R5) title(x
1
,y) ∧ title(x
2
,y) → x
1
≈ x
2
,
(R6) Author(x) → ∃y(authorO f (x,y) ∧ Paper(y)).
Faceted Queries in Ontology-based Data Integration
153

Sample RDF graphs, G
1
and G
2
, of two local
databases are given in, respectively, Figure 3 and Fig-
ure 4. These graphs are built over signatures, respec-
tively, Σ
1
and Σ
2
, being subsets of Σ, and over a set of
constants, Const, and a set of labeled nulls LabNull.
In this case John,Ann,2014,2013,KB,AI, NY, LA,
ACMCon f , and IEEECon f are in Const, and
p
1
,a
1
,a
2
are in LabNull. Labeled nulls are used as
identifiers of anonymous nodes and can be replaced
with other labeled nulls or with constants. So, they
are like variables (Fagin et al., 2005).
Paper
p
1
type
KB
title
Author
John
Ann
NY
LA
type
type
univ
univ
authorOf
authorOf
Figure 3: RDF graph G
1
of a local database DB
1
.
The FOL form of G
1
:
Paper(p
1
),title(p
1
,KB),Author(John),
Author(Ann),authorO f (John, p
1
),
authorO f (Ann, p
1
),univ(John, NY ),univ(Ann,LA),
and of G
2
:
Paper(a
1
),Paper(a
2
),title(a
1
,KB),
atCon f (a
1
,ACMCon f ),cyear(ACMCon f , 2014),
title(a
2
,AI),atCon f (a
2
,IEEECon f ),
cyear(IEEECon f ,2013),Author(Ann),
authorO f (Ann,a
1
),authorO f (Ann,a
2
).
If we evaluate query (2) against G
1
or/and G
2
, then
the answer is empty (in particular, the binary relation
ACMAuthor does not even exist). However, if we con-
sider also the set of rules in the ontology and apply
them to infer new facts, we see that (2) is satisfied by
John. So John is the answer to the query under con-
sideration. Thus, to obtain the answer we have to:
• merge database states,
• take into account deductive rules from the ontol-
ogy,
• apply deductive rules to infer new facts from the
result of merging,
• evaluate the query over the set of all facts.
Note, however, that a naive performance of these
operations can be rather inefficient. For example, we
ACMCon f
a
1
atConf
2014
cyear
KB
title
IEEECon f
a
2
atConf
Paper
type
type
2013
cyear
AI
title
Ann
authorOf
authorOf
Author
type
Figure 4: RDF graph G
2
of a local database DB
2
.
can merge whole database states – which is rather
very inefficient, or we can take into consideration only
such subgraphes which are relevant to obtain the an-
swer. Further on in the paper, we will discuss how
these relevant subgraphs can be chosen.
5 ANSWERING FACETED
QUERIES
5.1 Creating Global Query Patterns
Now, we will discuss the problem of selecting some
facts (edges) from RDF graphs (step (4) in Figure 2)
which should be sent to the merge stage (step (5) in
Figure 2). The general assumption about the selection
is that there must be justification to select an edge.
The selection of an edge (x,P,y) is justified if:
• predicate P occurs in the query;
• predicate P occurs in the left hand site of an on-
tology rule, and there is a justification to select a
predicate P
0
occurring on the right hand site of this
rule;
• P is functional or a key (P
−
is functional) and can
be used to infer an equality between some data
involved in the answer to the query.
A facet graph G for a facet query Q represented by a
FOL formula JQ(x)K, is the graph G = (V,E), where:
1. V is a set of unary predicate names, variable
names, constants and labeled nulls, occurring in
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
154

ACMAuthor
x
type
w
univ[f]
NY
≈
y
authorOf
z
pyear[f]
2014
≈
ACMPaper
type
u
atConf[f]
t
cyear[f]
ACMCon f
≈
v
title[key]
Figure 5: Extended query graph E.
JQ(x)K.
2. The set E of edges is defined as follows:
• if C(v) is in JQ(x)K, then (v,type,C) is in E,
• if P(v
1
,v
2
) is in JQ(x)K, then (v
1
,P,v
2
) is in E,
• if v ≈ a is in JQ(x)K, then (v, ≈, a) is in E.
In Figure 5, the subgraph with greyed nodes con-
stitutes the query graph for the faceted query in Figure
1 and its FOL interpretation (2). Additionally, in Fig-
ure 5 some edges are qualified with: [ f ], to denote that
the corresponding binary predicate is a function (rule
(R4)), and [key], to denote that the corresponding bi-
nary predicate is a key, i.e., its inversion is a function
(rule (R5)).
Next, the query graph G is extended to an ex-
tended query graph (or global query pattern), E =
(V
E
,E
E
), by adding some edges implied by ontology
rules. We take into account rules which are adjacent
to the current form of the extended query graph. We
proceed as follows:
1. We start with assuming E = (V
E
,E
E
) equal to
G = (V, E).
2. Let ϕ → C(v) be a rule and (x,type,C) be in E
E
,
for some variable x. Then:
• rename all variables occurring in ϕ, with the ex-
ception of variable v, in such a way that new
names are different from those occurring in V
E
;
• rename v to x,
• match the renamed form of ϕ to edges in E
E
,
and rename variables accordingly. The result
denote by ϕ
0
,
• extend E
E
as follows:
– if C(w) is in ϕ
0
and not in E
E
, then add the
edge (w,type,C) to E
E
,
– if P(w
1
,w
2
) is in ϕ
0
and not in E
E
, then add
(w
1
,P,w
2
) to E
E
,
– if w ≈ a is in ϕ
0
and not in E
E
, add (w, ≈, a)
to E
E
.
3. Let ϕ → P(v
1
,v
2
) be a rule and (x,P,y) be in E
E
,
for some variables x and y. Then:
• rename all variables occurring in ϕ, with the ex-
ception of variables v
1
and v
2
, in such a way
that new names are different from those occur-
ring in V
E
;
• rename v
1
to x, and v
2
to y,
• match the renamed form of ϕ to edges in E
E
,
and rename variables accordingly. The result
denote by ϕ
0
,
• extend E
E
analogously to the extension de-
scribed in (2).
4. Let ϕ be a rule defining functionality of a binary
predicate P(v
1
,v
2
). Let x be a variable in V
E
de-
fined over the range of P. Then rename v
2
to x,
and v
1
to an appropriate name w, and add (w, P, x)
to E
E
.
5. Let ϕ be a rule defining functionality of inversion
of a binary predicate P(v
1
,v
2
), i.e., determining
that P is a key. Let x be a variable in V
E
defined
over the domain of P. Then rename v
1
to x, and v
2
to an appropriate name w, and add (x,P,w) to E
E
.
In Figure 5, edges with white nodes were added
according to the above procedure. Dashed arrows
indicate which edges are needed to infer another
edges. In particular, (y,type,ACMPaper) is neces-
sary to infer (x,type,ACMAuthor) (rule (R2)). To in-
fer (y, type,ACMPaper), we need (y, atCon f , u) and
(u, ≈, ACMCon f ) (rule (R1)). To infer (y, pyear,z),
the edge (u,cyear,t) is needed, (rule (R3)). Finally,
(y,title,v) is added since title is a key, i.e., its inver-
sion, title
−
, is a function (rule (R5)).
5.2 Local Answers to Graph Patterns
Restrictions of graph E (Figure 5) to DB
1
and DB
2
are extended graphs (local query patterns), E
1
and
E
2
, presented in Figure 6 and Figure 7, respectively.
x
w
univ
NY
≈
y
authorOf
v
title
Figure 6: Extended query graph E
1
= τ
Σ
1
(E).
Faceted Queries in Ontology-based Data Integration
155

x
y
authorOf
u
atConf
t
cyear
ACMCon f
≈
v
title
Figure 7: Extended query graph E
2
= τ
Σ
2
(E).
Subgraphs G
0
1
= E
1
(G
1
) and G
0
2
= E
2
(G
2
), which
are answers to pattern queries E
1
and E
2
, respectively,
are presented in Figure 8 and Figure 9, respectively.
John
NY
univ
p
1
authorOf
KB
title
Figure 8: Answer G
0
1
= E
1
(G
1
).
Ann
a
1
authorOf
ACMCon f
atConf
2014
cyear
KB
title
Figure 9: Answer G
0
2
= E
2
(G
2
).
Next, RDF subgraphs G
0
1
and G
0
2
, are sent to the
merging service.
5.3 Merging Local Answers
Partial answers, like G
0
1
and G
0
2
, must be merged to
produce a RDF graph over which the user query Q can
be evaluated. Now, we propose a method to perform
the merging. The merge is done by means of map-
ping rules produced from the extended query graph
E and from the set R of ontology rules belonging to
the global schema. These rules are used to define the
chase procedure as it was proposed in data exchange
theory (Fagin et al., 2005), (Calvanese et al., 2007b).
Predicates prefixed by s refer to source data, i.e., to
G
0
1
and G
0
2
. Predicates without prefixes, refer to tar-
get data, i.e., to the result of the merge, and are un-
derstood as targed constraints. In our case, the set of
generated mapping rules used for merging is given in
Figure 10.
s.authorO f (x,y) → authorO f (x,y),
s.univ(x,y) → univ(x,y),
s.title(x,y) → title(x,y),
s.atCon f (x, y) ∧ y ≈ ACMCon f → ACMPaper(x),
authorO f (x,y) ∧ ACMPaper(y) → ACMAuthor(x),
s.atCon f (x, y) ∧ s.cyear(y,z) → pyear(x,z),
title(x
1
,y) ∧ title(x
2
,y) → x
1
≈ x
2
.
Figure 10: Mapping rules used in merging.
In particular, the last rule enforces a
1
≈ p
1
. So,
in the result RDF graph all occurrences of a
1
are re-
placed by p
1
. The result of merge is given in Figure
11.
ACMAuthor
Ann
John
NY
univ
p
1
authorOf authorOf
type
type
KB
title
ACMPaper
type
2014
pyear
Figure 11: Result of merging, G
0
= Merge(G
0
1
,G
0
2
), by
means of mapping rules from Figure 10.
5.4 Obtaining Final Answers
The result of merging of local answers to local graph
patterns, as G
0
= Merge(G
0
1
,G
0
2
) in Figure 11, consti-
tutes a dataset which is the object to evaluate a faceted
query under consideration. The first order representa-
tion of the query, in our case (2), is a monadic PEQ
resulting from a faceted query. So, the answer can be
found in polynomial time. It is easily seen that the
answer is John.
So called refocussing functionality in faceted
queries allows for changing the free variable of the
query Q. In consequence, the answer consists of
all valuations of this free variable. In our example,
if we want to now information about papers written
by ACM authors, we should refocus our attention to
the variable being the second argument of authorO f
predicate.
6 CONCLUSION
In this paper, we have discussed an ontology-based
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
156

data integration system with faceted query interface.
In such a system we have both, extensional and in-
tentional knowledge. The extensional knowledge is
stored as RDF graphs in local databases, and the in-
tentional knowledge is given as a set of rules consti-
tuting a set of axioms of a global ontology. A user
formulates faceted queries in a user-friendly way us-
ing a simple graphical interface. Next, local databases
are queried about data which is indirectly or directly
(to infer new facts by means of ontology rules) neces-
sary to answer the query. The set of local answers are
merged and finally the expected answer is obtained.
The proposed method is a base to introduce new func-
tionality into our system of data integration.
REFERENCES
Arenas, M., Grau, B. C., Kharlamov, E., Marciuska, S.,
and Zheleznyakov, D. (2014). Faceted search over
ontology-enhanced RDF data. In ACM CIKM 2014,
pages 939–948. ACM.
Baader, F., Calvanese, D., McGuinness, D., Nardi, D., and
Petel-Schneider, P., editors (2003). The Description
Logic Handbook: Theory, Implementation and Appli-
cations. Cambridge University Press.
Barcel
´
o, P. and Fontaine, G. (2015). On the data complexity
of consistent query answering over graph databases.
In ICDT 2015, volume 31 of LIPIcs, pages 380–397.
Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik.
Bernstein, P. A. and Haas, L. M. (2008). Information inte-
gration in the enterprise. Commun. ACM, 51(9):72–
79.
Cal
`
ı, A., Calvanese, D., Giacomo, G. D., and Lenzerini, M.
(2004). Data integration under integrity constraints.
Information Systystems, 29(2):147–163.
Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M.,
Poggi, A., and Rosati, R. (2007a). Ontology-based
database access. In SEBD 2007, pages 324–331.
Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M.,
Rosati, R., and Ruzzi, M. (2010). Using OWL in Data
Integration. In Semantic Web Information Manage-
ment. Chapter 17, pages 397–424. Springer.
Calvanese, D., Giacomo, G. D., et al., (2007b). EQL-Lite:
Effective First-Order Query Processing in Description
Logics. In IJCAI, International Joint Conference on
Artificial Intelligence, pages 274–279.
Calvanese, D., Giacomo, G. D., Lenzerini, M., and Rosati,
R. (2004). Logical Foundations of Peer-To-Peer Data
Integration. In PODS, pages 241–251.
Cruz, I. F. and Xiao, H. (2009). Ontology driven data inte-
gration in heterogeneous networks. In Complex Sys-
tems in Knowledge-based Environments, pages 75–98.
Das, S., Chong, E., Eadon, G., and Srinivasan, J. (2004).
Supporting Ontology-Based Semantic Matching in
RDBMS. In Proc. of the 30th International Confer-
ence on Very Large Data Bases, VLDB 2004, Toronto,
Canada, pages 1054–1065.
Eklund, P. W., II, R. J. C., and Roberts, N. (2004). Re-
trieving and exploring ontology-based information. In
Staab, S. and Studer, R., editors, Handbook on On-
tologies, pages 405–414. Springer.
Fagin, R., Haas, L. M., Hern
´
andez, M. A., Miller, R. J.,
Popa, L., and Velegrakis, Y. (2009). Clio: Schema
mapping creation and data exchange. In Concep-
tual Modeling: Foundations and Applications, vol-
ume LNCS 5600, pages 198–236.
Fagin, R., Kolaitis, P. G., Miller, R. J., and Popa, L.
(2005). Data exchange: semantics and query answer-
ing. Theor. Comput. Sci, 336(1):89–124.
Hahn, R., Bizer, C., Sahnwaldt, C., Herta, C., Robinson,
S., B
¨
urgle, M., D
¨
uwiger, H., and Scheel, U. (2010).
Faceted Wikipedia Search. In BIS 2010, volume 47
of Lecture Notes in Business Information Processing,
pages 1–11. Springer.
Halevy, A. Y., Rajaraman, A., and Ordille, J. J. (2006). Data
integration: The teenage years. In Dayal, U., Whang,
K.-Y., Lomet, D. B., Alonso, G., Lohman, G. M.,
Kersten, M. L., Cha, S. K., and Kim, Y.-K., editors,
VLDB, pages 9–16. ACM.
Lenzerini, M. (2002). Data integration: A theoretical per-
spective. In Popa, L., editor, PODS, pages 233–246.
ACM.
Oren, E., Delbru, R., and Decker, S. (2006). Extending
faceted navigation for RDF data. In ISWC 2006,
volume 4273 of Lecture Notes in Computer Science,
pages 559–572. Springer.
OWL 2 Web Ontology Language Profiles (2009).
www.w3.org/TR/owl2-profiles.
Resource Description Framework (RDF) Model and Syn-
tax Specification (1999). www.w3.org/TR/PR-rdf-
syntax/.
Skjæveland, M. G., Giese, M., Hovland, D., Lian, E. H., and
Waaler, A. (2015). Engineering ontology-based ac-
cess to real-world data sources. J. Web Sem., 33:112–
140.
SPARQL Query Language for RDF (2008).
http://www.w3.org/TR/rdf-sparql-query.
Ullman, J. D. (1997). Information integration using logical
views. in: Database Theory - ICDT 1997. Lecture
Notes in Computer Science, 1186:19–40.
Wache, H., Vgele, T., Visser, U., Stuckenschmidt, H.,
Schuster, G., Neumann, H., and Hbner, S. (2001).
Ontology-Based Integration of Information - A Sur-
vey of Existing Approaches. In IJCAI 2001, pages
108–117.
Yee, K.-P., Swearingen, K., Li, K., and Hearst, M. (2003).
Faceted metadata for image search and browsing. In
Proceedings of the SIGCHI Conference on Human
Factors in Computing Systems, CHI ’03, pages 401–
408. ACM.
Faceted Queries in Ontology-based Data Integration
157