Analysis of Brillouin Frequency Shift in Distributed Optical Fiber
Sensor System for Strain and Temperature Monitoring
Nageswara Lalam, Wai Pang Ng, Xuewu Dai, Qiang Wu and Yong Qing Fu
Smart Sensors Research Group, Northumbria University, Newcastle upon Tyne, U.K.
Keywords: Brillouin Frequency Shift (BF
S), Distributed Optical Fiber Sensors, Brillouin Scattering.
Abstract: In this paper, we have analyzed Brillouin frequency shift (BFS) in single mode silica optical fiber. The BFS
is analyzed in conventional Brillouin optical time domain analysis (BOTDA) at operating wavelength of
1550 nm by a pump-probe technique. The effects of strain and temperature on BFS are fully characterized.
We found that, the BFS change of 0.06 MHz/µ-strain and 1.26 MHz/
o
C, respectively. The BFS changes in
Brillouin gain and Brillouin loss mechanism have been analyzed. In addition, we also presented Brillouin
linewidth and peak gain variations of Brillouin gain spectrum with various temperature and strain values.
The results demonstrate, the BFS have a strong linear relationship with strain and temperature along the
sensing fiber.
1 INTRODUCTION
In Brillouin based distributed optical fiber sensors,
the basic principle for measuring strain and
temperature is based on the frequency difference
between the incident light and the backscattered
Brillouin light at every point along the fiber. The
distributed optical fiber sensor [DOFS] based on
Brillouin scattering is an attractive technique to
monitor the strain and temperature simultaneously
and independently. Compared to conventional
optical sensors such as fiber Bragg grating (FBG)
and Raman scattering based sensors, the Brillouin
based DOFS offers, capability of monitoring both
strain and temperature with high spatial resolution
and sensing range over tens of kilometers. As FBG
sensors are point type sensors, they are just good at
monitoring a specific location of interest. Raman
based distributed sensors are intensity based sensors
and only sensitive to the temperature, and also its
receiver has most complex structure compared to the
other fiber sensor techniques (Bao and Chen, 2011).
DOFS based on Brillouin scattering techniques
offers cost-effective and structural health monitoring
applications such as rail-track monitoring, pipeline,
bridge, dam, power line, slopes and boarder security
monitoring in real-time. Brillouin sensors are also an
excellent for corrosion and micro-crack detection in
large scale structures (Agarwal, 2000).
For simultaneous monitoring of strain and
temperature, the Brillouin optical time domain
reflectometry (BOTDR) (Kurashima et al., 1990)
based on spontaneous Brillouin scattering and the
Brillouin optical time domain analysis (BOTDA)
(Horiguchi et al., 1993) based on stimulated
Brillouin scattering (SBS) are introduced. The
BOTDR features with simple implementation
schemes (Maughan et al., 2001), while BOTDA
allows higher sensing range and high resolution in
the measurement, but requires access to the both
ends of the same fiber (Minardo et al., 2003). The
BOTDA is more dominant technique as it uses SBS
method through pump beam and counter propagating
probe beam. Due to the strong backscattered signal
strength, BOTDA system has an accurate strain and
temperature measurements and longer sensing range
compared to BOTDR technology (Kurashima et al.,
1993). Distributed strain and temperature monitoring
both in BOTDR and BOTDA systems are based on
Brillouin frequency shift (BFS), the BFS changes
linearly with both strain and temperature along the
sensing fiber.
In this paper, we focus on BFS in Brillouin based
DOFS system. In particular, the BFS is investigated
in conventional BOTDA. In section 2, a short
description of Brillouin sensing principle in BOTDR
and BOTDA is discussed, and the BFS is described
in Brillouin gain/loss mechanism in section 3. In
section 4, the BFS, Brillouin linewidth and peak gain
Lalam N., Ng W., Dai X., Wu Q. and Fu Y.
Analysis of Brillouin Frequency Shift in Distributed Optical Fiber Sensor System for Strain and Temperature Monitoring.
DOI: 10.5220/0005842803330340
In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 333-340
ISBN: 978-989-758-174-8
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
333

variations for different strain and temperature values
are analyzed and demonstrated. Finally, the BFS
dependence on micro-strain has been investigated
and reported in section 5.
2 BRILLOUIN SENSING
PRINCIPLE IN DISTRIBUTED
OPTICAL FIBER SENSOR
When a light beam injected into the optical fiber, a
small part of the light is backscattered due to the
Brillouin interaction between input pump photons
and acoustic phonons within the fiber. Because of
this interaction, the injected pump beam frequency is
down shifted (stokes) and up shifted (anti-stokes).
The down shifted frequency linearly changes with an
acoustic wave frequency within the sensing fiber.
During this inelastic scattering process, the energy is
shifted or converted. This affiliated frequency shift
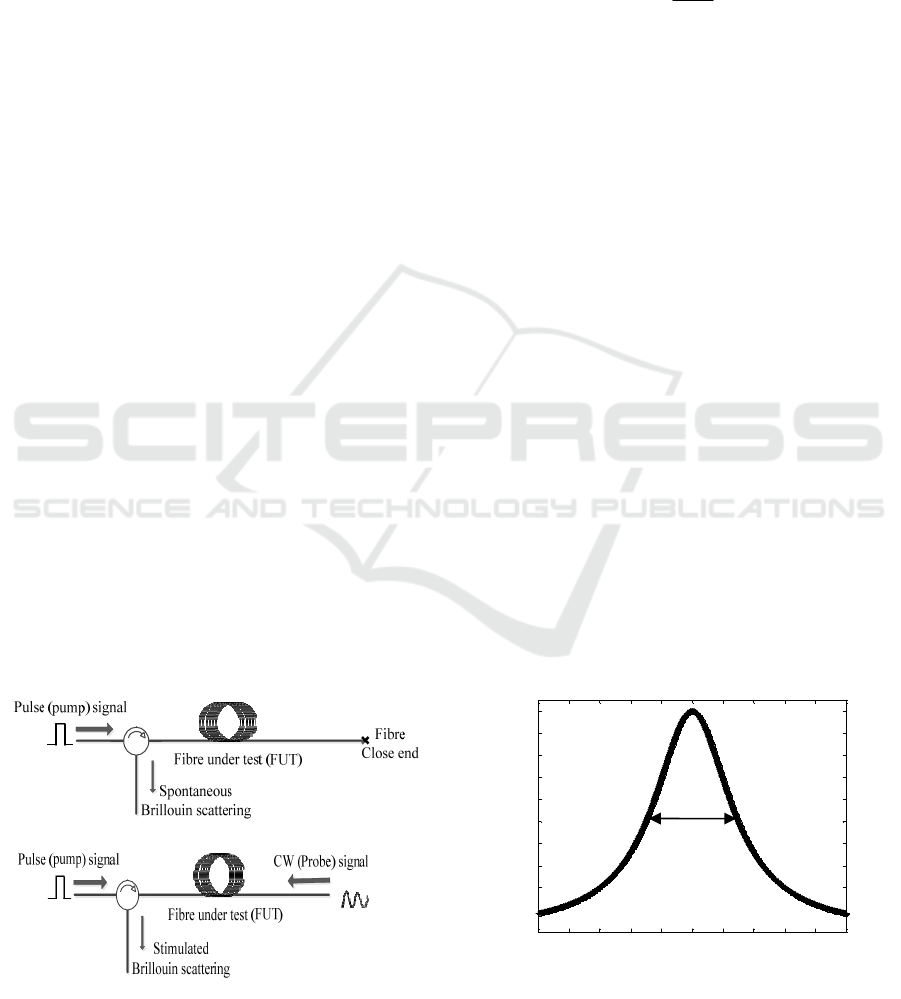
is known as BFS. The BOTDR system has a simple
implementation setup, as it requires access to the
only at one end of the fiber, as shown in Figure 1(a).
BOTDR system has a weak backscattered Brillouin
signal, thus the sensing range is limited compared to
the BOTDA.
The simplified BOTDA measurement setup is
shown in Figure 1(b), where the pulse light (also
known as pump) is propagate through one end of the
fiber, while a counter propagating continuous wave
(also known as probe) is injected at the other end of
the fiber. The BOTDA system utilizes the amplified
Brillouin scattering within the fiber, when the
spontaneous Brillouin scattering light interacts with
the counter propagating continues wave probe beam.
The frequency difference between the pump beam
and probe beam modulates the refractive index of
1
v
(a)
)(
1 b
vv

1
v
(b)
Figure 1: A simplified measurement setup of (a) BOTDR
and (b) BOTDA.
the fiber via electrostriction process, and then excites
an acoustic wave (phonons), which moves same
direction as pump beam (Agarwal, 2008). As a
result, small fraction of pump light is backscattered
into the SBS light. The SBS light frequency is
downshifted by the stokes frequency, this frequency
shift is BFS, and described as,
p
a
B
nv
v

2

(1)
where n is the refractive index,
a
v
is the acoustic
velocity and
p

is the pump wavelength of the fiber.
The relationship between the strain change
)(


,
temperature change
)( T

and BFS change
)(
B
v

is
described as (Bao and Chen, 2012),







CTCTv
TB
)/(
(2)
where
C)MHz/ (1.26
o

T
C
and
strain)-MHz/µ (0.06

C
are the temperature and strain coefficients at 1550
nm for a single mode silica fiber (Thévenaz, 2010).
These coefficients changes slightly for different
types of single mode fibers. Whenever the
temperature and strain changes, the Brillouin peak
frequency will shift linearly. As stated before,
BOTDA is the most preferred technique compared
to BOTDR, therefore, in this paper all measurements
has done in conventional BOTDA system. Figure 2
is a measured Brillouin gain spectrum (BGS) with a
central frequency of 12.90 GHz. The BGS in
standard single mode silica fiber is perfectly fit with
Lorentz profile shape. The fitted Lorentz curve
reveals the spectrum peak frequency, gain and
linewidth at full width at half maximum The BGS
spectrum varies from Lorentz shape to Gaussian
shape, if the input power greater than the threshold
value (Bao and Chen, 2012). From the BGS
Figure 2: Brillouin gain spectrum (BGS) of single mode
fiber with Brillouin frequency (
B
v
) = 12.90 GHz and
spectral linewidth (FWHM) = 30 MHz at room
temperature and strain free.
1.24 1.25 1.26 1.27 1.28 1.29 1.3 1.31 1.32 1.33 1.34
x 10
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Brillouin Gain Spectrum (BGS)
Frequency
Normalised intensity
Linewidth @
FWHM= 30
MHz
OSENS 2016 - Special Session on Optical Sensors
334

spectrum for each point along the fiber, we can
calculate strain/temperature along the sensing fiber
based on the time resolved measurement.
3 BFS CHANGES IN BRILLOUIN
GAIN AND BRILLOUIN LOSS
MECHANISM
In BOTDA system, a short pump pulse (≥10 ns) is
injected into one end of the fiber, while a continuous
wave (CW) probe beam is injected at another end of
the same fiber. From the quantum mechanism in
optical fiber, the pump wave and acoustic phonon
creates a Brillouin scattering at the same time. If the
CW probe beam set at Brillouin stokes frequency
)(
mo
fv 
, the energy transferred from the pump
wave to stokes wave, then the CW stokes beam
experiences Brillouin gain. If the CW probe beam
set at anti-stokes frequency
)(
mo
fv 
, then the energy
transferred from the probe wave to pump wave, then
CW anti-stokes wave experiences Brillouin loss,
respectively (Smith, 1999). In this mechanism the
pump wave acts as a donor and receiver for both
Brillouin gain and Brillouin loss mechanism. The
schematic representation of the energy transfer
process between pump wave and probe stokes and
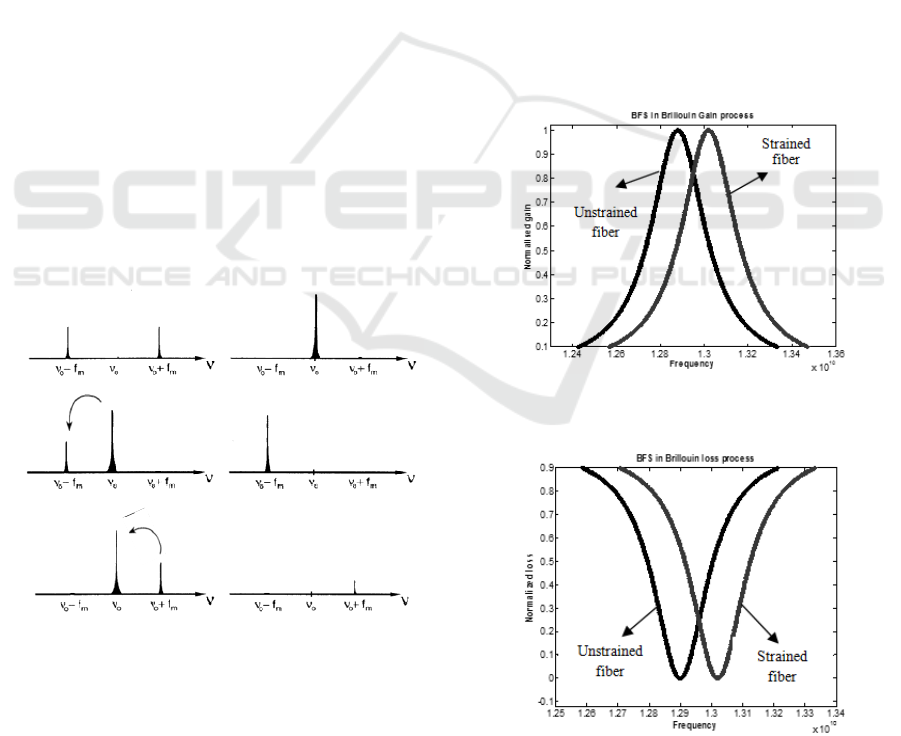
anti-stokes wave is illustrated in Figure 3.
The BGS of single mode silica fiber has a BFS
Figure 3: Schematic diagram of Brillouin gain and
Brillouin loss mechanism (a) Probe wave with stokes
)(
mo
fv 
, anti-stokes
)(
mo
fv 
and pump wave with
frequency
)(
o
v
before interaction. (b) Stokes wave set as
probe wave (Brillouin gain), probe wave experiences gain
after interaction with pump wave. (c) Anti-stokes wave set
as probe wave (Brillouin loss), probe wave experiences
loss after interaction with pump wave.
of 12.90 GHz, at strain free and ambient room
temperature. The 0.2% (2000 µε) tensile strain is
applied on sensing fiber; then the BFS is shifted to
13.02 GHz as shown in Figure 4. In this mechanism,
the CW signal is in stokes frequency
)(
mo
fv 
than
anti-stokes frequency
)(
mo
fv 
, so that the CW signal
experiences gain, while the BFS is shifted with
applied 0.2% strain. The strain induced BFS is
equivalent to 120 MHz (Lalam et al., 2015). In this
process, the energy transferred from pump to probe
beam, therefore, the pump acts as a donor while
probe stokes wave acts as a receiver in energy flow
mechanism. The pump and stokes beam, which are
propagating in opposite direction is assumed to be
linearly polarized along their propagation directions.
If we use polarization maintaining fiber, the states of
polarization (SOP) of the two beams will coincide,
otherwise, polarization noise will distort the
backscattered traces. This noise significantly leads to
BFS measurement error. Therefore, SOP plays an
important role in DOFS system, therefore
polarization scrambler (PS) is employed to maintain
Figure 4: Brillouin frequency shift obtained for 0.2%
tensile strain to the fiber in Brillouin gain mechanism.
Figure 5: Brillouin frequency shift obtained for 0.2%
applied tensile strain to the fiber in Brillouin loss
mechanism.
Probe
stoke
Probe wave
after
Interaction
Brillouin
Loss
Brillouin
gain
Pump
wave
Pump
wave
Probe wave
after
Interaction
Probe
stokes
Probe
Anti-stokes
Pum
p
wave
Analysis of Brillouin Frequency Shift in Distributed Optical Fiber Sensor System for Strain and Temperature Monitoring
335

the SOP, as shown in system block diagram. Figure
5, shows a Brillouin loss spectrum and BFS changes
with a 0.2% applied strain. In this case, the probe
signal is set at anti-stokes frequency, so that probe
beam experiences energy loss. The energy
transferred from probe to pump, therefore, the pump
wave switches from donor to receiver, while probe
beam acts as a donor in energy flow process. For
0.2% applied strain in Brillouin loss mechanism the
frequency shift is found as 120 MHz. Therefore, the
amount of frequency shift is same in both Brillouin
gain and Brillouin loss mechanism.
4 TEMPERATURE AND STRAIN
EFFECTS ON BRILLOUIN
FREQUENCY SHIFT AND
BRILLOUIN GAIN
As described in equation (1), the BFS depends on
the refractive index n
, pump wavelength
p

and
acoustic velocity
a
v
of the fiber. The group velocity
of an acoustic wave is given by,

k
v
a

(3)
(a)
(b)
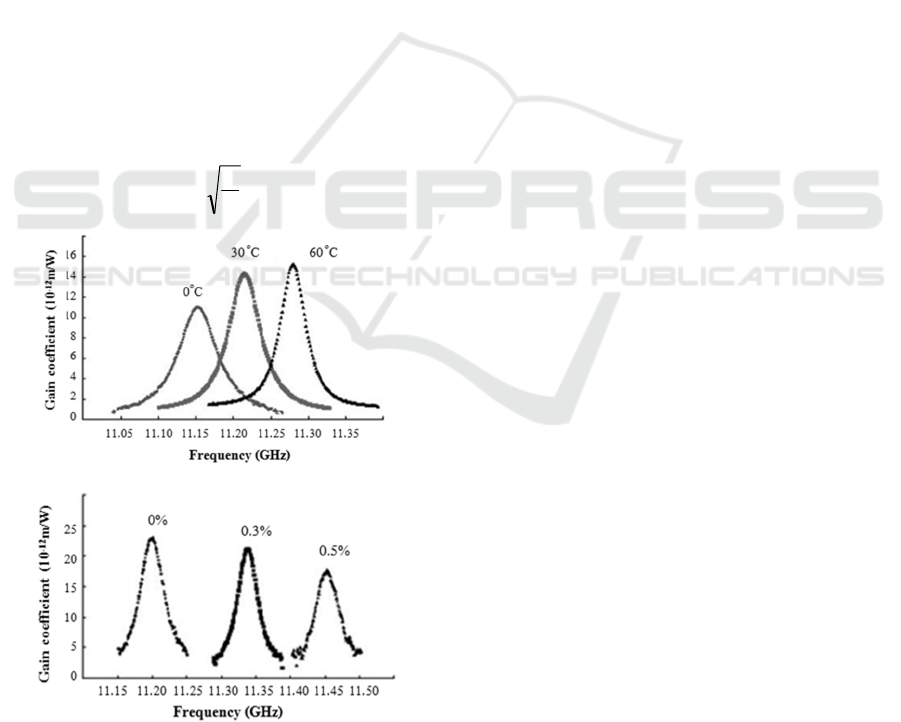
Figure 6: Brillouin frequency shift, linewidth and peak
gain variations of single mode silica sensing fiber for (a)
different temperatures (b) different strains.
change, hence result in a shift in Brillouin frequency
material density of sensing fiber. The material where
k is the bulk modules, ρ is the average density
changes when strain and temperature By analyzing
the back scattered BGS consists of BFS and
Brillouin gain coefficient, it is possible to measure
the distributed strain and/or temperature along the
sensing fiber.
Figure 6 shows, the BFS, Brillouin gain and
linewidth changes with different strain and
temperature applied on sensing fiber (Nikles et al.,
1997). By measuring Brillouin gain coefficient and
BFS changes, the strain/ temperature information
along the fiber can be determined. The performance
of BOTDA system certainly depends on three
parameters namely, the spatial resolution,
measurement accuracy, and the sensing range. The
spatial resolution is determined as, the smallest fiber
length which measurement can be detected. The
measurement accuracy is difference between the
measured value and expected value of
strain/temperature along the fiber. The sensing range
indicates the longest length of the fiber, which we
can extract the information from the received BGS.
Three fundamental parameters that characterize the
BGS, which are the Brillouin linewidth, measured at
full width at half maximum, the BFS and the
Brillouin gain coefficient. An interesting feature
from Figure 6(a) is the Brillouin spectrum linewidth
is decreases when the temperature increases. The
linewidth dependence is not linear with the
temperature and tends to meet at a constant value at
higher temperature for all different fibers (Pine,
1969). The Brillouin gain increases according to the
temperature increase due to its spectral narrowing
and thus phonon absorption. The two parameters;
Brillouin gain and BFS linearly changes with
applied different temperatures. Another important
feature observed from Figure 6(b) is the Brillouin
gain decreases with increase strain values up to the
fiber breaking point (~1% elongation), while the
linewidth remains unchanged. An important
observation from Figure 6(b), the BFS linearly
varies with applied strain values, while the Brillouin
linewidth is invariant. From Figure 6, we can
conclude that, the Brillouin linewidth decreases
when the temperature increases, and unchanged with
applied strain. Therefore, the changes of two
fundamental parameters; namely BFS and Brillouin
gain were considered in BGS for measuring the
strain and temperature along the sensing fiber. The
BFS determines the strain/temperature range, while
Brillouin gain discriminates, which is strain and
temperature, simultaneously.
OSENS 2016 - Special Session on Optical Sensors
336

(a)
(b)
Figure 7: Brillouin frequency shift changes with (a)
temperature (
o
C) and (b) strain (µε).
Table 1: Measured coefficient values of BFS and gain for
temperature and strain.
Description Measured value
Change in Brillouin
frequency versus strain
0.06 MHz/(µ-strain)
Change in Brillouin
frequency versus
temperature
1.26 MHz/
o
C
change in Brillouin gain
versus strain
-9×10
-4
%/(µ-strain)
change in Brillouin gain
versus temperature
0.416 %/K
The summary graph of different strain and
temperature vs BFS is depicted in Figure 7. It shows
a linear relationship between the applied strain and
temperature with Brillouin frequency shift. The
Brillouin gain
)(vg
B
is expressed as (Robert and
Norcia-Molin,
2006),
22
2
)2()(
)2(
)(
BWB
BW
oB
vvv
v
gvg


(3)
where
o
g
is the Brillouin gain coefficient,
BW
v
is the
Brillouin linewidth at full width at half maximum
v
is the pump frequency and
B
v is the Brillouin center
frequency. The Brillouin gain factor
o
g
is expressed
as follows (Lanticq et al., 2009),
BWaP
o
vvc
pn
g
2
2
2
12
2



(4)
the gain coefficient
o
g
depends on many structural
parameters as shown in equation (5). The value of
peak Brillouin gain coefficient changes between
5×10
-11
m/w to 7×10
-14
m/w at 1550 nm wavelength.
The parameters used for Brillouin gain coefficient
calculation are shown in Table 2 (Benassi, 1993),
Table 2: Parameters used for calculation of Brillouin gain
coefficient.
Parameter Symbol Value
Refractive index n
1.44
Electro-optic constant
12
p
0.29
Polarization factor γ 0.5
Pump wavelength λ
p
(nm) 1550
Fiber density ρ (kg/m
3
) 2330
Acoustic velocity
a
v
(m/s)
5996
Brillouin linewidth at
FWHM
BW
v
(MHz)
30
5 MICRO-STRAIN DETECTION
USING BFS TECHNIQUE IN
BOTDA SYSTEM
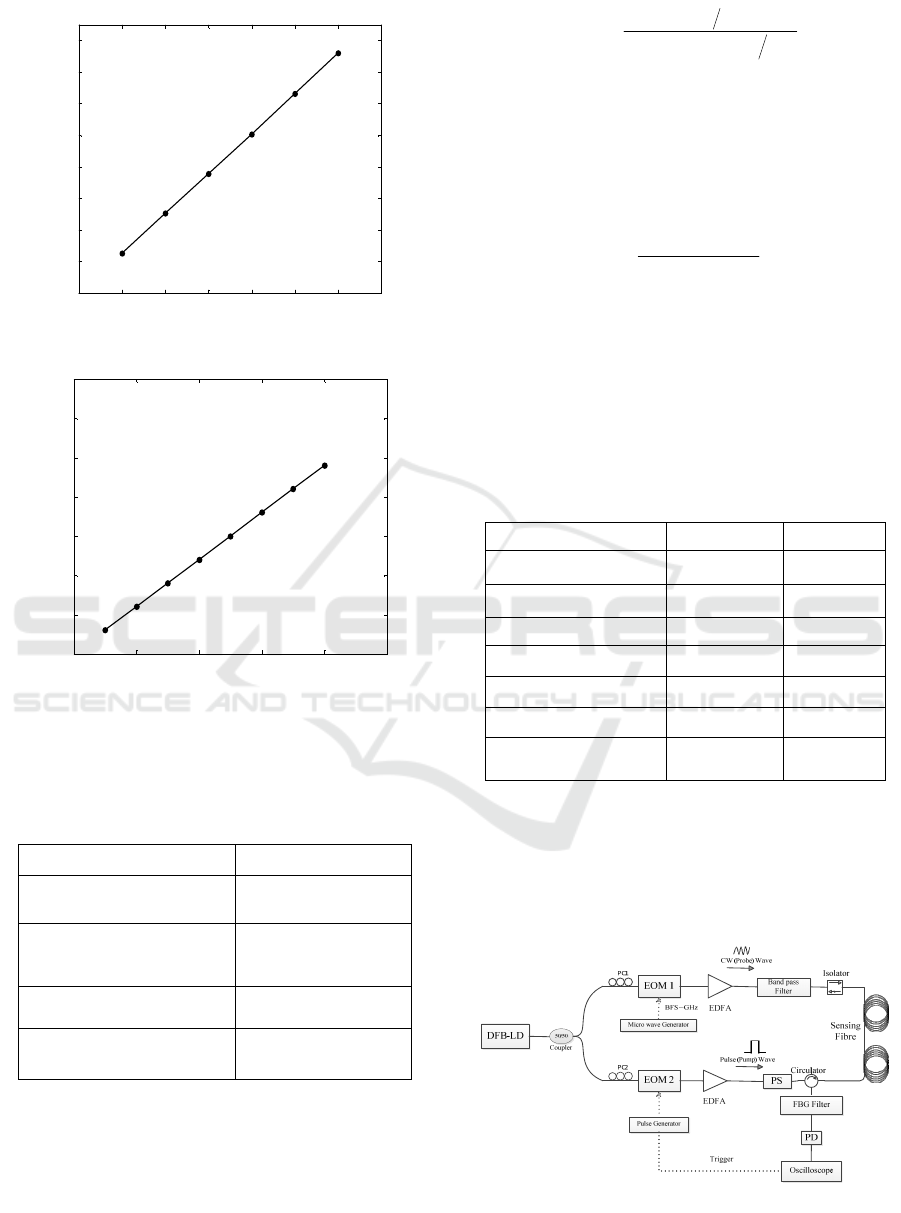
Figure 8: BOTDA system setup for measuring Brillouin
frequency shift (BFS).
0 20 40 60 80 100 120 140
0
20
40
60
80
100
120
140
160
Temperature ( C)
Frequency shift (MHz)
Brillouin frequency shift vs Temperature
o
0 2000 4000 6000 8000 10000
0
100
200
300
400
500
600
700
Strain (µ-strain)
Frequency shift (MHz)
Brillouin frequency shift vs applied strain
Analysis of Brillouin Frequency Shift in Distributed Optical Fiber Sensor System for Strain and Temperature Monitoring
337

Figure 9: Three-dimensional Brillouin gain spectrum of 40
m long SMF at room temperature and strain free.
Figure 10: The 0.1% strain applied induced BFS on 5 m
section of the fibre.
The system block diagram for BFS based micro-
strain measurement is shown in Figure 8. A
distributed feedback laser diode (DFB-LD) is used
as a laser source at 1550 nm. The laser output is split
into two beams, the pump and probe beam using a
50/50, 3 dB coupler. The polarization controller
(PC) controls the state of polarization of the injected
beam, in order to control the polarization sate of
input beam. An electro- optic modulator (denoted as
EOM2 in Figure 8), which convert the electrical
pulses into optical and to set high extinsion ratio.
EOM1 modulates the input signal around the fiber
BFS (~ 11 GHz), driven by an external microwave
signal generator. The output signal consists of two
sidebands, the upper sideband and fundamental
frequency is filtered out using an optical filter, while
the lower sideband set as probe wave. After that, the
probe signal is amplified by erbium doped fiber
amplifier (EDFA). In this paper, we consider a
Brillouin gain process, as lower sideband set as CW
probe beam. In general, the lower sideband
represents as a stoke beam with respect to the pulse
Figure 11: The 0.2% strain applied induced BFS on 5 m
section of the fibre.
Figure 12: The 0.3% strain applied induced BFS on 5 m
section of the fibre.
signal and amplifies during propagation. The upper
sideband acts as an anti-stokes wave experiences
depletion. The upper sideband and fundamental
frequency introduces negative effect to the SBS gain
process. Using the EOM2, we can set high extinction
ratio and the electrical pulses generated from a pulse
generator will convert into optical pulses. The pulse
width in conventional BOTDA is limited to 10 ns,
because of an acoustic wave life time (decay time) is
~10 ns, below this time no more information about
BFS can be obtained. Brillouin scattering is a
polarization sensitive process; therefore we employ a
polarization scrambler (PS) in setup. The received
backscattered signal is sent to the optical filter,
which eliminates the Raleigh and Raman
components. Then the Brillouin stokes signal is sent
to photo detector (PD) and analyzed by oscilloscope.
Figure 9, shows the Brillouin gain spectrum
detected at room temperature without any applied
strain. Therefore, no frequency shift is found along
the sensing fiber. As described before, the BGS
spectrum shape is well fitted by a Lorentz curve
OSENS 2016 - Special Session on Optical Sensors
338

profile shape. However, the BGS profile gradually
changes from a Lorentz shape to a Gaussian shape,
when the pulse width approaches near to the phonon
lifetime. As described in section 4, the Brillouin
linewidth does not vary with applied strain and
experiences a very small dependence on
temperature, ~-0.1 MHz/
o
C. Therefore, the Brillouin
linewidth would be a limited use for distributed
strain/temperature measurements. This is the reason
why we consider the two fundamental parameters;
the Brillouin gain and BFS for measuring distributed
strain and temperature, simultaneously.
Figure 10, shows a BGS corresponding to a 5 m
section of fiber under 0.1% tensile strain. The
frequency is shifted away from the spectrum to 60
MHz. The strain is increases to 0.2%, 0.3%
respectively, and then the strained section frequency
is shifted to 120 MHz and 180 MHz far away from
the spectrum, respectively, as shown in Figure 11
and Figure 12. Therefore, we observe that, for 0.1%
(1000µ-strain), the frequency shift is 60 MHz. For
0.2% (2000µ-strain), the frequency shift is 120
MHz, for 0.3% (3000µ-strain), the frequency shift is
180 MHz. As a result, for each µ-strain, the
frequency shift is found as 0.06 MHz, as perfectly
matched with strain coefficient

C
(0.06 MHz/µ-
strain) as given by equation (2). The pump pulse
width is set at 10 ns in measurement, corresponding
to a 1 m spatial resolution.
6 CONCLUSIONS
In conclusion, we have analyzed Brillouin frequency
shift in distributed optical fiber sensor system. The
measurements performed for different strain and
temperature values. The results demonstrate that, the
BFS has a strong linear relationship with strain and
temperature along the sensing fiber. Brillouin
gain/loss measurements performed based on stokes
and anti-stokes of the probe wave. BOTDA is a
frequency based technique system as compared to
Raman systems, which are intensity based technique.
Brillouin frequency technique is more accurate,
since intensity based techniques suffer from
sensitivity to frequency drifts. Therefore, distributed
fiber sensor systems based on Brillouin scattering is
a better technique for structural health monitoring
utilizing BFS.
Brillouin peak gain and linewidth variations
under different temperature and strain conditions are
characterized. We can conclude that, the Brillouin
linewidth does not vary linearly with temperature
and unchanged with applied strain. The Brillouin
gain increases with increased temperature due to
phonon absorption and very small gain decrement
with applied strain. Therefore, we found BFS have a
strong linear relationship with both applied strain
and temperature along the fiber. As a result, the BFS
change is used for strain and temperature
measurements, while the Brillouin gain changes
discriminate that, which is temperature and which is
strain simultaneously. From the measurement
results, it is evident that, for each µ-strain and
temperature on sensing fiber, the BFS found as 0.06
MHz/µ-strain and 1.26 MHz/
o
C, respectively.
Therefore, the BOTDA sensing system based on
BFS technique is a promising technique for
structural health monitoring in real-time.
REFERENCES
Bao, X., and Chen, L., 2001. "Recent Progress in
Brillouin.
Scattering Based Fiber Sensors," Sensors, vol. 11, pp.
4152-4187, 2011.
Agarwal, G.,2000. Applications of nonlinear fiber optics:
Academic press.
Kurashima, T., Horiguchi, T., Izumita, H., Furukawa, S.,
and Koyamada, Y., 1990. "Brillouin optical-fiber time
domain reflectometry,"
IEICE Trans. Commun, vol.
E76-B.
Horiguchi, T., Kurashima, T., and Tateda, M., 1993 "A
technique to measure distributed strain in optical
fibers," Photonics Technology Letters, IEEE, vol. 2,
pp. 352-354.
Maughan, S, M., Kee, H, H., and Newson, T, P., 2001.
"Simultaneous distributed fiber temperature and strain
sensor using microwave coherent detection of
spontaneous Brillouin backscatter,"
Meassurement
science and technology,
vol. 12, pp. 834-842.
Minardo, A., Bernini, Z., and Zeni, L., 2003
. "Accurate
distributed temperature measurements by Brillouin
Scattering fiber-optic sensor," in Sensors, Proceedings
of IEEE
, 2003, pp. 348-352 Vol.1.
Kurashima, T., Horiguchi, T., and Tateda, M., 1990.
"Distributed-temperature sensing using stimulated
Brillouin scattering in optical silica fibers,"
Optics
Letters,
vol. 15, pp. 1038-1040.
Agrawal, G, P., 2008. "Nonlinear fiber optics," in
Nonlinear fiber optics, book chapter, 4th ed.
Bao, X., and Chen, L., 2012. "Recent Progress in
Distributed Fiber Optic Sensors," Sensors, vol. 12, p.
8601.
Thévenaz, L., 2010. "Brillouin distributed time-domain
sensing in optical fibers: state of the art and
perspectives," Frontiers of Optoelectronics in China,
vol. 3, pp. 13-21.
Analysis of Brillouin Frequency Shift in Distributed Optical Fiber Sensor System for Strain and Temperature Monitoring
339

Bao, X., and Chen, L., 2011. "Recent Progress in
Distributed Fiber Optic Sensors,"
Sensors, vol. 12, pp.
8601-8639.
Smith, J., 1999. "Characterization of the Brillouin Loss
Spectrum for Simultaneous Distributed Sensing of
Strain and Temperature," M. Sc thesis, University of
New Brunswick.
Lalam, N., Ng, W, P., Dai, X., and Al-Musawi, A, K.,
2015. "Characterization of Brillouin frequency shift in
Brillouin Optical Time Domain Analysis (BOTDA),"
in
Networks and Optical Communications (NOC),
20th European Conference on
, pp. 1-4.
Nikles, M., Thevenaz, L., and Robert, P, A., 1997.
"Brillouin gain spectrum characterization in single-
mode optical fibers,"
Lightwave Technology, Journal
of,
vol. 15, pp. 1842-1851.
Pine, A, S., 1969. "Brillouin Scattering Study of Acoustic
Attenuation in Fused Quartz," Physical Review, vol.
185, pp. 1187-1193.
Robert, B., Norcia-Molin, S., Dolfi, D., Tonda, S.,
Huignard, J, P., Frey
, R., et al., 2006. "Optically
carried microwave signal modulation depth
enhancement by stimulated Brillouin scattering in
PCFs,"
Electronics Letters, vol. 42, pp. 108-109.
Lanticq, V., Jiang, S., Gabet, R., Jaouen, Y., Taillade, F.,
Moreau,G., et al., 2009. "Self-referenced and single-
ended method to measure Brillouin gain in monomode
optical fibers," Opt Lett, vol. 34, pp. 1018-20, Apr.
Benassi, P., Mazzacurati, V., Ruocco, G., and Signorelli,
G., 1993. "Elasto-optic constants in silicate glasses:
Experiment and theory,"
Physical Review B, vol. 48,
pp. 5987-5996.
OSENS 2016 - Special Session on Optical Sensors
340