Extracting Dynamics from Multi-dimensional Time-evolving Data

using a Bag of Higher-order Linear Dynamical Systems

Kosmas Dimitropoulos, Panagiotis Barmpoutis, Alexandors Kitsikidis and Nikos Grammalidis

Information Technologies Institute, Centre for Research and Technology Hellas, Thessaloniki, Greece

Keywords: Linear Dynamical Systems, Human Action Recognition, Dynamic Texture Analysis, Higher Order

Decomposition.

Abstract: In this paper we address the problem of extracting dynamics from multi-dimensional time-evolving data. To

this end, we propose a linear dynamical model (LDS), which is based on the higher order decomposition of

the observation data. In this way, we are able to extract a new descriptor for analyzing data of multiple

elements coming from of the same or different data sources. Each sequence of data is modeled as a

collection of higher order LDS descriptors (h-LDSs), which are estimated in equally sized temporal

segments of data. Finally, each sequence is represented as a term frequency histogram following a bag-of-

systems approach, in which h-LDSs are used as feature descriptors. For evaluating the performance of the

proposed methodology to extract dynamics from time evolving multidimensional data and using them for

classification purposes in various applications, in this paper we consider two different cases: dynamic

texture analysis and human motion recognition. Experimental results with two datasets for dynamic texture

analysis and two datasets for human action recognition demonstrate the great potential of the proposed

method.

1 INTRODUCTION

Machine learning problems often involve sequences

of real-valued multivariate observations. To model

the statistical properties of such data, it is assumed

that each observation is correlated to the value of an

underlying latent variable that is evolving over the

course of the sequence. If the state is real-valued and

the noise terms are assumed to be Gaussian, the

model is called a linear dynamical system (LDS)

(Boots, 2009). Thus, a linear dynamical system is

associated with a first order ARMA process with

white zero means IID Gaussian input (Doretto et al.,

2003). Linear dynamical systems are an important

tool for modeling time series in engineering,

controls and economics, as well as the physical and

social sciences and they have been successfully used

in the past for various vision tasks such as: dynamic

texture analysis, synthesis, segmentation,

registration and categorization (Soatto et al., 2001).

They have also been employed for the categorization

of video sequences in multimedia databases and

more recently in human action recognition tasks.

More specifically, in the field of video

categorization a lot of methods have adopted LDSs

focusing mainly on the definition of a suitable

distance or kernel between the model parameters of

two dynamical systems (Doretto et al., 2003); (Chan

and Vasconcelos, 2005); (Chan and Vasconcelos,

2007); (Vishwanathan et al., 2007). In addition,

Turaga et al., (2011) showed that the parameters of

linear dynamic models are finite dimensional linear

subspaces that can be described using the unified

framework of Grassmann and Stiefel manifolds and

proposed algorithms for supervised and

unsupervised clustering for activity recognition, face

recognition and video clustering. More recently, a

new method was introduced by Ravichandran et al.,

(2013) aiming to model video sequences with a

collection of LDSs, which are then used as features

in a bag of systems approach, while Luo et al.,

proposed the modelling of motion dynamics with

robust LDSs using the model parameters as motion

descriptors.

Nevertheless, a limitation of linear dynamical

systems is that they exploit information from only

one element, i.e., channel, thus, in the case of

multidimensional data the concatenation of different

components into one single element is required. To

this end, in this paper we propose a more efficient

Dimitropoulos, K., Barmpoutis, P., Kitsikidis, A. and Grammalidis, N.

Extracting Dynamics from Multi-dimensional Time-evolving Data using a Bag of Higher-order Linear Dynamical Systems.

DOI: 10.5220/0005844006830688

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 683-688

ISBN: 978-989-758-175-5

683

way to model dynamics by taking advantage of the

multidimensionality of data. More specifically, we

present a higher-order LDS model in order to extract

a new descriptor for analyzing data coming from

multiple elements, e.g., channels in the case of video

sequences or joint coordinates in the case of skeleton

animation data. The proposed model is based on the

higher order decomposition of the multidimensional

data and enables the analysis of dynamic time-series

using information from the same or different data

sources, e.g., colour visible range cameras, infrared

sensors of various spectral ranges, or even

synthesized images.

The proposed h-LDS descriptors are estimated in

equally sized temporal segments, while a bag of

systems approach is adopted, in which the h-LDSs

are used as feature descriptors. For the formation of

the codebook, a k-medoids (Kaufman and

Rousseeuw, 1987) classification method is applied,

where the K codewords correspond to K

representative higher order LDSs. Each data

sequence is then represented as a Term Frequency

(TF) histogram of the predefined codeword of h-

LDSs and is provided to a SVM classifier.

For evaluating the performance of the proposed

methodology to extract dynamics from time series

and using them for classification, in this paper we

deal with the problems of dynamic texture analysis

and human action recognition.

2 HIGHER-ORDER LINEAR

DYNAMICAL ANALYSIS

2.1 Estimation of the h-LDS Descriptor

As was mentioned above a linear dynamical system

is associated with a first order ARMA process with

white zero mean IID Gaussian input. More

specifically, the stochastic modeling of both

dynamics and appearance is encoded by two

stochastic processes, in which dynamics are

represented as a time-evolving hidden state process

x(t)∈ 



and observed data y(t)∈ 



as a linear

function of the state vector:





1

















(1)

























(2)

where ∈ 



is the transition matrix of the

hidden state (n is the dimension of hidden state with

n≤d), while ∈



is the mapping matrix of the

hidden state to the output of the system. The

quantities w(t) and Bv(t) are the measurement and

process noise respectively, with w(t)~N(0,R) and

Bv(t)~N(0,Q). The main advantage of the LDS

descriptor   ,, is that it contains both the

appearance information of the data segment, which

is modeled by , and its dynamics that are

represented by .

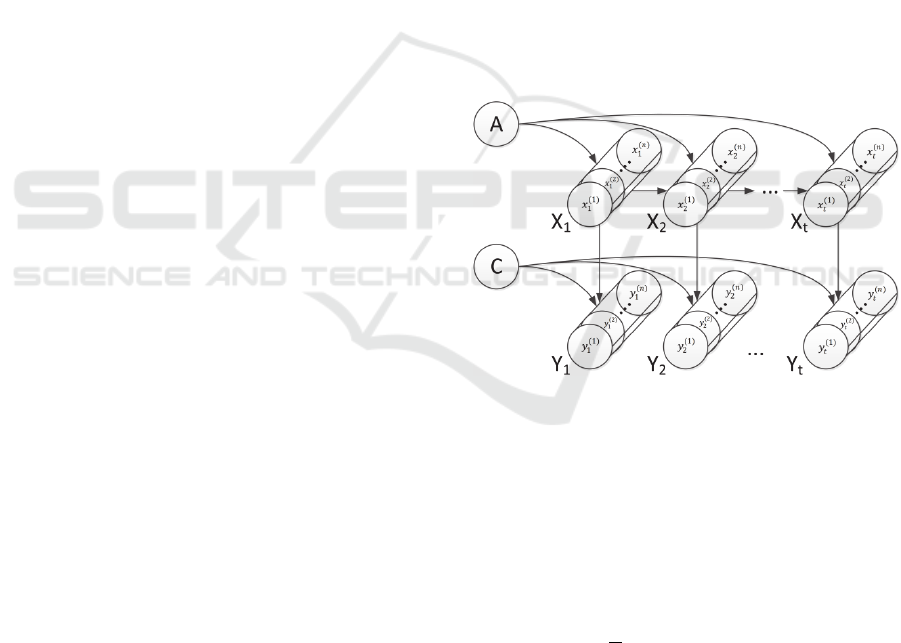
In the case of multidimensional data,

observations can be represented by a tensor Y∈



….

of order n, where d

, d

,....,d

are integer

numbers indicating the number of elements in each

dimension. For instance, if we consider a colour

video sequence of F frames, the order of tensor Y (in

the rest of the paper the term 'tensor' is used to

indicate a matrix of order higher than two) is four,

where d

and d

indicate the width and height of the

image respectively, d

is the number of image

elements (d

=3) and d

is the number of frames. In

order to estimate the matrices A and C containing the

dynamics and appearance information respectively

(see Figure 1), we need to decompose the n-order

tensor Y, so that the columns of the mapping matrix

C are orthonormal (Doretto et al., 2003).

Figure 1: A graphical representation of the h-LDS model.

To satisfy the aforementioned requirement, we

use the HOSVD (Kuo, 2013), which is a

generalization of the singular value decomposition

for higher order tensors. More specifically, we first

subtract from Y the temporal data average 



in order

to construct a zero mean matrix in the time axis,

where the temporal average is computed as:















,



,…..,



,







(3)

and then we decompose tensor Y as follows:

















…







(4)

where U

(1)

(2)

,....U

(n)

are orthogonal matrices

containing the orthonormal vectors spanning the

column space of the i-mode matrix unfolding Y

(i)

and

RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,

Industrial Applications

684





denotes the i-mode product between a tensor and

a matrix (Kuo, 2013), with i=1,2...n. Since, the

choice of matrices A, C and Q in equations (1) and

(2) is not unique, in the sense that there are infinitely

many such matrices that give rise to exactly the

same sample paths starting from suitable initial

conditions (Doretto et al., 2003), we can consider

)(n

, where

)(n

is an orthogonal matrix and

X=















…







(5)

Hence, equation (4) can be reformulated as follows:







(6)

The n-mode product of tensor X∈ 

….

with

matrix C∈



can be defined as:





⇔







(7)

The transition matrix A, containing the dynamics of

the multidimensional data, can then be easily

computed by using least squares:



























(8)

where the matrices 













,





,…,



1





and











,





,…,







 are formed from the

unfolding X

(n)

of tensor X along the n

dimension.

2.2 Codebook Creation and

Classification

For the formation of the codebook, k-medoids

clustering is applied, however, before that we need

to define a similarity metric between two descriptors









,



 and 







,



 that will be

applicable to the non-Euclidean space of h-LDSs.

Since h-LDS descriptor consists of a pair of two-

dimensional matrices, we can easily use as a

similarity metric the Martin distance between 





and 

















,









ln







(9)

where θ

are the subspace angles (Cock and Moor,

2002) between the two models. The cosine of θ

can

be calculated as the square root of the i-th

eigenvalue of the matrix P













cos





i



eigenvalue

















(10)

where the estimation of matrix















2221

1211

is performed by solving the Lyapunov equation



PAP  C



C, where















and





CCC 

The codebook can then be created by using h-LDS

as feature descriptors. Specifically, the training

dataset of the h-LDS descriptors is fed into k-

medoids algorithm for the creation of a codebook of

K codewords corresponding to K representative h-

LDSs, as shown in Figure 2. Finally, each data

segment is then represented as a Term Frequency

(TF) histogram of the predefined codeword of h-

LDSs.

Figure 2: h-LDS codebook creation and classification.

3 EXPERIMENTAL RESULTS

For evaluating the performance of the proposed

methodology to extract dynamics from time

evolving multidimensional data and using them for

classification, in this paper we consider two different

applications: i) dynamic texture analysis and ii)

human motion recognition. In the former case, the

proposed high order LDS descriptor is used to model

the temporal evolution of pixels intensities, while in

the latter the evolution of skeleton joints positions

during the performance of a motion is considered as

a multidimensional time series.

3.1 Dynamic Texture Analysis

In this section we present experimental results using

two video datasets for dynamic texture analysis.

More specifically the first dataset (Dimitropoulos et

al., 2015) contains videos with flame and flame-

Extracting Dynamics from Multi-dimensional Time-evolving Data using a Bag of Higher-order Linear Dynamical Systems

685

colored objects, while the second one contains

videos with smoke and non-smoke frames

(Barmpoutis et al., 2014). In both cases, each frame

of the video sequence is divided into image patches

of size 16x16, which is a typical approach in video-

based fire detection systems and then a pre-

processing step is applied aiming to identify

candidate image patches i.e., patches containing a

sufficient number of flame or smoke colored moving

pixels. To this end, we initially apply an Adaptive

Median algorithm (McFarlane and Schofield, 1995),

(Dimitropoulos et al., 2012), which is fast and very

efficient algorithm for detecting moving pixels, and

then we use a fire probability model (Dimitropoulos

et al., 2015) or a HSV smoke color model

(Avgerinakis et al., 2012) to identify candidate flame

or smoke image patches respectively.

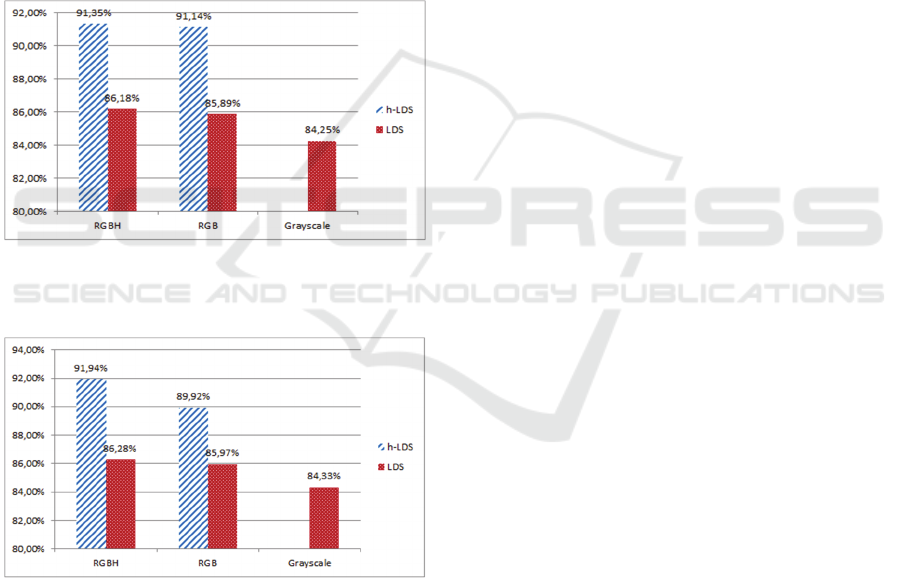
Figure 3: Comparison of LDS and h-LDS with grayscale,

RGB and RGBH data using the dataset containing flame

and flame colored objects.

Figure 4: Comparison of LDS and h-LDS with grayscale,

RGB and RGBH data using the dataset containing smoke

and smoke colored objects.

For each candidate image patch we estimate a h-

LDS descriptor using a temporal length of 16

frames. In addition, for the classification of each

frame, we create histogram representations

corresponding to the sub-sequences of T previous

frames (in our experiments T=100). In the

experimental results, we estimated the number of

correctly detected frames out of the total number of

frames in each dataset. As can be seen in Figures 3

and 4, the proposed descriptor outperforms standard

LDSs in both cases i.e., flame and smoke

identification respectively. In order to validate the

performance of both descriptors with a different

number of elements, apart from the use of grayscale

and RGB data (i.e., three elements), we also created

a fourth channel by visualizing the feature space of

HOG descriptor as in (Vondrick et al., 2013) (i.e.,

RGBH data). Especially in the case of smoke, the

fourth channel seems to improve significantly the

results, while LDS descriptor does not seem to

change significantly its detection rate.

3.2 Human Action Recognition

In this section we deal with the problem of human

action recognition in game-like applications. More

specifically, for capturing the human motion, depth

sensors are used, while the evolution of skeleton

joints positions during the performance of a motion

is considered as a multidimensional time series. To

extract the dynamics of the body motion, we

segment the multidimensional signal into equally

sized elementary segments using a sliding time

window of 16 frames. In this way we accomplish a

better representation of human motion, instead of

using the whole non-linear sequence of data, as each

elementary segment can be efficiently modelled by a

linear dynamical system.

Experimental results with two datasets for human

action recognition show that the proposed method

outperforms the different variants of LDSs on the

recognition task of body motion. More specifically,

for the validation of the proposed method we created

a new Kinect gesture dataset consisting of 360

motions, while we also used a well-known dataset

such as MSRC-12 (Fothergill et al., 2012). More

specifically the new dataset contains 6 actions (bend

forward, left kick, right kick, raise hands, hand

wave, push with hands) performed by 6 subjects,

each repeated 10 times (360 motions in total) and the

Microsoft Research Cambridge-12 Kinect gesture

data set (MSRC-12) comprises of 594 sequences

collected from 30 people performing 12 gestures.

The MSRC-12 dataset is partitioned along different

methods of instruction given to the subjects such as

text and video. We used the part of the dataset where

video only instructions were given. Both datasets

contain tracks of 20 skeleton joint position

coordinates estimated using the Kinect Pose

Estimation pipeline.

RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,

Industrial Applications

686

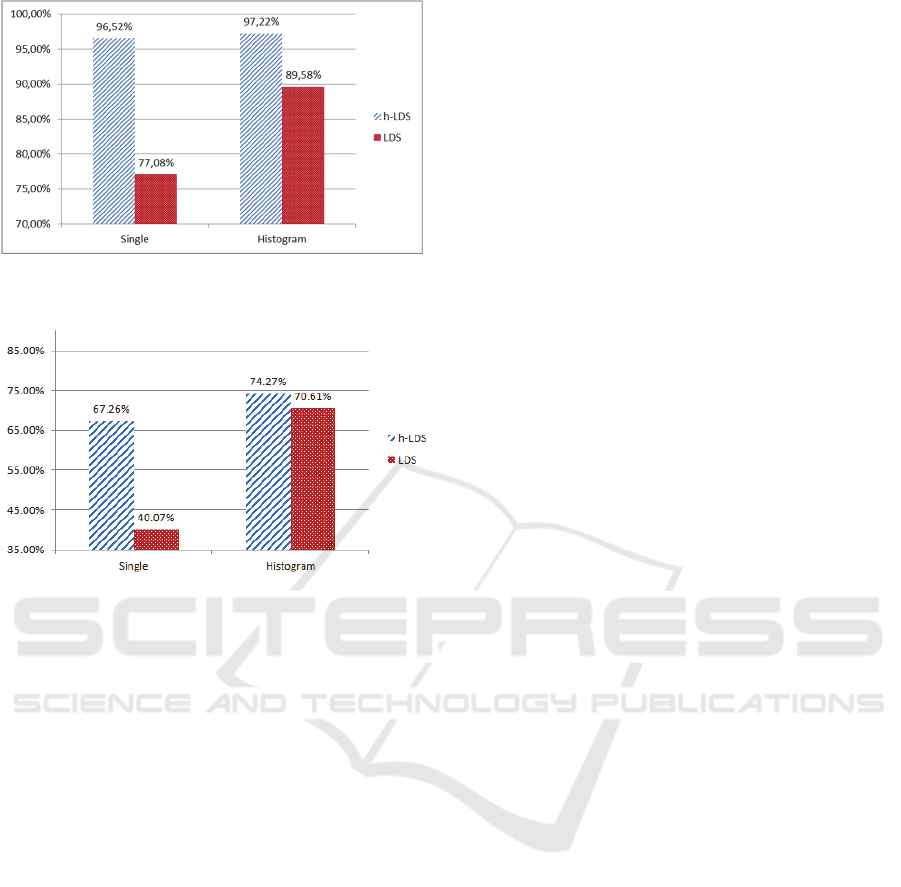
Figure 5: Comparison of LDS and H-LDS descriptor

performance on our dataset.

Figure 6: Comparison of LDS and H-LDS descriptor

performance on MSRC-12 dataset.

As seen in Figures 5 and 6 the histogram of

LDSs offer an improvement in classification results

compared to using a single descriptor for the whole

motion. Additionally, the h-LDS descriptor clearly

outperforms the simple LDS descriptor in each case.

This extends to the case of histogram of LDSs,

where the same behavior can be observed.

4 CONCLUSIONS

In this paper, we introduced a higher order linear

dynamical systems (h-LDS) descriptor for extracting

dynamics from multidimensional time evolving data.

By applying higher order decomposition in the

observation data, we showed that we can achieve

higher detection rates than standard linear dynamical

systems both in the case of dynamic texture analysis

and human action recognition. In the future, we are

planning to use data from different sources, e.g.,

multispectral imaging in the case of flame detection

or skeletal data and depth data in the case of human

action recognition.

ACKNOWLEDGEMENTS

The research leading to these results has received

funding from the European Community's Seventh

Framework Programme (FP7-ICT-2011-9) under

grant agreement no FP7-ICT-600676 ''i-Treasures:

Intangible Treasures - Capturing the Intangible

Cultural Heritage and Learning the Rare Know-How

of Living Human Treasures''.

REFERENCES

Avgerinakis, K., Briassouli, A., Kompatsiaris, I., 2012.

"Smoke Detection Using Temporal HOGHOF

Descriptors and Energy Colour Statistics from Video,"

in Int'l Workshop on Multi-Sensor Systems and

Networks for Fire Detection and Management.

Barmpoutis, P., Dimitropoulos, K., Grammalidis, N.,

2014. "Smoke Detection Using Spatio-Temporal

Analysis, Motion Modeling and Dynamic Texture

Recognition", 22nd European Signal Processing

Conference (EUSIPCO 2014), Lisbon, Portugal, 1-5

September.

Boots, B., 2009. Learning stable linear dynamical systems.

M.S. Thesis in Machine Learning, Carnegie Mellon

University.

Chan, A., Vasconcelos, N., 2005. "Probabilistic Kernels

for the Classification of Auto-Regressive Visual

Processes," in IEEE Conf. Computer Vision and

Pattern Recognition.

Chan, A., Vasconcelos, N., 2007. "Classifying Video with

Kernel Dynamic Textures," in IEEE Conf. Computer

Vision and Pattern Recognition.

Cock, K. D., Moor, B. D., 2002. "Subspace angles and

distances between ARMA models," System and

Control Letters, vol. 4, pp. 265-270.

Dimitropoulos, K., Tsalakanidou, F., Grammalidis, N.,

2012. "Flame detection for video-based early fire

warning systems and 3D visualization of fire

propagation," in 13th IASTED Int'l Conf. on Computer

Graphics and Imaging.

Dimitropoulos, K., Barboutis, P., Grammalidis, N., 2015.

"Spatio-Temporal Flame Modeling and Dynamic

Texture Analysis for Automatic Video-Based Fire

Detection", IEEE Transactions on Circuits and

Systems for Video Technology, vol. 25, no. 2, pp.

339-351.

Doretto, G., Chiuso, A., Wu, Y. N., Soatto, S., 2003.

"Dynamic Textures," Int'l J. of Computer Vision, vol.

51, no. 2, pp. 91-109.

Fothergill, S., Mentis, H. M., Kohli, P., Nowozin, S.,

2012. Instructing people for training gestural

interactive systems. In J. A. Konstan, E. H. Chi, and

K. Hook, editors, CHI, pages 1737–1746. ACM.

Kaufman, L., Rousseeuw, P.J., 1987. Clustering by means

of Medoids. In Statistical Data Analysis Based on the

L1–Norm and Related Methods, edited by Y. Dodge,

Extracting Dynamics from Multi-dimensional Time-evolving Data using a Bag of Higher-order Linear Dynamical Systems

687

North-Holland, 405–416.

Kuo, C. T., 2013. "Higher order SVD: theory and

algorithms".

McFarlane, N., Schofield, C., 1995. "Segmentation and

tracking of piglets in images," British Machine Vision

and Applications, vol. 8, pp. 187-193.

Ravichandran, A., Chaudhry, R., Vidal, R., 2013.

"Categorizing dynamic textures using a bag of

dynamical systems," IEEE Trans. on Pattern Analysis

and Machine Intelligence, vol. 35, no. 2, pp. 342-353,

February.

Soatto, S., Doretto, G., Wu, Y., 2001. Dynamic Textures.

Intl. Conf. on Computer Vision.

Turaga, P., Veeraraghavan, A., Srivastava A. Chellappa

R., 2011. "Statistical Computations on Grassmann and

Stiefel Manifolds for Image and Video based

Recognition," IEEE Trans. on Pattern Analysis and

Machine Intelligence, November.

Vishwanathan, S., Smola, A., Vidal, R., 2007. "Binet-

Cauchy Kernels on Dynamical Systems and Its

Application to the Analysis of Dynamic Scenes," Int'l

J. Computer Vision, vol. 73, no. 1, pp. 95-119.

Vondrick, C., Khosla, A., Malisiewicz T., Torralba, A.,

2013. "HOGgles: Visualizing Object Detection

Features," in Int'l Conf. on Computer Vision, Sydney,

Australia, December.

RGB-SpectralImaging 2016 - Special Session on RBG and Spectral Imaging for Civil/Survey Engineering, Cultural, Environmental,

Industrial Applications

688