
Energy Cost Minimization with Risk Rate Constraint for Internet
Data Center in Deregulated Electricity Markets
Zhongjin Li
1
, Jidong Ge
1
, Chuanyi Li
1
, Hongji Yang
2
, Haiyang Hu
3
and Bin Luo
1
1
State Key Laboratory for Novel Software Technology, Software Institute, Nanjing University, Nanjing, China
2
Centre for Creative Computing (CCC), Bath Spa University, England, U.K.
3
School of Computer, Hangzhou Dianzi University, Hangzhou, China
Keywords: Internet Data Center, Risk Rate Constraint, Energy Cost Minimization, Deregulated Electricity Markets.
Abstract: With the large-scale development of internet data center (IDC), the energy cost is increasing significantly and
has attracted a great deal of attention. Moreover, existing scheduling optimization methods for cloud
computing applications disregard the security services. In this paper, we propose a long-term energy cost
minimization (ECM) algorithm with risk rate constraint for an internet data center in deregulated electricity
markets. First, we formulate the stochastic optimization problem taking the temporal diversity of electricity
price and risk rate constraint into account. Then, an operation algorithm is designed to solve the problem by
Lyapunov optimization framework, which offers provable energy cost and delay guarantees. Extensive
evaluation experiments based on the real-life electricity price demonstrate the effectiveness of proposed
algorithm.
1 INTRODUCTION
Cloud computing supported by the infrastructure
called internet data center (IDC) is a large-scale
distributed computing platform to meet the
skyrocketing demand of online applications and
services. Recently, a cloud and non-cloud storage is
deployed for biomedical scientists to conduct the
performance comparisons, which show that the cloud
system outperforms the non-cloud system on
execution time, consistency, efficiency improvement
(Chang and Wills, 2015). As an IDC typically
comprises thousands of servers, energy consumption
or energy cost is one of the critical problems.
Recently, IDC operators have developed many
scheduling strategies to minimize the energy cost by
exploiting the electricity price dynamics across
geographically distributed regions (Rao et al., 2010,
2011). In the real life, electricity price manifests not
only spatial diversity but also temporal diversity. For
instance, in North America, due to the different power
generation profiles, many electricity markets have
been deregulated in which the electricity prices are
not constant but vary on an hourly or 15-min basis
(Shao et al., 2014).
Besides energy consumption and energy cost,
security is another critical concern for IDC on a wide
range of applications. Nowadays, several recent
works tackle the security problem on clusters (Xie
and Qin, 2006), grid computing (Song et al., 2006),
heterogeneous distributed system (Xie and Qin, 2007;
Tang et al., 2011) and cloud computing (Zeng et al.,
2015; Chang, 2014, 2015; Chang et al., 2015).
Unfortunately, since distributed computing is built to
execute a broad spectrum of unverified user-
implemented applications by a vast number of users,
both applications and users can be sources of security
threats to computing environments (Yurcik et al.,
2004). However, many existing cloud computing
environments have not employed any security
mechanism to counter the security threats (Ali et al.,
2015).
In this paper, we propose an energy cost
minimization (ECM) algorithm for an IDC in an
environment where the electricity price exhibits
temporal diversity and the workload is dynamic. The
security services are incorporated into the tasks
arrived, and the average risk rate constraint of all
executed tasks must be satisfied. The energy cost
minimization framework is shown in Figure 1. First,
all tasks arrived in IDC are enqueued into a FIFO
queue. Then, the workload shaping method is
employed to measure the workload based on the task
itself and security services. Finally, we apply the
Li, Z., Ge, J., Li, C., Yang, H., Hu, H. and Luo, B.
Energy Cost Minimization with Risk Rate Constraint for Internet Data Center in Deregulated Electricity Markets.
DOI: 10.5220/0005851104070418
In Proceedings of the International Conference on Internet of Things and Big Data (IoTBD 2016), pages 407-418
ISBN: 978-989-758-183-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
407

Figure 1: The energy cost minimization framework.
ECM algorithm which based on the Lyapunov
optimization framework to solve the problem. In
ECM algorithm, our purpose is to minimize energy
cost by deciding: 1) how many tasks should be
processed in each time slot; 2) which security levels
should be selected for these tasks; and 3) how many
resources should be provided by IDC.
The main contributions of this paper can be
summarized as follows:
We present an energy cost minimization
algorithm for IDC while incorporating the
security services of application. Furthermore,
the time average risk rate constraint for the
queue system is satisfied.
We exploit the temporal diversity of electricity
price to minimize the energy cost in
deregulated electricity markets by scheduling
workload in a temporal context.
We design a polynomial time complexity
algorithm to solve the problem based on
Lyapunov optimization technique, which can
facilitate energy cost versus delay trade-off for
internet data center.
The rest of this paper is organized as follows.
Section 2 summarizes the related work. Section 3
describes some system models and problem
formulation. Section 4 introduces the algorithm
design and performance analysis. The performance
evaluation approaches and results are conducted in
Section 5. Section 6 concludes this paper and
envisages our future work.
2 RELATED WORK
Security is one of the critical problems in distributed
computing environment. However, only few groups
of researchers investigate the security-driven
scheduling policy from different points of view. Song
et al. (2006) develop three risk-resilient strategies and
a genetic algorithm to provide security assurance in
grid job scheduling. Xie and Qin (2006, 2007) study
a family of dynamic security-aware scheduling
algorithms for homogeneous clusters and
heterogeneous distributed systems. Tang et al. (2011)
design a security-driven scheduling architecture that
can dynamically measure the trust level of each node.
Zeng et al. (2015) introduce a security-aware and
budget-aware workflow scheduling strategy (SABA),
to provide customers with shorter makespan and
security services. Chang (2014) uses business
intelligence as a service in the cloud (BIaaS) to permit
organizations to break the constraints of the desktop.
Then, a revised and improved technique,
organizational sustainability modelling (OSM), is
proposed to consider the application of capital asset
price modelling (Chang et al., 2015).
For IDC service providers, high energy
consumption means enormous electricity cost
budgets. Qureshi et al. (2009) investigate the feature
of electricity price in deregulated electricity markets,
i.e., electricity prices exhibit both temporal and
spatial variations. Rao et al. (2010) study the problem
of minimizing the total electricity cost under multiple
electricity markets environment. Shao et al. (2014)
take the transmission delay into their design
consideration and formulate a mixed-integer
nonlinear programming (MINLP) problem with
coupled constraint. Luo et al. (2014) study an
important energy management problem and propose
a novel two-stage design and the eco-IDC (energy
cost optimization-IDC) algorithm to exploit the
temporal diversity of electricity price. Yu et al. (2014)
propose a risk-constrained decision framework to
achieve the optimal tradeoff between expected energy
cost and operation risk.
A number of recent works introduce new aspects
in better usage of power in data centers. Urgaonkar
et al. (2011) investigate cost reduction opportunities
that arise by the use of uninterrupted power supply
(UPS) units as energy storage devices. Yu et al. (2015)
minimize energy cost by scheduling workload and
battery jointly, which can fully exploit the temporal
diversity of electricity price. Guo et al. (2013)
develop an online algorithm to minimize energy cost
with batteries, which can utilize the temporal
diversity of electricity price.
Liu et al. (2012) consider
server management together with cooling and usage of
renewable energy.
Then, they investigate the problem
of minimizing the long-term energy cost with the
uncertainties in electricity price, workload, renewable
energy generation, and power outage state (Liu et al.,
2015).
However, both energy cost and security are
critical for IDC. Different from the above works, our
research investigates the energy cost minimization
with risk rate constraint for internet data center in
deregulated electricity markets.
IoTBD 2016 - International Conference on Internet of Things and Big Data
408
3 MODELS AND PROBLEM
FORMULATION
In this section, we model an IDC system and
formulate a long-term energy cost optimization
problem. For ease of understanding, we summarize
the major notations and their meanings used in this
paper in Table 1.
3.1 IDC Resource Capacity
We consider a discrete-time system evolving over a
sequence of equal-length time slots. The IDC
resources are quantified in unit of basic resource unit
(Luo et al., 2014). A basic resource unit may include
a number of microprocessor cores, an amount of
memory and so on. Thus, an IDC resource capacity is
in unit of basic resource unit· time slot. When an IDC
receiving service requests, it needs to allocate a
certain amount of resource
)(tR
for them according to
the workload requirement in time slot
t
. We also
assume that there exists
min
R
and
max
R
such that
maxmin
)( RtRR ≤≤
and the scaling time of which can
be negligible related to unit time slot.
Generally, an IDC task can be generally classified
as delay-sensitive, or delay-tolerant (Luo et al., 2014).
In this paper, we focus on the tasks in delay-tolerant
requests which include compute-intensive or data-
intensive jobs, such as scientific computing and data
intensive applications. For example, it is indicated
that Google often has a large number of “ long
duration” jobs running on back-end servers (Mishra
et al., 2010).
3.2 Security Model
Since snooping, alteration, and spoofing are three
common attacks in cloud environments, we consider
three security services (i.e., authentication service,
integrity service and confidentiality service) to guard
against the common threats (Xie and Qin, 2006).
We consider that each task may require three
security services with various security levels. For
example,
i
sl
is the set of security levels of task
i
t
provided by IDC operator, which can be specified as
a K-vector
),...,...,,(
21 K
i
k
iiii
slslslslsl =
, where
k
i
sl
represents the security level of
thk
security service
and
3=K
. An example of security levels of
cryptographic algorithm for confidentiality is shown
in Table 2. For the sake of simplicity, we use letters
a, g and c to represent the authentication, integrity and
confidentiality respectively.
Table 1: Notations.
Symbol Definition
)(tR Resource capacity in time slot
t
;
i
sl
The set of security levels of task
i
t
;
k
i
sl
Security level of
thk
security service;
k
SL
The set of security service;
)(ta The number of tasks arriving at IDC;
)(tb The number of tasks is processed ;
k
i
SW
Security workload;
i
SW
Total security workload of task
i
t
;
i
EW
Execution workload of task
i
t
;
i
W
Total workload of task
i
t
;
)(
k
i
i
slr
Risk rate of the
thk
security service;
)(tr
i
The risk rate of task
i
t
in time slot
t
;
)(tu Average risk rate of tasks;
λ
Average task arrival rate;
)(tC Energy cost of IDC in time slot
t
;
)(tp Electricity price in time slot
t
;
)(tQ Queue backlog in time slot
t
;
)(tZ Virtual queue;
))(( tL Θ Lyapunov function;
))(( tΘΔ Conditional Lyapunov drift.
Table 2: Cryptographic Algorithm for Confidentiality.
Cryptographic
Algorithms
c
sl
: Security
Level
Processing
Rate: KB/ms
SEAL 0.08 168.75
RC4 0.14 96.43
Blowfish 0.36 37.50
Knufu/Khafre 0.40 33.75
RC5 0.46 29.35
Rijndael 0.64 21.09
DES 0.90 15.00
IDEA 1.00 13.50
3.3 Task Arrival and Workload
Shaping
We consider the IDC which has one service queue for
delay-tolerant tasks and denote the corresponding
queue as
)(tQ
which is assumed to operate in a
discrete time-slot manner, i.e.,
,...2,1,0=t , where
)(tQ
represents the queue backlog. In every time slot
t
, we denote the amount of newly arrived tasks as
)(ta
. The variable
)(ta
is the stochastic arrival with
λ
=)}({ taE , and it is assumed to be non-negative.
This process is assumed to be independent of the
Energy Cost Minimization with Risk Rate Constraint for Internet Data Center in Deregulated Electricity Markets
409

current amount of unfinished tasks in the queue
system and has finite second moment. Moreover,
suppose that there exists a maximum
max
A
such that
max
Ata ≤)(
for all time slot
t
. All arriving tasks,
which are computation-intensive, are queued into the
FIFO queue that is shown in Figure 1, and CPU
resource is the bottleneck resource. For simplicity, we
assume that all tasks arrive at the end of each time
slot.
For each task arriving at IDC, it needs security
services to ensure its successful execution. The
security service also introduces some time overhead
to the computing systems. The definitions of time
overhead of
thk
security service can be found in
detail in (Xie and Qin, 2006, 2008). Different from
the time overhead, each security service is inverted
into the security workload which is denoted by:
},{),,( cgkdslFSW
k
i
k
i
kk
i
∈=
(1)
where symbol
k
i
SW
represents the security workload
(in basic resource unit) of
thk
security service and
k
i
d
is the data of task
i
t
to be protected. The function
),( ⋅⋅
k
F
can be induced from (Xie and Qin, 2006), and
we can easily get the following property:
Property 1. The function
}),{)(,( cgkF
k
∈⋅⋅
should
satisfy the following conditions:
If
0=
k
i
sl
or
0=
k
i
d
, then
0)0,( =
k
i
k
slF
or
0),0( =
k
i
k
dF
;
If
kk
slsl
21
=
and
kk
dd
21
<
, then
),(),(
2211
kkkkkk
dslFdslF <
;
If
kk
dd
21
=
and
kk
slsl
21
<
, then
),(),(
2211
kkkkkk
dslFdslF <
;
The three conditions reflect the security service
workload associated with security levels and the
protected data. However, the security overhead of each
authentication service is a constant value which only
depends on the service type. Hence, the security
workload of authentication service is computed by Eq.
(2).
}{),( akslFSW
k
i
kk
i
∈=
(2)
We can also have the same property that
0)0( =
a
F
and
)()(
21
aaaa
slFslF <
when
aa
slsl
21
<
.
Then, the total security workload of task
i
t
is
represented by Eq. (3).
∈
=
},,{ cgak
k
ii
SWSW
(3)
Finally, the workload of task
i
t
is denoted as follows:
iii
SWEWW +=
(4)
where
i
EW
is the execution workload of task
i
t
. So,
different from the existing work, the workload of a
task includes two components.
3.4 Time-average Risk Rate
In this risk rate model, we derive the risk probability
to quantitatively analyze the risk rate for a task
i
t
with
different security levels. We assume that the risk rate
is a function of security levels and the distribution of
the risk for any fixed time interval follows a Poisson
probability distribution. The risk rate model is used
for illustration purpose only. Thus, the task’s risk rate
of the
thk
security service can be presented by an
exponential distribution as follows (Xie and Qin,
2007; Tang et al., 2011):
},,{)),1(exp(1)( cgakslslr
k
i
kk
ii
∈−−−=
λ
(5)
In IDC, the risk coefficient
k
λ
is different from
one to another. The negative exponent indicates that
failure probability grows with the difference
k
i
sl−1
,
where we assume that the maximum security level of
each security service is 1 (e.g. see Table 2). The risk
rate of task
i
t
in time slot
t
can be obtained below by
considering all the security services. Consequently,
we have the following Eq. (6).
∏
∈
−−=
},,{
))(1(1)(
cgak
k
iii
slrtr
(6)
Let
)(tb
represent the amount of tasks processed
by IDC in time slot
t
, and
ttbB
max
∀≥ ),(
denotes the
maximum number of tasks that can be served in a time
slot. As the risk rate of each task is only related to the
security levels, we assume that all tasks served in time
slot
t
have the same security services, and hence the
same of risk rate. Thus, we have
)}(,...,2,1{),()( tbitrtr
i
∈=
(7)
This is the fairness for these tasks served in the same
time slot
t
. Then, we define the average risk rate
u
of the IDC as follows:
)()(
)(
1
lim
1
0
1
0
ττ
τ
τ
τ
rb
b
u
t
t
t
⋅=
−
=
−
=
∞→
(8)
IoTBD 2016 - International Conference on Internet of Things and Big Data
410

where
−
=
1
0
)(
t
b
τ
τ
and
)()(
1
0
ττ
τ
rb
t
⋅
−
=
are the total
number of tasks and risk rates respectively.
Nevertheless, when
∞→
t
, the time-average arrival
rate is equal to the time-average service rate, which is
represented by Eq. (9).
−
=
−
=
∞→∞→
===
1
0
1
0
)(
1
lim)(
1
lim
tt
a
t
ab
t
b
tt
ττ
ττ
(9)
We can also know that
λ
== ataE )}({ . Then, the
Eq. (8) can be rewritten as follows.
)()(
11
lim
1
0
ττ
λ
τ
rb
t
u
t
t
⋅⋅=
−
=
∞→
(10)
Denote the average risk rate of tasks in time slot
t
as
)()(/1)( trtbtu ⋅⋅=
λ
, and then
u
represents the time-
average risk rate of
)(tu
.
3.5 Energy Cost Model
At time slot
t
, IDC operator provides
)(tR
resource
capacity for the current queued tasks according to the
tasks workloads. The power requirement of resource
capacity is denoted as
))(( tRP
. Symbol )(⋅P is the
power function associated with resource capacity. We
assume that the power function is known to IDC, and
there exists a maximum value
max
P
such that
max
PtRP ≤))((
for all time slot
t
. Such power
consumption will in turn incur some monetary cost
for the data center of the form “power × price”. To
also model the fact that each IDC may face different
electricity prices at time slot
t
in deregulated
electricity markets, we denote it as
)(tp
. We assume
that
)(tp
is independent in every time slot
t
and takes
a value in the finite state space. Then, the energy cost
)(tC
of IDC in time slot
t
is computed by Eq. (11).
)())(()( tptRPtC ⋅=
(11)
We define
max
p
as the maximum electricity price
that the IDC can experience. It is easy to see that if
we have
maxmaxmax
pPC ⋅=
, then
max
CtC ≤)(
for all
t
.
3.6 Problem Formulation
In this paper, we are interested in minimizing the
time-average expected energy cost which is
represented as follows.
})({
1
suplim
1
0
−
=
∞→
=
t
CE
t
C
t
τ
τ
(12)
The electricity price
)(tp
is changing in each time
slot. If the IDC processes all the tasks in the queue
)(tQ in spite of the price, it will incur high energy cost
but low service delay. On the contrary, if the IDC
serve the tasks only when the electricity price is low,
then the queue backlog
)(tQ
will increase rapidly,
consequently leading to large unacceptable delay.
Hence, there is a cost-delay tradeoff in conducting the
tasks execution. To balance such a tradeoff, we
require the queue to be stable in the time average
sense, i.e.,
∞<=
−
=
∞→
1
0
)}({
1
suplim
t
QE
t
Q
t
τ
τ
(13)
where
)(tQ
represents the time-average queue
backlog, and the queueing dynamics can be
characterized by Eq. (14).
)(]0),()([)1( tatbtQmaxtQ +−=+
(14)
Condition (14) implies that all tasks arriving at the
queue in IDC will be processed in bounded time. A
larger value
Q
means a longer delay for tasks.
In order to ensure the security of all tasks, the
time-average risk rate must subject to risk rate
constraint, that is
av
uu ≤
, where
av
u
represents a pre-
specified average risk rate constraint. In each time
slot
t
, the IDC operator makes an online decision to
minimize the energy cost under queue stability and
time-average risk rate constraint.
Minimize:
})({
1
suplim
1
0
−
=
∞→
=
t
CE
t
C
t
τ
τ
(15a)
Subject to:
∞<Q
(15b)
av
uu ≤
(15c)
],[)(,)(
)(
1
maxmin
tb
i
i
RRtRtRW ∈≤
=
(15d)
},,{, cgakSLsl
kk
i
∈∈
(15e)
)}(,...,2,1,0{)( tntb ∈
(15f)
Inequality (15d) means that the resource capacity
of IDC in time slot
t
should be equal or more than the
task workload needed to be processed. For Eq. (15e),
there are only limited levels for each security service.
Let
)(tn represent the number of tasks of queue
)(tQ
in time slot
t
, which is the maximum number of tasks
that can be serviced by IDC. Therefore, parameter
)(tb has
)1)(( +tn
choices for the FIFO queue system
in time slot
t
.
Security services are used to prevent the tasks
from tampering maliciously and accessing illegally.
However, if users apply better security services for
Energy Cost Minimization with Risk Rate Constraint for Internet Data Center in Deregulated Electricity Markets
411

tasks, it will incur longer processing time, which will
also result in more cost and larger delay. Hence, users
can select proper risk rate constraint for all the tasks
execution.
4 ALGORITHM DESIGN AND
PERFORMANCE ANALYSIS
In this section, we design an ECM algorithm along
with queue stability and average risk rate constraint
based on the Lyapunov optimization framework
(Georgiadis et al., 2006). This framework allows us
to include energy cost into the Lyapunov drift
analysis, a well-known technique for designing stable
control algorithms. We now highlight the key steps in
deriving ECM and then characterize its performance.
4.1 Algorithm Design
To ensure that the constraint Eq. (15c) is satisfied, we
use a virtual queue
)(tZ
with update equation as
follows:
}0,)()({)1(
av
ututZmaxtZ −+=+
(16)
Specifically, from Eq. (16) it is clear that
av
av
ututZ
ututZmaxtZ
−+≥
−+=+
)()(
}0,)()({)1(
(17)
and hence
−
=
≥+
−
1
0
)(
1
)0()(
t
av
u
t
u
t
ZtZ
τ
τ
(18)
Taking expectations of both sides and using
0)0( =Z
yields
uu
t
tZE
av
≥+
)}({
(19)
It follows from Eq. (19) that if
0/))(( →ttZE
, then
av
uu ≤
. Stabilizing this virtual queue ensures that the
time-average value of
)(tu
is less than or equal to the
time average risk rate constraint, which ensures Eq.
(15c) (Neely, 2010).
Next, we first define the Lyapunov function,
))(( tL Θ , which represent a scalar metric of queue
backlog for reflecting delays of tasks, as follows:
])()([
2
1
)(
2
1
))((
222
tZtQttL +=Θ=Θ
(20)
where
)(tΘ is defined as )](),([)( tZtQt =Θ which can
evolve over slot
,...}2,1,0{∈t
, and
ttL ∀≥ ,0))((Θ
. To
keep the system stable by persistently pushing the
Lyapunov function towards a lower congestion state,
we introduce the Lyapunov drift
))(( tΘΔ
as follows:
)}(|))(())1(({))(( ttLtLEt ΘΘΘΘ −+=Δ
(21)
Eq. (21) is the expected change in the Lyapunov
function over one time slot, given that the current
state in time slot
t
is )(tΘ . Following the Lyapunov
optimization approach (Neely, 2010), we incorporate
the expected energy cost over one time slot, to both
sides of Eq. (21), which leads to drift-plus-penalty
term:
)}(|)({))(( ttCΕVt ΘΘ ⋅+Δ , where control
parameter
0>V
that represents an important weight
on how much the IDC operator emphasizes energy
cost minimization. Such a control decision can be
motivated as follows: we want to make
))(( tΘΔ
small to push queue backlog towards a lower
congestion state, but we also want to make
)}(|)({ ttCΕ Θ
small so that we do not incur large
energy cost expenditure. We thus decide according to
the above weighted sum.
Then, a key derivation step is to obtain an upper
bound on this term. The following lemma defines
such an upper bound for our case.
Lemma 1. For any possible action under constraints
(15b) - (15f) that can be implemented at slot
t
, we
have
)}(|)({)(
)}(|)()({)(
)}(|)({
)}(|)({))((
tutuEtZ
ttbtaEtQ
ttCΕVD
ttCΕVt
av
Θ
Θ
Θ
ΘΘ
−⋅+
−⋅+
⋅+≤
⋅+Δ
(22)
where
)(,)1[(
2
1
)(
2
1
2222 avav
maxmax
uumaxBAD −⋅++⋅=
(23)
Proof. According to Eq. (20), we have
])()1([
2
1
])()1([
2
1
))(())1((
22
22
tZtZ
tQtQtLtL
−++
−+=−+ ΘΘ
(24)
Then, using the fact that for any real number
x
,
22
])0,[( xxmax ≤ , we have
)]()([)(2
)()()()1(
2222
tbtatQ
tbtatQtQ
−⋅+
+≤−+
(25)
In the same way, we get:
IoTBD 2016 - International Conference on Internet of Things and Big Data
412

])([)(2
))(()()1(
222
av
av
ututZ
ututZtZ
−⋅+
−≤−+
(26)
Then,
)}(|])({[)(
)}(|))({(
2
1
)}(|)]()({[)(
)}(|])()({[
2
1
)}(|))(())1(({))((
2
22
tutuEtZ
tutuE
ttbtaEtQ
ttbtaE
ttLtLEt
av
av
Θ
Θ
Θ
Θ
ΘΘΘΘ
−⋅+
−+
−⋅+
+≤
−+=Δ
(27)
As
max
Ata ≤)(
,
max
Btb ≤)(
, and
1)(0 ≤≤ tu
, we have
])(,)1[(
2
1
)(
2
1
)}(|))({(
2
1
)}(|])()({[
2
1
2222
222
avav
maxmax
av
uumaxBA
tutuEttbtaE
−++≤
−++ ΘΘ
(28)
Then, we get
)}(|)({)(
)}(|)()({)())((
tutuEtZ
ttbtaEtQDt
av
Θ
ΘΘ
−⋅+
−⋅+≤Δ
(29)
Now adding
)}(|)({ ttCΕV Θ⋅
to both sides prove the
lemma 1.
Following the design principle of Lyapunov
framework, the underlying objective is to minimize
the upper bound of the drift-plus-penalty term. Rather
than directly minimize drift-plus-penalty term every
slot
t
, our strategy actually seeks to minimize the
bound given in the right-hand-side of (22). This is
done via the framework of opportunistically
minimizing a conditional expectation. Then, our
algorithm finally minimizes the R.H.S of Eq. (22) by
minimizing the following simplified term:
Minimize
)()(
1
)(
)()()())((
)()()()()(
trtbtZ
tbtQtptRPV
tutZtbtQtCV
⋅⋅+
⋅−⋅⋅=
⋅+⋅−⋅
λ
(30a)
Subject to (15d), (15e) and (15f) (30b)
As
)(tQ
, )(tZ and )(tp can be observed at the
beginning of every time slot
t
, there are only three
variables in Eq. (30a), namely
)(tb
, )(tr and )(tR ,
respectively. Nevertheless, if we determine how
many tasks to be processed and which security levels
to be selected for these tasks in time slot
t
, that is if
we determine the parameters
)(tb and )(tr , the total
workload of these tasks can be computed by Eq. (4).
Then, we can calculate how many resources
)(tR
should be provided by IDC. Finally, the value of Eq.
(30a) can be got.
Note that variable
)(tb
and
)(tr
are discrete and
there are three authentication services, seven integrity
services and eight confidentiality services in the real-
world applications (Xie and Qin, 2006). So, there are
k
possibilities for risk rate )(tr in every time slot
t
,
i.e.
984 ××=k
. Furthermore, variable
)(tb
only has
)1)(( +tn
choices for the FIFO queue system in time
slot
t
. Hence, we can use the enumeration method to
minimize Eq. (30a) subjects to constraint (30b).
The pseudo code of ECM algorithm is outlined in
Figure 2. Note that all tasks have the same security
services in time slot
t
. Therefore, for a fixed value
)}(,...,2,1,0{)( tntb ∈
in time slot
t
, we calculate all the
security levels profile and then select the local
optimal profile which can minimize the value of Eq.
(30a) (lines 5-13). Then, we enumerate
)1)(( +tn
possibilities for all the tasks in the queue system to
get access to the global minimization energy cost
(lines 3-18). Finally, the IDC operator processes tasks
according to optimal number of tasks, security levels
profile and required resource and updates the actual
queue
)1( +tQ
and virtual queue )1( +tZ at the end of
time slot
t
(lines 19-20). We can conclude that the
time complexity of ECM algorithm by enumeration
method is
)(knO
in time slot
t
, where )(tnn = , which
is polynomial associated with
)(tn
in current queue
)(tQ .
Considering a fixed
V
, if we do not want to
process any task in time slot
t
, that is
0)( =tb
, we
have
0)( =tR , and then the expression of Eq. (30a) is
zero. As we only minimize the Eq. (30a), the IDC
operator executes the tasks when the value of Eq.
(30a) is negative. It happens when either the
electricity price
)(tp
is low, or the queue
)(tQ
is
already congested in time slot
t
. Therefore, our ECM
algorithm will process tasks in the following
conditions: 1) when the electricity price
)(tp
is low
enough, the IDC operator will catch the chance to
execute more tasks with low risk rate; 2) when the
queue
)(tQ
is congested, tasks must be finished to
guarantee the queue stability.
4.2 Performance Analysis
The performance bounds of ECM algorithm are stated
in the following theorem.
Theorem 1. Assume that the task arrival rate
λ
is
strictly within the network capacity region Λ, and the
Energy Cost Minimization with Risk Rate Constraint for Internet Data Center in Deregulated Electricity Markets
413

ECM algorithm is applied at each time slot
t
. For any
control parameter
0>V
, it generates the time-
average energy cost
C
and queue backlog Q
satisfying that:
V
D
CCE
t
C
t
t
+≤=
−
=
∞→
*
1
0
)}({
1
suplim
τ
τ
(31)
ε
τ
τ
*
1
0
)}({
1
suplim
VCD
QE
t
Q
t
t
+
≤=
−
=
∞→
(32)
where
D
and
ε
are positive constants, and
*
C
is the
theoretical optimal time-average energy cost.
Proof. Since the arrival process is strictly within the
network capacity region, there exists one stationary
randomized scheduling policy that can stabilize the
queue (Neely, 2010), which satisfies the following
properties:
*
)}({ CCE =
τ
(33)
0})({ ≤−
av
uuE
τ
(34)
ε
τ
τ
−≤− )}()({ baE
(35)
For any slot
τ
, by applying Eqs. (33), (34) and (35)
to Eq. (22), we have:
*
)(
)}(|)({))((
CVQD
CΕV
⋅+⋅−≤
⋅+Δ
τε
τ
τ
τ
ΘΘ
(36)
Taking the expectation of Eq. (36) with respect to the
distribution of
)(
τ
Q
and applying the iterative
expectation law, we get
*
)}({
)}({))}(())1(({
CVQED
CEVLLE
⋅+⋅−≤
⋅+−+
τε
τ
τ
τ
ΘΘ
(37)
Summing the series over all time slots
}1,...,1,0{ −∈ t
τ
and using the law of telescoping sums yields:
−
=
−
=
⋅−⋅⋅+≤
⋅+−
1
0
*
1
0
)}({)(
)}({))}0(({))}(({
t
t
QEtCVD
CEVLEtLE
τ
τ
τε
τ
ΘΘ
(38)
Rearranging terms and neglecting non-negative
terms when appropriate, it is easy to show that the
above inequality directly implies the following two
inequalities for all
0>t
:
Vt
LE
V
D
CCE
t
t
))}0(({
)}({
1
1
0
*
Θ
++≤
−
=
τ
τ
(39)
t
LE
VCD
QE
t
t
εε
τ
τ
))}0(({
)}({
1
*
1
0
Θ
+
+
≤
−
=
(40)
where Eq. (39) follows by dividing Eq. (38) by
V
t
,
and Eq. (40) follows by dividing Eq. (38) by
t
ε
.
Algorithm 1: ECM algorithm.
BEGIN
01. Set
∞=minC
to record the minimum energy cost;
02. Use
)(
*
tb
, ),,(
*** cga
slslsl and )(
*
tR to record the
optimal number of tasks, security levels profile and
required resource under minimum energy cost;
03.
for
0)( =tb
to )(tn in time slot
t
04. Set
∞=))(( tbCost
to record the local minimum
energy cost;
05.
for any security levels profile
),,(
cga
slslsl
06. Calculate the total workload
=
)(
1
tb
i
i
W
of
)(tb
tasks according to Eq. (4);
07. Get
)(tR
based on condition constraint (15d);
08. Compute the value
value
of Eq. (30a);
09.
if
))(( tbCostvalue <
10. Set
valuetbCost =))((
;
11. Record
),,(
cga
slslsl
and )(tR ;
12.
end if
13.
end for
14.
if
minCtbCost <))((
15. Set
))(( tbCostminC =
;
16. Update the
)(
*
tb
, ),,(
*** cga
slslsl and )(
*
tR ;
17.
end if
18.
end for
19. IDC operator conduct processing actions according
to
)(
*
tb
, ),,(
*** cga
slslsl and )(
*
tR ;
20. Update actual queue
)1( +tQ
and virtual queue
)1( +tZ when the current time slot
t
ends according to
the Eq. (14) and Eq. (16) respectively.
END
Figure 2: The pseudo code of ECM algorithm.
Taking limits of the above as
∞→t
proves Eqs. (31)
and (32).
Theorem 1 can be understood as follows: If for
any parameter
0>V
, we can use the ECM algorithm
to ensure the drift condition (36) is satisfied on every
time slot, then the time average expected penalty
satisfied Eq. (31) and hence is either less than the
target value
*
C
, or differs from
*
C
by no more than
the value
VD /
, which can be made arbitrarily small
as
V
is increased. However, the time average queue
backlog bound increases linearly in the
V
parameter,
as shown by Eq. (32). This presents a cost-backlog
tradeoff of
)](),/1([ VOVO
. Such a cost-delay tradeoff
allows ECM algorithm to make flexible design
choices according to different application types and
user contexts.
IoTBD 2016 - International Conference on Internet of Things and Big Data
414

5 PERFORMANCE EVALUATION
In this section, we evaluate the performance of the
proposed algorithm based on real-world electricity
prices.
5.1 Experimental Setup
System parameters Suppose that an IDC has
10000=N
servers, and power function
))(( tRP
is we
modelled as follows:
))(())((
3
idle
PtfNtRP +⋅⋅=
α
(41)
In Eq. (41),
α
and
idle
P
are constants determined by
IDC. Specifically,
idle
P
is the average idle power
consumption of a server, and
idle
Ptf +⋅ )(
3
α
gives the
power consumption of a server running at computing
frequency
)(tf
. Then, the resource capacity of the
IDC is
)()( tfNtR ⋅=
(in basic resource unit), where
the computing frequency is in the range [1.2, 3.2]
(Cao and Zhu, 2013). In our experiments, we choose
1.6=
α
and
W100=
idle
P
such that the peak power
consumed by a server is 250W.
The model (41) is
based on the measurements reported in
(Gandhi et al.,
2009;
Yao et al., 2014).
Task workload Suppose that the number of tasks
arrive in each slot
)(ta
follows a Poisson distribution
with parameter 5 and the execution workload follows
a uniform distribution in the range [1000, 4000] (in
basic resource unit). In order to meet the security
requirement of each task, the IDC should process the
security workload. The risk coefficients of three
attacks are set
0.3=
a
λ
,
5.2=
g
λ
and
8.1=
c
λ
,
respectively. For the integrity service and
confidentiality service, the workload function (in
basic resource unit) is devised as follows.
},{,),( cgkdsldslF
kkkkkk
∈⋅⋅=
β
(42)
We can see that Eq. (42) satisfies the property 1.
As to authentication service, the workload function is
represented by Eq. (43).
}{,)( akslslF
kkkk
∈⋅=
β
(43)
For each arrived task, the protected data
k
d
is in
the range [0.1, 1] GB, and
1600=
a
β
, 2400=
g
β
and
800=
c
β
. These parameters are derived and deduced
from (Xie and Qin, 2006)
.
Electricity Price We downloaded the hourly
electricity prices of Palo Alto in real-time electricity
market (Nyiso, 2015), and the time horizon we
consider in this paper is from June 1 to June 30, 2015.
To fully exploit the cost savings due to temporal
power price variations, we would have preferred to
have prices at a time granularity that exhibits high
variability, for example, the length of a time slot is set
to 5 minutes (Qureshi et al., 2009). However, since
we had access to only the hourly prices, we use
interpolation to generate prices at 5-minute intervals
(Yao et al., 2014). Thus, the time horizon in the
evaluations is 8640 slots.
Algorithms in Comparison The following four
algorithms are compared in terms of energy cost and
queue delay in the experiments:
Algo-1: The Lyapunov optimization technique is not
utilized in this algorithm. Thus, arriving tasks are not
queued. It starts to execute tasks when they are
received. Moreover, these tasks are executed without
security services.
Algo-2: This algorithm starts to execute all arriving
tasks when they are received. However, each task
requires security services to ensure its security
execution. Furthermore, all the levels of service are
set to 1.
Algo-3: It uses our proposed ECM algorithm but with
no risk rate constraint, i.e.,
1=
av
u
. Different from
Algo-1 and Algo-2, the arrived tasks are queued in the
IDC, which will be processed when the electricity
price is low or the queue is congested.
Algo-4: This is our ECM algorithm, the purpose of
which is to minimize the total energy cost with risk
rate constraint for IDC.
5.2 Performance Comparison of Four
Algorithms
We fix the parameter
10=V
and
0=
av
u
for Algo-4
and conduct the four algorithms in TEC and average
delay. As shown in Figure 3 (a), we can make the
following observations about TEC: 1) Compared with
Algo-1 and Algo-2 respectively, Algo-3 and Algo-4
have the Lower TEC. This is because Algo-3 and
Algo-4 uses the Lyapunov optimization technique to
minimize the energy cost. The arrived tasks are
queued in the IDC, which can be processed when the
electricity price is low, i.e., the IDC operator can fully
exploit the temporal diversities of electricity price; 2)
Algo-2 exhibits more energy cost than Algo-1. This is
reflected by the fact that each task in Algo-2 requires
security services to ensure its security execution,
which will incur a great amount of security workload
and power demand for IDC (see Section 3.3). There
is the same relationship between Algo-3 and Algo-4.
Energy Cost Minimization with Risk Rate Constraint for Internet Data Center in Deregulated Electricity Markets
415
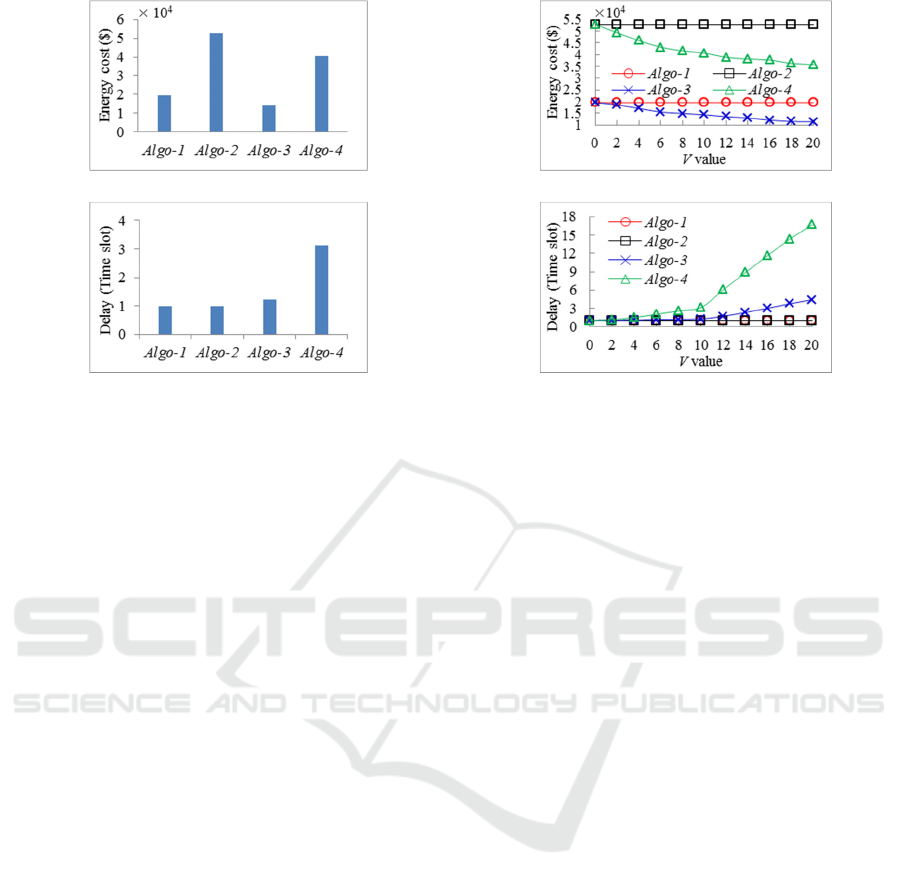
(a) Energy cost
(b) Delay
Figure 3: Energy cost and delay of four algorithms.
As for average delay shown in Figure 3 (b), Algo-
1 and Algo-2 have the same and lowest delay, which
results from the fact that arrived tasks are not queued,
and IDC operator executes these tasks in the same slot
when they are received. The Algo-4 tends to have the
longer average delay due to two reasons that: 1)
arrived tasks in the queue are waiting for low
electricity price; 2) security services result in more
workload while IDC only processes fewer tasks in
one time slot, which increases the length of task
queue. The Algo-3 has no security services but with
task queue, the delay of which is medium.
5.3 Performance Vary under Different
Parameters
Figure 4 illustrates the performance of four
algorithms under varying control parameter
V
. As
Aglo-1 and Aglo-2 are independent of parameter
V
,
we plot them as baselines in contrast with Algo-3 and
Algo-4. The parameter
V
controls the energy-delay
tradeoff of Algo-3 and Algo-4. As shown in Figure 4,
given
0=
av
u
, the TEC drops and the time-average
delay grows as
V
goes from 0 to 20. The TEC of
Algo-1 and Algo-2 are always larger than Algo-3 and
Algo-4, respectively, while they are equal when
0=V
. This is because security services incur lots of
energy cost, and we only care about the queue delay
when parameter
V
is set to 0. Note that energy cost
falls quickly at the beginning and then tends to
descend slowly while the time-averaged queue
backlog grows linearly with
V
. This finding confirms
(a) Energy cost
(b) Delay
Figure 4: Energy cost and delay under different
V
.
the
)](),/1([ VOVO
energy-delay tradeoff as captured
in Eqs. (31) and (32). Particularly, there exists a spot
of
V
(e.g.,
10=V
), beyond which increasing
V
leads
to marginal energy conservation yet consistently
growing delays.
5.4 Impact of Risk Rate Constraint
For purpose of revealing the impact of risk rate
constraint of our ECM algorithm, we fix
10=V
and
vary
av
u
from 0.1 to 1. The performance effects of
varying risk rate constraint are reported in Figure 5. It
can be seen that the TEC and delay become lower as
risk rate
av
u
increases. This phenomenon can be
explained as follows: given a large risk rate
constraint, the workload of security service is small
according to Eqs. (1) and (2). Then, we need less
electricity energy to execute the arrived tasks. What
is more, The IDC operator can process more tasks in
one time slot under the same computing resource that
leads to lower average delay. Overall, though larger
risk rate constraint will reduce the TEC and delay, the
tasks may experience more threats and attacks when
being executed in IDC.
5.5 Impact of Three Risk Coefficients
As mentioned in Section 3.4, the risk rate is highly
correlated with the risk coefficient. This section is
focused on the performance impact of the three risk
coefficients on our ECM algorithm. We fix
V
to be 10
and use shortening Authe_only, Integ_only and
Confi_only to represent authentication service only,
IoTBD 2016 - International Conference on Internet of Things and Big Data
416

(a) Energy cost
(b) Delay
Figure 5: Energy cost and delay under different risk rate
constraints.
integrity service only and confidentiality service only,
respectively. Authe_only means that there is only
authentication service for tasks, and this is the same
interpretation with other two shortenings.
The simulation results are given in Figure 6 for
three risk coefficients. Overall, the Confi_only
achieves the lowest TEC and delay, Authe_only has
the medium performances and Integ_only performs
the worst. This can be explained by the fact that we
set
gac
βββ
<<
, and a larger parameter
β
will lead
to more security workload. We can also see from
Figure 6 that the three curves are higher slope when
parameter
},,{,5.1 cgak
k
∈≤
λ
, beyond which curves
become flat. The explanation is that the risk rate
changes dramatically when the risk coefficient varies
in a small range in terms of Eq. (5), then the TEC and
delay change with the same pace. In a word, different
risk coefficients make different impacts on our energy
cost minimization framework.
6 CONCLUSION AND FUTURE
WORK
In this paper, we propose a long-term energy cost
minimization (ECM) algorithm for an internet data
center in deregulated electricity markets. We
formulate the stochastic optimization problem taking
the temporal diversity of electricity price and risk rate
constraint into account. Then, an operation algorithm
is designed to solve the problem by Lyapunov
(a) Energy cost
(b) Delay
Figure 6: Impact of three risk coefficients.
optimization framework, which offers provable
energy cost and delay guarantees.
As a future work, we are going to consider some
new aspects in better usage of power in IDC, such as
renewable energy, energy storage, battery and so on.
We also plan to exploit spatial variations in the
workload arrival process and the power prices to
reduce energy cost for IDC.
ACKNOWLEDGEMENTS
This work was supported by the National 863
Program (2015AA01A203), the National Natural
Science Foundation, China (No.61572251,
61272188, 61572162), the Natural Science
Foundation of Jiangsu Province (No.BK20131277),
the Fundamental Research Funds for the Central
Universities, the Open Foundation of State Key
Laboratory for Novel Software Technology of
Nanjing University (KFKT2014B15). Jidong Ge is
the corresponding author.
REFERENCES
Ali, M., Khan, S.U., Vasilakos, A.V., 2015. Security in
Cloud Computing: Opportunities and Challenges,
Information Science, 305, 357-383.
Cao, F., Zhu, M.M., 2013. Energy-aware Workflow Job
Scheduling for Green Clouds. 2013 IEEE International
Conference on Green Computing and Communications
and IEEE Internet of Things and IEEE Cyber, Physical
and Social Computing, pp. 232-239.
Energy Cost Minimization with Risk Rate Constraint for Internet Data Center in Deregulated Electricity Markets
417

Chang, V., 2014. The Business Intelligence as a Service in
the Cloud. Future Generation Computer Systems, 37,
512-534.
Chang, V., 2015. Towards a Big Data System Disaster
Recovery in a Private Cloud. Ad Hoc Networks, 1-18.
Chang, V., Walters, R.J., Wills, G.B., 2015. Organisational
Sustainability Modelling-An Emerging Service and
Analytics Model for Evaluating Cloud Computing
Adoption with Two Case Studies, International Journal
of Information Management.
Chang, V., Wills, G., 2015. A model to compare cloud and
non-cloud storage of Big Data, Future Generation
Computer Systems.
Gandhi, A., Harchol-Balter, M., Das, R., Lefurgy, C., 2009.
Optimal Power Allocation in Server Farms.
Proceedings of the Eleventh International Joint
Conference on Measurement and Modeling of
Computer Systems, SIGMETRICS/Performance 2009,
pp. 157-168.
Georgiadis, L., Neely, M.J., Tassiulas, L., 2006. Resource
Allocation and Cross-Layer Control in Wireless
Networks. Foundations and Trends in Networking.
Liu, Z., Chen, Y., Bash, C., Wierman, A., Gmach, D.,
Wang, Z., Marwah, M., Hyser, C., 2012. Renewable
and Cooling Aware Workload Management for
Sustainable Data Centers. Proceedings of the 2012
ACM SIGMETRICS International Conference on
Measurement and Modeling of Computer Systems,
SIGMETRICS 2012, pp. 175-186.
Liu, Z., Lin, M., Wierman, A., Low, S.H., Andrew, L.L.H.,
2015. Greening Geographical Load Balancing.
IEEE/ACM Transactions on Networking, 23 (2), 657-
671.
Luo, J., Rao, L., Liu, X., 2014. Temporal Load Balancing
with Service Delay Guarantees for Data Center Energy
Cost Optimization. IEEE Transactions on Parallel and
Distributed Systems, 25, 775-784.
Mishra, A.K., Hellerstein, J.L., Cirne, W., Das, C.R., 2010.
Towards Characterizing Cloud Backend Workloads:
Insights from Google Compute Clusters. SIGMETRICS
Performance Evaluation Review, 37 (4), 34-41.
Neely, M. J., 2010. Stochastic Network Optimization with
Application to Communication and Queueing Systems.
Synthesis Lectures on Communication Networks,
Morgan & Claypool publishers.
Nyiso, http://www.nyiso.com/, 2015.
Qureshi, A., Weber, R., Balakrishnan, H., Guttag, J.,
Maggs, B., 2009. Cutting the Electric Bill for Internet-
Scale Systems. Proceeding of ACM SIGCOMM,
pp.123-134.
Rao, L., Liu, X., Ilic, M.D., Liu, J., 2011. Distributed
Coordination of Internet Data Centers under
Multiregional Electricity Markets. Proceeding of IEEE,
100 (1), 269-282.
Rao, L., Liu, X., Xie, L., Liu, W., 2010. Minimizing
Electricity Cost: Optimization of Distributed Internet
Data Centers in a Multi-Electricity-Market
Environment. IEEE INFOCOM, pp. 1-9.
Shao, H.J., Rao, L., Wang, Z., Liu, X., Wang, Z.B., Ren,
K., 2014. Optimal Load Balancing and Energy Cost
Management for Internet Data Centers in Deregulated
Electricity Markets. IEEE Transactions on Parallel and
Distributed Systems, 25, 2659-2669.
Song, S., Hwang, K., Kwok, Y.K., 2006. Risk-resilient
Heuristics and Genetic Algorithms for Security-assured
Grid Job Scheduling. IEEE Transactions on
Computers, 55 (6), 703-719.
Tang, X., Li, K., Zeng, Z., Veeravalli, B., 2011. A Novel
Security-driven Scheduling Algorithm for Precedence
Constrained Tasks in Heterogeneous Distributed
Systems. IEEE Transactions on computers, 60 (7),
1017-1029.
Urgaonkar, R., Urgaonkar, B., Neely, M.J.,
Sivasubramaniam, A., 2011. Optimal Power Cost
Management Using Stored Energy in Data Centers.
Proceedings of the 2011 ACM SIGMETRICS
International Conference on Measurement and
Modeling of Computer Systems, SIGMETRICS 2011,
pp. 221-232.
Xie, T., Qin, X., 2006. Scheduling Security-Critical Real-
Time Applications on Clusters. IEEE Transactions on
Computers, 55 (7), 864-879.
Xie, T., Qin, X., 2007. Performance Evaluation of a New
Scheduling Algorithm for Distributed Systems with
Security Heterogeneity. Journal of Parallel and
Distributed Computing, 67 (10), 1067-1081.
Xie, T., Qin, X., 2008. Security-aware Resource Allocation
for Real-Time Parallel Jobs on Homogeneous and
Heterogeneous Clusters. IEEE Transactions on
Parallel and Distributed Systems, 19 (5), 682-697.
Yao, Y., Huang, L.B., Sharma, A.B., Golubchik, L., Neely,
M.J., 2014. Power Cost Reduction in Distributed Data
Centers: A Two-Time-Scale Approach for Delay
Tolerant Workloads. IEEE Transactions on Parallel
and Distributed Systems, 25, 200-211.
Yu, L., Jiang, T., Cao, Y., 2015. Energy Cost Minimization
for Distributed Internet Data Centers in Smart
Microgrids Considering Power Outages. IEEE
Transactions on Parallel Distributed System, 26 (1),
120-130.
Yu, L., Jiang, T., Cao, Y., Qi, Q., 2015. Joint Workload and
Battery Scheduling with Heterogeneous Service Delay
Guarantees for Data Center Energy Cost Minimization.
IEEE Transactions on Parallel and Distributed
Systems, 26, 1937-1947.
Yu, L., Jiang, T., Cao, Y., Zhang, Q., 2014. Risk-
constrained Operation for Distributed Internet Data
Centers in Deregulated Electricity Markets. IEEE
Transactions on Parallel and Distributed Systems, 25
(5), 1306-1316.
Yurcik, W., Meng, X., Koenig, G., Greenseid, J., 2004.
Cluster Security as a Unique Problem with Emergent
Properties. Fifth LCI International Conference on
Linux Clusters: The HPC Revolution 2004.
Zeng, L.F., Veeravalli, B., Li, X.R., 2015. SABA: A
Security-aware and Budget-Aware Workflow
Scheduling Strategy in Clouds. Journal of Parallel and
Distributed Computing, 75, 141-151.
IoTBD 2016 - International Conference on Internet of Things and Big Data
418
