
Towards a Temporal Extension to OWL 2: A Study based on tOWL
Language
Deborah Mendes Ferreira and Flavio de Barros Vidal
Department of Computer Science, University of Brasilia,
C.P. 4466, Brasilia - DF, 70910-900, Brazil
Keywords:
Semantic Web, Description Logics, OWL, tOWL, Decidability.
Abstract:
The Semantic Web is becoming fundamental in the Web. The amount of data available in the Web is increasing
in great proportions, it is very important to find ways to deal with this trend. The Semantic Web can help with
this, by giving meaning to this data in a way that machines can understand what information it contains
and automatically process it. In this paper we present a study about the compatibility between the latest
version of the Web Ontology Language (OWL 2) and the Temporal Web Ontology Language (tOWL), based
on the first version of OWL. We analyze which constructs of tOWL can be used and modified into OWL 2
maintaining decidability aspects. The current version of OWL does not have resources to represent complex
time information and the main contribution of this work is a new proposal to represent time in OWL 2.
1 INTRODUCTION
One of the biggest obstacle to provide better support
for Web users is the fact that a large part of the Web
content is not accessible by machines (Berners-Lee
et al., 2001). There are tools capable of collecting
texts, separating it in parts, verifying its orthography
and counting words. However, regarding the interpre-
tation of phrases and extracting useful information for
the users, the current tools are very limited (Staab and
Studer, 2013). To be able to understand the content
of information contained in the Web, machines and
humans need to share some understanding of the real
world, i.e, we need to be able to represent the world
or parts of the world inside the machine.
The Semantic Web has several tools that provide
aid for machines to understand the meaning of texts
contained in the Web, optimizing the communication
between humans, machines, as well as communica-
tion between humans and machines. Using Semantic
Web tools we can represent real aspects of the world
inside the computer and reason with that representa-
tion (Davis et al., 1993).
When representing the world, we want this repre-
sentation to be as close to reality as possible to avoid
making false assumptions about the world. To be
able to do this, we also need to be capable of rep-
resenting time. Time is an important aspect of human
life. Many environments require temporal awareness,
one known example is air traffic control, each air-
craft needs to follow a strict schedule to avoid any
incidents. Therefore, time should also be part of real
world representations.
The Web Ontology Language (OWL) is the offi-
cial standard for representing ontologies in the Se-
mantic Web (Group et al., 2009), with this lan-
guage we can represent several aspects of the world
inside computers, but not complex time informa-
tion. The underlying semantics of this language is
based on a Description Logics (DL) fragment called
SR OI Q (Horrocks et al., 2006). This fragment has
been proved to be decidable, that means we can rea-
son with our world representation, finding implicit
knowledge from it and verifying its consistency.
The Temporal Ontology Language (tOWL) (Milea
et al., 2012) is a temporal language built as an exten-
sion of the first version of OWL. With tOWL we can
represent complex aspects of time, such as points in
time and intervals. This language adds Concrete Do-
mains to OWL, making it possible to use Concrete
Domains predicates and datatypes, but limiting the
expressiveness of the language to avoid undecidabil-
ity (Baader and Hanschke, 2011).
In this paper we perform a study on the compat-
ibility between tOWL and OWL 2, verifying which
structures of tOWL are compatible with OWL 2 and
which ones need some modification to keep decidabil-
ity. The first version of OWL has been very success-
Ferreira, D. and Vidal, F.
Towards a Temporal Extension to OWL 2: A Study based on tOWL Language.
In Proceedings of the 12th International Conference on Web Information Systems and Technologies (WEBIST 2016) - Volume 2, pages 227-234
ISBN: 978-989-758-186-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
227

ful, but lacked several important elements for ontol-
ogy modelers (Grau et al., 2008a). One of these el-
ements is qualified cardinality restriction. With this
structure we can represent not only cardinality, limit-
ing the number of elements that a property can take,
but we can also qualify this cardinality, limiting the
type of elements a property can take. This structure
is added to OWL 2, however, since tOWL is based on
OWL 1, we can’t use this structure with tOWL.
As a result of this study, we present modifica-
tions to the tOWL language, allowing it to have the
expressiveness of OWL 2 without compromising the
decidability of the language. If both languages have
the same expressiveness, we can use all OWL 2
constructs, including qualified cardinality restriction,
next to tOWL constructs, providing a temporal exten-
sion for OWL 2.
Since OWL 2 does not use Concrete Domains, the
use of tOWL structures together with OWL 2 could
lead to undecidability. We modify some of the exis-
tents OWL 2 constructs in such a way that we can
add the temporal constructs from tOWL, maintain-
ing decidability at the same time. We present a new
layer to tOWL, replacing the Layer of Concrete Do-
mains. This new layer acts as a glue between tOWL
and OWL 2.
This paper is organized as follows: Section 1
presented the introduction for this work. Section 2
presents a theoretical background for this study, pre-
senting a short introduction on Description Logics,
OWL 2 and tOWL. Section 3 presents the modifi-
cations and adaptations that were made into tOWL,
making it compatible with OWL 2. Section 4 presents
an application for this modified version of tOWL next
to OWL 2. At Section 5 we present the conclusion for
this work and possible future work.
2 BACKGROUND
This Section presents some definitions for the De-
scription Logics SR OI Q , which is the basis for the
semantics of OWL 2. We also present some of OWL
2 principles and the tOWL language.
2.1 SR OI Q
Description Logics (Baader and Nutt, 2003) is a
name given to a family of formalism from Knowl-
edge Representation that represents concepts from a
domain and uses these concepts to specify proper-
ties of objects and individuals that are in this do-
main. A Knowledge Representation system provides
the resources to define knowledge bases, reason about
its content and also manipulate it (McGuinness and
Borgida, 1995).
A knowledge base usually contains two elements,
the TBox and the ABox (Kr
¨
otzsch et al., 2012). The
TBox presents the vocabulary of the application do-
main and the ABox contains assertions about the in-
dividuals named according to the vocabulary. The
vocabulary is composed by concepts (or classes) and
roles (or properties), which denotes the set of individ-
uals and express binary relations between such indi-
viduals, respectively.
There are many fragments for Description Logics
and they are named according to the allowed opera-
tors. The OWL 2 semantics (Motik et al., 2009b) is
based on the fragment SR OI Q of Description Log-
ics, where S is for the AL (attributive language, a ba-
sic fragment for DL) with C (complex concept nega-
tion), R is for complex role inclusion axioms, O is
for nominals, I is for inverse properties and Q is for
qualified cardinality restrictions.
Formally, each DL ontology is based on three fi-
nite set of symbols, a set N
I
of individual names, a set
N
C
of concept names and a set N
R
of roles names. The
set of roles expressions R is defined by the following
grammar (Kr
¨
otzsch et al., 2012) (Eq.1):
R ::“ U | N
R
| N
´
R
(1)
where U is the universal role and N
´
R
is the inverse
of N
R
.
The set of concept expressions C is defined as:
C ::“N
C
|pC [Cq|pC \Cq| C | J | K |
DR.C | @R.C | ě nR.C | ď nR.C |DR.Sel f | tN
I
u
(2)
The axioms can be defined by Eqs.3, as follow:
ABox : CpN
I
q RpN
I
, N
I
q N
I
« N
I
N
I
ff N
I
T Box : C Ď C C ” C
RBox : R Ď R R ” R R ˝ R Ď R Dis jointpR, Rq
(3)
The fragment S R OI Q has been proved to be de-
cidable (Horrocks et al., 2006), that implies we can
reason with this fragment.
2.2 OWL 2
OWL is the acronym for Web Ontology Lan-
guage (Hitzler et al., 2009a), is a Web Semantic lan-
guage developed to represent knowledge about things,
group of things and relationship between things. It
is used to represent ontologies as a logic based lan-
guage. This implies that the knowledge expressed in
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
228

OWL can be reasoned by software to verify the con-
sistence of the knowledge base and to find new im-
plicit knowledge (Hitzler et al., 2009a).
The basic concepts of OWL are:
• Axioms: Basic expression declarations that can
be true or false. A set of declarations can be con-
sistent when all declarations are true in the same
situation, or inconsistent when it is not possible
to find such situation. The reasoners (Sirin et al.,
2007; Shearer et al., 2008) are tools for OWL that
can automatically compute if a declaration is con-
sequence of others.
• Entities: Elements used to refer to real world ob-
jects (Group et al., 2009). They are atomic con-
cepts of declarations, such as, objects, categories,
relationships, etc. OWL objects are treated as in-
dividuals, categories are treated as classes and re-
lationship are treated as properties. The properties
are divided in object properties, datatype proper-
ties and annotation properties.
• Expressions: Combinations of entities to form
complex descriptions from basic elements. We
can combine entities names into expressions us-
ing constructors. For example, the atomic classes
“animal” and “mammal” can be combined to de-
scribe classes of animals that are mammals. This
new class would be represented in OWL by a class
expression, that could be used in declarations or in
other expressions.
2.3 tOWL
The tOWL (Milea et al., 2012) (Temporal Web Ontol-
ogy Language) is an OWL extension that allows the
communication between machines in contexts includ-
ing temporal information. The tOWL language allows
inferences of implicit knowledge in contexts that need
temporality when a temporal dimension is involved.
This language was developed as an extension of
OWL DL (Motik et al., 2009a), a profile from the first
version of OWL, with addition of the time unit. The
OWL DL fragment considered was S H I N pDq, i.e.,
OWL without the use of nominals, refereed as OWL
DL
´
.
The tOWL implements two aspects of time: tem-
poral infrastructure and change. Temporal infrastruc-
ture refers to the representation of time as intervals or
instants.
Using tOWL, changes can happen in values of
concrete attributes, in relationship between entities
and in transition of states.
The language was developed in three layers: (i)
Layer of Concrete Domains, (ii) Layer of Temporal
Reference and (iii) Layer of 4D Fluents.
2.3.1 Layer of Concrete Domains
This layer allows representation of restrictions using
binary predicates from concrete domains. In tOWL
we can represent feature chains, f
1
... f
n
, composed
with a concrete feature g, creating a concrete feature
path (CFP), which is equivalent to the following com-
position:
f
1
˝ f
2
˝ ... f
n
˝ g, (4)
where n P N. The CFP is added to tOWL as the
construct ConcreteFeatureChain. One example of
such composition would be the abstract feature time
composed with the concrete feature start, in the fol-
lowing manner:
time ˝ start. (5)
This construction denotes the beginning of a point
in an interval. Table 1 summarizes the semantics in-
troduced for this layer, with the abstract syntax pro-
posed for the tOWL constructs.
2.3.2 Layer of Temporal Reference
This layer presents timepoints, relationships between
timespoints and intervals. The intervals are defined
using the predicate of concrete domain ă and two
concrete features, start and end, to define that the
beginning of an interval must be strictly smaller than
the end of the interval, as described in Eq.6.
ProperInterval ” Dpbegin, endq. ă (6)
2.3.3 Layer of 4D Fluents
This layer presents a perdurantist view of individuals,
allowing representation of complex temporal aspects,
as state transitions in processes. Table 2 presents the
axioms of TBox corresponding to the timeslices/flu-
ents layer.
The language tOWL is limited in expressiveness
compared to OWL 2. It is based on the frag-
ment S H I N pDq while OWL 2 uses the fragment
SR OI Q . Thus, several constructs that are available
for OWL 2 cannot be used with tOWL.
One of the main innovations of OWL 2 is the ad-
dition of qualified cardinality restriction (Grau et al.,
2008a). With this construct we can represent sen-
tences such as “this airplane has 108 seats of the type
economic class and 48 seats of the type first class”.
That means we can add not only cardinality to prop-
erties, we can also qualify it, this is not possible in
tOWL and it is fundamental for the development of
several ontologies (Horrocks et al., 2006).
Towards a Temporal Extension to OWL 2: A Study based on tOWL Language
229

Table 1: Semantics for the Layer of Concrete Domains (Milea et al., 2012).
tOWL abstract syntax Theoretical Model semantics
ConcreteFeatureChain( f
1
f
2
... f
n
g) tpa
1
, bq P ∆
I
ˆ ∆
D
| D!a
2
P ∆
I
, ..., D!a
n`1
P
P ∆
I
^ ^ D!b P ∆
D
: pa
1
, a
2
q P f
I
1
, ...
pa
n
, a
n`1
q P f
I
n
^ g
I
pa
n`1
q “ bu.
dataSomeValuesFrompu
1
u
2
p
d
q tx P ∆
I
| D!q
1
P ∆
D
, D!q
2
P ∆
D
:
u
I
1
pxq “ q
1
^ u
I
2
pxq “ q
2
^ pq
1
, q
2
q P p
I
d
u.
dataAllValuesFrompu
1
u
2
p
d
q tx P ∆
I
| @q
1
P ∆
D
, @q
2
P ∆
D
:
u
I
1
pxq “ q
1
^ u
I
2
pxq “ q
2
^ pq
1
, q
2
q P p
I
d
qu.
Table 2: tOWL axioms for the Layer of 4D Fluents (Milea et al., 2012).
Constructs tOWL 4dFluents tOWL Axioms in OWL-DL
´
Class(TimeSlice) Dtime.Interval [ p“ 1 timeq [ DtimeSliceOf.
pTimeSlice \ Interval \ rdfs:Literalq[
p“ 1 timeSliceOfq
Class(Interval) Dpstart, endq. ď [Dstart.dateTime[
[Dend.dateTime [ p“ 1 startq [ p“ 1 endq
Class(FluentProperty) FluentProperty < rdf:Property
Class(FluentObjectProperty) FluentObjectProperty < FluentProperty
Class(FluentDatatypeProperty) FluentDatatypeProperty < FluentProperty
Property(timeSliceOf) ě 1 timeSliceOf Ď TimeSlice
J Ď @timeSliceOf. pTimeSlice \ Interval\
\rdfs:Literalq
Property(time) ě 1 time Ď TimeSlice
J Ď @time.Interval
Property(start) ě 1 start Ď Interval
J Ď @start.dateTime
Property(end) ě 1 end Ď Interval
J Ď @end.dateTime
Furthermore, OWL 2 also adds the complex roles
inclusion and a richer set of datatypes compared to
the first version of OWL (Grau et al., 2008a).
Unfortunately, we cannnot simply use tOWL with
OWL 2 because of the undecidability added by the
concrete domains constructs used in tOWL (Milea
et al., 2012). To be able to use tOWL with the level
of expressiveness of OWL, some modifications are
needed.
3 COMPATIBILITY OF TOWL
CONSTRUCTS WITH OWL 2
In this Section, we describe the main constructs
changes made in tOWL to achieve compatibility with
OWL 2.
3.1 Layers
OWL 2 does not allow the full use of concrete do-
mains since the use of concrete domains next to nom-
inals can lead to undecidability (Milea et al., 2012).
The current version of OWL (Hitzler et al.,
2009a) uses datatype maps to add concrete roles and
datatypes to the language, unlike the first version,
which used a simplified version of concrete domains
to represent datatypes (Grau et al., 2008b).
To be able to use tOWL as OWL 2 constructs, we
need to make a few modifications in the language,
specially in the aspects related to Concrete Domains.
Considering this, we propose the following layers
as an extended version of tOWL: Layer of Concrete
Path, Layer of Temporal Reference and Layer of 4D
fluents, as described in Figure 1.
The Layer of Concrete Path adds constructs that
are equivalent to the ones in the tOWL Layer of
Concrete Domains using constructs that are sim-
ilar to ones already present in OWL 2, not af-
fecting the decidability of the language. All the
constructs of the Layer of Concrete Domains were
removed from the original tOWL and the fol-
lowing ones are added: DatatypePropertyChain
and SubDatatypePropertyOf. These constructs
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
230

Figure 1: Layers of tOWL compatible with OWL 2.
will be explained in detail in the next subsec-
tion. The constructs dataSomeValuesFrom and
dataAllValuesFrom already have a version in OWL
2, so we don’t need to add this constructs to this layer,
as shown in Table 3. In the Table 3 u
1
and u
2
are con-
crete feature chains, p
d
is a concrete domain predi-
cate, S
1
... S
n
are concrete roles and dr is a data range.
The Layer of Temporal Reference defines the in-
tervals and points in time, we add to this layer the
Allen’s 13 intervals relations (Allen, 1981) to estab-
lish relations between intervals, tOWL also imple-
ments these relations, but the details were not made
available. An interval i is considered a pair of real
ordered numbers, px
1
, x
2
q, with x
1
ď x
2
. Considering
this, an interval can be defined as shown in Eq.7.
Interval “ pstart ď endq (7)
A pair of intervals groups two intervals as first and
second:
Pair “ D first.Interval [ Dsecond.Interval (8)
The Layer of 4D Fluents adds temporality for in-
tervals, including the concept of fluents defined as
properties which the value can change with time. This
layer also adds the concept of timeslides, timeslices
are intervals when a certain fluent is valid. For ex-
ample, an aircraft can have as a fluent the property of
phase of the flight, and we could have a timeslice for
the interval when this aircraft is on the phase of taking
off. This layer does not need any modification to be
compatible with OWL 2. These constructs have been
already presented in Table 2.
3.2 DatatypePropertyChain and
SubDatatypePropertyOf
One of the reasons the Layer of Concrete Domains
was added into tOWL was to allow the use of the Con-
crete Feature Path (CFP). An example of a CFP was
presented in Equation 4 and is represented in tOWL
as the construct ConcreteFeatureChain. This con-
struct is fundamental for the tOWL language, since
we need composition of features to represent con-
structs related to time, such as the one shown in Equa-
tion 5. The tOWL language uses features, i.e., func-
tional properties that can assume abstract or concrete
values. Features are also part of Concrete Domains.
Since OWL 2 does not use Concrete Domains, we
are not able to use elements from Concrete Domains,
such as concrete and abstract features. Since we can-
not use features, we are also not able to represent
CFP as defined in tOWL. However, in OWL 2, we
have similar definitions to features: concrete roles and
abstract roles (Hitzler et al., 2009b). Abstract roles
connects individuals to individuals and concrete roles
connects individuals to data values, i.e., elements that
have datatypes.
To make this glue between tOWL and OWL 2, we
need to be able to represent Concrete Feature Path us-
ing elements that are present in OWL 2.
In OWL 2, we can have the composition of ab-
stract roles, as shown in Table 4, where R
1
... R
n
are
concrete roles, with n P N.
Based on this construct, which already ex-
ists in OWL 2, we can create compatibility with
tOWL presenting a new construct with an equiv-
alent function to ConcreteFeatureChain: the
DatatypePropertyChain. This structure creates the
compatibility between tOWL and OWL 2, thereby, we
do not have to rely on Concrete Domains to represent
composition of abstract roles and concrete roles. We
can create compositions of n abstract roles and one
concrete role, as shown in Table 5.
Using the construct shown in Table 5, we also add
a new construct to increase the expressiveness of the
language: complex role inclusion with concrete roles.
This structure is not present in tOWL, we present this
as an addition to the language to simplify the repre-
sentation of concrete roles. With the expressiveness
of SR OI Q , we can have role axioms as described in
Eq.9.
R
1
˝ R
2
Ď R
3
, (9)
where R
1
, R
2
and R
3
are abstract roles.
Using the construct DataPropertyChain, we can
extend the construct shown in Eq. 9, named Complex
Role Inclusion, to also apply to concrete roles. Ta-
ble 6 introduces a new construct added to tOWL, de-
fined as SubDatatypePropertyOf, where R
1
... R
n
are abstract roles, and S
1
and S
2
are concrete roles.
Having defined this new construct, we can now
create new concrete roles using role composition. It
Towards a Temporal Extension to OWL 2: A Study based on tOWL Language
231

Table 3: tOWL constructs vs OWL 2 constructs.
tOWL Construct OWL 2 Construct
dataSomeValuesFrompu
1
u
2
p
d
q DataSomeValuesFrompS
1
... S
n
drq
dataAllValuesFrompu
1
u
2
p
d
q DataAllValuesFrompS
1
... S
n
drq
Table 4: Composition of abstract roles.
OWL 2 Construct DL Syntax DL Semantics
ObjectPropertyChain(R
1
... R
n
) R
1
˝ R
2
˝ ... ˝ R
n
tpa, bq P ∆
I
ˆ ∆
I
|
Dc P ∆
I
.pa, x
1
q P R
I
1
^ px
1
, x
2
q P
R
I
2
^ ... ^ px
pn´1q
, bq P R
I
n
u
Table 5: Semantics and Syntax of DatatypePropertyChain.
tOWL Construct DL Syntax DL Semantics
DataPropertyChain(R
1
... R
n
S) R
1
˝ R
2
˝ ... ˝ R
n
˝ S tpa, bq P ∆
I
ˆ ∆
D
|
Dc P ∆
I
.pa, x
1
q P R
I
1
^ px
1
, x
2
q
P R
I
2
^ ... ^ px
n´1
, bq P S
I
u
is possible to create a new role to denote the beginning
of an interval, using the composition shown in Eq. 5
combined with Eq.10.
time ˝ start Ď startO f Interval (10)
The same algorithm used to evaluate the compo-
sition of abstract roles can be adapted to evaluate the
concrete feature chain (Horrocks et al., 2006), keep-
ing decidability of the language.
4 CASE STUDY: PHASES OF
FLIGHT
In this section we present an application for the tOWL
version compatible with OWL 2. We propose an on-
tology for representing the phases of an airline flight.
Usually, a flight is divided in the following phases: (i)
take-off, (ii) climb, (iii) en route, (iv) descent and (v)
landing (Seyfarth et al., 2002).
In such an ontology, each flight is connected to
a flight phase in a certain timeslice. The timeslice
represents the interval when such a relation is true,
in this case, the interval when a flight is in a certain
phase.
Figure 2 presents an example for a flight that
is in the stage en route. We have two classes,
Flight and FlightPhase that are both subclass
of Class. We represent a flight of number
TK1041 as iFlight#TK1041, an instance of the class
Flight. Similarly, we present the phase en route as
iEnRoute, a instance of FlightPhase. The con-
structs iFlight#TK10141 TS1 and iEnRoute TS1
are both instances of the class TimeSlice, and
they are connected by the property timeSliceOf to
iFlight#TK1041 and iEnRoute, respectively. Each
timeslice is associate with an interval and since the
flight and the flight phase belong to the same times-
lice, the values of the intervals should be the same.
Using the constructs already presented in OWL 2,
we can represent the fact that the start of iInterval1
should be smaller than the end:
EquivalentClasses(iInterval1
DataAllValuesFrom(start end
DataComparison(Arguments(x y)
leq( x y ))))
However, without extending OWL 2 we cannot
represent a role that is made of a composition of an
abstract role and a concrete role. For example, to cre-
ate a new role that is the start of a interval. This can
be done with the constructs presented in this paper,
creating the role startOfInterval:
SubDatatypePropertyOf(
DataPropertyChain(time start)
startOfInterval)
We can use such a role in this ontology to define
the start of an interval for the timeslice that defines the
relation between flight TK1041 and the flight phase
en route:
DataPropertyAssertion( :startOfInterval
a:iInterval1 "2014-06-12T04:00:00-05:00"
ˆˆxsd:dateTime )
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
232
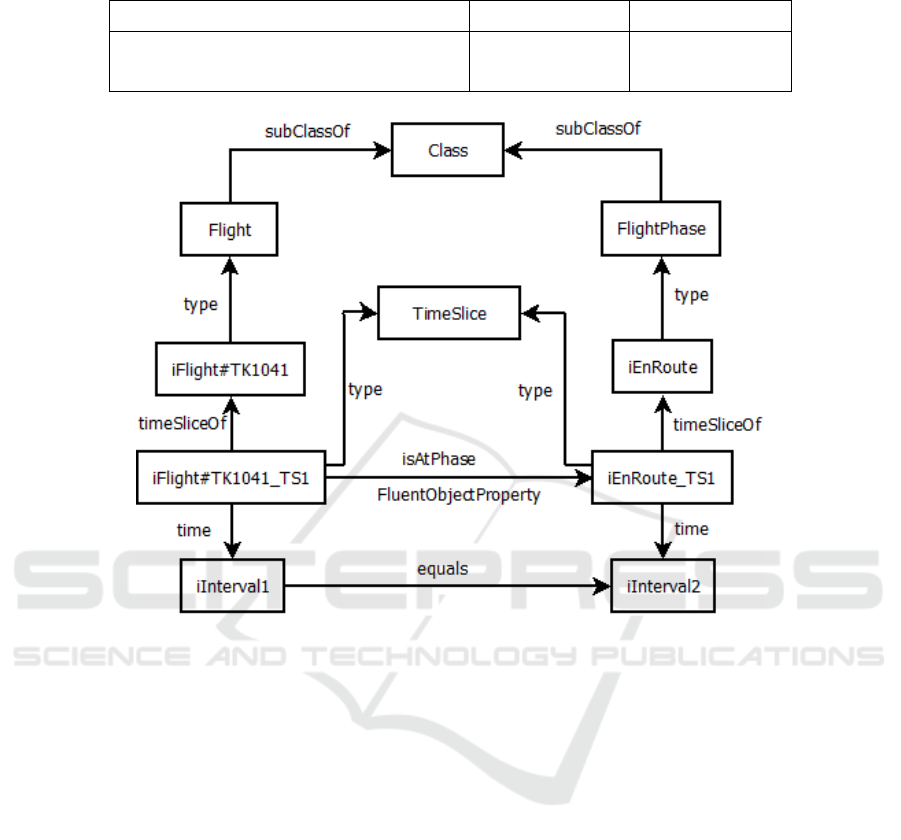
Table 6: Semantics and Syntax of SubDatatypePropertyOf.
tOWL Construct DL Syntax DL Semantics
SubDatatypePropertyOf( R
1
˝ R
2
˝ ... ˝ R
n
˝ R
I
1
˝ R
I
2
˝ ... ˝ R
I
n
˝
DataPropertyChain(R
1
... R
n
S
1
q S
2
) ˝S
1
Ď S
2
˝S
I
1
Ď S
I
2
Figure 2: Application of tOWL for stages of the flight.
In tOWL we don’t have enough expressiveness to
represent the fact that an aircraft can have 108 seats
of the type economic class and 48 seats of the first
class. With the extension shown in this paper, we can
use tOWL with the expressiveness of OWL. There-
fore, we can represent such a statement:
ClassAssertion(
ObjectMaxCardinality( 108 :hasSeats
:EconomicClass ) :iFlight#TK1041 )
ClassAssertion(
ObjectMaxCardinality( 48 :hasSeats
:FirstClass ) :iFlight#TK1041 )
5 CONCLUSION AND FUTURE
WORK
In this paper we presented a study on the compatibil-
ity between construct of the temporal language tOWL
and the Semantic Web language OWL 2. We propose
the addition of constructs that can replace the cause of
incompatibility: concrete domains. Using constructs
that are already in OWL 2, we can adapt tOWL con-
structs in a way that we keep decidability in the lan-
guage.
There are many advantages for adapting tOWL
to OWL 2, we have more expressiveness in the lan-
guage, we can use tools that are only available for the
newest version of OWL and we can be up-to-date with
the current standards from Semantic Web.
For future work, we will implement a reasoner ca-
pable of reasoning with time, adapting reasoners that
already exists for SR OI Q .
REFERENCES
Allen, J. F. (1981). An interval-based representation of tem-
poral knowledge. In IJCAI, volume 81, pages 221–
226.
Baader, F. and Hanschke, P. (2011). A scheme for integrat-
ing concrete domains into concept languages.
Baader, F. and Nutt, W. (2003). Basic description logics. In
Description logic handbook, pages 43–95.
Berners-Lee, T., Hendler, J., Lassila, O., et al. (2001). The
semantic web. Scientific american, 284(5):28–37.
Towards a Temporal Extension to OWL 2: A Study based on tOWL Language
233

Davis, R., Shrobe, H., and Szolovits, P. (1993). What is a
knowledge representation? AI magazine, 14(1):17.
Grau, B. C., Horrocks, I., Motik, B., Parsia, B., Patel-
Schneider, P., and Sattler, U. (2008a). Owl 2: The
next step for owl. Web Semantics: Science, Services
and Agents on the World Wide Web, 6(4):309–322.
Grau, B. C., Horrocks, I., Motik, B., Parsia, B., Patel-
Schneider, P., and Sattler, U. (2008b). Owl 2: The
next step for owl. Web Semantics: Science, Services
and Agents on the World Wide Web, 6(4):309–322.
Group, W. O. W. et al. (2009). tOWLu 2 web ontology
language document overview.
Hitzler, P., Kr
¨
otzsch, M., Parsia, B., Patel-Schneider, P. F.,
and Rudolph, S. (2009a). Owl 2 web ontology lan-
guage primer. W3C recommendation, 27(1):123.
Hitzler, P., Krotzsch, M., and Rudolph, S. (2009b). Foun-
dations of semantic web technologies. CRC Press.
Horrocks, I., Kutz, O., and Sattler, U. (2006). The even
more irresistible sroiq. KR, 6:57–67.
Kr
¨
otzsch, M., Simancik, F., and Horrocks, I. (2012).
A description logic primer. arXiv preprint
arXiv:1201.4089.
McGuinness, D. L. and Borgida, A. (1995). Explaining sub-
sumption in description logics. In IJCAI (1), pages
816–821.
Milea, V., Frasincar, F., and Kaymak, U. (2012). towl: a
temporal web ontology language. Systems, Man, and
Cybernetics, Part B: Cybernetics, IEEE Transactions
on, 42(1):268–281.
Motik, B., Grau, B. C., Horrocks, I., Wu, Z., Fokoue, A.,
and Lutz, C. (2009a). Owl 2 web ontology language:
Profiles. W3C recommendation, 27:61.
Motik, B., Patel-Schneider, P. F., and Grau, B. C. (2009b).
Owl 2 web ontology language direct semantics. W3C
Recommendation, 27.
Seyfarth, A., Geyer, H., G
¨
unther, M., and Blickhan, R.
(2002). A movement criterion for running. Journal
of biomechanics, 35(5):649–655.
Shearer, R., Motik, B., and Horrocks, I. (2008). Hermit:
A highly-efficient owl reasoner. In OWLED, volume
432, page 91.
Sirin, E., Parsia, B., Grau, B. C., Kalyanpur, A., and Katz,
Y. (2007). Pellet: A practical owl-dl reasoner. Web
Semantics: science, services and agents on the World
Wide Web, 5(2):51–53.
Staab, S. and Studer, R. (2013). Handbook on ontologies.
Springer Science & Business Media.
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
234
