
Binary Programing Model to Optimize RSU Placement for
Information Dissemination
Hamid Reza Eftekhari
1
, A. Jalaeian Bashirzadeh
1
and Mehdi Ghatee
1,2
1
Departments of Mathematics and Computer Science, Amirkabir University, Tehran, Iran
2
Intelligent Transportation Systems Research Institute, Amirkabir University of Technology, Tehran, Iran
Keywords: Binary Programming (BP), Location Problem, RSU Placement, Vehicular Communication Systems.
Abstract: Vehicular communication systems are developed not only to increase safety but also for mobility of road
transportation. Roadside units (RSU) are the prominent elements of this technology. This equipment is
installed on roadsides and at intersections to gather traffic information from vehicles and send messages and
alarms to vehicles. Due to the costly implementation and maintenance of this equipment, determining the
number of RSUs and their placement are the important problems. In this paper, we propose a novel binary
programming (BP) model to the placement of RSUs beside a road to maximize information dissemination to
vehicles. This approach makes decisions based on the number of curves, number of on-ramps, accident rate,
weather condition, and cost limitations. The proposed model is applied on Tehran to Pardis Freeway.
According to the computational experiments, four operational phases are obtained to equip the whole road for
information dissemination.
1 INTRODUCTION
To begin with, vehicular communication system
(VCS) is a one of the new technologies in
transportation system for increasing safety and
mobility. This technology includes two primary
elements. Generally put, on-board units (OBUs) are
installed in vehicles in order to gather sensor data,
particularly vehicles' speed and position, and also
send and receive messages to/from other elements.
The next element is a roadside unit (RSU) which can
be installed on roadsides. RSUs can act similar to a
wireless LAN access point and provide
communications with the infrastructure and OBUs of
vehicles through dedicated short-range
communication (DSRC). To elaborate on, RSUs have
two main functionalities: analyzing traffic conditions
based on data received from OBUs and disseminating
travel and safety information to vehicles. We have
appointed the name information dissemination, which
includes the following information to drivers:
Weather condition, in particular rainy, foggy, or
slippery roads;
Road speed limits in curves and intersections;
Alerting vehicles for entering from an on-ramp;
Alerting drivers for decreasing speed or changing
path when an accident is occurring on a road.
The entire area of the road must be completely
covered in order to take advantage of the highest level
of safety in connecting vehicles until the position of
the vehicle is accessible by infrastructure online.
Nevertheless, due to the high cost of equipping the
entire road, we can consider a step by step strategy
according to the importance of each segment of the
road. Because of the limitation of technology, RSU
antennas cover 500m surrounding area. Therefore,
RSUs must be installed every 1km to provide
continuing coverage on a road. It is preferable to
cover part of the road and select some appropriate
locations for installing RSUs because of the high cost
of implementation and lack of market penetration of
vehicular communication system. Besides,
appropriate locations are those with high potential for
disseminating the above information at the right time
(see Fig. 1).
As a case in point, suppose that there are 80
candidates for installing RSU on a freeway with the
length of 80 km; if we want to install 10 RSUs on this
road, then 3.5 10
different modes can be
expected. The subject of this paper is to determine the
optimal placement with the strategy of maximum
nformation dissemination.
Eftekhari, H., Bashirzadeh, A. and Ghatee, M.
Binary Programing Model to Optimize RSU Placement for Information Dissemination.
In Proceedings of the International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2016), pages 227-231
ISBN: 978-989-758-185-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
227

Aslam (Aslam,2011) posed the problem by
obtaining optimal placement of RSUs along freeways
with the goal of minimizing the average time taken
for a vehicle to report an event to a nearby RSU.
Ignoring the importance of alert as well as lack of
consideration of various RSUs in segments, in which
the probability of accidents is higher, are the
disadvantages of this work.
Figure 1: RSUs placement schema.
Cavalcante et al. (Cavalcante,2012) followed the
issue with utilizing genetic and greedy algorithms and
determined the placement of RSUs in urban areas
with the maximum coverage of circulating vehicles.
Rashidi (Rashidi,2012) proposed a method to
calculate the distance between RSUs (gap) on a
freeway based on the data delivery ratio, data
collection update interval, and size of measured data.
Indeed, in these studies, no limitations are
considered for cost; furthermore, the number and
location of RSUs have been calculated on the basis of
limited data buffering. Similar works for the location
and placement can be pointed out for the
determination of locations for RSUs in a city. The
main difference between these works is the
dependence of placement on traffic and network
topology.
Rizk (Rizk,2014) presented a greedy method for
RSU placement in urban and rural roads, which
covered the whole road districts and minimized the
overlap between RSUs.
When all parts of the road are covered by RSUs,
it is possible to inform any vehicles in all parts, which
is called full information dissemination. The aim of
this research is to obtain a greater level of information
dissemination to vehicles according to the restrictions
on the cost of equipment and importance of segments.
The main contribution of this paper is to propose a
novel binary programming model for the placement
of optimal roadside units beside freeways to
maximize information dissemination of the road
based on cost constraint and segment characteristics.
In Section 2, the proposed model is fully introduced.
The computational results and discussion of the
model's performance are presented in Section 3. In the
last section, some conclusions from the research
output and their limitations are reported.
2 MATHEMATICAL MODEL
Informed vehicles that are on the border of coverage
and moving toward the scene of accident act as
temporary RSUs for a certain period of time. These
vehicles make a brief stop and periodically
rebroadcast the safety message to mimic the function
of the conventional roadside units (Mehar,2015).
When an accident occurs, wireless technologies
enable vehicles to share warning messages with other
vehicles using vehicle to vehicle (V2V)
communications. Since RSUs are usually very
expensive to install, authorities limit their number,
especially in the suburbs and areas with large
population, making RSUs a priceless resource in
vehicular environments. Additionally, opting
locations near on-ramps, curves, and hazardous
segments could have more benefits.
In this section, first, a BP model is introduced for
optimizing RSU placement for information
dissemination. In this mathematical model, the
selected locations should have a greater impact on the
objective function optimization. If each RSU covers
within the radius of r and L is the length of the road,
therefore /2 ∗ represents the locations or
segments which are candidates for installing RSUs
and, in fact, some of them should be selected with
regard to the financial restrictions. The proposed
model for RSU placement can be expressed as
follows:
()
M
ax C W y
iii
iI
Subject to
(1)
(1 y ) , , , , ;
1
WW kiy z iI jJ
k
iz kj
j
k
(2)
,;CART iI
iiii
(3)
.,yF
i
Total
iI
(4)
y{0,1}, ;iI
i
(5)
where
is a decision variable for installing RSUs. It
is equal to one if RSU is installed in the i
th
segment;
otherwise, it is zero ─ each road is divided into
VEHITS 2016 - International Conference on Vehicle Technology and Intelligent Transport Systems
228
segments and each segment is equal to 1 km.
Meanwhile, indicates the segment ∈ ;
1,…, and shows weather zone ∈;
1,…,, in which ;
shows the accident rate
of the i
th
segment that should be normalized,
represents the weather indicator of the i
th
segment,
implies the number of the on-ramp in the i
th
segment;
represents the number of road curves in
the i
th
segment;
is the number of all accidents
occurring in the i
th
segment once a year;
suggests
the volume of annual average of daily traffic
(AADT);
reveals a set of segments located in the
j
th
weather zone of a road; and
represents the
weather indicator of the j
th
zone, which is between
zero and one (
∈ 01). Moreover, some other
parameters are defined as follows:
: Total
financial budget for implementing the whole
project;ŋ: Implementation cost for an RSU; : Radius
of an RSU coverage area; : Length of the road; and
: Number of candidate RSU locations. Additionally,
by defining accident rate ─ the average number of
accidents per 1.000.000 km of driving in each
segment, according to (Golembiewski,2011)we
conclude that:
1,000,000
365 2
Q
i
A
i
Vr
i
(6)
Furthermore, objective function (1) optimizes the
location of RSUs, in which maximum information
dissemination to vehicles is achieved. Constraint (2)
reflects that there is just one weather indicator value
for all segments, in particular ∈ zone. Besides,
sending weather condition information is sufficient
just by one RSU to the next zone (1.
Consequently, the influence of one of them is
considered in the objective function. In other words,
the effect of weather indicator should not be
calculated in the segments under one zone.
∈
includes segments within the
th
zone. The
coefficient of
in objective function includes a
number of the on-ramps, curves, and accident rate in
the i
th
segment which is considered in constraint (3).
Constraint (4) ensures that financial limitation is met
and constraint (5) defines the decision variables only
for the segments in which the RSU can be installed.
3 COMPUTATIONAL
EXPERIMENTS
To analyze the impact of the proposed model on
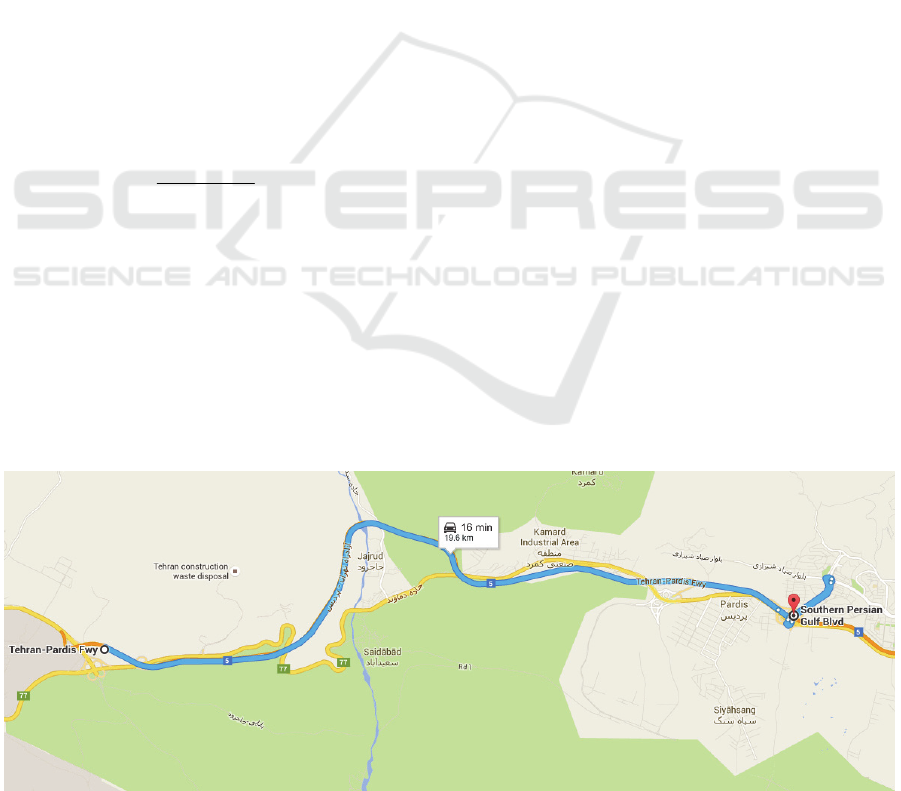
information dissemination, a real case study ─ Tehran
to Pardis Freeway (see Fig. 2) ─ with 11 curves, 13
ramps of about 20 km with 0.37 total average accident
rate, and 4 zones were considered, the full description
of which is presented in Table 1.
In general, for normalizing the accident rates, we
divided each accident rate into the segments on the
maximum value of all accident rates. In addition, the
history of the road for determination weather
indicator during a year was investigated and a number
between 0 and 1 was assigned to each segment; 1
represents an unfavorable weather, such as foggy or
rainy realm on most days or slipping road condition
during cold days, and 0 indicates pleasant weather as
well as road surface condition in that area during a
year. Weather conditions are the same in a number of
adjacent segments (because of the segment size).
Besides, we considered weather zones (z
j
) and
assigned segments within the respective zone.
Considering an RSU throughout a zone was adequate
to warn drivers.
Figure 2: The map of Tehran to Pardis Freeway.
Binary Programing Model to Optimize RSU Placement for Information Dissemination
229
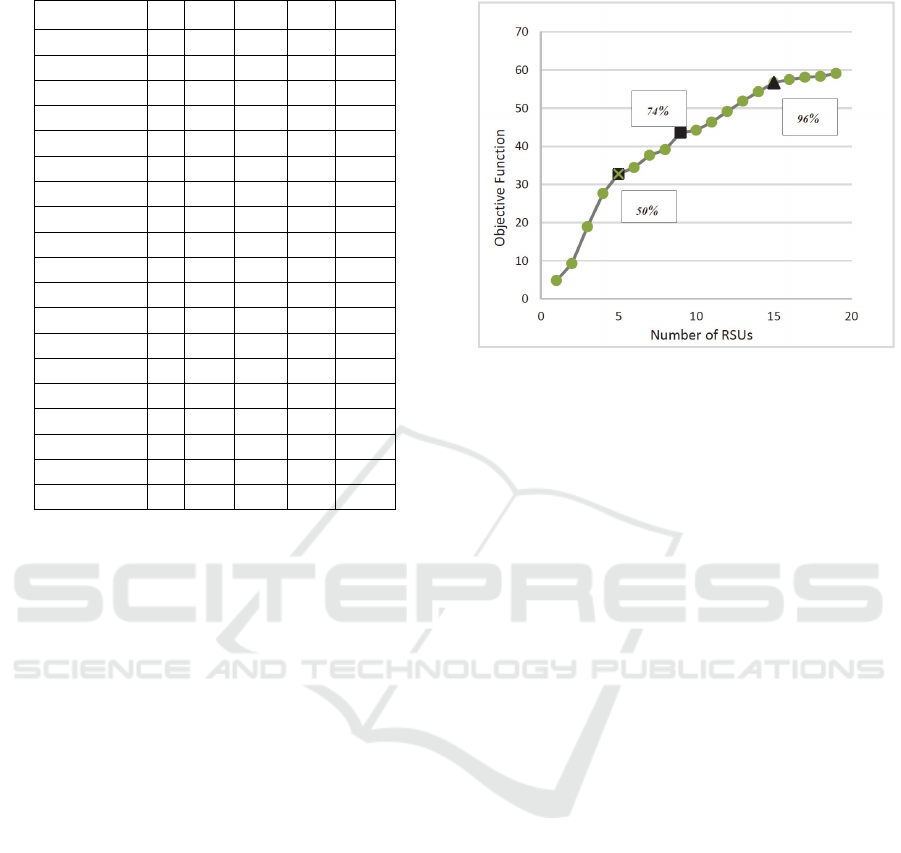
Table 1: Detail of Tehran to Pardis Freeway case study.
Segments (i)
(
) (
)
(
)
(
)
1 1 1 0.41
0.2
2 1 1 0.45
0.2
3 0 2 0.63
0.2
4 1 0 0.3
0.2
5 0 0 0.24
0.2
6 2 1 0.81
0.3
7 1 0 0.4
0.3
8 0 0 0.16
0.3
9 1 0 0.24
0.3
10 0 2 0.67
0.3
11 0 0 0.19
0.7
12 1 0 0.39
0.7
13 0 1 0.27
0.7
14 1 0 0.3
0.5
15 1 2 0.79
0.5
16 0 1 0.1
0.5
17 0 0 0.1
0.5
18 0 1 0.21
0.5
19 1 1 0.55
0.5
Additionally, even though the objective function (1)
includes binary variables, constraint (2) is not a linear
equation. Ergo, to transform this constraint into a
linear one, some new binary variables are defined
(Chen,2010). For example, for
, we can define
,
,
which is equivalent to the multiplication of two
binary variables and related constraints as follows.
These constraint ensure that variable
,
is 1 if and
only if the related two variables are equal to 1;
otherwise, it is zero. For further details, see the related
book (Chen,2010), page 66. As a case in point, if
weather zone
includes
,
, and
segments,
constraint (2) can be transformed into the following
constraints by defining
,
.
:
11
3
WW
z
(7)
.(1 y )
12 11
3
WW
z
(8)
.(1 y y u )
13 11 12 11,12
3
WW
z
(9)
2u , 1 u
11,12 11 12 11 12 11,12
yy yy
(10)
u{0,1}
11,12
(11)
where the values of
,
,
are the
coefficients of
,
,
in the objective
function (1); using the modified variables repeatedly,
the model could turn into a BP model. Considering
Figure 3. The trend of the objective function.
this matter, the model is a binary programming (BP)
problem and can be solved using common solvers. If
the segments have great length, the number of
auxiliary variables will increase for solving the
problem. As a case in point, if a segment has 20 RSU,
we need 19 auxiliary variables for linearization in
addition to the 20 binary variables. The simple case
study was solved by the binary programming solver
CPLEX 12.3 with AIMMS 3.12 software. We used
the default parameters of CPLEX. Experiments were
carried out on an MSI laptop, 4GB of RAM memory,
a 2.2-GHz processor. Fig. 1 shows the situations in
which the number of RSUs was increased from 1 to
full coverage of freeway (19 RSUs). When all parts
of the road were covered by RSUs, it is possible to
inform any vehicles in all parts; then, we can achieve
full information dissemination. The aim of this
research is to obtain a greater level of information
dissemination to vehicles according to the restrictions
on the cost of equipment and importance of segments.
Results show that, with the placement of 5 RSUs, we
can achieve more than 50 percent of full information
dissemination. Moreover, sensitivity analysis on the
number of RSUS indicates that more than 15 RSUs
beside the road do not have a significant effect on the
objective function.
The effect of adding each RSU to the objective
function is shown in Fig 2. According to Fig 2, major
changes can be seen after the ninth RSU, when 74
percent of full information dissemination is achieved.
According to the results, investors can present a
pattern for funding and phasing the project, as one of
the best characteristics of the proposed model. Hence,
freeway equipment can be done in four phases. The
first phase, placement of 5 RSUs, is equivalent to
VEHITS 2016 - International Conference on Vehicle Technology and Intelligent Transport Systems
230
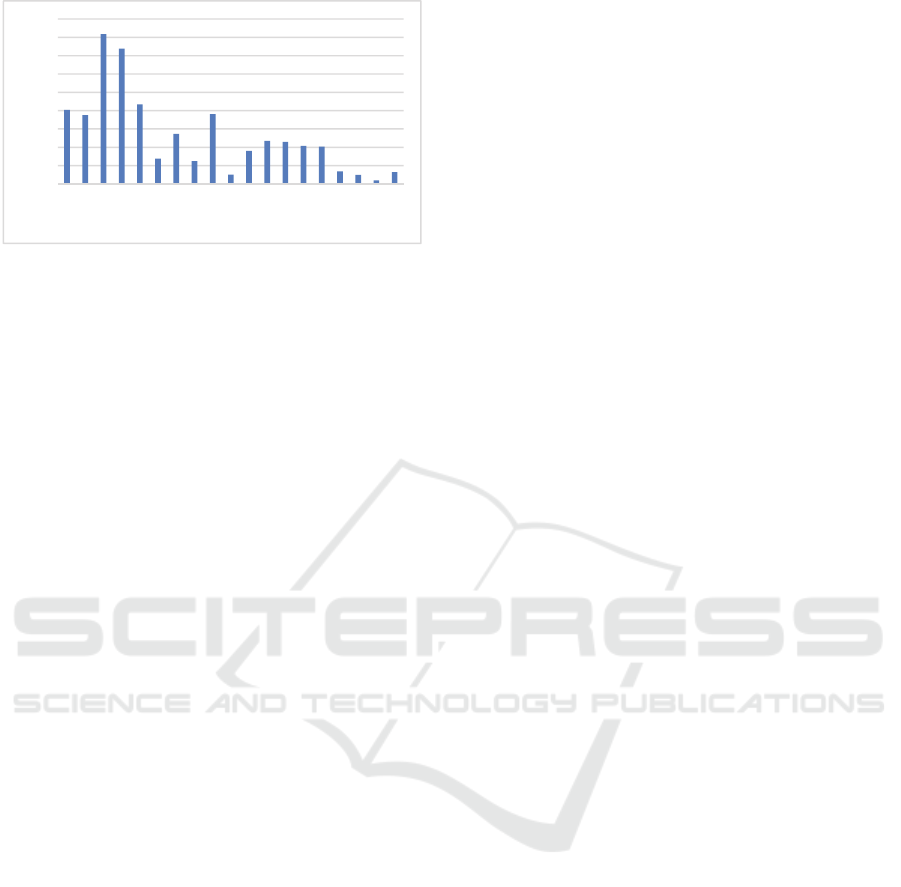
Figure 4: The effect of increasing each RSU on objective
function.
achieving more than 50 percent of full information
dissemination. The second phase, placement of 4 next
RSUs, is equivalent to fulfilling almost 74 percent of
full information dissemination (totally 9 RSUs). The
third phase, placement of 6 other RSUs, achieves 96
percent and, in the last phase, 4 final RSUs have slight
effect on the objective function.
4 CONCLUSION AND FUTURE
WORK
By the same token, Roadside unit (RSU) is one of the
substantial elements in vehicular communication
systems. This equipment could be installed around a
road and send messages to vehicles. These messages
such as weather condition, limit speed warning, and
accident warning alerts are important for drivers in
order to have safe and efficient driving. Also, it is
ideal to cover the whole road by RSUs; nonetheless,
it is not a cost-effective solution due to the costly
implementation and maintenance of this equipment
and lack of market penetration of vehicular
communication system. In this paper, a BP
optimization model was proposed to choose an
appropriate placement for RSUs. This approach made
decisions based on the number of curves, number of
on-ramps, accident rate, weather condition, and cost
limitations. The proposed model was applied to one
of the suburbs of Tehran freeway ─Tehran to Pardis.
This model was solved precisely using CPLEX 12.3.
We would like to point out that the results indicated
that, with the placement of 5 out of 19 RSUs, more
than 50 percent of full information dissemination can
be achieved. Furthermore, equipping the freeway can
be classified in four phase operational budget. The
first phase, placement of 5 RSUs, is equivalent to
achieving more than 50 percent of full information
dissemination. The second phase, placement of 4 next
RSUs, is equivalent to fulfilling almost 74 percent of
full information dissemination (totally 9 RSU). The
third phase, placement of 6 other RSUs, achieves 96
percent and, in the last phase, 4 final RSUs have alight
effect on the objective function. In future works, in
addition to the listed parameters, the parameters
regarding volume of traffics can be applied.
REFERENCES
Aslam, Baber, Cliff C. Zou, 2011 ,“Optimal roadside units
placement along highways,” Consumer
Communications and Networking Conference (CCNC),
2011 IEEE, pp. 423-429.
Chen, Der-San, Robert G. Batson, and Yu Dang,2010,
“Applied integer programming: modeling and
solution,” John Wiley & Sons.
E. S. Cavalcante, L.L. Aquino, G.L. Pappa, A.F. Loureiro,
2012 ,“Roadside unit deployment for information
dissemination in a VANET: An evolutionary
approach,” Proceedings of the 14th annual conference
companion on Genetic and evolutionary computation.
ACM, pp. 27-34.
G.A. Golembiewski, B. Chandler, 2011,“Roadway
Departure Safety: A Manual for Local Rural Road
Owners Federal Highway,” Administration U.S.
Department of Transportation Report No. FHWA SA-
11-09.
M. Rashidi, I. Batros, T. Madsen, T. Riaz, T. Paulin, 2012,
“Placement of Road Side Units for floating car data
collection in highway scenario,” (ICUMT), 2012 4th
International Congress on. IEEE, pp. 114-118.
Rizk, Ramy, Robil Daher, and A. Makkawi. 2014, “RSUs
placement using overlap based greedy method for urban
and rural roads,” Communication Technologies for
Vehicles (Nets4Cars-Fall), 2014 7th International
Workshop on. IEEE, pp. 12-18.
S. Mehar, SM Senouci, 2015, “An Optimized Roadside
Units (RSU) placement for delay-sensitive applications
in vehicular networks,” Consumer Communications
and Networking Conference (CCNC), 2015 12th
Annual IEEE.
0
2
4
6
8
10
12
14
16
18
1 2 3 4 5 6 7 8 9 10111213141516171819
Theeffectofincreasing
Number of RSUs
Binary Programing Model to Optimize RSU Placement for Information Dissemination
231
