
The Spanning Tree based Approach for Solving the Shortest Path
Problem in Social Graphs
Andrei Eremeev
1
, Georgiy Korneev
1
, Alexander Semenov
2
and Jari Veijalainen
2
1
Department of Computer Technologies, ITMO University, Saint Petersburg, Russia
2
Department of Computer Science and Information Systems, University of Jyvaskyla, Jyvaskyla, Finland
Keywords: Social Graph, Social Network Analysis, Shortest Path Problem, Odnoklassniki, the Atlas Algorithm.
Abstract: Nowadays there are many social media sites with a very large number of users. Users of social media sites
and relationships between them can be modelled as a graph. Such graphs can be analysed using methods
from social network analysis (SNA). Many measures used in SNA rely on computation of shortest paths
between nodes of a graph. There are many shortest path algorithms, but the majority of them suits only for
small graphs, or work only with road network graphs that are fundamentally different from social graphs.
This paper describes an efficient shortest path searching algorithm suitable for large social graphs. The
described algorithm extends the Atlas algorithm. The proposed algorithm solves the shortest path problem
in social graphs modelling sites with over 100 million users with acceptable response time (50 ms per
query), memory usage (less than 15 GB of the primary memory) and applicable accuracy (higher than 90%
of the queries return exact result).
1 INTRODUCTION
The emergence of online social networking sites is
changing the way social scientists study the structure
of human relationships. Social network analysis has
gained a significant popularity in computer science,
political science, communication studies and
biology. Since individuals record many of their
social relationships at online social networking sites,
previously invisible social structures can be explored
to determine social processes. The overall modeling
framework we will apply in the sequel was
presented in our previous research (Semenov et al.,
2013). Accordingly, social networks modelled and
observable at the social media sites (1
st
level models,
or site ontologies) can be further modeled as graphs
(2
nd
level models); hence, the methods of graph
theory can be applied for analysis of the original
social networks. The methods can be used to
investigate kinship patterns, community structures,
information diffusion and many other problems
(Marcus et al., 2007).
Additionally, information left by users on social
networking sites can be used, for instance, in
predicting the results of elections (Wang et al., 2012;
Tumasjan et al., 2010). Also, social networks
analysis is used to identify money laundering and
terrorists (Zhang et al., 2003). Moreover, social
networks were broadly used in organizing mass riots
and violence during the Arab Spring (Semenov,
2013). The National Security Agency (NSA) has
been performing analysis of call records since the
September 11 attacks, and analysis of collected
Internet communications since 2007, known as
surveillance program PRISM (Greenwald et al.,
2013).
Some of the problems which need to be solved
during graph data aggregation and analysis require
large numbers of shortest path computations
between a pair of vertices in a graph. These
problems involve calculations of such metrics as
betweenness centrality, closeness centrality,
harmonic centrality and others. The shortest path
problem is defined as searching for such a path that
the sum of weights of edges that belong to the path
is minimized. Graphs that model social networking
sites are usually unweighted, i.e. all edges in the
graphs have weight one. Many shortest path
calculation algorithms have been developed,
however they do not perform well on large graphs
that contain hundreds of millions of nodes and
billions of edges – typical of graphs modeling major
social media sites.
42
Eremeev, A., Korneev, G., Semenov, A. and Veijalainen, J.
The Spanning Tree based Approach for Solving the Shortest Path Problem in Social Graphs.
In Proceedings of the 12th International Conference on Web Information Systems and Technologies (WEBIST 2016) - Volume 1, pages 42-53
ISBN: 978-989-758-186-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

The current paper suggests an algorithm based
on the Atlas algorithm (Cao et al., 2011) that solves
the single-pair shortest path problem in large
unweighted social graphs with acceptable accuracy
(91%), performance (50 ms per a query) and
memory usage. Also, if the Atlas+ algorithm makes
a mistake, then the length of the found result is not
longer than the length of a correct (shortest) path
plus one. These kinds of mistakes lead to incorrect
statistics if the algorithm is used in graph analysis.
Furthermore, the algorithm does not make mistakes
in the case of short paths (less than three edges). If a
shortest path algorithm is deployed as a standalone
service, its results can be easily checked by the users
for short paths. Hence, if a user realizes that the
algorithm returns wrong results, then it could lead to
lowering the prestige of the social networking site.
As for the Atlas algorithm, Atlas demonstrates
excellent performance (0.5 ms per query) and
performs well in such application as ranked social
search (searching for top k closest vertices from a set
of vertices) (Cao et al., 2011). Nevertheless, the
accuracy of the algorithm is not acceptable (25-
30%).
Social graphs are very dynamic (Wilson et al.,
2009). The proposed algorithm is also able to handle
dynamic social graphs.
2 DEFINITIONS
A graph is an ordered pair
,
comprising a
finite nonempty set of vertices (points) and
together with a set of edges (lines), which is a
subset of Cartesian product of the set of vertices, i.e.
⊂. Each pair of vertices
,
∈is
an edge and it is said that e connects and . Hence,
vertices and are adjacent vertices. Vertex and
edge are incident with each other; as well as v and
e. Moreover, if two distinct edges and ′ are
incident with a common vertex, then they are said to
be adjacent edges. A directed graph or digraph is a
graph which consists of a finite nonempty set V of
vertices and a set of ordered pairs which are named
directed edges or arcs. An undirected graph is a one
where for each edge
,
in E it holds that there is
an edge
,
in E.
A path (walk) in a graph can be defined as a
finite sequence of vertices and edges
…
in
which each edge is incident with the preceding and
following vertices, so
,
. The edges can
be omitted in the notation, so the path between two
vertices can be denoted as
…
. The edges are
evident by context. If the first and last vertices are
the same, i.e.
, then the path is called a
closed path in a directed graph. A closed path in a
undirected graph is a path in which the first and last
vertices are the same, and
. A cycle
in a graph is an equivalence class of closed paths
with such equivalence relation as, two paths is
equivalent if and only if ∃∀ ∶
where
are edges of the first path and ′
are edges
of the second one. In other words, this definition
means that there exists such a shift of indices that
there is the same number of edges in both paths and
the adjacent vertices are identically numbered.in
both paths.
The length of a path in an unweighted graph is
the number of edges which comprise the path. In a
weighted graph the length of a path is the sum of
weights of edges which belongs to the path. In other
words,
∑
. A shortest path between
two vertices is a path where the length of path
between these vertices is minimized. The diameter
of a graph is the longest shortest path between any
pair of vertices of the graph if the graph is
connected. Otherwise it is infinite.
If each pair of vertices of an undirected graph is
connected by a path, then this graph is called
connected. A connected component or simply a
component is a connected subgraph of an undirected
graph that is maximal with regards to inclusion.
Thus, the connected components of an undirected
graph are equivalence classes in which pair
connectivity induces an equivalence relation.
Relying on the definition of cycles and
connected components the terms tree and forest can
be defined. A graph is called acyclic if it does not
have cycles. A tree is a connected acyclic undirected
graph. Any graph without cycles is a forest. Thus,
the connected components of a forest are trees. A
subgraph ′ of a graph is called a spanning tree if
and only if is a tree and contains all vertices of the
graph .
The neighborhood graph of a vertex is a
subgraph which is comprised of the adjacent vertices
of the vertex and edges between them. The degree d
of vertex v is the number of edges where v occurs.
So local clustering coefficient lcc of vertex v is a
metric that equals to the number of edges in the
neighborhood graph divided by the degree d of
vertex v. Thus, 2#/ 1.
3 BACKGROUND
The Atlas algorithm (Cao et al., 2011) is comprised
The Spanning Tree based Approach for Solving the Shortest Path Problem in Social Graphs
43

of two phases: building a search index (the pre-
computation step) and subsequent queries to the
built search index. The search index consists of a set
of spanning trees that are stored on the hard drive.
The tree construction algorithm takes the number of
spanning trees to be built as a parameter and builds
the specified number of trees. The strategies of the
selection of starting vertices and adding new edges
to the tree are described below.
To build a spanning tree, the strategy of selection
of the starting vertex and the strategy of selection of
the edges should be chosen. Cao et al. (2011) have
evaluated the following strategies for the selection of
the starting vertices:
The top k-centrality strategy in which k most
popular vertices (k with the highest degree) are
chosen as the starting vertices;
The scattered top k-centrality strategy in which
k most popular vertices are chosen in such a
way that distance between a pair of the chosen
vertices is at least two edges;
The random selection strategy in which the
starting vertices are chosen randomly.
In Cao et al. (2011) the best characteristics had the
top k-centrality strategy.
At each step of the Atlas algorithm an edge is
probed and decided whether it can be added to the
spanning tree under construction. In the paper three
strategies of edge selection has been evaluated:
Breadth-first search with random tie-break in
which a random edge among the possible edges
is added;
Breadth-first search with complementary tie-
break in which the least used edge among the
possible edges is added;
The least covered edge first strategy in which
the edge least used in the previous trees is
added to the tree under construction.
The best accuracy was demonstrated by the breadth-
first search with complementary tie-break.
Overall, the starting vertices of the trees are
chosen according to their popularity in a social
graph, i.e. based on the degree of vertices. To cover
as much edges as possible, at each step of the
algorithm the least used edge is added to the
building tree, but this strategy leads to use too much
memory for storing counters for each edge. Also if
trees are built concurrently, synchronization between
threads are needed that decreases the performance of
the tree construction.
Handling of dynamic graphs is done as follows.
Several old trees are replaced with new trees. Also,
it was shown that changes in social graphs do not
impact much the built spanning trees.
To find the shortest path between vertices s and t,
the Atlas algorithm finds the shortest path in each
spanning tree and selects the shortest path among the
found paths.
The Atlas algorithm demonstrates excellent
performance (0.5 ms per query). Nevertheless, the
accuracy of the algorithm is not acceptable
(25-30%) (Cao et al., 2011). Thus, it was decided to
improve its accuracy with regards to its performance
and memory usage.
4 Atlas+ ALGORITHM
DESCRIPTION
The following section describes the changes in the
Atlas algorithm that improve its accuracy. The
improvement is based on the large value of the local
clustering coefficient. After that, properties of the
new algorithm, Atlas+, are analyzed, and according
to them, two versions of Atlas+ are suggested.
The tree construction phase of Atlas+ is taken
from the Atlas algorithm as is. K most popular
vertices are selected as starting vertices, but the
breadth-first search with random tie-break is used as
edge selection strategy. BFS with random tie-break
has been selected because it allows isolated tree
construction.
4.1 The Proposed Algorithm
The modifications of Atlas+ attempt to improve the
efficiency of the second phase of Atlas. The local
clustering coefficient describes the neighborhood
graph of a vertex, the probability that a pair of
adjacent vertices of a vertex is connected by an
edge. The local clustering coefficient is large for
social graphs, for example, Facebook – 0.15
(Ugander, Karrer, Backstrom, & Marlow, 2011), a
subgraph of LiveJournal – 0.13 (Stanford Network
Analysis Project, 2015). It means that the probability
that adjacent vertices of a vertex are connected by an
edge was 15% for Facebook 5 years ago and 13%
for the subgraph of LiveJournal. Thus, a path
between a pair of vertices can be shortened. In Fig. 1
a path between vertices u and v is shown. The
dashed edge connects the adjacent vertices of vertex
w. Thus, the path between vertices u and v can be
shortened through the dashed edge. Hence, the result
of the Atlas algorithm can be improved with help of
some adjacent vertices of the vertices obtained by
the Atlas algorithm. The proposed algorithm looks
as in Listing 1.
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
44

Figure 1: Shortening a path by bypassing node w.
Listing 1: Shortest path between s and t
1 long[] path(long s, long t)
2 paths = atlas(s, t)
3 adjLists = getAdjLists(paths)
4 graph = buildGraph(adjLists)
5 return bfs(graph)
The new algorithm, first, searches for the shortest
paths in the spanning trees (the atlas method, line 2).
Thereafter, the adjacent vertices of the vertices
obtained by Atlas are requested (the getAdjLists
method, line 3). Based on that, a graph is built (the
buildGraph method, line 4) in which BFS finds the
shortest path between the source and the destination
vertices (the bfs method, line 5). The found path is
the result of the algorithm. The building graph is
stored in a hash table in which keys are ids of
vertices and values are lists of adjacent vertices.
Let us call the vertices retrieved at the 4 line of
the algorithm new vertices. To analyze Atlas+, the
paths returned by the Atlas algorithm and the paths
obtained by the proposed algorithm have been
compared. From the comparison of the paths, it was
observed that the shortened path may be comprised
of pieces of the paths obtained by the Atlas
algorithm and no more than one vertex was added to
those returned by Atlas. Hence, the new algorithm
only needs to store two edges on which the shortest
distances to the source and the destination vertices
are reached for each vertex. For the analysis, 148789
pairs of vertices were selected randomly from the
Odnoklassniki social graph. Shortest paths between
each pair were calculated by BFS.
Thus, the second version looks as in Listing 2.
Listing 2: The enhanced algorithm
1 long[] path(long s, long t)
2 paths = atlas(s, t)
3 adjLists = getAdjLists(paths)
4 graph = buildGraph(paths, adjLists)
5 treeS = bfs(s, graph);
6 treeT = bfs(t, graph);
7 minV = findMinimum(s, t, tS, trT);
8 bfsPath = getPath(tS, t)
9 path = getPath(minV, tS, tT)
10 return shortestOf(bfsPath, path)
The new algorithm, first, searches for the shortest
paths in the spanning trees (the atlas method, line 2).
Thereafter, the adjacent vertices of the vertices
obtained by Atlas are requested (the getAdjLists
method, line 3), as in the first version. After that, a
graph comprised of the vertices obtained by the
Atlas algorithm and those edges obtained after the
request where vertices are among those obtained by
the Atlas algorithm (the buildGraph method, line 4).
In 5-6 lines two trees of shortest paths rooted at
vertex s and at vertex t are built by BFS. The
findMinimum method finds a vertex on which
minimum sum of distances from the vertex to s and t
is reached. The findMinimum method stores all new
vertices in a hash table in which keys are ids of the
new vertices and values are objects of the Vertex
type storing distances to vertices s and t. After that,
the shortest path is selected from the paths counted
by BFS (line 8) and the final path found on line 9.
The bfs method returns a tree of shortest paths. A
tree of shortest paths is comprised of a map in which
keys are ids of vertices and values are ids of parent
vertices; parents of root vertices are set to -1. Thus,
to find the shortest path between vertex s and
another vertex u, the algorithm iterates and queries
parents of the current vertex starting from u until a
root vertex (the getPath method, line 8). The Vertex
type is a type comprised of id of the vertex and two
other ids of adjacent vertices on which minimal
distances to vertices s and t are reached. The second
getPath method (line 9) is presented in Listing 3 and
works as follows. First, paths in the both BFS trees
are found. If one of them does not exist, then the
algorithm returns null, otherwise, the algorithm
returns the shortest path which goes through vertex
v.id.
Listing 3: Find the shortest path in the
trees
1 long[] getPath(Vertex v, Tree tS, Tree tT)
2 toS = getPath(tS, v.idToS);
3 toT = getPath(tT, v.idToT);
4 if (toS == null || toT == null)
5 return null;
6 return toS + v.id + toT.reverse();
Table 1 contains the number of vertices and edges
utilized in the first version of the Atlas+ algorithm
and the number of vertices the degree of which
equals to one among those vertices. According to
Table 1, 339859 of the new vertices (67%) cannot be
used in the improvement of paths, as their degree
equals to one.
Table 1: Analysis of the first version of the algorithm.
Vertices Edges Vertices with degree equal 1
501324 10524245 339859
Thus, the number of stored edges has decreased to
2N in the second version of Atlas+, where N is the
number of vertices in the built graph. For example,
in this case, N is 501324
,
the number of stored edges
The Spanning Tree based Approach for Solving the Shortest Path Problem in Social Graphs
45

is decreased in ten times (1002648 against
10524245).
The second version of Atlas+ is depicted in
Fig. 2-Fig. 5. Let the proposed algorithm search for
the shortest path between vertices
and
in the
unweighted social graph shown in Fig. 2.
First, the Atlas algorithm finds two paths
between the vertices, path
is drawn
by dashes and path
is drawn by dots.
Fig. 3 shows the two paths found by the Atlas
algorithm. Other vertices and edges of the original
graph are marked by gray color.
Figure 2: The original graph.
Fig. 4 depicts the graph that consists of the
previously obtained vertices and of the additional
edges queried from the original graph that connect
the vertices.
In Fig. 5 the algorithm looks for a new adjacent
vertex that is not in the built graph, on which the
shortest path between
and
is reached. The
shortest path, marked with gray vertices, between
and
is
.
Figure 3: The two paths found by the Atlas algorithm.
Figure 4: The graph with adding edges queried from the
original graph.
According to the scale-freeness of social graphs, the
shortest paths between vertices have tendency to go
through popular vertices. Hence, the algorithm can
Figure 5: The found shortest path.
be accelerated if only a small portion of the adjacent
vertices are queried, not the whole adjacency list. It
also decreases the number of vertices stored in the
hash table. If a social graph is stored on another
machine, as is done in social networking sites, the
volume of data sent via a network decreases
(querying adjacent vertices). Thus, the heuristic may
improve performance of both the network query and
the processing of the responses.
Let a query “get at least k vertices or vertices
with degree more than some bound d” be named as a
query of the popular adjacent vertices. To find a
reasonable value for the degree d, the following plot
in Fig. 6 is utilized. The degrees of vertices queried
in the original graph that shorten the shortest path
obtained by the Atlas algorithm have been assessed.
If the proposed algorithm in Listing 2 is able to find
several shortest paths between a pair of vertices, the
path in which the degree of such vertex is largest is
selected. The plot in Fig. 6 shows the cumulative
normalized number of vertices that shortens the
paths with regards to their degree. According to the
diagram, the shortest path is shortened through very
popular vertices; only 2-3% of all paths are
improved through vertices with degrees circa
100 - 200 which are also rather popular vertices.
According to the analysis of degree distribution in
the Odnoklassniki social graph, only 7% of vertices
of the social graph have degree more than 200. Thus,
Figure 6: Cumulative share of vertices through which
paths are shortened depending on the degree of the
vertices.
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
46

if adjacent vertices the degree of which is more than
some fixed threshold are requested, the volume of
sent and processed data decreases essentially. As a
trade off the accuracy of the algorithm decreases by
1-2% which is still acceptable if the threshold is 200.
Thus, by setting the threshold d at 200, only 7% of
the vertices are returned to the query of the popular
adjacent vertices above, by among them are all those
that have up to 5000 adjacent vertices.
4.2 Handling of Dynamic Graphs
Social networking sites are very dynamic as
concerns the addition of new users and additions and
deletions of relationships between users. According
to the study even 50% of actions of users of social
networking site per day relates to changes in their
friend lists (Wilson et al., 2009). An algorithm for
searching the shortest path between two vertices
should always return the relevant path. Thus,
changes in the social graph have to be reflected the
graph model, in this case, in the spanning trees
impacted by them. Rebuilding all trees takes too
much resources and too much time. We have
observed that building a spanning tree takes for the
Odnoklassniki social networking site with the
current number of users 1 hour and 20 minutes on
average (O(|E|), as the spanning trees are built by
BFS). Hence, only a part of the built trees or a part
of a tree should be rebuilt per day. The current paper
utilizes the replacement strategy suggested in Cao et
al. (2011) and suggests local modifications of the
trees rather than complete rebuilding.
The replacement of trees is assumed to be done
once a day; and the task should take at most a couple
of hours for the graph of the Odnoklassniki social
networking site. Local modifications of a spanning
tree should be done if it is not a tree of the breadth-
first search. The impacted tree is modified in such a
way that it will become a breadth-first search tree
again. The following changes can occur in a network
at the site that are reflected into the modelling graph:
adding a new friend: add an edge;
adding a new user: add a vertex;
removing a friend: remove an edge;
removing a user: remove a vertex.
Let uv be a new edge between existing vertices u
and v. Adding a new edge does not impact the
functionality of the spanning trees before the
difference between the depth of the vertices is more
than one. If the difference is more than one, then the
highest vertex should become a child of the second
vertex. The needed tree modification is shown in
Fig. 7. In the picture vertex v is deeper than vertex u
in the tree; vertex w is a descendant of vertex u and
the shortest path between vertices u and v is of
length 2 or more in the tree. The modification needs
to calculate the depth of the vertices (from the root)
and change the parent pointer of the lowest vertex;
in the picture vertex u becomes the parent of vertex
v. Thus, time complexity of the modification is O(L
+ 1) = O(L) where L is the depth of the tree. In the
implementation of Atlas+ only the pointer to the
parent vertex of a vertex in a tree is needed. Thus,
edges in the spanning trees are directed from a child
to its parent.
Figure 7: Modification when edge uv is added.
Adding a new vertex does not impact built trees until
an edge connecting the vertex and another
component of the social graph is added. This can
occur if, for instance, a new just registered user at a
social networking site connects with another user.
Removing an edge from the social graph may
split a tree into two unconnected components. Let a
vertex v be the parent of a vertex u in a spanning tree
and the edge uv has been removed. Then such a
vertex w should be found that vertex w should be an
adjacent vertex of vertex u, vertex w should be
connected in the modified tree, and after setting the
parent of u to w the tree should become a breadth-
first search tree. Since the depth of a tree should be
as small as possible, vertex w is sought in the
following groups of the vertices. The adjacent
vertices of vertex u are split into three groups:
vertices the depth of which equals to the depth of
vertex u minus one, the vertices the depth of which
equals to the depth of vertex u and the vertices the
depth of which equals to the depth of vertex u plus
one. If such a vertex w cannot be found, then such a
vertex y is found among the adjacent vertices of w
for which vertex y is not an ancestor of vertex w. If
such a vertex y exists, then vertex y becomes the
parent of w and edge vw is inverted. If vertex y does
not exist, then the algorithm is repeated recursively
The Spanning Tree based Approach for Solving the Shortest Path Problem in Social Graphs
47
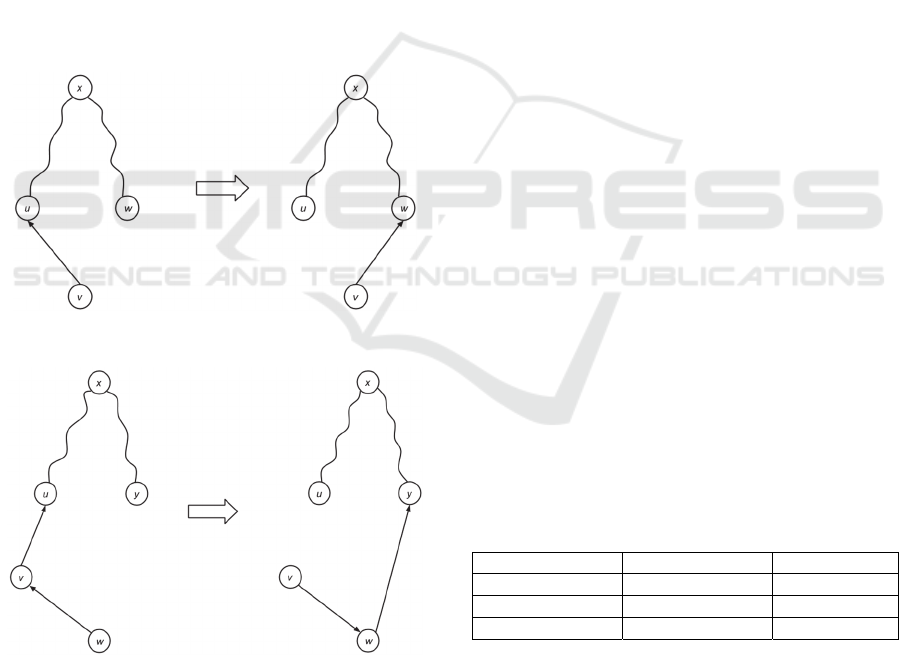
for all adjacent vertices of vertex w until a suitable
vertex is found. A suitable vertex may not be found
if all vertices of the subtree rooted at vertex v do not
have adjacent vertices in the original graph from
another subtree of the spanning tree being modified.
This means that edge uv is a bridge edge (cut-edge),
an edge of a graph whose deletion from the graph
increases its number of connected components
(Harary, 1969). Thus, in this case, no modifications
are needed. Nevertheless, this scenario very rarely
occurs in practice, since the social networks tend not
to have just one connection two subgroups of users.
To perform the modification, calculating the
depth of some vertices is needed. Since the
modification algorithm has to process the whole
subtree rooted at vertex v and query the adjacent
vertices of all vertices of the subtree in the worst
case, the time complexity of modification is O(|E|).
The modification is depicted in Fig. 8-Fig. 9. In
the pictures edge between vertices u and v is removed
and the tree is modified as explained above.
Figure 8: Modification when edge uv is removed.
Figure 9: Modification for removing edge uv (worst case).
Removing a vertex is similar to removing all edges
incident to the vertex. Thus, this case is covered by
the previous modification. It is implemented by
repeating the procedure above for every removed
edge the vertex.
4.3 Time and Space Complexity
To measure the time complexity of the Atlas+
algorithm, analysis of the each step is needed.
Finding of the shortest path in a tree takes time
linear with regards to the depth L of the tree O(L).
Search of k shortest paths in k trees takes time
O(kL). The number of edges queried by the Atlas+
algorithm is bounded by dkL, where d is the
maximal degree of vertices in the original social
graph. Thus, the breadth-first search algorithm
works in O(dkL) in the worst case. Thus, the
summarized time complexity of the proposed
shortest path searching algorithm depends on the
depth of trees, number of trees and the maximal
degree of vertices in the social graph and equals to
O(dkL). Also, some social networking sites limit the
maximal number of friends. Therefore, d is assumed
to be a constant.
The time complexity of Atlas algorithm is O(kL),
since the algorithm searches for shortest paths in k
spanning trees. Thus, the time complexity of Atlas+
is worse than the one of Atlas.
The number of edges queried by Atlas+ is
O(dkL), therefore, its space complexity is O(dkL).
While Atlas requires O(L) memory. Thus, Atlas+
requires more memory than Atlas.
5 EVALUATION
This section describes how the proposed algorithm
Atlas+ is evaluated and the results of the evaluation.
For the evaluation of Atlas+ LiveJournal and Orkut,
obtained from SNAP (Stanford Network Analysis
Project, 2015), and the real social graph of the
Odnoklassniki social networking site have been
utilized. Table 2 shows the size of the (social)
graphs used in evaluation.
Table 2: Graph data used in evaluation.
Graph Vertices Edges
Odnoklassniki 205M 25000M
LiveJournal 3997962 34681189
Orkut 3072441 117185083
5.1 Implementation Details
The algorithm has been implemented in the Java
programming language.
Spanning trees is stored as an array of integers
on the hard drive. All vertices of the initial social
graphs are fetched and are enumerated from 1 to N,
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
48

where N is the number of vertices in the graph. Let p
be an array of integers in which a tree is stored and i
be the id of a vertex. Thus, p[i] stores the id of the
parent of vertex i. Generated trees are too large to
be stored in the heap, circa 14-16 GB in total for the
graph of the Odnoklassniki social networking site.
Additionally, mapping from social graph ids, unique
8 bytes long integers, to tree ids should be stored in
the primary memory. To overcome the memory
problem, the files that contain the spanning trees, are
mapped to the virtual memory. Also, to store the
mapping of social graphs ids to tree ids in the
primary memory, the one-nio library of the
Odnoklassniki API is utilized (One-NIO, 2015).
The benefits of the suggested solution are (Bach,
1986):
demand paging, i.e. files are loaded into
physical memory by pages, and only when that
page is referenced;
page cache, i.e. several processes can share
memory mapped files between each other.
Hash tables are utilized in the first version and in the
second version of the algorithm. Standard Java
collections may only store objects. This means that
primitive types, like long, integer, have to be boxed
to class wrappers, e.g the Long class is for long
integer. Using the standard Java collections for
primitive types leads to the following problems with
performance and memory usage:
more heap memory than necessary is used,
since the corresponding Java object contains
headers and other meta information in addition
to primitive types;
objects need to be garbage collected, while
memory for primitive types can be allocated
directly in the stack memory;
indirect access to primitive types which leads
to slowing down program execution;
problems with caching: an array is supposed to
be stored contiguously; thus, arrays are easy to
be cached in order to decrease access time to
elements of the array, but as concerns the
boxed integers, the array is as an array of
pointers to objects randomly spread around the
heap. Thus, the data cannot be cached into a
contiguous memory area.
To eliminate the mentioned problems,
implementation of the hash table provided by Trove
is utilized (Trove, 2015). In the Trove library hash
tables are implemented as open-addressing hash
tables with double hashing. Nevertheless, the
performance of Trove's hash table does not fit the
requirements of the proposed algorithm. Thus, to
speed up the algorithm an open-addressing lock-free
hash table has been implemented. Since the
proposed algorithm only adds or makes queries to
the hash table, rehashings in the hash table can be
optimized. Let k be a maximal number of probes
done during insertion to the open-addressing hash
table. If elements are not removed, then the
searching element e cannot lie further than k
iterations from the h(e) cell, where h(e) is the hash
value of element e. Thus, the searching algorithm
does not need to make more than k rehashings. For
generation of probing sequences quadratic probing is
utilized (Cormen, Leiserson, Rivest, & Stein, 2001).
Moreover, the implementation of the hash is lock-
free.
5.2 Evaluation of Accuracy
To analyze the accuracy of the algorithm, pairs of
vertices from the above-mentioned social graphs
have been randomly selected. Table 3 shows the
number of paths grouped by the length of the paths.
Due to the properties of social networks, the shortest
paths with length more than five edges in the
modeling graphs are very rare. Thus, the selected
sets of paths are representative for the algorithm
evaluation.
Table 3: Paths grouped by the length of the paths.
Social graph 3 4 5 6 Total
Odnoklassniki
7439
(5%)
61004
(41%)
71419
(48%)
8927
(6%)
148789
LiveJournal
5151
(10%)
18484
(37%)
25061
(50%)
1304
(3%)
50000
Orkut
3121
(6%)
20531
(41%)
23482
(47%)
2866
(6%)
50000
The suggested algorithm has calculated a path
between each pair of the vertices; after that, the
result of the algorithm has been compared with the
actual shortest path. The correct shortest paths have
been computed by BFS. In addition, the accuracy of
the algorithm grouped by the length of paths has
been calculated. Fig. 10-Fig. 13 show that the
accuracy of the algorithm depending on the number
of trees used in search. Hence, 25-30 spanning trees
are enough to obtain the desirable accuracy, more
than 90%, which is much better than the accuracy of
the Atlas algorithm (30 %), and desirable
performance (shown in Table 6). The accuracy is the
rate of that the found path is not the shortest one
normalized by the amount of the paths used in the
evaluation.
The Spanning Tree based Approach for Solving the Shortest Path Problem in Social Graphs
49

Figure 10: The accuracy of the proposed algorithm with
regards to the number of used spanning trees.
Figure 11: The accuracy grouped by the length of the
paths (Odnoklassniki).
Figure 12: The accuracy grouped by the length of the
paths (LiveJournal).
Additionally, according to Fig. 10-Fig. 13, the
accuracy of the algorithm for long paths (four-five
edges) is better than for shorter paths (two-three
edges), but the difference is insignificant. If the
algorithm makes a mistake, the difference in path
Figure 13: The accuracy grouped by the length of the
paths (Orkut).
length is not more than one edge. Overall, the
proposed algorithm has acceptable accuracy in the
intended environments.
Table 4 shows the comparison of the accuracy of
the Atlas and Atlas+ algorithms. In the accuracy
evaluation the same sets of paths were utilized.
According to the table, the Atlas+ has much better
accuracy.
Table 4: The accuracy of Atlas and Atlas+.
Algorithm Odnolassniki LiveJournal Orkut
Atlas 30% 40% 56%
Atlas+ 91% 90% 96%
5.3 Evaluation of Performance
This section is devoted to performance of the
algorithm depending on parameters and
modifications of the algorithm. Table 5 shows the
time required to build spanning tree for the selected
social media site data, as well as average query time
for shortest path query between two random
vertices.
Table 5: Performance of the algorithm.
Social graph Size of a
tree
Number
of
vertices
Tree
construction
time
Query
time
Odnoklassniki 572 MB 150M 80 minutes 51 ms
LiveJournal 15 MB 3997962 20 seconds 17 ms
Orkut 11 MB 3072441 83 seconds 21 ms
Table 6 contains the average time needed for
searching the shortest path between two vertices
using 25 spanning trees on Odnoklassniki. The
performance of each step of the algorithm has been
measured, as well. The measurement has been
performed on machine with Intel Core i7-4702MQ
CPU 64 GB of the primary memory and Linux
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
50

(Ubuntu 14.04). Requests of adjacent vertices is
done via a computer network, since the
Odnoklassniki social graph is stored on a machine
cluster. In the table row Tree query relates to Atlas.
Thus, Atlas is 100 times faster than the proposed
one.
Table 6: Performance of the steps of Atlas+.
Step of algorithm First
version
Second
version
Tree query (Atlas) 0.5 ms 0.5 ms
Request of adjacent vertices 32 ms 32 ms
Building of a hash table 61 ms 20 ms
BFS 33 ms 9 ms
Total 127 ms 51 ms
According to the table, despite of the suggested
modifications to improve the algorithm, the
performance of the algorithm is observed to be
unacceptable and can be improved. Indeed, the
average number of the vertices for which adjacency
lists are requested is circa 100. Since the spanning
trees are built around popular vertices, the responses
for the requests appear to be large (more than 2
MB). Additionally, as is shown in Section 4.2 the
most part of edges cannot be used in improving the
paths. Moreover, most part of the time for one
search is consumed by the network requests. Section
4.2 shows that the number of requested vertices can
be bounded without significant decreasing of the
accuracy of the algorithm.
Unfortunately, the API of the Odnoklassniki
social network site does not support the query of
popular adjacent vertices. That is why the
performance of using only popular adjacent vertices
has not been measured.
5.4 Evaluation on Dynamic Graphs
The current section analyzes accuracy of the
algorithm on dynamic graphs. The section also
analyzes the proposed modifications of the trees to
handle changes in the social network. To analyze
accuracy of the algorithm on dynamic graphs, a
subgraph of the graph modeling Odnoklassniki is
utilized. The subgraph consists of vertices for users
who mention Latvia as their country of origin in
their profile and ties between them induce the edges.
The subgraph contains 515000 vertices and 25
million edges. To emulate the dynamics of the
subgraph, a log of relevant changes that occurred at
the site during a week is utilized. The log only
includes adding and removing ties. Hence, two
versions of the graph are generated. The first is
modeling the state of the above subgraph at the
beginning of the week and the second at the end of
the week, after the tie changes recorded into the log
have been reflected into the edge set of the
subgraph.
As was mentioned above, spanning trees should
be changed in case of adding an edge for which the
difference in the depth of the vertices the edge
connects is more than one and in case of removing
an edge that occurs in the trees. Table 7 shows the
number of added edges grouped by difference in
depth. Thus, trees are impacted by adding of new
edges only in 0.03% of the additions. Concerning
dropping of edges, only 0.07% of removals of edges
impact the built trees. Thus, the built trees still are
able to approximate the modified graph rather well.
Table 7: Difference of depth of the vertices of edges.
Difference in depth Dist. Of adding an edge
0 54.17%
1 45.8%
2 0.03%
3 0%
Local modifications of trees are evaluated as
follows. First, 20000 of shortest paths have been
calculated in both the subgraph of Latvia and the
modified subgraph of Latvia. Thereafter, 30
spanning trees have been built for the subgraph.
Accuracy of the proposed algorithm has been
measured on the initial graph (97%) and on the
modified graph (95%). After that, the modifications
suggested in Section 5.4 have been applied to the
built spanning trees. Using the modified spanning
trees accuracy of the algorithm is 96%. Thus, the
local modifications increase accuracy of the
algorithm slightly.
The accuracy of the algorithm grouped by length
of shortest paths is depicted in Fig. 14. According to
the diagram, changes in the graph influence the
accuracy of the algorithm on short paths (3 edges),
while the accuracy on longer paths (more than 4
edges) does not change considerably. Local
modifications of trees increase accuracy of the
algorithm on short paths.
The replacement strategy is evaluated as follows.
As well as for local modifications, 20000 of shortest
paths have been calculated in the subgraph of Latvia
and in the modified graph of Latvia. Thereafter,
some number of old trees are replaced with new
ones. Fig. 15 demonstrates accuracy of the algorithm
depending on the number of replaced trees.
According to the picture, replacement of 14 trees
increases accuracy of the algorithm.
The Spanning Tree based Approach for Solving the Shortest Path Problem in Social Graphs
51
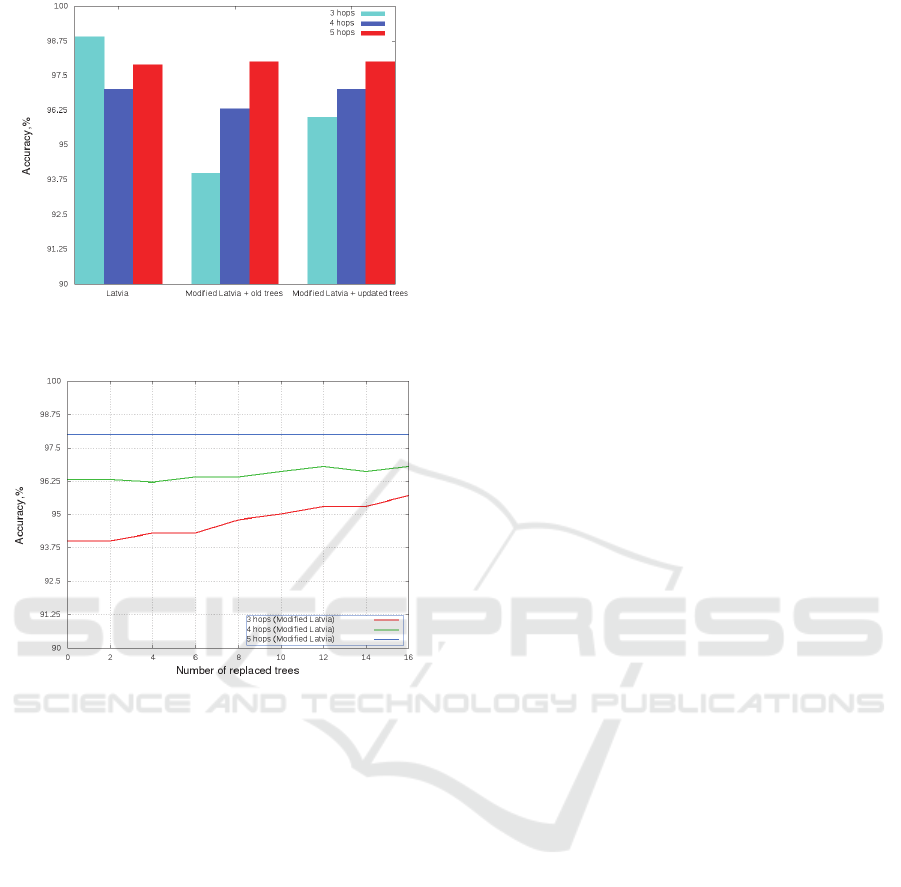
Figure 14: Accuracy of the algorithm (local modifications
of spanning trees).
Figure 15: Accuracy of the algorithm (replacement of
spanning trees).
6 RELATED RESEARCH
This section is devoted to other existing algorithms
using for solving the shortest path problem or for
distance estimation in social graphs.
Fu et al. (2013) suggest extracting the core-net
which is a subgraph consisting of popular vertices,
bridge vertices and edges that make it to form only
one connected component. Thereafter, distances
between all pairs of the core-net are calculated. The
shortest distance between a pair of vertices is found
as follows. First, the friend and friend-of-friends lists
of the two vertices are calculated, thereafter, they are
checked for intersection. If the lists have common
vertices, then distance is found. Otherwise, the lists
and the core-net are checked for intersection. If they
intersect, the distance is calculated, according to the
distance matrix. The time complexity of the
algorithm is|
||
| ||, where
and
are sets of friend-of-friends vertices and C is a
core-net of the graph. Also, researchers widely use
landmark-based approaches to estimate distances in
large graphs. These approaches select a subset of
nodes which are named landmark and pre-compute
the distances from each landmark to all other nodes
in the graph. The algorithm finds shortest paths
through the landmarks and returns the shortest one
as the answer to a query. Kleinberg et al. (2004)
show that landmarks can be picked randomly with
good theoretical results. Potamias et al. (2009) build
landmarks according to the basic metrics with better
result than in the previous work and also prove that
selecting the optimal landmark set belongs to the
class of NP-hard languages. All of the above
mentioned landmark-based approaches estimates the
lengths of the shortest path in ||, where L is a
set of landmarks. Finally, the Orion system, offered
in Zhao et al. (2010), embeds a graph into a
Euclidean space and distance between two vertices
is estimated according to Euclidean distance
between them. The time complexity time of Orion is
1, as calculation of the Euclidean distance
between a pair of vertices is needed. The main
disadvantage of the mentioned algorithms is that
they are only able to estimate distance between
vertices, not to calculate an actual path. Qi et al.
(2013) combine a landmark-based approach and an
embedding of vertices into a Euclidean space. Akiba
et al. (2015) propose the method that quickly
answers top k distance queries on large networks.
The method has been evaluated on real-world social
and web graphs. The Atlas algorithm (Cao et al.,
2011) reduces the shortest path problem in a graph
to the one in a tree.
According to the papers, it can be concluded that
researches mostly invest in algorithms which only
estimate the shortest distance between a pair of
vertices, not in the development of the shortest path
searching algorithm. For the most part of
applications, like ranked social search (find top k
closest vertices to a vertex from a set of vertices),
distance estimations are enough.
7 CONCLUSIONS
The Atlas algorithm builds a set of spanning trees
and reduces the shortest path problem to the least
common ancestor problem. The accuracy of the
Atlas algorithm is not acceptable for the envisioned
environment. The current paper has proposed a new
algorithm, Atlas+, based on the Atlas algorithm. The
proposed algorithm adopts the precomputation step,
i.e. the spanning tree construction of the Atlas
WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies
52

algorithm. The second part of Atlas, the path
searching is improved by the query to the entire
graph in order to find a vertex through which the
paths found by the original Atlas can be shortened.
Also, the paper has analysed several variations of the
proposed algorithm, as its initial version did not fit
the performance requirements. Some of the steps of
Atlas+ have been parallelized and a new lock-free
hash table has been suggested. The queries asking
for adjacent vertices on found paths are often done
via a communication network. Therefore, the paper
has discussed how the network time could be
reduced, but the suggested improvements would
require changes of the API at the server side and
they could not be tested. Finally, one has also
evaluated the proposed algorithm on dynamic
graphs. It is plausible to argue that the proposed
Atlas+ would exhibit high enough performance on a
real social network, as the evaluation against the
Odnoklassniki social network site demonstrated.
In the future work, the time of the network
queries can be investigated more precisely. In
addition, the algorithm is needed to be shipped with
the API of a social network site in order to
investigate the impact of the dynamics of social
networks on the algorithm. The proposed algorithm
might also be extended to answer top k shortest
paths between a pair of vertices.
REFERENCES
API OK. (2015, February 15). Retrieved from API OK:
https://apiok.ru/wiki/display/api/friends.get.
One-NIO. (2015). Retrieved from One-NIO:
https://github.com/odnoklassniki/one-nio.
Stanford Network Analysis Project. (2015, May 14).
Retrieved May 14, 2015, from
http://snap.stanford.edu.
Akiba, T., Hayashi, T., Nori, N., Iwata, Y., & Yoshida, Y.
(2015). Efficient Top-k Shortest-Path Distance
Queries on Large Networks by Pruned Landmark
Labeling. In 29th AAAI Conference on Artificial
Intelligence.
Bach, M. J. (1986). The design of the UNIX operating
system. Vol. 5. Englewood Cliffs: NJ: Prentice-Hall.
Cao, L., Zhao, X., Zheng, H., & Zhao, B. Y. (2011). Atlas:
Approximating shortest paths in social graphs. Santa
Barbara: Tech. rep. 2011-09, Department of Computer
Science, University of California.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C.
(2001). Introduction to algorithms. Cambridge: MIT
press.
Faloutsos, M., Faloutsos, P., & Faloutsos, C. (1999). On
power-law relationships of the internet topology. In
ACM SIGCOMM Computer Communication Review
29, 4. ACM, 251–262.
Greenwald, G., & MacAskill, E. (2013). NSA Prism
program taps in to user data of Apple, Google and
others. The Guardian, 7(6), 1-43.
Harary, F. (1969). Graph theory. Reading, MA: Addison-
Wesley.
Marcus, S., Moy, M., & Coffman, T. (2007). Social
network analysis. Mining graph data, 443-467.
Qi, Z., Xiao, Y., Shao, B., & Wang, H. (2013). Toward a
distance oracle for billion-node graphs. Proceedings of
the VLDB Endowment, 7(1), 61-72.
Semenov, A. (2013). Principles of social media
monitoring and analysis software. Jyväskylä Studies in
Computing, 168.
Semenov, A., & Veijalainen, J. (2013). A modelling
framework for social media monitoring. International
Journal of Web Engineering and Technology 8.3, 217-
249.
Trove. (2015, February 13). Retrieved from High
Performance Collections for Java: http://
trove.starlight-systems.com/
Tumasjan, A., Sprenger, T. O., Sandner, P. G., & Welpe,
I. M. (2010). Election Forecasts With Twitter: How
140 Characters Reflect the Political Landscape. Social
Science Computer Review.
Ugander, J., Karrer, B., Backstrom, L., & Marlow, C.
(2011). The anatomy of the facebook social graph.
Wang, H., Can, D., Kazemzadeh, A., Bar, F., &
Narayanan, S. (2012). A system for real-time twitter
sentiment analysis of 2012 US presidential election
cycle. Proceedings of the ACL 2012 System
Demonstrations. Association for Computational
Linguistics.
Wilson, C., Boe, B., Sala, A., Puttaswamy, K. P., & Zhao,
B. Y. (2009). User interactions in social networks and
their implications. In Proceedings of the 4th ACM
European conference on Computer systems, 205–218.
Zhang, Z. M., Salerno, J. J., & Yu, P. S. (2003). Applying
data mining in investigating money laundering crimes.
9th ACM SIGKDD international conference on
Knowledge discovery and data mining, 747-752.
The Spanning Tree based Approach for Solving the Shortest Path Problem in Social Graphs
53
