Towards a Trace-based Evaluation Model for Knowledge Acquisition and
Training Resource Adaption
Soraya Chachoua, Nouredine Tamani, Jamal Malki and Pascal Estraillier
L3i Laboratory, University of La Rochelle, Avenue Michel Cr
´
epeau, La Rochelle, France
Keywords:
e-Assessment, Scoring, Temporel Trace, Attempts Trace, Training Quality, Learner Behaviour, Resource
Adaption.
Abstract:
e-Assessment in an e-learning system is aimed at evaluating learners regarding their knowledge acquisition.
Available assessment methods are usually used at the end of a training activity in order to state if a given
learner has either passed or failed a training unit or level, based on the grading results obtained. Most of
grading processes follow the SCORM norm in the matter (Scorm, 2006) and make use of duration and number
of attempts to compute the scores. These information are valuable in grading but they can also be exploited
to capture the learner bahaviour during a training activity, and then assess both learner knowledge acquisition
and training resource quality in terms of adequacy. Therefore, we consider in this paper duration and number
of attempts as modeled traces, upon which we build a theoretical model for automated evaluation of learners’
knowledge acquisition evolution as a training activity progresses. The values obtained can be used to adapt
training strategies and resources to improve both learner’s knowledge level and e-learning platform quality.
1 INTRODUCTION AND
MOTIVATION
In recent years, the use of e-learning platforms has
seen a tremendous increase in the training field. The
more so with the large adoption of ICT in teach-
ing processes (Martin, 2008), in which a learner is
empowered with tools and materials to acquire new
knowledge such as courses, exercises, quizzes, etc.,
which are organized in such a way that learners can
manage and monitor by themselves the training ac-
tivities. In order to be able to track their progress in
terms of knowledge acquisition, learners have to take
tests and exams in the form of multiple-choice ques-
tions and/or fill-in-the-blank exercises (Nicol, 2007;
Crisp, 2009), which deliver a static evaluation based
on learner’s answers. These evaluation methods, in
the sense of grading or scoring (Crooks, 1988) func-
tions, are parts of a so-called e-Assessment compo-
nent widely integrated into e-learning platforms.
As stated in (Wandall, 2011), testing and test re-
sults can be used in order to assess the learner’s
knowledge and competencies, as a pedagogical tool
to assess the effect of the teaching, but also for admis-
sion, regulation, controlling, rewarding/punishment
of individuals/schools. Early student evaluation is
important in any pedagogical process. Its role is
twofold; first, it gives the possibility to quantify the
level of the learner and thus optimally adapt learning
materials and processes accordingly, and second, it
can identify learner progress patterns after some train-
ing sessions. Therefore, more sophisticated student
evaluation or scoring approaches have been proposed
which harness some additional information, called
traces, such as in (Kumar et al., 2015; Papamitsiou
and Economides, 2015). In (Papamitsiou and Econo-
mides, 2015), temporal trace data visualization dur-
ing the assessment has been proposed to help actors
involved in the activity to intuitively interpret and
quickly perceive a concealed feature. In (Kumar et al.,
2015), an on-line platform called Learnform has been
developed for problem solving in the domain of Elec-
tricity and Magnetism. Student progress evaluation is
based on platform’s logs, upon which Cohen’s statisti-
cal approach (Cohen, 1977) has been applied to com-
pare between student’s post-test scores with his/her
pre-test ones and state either the student has improved
or not his/her knowledge.
Given the possibility to attach the duration and
number of attempts in an interactive training activ-
ity, we can make use of these information as traces
to evaluate both learner level and progress. Indeed,
traces generated by a learner during his/her train-
ing activity are valuable in the process of evaluation
Chachoua, S., Tamani, N., Malki, J. and Estraillier, P.
Towards a Trace-based Evaluation Model for Knowledge Acquisition and Training Resource Adaption.
In Proceedings of the 8th International Conference on Computer Suppor ted Education (CSEDU 2016) - Volume 2, pages 121-128
ISBN: 978-989-758-179-3
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
121

of his/her knowledge acquisition level (Lebis et al.,
2015). Moreover, trace-based evaluation process al-
lows to compute relevant indicators that permit the
personalization of the analysis (Settouti et al., 2009c),
since traces can be attached to a unique user, and by
personalization we can obtain more accuracy in the
behavior modeling and analysis. For instance, a stu-
dent who took twice as much time as recommended
to solve a kind of problem can reveal some difficul-
ties faced by the learner to acquire the corresponding
knowledge. The reason could be related to student de-
ficiencies in prerequisite skills or the training strategy
(training materials and processes) is not adequate, or
both. Therefore, traces can disclose and reveal new
knowledge about both learners and teaching strate-
gies, which are actually difficult to reach with the
traditional evaluation methods. Again, traces about
the number of tries or attempts students carried out
to solve a problem, for instance, can inform experts
about both the level of knowledge the learners mas-
tered and the adequacy of the teaching materials to
learners’ profiles.
Subsequently, we introduce in this paper a theoret-
ical model for both student level and progress rhythm
evaluation based on two types of trace, namely, (i)
time spent to solve a problem, (ii) the number of
attempts or tries to solve it. Their combination is
also taken into account. In practical terms, we pro-
pose three mathematical functions which compute
learner’s performance indicators (we refer the reader
to (Wilhelm, 2009) for more details about perfor-
mance indicators in computer-based assessment) and
refined scores for the level of knowledge the learner
has acquired, and the way he/she managed to handle
training activities. The proposed approach is a first
step towards a trace-based learner behavior model for
knowledge acquisition and training resource adaption.
The significance of our approach is twofold:
• computing personalized e-learning performance
indicators for training materials and process adap-
tion. For instance, if the system notices that
a learner frequently fails to solve a given kind
of problem, then its recommends some actions
to be performed to adapt the contents and/or in
the training processes to knowledge level of the
learner,
• computing a personalized and refined assessment
of a learner regarding his/her knowledge acqui-
sition; thus the approach proposed can be seen
as a scoring or a grading method. In effect, the
approach introduced can distinguish between stu-
dents having answered correctly to a given test ac-
tivity but in different duration and number of at-
tempts.
The remainder of the paper is organized as fol-
lows. Section 3 summarizes some definitions about
traces and learner evaluation; then describes the posi-
tioning of our approach within a modeled trace-based
assessment process. Section 4 details our trace-based
assessment model. Section 2 discusses some related
work in the domain of e-Assessment. Finally, Sec-
tion 5 concludes the paper and gives some perspec-
tives for further research.
2 RELATED WORK
Automatic assessment or computer-based assessment
is considered as an important tool in educational sys-
tem as detailed in the large report of the European
Union (Scheuermann and Bj
¨
ornsson, 2009). This lat-
ter is a collection of articles and studies about the as-
sessment topic from diverse standpoints encompass-
ing assessment needs in European countries, Com-
puter Adaptive Testing (CAT), and methodologies of
computer-based testing and benchmarking, to name
a few. Amongst this collection, the authors of study
(Kozma, 2009) pointed out the limitation of tradi-
tional assessment methods as tools for measuring the
competencies and skills that are needed to be mas-
tered by the learners. Our proposed approach can be
seen as an improvement of such methods and also as
a step towards a computer adaptive testing based on
learners’ traces.
In (Crisp, 2009) three kinds of assessment and
their relationships have been introduced, namely: (i)
diagnostic which is performed before the learning
to estimate the level of students, (ii) formative
which is applied during the learning to test the
knowledge evolution and (iii) summative which is
considered after the learning to assess the knowledge
acquired. These assessment steps allow learners
to follow their progress and track their objectives
targeted during a given activity in order to know
if they passed or failed a given training level. In
(Amelung et al., 2011), the authors designed and
implemented a generic support of assessment for
assignments in programming languages, which
could be integrated into on-line laboratory (Guo,
2013). They also developed an eduComponents
(http://wdok.cs.ovgu.de/eduComponents/) module
for student evaluation, which only provides a semi-
automated and static assessment which is performed
by the tutor under the guidance of the tool. Thus,
the formative and summative assessments are carried
out by the instructor. However, eduComponents
offers only a semi-automated and static assessment
which is done by the tutor and assisted by the tool
CSEDU 2016 - 8th International Conference on Computer Supported Education
122

during student evaluation process. In (Nicol and
Macfarlane-Dick, 2006; Nicol, 2007), a large study of
formative assessment and feedback has been carried
out in order to identify how assessment processes
can help the enhancement and the development of
learner’s self-direction and regulation. Our approach
is actually a technical solution which covers the three
assessment types, since time and number of attempts
are useful traces for diagnostic processes to evaluate
learners knowledge level. The proposed approach
can also be used during the training process, pro-
viding formative evaluation or after training session
implementing a summative evaluation.
Finally, it is noteworthy that SCORM norm
(Scorm, 2006) considers both duration and attempts
in test activities, such as those implemented in lan-
guage e-learning platforms, IT certification courses
and exams, hiring tests, etc. In this case, duration
and number if attempts are not considered as traces,
as in our model, but as parameters to set for a test
or an exam, in order to put learners under a temporal
stress by imposing on them to answer some questions
or solve puzzles in a given time, usually short, even-
tually combined with a limited number of authorized
tries or attempts, beyond which the system consid-
ers that the candidate failed to answer the question or
solve the problem.
3 CONTEXT AND DEFINITIONS
In this section we briefly define some concepts useful
for the description of our approach. Section 3.1 intro-
duces definitions of trace and their related concepts.
Section 3.2 gives our definition of evaluation function
in an assessment process.
3.1 Trace Definition
In literature, the notion of trace often refers to log files
describing events happened in a given system (An-
drews, 1998). In (Djouad et al., 2010) a trace is a
series of things left by any action related to a being
or an object; a series of imprints or marks left by the
passage of an object or a being, which reveals that
something has existed. In our context, a digital trace
is any piece of information captured by observation
processes within an e-Learning activity. It represents
a residual footprint of interactions between learners
and training processes. A digital trace about an activ-
ity consists of objects which are chronologically ob-
served, captured and saved on a support. Such traces
are collected and analyzed by Trace-Based Systems
(TBS) (Settouti et al., 2009a; Laflaquiere et al., 2006).
A TBS considers three components as described in
(Mille et al., 2013).
• Observer: it is a system agent called obsel, which
is attached to event occurred during an execution
of an application. Each Obsel is characterized by
a name, a timestamp, and a set of properties.
• Trace model: is an abstract description of trace el-
ements. In other terms, it represents a trace vocab-
ulary and each trace can be associated to a model.
• M-Trace (for Modeled Trace): it is a trace at-
tached with its model, and managed by an m-
Trace-Based System (m-TBS). Figure 1 illustrates
two examples of Obsels: User and Training situ-
ation, and their recorded traces modeled respec-
tively by {user identifier (UserID), Date} and
{Name, Duration, Score, Attempts}.
The aforementioned modeled traces can be ex-
ploited within an e-Assessment component in both
training and learner evaluation.
3.2 Assessment Definition
To the best of our knowledge, grading or scoring func-
tions have been only considered in few work. For in-
stance, the authors in (Burstein et al., 2001) defined
the scoring function in a context of essay as a lin-
ear equation, and in (Yang et al., 2002), authors con-
sider automated scores are consistent with the scores
from expert human graders, fair and have been vali-
dated against external measures. As stated in (Kozma,
2009), there is a need for new theories and models
of scoring the students’ processes and strategies dur-
ing assessments, as well as outcomes. As stated in
(Williamson et al., 2012), the field of study of auto-
mated scoring remains new enough that the guidelines
of best practice are still evolving.
In our case, we combine both aspects by defining
a quantitative evaluation function, which computes a
value in R in contrast with symbolic evaluation func-
tion which returns a qualitative grading value such as
{A
+
, A, B, ..., F}.
Definition 1 (Quantitative Scoring Function). A
quantitative scoring function is any function f defined
from 2
A
, such as A is the set of all correct answers,
to [0, M], such as M ∈ N is the maximum mark, and
satisfies the following properties:
• f is fair: in the sense that f is a non-decreasing
function over the set 2
A
,
• f is bounded: f (
/
0) = 0 and f (A ) = M,
• minimality in the sense that any set of answers B
containing A, f (B ) should be less than f (A ).
Towards a Trace-based Evaluation Model for Knowledge Acquisition and Training Resource Adaption
123

We extend the definition of quantitative scoring
function to traces to define trace-based quantitative
scoring function.
Definition 2 (Trace-Based Quantitative Evaluation
Function). Let f be a quantitative scoring function
defined from 2
A
to [0, M], and T a trace defined over
a domain D. A trace-based quantitative scoring func-
tion is a binary function g defined from 2
A
× D to
[0, M] as follows.
2
A
× D −→ [0, M]
(A, d) 7−→ g( f (A), d)
such that g is bounded and fair.
3.3 Trace-based Automated Scoring
Process
Figure 2 describes the components of the trace-based
automated scoring process considered as follows:
• e-Learning system, equipped with a user interface
to interact with users,
• e-Assessment module which implements the scor-
ing and evaluation functions, and delivers the re-
sults to both learners and teachers/experts,
• m-trace database which is put between the e-
learning system and the e-Assessment module. It
is fed by the former with users’ traces, and it feeds
the latter with saved traces.
Its steps are also described as follows. Users in-
teract with the system (e-Learning platform, on-line
laboratory, etc.) in order to do a training activity.
Their interaction actions are tracked and the traces are
saved in trace database. The traces are then modeled
based on the three phases of (i) data collection, (ii)
data transformation, (iii) data analysis; this process is
out of the scope of this paper. We refer the reader to
(Settouti et al., 2009b) for more details. Then a test-
ing phase (see (Patelis, 2000; Thompson and Wiess,
2009; Sireci and Luecht, 2012)) is launched to check
whether the answer is correct or false. Other traces
are also generated from this process which are use-
ful to our evaluation function. After that, we apply
one of our assessment models: (i) time trace-based
model, (ii) attempt trace-based model and (iii) com-
bined time and attempt trace-based model for both
learner progression and training activities. Finally, a
performance step can be carried out to compute indi-
cators about learners progress and training resources
and/or strategies adequacy, in the evolution phase of
the e-Assessment process. The performance indica-
tors are delivered to experts to act accordingly by
adapting the training situations.
Figure 1: Examples of m-traces.
The following section details the trace-based
model we propose.
4 TRACE-BASED ASSESSMENT
AND EVALUATION MODEL
In this section we detail our evaluation models based
on traces left by a learner during his/her training activ-
ity. In Subsection 4.1 a time trace model considering
durations spent to solve a problem is introduced. In
subsection 4.2, our second model based on number
of tries is detailed. The combination of both traces is
introduced in Subsection 4.3.
4.1 Time Trace-based Evaluation Model
We suppose that traces are considered regarding a sin-
gle learner. A training activity can be attached with
two timestamps corresponding respectively to its start
instant and finish instant. These timestamps returns
the duration spent by the learner to perform the con-
sidered activity. As mentioned in the introduction the
time spent by the learner is useful for his/her evalua-
tion. The intuition behind our time trace-based model
is as follows.
• let a training objective be modeled as a set of m
testing activities O = {A
1
, ..., A
m
}, a testing activ-
ity can be any fill in blank exercise, reordering ex-
ercise, value to compute problem, single/multiple
choice question, etc.
• each exercise or activity A
i
with i = 1, ..., m, is
characterized by a full maximum mark, denoted
by M
A
i
, which can be set by an expert and/or a
trainer in the e-Learning system, or computed by
a quantitative scoring function f (see Definition
1), and an optimal duration, denoted D
A
i
,
• from temporal traces, it is possible to compute the
duration a learner took to answer the problem; let
us denote this duration by d,
• if the answer of the leaner is wrong, then his/her
score is 0,
CSEDU 2016 - 8th International Conference on Computer Supported Education
124

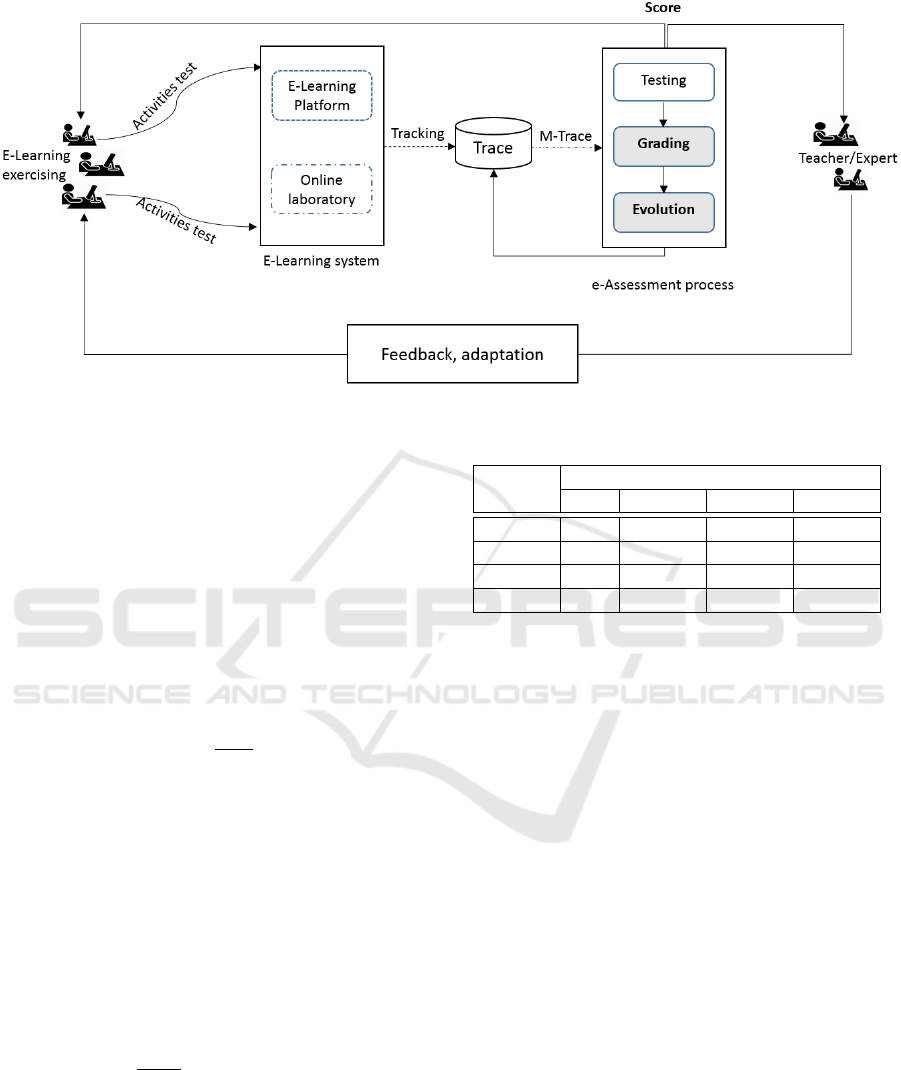
Figure 2: Traced-Based assessment process.
• if the learner answers well to the exercise in a du-
ration less than or equal to the optimal duration
D
A
i
, then he/she obtains the full mark M
A
i
,
• if the learner took more than the optimal duration,
then the longer the extra time he took to correctly
answer the question, the less the mark will be.
The mark obtained by the learner for the testing
activity A
i
, is computed by the trace-based binary
function M
A
i
(M
A
i
, d) (as introduced in Definition 2),
and defined by the following formula (1) based on the
duration taken to achieve it.
M
A
i
(M
A
i
, d) =



M
A
i
if (d ≤ D
A
i
),
M
A
i
e
−α(
d−D
A
i
D
A
i
)
otherwise.
(1)
such that:
• α ∈ [0, 1] is an attenuation constant. It allows
to compute a score in [0, M
A
i
], which indicates
that M
A
i
(M
A
i
, d) is bounded. If α is close to 0,
then M
A
i
(d) approaches M
A
i
. Otherwise if α ap-
proaches 1 then M
A
i
(M
A
i
, d) approaches 0. The
closer to 1 α is, the harsher the attenuation will
be. Moreover, for a fixed value for parameter α,
the longer the duration d is, the lower the mark
computed is, which shows the fairness of the bi-
nary function M
A
i
(M
A
i
, d),
• the fraction (
d−D
A
i
D
A
i
) aims at normalizing the dura-
tion to eliminate the effect of its unit of measure-
ment, and so for the mark computed.
It is worth noticing that the parameterized expo-
nential term in Formula (1) permits to capture the nat-
ural fading effect of the mark when the extra time in-
creases. Moreover, it well models the ability to ex-
press the importance of the skill the learner should
Table 1: Example of time trace-based model instantiation.
Learner
M
A
i
(M
A
i
, d)
d(s) α = 0.2 α = 0.5 α = 0.8
l
1
200 5 5 5
l
2
300 5 5 5
l
3
530 4.29 3.41 2.71
l
4
620 4.04 2.93 2.13
acquire in a given training activity by configuring the
constant parameter α. Indeed, the more important the
skill is, the closer to 1 α should be. This flexibility is
not easy to implement with a linear model. Besides,
when α = 0 then formula (1) reduces to a traditional
scoring function, which returns the full mark if the
answer is correct, independently of temporal traces.
Example 1. Let us suppose an e-Learning system for
SQL training. Let us suppose an exercise about an
SQL query for which we set the following parameters:
(i) M
A
i
= 5, (ii) D
A
i
= 300 seconds. To illustrate the
behavior of the model (formula (1)), we ran it thrice
with three different values of α such that α = 0.2 (low
importance level activity), α = 0.5 (medium impor-
tance level activity), and α = 0.8 (high importance
level activity). Table 2 summarizes the results ob-
tained for 4 learners {l
1
, l
2
, l
3
, l
4
} with their diverse
duration taken to solve the exercise.
We notice that the marks decrease according to
the extra-time took by the learner to do the activity.
With α = 0.2 the mark of learner l
4
has been dimin-
ished by about 20% compared with the full mark, even
though he/she took more than twice as much time as
recommended, and by more than 57% when α = 0.8.
Towards a Trace-based Evaluation Model for Knowledge Acquisition and Training Resource Adaption
125

4.2 Attempt Trace-based Model
In this subsection we define our second model which
is based on number of attempts (t). As mentioned in
the introduction the number of attempts performed by
the learner is also useful for his/her evaluation. The
intuition behind the model is as follows.
• in this case, each exercise or activity A
i
is char-
acterized by a full maximum mark M
A
i
, which
can be set by an expert and/or a trainer in the e-
Learning system, or computed by a quantitative
scoring function f (see Definition 1), and a num-
ber of allowed attempts, denoted T
A
i
,
• from attempt traces, it is possible to compute the
number of tries a given learner did to solve the
problem; let us denote this attempt number by t,
• if the answer of the leaner is wrong, then his/her
score is 0,
• if the learner answers well to the exercise in a
number of tries less than or equal to T
A
i
, then
he/she obtains the full mark M
A
i
,
• if the learner made more attempts than T
A
i
, then
the greater number of attempts he/she makes to
answer the question, the less the mark will be.
The mark obtained by the learner for the testing
activity A
i
, is computed by the trace-based binary
function M
A
i
(M
A
i
,t) (as introduced in Definition 2)
defined by the following formula (2) based on the
number of attempts t to achieve it.
M
A
i
(M
A
i
,t) =



M
A
i
if (t ≤ T
A
i
),
M
A
i
e
−β(
t−T
A
i
T
A
i
)
otherwise.
(2)
such that:
• β ∈ [0, 1]: is an attenuation constant. It allows to
compute a score in [0, M
A
i
], therefore M
A
i
(M
A
i
,t)
is bounded. If β is close to 0, then M
A
i
(M
A
i
,t)
approaches M
A
i
. Otherwise, if β approaches 1
then M
A
i
(M
A
i
,t) approaches 0. The closer to 1 β
is, the harsher the attenuation will be. Moreover,
for a fixed parameter β, the greater the number
of attempts t is, the lower the mark computed is.
Therefore, function M
A
i
(M
A
i
,t) is fair,
• The fraction (
t−T
A
i
T
A
i
) normalizes the number of
tries, and so for the mark computed by the func-
tion M
A
i
(M
A
i
,t).
We note that properties of formula (1) are still
valid for formula (2). Formula (2) is flexible enough
(by the exponential term) to catch the fading effect,
to express the importance of the training activity A
i
,
and behaves like a traditional scoring function when
β = 0.
Table 2: Example of attempt trace-based model instantia-
tion.
Learner
M
A
i
(M
A
i
,t)
Tries t β = 0.2 β = 0.5 β = 0.8
l
1
1 5 5 5
l
2
4 4.68 4.23 3.83
l
3
2 5 5 5
l
4
6 4.09 3.03 2, 25
Example 2. Let us consider the same exercise of Ex-
ample 1 for which the model parameters are set as fol-
lows: (i) M
A
i
= 5, and (ii) the number of allowed tries
T
A
i
= 3 . To illustrate the behavior of the model (for-
mula (2)), we consider 4 learners {l
1
, l
2
, l
3
, l
4
} and
their respective number of attempts to resolve the ex-
ercise. Table 2 summarizes the results obtained for
the learners, under the following values of β: 0.2 (low
importance level activity), 0.5 (medium importance
level activity), 0.8 (high importance level activity).
We notice the same effect of attenuation in the re-
sults and its severity when β increases (i.e becomes
close to 1).
4.3 Combination of Time and Attempt
Traces
In this subsection we define a combined model based
on both duration and number of attempts traces. We
recall that an activity A
i
has a full mark M
A
i
, which
can be set by an expert and/or a trainer in the e-
Learning system, or computed by a quantitative scor-
ing function f (see Definition 1), an optimal duration
D
A
i
,and an authorized number of tries T
A
i
. Let us de-
note the duration taken by a learner and his/her num-
ber of attempts by d and t respectively. Therefore, the
evaluation of the learner, denoted by M
A
i
(M
A
i
, d, t),
according to these parameters is as follows.
• if (d ≤ D
A
i
) and (t ≤ T
A
i
) then M
A
i
(M
A
i
, d, t) =
M
A
i
(the full mark),
• if (d > D
A
i
) and (t ≤ T
A
i
) then M
A
i
(M
A
i
, d, t) =
M
A
i
(M
A
i
, d) (by using Formula (1))
• if (d ≤ D
A
i
) and (t > T
A
i
) then M
A
i
(M
A
i
, d, t) =
M
A
i
(M
A
i
,t) (by using Formula (2))
• if (d > D
A
i
) and (t > T
A
i
) then we aggregate both
traces intuitively by summing the extra-time and
the extra number of attempts, then we apply the
same reasoning as for Formulas (1) and (2) to de-
fine the evaluation function of three parameters
M
A
i
(M
A
i
, d, t). Therefore, the combined model
can be expressed by Formula (3) as follows.
CSEDU 2016 - 8th International Conference on Computer Supported Education
126

Table 3: Example of combined duration and attempts traces
instantiation.
Learner
M
A
i
(M
A
i
, d, t)
d t γ = 0.2 γ = 0.5 γ = 0.8
l
1
200 1 5.00 5.00 5.00
l
2
300 4 4.68 4.23 3.83
l
3
530 2 4.29 3.41 2.71
l
4
620 6 3.31 1.78 0.96
M
A
i
(M
A
i
, d,t) =



















M
A
i
if (d ≤ D
A
i
) ∧ (t ≤ T
A
i
)
M
A
i
(M
A
i
, d) if (d > D
A
i
) ∧ (t ≤ T
A
i
)
M
A
i
(M
A
i
,t) if (d ≤ D
A
i
) ∧ (t > T
A
i
)
M
A
i
e
−γ(
t−T
A
i
T
A
i
+
d−D
A
i
D
A
i
)
otherwise.
(3)
such that:
• γ ∈ [0, 1] is an attenuation constant. It allows to
compute a score in [0,M
A
i
], therefore the function
M
A
i
(M
A
i
, d, t) is bounded. If γ is close to 0, then
M
A
i
(M
A
i
, d, t) approaches M
A
i
. Otherwise if γ ap-
proaches 1 then M
A
i
(M
A
i
, d, t) approaches 0. The
closer to 1 γ is, the harsher the attenuation will be.
Moreover, for a fixed parameter γ, the longer the
duration d and the greater the number of attempts
t are, the lower the mark computed is. Therefore,
function M
A
i
(M
A
i
, d, t) is fair.
Formula (3) has the same properties as Formulas
(1) and (2) in terms of fading effect, flexibility and
regular scoring.
Example 3. Let us consider the same learners of both
Examples 1 and 2. We recall the training activity pa-
rameters are as follows: the full mark M
A
i
= 5 points,
the optimal duration D
A
i
= 300 seconds, and the au-
thorized number of tries is T
A
i
= 3. To illustrate the
behavior of the model (formula (3)), we consider the
same traces obtained for the learners {l
1
, l
2
, l
3
, l
4
}.
Table 3 summarizes the results obtained for the four
learners under the following values for γ: 0.2 (low im-
portance level activity), 0.5 (medium importance level
activity), 0.8 (high importance level activity).
We notice in Table 3 the double effect of penal-
ties for leaner l
4
due to the extra time taken to solve
the problem and the number of tries which exceeds by
twice the authorized number.
5 CONCLUSION
We have developed in this paper a generic model for
evaluation of both learners and training strategies and
resources through performance indicators, based on
duration, number of attempts , and their both combi-
nation, which are considered here as modeled traces.
We have also illustrated the behavior of the model
through some simple examples. The proposed model
assesses in a flexible way the learner’s performance
and knowledge acquisition during a training activity.
It can also capture some patterns of behavior of the
learner during training sessions. In addition, the ex-
perts can configure in the model the importance of
a training activity from skill and knowledge acquisi-
tion standpoint, or limit the model to perform a reg-
ular scoring by setting the attenuation constants to 0.
This kind of evaluation allows, on the one hand, per-
sonalizing and adapting learner training strategy and
resources, and personalizing assessment of the knowl-
edge acquisition which helps learner’s categorization
and ranking, on the other hand.
The next step in our work is the implementation
and test of the model we proposed in an online lab-
oratory for SQL training, which is already developed
in our research team. We need particularly to empir-
ically compute the appropriate attenuation constants
used in the model. We also plan to develop the
adaption process combining the performance indica-
tor proposed and semantics rules describing the ac-
tions and tasks to undertake to adapt learning strate-
gies and resources to cope with pedagogical objec-
tives the learner has to achieve in his/her training ac-
tivities. An implementation of the extended approach
is also planned for its validation through real world
use cases.
REFERENCES
Amelung, M., Krieger, K., and Rosner, D. (2011). E-
assessment as a service. Learning Technologies, IEEE
Transactions on, 4(2):162–174.
Andrews, J. H. (1998). Testing using log file analysis: tools,
methods, and issues. In Automated Software Engi-
neering, 1998. Proceedings. 13th IEEE International
Conference on, pages 157–166. IEEE.
Burstein, J., Leacock, C., and Swartz, R. (2001). Automated
evaluation of essays and short answers.
Cohen, J. (1977). Statistical power analysis for the behav-
ioral sciences (rev. Lawrence Erlbaum Associates,
Inc.
Crisp, G. (2009). Interactive e-assessment: moving be-
yond multiple-choice questions. Centre for Learning
and Professional Development. Adelaide: University
of Adelaide, 3:12–31.
Crooks, T. J. (1988). The impact of classroom evaluation
practices on students. Review of educational research,
58(4):438–481.
Djouad, T., Settouti, L. S., Pri
´
e, Y., Reffay, C., and Mille,
Towards a Trace-based Evaluation Model for Knowledge Acquisition and Training Resource Adaption
127

A. (2010). Un syst
`
eme
`
a base de traces pour la
mod
´
elisation et l
´
elaboration dindicateurs dactivit
´
es
´
educatives individuelles et collectives. mise
`
a l
´
epreuve
sur moodle. Mise
`
a l
´
epreuve sur Moodle. Technique
et Science Informatiques.
Guo, P. J. (2013). Online Python Tutor: Embeddable web-
based program visualization for CS education. In
Proceedings of the 44th ACM Technical Symposium
on Computer Science Education, SIGCSE ’13, pages
579–584, New York, NY, USA. ACM.
Kozma, R. (2009). Transforming education: Assessing
and teaching 21st century skills. The transition to
computer-based assessment, 13.
Kumar, R., Chung, G. K., Madni, A., and Roberts, B.
(2015). First evaluation of the physics instantiation
of a problem-solving-based online learning platform.
In Artificial Intelligence in Education, pages 686–689.
Springer.
Laflaquiere, J., Settouti, L. S., Pri
´
e, Y., and Mille, A.
(2006). Trace-based framework for experience man-
agement and engineering. In Knowledge-Based In-
telligent Information and Engineering Systems, pages
1171–1178. Springer.
Lebis, A., Lefevre, M., Guin, N., and Luengo, V. (2015).
Capitaliser les processus danalyses de traces dappren-
tissage ind
´
ependamment des plates-formes danalyses
de traces. Technical report, LIG-LIRIS. ANR Project
HUBBLELEARN.
Martin, R. (2008). New possibilities and challenges for as-
sessment through the use of technology. Towards a re-
search agenda on computer-based assessment, page 6.
Mille, A., Champin, P.-A., Cordier, A., Georgeon, O., and
Lefevre, M. (2013). Trace-based reasoning-modeling
interaction traces for reasoning on experiences. In The
26th International FLAIRS Conference, pages 1–15.
Nicol, D. (2007). E-assessment by design: using multiple-
choice tests to good effect. Journal of Further and
Higher Education, 31(1):53–64.
Nicol, D. J. and Macfarlane-Dick, D. (2006). Formative
assessment and self-regulated learning: A model and
seven principles of good feedback practice. Studies in
higher education, 31(2):199–218.
Papamitsiou, Z. and Economides, A. A. (2015). Tem-
poral learning analytics visualizations for increasing
awareness during assessment. RUSC. Universities and
Knowledge Society Journal, 12(3):129–147.
Patelis, T. (2000). An overview of computer-based testing.
Scheuermann, F. and Bj
¨
ornsson, J. (2009). The transition to
computer-based assessment. Luxembourg: Office for
Official Publications of the European Communities.
Scorm (2006). SCORM 2004 Handbook. The e-Learning
Consortium, Japan. Version 1.04.
Settouti, L. S., Pri
´
e, Y., Champin, P.-A., Marty, J.-C., and
Mille, A. (2009a). A trace-based systems framework:
Models, languages and semantics.
Settouti, L. S., Pri
´
e, Y., Cram, D., Champin, P.-A., and
Mille, A. (2009b). A trace-based framework for sup-
porting digital object memories. In Workshops Pro-
ceedings of the 5th International Conference on Intel-
ligent Environments, Barcelona, Spain, 19th of July,
2009, pages 39–44.
Settouti, L. S., Pri
´
e, Y., Marty, J., and Mille, A. (2009c).
A trace-based system for technology-enhanced learn-
ing systems personalisation. In The 9th IEEE Inter-
national Conference on Advanced Learning Technolo-
gies, ICALT 2009, Riga, Latvia, July 15-17, 2009,
pages 93–97. IEEE Computer Society.
Sireci, S. and Luecht, R. M. (2012). A review of models for
computer-based testing.
Thompson, N. and Wiess, D. (2009). Computerised and
adaptive testing in educational assessment. The tran-
sition to computer-based assessment. New approaches
to skills assessment and implications for large-scale
testing, pages 127–133.
Wandall, J. (2011). National tests in denmark–cat as a ped-
agogic tool. Association of Test Publishers, 12(1).
Wilhelm, O. (2009). Issues in computerized ability mea-
surement: Getting out of the jingle and jangle jungle.
The transition to computer-based assessment, pages
145–150.
Williamson, D. M., Xi, X., and Breyer, F. J. (2012). A
framework for evaluation and use of automated scor-
ing. Educational Measurement: Issues and Practice,
31(1):2–13.
Yang, Y., Buckendahl, C. W., Juszkiewicz, P. J., and Bhola,
D. S. (2002). A review of strategies for validating
computer-automated scoring. Applied Measurement
in Education, 15(4):391–412.
CSEDU 2016 - 8th International Conference on Computer Supported Education
128