
An Analysis of Factors Affecting Automatic Assessment based on
Teacher-mediated Peer Evaluation
The Case of OpenAnswer
Maria De Marsico
1
, Andrea Sterbini
1
and Marco Temperini
2
1
Department of Computer Science, Sapienza University, Rome, Italy
2
Department of Computer, Control and Management Engineering, Sapienza University, Rome, Italy
Keywords: Peer Assessment, OpenAnswer Questions, Automatic Grade Prediction.
Abstract: In this paper we experimentally investigate the influence of several factors on the final performance of an
automatic grade prediction system based on teacher-mediated peer assessment. Experiments are carried out
by OpenAnswer, a system designed for peer assessment of open-ended questions. It exploits a Bayesian
Network to model the students’ learning state and the propagation of information injected in the system by
peer grades and by a (partial) grading from the teacher. The relevant variables are characterized by a
probability distribution (PD) of their discrete values. We aim at analysing the influence of the initial set up
of the PD of these variables on the ability of the system to predict a reliable grade for answers not yet
graded by the teacher. We investigate here the influence of the initial choice of the PD for the student’s
knowledge (K), especially when we have no information on the class proficiency on the examined skills,
and of the PD of the correctness of student’s answers, conditioned by her knowledge, P(C|K). The latter is
expressed through different Conditional Probability Tables (CPTs), in turn, to identify the one allowing to
achieve the best final results. Moreover we test different strategies to map the final PD for the correctness
(C) of an answer, namely the grade that will be returned to the student, onto a single discrete value.
1 INTRODUCTION
Peer assessment is widely deemed to be a useful
exercise to challenge as well as improve one’s
understanding of a topic but also to achieve higher
metacognitive abilities. Actually, according to
Bloom’s taxonomy of educational objectives in the
cognitive domain (Bloom et al., 1956), learner’s
abilities increase when passing from pure knowledge
(the ability to remember a topic is considered at the
lower level), to comprehension, application,
analysis, evaluation and finally synthesis. In
(Anderson et al., 2000) a revised version of the
taxonomy is proposed, where remember, understand
and apply lay at increasing levels, while analyse,
evaluate and create lay at the same top level. In any
case, the ability to evaluate is considered a higher
one. It is a metacognitive skill going beyond the
proficiency in a single topic, though requiring it. As
a matter of fact, as discussed by Metcalfe and
Shimamura (1994), metacognitive activities require
not only knowing but also knowing about knowing.
The accepted definition of metacognition refers to
higher order thinking, entailing the ability to
exercise an active control over the cognitive
processes underlying learning. Planning strategies
and schedules to carry out a learning task,
monitoring one’s and others’ comprehension of a
topic and the progress towards the completion of a
task, and being aware of how to apply newly
acquired concepts and rules, all play a critical role in
successful learning. Therefore, besides exercising
cognitive skills, also metacognitive ones should be
cared for in educational planning. Peer assessment
can be exploited to this aim. The framework
implemented through the OpenAnswer system
(Sterbini and Temperini, 2012, 2013a, 2013b)
adopted for the experiments presented in this paper
allows (semi-)automated grading of open answers
through peer assessment, with the further goal of
relieving the teacher from part of the burden of
grading the complete set of answers. As a matter of
fact, while this kind of exercise provides a much
more reliable evaluation of students’ proficiency
with respect to, e.g., multiple-choice tests (Palmer
Marsico, M., Sterbini, A. and Temperini, M.
An Analysis of Factors Affecting Automatic Assessment based on Teacher-mediated Peer Evaluation - The Case of OpenAnswer.
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 2, pages 49-61
ISBN: 978-989-758-179-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
49

and Richardson, 2003), they are also much more
demanding for the teacher too since they require a
longer revision activity. Of course, the condition for
the system to be useful is to provide reliable
outcomes, and we are investigating several factors
that could affect them. During an OpenAnswer
assessment session, each student is requested to
grade some (e.g., 3) of her/his peers’ answers. The
validity of results of peer evaluation is enforced by
requiring that a subset of answers (chosen according
to some relevant criterion which will be discussed in
the following) is further graded by the teacher.
Information provided by peers’ and teacher’s
assessments is fed and propagated within a Bayesian
Network (BN). In such network the students are
modelled by their Knowledge level on the topic (K),
and by the correctness of their evaluations, denoted
as Judgment (J). In the network, the answers of a
single student have an estimated Correctness (C).
Such value can be updated by evidence propagation.
When a student marks an answer by a peer, a
corresponding Grade (G) is injected into the
network, and propagates its effects depending on
both J of the grading student and on current
estimation of C of the peer answer. Variables C and
J are assumed to be conditioned by K (C|K and J|K),
therefore for each of them we have a Conditional
Probability Table (CPT). In this process, students
can both understand how the grading process should
work, by matching the grades they assigned with
final ones (possibly by the teacher, or inferred by the
system through the BN), and learn from smarter
peers how to improve their results (Sadler and Good,
2006). Providing to the students the final values of
their own K and J returned by the system, besides
the pure exercise grade, can spur further
metacognitive awareness.
In the present work we first use traditional
assessment (done by the teacher in the whole, and
being our ground truth) to systematically evaluate
and compare with it the grading accuracy achievable
by different policies to use our teacher-mediated
peer assessment. These strategies range from pure
manual peer assessment to peer assessment
propagated by OpenAnswer without teacher’s
grading, to complete exploitation of OpenAnswer
potentialities with peer assessment complemented by
teacher's (partial) grading in OpenAnswer, with
different strategies for the choice of next answer to
grade and for termination (no further grading is
required from the teacher). In this respect, we
introduce new strategies for the choice of the next
answer, namely maxInfoGain, maxStrangeness, and
maxTotalEntropy, which will be detailed in the
following. We evaluate the influence of some
preliminary choices on system performance. More
important, we want to show how the work by the
teacher in our framework can improve the pure peer
assessment accuracy. In this context we investigate
the effect of different choices for the initial
distribution of K values (for each student) on system
evaluation performances, especially when no or little
knowledge is available on specific students’ skills on
the topic at hand. We evaluated different choices for
the initial CPT of C|K, that then evolves to a final
value during the peer assessment/teacher grading.
Then we compared different strategies to map the
grade distribution (C), achieved by each student,
onto a single final grade.
2 RELATED WORK
The automatic analysis of open answers is a
powerful means to manage assessment in education,
also known as knowledge tracing (Anderson et al.,
1995). It is met, though, in other fields, such as in a
context of marketing applications, where techniques
of data mining and natural language processing are
used to extract customer opinions and synthesize
products reputation (Yamanishi and Li, 2002). In
(Jackson and Trochim, 2002) concept mapping and
coding schemes are used with the same goal. The
(semi-)automatic assessment of open-answers
proposed in (Castellanos-Nieves et al., 2011) relies
on ontologies and semantic web technologies. The
ontology models the knowledge domain related to
the questions, and also aspects of the overall
educational process. In (El-Kechaï et al., 2011) open
answers are examined to identify and treat students
misconceptions which hinder learning
Peer-assessment is the activity in which a
learner, or a group of learners, assesses the product
of other learners (the peers) meanwhile engaging in
a notoriously high cognitive level activity (Bloom et
al., 1956). Peer-assessment can be used to pursue
both formative and summative aims (Topping,
1998): in the first case the aim is to allow the learner
to appreciate her cognitive situation (such as level of
knowledge, or lacks therein) and monitor her
progress. In the second case not all the available
information might reach the learner, and the aim is
to evaluation and possible support to the selection of
remedial activities.
Li et al. (2010) states that a relationships does
exist between the quality of the peers feedback, on a
learner's job, and the quality of the final project
submitted by the learner. A comprehensive study of
CSEDU 2016 - 8th International Conference on Computer Supported Education
50

peer assessment in a prototype educational
application is in Chung et al. (2011).
The OpenAnswer system relies on the evaluation
of answers coming from peer-assessment, and on the
student modelling managed by Bayesian Networks.
Another machine learning approach to student
modelling is in (Conati et al., 2002), where Bayesian
Network techniques are used to support learner's
modelling in an Intelligent Tutoring System (ITS).
The modelling is devised to support activities
relevant in an ITS: knowledge assessment, plan
recognition and prediction, the last two deemed to
see what intentions are behind a learner's choice, and
what following choices might be, during the phase
of problem solving.
In OpenAnswer the peer is presented with a set
of assessing criteria, to refer to while marking; the
criteria are defined by the teacher, and are supposed
to be adhered to by the teacher, during her grading
too. In our experience too many criteria might result
cumbersome for the peers. We have not investigated,
though, on this aspect. In literature the specificity of
"scoring criteria" has been identified as an important
factor against the problem of having assessors that
limit the range of their marks to a subset (typically
in the high end) of the scale; in this case the problem
is twofold, involving both peers leniency and
shrinking of the marking scale (Miller, 2003).
An aspect of research in peer-assessment regards
the number of peer-evaluations that a same job
should undergo during the peer-evaluation process.
In OpenAnswer this is configurable, with default to
3. In literature it is found that more feedbacks on the
same job make the peer performing more complex
revisions on her product, ending up with a better
result (Cho and MacArthur, 2010).
3 OpenAnswer SYSTEM
The intended use of OpenAnswer system is to
support semi-automatic grading of answers to open-
ended questions (open answers) through peer
assessment. From one side, it can be used by the
teacher to spur students’ evaluation metacognitive
ability, and therefore to also evaluate their
performance in assessing the answers of their peers,
thus getting further information on their deep
understanding of topics. From the other side, it may
underlie strategies to limit the amount of teacher’s
grading effort. Many proposed systems are
developed along the first line. We pursue both. After
all, automatic grading techniques relying exclusively
on peer assessment are still not reliable enough.
OpenAnswer (Sterbini and Temperini, 2012, 2013a,
2013b), as well as similar previous work (Sterbini
and Temperini, 2009), rather adopts a mixed
approach, to pursue both goals at the same time. In
order to enforce/emend the results of peer
evaluation, and therefore increase the reliability of
final grades, the teacher is required to assess some
part of the answers, whose number and identification
depends on the chosen corresponding strategies that
will be presented in the following. In this way the
teacher’s grading workload will be reduced,
therefore encouraging a more frequent use of an
educational strategy entailing open answer tests and
peer assessment, while students will receive both the
grading of their answers and be able to compare
their peer grading with the correct one. As further
detailed below, the system suggests to the teacher
the order of answers to manually grade, according to
a selection strategy chosen in advance among a
number of available ones. Manual grading can stop
when some pre-defined termination criterion is met.
Even in this case, a number of criteria are available.
After the termination criterion is met, the system
automatically completes the grading task for the
remaining answers using the correctness information
collected so far, together with the results of the peer
grading. The OpenAnswer approach relies on a
simple Bayesian network model. The individual
student model is represented by a Bayesian network.
The variables defining the model include an
assumed value for the learner’s state of knowledge
on the exercise topic (K), and the ability to judge (J)
answers given by peers on the same topic. Actually,
as it is quite natural, we assume that the value of J is
conditioned by the value of K. These variables are
exploited in the system state evolution and affect the
way information is weighted while propagated. For
each peer assessment session, the individual student
networks are interconnected depending on the
current sets of answers that each student receives to
grade. Therefore, different sessions may entail
different interconnection patterns. Each answer is
characterized by its correctness (C), measuring the
student ability to provide a correct solution, and by
the grades (G) assigned by the peers to it. C is a
variable depending on the student K value and is
characterized by a conditional PD, that reduces to a
single grade once the answer is manually graded by
the teacher. All variables are characterized by a
probability distribution (PD) of discrete values that
follows the same convention of grading. In our case,
depending on the datasets used as testbed, this
entails 6 (from A to F) or 5 (A, B, C, D, F) values,
with F=Fail.
An Analysis of Factors Affecting Automatic Assessment based on Teacher-mediated Peer Evaluation - The Case of OpenAnswer
51

It is worth underlying that, according to Bloom’s
taxonomy and building on results presented in (De
Marsico et al., 2015), we chose a PD which, for each
value of J|K=k, has its maximum on k-1. This is
supported by the assumption, confirmed by
evidence, that judging the work of a peer is more
engaging that carrying out the same work. In this
work we want to assess if this choice is also suitable
for P(C|K). To this aim we investigate the influence
of different definitions for P(C|K) on system
outcome reliability.
C and G control evidence propagation according
to the possible matching between teacher's and peer
assessments. In particular, the J of a student is
connected to the Cs corresponding to the evaluated
peer answers through the assigned grades G. The
resulting compound network is continuously
updated. Figure 1 shows an example BN fragment
for a student that graded three peers. Evidence
propagation happens in two phases. The first one is
only based on peer assessment grades (G).
Afterwards, when the teacher starts grading, the
grades provided affect the C variables of
corresponding answers (they become fixed values,
i.e. the conditional PD concentrates on a single
value), therefore affecting J values of grading peers
through the Gs that they assigned to the same
answers. In turn, this indirectly affects J and K
variables of the student author of the answer, and
indirectly the J and K values of grading peers.
Figure 1: An example fragment of Bayesian Network in
OpenAnswer: student S1 grades the answers of students
S3, S5 and S21, and notwithstanding the most probable
value of D for K, presents a current most probable grade F
for his/her answer.
During the following manual grading phase, the
system supports the teacher by suggesting the next
“best” answer to grade according to one of the
selection criteria detailed below, and by propagating
in the network the added information provided by
the teacher’s grade. After each evidence propagation
step, the teacher grading step is iterated until a
termination condition is met. In practice, the latter
states that new information from additional teacher’s
grades would be less decisive. When the teacher
stops grading after a sufficient number of answers,
the information collected so far allows to
automatically grade those answers that were not
directly graded by the teacher. In practice, grades
not directly given by the teacher are inferred
according to the current probability distribution
associated to the C values. Of course, it is necessary
to devise also a suitable mapping strategy from PDs
to single values to return to students.
The possible system strategies to suggest the
next answer to grade are:
• max_wrong: the system suggests to grade the most
probably incorrect answer, i.e. the one with highest
probability of having C=’F’;
• max_entropy: the system suggests to grade the
answer presenting the highest entropy (the answer
the system knows less about, or about which has
less information for inference); the entropy of an
answer is the entropy of the corresponding C
variable;
• maxInfoGain: the system chooses the answer that
guarantees the greater assured information
variation; the latter is the minimum variation of
total entropy of the network that is produced by
each of the possible grades that the teacher might
assign to a certain answer, by propagating the
grade choice in the network; the total entropy of
the network is the sum of entropies computed for
all K, J and C variables of all students in the BN;
of course this strategy is the slowest one, but no
real time outcome is required;
• maxStrangeness: the system chooses the answer
with the greater strangeness; strangeness is the
absolute value of the difference between J and C
(after mapping their current respective PDs as
computed by the network into single values); this
is to capture the two peculiar cases of a student
with high C but low J (good knowledge but low
judgment ability) and vice versa;
• maxTotalEntropy: the system chooses the answer
by the student with maximum total entropy, with
total entropy of a student being the sum of the
entropies of the associated C, J and K variables;
• random: the next answer to grade is chosen at
random; this strategy is mostly used for testing
purposes, as it should provide a comparison with
totally random choices, and indirectly information
CSEDU 2016 - 8th International Conference on Computer Supported Education
52

on the effectiveness of chosen alternatives; it is not
used in the present work;
The termination criterion can be chosen among
the following:
• none: no answer at all is graded by the teacher,
therefore this corresponds to “pure” peer
assessment yet with the evidence propagation
provided by OpenAnswer;
• no_wrong: no more ungraded answers exist which
would be automatically graded as wrong (C='F')
once the PD of C is mapped onto a grade;
• no_wrong2: for all remaining answers P(C=’F’)
≤
1/2;
• no_wrong3: for all remaining answers P(C=’F’)
≤
1/3;
• no_flip(N): the automatically computed grades
remained stable in the last N correction steps.
In general, max_wrong is best associated with
no_wrong<p> and max_entropy with no_flip(N),
while random can be associated with both the
termination criteria.
4 ASPECTS INVESTIGATED IN
THE EXPERIMENTS
In the present work, we explored different
evaluation settings for OpenAnswer system. First,
we matched grading accuracy achievable through
peer assessment against traditional assessment
(completely by the teacher, our ground truth) in
different settings: 1) pure peer assessment (without
OpenAnswer system), 2) peer assessment with
OpenAnswer without teacher's contribution
(propagation of peer grades through the Bayesian
network in OpenAnswer, without any grading by the
teacher, i.e. termination=none), 3) peer assessment
complemented by teacher's (partial) grading in
OpenAnswer, with different policies for the choice
of next answer to grade and for termination (no
further grading is required from the teacher). To this
respect, we introduce new strategies for the choice
of the next answer, namely maxInfoGain,
maxStrangeness, and maxTotalEntropy, described in
the previous section. Our main goal is to evaluate
the influence of some preliminary choices on system
performance, i.e., on the quality of assessment, on its
reliability (rate of grades correctly inferred), and on
the work requested by the teacher.
In this context we investigated also the effect of
different choices for the initial distribution of K
values (for each student) on system evaluation
performances. We have two possible alternatives.
The first one can only be used in experimental
settings, and entails an ex-post knowledge of the
group of students and their learning state on the
specific topic being assessed. The assumption is that
having such knowledge can improve the quality of
information propagation in the BN. In this case we
exploit two sub-choices. The first, more relaxed one
is to assume for all students the same probability
distribution for K, which is equal to the distribution
obtained for the manual exercise grading (performed
completely by the teacher) that is used as ground
truth. This is reported by columns labelled as
TgrDist (Teacher’s Grade Distribution) in the tables
reporting experimental results. It is worth
underlining that this choice can also realistically
model cases, that we do not consider here, when we
can inherit and exploit the distribution of knowledge
of the class obtained in previous assessment sessions
on a similar topic. The second entails assigning to
each student with probability=1 the level of
knowledge corresponding to the grade achieved,
again obtained from teacher’s grading. This is
reported by columns labelled as Tgrade (Teacher’s
Grades) in the tables reporting experimental results.
The Tgrade distribution is the less realistic one and
can be considered as an upper bound, as we will
discuss in more detail in the following.
The second situation is the realistic one, and
entails ex-ante attempts to model students in a
starting setting, where no or little knowledge is
available on specific students’ skills on the topic at
hand. In this case we have further two sub-choices,
namely: to assume for each student an equal
probability for all K levels, reported by columns
labelled as flat in the tables reporting experimental
results, or to apply to all students a same, synthetic
and “reasonable” PD for K, reported by columns
labelled as synthetic. The synthetic PDs for K for 6
or 5 grade values are shown if Figure 2.
A 0,10
B 0,20 A 0,15
K
C
0,30 B 0,30
D 0,20
K
C 0,30
E 0,10 D 0,15
F 0,10 E 0,10
Figure 2: Synthetic PDs, stating initial values of K, in the
cases of 6-valued and 5-valued scale for the value of K.
We use the “artificial” setting, in particular
Tgrade, to evaluate an upper bound to achievable
results. Once we identify the combination <strategy,
termination> achieving the best results, we can
An Analysis of Factors Affecting Automatic Assessment based on Teacher-mediated Peer Evaluation - The Case of OpenAnswer
53
observe which is the best realistic distribution for K
values to adopt with this combination.
As a further element that can affect final
effectiveness of OpenAnswer assessment, we tested
different Conditional Probability Tables (CPTs) for
the level of correctness P(C|K). We started from the
same CPT as for J|K, which entails a distribution
that for each value of C|K=k has its maximum on k-
1. We show the corresponding CPTs (labelled as
CPT1) (in Figure 3 the two cases of 6-valued and 5-
valued grading scale are shown). This CPT differs
from the others for both the choice of the value of C
with maximum probability for each value of K, and
for the fraction of probability assigned to such value.
It is worth underlining that at the moment this is the
same CPT that we use in all experiments for P(J|K).
In the future we plan to test different choices for
P(J|K) too.
C|K A B C D E F
A 0,20 0,09 0,01 0,01 0,01 0,01
B 0,40 0,20 0,09 0,07 0,06 0,01
C 0,20 0,40 0,20 0,12 0,10 0,01
D 0,12 0,20 0,40 0,20 0,18 0,07
E 0,07 0,09 0,20 0,40 0,25 0,20
F 0,01 0,02 0,10 0,20 0,40 0,70
C|K A B C D F
A 0,20 0,09 0,01 0,01 0,01
B 0,40 0,20 0,09 0,07 0,01
C 0,20 0,40 0,20 0,12 0,01
D 0,17 0,26 0,55 0,40 0,12
F 0,03 0,05 0,15 0,40 0,85
Figure 3: CPT1: for each k the probability distribution of
P(C|K=k) in column k, has its maximum on row C=k-1
(the upper table shows the values for the 6-valued grading
scale; the lower table is related to the 5-valued scale).
C|K A B C D E F
A 0,40 0,05 0,05 0,05 0,05 0,02
B 0,30 0,40 0,05 0,05 0,05 0,03
C 0,15 0,25 0,45 0,15 0,10 0,10
D 0,10 0,15 0,20 0,45 0,15 0,15
E 0,04 0,10 0,15 0,15 0,45 0,25
F 0,01 0,05 0,10 0,15 0,20 0,45
C|K A B C D F
A 0,40 0,05 0,05 0,05 0,02
B 0,30 0,40 0,05 0,05 0,03
C 0,15 0,25 0,45 0,15 0,10
D 0,12 0,20 0,28 0,55 0,27
F 0,03 0,10 0,17 0,20 0,58
Figure 4: Second tested CPT2: for each value K=k we
devised a “reasonable” distribution for C values. Again the
two cases of 6- and 5-valued grading scale are shown.
As a second alternative we tested a ”reasonable”
distribution of C values for each value K=k. Figure 4
shows the corresponding CPTs (CPT2). Then we
tested two other CPTs for C that not only
concentrate the highest probability on c=k, but also
assume such probability P(C=k|K=k)=0.5. In both
cases, half conditional probability is concentrated on
the same value the student achieves for K, while the
remaining 0.5 is divided according to some criteria
among the other grades. And in both cases we
assumed a higher probability to achieve a
correctness value which is lower than K than a
higher one. For the first case, we created the
conditional probability distributions P(C|K=’A’) and
P(C|K=’F’), (corresponding to the first and last
column in the CPT), which represent extreme cases,
establishing some “reasonable” relations among
such probabilities. As for the other columns, we
assumed 2/5 of the remaining probability (total 0.20)
to achieve a higher grade, and 3/5 (total 0.30) to
achieve a lower one. Given m the number of higher
(lower) grades to handle, we then computed
=
∑
1
, and assigned to the less probable
grade 0.20 × , to the second less probable
the grade 0.20 × 2 × , and so on
(respectively, 0.20 × , 0.20 × 2 × ,
and so on). Figure 4 shows the resulting CPTs.
C|K A B C D E F
A 0,50 0,20 0,07 0,03 0,02 0,01
B 0,30 0,50 0,13 0,07 0,04 0,03
C 0,10 0,12 0,50 0,10 0,06 0,06
D 0,06 0,09 0,15 0,50 0,08 0,10
E 0,03 0,06 0,10 0,20 0,50 0,30
F 0,01 0,03 0,05 0,10 0,30 0,50
C|K A B C D F
A 0,50 0,20 0,07 0,03 0,02
B 0,30 0,50 0,13 0,07 0,08
C 0,10 0,15 0,50 0,10 0,10
D 0,08 0,10 0,20 0,50 0,30
F 0,02 0,05 0,10 0,30 0,50
Figure 5: CPT3, 6-valued (up) and 5-valued grading
scale): half probability is concentrated on C=k|K=k.
The last CPT tested follows the rules above also
for the first and last columns (K=’A’ and K=’F’),
except that the amount of probability which is not
applicable (the probability to increase the grade for
K=’A’ or decrease it for K=’F’) is summed to
P(C=k|K=k).
We finally evaluated different strategies to map
back the correctness distribution (C) achieved by
each student at the end of the evaluation session into
CSEDU 2016 - 8th International Conference on Computer Supported Education
54
a single grade (parameter P2VAL - prob2value in
the tables below). We explored different solutions:
1) take the centre of the interval corresponding to the
grade with highest probability (label max1P in the
experiment tables); 2) take the weighted and
normalized sum of the two grades in the distribution
with the highest probabilities (label max2P), where
weights are the achieved probabilities; 3) take the
weighted and normalized sum of the three grades in
the distribution with the highest probabilities (label
max3P); 4) take the weighted and normalized sum
of all grades in the distribution (weightedSum -
wSum in the tables below); 5) take the weighted
sum of the most probable values, till to reach 75% of
accumulated probability (label best75%).
C|K A B C D E F
A 0,70 0,20 0,07 0,03 0,02 0,01
B 0,10 0,50 0,13 0,07 0,04 0,03
C 0,08 0,12 0,50 0,10 0,06 0,04
D 0,06 0,09 0,15 0,50 0,08 0,05
E 0,04 0,06 0,10 0,20 0,50 0,07
F 0,02 0,03 0,05 0,10 0,30 0,80
C|K A B C D F
A 0,70 0,20 0,07 0,03 0,02
B 0,12 0,50 0,13 0,07 0,04
C 0,09 0,15 0,50 0,10 0,06
D 0,06 0,10 0,20 0,50 0,08
F 0,03 0,05 0,10 0,30 0,80
Figure 6: CPT4: half probability is concentrated on
C=k|K=k plus, in first and last columns, the total
probability of increasing or decreasing the grade.
5 EXPERIMENTAL RESULTS
The datasets we exploited for experiments are
collections of exercises with their corresponding
peer assessment data. In addition, each peer
assessment session is integrated by the teacher
complete grading: it is used as ground truth to
evaluate the reliability of the semi-automatic grading
results returned by OpenAnswer. Datasets come
from different educational contexts, namely
University or High School, and exercises deal with
different topics, from both scientific and social
sciences courses.
Table 1 reports the composition of each
collection.
Table 1: The composition of the used benchmark data.
Dataset Level Topic Groups Students
A-6-1 Univ.
4 exercises on multi-
level cache systems
2 7 to 15
M-6-1 Univ.
3 exercises on C
programming
2 9 to 13
I-6-1
High
School
1 physics exercise
2 14 and 12
A2-5-4 Univ.
1 essay on social
tools
5 12
Near to each collection label we report the
number of values used for grade/levels, that are used
in turn to model the discrete Bayesian variables, and
the number of teachers involved. When more
teachers graded the same exercise, we run an
independent simulation for each of them, using the
same data from students, with different teacher
grading. We first report the average performance of
pure peer assessment over the different sessions on
the different datasets, i.e., the accuracy of students’
grading w.r.t. the ground truth of teachers’ grading.
Table 2 reports the average percentage of correct
(i.e. equal to teacher’s) peer grades (OK/TOTAL)
and of grades within 1 mark (IN1/TOTAL) from the
teacher grade. Regarding rows labelled as “A2 avg”
and “A2 median” in Table 2, we remind that in
dataset A2 the students’ answers were graded by 4
different teachers. In the first row in Table 2, the
grade set of each teacher is considered as a separate
experiment, and the average results of the 4 are
reported, while in “A2 avg” and “A2 median” we
considered a single experiment using as grades
either the average or the median grades over the four
teachers, respectively.
Table 2: OK/TOTAL represents the average percentage
over different datasets of peers’ grades equal to teacher’s
grades, while IN1/TOTAL represents the average
percentage over different datasets of peers’ grades within
one grade from teacher’s (still considered acceptable).
DATASET DOMAIN OK/TOTAL IN1/TOTAL
A2 5 47.13% 91.57%
A2 avg 5 58.82% 94.12%
A2 median 5 58.82% 95.59%
A 6 37.84% 67.57%
I 6 57.69% 96.15%
M 6 27.94% 72.06%
A+M+I+A2
(weighted)
6 and 5 42.72% 84.16%
The test provides an overall average rate of
correct grades of 42.72%, while if we admit a
An Analysis of Factors Affecting Automatic Assessment based on Teacher-mediated Peer Evaluation - The Case of OpenAnswer
55

difference of ±1 grade we get 84.16%. The overall
average is weighted with respect to the number of
experiments in each dataset. It is interesting to notice
that when using “A2 avg” and “A2 median” as
ground truth, better performance are obtained. This
seems to suggest that the difference in grading
criteria among different teachers has a clear
influence on the evaluation of the results of peer
assessment. In practice, the students’ assessment is
closer to the assessment carried out by an “average”
or “median” teacher, so that individual episodic
differences are smoothed.
In the experiments presented in the following we
do not enter anymore into details regarding the
single collections, but rather discuss the obtained
average results over all simulations. As a first step,
we compare the above “correctness” rates with those
obtained by having OpenAnswer just propagate peer
grades as they are across the BN (i.e., we select
termination = none). The results show how different
initial settings for P(K) and P(C|K) and different
mapping rules from P(C|K) (a distribution) to the
final grade (a single value) can influence the
reliability of outcomes. Table 3 shows the obtained
results. The first observation is that, among the
Conditional Probability Tables (CPTs) tested in our
experiments, the best one is the one modelled
manually by an experienced teacher (CPT2). In fact,
using the other CPTs, also the results obtained
adding some amount of teacher grading achieved a
lower accuracy. We will therefore continue our
presentation of experimental results only referring to
that CPT. It is further interesting to notice that this
CPT causes a fair behaviour of the BN. When no
information is provided about the class, the network
is quite neutral (the results are very close to those
obtained by pure peer assessment). On the contrary,
when some amount of knowledge about the class
learning state is added by exploiting the teacher’s
grade distribution from the ground truth (TgrDist), a
significant improvement is obtained using the BN.
Of course the best result is obtained by using the
true teacher’s grades as initial knowledge about the
class (Tgrade), entailing to know the exact grade in
advance (as noticed, this is an upper bound). In the
following, we will compare the more realistic flat
(no knowledge at all on the class) and TgrDist (past
knowledge) distributions. As a further observation,
the weighted sum (wSum) rule to map a grade
distribution onto a final value gives the best results
in most cases even in the following experiments.
Therefore, we will always report results obtained by
this strategy.
Results in Table 3 confirm our hypothesis that
pure peer assessment without OpenAnswer
information propagation can be considered as a
lower bound of the achievable accuracy (agreement
with teacher’s grades). As a matter of fact, using a
BN propagation, based on a suitable starting
assumption/knowledge for the P(K) of the class,
provides some improvements on the accuracy, even
without any teacher’s grading. We continue our
experimentation by searching for an upper bound of
the achievable accuracy. To this aim, we assume a
fictitious initial exact knowledge of the outcome
(Tgrade), i.e., a distribution of values for K such
that, for each student, P(K)=1 on the grade actually
achieved by the student. Our next hypothesis is that
the full use of OpenAnswer with such exact
knowledge about the class proficiency should
represent the searched upper bound. It is worth
underlining that, since grades are partly inferred
anyway, a 100% accuracy will not be achieved in
this case neither. As a final hypothesis, we want to
verify that full use of OpenAnswer with a more
realistic set-up of P(K) provides results that are
between BN propagation without teacher’s grading
and the use of teacher’s grading with the best
possible knowledge (actually, knowing results in
advance). Of course this would not necessarily hold
for all possible combinations of the CPT for C|K, the
initial setting for P(K), the mapping from
distribution to grade, and the strategy next answer
choice/termination: our goal is just to find out the
best such combinations.
Table 4 and Table 5 present the results that we
obtained for the best candidates identified from
Table 3 (CPT2, wSum) with different next answer
choice/termination strategies for flat and TgrDist
initial distributions for P(K), respectively.
In Tables 4 and 5 the groups of rows labelled
L/TOTAL report, for each choice strategy for the
next answer to grade and for each termination
condition, the percentage of questions manually
graded by the teacher (a measure of the teacher’s
effort). The groups of rows labelled as
(OK+L)/TOTAL report the total percentage of
answers correctly graded (either by the teacher or by
the system through peer assessment), while groups
(IN1+L)/TOTAL report a similar value for answers
finally graded by a value that is ±1 the correct grade.
We remind that correct grades are available as
ground truth for experimental evaluation. In both
Table 4 and Table 5, the column none (for
termination condition) reports the same values for all
strategies, since it corresponds to the situation where
the teacher does not correct any answer, and
therefore neither next choice strategies nor
CSEDU 2016 - 8th International Conference on Computer Supported Education
56
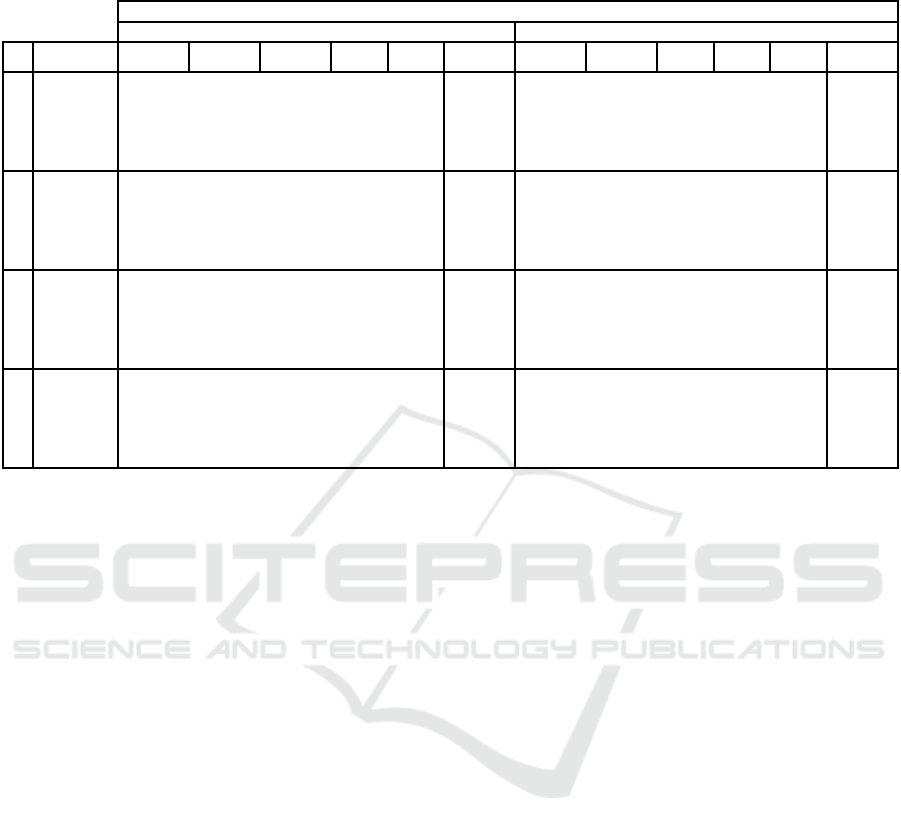
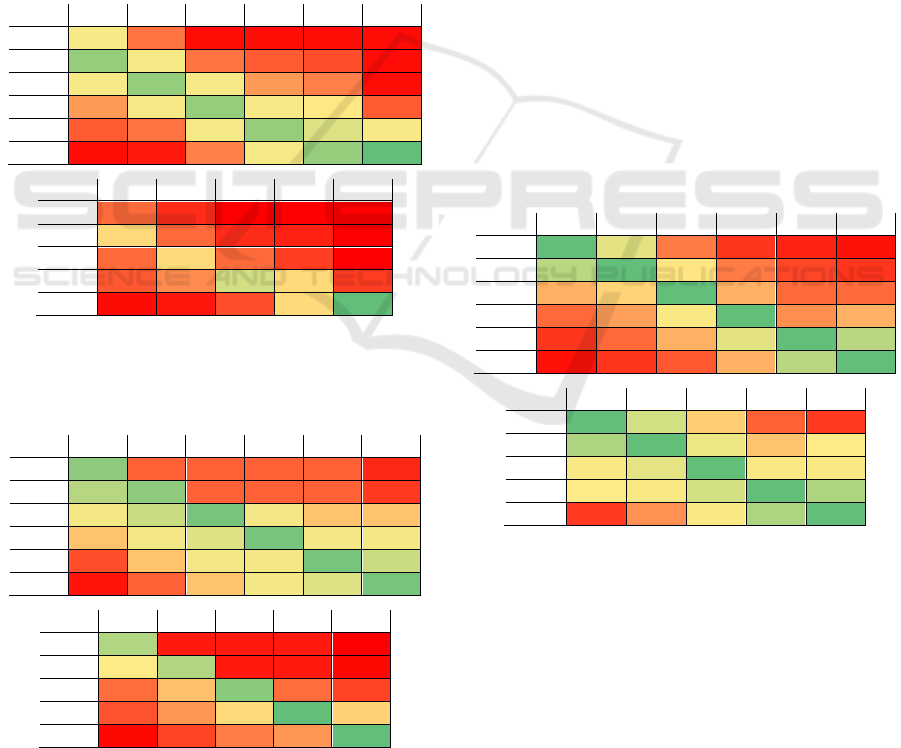
Table 3: Results obtained for pure peer assessment supported by BN propagation, using different CPTs, different initial
settings for P(K) and different procedures to map a probability distribution onto a single vote; no teacher grading is entailed.
TERMINATION=none (no teacher correction)
Average - OK/TOTAL Average - IN1/TOTAL
P ( K ) best75
max1P
max2P
max3P
wSum
Increment
best75
max1P
max2P max3P
wSum
Increment
C
P
T
1
flat 39,01% 38,62% 36,96% 39,72 39,44 -3,00% 81,44% 81,25% 80,56 80,86 81,22 -2,72%
synthetic 38,79% 36,56% 35,51% 39,90 39,30 -2,83% 82,76% 80,44% 79,66 83,25 81,68 -0,91%
Tgrade 39,76% 29,80% 28,60% 46,23 40,86 3,50% 92,83% 94,74% 92,72 90,83 91,29 10,58%
TgrDist 39,60% 37,34% 37,35% 40,72 42,01 -0,72% 85,81% 82,32% 81,00 83,65 84,41 1,65%
C
P
T
2
flat 40,30% 37,85% 36,18% 40,24 42,12 -0,60% 81,16% 81,02% 80,73 84,12 85,45 1,29%
synthetic 40,68% 40,34% 39,56% 40,40 41,85 -0,87% 82,17% 80,83% 81,09 84,66 86,04 1,88%
Tgrade 64,03% 82,96% 73,83% 55,04 58,28 40,23% 93,72% 93,26% 92,48 94,21 93,94 10,05%
TgrDist 43,67% 48,44% 46,04% 44,63 45,60 5,72% 85,71% 84,02% 83,72 86,89 87,05 2,89%
C
P
T
3
flat 38,56% 36,67% 35,75% 40,33 40,87 -1,85% 80,94% 81,03% 81,12 83,61 84,43 0,27%
synthetic 37,90% 37,22% 35,76% 38,15 42,50 -0,23% 80,90% 82,06% 81,59 82,59 84,19 0,03%
Tgrade 70,39% 81,10% 72,24% 63,07 66,51 38,38% 94,94% 94,61% 94,81 95,43 94,54 11,27%
TgrDist 40,71% 43,12% 41,59% 40,37 43,32 0,60% 82,86% 84,29% 83,83 84,90 85,69 1,53%
C
P
T
4
flat 37,10% 32,02% 33,52% 37,12 39,34 -3,38% 79,92% 72,38% 76,32 81,41 83,44 -0,72%
synthetic 36,68% 35,24% 35,52% 37,06 41,09 -1,63% 79,43% 77,68% 78,27 82,44 84,21 0,05%
Tgrade 72,25% 81,48% 74,37% 67,80 71,22 38,75% 95,41% 94,34% 95,01 95,90 94,77 11,74%
TgrDist 39,10% 42,10% 39,76% 39,46 43,50 0,78% 81,61% 80,28% 81,24 83,64 84,22 0,06%
termination conditions are involved. The value only
changes when passing from OK (correctly inferred)
to IN1 (correctly inferred plus those inferred at a
distance of ±1 grade). For the same reason, the rows
corresponding to L/TOTAL are empty and
(OK+L)/TOTAL in this column has always a value
equal to OK/TOTAL. Finally notice that values
OK/TOTAL and IN1/TOTAL under column none
report the same values in the corresponding settings
as reported in Table 3.
In Table 4 it is possible to notice that inferred
grades alone do not reach the accuracy of pure peer
evaluation with propagation (column none).
However, if we add some teacher’s work, we can
observe a significant improvement in accuracy, even
though this is obtained at the expense of more
teacher’s effort (see discussion in the next section).
Using MaxTotalEntropy with noFlip3, we reach
80.63% (OK+L)/TOTAL and 95.32% for
(IN1+L)/TOTAL at the expense of about 68%
answers manually graded. It is also possible to
consider, by comparing values in the different
combinations, that the earliest the system stops (e.g.,
noFlip1 vs. noFlip3) the lower the teacher’s work
but the lower the accuracy too. Though these results
seem not brilliant, it is to consider that Table 4 refers
to a situation where we assume no knowledge about
student’s learning state, therefore we start from an
initial setting for P(K) where all values are equally
probable. Table 5 demonstrates that a certain amount
of preliminary knowledge of the class learning
achievements can improve accuracy results.
6 DISCUSSION
A first observation is in that the better results
obtained using CPTs, for the conditional probability
P(C|K), seem to suggest that simple mathematical
relations cannot satisfactorily model the anticipation
of possible correctness of student responses, just
basing on their level of knowledge on a topic.
Then, the better results obtained with “manually”
produced CPTs seem to testify that the experience
gained by a teacher is of paramount importance in
carrying out such kind of modelling.
As a further consideration, we can discuss the
often better accuracy of results, in terms of
(OK+L)/TOTAL, obtained by the random strategy to
choose the next answer to grade. This is not the
contradiction it might appear to be: using this
strategy (that is, avoiding to use any strategy), we
cannot neither choose nor anticipate in any way the
amount of information that the next grading will
allow to propagate in the BN. So the teacher will
grade more answers (corresponding to a higher value
for L/TOTAL) in order to feed the automatic
inference with sufficient information. In other
words, the final accuracy will be higher because,
with a random choice of the next answer to grade,
An Analysis of Factors Affecting Automatic Assessment based on Teacher-mediated Peer Evaluation - The Case of OpenAnswer
57

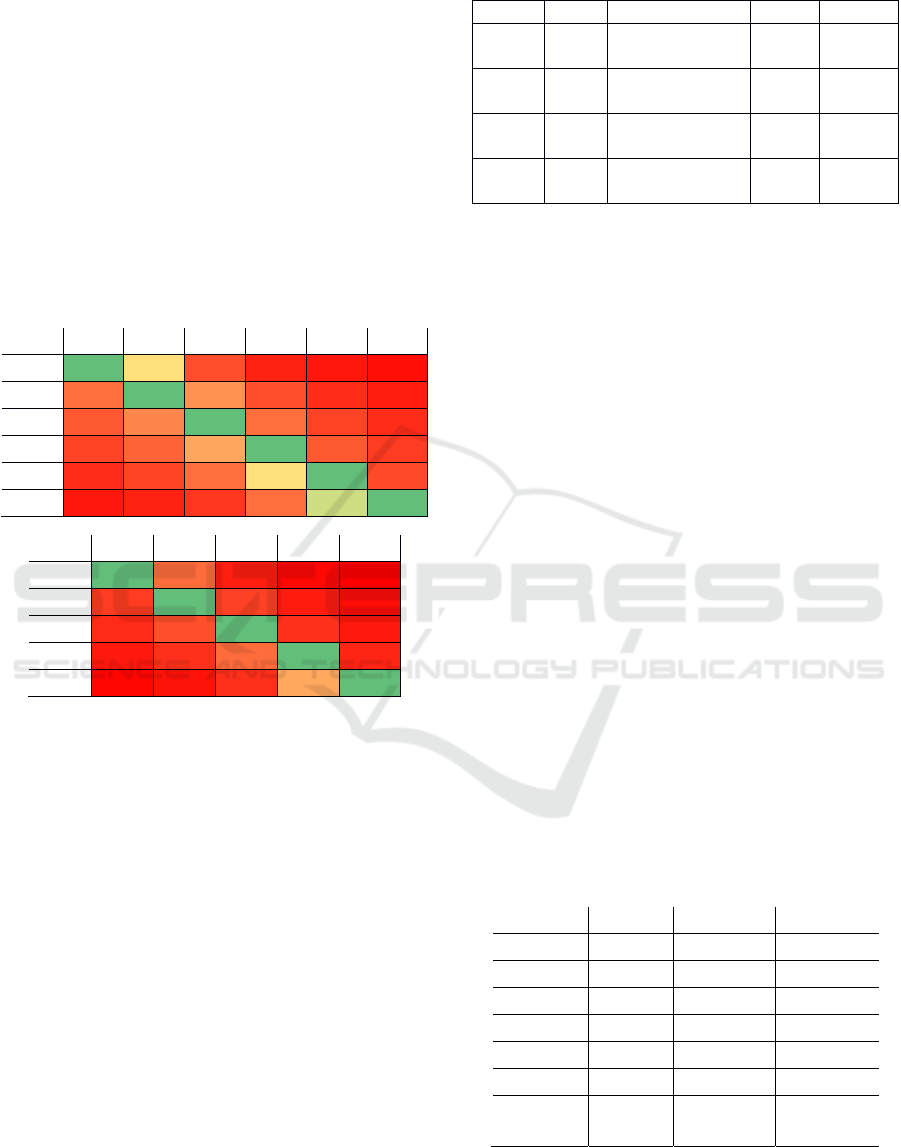
Table 4: Results obtained by adding teacher’s grade with P(K)=flat (no assumption on class knowledge) and for probability
to value (label P2VAL) = wSum, using CPT2; teacher grading is carried out using different strategies to choose the next
answer to grade, and different termination conditions.
P(K)=flat P2VAL=wSum TERMINATION
Data STRATEGY noFlip1 noFlip2 noFlip3 none noWrong noWrong2 noWrong3
Average -
OK/TOTAL
maxEntropy 35,97% 24,85% 17,34% 42,12% 31,08% 31,59% 31,08%
maxInfoGain 32,40% 26,24% 18,08% 42,12% 31,77% 32,27% 31,45%
maxStrangeness 29,41% 23,23% 15,22% 42,12% 34,36% 35,08% 34,36%
maxTotalEntropy 33,65% 25,33% 12,87% 42,12% 31,44% 32,80% 31,73%
maxWrong 30,06% 17,96% 11,95% 42,12% 38,59% 40,40% 38,59%
random 30,05% 22,64% 15,02% 42,12% 34,42% 37,67% 33,76%
Average -
L/TOTAL
maxEntropy 18,63% 43,25% 60,44% 34,44% 30,61% 34,44%
maxInfoGain 18,81% 33,86% 53,85% 32,56% 29,13% 32,88%
maxStrangeness 29,01% 44,36% 61,67% 24,69% 20,03% 24,69%
maxTotalEntropy 17,81% 37,92% 67,76% 31,49% 27,47% 30,60%
maxWrong 25,58% 52,46% 66,41% 8,86% 5,02% 8,84%
random 21,74% 44,70% 65,89% 23,41% 13,63% 24,60%
Average -
OK+L/TOTAL
maxEntropy 54,60% 68,10% 77,78% 42,12% 65,52% 62,20% 65,52%
maxInfoGain 51,22% 60,10% 71,93% 42,12% 64,33% 61,40% 64,33%
maxStrangeness 58,43% 67,58% 76,89% 42,12% 59,04% 55,12% 59,04%
maxTotalEntropy 51,46% 63,25% 80,63% 42,12% 62,92% 60,26% 62,34%
maxWrong 55,64% 70,41% 78,36% 42,12% 47,44% 45,42% 47,43%
random 51,79% 67,34% 80,91% 42,12% 57,83% 51,30% 58,36%
Average -
IN1+L/TOTAL
maxEntropy 88,66% 93,19% 95,10% 85,45% 94,42% 93,18% 94,42%
maxInfoGain 89,75% 91,83% 93,83% 85,45% 93,70% 92,76% 93,70%
maxStrangeness 88,32% 90,84% 92,84% 85,45% 92,59% 90,26% 92,59%
maxTotalEntropy 87,78% 91,70% 95,32% 85,45% 93,54% 92,30% 92,95%
maxWrong 90,60% 93,76% 95,14% 85,45% 88,56% 86,96% 88,56%
random 88,05% 91,27% 93,91% 85,45% 92,54% 89,55% 92,29%
the teacher will do more work, and therefore feed
more information into the BN. As a matter of fact,
the role of choice and termination strategies is just to
find out the best way to save teachers’ work while
preserving a reliable inference.
Last but not least, by comparing gain in accuracy
(OK+L)/TOTAL and lengthier grading L/TOTAL,
we can see a kind of “effort leak” on teacher’s side:
the increase in accuracy is somehow not
proportional to the additional work (lower, infact).
In other words, a greater teacher’s effort does not
correspond to an equally higher accuracy of inferred
grades. For this reason, more investigation is
required regarding the CPT tables used for both C|K
and J|K, and the starting P(K), since these elements
can significantly affect information propagation and
therefore the final outcome.
7 CONCLUSIONS
This paper has presented an analysis of factors
affecting automatic assessment based on teacher-
mediated peer evaluation. We presented results from
experiments involving the OpenAnswer system,
designed to support peer evaluation of open ended
questions. The goal of the devised approach is to
improve efficacy and efficiency of semi-automatic
grading of open answer tests, as well as to teach the
students evaluation skills.
CSEDU 2016 - 8th International Conference on Computer Supported Education
58

Table 5: The results are obtained by adding teacher’s grade with P(K)=TgrDist (we assume to know the class knowledge
state as a distribution, not as individual values) and for probability to value (label P2VAL) = wSum, using CPT2; teacher
grading is carried out using different strategies to choose the next answer to grade, and different termination conditions.
TgrDist wSum TERMINATION
Data STRATEGY noFlip1 noFlip2 noFlip3 none noWrong noWrong2 noWrong3
Average -
OK/TOTAL
maxEntropy 38,76% 31,01% 21,53% 45,60% 34,41% 35,97% 34,41%
maxInfoGain 39,03% 30,87% 23,68% 45,60% 35,53% 37,02% 35,53%
maxStrangeness 38,63% 28,11% 21,84% 45,60% 37,91% 40,01% 37,91%
maxTotalEntropy 40,11% 33,95% 21,28% 45,60% 34,55% 36,77% 34,55%
maxWrong 38,06% 27,55% 20,99% 45,60% 41,77% 43,61% 42,25%
random 35,99% 27,16% 18,31% 45,60% 38,74% 41,23% 38,74%
Average -
L/TOTAL
maxEntropy 16,72% 33,24% 53,99% 33,21% 25,81% 33,21%
maxInfoGain 15,86% 35,74% 51,83% 30,42% 22,93% 30,21%
maxStrangeness 16,59% 38,99% 54,60% 22,46% 16,42% 22,46%
maxTotalEntropy 15,94% 31,68% 54,37% 30,54% 24,09% 30,54%
maxWrong 16,61% 39,08% 53,51% 10,55% 3,85% 8,71%
random 16,78% 41,27% 59,94% 23,88% 13,57% 23,88%
Average -
OK+L/TOTAL
maxEntropy 55,48% 64,25% 75,51% 45,60% 67,63% 61,78% 67,63%
maxInfoGain 54,89% 66,61% 75,51% 45,60% 65,95% 59,95% 65,74%
maxStrangeness 55,22% 67,10% 76,44% 45,60% 60,37% 56,43% 60,37%
maxTotalEntropy 56,05% 65,63% 75,65% 45,60% 65,08% 60,86% 65,08%
maxWrong 54,67% 66,63% 74,50% 45,60% 52,32% 47,46% 50,97%
random 52,76% 68,43% 78,26% 45,60% 62,62% 54,80% 62,62%
Average -
IN1+L/TOTAL
maxEntropy 90,92% 93,29% 95,42% 87,05% 94,68% 93,19% 94,68%
maxInfoGain 89,82% 93,09% 95,10% 87,05% 94,35% 93,39% 94,35%
maxStrangeness 88,19% 90,32% 92,55% 87,05% 91,38% 90,16% 91,38%
maxTotalEntropy 91,43% 93,17% 95,98% 87,05% 93,61% 92,70% 93,61%
maxWrong 90,07% 93,84% 95,61% 87,05% 90,44% 88,02% 89,26%
random 88,23% 92,97% 95,80% 87,05% 92,32% 90,07% 92,32%
The educational practice of open ended
questionnaires represents a very effective assessment
tool but requires much grading effort by the teacher.
On the other hand the practice of peer assessment
would train the meta-cognitive abilities of students.
So, the goals mentioned above also aim to provide
the teacher with an effective environment, where a
wider usage of open answer questionnaires is
encouraged and supported, while the teacher is
relieved of a significant part of the consequent
grading work, so to concentrate on higher level
tasks, such as the definition of questions and of the
criteria to assess them.
It appears that it is still necessary to gain a
deeper understanding of the effect of different set-up
choices and modelling parameters on the final
results. The reason why this kind of investigation is
crucial for the final outcomes, is because the
elements conditioning the system behaviour do not
represent pure operation parameters, but should
reflect a real understanding of pedagogical and
educational issues. The fact to reflect on is that some
“manual” adjustments of probability distributions,
obtained through a field experience in educational
tasks, achieve better result than “reasonable”
mathematical considerations. Moreover, even in the
best starting set-up, the work of the teacher still
appears to be of crucial importance for the overall
system reliability. This is due to a kind of implicit
knowledge that is entailed in the educational
process, a thing that is difficult to formalize through
automatic operational rules.
An Analysis of Factors Affecting Automatic Assessment based on Teacher-mediated Peer Evaluation - The Case of OpenAnswer
59

About future work, on the side of experimental
settings we are pursuing application of the
framework to the case of formal algebra (Formisano
et al. 2000, 2001), on the spur of work done in (El-
Kechaï et al. 2011). Another application of the
OpenAnswer approach to peer-evaluation will be in
regard to the support for teachers of the retrieval and
selection of learning objects in courses contruction,
in the line of work done in (Limongelli et al. 2012,
2013, 2015, 2016; Gentili et al. 2001; Sciarrone
2013). Regarding the development of the
framework, we will investigate in particular the role
of propagation of information between a sequence of
assessment sessions. We are encouraged in doing
this by the good results obtained when using a
distribution of values for the expected initial student
knowledge that is given by considering the overall
class state. In the present work, we carried out a kind
of systematic investigation on the dependence of the
correctness of a learner’s answer, from her state of
knowledge (C|K). Another point to investigate in the
future will be the best distribution to use for J|K, i.e.,
the ability to judge given e certain state of
knowledge. Actually, this reasonably appears to be a
further crucial parameter in modelling the inference
process.
REFERENCES
Anderson, L. W., Krathwohl, D. R. (eds.), 2000. A
taxonomy for learning, teaching, and assessing: A
revision of Bloom's taxonomy of educational
objectives. Allyn and Bacon.
Anderson, J.R., Corbett, A.T., Koedinger, K.R., Pelletier,
R., 1995. Cognitive Tutors: Lessons Learned. The
Journal of the Learning Sciences, 4(2), 167-207.
Bloom, B.S., Engelhart, M.D., Furst,. E.J., Hill, W.H.,
Krathwohl, D.R., 1956. Taxonomy of educational
objectives: The classification of educational goals.
Handbook I. McKay.
Castellanos-Nieves, D., Fernández-Breis, J., Valencia-
García, R., Martínez-Béjar, R., Iniesta-Moreno, M.,
2011. Semantic Web Technologies for supporting
learning assessment, Inf. Sciences, 181:9.
Cho, K., MacArthur, C., 2010. Student Revision with Peer
and Expert Reviewing. Learning and Instruction
20(4).
Chung, H., Graf, S., Robert Lai, K., Kinshuk, 2011.
Enrichment of Peer Assessment with Agent
Negotiation. IEEE TLT Learning Technologies, 4(1),
pp.35-46.
Conati, C., Gartner, A. , Vanlehn, K., 2002. Using
Bayesian Networks to Manage Uncertainty in Student
Modeling. User Modeling and User-Adapted
Interaction 12, pages 371-417.
De Marsico, M., Sterbini, A., Temperini, M., 2015.
Towards a quantitative evaluation of the relationship
between the domain knowledge and the ability to
assess peer work. Proc. ITHET 2015 (pp. 1-6). IEEE.
El-Kechaï, N., Delozanne, É., Prévit, D., Grugeon, B.,
Chenevotot, F., 2011. Evaluating the Performance of a
Diagnosis System in School Algebra, ICWL, LNCS
7048.
Formisano, A., Omodeo, E.G., Temperini, M., 2000.
Goals and benchmarks for automated map reasoning,
Journal of Symbolic Computation, 29(2), pp. 259-297,
Elsevier.
Formisano, A., Omodeo, E.G., Temperini, M., 2001.
Layered map reasoning: An experimental approach put
to trial on sets. El. Notes in Theor. Comp. Sci., 48, pp.
1-28, Elsevier.
Gentili, G.L., Marinilli, M., Micarelli, A., Sciarrone, F.,
2001. Text categorization in an intelligent agent for
filtering information on the web. Int. J. of Patt. Rec.
and A. I. 15(3).
Jackson, K., Trochim, W., 2002. Concept mapping as an
alternative approach for the analysis of open-ended
survey responses. Organizational Research Methods,
5, Sage.
Li, L.X., Liu, X. , Steckelberg, A. L., 2010. Assessor or
Assessee: How Student Learning Improves by Giving
and Receiving Peer Feedback. Br. J. of Ed. Tech. 41
(3), pages 525–536.
Limongelli, C., Miola, A., Sciarrone, F., Temperini, M.,
2012. Supporting Teachers to Retrieve and Select
Learning Objects for Personalized Courses in the
Moodle LS Environment. In Proc. 14th IEEE ICALT,
Workshop SPEL,pp. 518-520, IEEE Computer
Society.
Limongelli, C., Lombardi, M., Marani, A., Sciarrone, F.,
2013. A teaching-style based social network for
didactic building and sharing, LNAI 7926, pp.774-
777, Springer.
Limongelli, C., Sciarrone, F., Temperini, M., 2015. A
social network-based teacher model to support course
construction. Comp. in Human Behav., 51, Elsevier.
Limongelli, C., Lombardi, M., Marani, A., Sciarrone, F.,
Temperini, M., 2016. A recommendation module to
help teachers build courses through the Moodle
Learning Management System. New Review of
Hypermedia and Multimedia, 22(1-2), Taylor &
Francis.
Metcalfe, J., Shimamura, A. P., 1994. Metacognition:
knowing about knowing. Cambridge, MA: MIT Press.
Miller, P., 2003. The Effect of Scoring Criteria Specificity
on Peer and Self-assessment. Assessment &
Evaluation in Higher Education, 28/4.
Palmer, K., Richardson, P., 2003. On-line assessment and
free-response input-a pedagogic and technical model
for squaring the circle. In Proc. 7th CAA Conf. (pp.
289-300).
Sadler, P. M., E. Good, P. M., 2006. The Impact of Self-
and Peer-Grading on Student Learning. Ed. Ass.,
11(1).
CSEDU 2016 - 8th International Conference on Computer Supported Education
60

Sciarrone, F., 2013. An extension of the Q diversity metric
for information processing in multiple classifier
systems: A field evaluation, Int. Journal of Wavelets,
Multiresolution and Information Processing, 11(6).
Sterbini, A., Temperini, M., 2009. Collaborative Projects
and Self Evaluation within a Social Reputation-Based
Exercise-Sharing System. Proc. IEEE/WIC/ACM WI-
IAT'09, Vol. 3, Workshop SPEL, pp. 243-246.
Sterbini, A., Temperini, M., 2012. Dealing with open-
answer questions in a peer-assessment environment.
Proc. ICWL 2012. LNCS, vol. 7558, pp. 240–248.
Springer, Heidelberg.
Sterbini, A., Temperini, M., 2013a. OpenAnswer, a
framework to support teacher's management of open
answers through peer assessment. Proc. 43th Frontiers
in Education (FIE 2013).
Sterbini, A., Temperini, M., 2013b. Analysis of
OpenAnswers via mediated peer-assessment. Proc.
17th IEEE Int Conf. on System Theory, Control and
Computing (ICSTCC 2013).
Topping, K., 1998. Peer assessment between students in
colleges and universities, Rev. of Ed. Research, 68, pp.
249–276.
Yamanishi, K. , Li, H. , 2002. Mining Open Answers in
Questionnaire Data, IEEE Int. Systems, Sept-Oct, pp
58-63.
An Analysis of Factors Affecting Automatic Assessment based on Teacher-mediated Peer Evaluation - The Case of OpenAnswer
61
