Unsupervised Clustering on PMU Data for Event Characterization on

Smart Grid

Eric Klinginsmith, Richard Barella, Xinghui Zhao and Scott Wallace

School of Engineering and Computer Science, Washington State University Vancouver,

14204 NE Salmon Creek Ave., Vancouver, WA, 98686 U.S.A.

Keywords:

Smart Grid, Phasor Measurement Unit (PMU), Synchrophasors, Machine Learning, Clustering, Event

Characterization.

Abstract:

In the past decade, with the world-wide initiative of upgrading the electrical grid to smart grid, a signiﬁcant

amount of data have been generated by the grid on a daily basis. Therefore, there has been an increasing

need in handling and processing these data efﬁciently. In this paper, we present our experience in applying

unsupervised clustering on PMU data for event characterization on the smart grid. We show that although the

PMU data are time series in nature, it is more efﬁcient and robust to apply clustering methods on carefully

selected features from the data collected at certain instantaneous moments in time. These features are more

representative at the moments when the events have the most impact on the grid. Experiments have been

carried out on real PMU data collected by Bonneville Power Administration in their wide-area monitoring

system in the paciﬁc northwest, and the results show that our instantaneous clustering method achieves high

homogeneity, which provides great potentials for identifying unknown events in the grid without substantial

training data.

1 INTRODUCTION

The emerging smart grid technology provides oppor-

tunities to implement a more reliable, intelligent, and

highly automated energy delivery network, harness-

ing the advances in communication and information

technologies. A key component in the smart grid is

the Phasor Measurement Unit (PMU), or synchropha-

sor, which measures phase angles and magnitudes of

the electrical waves in real time, at a high frequency,

ranging from 30 measurements per second to hun-

dreds of measurements per second. Data generated

by these devices contain valuable information about

the operation status of the power grid. A signiﬁcant

amount of work has been done to detect or monitor

certain conditions of a power grid by leveraging in-

formation extracted from PMU data. Potential appli-

cations include fault detection (Liang et al., 2014), lo-

calization (Jiang et al., 2000), tracking (Chang et al.,

2008), and oscillation detection (Liu and Venkatasub-

ramanian, 2008). A comprehensive survey on vaious

applications using PMU data can be found in (Singh

et al., 2011).

Over the last 5 years, the PMU deployment has

been signiﬁcantly increased in the U.S., from 200

PMUs in 2009 (North American Electric Reliabil-

ity Corporation, 2014) to approximately 1700 in

2014 (Americans for a Clean Energy Grid, 2014).

However, with the number of PMUs rapidly increas-

ing, the volume of the data generated by those PMUs

presents challenges for efﬁcient processing. An in-

stallation of 100 PMUs produces data in the scale of

3-4TB per month, which will quickly become inac-

cessible for traditional workﬂow. A more automated

and efﬁcient approach for data processing is essential,

in order to take advantage of the valuable information

in PMU data. The efﬁciency of the data processing

is even more critical for real-time monitoring of the

power grid.

Machine learning techniques provide potentials

for automated information extraction from large data

sources, and therefore become the most widely

used approach for address the big data challenge.

Among machine learning techniques, clustering (Bai-

ley, 1994) is an exploratory approach which can po-

tentially identify unknown signatures by grouping

data objects based on their similarities. In this paper,

we apply various clustering methods on PMU data

streams collected from a large power grid in paciﬁc

northwest. The goal is to explore the applicability of

Klinginsmith, E., Barella, R., Zhao, X. and Wallace, S.

Unsupervised Clustering on PMU Data for Event Characterization on Smart Grid.

In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 233-240

ISBN: 978-989-758-184-7

233

different clustering technique in identifying known or

unknown events which occur in the power grid.

The remainder of the paper is organized as fol-

lows. Section 2 reviews related work in applying ma-

chine learning techniques on PMU data. Section 3 in-

troduces the dataset we use in this research, as well as

the feature selection for the clustering method. Sec-

tion 4 presents our work in applying hierarchical clus-

tering on PMU time series, and the experimental re-

sults. Section 5 presents a different approach for clus-

tering instantaneous data, as well as experimental re-

sults. Section 6 concludes the paper and proposes fu-

ture directions for this work.

2 RELATED WORK

PMUs are widely used to monitor the operational sta-

tus of a power grid with the aim of enhancing the sit-

uation awareness for power system operators. A sig-

niﬁcant amount of work has been done to detect or

monitor certain conditions of a power grid by lever-

aging information extracted from PMU data. Jiang et

al. propose an online approach for fault detection and

localization using SDFT (smart DFT) (Jiang et al.,

2000). Liu et al. use Frequency Domain Decompo-

sition for detecting oscillations (Liu and Venkatasub-

ramanian, 2008). Kazami et al. propose a multivari-

able regression model to track fault locations (Chang

et al., 2008). Besides voltage and current magnitudes,

which are the most commonly used features in detect-

ing faults, phase angle measurements can also be used

in detecting outages (Tate and Overbye, 2008).

Most recently, with the emergence of big data an-

alytics, new technologies are introduced to PMU data

storage and processing. Most importantly, a variety

of machine learning techniques have been applied to

analyze PMU data for the purpose of recognizing pat-

terns or signatures of events. Two widely adopted

techniques are classiﬁcation and clustering.

Classiﬁcation methods employ supervised learn-

ing and therefore, after training, can identify known

signatures or patterns. In (Nguyen et al., 2015),

Nguyen et al. develop a decision tree based on the

J48 algorithm, for the purpose of detecting line events

on the power grid using PMU data streams. Zhang

et al. propose a classiﬁcation method for ﬁnding

fault locations based on pattern recognition (Zhang

et al., 2011). The key idea is to distinguish a class

from irrelevant data elements using linear discrimi-

nant analysis. The classiﬁcation is carried out based

on two types of features: nodal voltage, and neg-

ative sequence voltage. Similar classiﬁcation tech-

niques are used to detect voltage collapse (Diao et al.,

2009) and disturbances (Ray et al., 2014) in power

systems. Speciﬁcally, Diao et al. develop and train a

decision tree using PMU data to assess voltage secu-

rity (Diao et al., 2009). Ray et al. build Support Vec-

tor Machines and decision tree classiﬁers based on a

set of optimal features selected using a genetic algo-

rithm (Ray et al., 2014). Support Vector Machine-

based classiﬁers can also be used to identify fault lo-

cations (Salat and Osowski, 2004), and predict post-

fault transient stability (Gomez et al., 2011).

Although classiﬁcation methods usually can pro-

vide high accuracy, they require a substantial amount

of labeled data for training. Unlike classiﬁcation,

clustering methods with unsupervised learning do not

require labeled training data. Antoine et al. propose to

identify causes for inter-area oscillations by clustering

a number of parameters provided by PMUs, includ-

ing mode frequency, the voltage angle differences be-

tween areas and the mode shapes (Antoine and Maun,

2012). It has been shown that by clustering these pa-

rameters, changes in inter-area oscillations can be ex-

plained. Clustering methods have also been proven

to be effective in identifying different types of distur-

bances (Dahal et al., 2014).

In this paper, we investigate PMU data collected

from a wide-area monitoring system, extract useful

features, and evaluate different unsupervised cluster-

ing methods on PMU data for the purpose of events

characterization. To the best of our knowledge, this is

the ﬁrst work which applies unsupervised clustering

methods to real PMU data for this characterizing line

events.

3 DATASET AND FEATURE

SELECTION

Our dataset was obtained from Bonneville Power Ad-

ministration (BPA), one of the ﬁrst transmission oper-

ators to adopt synchrophasor technology. In this sec-

tion, we describe the dataset we use in this research,

as well as the features we extracted for the clustering

methods.

3.1 Dataset

At the time our data was collected, BPAs instal-

lation base contained 31 phasor measurement units

from across the paciﬁc northwest. These PMUs mea-

sure line and/or bus voltage across all three phases.

They also record positive sequence voltage and cur-

rent phasors, frequency and rate-of-change of fre-

quency. At each PMU, the data is recorded at 60Hz.

Measurements from our dataset are primarily from

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

234

(a) A Typical Single-Line-to-Ground Fault (b) A Typical Line-to-Line Fault

Figure 1: Typical Line Events on a Smart Grid.

500KV and 230KV buses, although a small number

of smaller voltage transmission lines are also covered.

Our dataset was collected from the period October 17,

2012 to September 16, 2013 and contains 114 docu-

mented faults that occur at a bus or on a transmission

line instrumented with at least one PMU. The faults

include instances of single-line-to-ground faults, line-

to-line faults, three-phase faults, in that order of rela-

tive frequency, and no-fault data. The data set used for

clustering contains 100 of the 114 documented fault

events and 19 no fault events, i.e., 119 events in to-

tal. Since not all events or locations on the electrical

grid have all the required data for calculating of the

features required for our clustering, those events and

locations were dropped. On average we gathered data

at 56 different locations on the electrical grid for each

of the 119 events, resulting in 6676 data points in to-

tal. Of the 6676 data points 4935 are Line to Ground

faults, 331 are Line to Line, 196 are Three Phase, and

1214 are marked as No Fault.

3.2 Feature Selection

In our dataset, the measurements recorded by the

PMUs are voltage magnitude and phase angle (pos-

itive sequence and A, B, C phases), current magni-

tude and phase angle (positive sequence only), and

frequency (60Hz). It has been shown in previous

work that the per-phase voltage magnitude is an ef-

fective measurement to identify different types of line

events (Liang et al., 2014).

Figure 1 shows the per-phase voltage magnitude

over time for two typical line events, single-line-to-

ground fault, and line-to-line fault. Note that the

voltage magnitude values are normalized based on

the steady state voltage. As shown in in Figure 1,

the voltage sags behave differently in different types

of events, which provides potentials for separating

events into different groups via clustering. This obser-

vation serves as the guideline for developing features

for our the clustering method.

To enable efﬁcient clustering in a two dimension

space while retaining all the information contained

in the three phase voltage magnitudes, we devel-

oped two new features, RelativeP hase2over1, and

RelativeP hase3over1, by synthesizing the three

per-phase voltage values. These two features are

calculated in 3 steps. First, we calculate the rela-

tive phase deviations (RP) from steady state for three

phases, as shown in equation 1, 2, and 3.

(1)RP

= |1.0 −

(2)RP

= |1.0 −

(3)RP

= |1.0 −

In the above equations, v values are per-phase

voltage magnitudes, ss values are steady state volt-

ages on the corresponding phases, and the values are

normalized based on the steady state voltages. We

then sort these relative phase deviations in ascending

order, resulting in a tuple, as shown in equation 4.

(4)[RP

, RP

] = sort([RP

, RP

])

Note that sorting the relative phase deviations sim-

pliﬁes the complexity of our feature space. Although

by doing that we lose the information about deviations

on speciﬁc phases, the relative deviation magnitudes

among three phases are captured, which still enable

us to differentiate fault types.

In the last step, we use the values in the relative

phase deviation tuple to calculate the two new fea-

tures, as shown in equation 5, and 6.

(5)RelativeP hase2over1 =

(6)RelativeP hase3over1 =

Unsupervised Clustering on PMU Data for Event Characterization on Smart Grid

235

These two features retain the information con-

tained in the three per-phase voltage values, yet pro-

vide a simpliﬁed two dimensional space for the clus-

tering methods. In addition, by normalizing the mag-

nitudes based on the steady state voltages, we elim-

inate the bias introduced by the absolute magnitude

deviations, so that the characteristics, or patterns of

different events can be better captured by the cluster-

ing methods.

4 TIME SERIES CLUSTERING

Given the fact that PMU data are time series data

in nature, we have applied the time series clustering

method (Liao, 2005) to our dataset. The technical

details and experimental results are described in this

section.

4.1 Data Processing and Distance

Metric

Time series clustering takes data on a window of time

as one data entry. For our case, one data entry is a

time window of data collected by one PMU. This ap-

proach provides an opportunity for clustering based

on the shape of the event over time, instead of a sin-

gle data point. However, events with longer duration

present challenges in data handling. To simplify the

data processing without losing the advantages of time

series clustering, we have applied the widely used

Piecewise Aggregate Approximation (PAA) (Keogh

and Pazzani, 2000) to reduce the number of points in

each time window. Speciﬁcally, each data window is

divided into n time slices. Then, the mean of each

time slice is calculated. These mean values are used

to replace of the actual data collected during the cor-

responding time slices.

Another challenge in time series clustering is to

deﬁne a meaningful similarity metric of two data en-

tries. One basic method is to calculate the euclidean

distance between the two time series. However, this

method can be inaccurate, as the same event can ap-

pear at different sites where one site sees the fault a

few cycles after the other, which results in the time

series on two sites out of sync. Therefore, it is criti-

cal to use a method that can take slight offsets in time

into account. To this end, we utilize Dynamic Time

Warping (DTW) (Keogh and Pazzani, 2000), a well

researched solution to this problem. DTW aligns the

sequences by locally stretching and shrinking one se-

quence to obtain the optimal ﬁt to the other sequence

and then calculates their relative distance given the

optimal alignment. This causes the time series to be

compared in a non-linear fashion instead of in lock-

step.

4.2 Clustering Results

For clustering, we chose the hierarchical clustering al-

gorithm (Rokach and Maimon, 2005), because it is

the most suitable method for the time series model,

and it allows customized distance metric, for which

we used the DTW distance metric described above.

In order to apply the hierarchical clustering

method to our data, we need to transform each event

into time series data with a ﬁxed window size. Since

most of the line events in our dataset last approxi-

mately 6 cycles (1/10th of a second), we choose a

window size of 10, which gives us extra space to

capture steady state data before and after the event.

Speciﬁcally, we process each event as follows. First,

for each event which lasts less than 8 cycles, we

add steady state data to both sides until the dura-

tion is greater or equal to 8. Second, we perform

PAA (Keogh and Pazzani, 2000) with a window size

of 8 to each event, so that the data is divided into 8

slices, or time steps. Third, we add a steady state data

point to each side of the event, forming a time series

data with a ﬁxed size 10.

After obtaining the 10 time steps for each event,

we calculate the features described in Section 3.2 for

each time step. Finally we apply the hierarchical clus-

tering method on these data points. Due to the limited

space of the paper, we only present the result time step

5. We chose time step 5 because it is located in the

middle of the event window, and carries the most rep-

resentative features of the event. The clustering result

for this time step is shown in Figure 2. Different col-

ors represent different groups of data entries. To as-

sociate the groups generated by the clustering method

with the event types in our dataset, we have calculated

the percentage breakdown of each event type in the 4

groups, and the results are shown in Table 1.

Figure 2: Hierachical Clustering at Time Step 5.

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

236

Table 1: Time Series Hierarchical Clustering % Break-

down.

LG LL TP NF

0 14.08% 9.37% 44.39% 28.25%

1 14.23% 29.00% 11.23% 29.41%

2 18.70% 38.37% 35.71% 40.94%

3 52.99% 23.26% 8.67% 1.40%

As shown in the results, half of the single-line-

to-ground (LG) events are clustered in group 3 while

the rest are split among the other three groups. Ma-

jority of the Line-to-line (LL) events are split among

three groups 1, 2, and 3. Majority of the three-phase

(TP) events are split among groups 0 and 2. Finally,

most of the no-fault (NF) data entries are split be-

tween groups 0, 1, and 2. Overall, hierarchical clus-

tering on PMU time series data does not work well,

which can be reﬂected by the low homogeneity score

of 0.156. Note that the homogeneity score (Rosen-

berg and Hirschberg, 2007) is a metric indicating how

well data points which belong to the same class are as-

signed to the same cluster. A perfectly homogeneous

solution has a homogeneity score of 1.

Since it has been shown that the combined volt-

age deviations, as illustrated in equation 7, is an effec-

tive metric for representing the impact of the event on

the PMU site (Liang et al., 2014). A greater value of

∆V represents higher impact of an event on a PMU.

In order to remove the events which occur at loca-

tions that are far away from the PMUs, we ﬁltered our

dataset by removing all the data entries with ∆V val-

ues less than 0.018, a threshold suggested in (Liang

et al., 2014). After this ﬁltering process, our dataset

contains 2211 data points. That is to say, 4462 data

points are ﬁltered out. These data points are signals

captured by PMUs which are far away from the loca-

tion where the event occurred.

∆V =

− ss

)

+ (v

− ss

)

+ (v

− ss

)

(7)

We then carried out the hierarchical clustering on

the ﬁltered dataset, and the results are shown in Fig-

ure 3 and Table 2.

Table 2: Time Series with ∆V ﬁlter Hierarchical Clustering

% Breakdown.

LG LL TP NF

0 15.24% 44.36% 0.00% 0.00%

1 19.52% 21.77% 31.43% 0.00%

2 27.80% 15.32% 58.10% 33.33%

3 37.44% 18.55% 10.47% 66.67%

The results of the hierarchical clustering on ﬁl-

tered dataset are similar to those on the original

Figure 3: Hierarchical Clustering on Filtered Data at Time

Step 5.

dataset, with an even lower homogeneity score of

0.027. This indicates that although PMU data are time

series, it is challenging to apply clustering methods on

these time series.

5 INSTANTANEOUS

CLUSTERING

Besides time series clustering, an alternative solution

is to represent each event using one single data point

at an instantaneous moment in time, and apply clus-

tering methods on these data points. In this section,

we describe our work in this direction.

5.1 Data Processing

In order to apply instantaneous clustering methods to

our data, we ﬁrst need to choose a data point to rep-

resent each event. As shown in the typical line events

in Figure 1, the best candidate is the moment when

the maximum voltage deviation is reached. However,

even though a given site may have a minimum at a

given cycle, that does not guarantee that another site’s

minimum is located at the same cycle. Instead of

choosing one site to represent all sites we developed

a better method that takes all sites into account. In

our method all sites vote on what cycle they say is

the minimum cycle of a given fault. The cycle with

the most votes from the sites is the one that is cho-

sen. This method allows us to get the point in time

where we see the largest deviation for the most sites.

Note that in order to take into consideration all three

phases, we use the metric ∆V shown in equation 7

in the voting process. In other words, for each event,

the cycle during which the largest number of sites ob-

serve their greatest ∆V value is chosen to represent

that event across the grid. We then apply instanta-

neous clustering methods on these data points.

Unsupervised Clustering on PMU Data for Event Characterization on Smart Grid

237

5.2 Clustering Results

For instantaneous clustering, we choose two widely

used methods, k-means (Wagstaff et al., 2001) and

DBSCAN (Density Based Spatial Clustering of Ap-

plications with Noise) (Ester et al., 1996) to perform

the clustering on our data points described above,

based on the two features presented in Section 3.2.

The results of the k-means clustering are shown in

Figure 4. The data points are divided into 4 different

groups, each of which is represented by a different

color. The percentage breakdown for different even

types are shown in table 3.

Figure 4: K-menas Clustering on Instantaneous Data.

Table 3: K-menas Clustering % Breakdown.

LG LL TP NF

Blue 1.72% 0.60% 98.98% 74.79%

Gray 64.84% 7.86% 0.00% 4.53%

Orange 3.49% 91.54% 1.02% 20.02%

Brown 29.95% 0.00% 0.00% 0.66%

In general, k-means clustering performs well in

separating different events into groups. Particularly,

three-phase (TP) events are well isolated from the rest

event types. However, some single-line-to-ground

(LG) events are mixed with line-to-line (LL) events,

and the no-fault (NF) data points are separated into

two main groups. Note that the over all homogene-

ity score of k-means clustering on the instantaneous

PMU data is 0.60, showing a major improvement over

the hierarchical clustering on time series data.

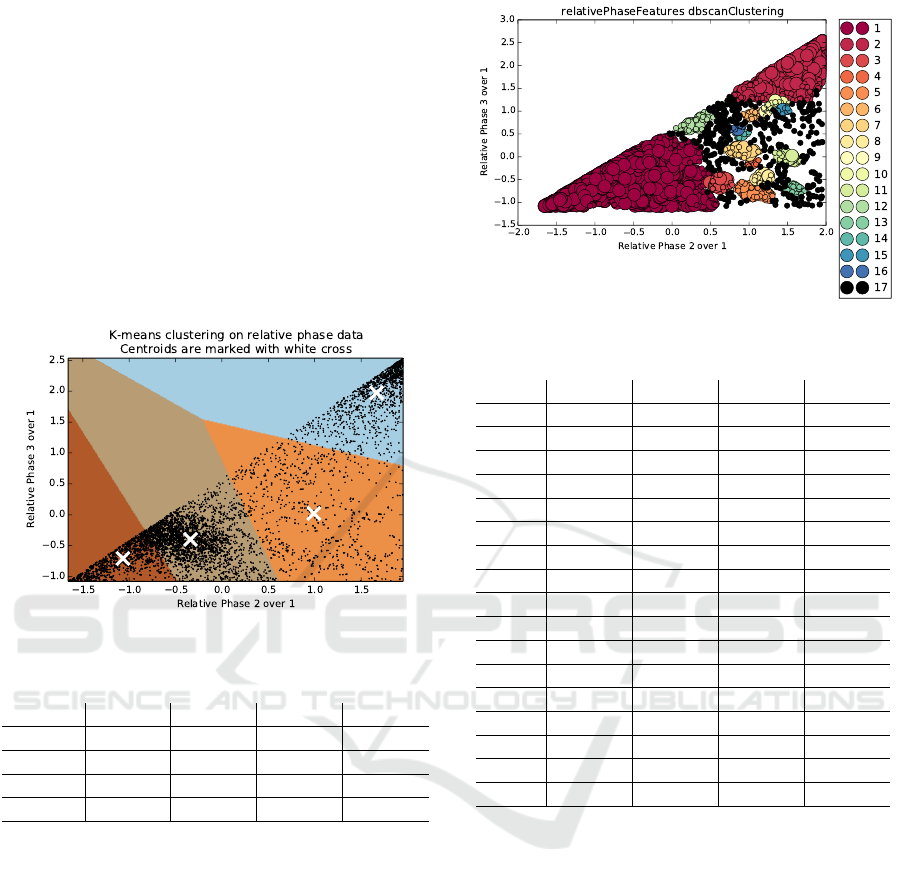
We then applied the density-based DBSCAN clus-

tering method on the same dataset, and the results are

shown in Figure 5 and Table 4.

When using DBSCAN the user does not provide

the number of clusters. Instead the algorithm breaks

down the data into as many clusters as it sees ﬁt. On

top of this it also adds an additional cluster for what

DBSCAN has determined to be noise in the data. In

Figure 5: Relative Phase Features.

Table 4: DBSCAN clustering % breakdown.

LG LL TP NF

1 95.16% 8.16% 0.00% 5.93%

2 1.62% 0.60% 98.98% 69.44%

3 0.55% 3.32% 0.00% 0.66%

4 0.00% 4.23% 0.00% 0.08%

5 0.04% 15.11% 0.00% 0.41%

6 0.10% 0.00% 0.00% 1.40%

7 0.16% 8.46% 0.00% 0.66%

8 0.04% 6.65% 0.00% 0.00%

9 0.00% 0.00% 0.00% 0.74%

10 0.04% 0.00% 0.00% 1.32%

11 0.00% 9.67% 0.00% 0.16%

12 0.63% 0.00% 0.00% 1.48%

13 0.00% 5.74% 0.00% 0.00%

14 0.06% 0.00% 0.00% 0.91%

15 0.02% 0.00% 0.00% 0.91%

16 0.10% 0.00% 0.00% 0.33%

Noise 1.48% 38.07% 1.02% 15.57%

this case DBSCAN divided the data into 16 groups.

Despite the large number of groups, DBSCAN per-

forms well in dividing LG and TP from the other

two type of events. However, instead of grouping LL

into a single cluster, DBSCAN has divided it into 7

groups. Also, most of the LL data are identiﬁed as

noise. Most of the No Fault data points are grouped in

the same cluster as TP, but a good portion of it is also

marked as noise. This clustering has a homogeneity

of 0.628.

We observed that there is quite a bit of data be-

ing labeled as noise. If we could reduce the amount

of noise, then that could help DBSCAN preform bet-

ter. In addition, reducing the amount of noise could

help separate no fault data from TP. With most faults

a higher ∆V signiﬁes that signal is closer to the loca-

tion of the fault.

Therefore, we execute the two instantaneous clus-

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

238

tering method on the ﬁltered dataset which con-

tains only data points with ∆V values greater than

0.018.The clustering results of k-means are shown in

Figure 6 and Table 5.

Figure 6: K-means Clutering on Filtered Instantaneous

Data.

Table 5: Filtered K-means Clustering % Breakdown.

LG LL TP NF

Blue 37.18% 0.00% 0.00% 0.00%

Gray 0.56% 0.81% 100% 100%

Orange 62.21% 0.00% 0.00% 0.00%

Brown 0.05% 99.19% 0.00% 0.00%

The results here show some improvements over

those on the non-ﬁltered data, although LG is still

split between two clusters. LL is predominately in

one cluster. Interestingly, all of TP is in a single clus-

ter with all NF data points. This is because that af-

ter the ∆V ﬁltering, only a small number of NF data

points are left in the dataset. The homogeneity score

of this method is 0.932, much higher than the results

on the non-ﬁltered dataset.

On the same ﬁltered dataset, we have also applied

the DBSCAN clustering method, and the results are

shown in Figure 7 and Table 6.

Figure 7: Relative Phase Features.

Table 6: Filtered DBSCAN clustering % breakdown.

LG LL TP NF

1 99.34% 0.00% 0.00% 0.00%

2 0.56% 0.81% 100% 100%

3 0.00% 84.68% 0.00% 0.00%

4 0.00% 6.45% 0.00% 0.00%

Noise 0.10% 8.06% 0.00% 0.00%

Comparing to the results on the original dataset,

this set of results show signiﬁcant improvement, be-

cause the ﬁltering help remove most of the noise.

With the ﬁlter DBSCAN preformed excellently well,

illustrated by its homogeneity score of 0.933. It was

able to cluster most of LG in cluster 1, LL in cluster

3 and 4, and all of TP in cluster 2. Similar to the k-

means method, No Fault data are mixed with TP in

cluster 2, because of the limited number of data sam-

ples after the ﬁltering.

6 CONCLUSION

Synchrophasor technology is widely used in modern

power systems, resulting in increasing amounts of

data being generated on a daily basis. Machine learn-

ing methods represent the future directions in process-

ing these data. Although supervised learning methods

have been applied for this purpose, in order to prepare

the training datasets for those methods, labeling data

requires a signiﬁcant amount of effort.

In this paper, we present our experience in ap-

plying unsupervised clustering methods on PMU data

collected on a smart grid. We have evaluated mul-

tiple clustering methods on two distinct representa-

tions of PMU data: time series and instantaneous data

points. Speciﬁcally, hierarchical clustering method

is used to cluster time series data, and both k-means

and DBSCAN are used to cluter instantaneous data

points. Interestingly, although PMU data are time se-

ries data in nature, our results show that clustering

on instantaneous data points with carefully selected

features performs much better in terms of homogene-

ity score. Among all the clustering methods we have

evaluated, DBSCAN achieves the highest homogene-

ity score. This work demonstrates potentials of iden-

tifying unknown events on a smart grid without sub-

stantial training data. For future work, we will apply

the clustering methods on a dataset which contains

unknown events, namely generator faults, for the pur-

pose of characterizing new events. In addition, we

will develop type-speciﬁc classiﬁcation methods on

different clusters to better classify events.

Unsupervised Clustering on PMU Data for Event Characterization on Smart Grid

239

ACKNOWLEDGMENTS

The authors would like to thank the Department of

Energy / Bonneville Power Administration for their

generous support through the Technology Innovation

Program (TIP# 319) and for providing the PMU data

used in this study.

REFERENCES

Americans for a Clean Energy Grid (2014). Syn-

chrophasors. http://cleanenergytransmission.org/wp-

content/uploads/2014/08/Synchrophasors.pdf. Ac-

cessed: 2015-09-08.

Antoine, O. and Maun, J.-C. (2012). Inter-area oscillations:

Identifying causes of poor damping using phasor mea-

surement units. In Power and Energy Society General

Meeting, 2012 IEEE, pages 1–6. IEEE.

Bailey, K. (1994). Numerical taxonomy and cluster analy-

sis. Typologies and Taxonomies.

Chang, G., Chao, J.-P., Huang, H.-M., Chen, C.-I., and

Chu, S.-Y. (2008). On tracking the source location

of voltage sags and utility shunt capacitor switching

transients. IEEE Transactions on Power Delivery,

23(4):2124–2131.

Dahal, O. P., Brahma, S. M., and Cao, H. (2014). Com-

prehensive clustering of disturbance events recorded

by phasor measurement units. IEEE Transactions on

Power Delivery, 29(3):1390–1397.

Diao, R., Sun, K., Vittal, V., O’Keefe, R., Richardson, M.,

Bhatt, N., Stradford, D., and Sarawgi, S. (2009). Deci-

sion tree-based online voltage security assessment us-

ing pmu measurements. IEEE Transactions on Power

Systems, 24(2):832–839.

Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In KDD, vol-

ume 96, pages 226–231.

Gomez, F. R., Rajapakse, A. D., Annakkage, U. D., and Fer-

nando, I. T. (2011). Support vector machine-based al-

gorithm for post-fault transient stability status predic-

tion using synchronized measurements. IEEE Trans-

actions on Power Systems, 26(3):1474–1483.

Jiang, J.-A., Yang, J.-Z., Lin, Y.-H., Liu, C.-W., and Ma,

J.-C. (2000). An adaptive pmu based fault detec-

tion/location technique for transmission lines. i. the-

ory and algorithms. IEEE Transactions on Power De-

livery, 15(2):486–493.

Keogh, E. J. and Pazzani, M. J. (2000). Scaling up dy-

namic time warping for datamining applications. In

Proceedings of the 6th ACM SIGKDD International

Conference on Knowledge Discovery and Data Min-

ing, pages 285–289. ACM.

Liang, X., Wallace, S., and Zhao, X. (2014). A technique

for detecting wide-area single-line-to-ground faults.

In Proceedings of the 2nd IEEE Conference on Tech-

nologies for Sustainability (SusTech 2014), SusTech

’14, pages 1–4. IEEE.

Liao, T. W. (2005). Clustering of time series dataa survey.

Pattern recognition, 38(11):1857–1874.

Liu, G. and Venkatasubramanian, V. (2008). Oscillation

monitoring from ambient pmu measurements by fre-

quency domain decomposition. In IEEE International

Symposium on Circuits and Systems (ISCAS 2008),

pages 2821–2824.

Nguyen, D., Barella, R., Wallace, S., Zhao, X., and Liang,

X. (2015). Smart grid line event classiﬁcation using

supervised learning over pmu data streams. In Proc-

cedings of the 6th IEEE International Green and Sus-

tainable Computing Conference.

North American Electric Reliability Corporation

(2014). Real-Time Application of Synchro pha-

sors for Improving Reliability. http://www.nerc.

com/docs/oc/rapirtf/RAPIR%20ﬁnal%20101710.pdf.

Accessed: 2015-09-08.

Ray, P. K., Mohanty, S. R., Kishor, N., and Catal

ao, J. P.

(2014). Optimal feature and decision tree-based clas-

siﬁcation of power quality disturbances in distributed

generation systems. IEEE Transactions on Sustain-

able Energy, 5(1):200–208.

Rokach, L. and Maimon, O. (2005). Clustering methods.

In Data mining and knowledge discovery handbook,

pages 321–352. Springer.

Rosenberg, A. and Hirschberg, J. (2007). V-measure: A

conditional entropy-based external cluster evaluation

measure. In EMNLP-CoNLL, volume 7, pages 410–

420.

Salat, R. and Osowski, S. (2004). Accurate fault location

in the power transmission line using support vector

machine approach. IEEE Transactions on Power Sys-

tems, 19(2):979–986.

Singh, B., Sharma, N., Tiwari, A., Verma, K., and Singh,

S. (2011). Applications of phasor measurement units

(pmus) in electric power system networks incorpo-

rated with facts controllers. International Journal of

Engineering, Science and Technology, 3(3).

Tate, J. E. and Overbye, T. J. (2008). Line outage detection

using phasor angle measurements. IEEE Transactions

on Power Systems, 23(4):1644–1652.

Wagstaff, K., Cardie, C., Rogers, S., Schr

odl, S., et al.

(2001). Constrained k-means clustering with back-

ground knowledge. In ICML, volume 1, pages 577–

584.

Zhang, Y.-G., Wang, Z.-P., Zhang, J.-F., and Ma, J. (2011).

Fault localization in electrical power systems: A pat-

tern recognition approach. International Journal of

Electrical Power & Energy Systems, 33(3):791–798.

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

240