Continuous Improvement of Proactive Event-driven Decision Making

through Sensor-Enabled Feedback (SEF)

Alexandros Bousdekis

, Nikos Papageorgiou

, Babis Magoutas

, Dimitris Apostolou

and Gregoris Mentzas

Information Management Unit, National Technical University of Athens, Athens, Greece

Department of Informatics, University of Piraeus, Piraeus, Greece

Keywords: Kalman Filter, Curve Fitting, Decision Support, Machine Learning, Manufacturing, Feedback.

Abstract: The incorporation of feedback in the proactive event-driven decision making can improve the

recommendations generated and be used to inform users online about the impact of the recommended action

following its implementation. We propose an approach for learning cost functions from Sensor-Enabled

Feedback (SEF) for the continuous improvement of proactive event-driven decision making. We suggest

using Kalman Filter, dynamic Curve Fitting and Extrapolation to update online (i.e. during action

implementation) cost functions of actions, with the aim to improve the parameters taken into account for

generating recommendations and thus, the recommendations themselves. We implemented our approach in

a real proactive manufacturing scenario and we conducted extensive experiments in order to validate its

effectiveness.

1 INTRODUCTION

Proactive, event-driven decision making is an

approach for deciding ahead of time about the

optimal action and the optimal time for its

implementation (Engel et al., 2012). Proactivity is

leveraged with novel information technologies that

enable decision making before a predicted critical

event occurs (Bousdekis et al., 2015). A proactive

event-driven Decision Support System (DSS) should

integrate different sensor data, provide real-time

processing of sensor data and combine historical and

domain knowledge with current data streams in

order to facilitate predictions and proactive

recommendations (Engel et al., 2012; Bousdekis et

al., 2015). The emergence of the Internet of Things

paves the way for enhancing the monitoring

capabilities of enterprises by means of extensive use

of sensors generating a multitude of data (Bousdekis

et al., 2015). The manufacturing domain can take

substantial advantage from proactive event-driven

decision making in order to turn maintenance

operations from “fail and fix” to “predict and

prevent” (Bousdekis et al., 2015). In addition, the

incorporation of feedback in the decision process

can, on the one hand, improve the recommendations

generated by the proactive event-driven DSS and, on

the other hand, be used to inform users online about

the impact of the recommended action following its

implementation. However, the noise existing in

manufacturing sensors makes proactive event-driven

decision making process vulnerable to inaccuracies.

Until now the embodiment of a feedback

functionality in proactive, event-driven decision

making has not been examined.

Our research objective is to examine how a

feedback loop can be implemented in a proactive

event-driven DSS so that data generated post action

implementation can be used to improve the decision

making process. Specifically, by focusing on

decision making processes that have a cost footprint

on the manufacturing process, we aim to investigate

how the cost functions of actions that are taken into

account for the provision of recommendations can

be updated and improved each time a recommended

action is implemented. Furthermore, we examine

what kind of data processing conducted by the

feedback loop is appropriate for informing online

users about the actual and the predicted cost of the

action during its implementation. Our approach is

followed by an application in a real industrial

environment and by extensive experiments for

validation.

The rest of the paper is organized as follows:

166

Bousdekis, A., Papageorgiou, N., Magoutas, B., Apostolou, D. and Mentzas, G.

Continuous Improvement of Proactive Event-driven Decision Making through Sensor-Enabled Feedback (SEF).

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 2, pages 166-173

ISBN: 978-989-758-187-8

Section 2 presents the related and background

works; Section 3 outlines our approach, while

Section 4 illustrates its application in a proactive

manufacturing scenario in the area of production of

automotive lighting equipment and presents

extensive experimental results in comparison to

Curve Fitting on noisy data, that prove the

effectiveness of our approach. Section 5 discusses

the results and concludes the paper.

2 RELATED AND BACKGROUND

WORKS

2.1 State-of-the-Art

There are several research works dealing with the

utilisation of feedback in Machine Learning

proposing algorithms based on Reinforcement

Learning (Lewis et al., 2012), iterative control

techniques (Lee and Lee, 2007), particle swarm

optimization (Tang et al., 2011) and incremental

learning (Chen et al., 2012). However, there is not a

methodology which enables the sensor noise

removal and the extraction of the function that these

sensor data follow in a way that can continuously

improve the recommendations provided by a

proactive event-driven system. Moreover, although

there are several applications in image processing

and robotics, learning from feedback has not been

used in order to update and improve costs of actions

that are expressed as a function of time. So, an

approach is needed for the continuous improvement

of a proactive event-driven system in terms of the

cost information that it handles, no matter which

decision method it uses.

For removing the noise from sensors and having

data closer to the real one, a Kalman Filter can be

used. Kalman Filters have been widely used for

removing noise in applications such as voltage

measurement, object tracking, navigation and

computer vision applications. Moreover, there are

some applications of Kalman Filters in prognosis of

manufacturing equipment (Sai Kiran et al., 2013).

However, a Kalman Filter is only able to provide the

corrected data based on the sensor measurements

and not to extract an estimation of the function that

these data follow. Curve fitting has been widely used

for extracting the linear, polynomial or exponential

function that a series of data follow and it can be

combined with extrapolation. However, when curve

fitting and extrapolation are applied to highly noisy

data, the level of confidence about the result is low,

since there is high uncertainty in both the actual

value of the measurement and the prediction that

extrapolation produces.

We argue that Kalman Filter, Curve Fitting and

extrapolation can be synergistically combined in

order to provide Sensor-Enabled Feedback (SEF) to

the decision making algorithms of a proactive event-

driven DSS about the actual cost functions that are

taken into account for the business performance

optimization and the provision of recommendations.

Although there are some research works proposing

such a combination, they address different problems

and in a different context (Sai Kiran et al., 2013),

while they assume the availability of historical data

or extensive domain knowledge (Yunfeng 2013).

2.2 Kalman Filter

Kalman Filter is an algorithm that uses a series of

measurements observed over time, containing

statistical noise and other inaccuracies in order to

provide estimations about the current values

(Kalman 1960). A Kalman filter is an optimal and

recursive estimator since it infers parameters of

interest from inaccurate observations as they arrive.

Moreover, it provides reliable results and is suitable

for online / real-time processing (Ertürk 2002). It is

suitable for linear systems, while, in cases of highly

non-linear systems, the Unscented Kalman Filter is

an accurate estimator (Kandepu et al., 2008).

Kalman Filter can be used for either uniform or non-

uniform sampling.

2.3 Curve Fitting and Extrapolation

Curve fitting is a numerical process that is used to

represent a set of experimentally measured (or

estimated) data points by some hypothetic analytical

functions (Vohnout 2003). Curve fitting can be

applied in several types of functions, e.g. linear (first

degree polynomial), polynomial, exponential. A

well-known curve fitting technique for linear

functions is the Linear Regression (Montgomery et

al., 2012). In the general form, for polynomial

functions, a widely used technique is Levenberg–

Marquardt algorithm (Lourakis 2005). For

exponential functions, a useful algorithm is Nelder-

Mead algorithm (Bűrmen 2006). Extrapolation

refers to the use of a fitted curve beyond the range of

the observed data and is subject to a degree of

uncertainty (Brezinski and Zaglia, 2013).

Extrapolation is implemented based on the curve

fitting results. Curve fitting and extrapolation can be

applied dynamically in a way that their output is

Continuous Improvement of Proactive Event-driven Decision Making through Sensor-Enabled Feedback (SEF)

167

updated in real-time as long as new data are gathered

from sensors.

3 OUR APPROACH

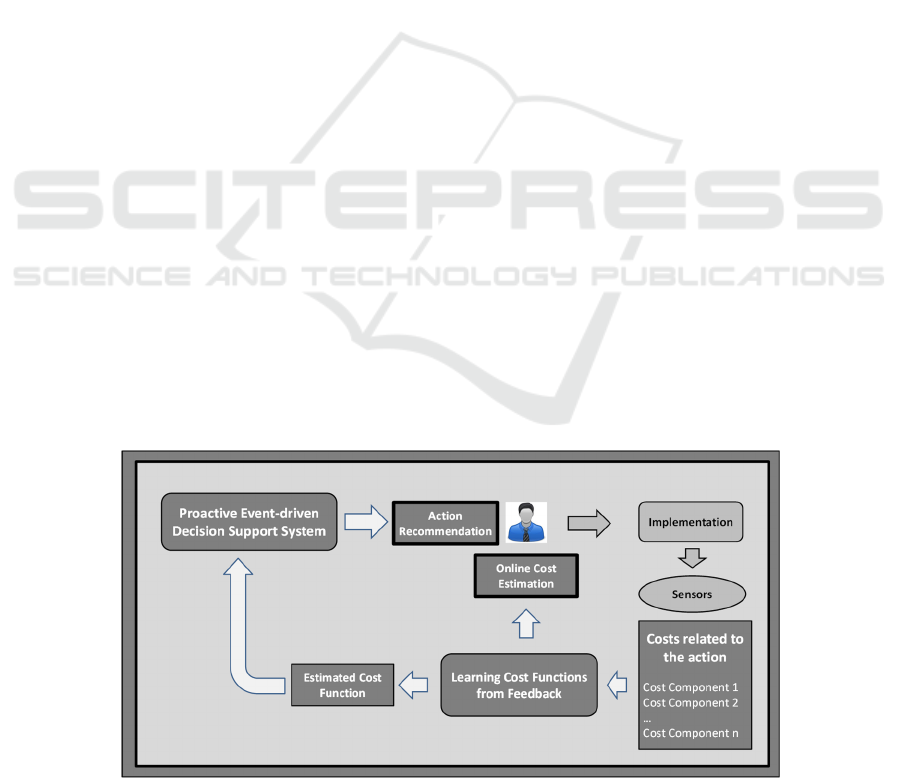
The overall approach for learning cost functions

from SEF for the continuous improvement of

proactive event-driven DSS is shown in Figure 1.

The proactive event-driven DSS provides a

recommendation about the optimal action and the

optimal time for its implementation on the basis of a

prediction of a future undesired event, so that the

utility function is maximised (Engel et al., 2012).

For this reason, the decision making algorithms

embedded in the system take into account the

prediction but also domain knowledge, such as the

costs of actions as a function of time. The specific

algorithms used are not described here for brevity

but can be found in Bousdekis et al. (2015).

Cost functions are provided typically by domain

experts during the configuration of the system. In the

case of manufacturing, the total cost function is

typically an aggregation of different cost

components such as labour cost, cost due to

downtime, cost due to scrapped parts, cost due to

warranty claims, cost of spare parts, etc. (Amorim-

Melo et al., 2014). During the implementation of the

action, data regarding the cost functions can be

collected from different sensors (hardware,

software-e.g. ERP production plan- or human

sensors); their sampling may vary from the one cost

component to the other, while each cost component

may follow a different type of function (e.g. fixed,

linear, polynomial, exponential). The type of cost

functions may be affected either by the cost model

itself (e.g. labour cost is a linear function which

corresponds to a pay rate of X euros per hour) or by

a business process that causes a cost increase (e.g.

the number of defects per unit time affects the cost

function due to scrapped parts).

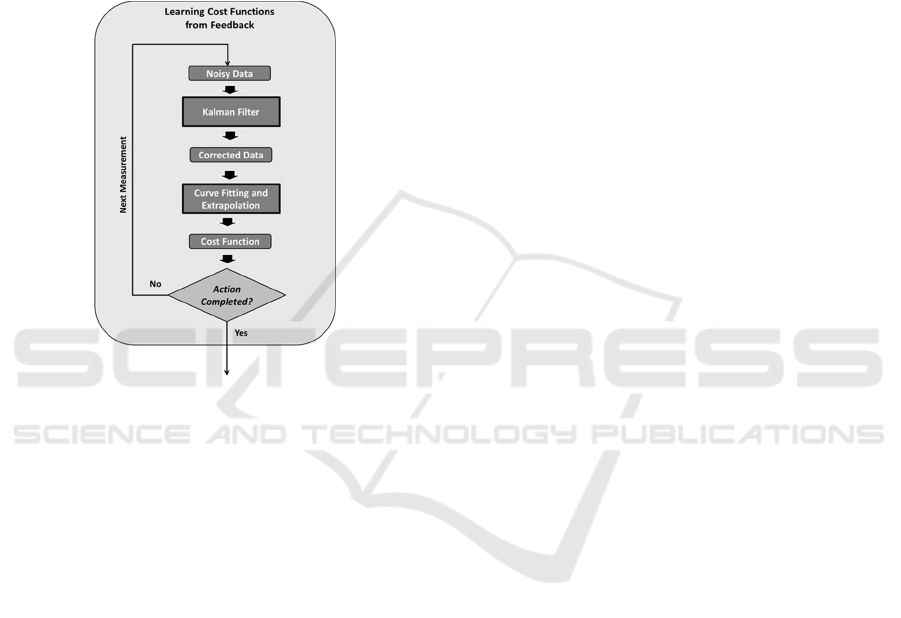
The process of learning cost functions from

feedback is shown in Figure 2. The figure provides a

more detailed explanation of the “Learning Cost

Functions from Feedback” block of Figure 1. For

each cost component, sensors generate noisy data

with a specific frequency either with uniform or with

non-uniform sampling. These noisy data include the

input of the Kalman Filter which removes the noise

and provides estimation about the current state (the

real current value of a cost component). In cases of

fixed and linear cost functions, the linear Kalman

Filter is used, while, for polynomial and exponential

cost functions, the Unscented Kalman Filter is used

(Kandepu et al., 2008). The Kalman Filter’s output

is provided as input to Curve Fitting, which is

applied during the implementation of the action and

is updated after every measurement. In case of fixed

and linear cost function, a linear regression

algorithm can be applied. In case of polynomial cost

function, a Levenberg–Marquardt algorithm can be

applied, while in case of exponential one, a Nelder-

Mead algorithm is suitable. The type of function has

been inserted into the system during its

configuration. Furthermore, at each measurement

time step, extrapolation is applied on the function

estimated by Curve Fitting in order to estimate the

future state of the system (i.e. future evolution of

cost function) until a pre-defined threshold. This

threshold can deal with the level of cost (e.g. the

action is going to stop in case of unpredictably high

costs, over a cost threshold) or the period of time (e.g.

the action is going to stop after a specific period of

time passes) or an average value of either cost or time.

Figure 1: Overall Approach.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

168

The process for learning cost functions is an

iterative process which takes place each time sensor

measurements exist. The user is informed online

about the estimated cost of action during its

implementation as shown in Figure 1. So, the user

becomes aware of the actual cost of the action and

its evolution until the end of the action. After the

implementation of the action, the updated cost

function of this action feeds into the proactive event-

driven DSS in order to be used in the next

recommendation in which this action is involved.

Figure 2: The process for learning cost functions from

feedback.

4 IMPLEMENTATION OF OUR

APPROACH

4.1 Application in a Real Industrial

Scenario

We validated our approach in a manufacturing

scenario in the area of production of automotive

lighting equipment. The production process includes

the production of the headlamps’ components. These

processes gather many data through embedded

quality assessment equipment using sensors and

measuring devices. A proactive event-driven DSS

embedding various decision methods would be able

to be developed based on a relevant architecture in

order to provide proactive recommendations

(Bousdekis et al., 2015). The proposed approach

could be coupled with such a proactive event-driven

DSS so that: (i) the user is informed online about the

estimated actual and future cost of action during its

implementation, and (ii) the updated cost function of

the specific action is used in the next recommendation

in which this action is involved. However, the cost

functions of actions that are taken into account for the

provision of recommendations are inserted in the

system only once, during the configuration stage

(Bousdekis et al., 2015) and the sensor measuring the

scrapped parts generates noisy data.

In the current scenario, there are two alternative

actions that can be recommended: the re-

configuration of the moulding machine during its

function (which results in higher scrap rate) or the

same action with downtime. The decision method of

the system calculates that the cost of production loss

due to downtime will be higher than the cost of

scrapped parts during moulding machine’s function.

So, the “re-configuration of the moulding machine

during its function” is the action that is

recommended along with the optimal time for its

implementation. This action may cause a

malfunction of the moulding machine which can

lead to an increase of scrapped parts during the

implementation. So, in this case, one cost component

exists: the cost due to the production of scrapped parts

when an action is implemented. The cost due to the

production of scrapped parts is represented by a linear

function. Each scrapped part has a cost of 100 € with

a constant rate at each time step equal to 1 scrapped

part per minute, as shown in Equation 1.

Cost Function = 100 * number of scrapped

parts * t

(1)

So, in this case, the noise exists in the number of

scrapped parts that the sensor measures during the

implementation of the action. Each time a part is

produced, the sensor sends a signal about whether it

is good or scrapped. When there is a signal of a

scrapped part, the cost of a unit part is added to the

cost till that time. The production rate of the

machine does not change, so there is a uniform

sampling since each time a part is produced, a

measurement is taken by a sensor. Based on domain

knowledge, the action will last approximately 2

hours. The function that has been given during the

configuration of the system is shown in Equation 2:

Cost = 100 * t (2)

Based on technical specifications and domain

knowledge, the sensor noise covariance for this

setup is equal to 6, therefore the cost noise

covariance will be:

Cost Noise Covariance = 6 * 100 € (3)

This has been calculated according to the formula:

Cost Noise Covariance = Sensor Noise

Covariance * unit cost

(4)

Continuous Improvement of Proactive Event-driven Decision Making through Sensor-Enabled Feedback (SEF)

169

The formulation of Kalman Filter is similar to a

position-constant velocity problem (Won et al.,

2010), but instead of position and velocity, there is

cost and rate of cost change. So, the equations of

Kalman Filter are modified accordingly. The

proposed approach was implemented in Python

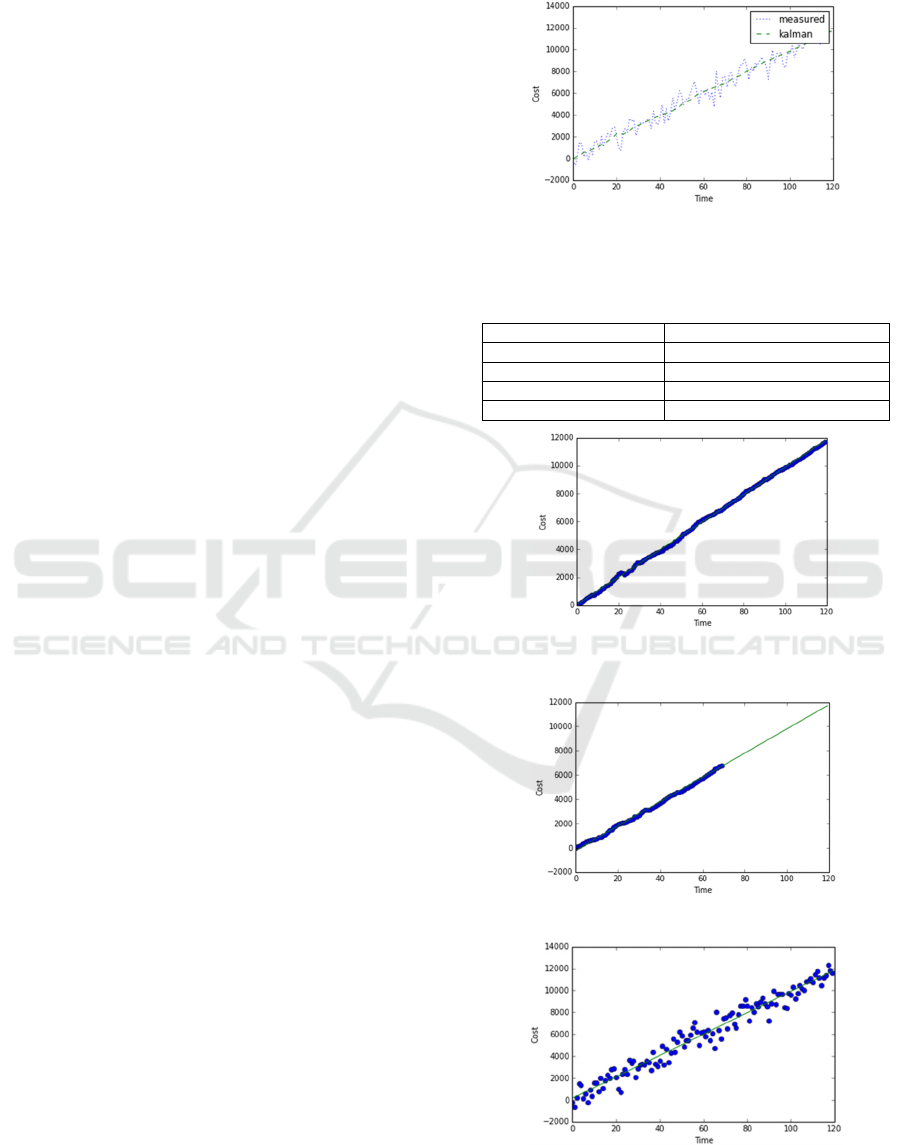
programming language. Figure 3 shows the

evolution of cost according to the noisy

measurements and according to the corrected

measurements after the implementation of Kalman

Filter. Since Kalman Filter cannot extract the

function, our approach applies dynamic curve fitting

in each iteration and in the final result. So, in this

example, linear regression is applied on the basis of

the points extracted from Kalman. The final result is

shown in Figure 4, where the output of the Kalman

Filter are data that approach a linear function and is

close to the line that linear regression creates.

The output of linear regression in the corrected

data is shown in Table 1. The equation is derived

from the results of Linear Regression about the slope

and the intercept (Montgomery et al., 2012). In this

example, R

is high and approaches 1, so the data

are fitted almost perfectly to the regression line. P-

value approaches 0, which means that the null

hypothesis can be rejected. Standard error is

0.225229389344, so the distance that the values fall

from the regression line is relatively low. The

sample size is equal to 120 as measurements are

taken every minute for 2 hours.

The final results, after the implementation of the

action, feeds into the proactive event-driven DSS

and updates the cost function of the specific action

which will be used in the next recommendation in

which this action is involved. At the same time, the

user is informed online about the estimated cost of

action during its implementation. This means that he

/ she is able to see the actual cost and its evolution

until now (through dynamic curve fitting) as well as

the estimated cost until a time threshold which in

this example is 2 hours (through extrapolation).

Figure 5 shows the dynamic curve fitting and

extrapolation technique at a specific time step of the

action implementation.

Since the objective is to extract the actual cost

function, we compare the results of our approach

with applying linear regression directly on the basis

of noisy data. This result is shown in Figure 6. The

output of linear regression in the corrected data is

shown in Table 2. R

is lower than the one in our

approach, so the data are fitted worse to the regression

line. P-value also approaches 0, but is slightly higher

than the one in our approach. Standard error is

1.79130743211, so the distance that the values fall

from the regression line is higher. The linear

regression is applied in the same sample size.

Figure 3: Cost evolution during the implementation of the

action.

Table 1: Output of curve fitting (linear regression) in the

corrected data for the scenario.

Equation

98.55 * t + 37.64

0.999384074129

P value

2.80148856911e-191

Standard Error

0.225229389344

Sample size

120

Figure 4: Curve Fitting (Linear Regression) on the basis of

corrected data.

Figure 5: Dynamic Curve Fitting and Extrapolation

Figure 6: Curve Fitting (Linear Regression) on the basis of

noisy data.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

170

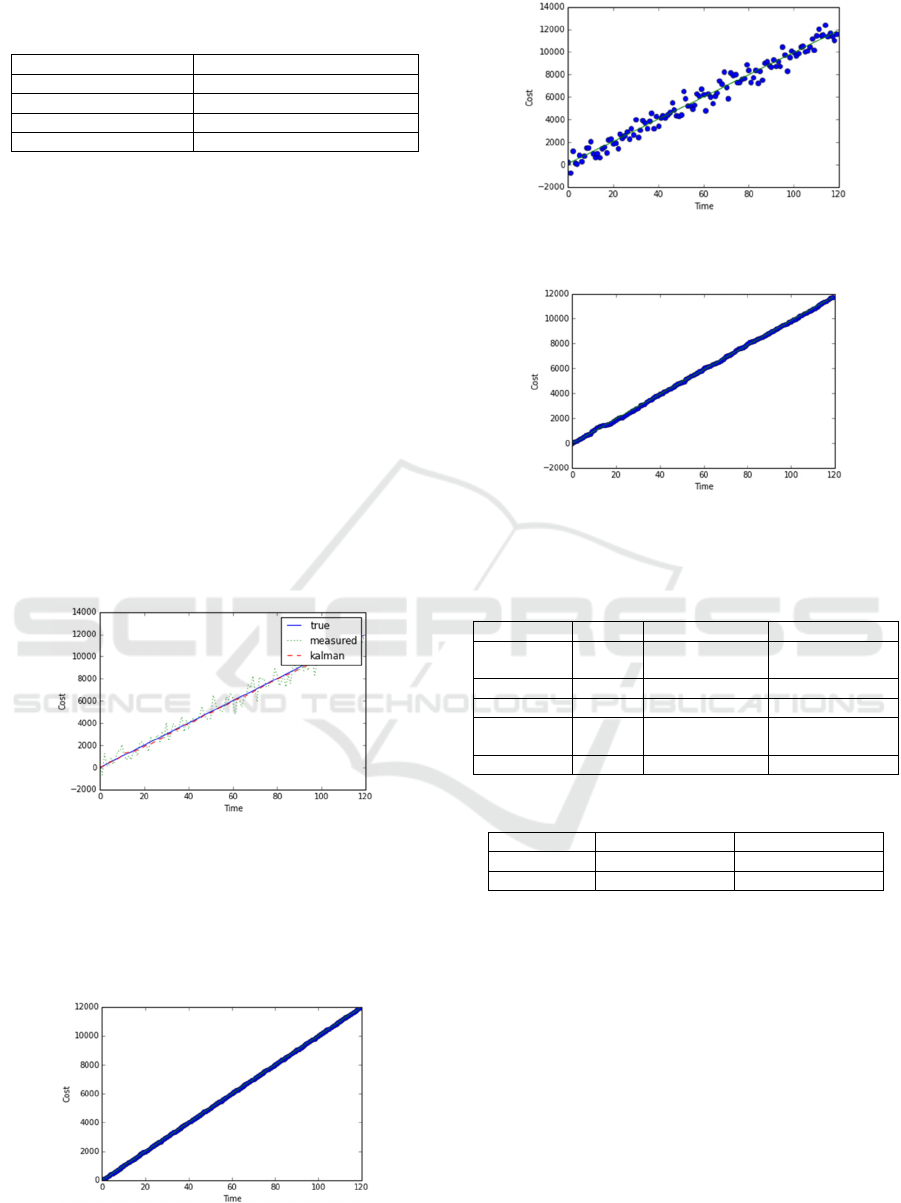
Table 2: Output of linear regression in the noisy data for

the scenario.

Equation

96.45 * t + 63.34

0.961777688176

P value

1.69862696613e-85

Standard Error

1.79130743211

Sample size

120

4.2 Experimental Results

4.2.1 Indicative Simulation Experiment

In order to validate the effectiveness of our

approach, we conducted simulations with various

noise levels and linear functions and we compared

the Mean Squared Error (MSE) and the Mean

Absolute Error (MAE) (Willmott, and Matsuura,

2005). The results show that our approach works

much better than applying linear regression on the

basis of noisy data. In other words, the resulting cost

function of our approach is closer to the true one

than the one of the linear regression applied to noisy

data. Figure 7 shows the results of one of the

simulation experiments. It shows the true function,

the measured noisy data and the data after the

implementation of Kalman Filter.

Figure 7: Result of a simulation experiment.

We applied Linear Regression to all the three

functions and the results for each one are shown in

Figure 8, in Figure 9 and in Figure 10. The output

results of Linear Regression are shown in Table 3.

Obviously, in the true function all the data fit

Figure 8: Curve Fitting (Linear Regression) on the basis of

the true data for the simulation example.

Figure 9: Curve Fitting (Linear Regression) on the basis of

the noisy data for the simulation example.

Figure 10: Curve Fitting (Linear Regression) on the basis

of corrected data for the simulation example.

Table 3: Output results of Linear Regression in the

simulation example.

True Measured Kalman

Equation

100 * t 98.65 * t +

78.76

98.66 * t - 22.79

1.0 0.973573107 0.999678

P value

0.0 5.92e-95 6.407e-208

Standard

Error

0.0 1.496 0.1629

Sample size

120 120 120

Table 4: Comparison of MSE and MAE.

Measured Kalman

MSE

433872.211071 12492.8947745

MAE

542.908521255 85.4088944024

perfectly to the regression line. The application of

Linear Regression on the basis of the data processed

by Kalman Filter gives better results. The plot data

are less scattered and more accurate due to the

application of Kalman Filter. This can also be

concluded by Table 4, which shows the values of

MSE and MAE of the two comparing approaches.

4.2.2 Overview of Experimental Results

In the simulation experiments, we applied Curve

Fitting on the basis of the measured noisy data and

on the basis of the corrected data (after the

implementation of Kalman Filter) for various Cost

Noise Covariances and Cost Functions. The results

Continuous Improvement of Proactive Event-driven Decision Making through Sensor-Enabled Feedback (SEF)

171

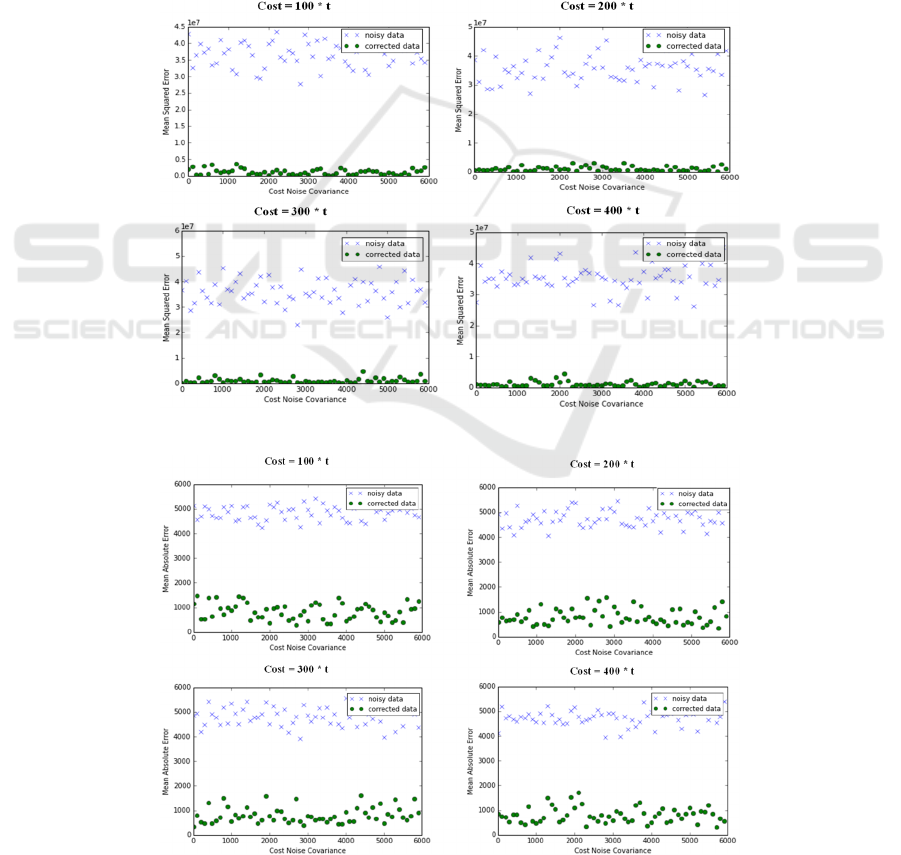
show that our approach provides more accurate

results. This was concluded by comparing the

resulting equations of the two approaches with the

true one. Thus, MSE and MAE were compared for

different Cost Functions and Cost Noise

Covariances, as shown in Figure 11 and in Figure 12

respectively. MSE and MAE of our approach is

always much lower for various Cost Noise

Covariances and for different Cost Functions.

5 CONCLUSIONS AND FUTURE

WORK

We propose an approach for learning cost functions

from SEF for the continuous improvement of

proactive event-driven decision making. We suggest

using Kalman Filter to update online cost functions

of actions, with the aim to improve the parameters

taken into account for generating recommendations

and thus, the recommendations themselves. More

specifically, our approach utilizes the capabilities of

Kalman Filter for removing noise from sensor data,

dynamic curve fitting on the basis of the corrected

data for extracting at each time step the cost function

and extrapolation on the basis of the corrected data

for predicting the evolution of cost until the end of

the implementation of the recommended action in an

accurate and reliable way. The SEF is received

during the recommended action implementation.

Figure 11: MSE for different Cost Functions and Cost Noise Covariances.

Figure 12: MAE for different Cost Functions and Cost Noise Covariances.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

172

The role of SEF is twofold: (i) The user is informed

online about the estimated cost of action during its

implementation, and (ii) The updated cost function

of the specific action is used in the next

recommendation in which this action is involved.

The proposed approach was tested in a real

industrial environment. In addition, simulation

experiments were conducted in order to prove its

effectiveness. Curve Fitting and extrapolation on

less noisy data (after the implementation of Kalman

Filter) gives more reliable results comparing to its

application to the sensor noisy measurements. In

other words, applying curve fitting in more accurate

and less noisy data can give a better insight about

the function that these data follow and can provide

more reliable predictions about the future values

through extrapolation. Regarding our future work,

we aim to add more cost models and validate our

approach for different functions for both uniform

and non-uniform sampling. Cost components may be

gathered from different sensors in a different

frequency, while some of them may conduct

uniform sampling and others non-uniform sampling.

We aim to examine the combination of all these

sensors and the aggregation of the total cost at each

time step.

ACKNOWLEDGEMENTS

This work is partly funded by the European

Commission project FP7 STREP ProaSense “The

Proactive Sensing Enterprise” (612329).

REFERENCES

Amorim-Melo, P., Shehab, E., Kirkwood, L., Baguley, P.

(2014). Cost Drivers of Integrated Maintenance in

High-value Systems. Procedia CIRP, 22, 152-156.

Bousdekis, A., Papageorgiou, N., Magoutas, B.,

Apostolou, D., Mentzas, G., 2015. A Real-Time

Architecture for Proactive Decision Making in

Manufacturing Enterprises. In On the Move to

Meaningful Internet Systems: OTM 2015 Workshops

(pp. 137-146). Springer International Publishing.

Brezinski, C., Zaglia, M. R., 2013. Extrapolation methods:

theory and practice. Elsevier.

Bűrmen, Á., Puhan, J., Tuma, T., 2006. Grid restrained

nelder-mead algorithm. Computational Optimization

and Applications, 34(3), 359-375.

Chen, X., Huang, J., Wang, Y., Tao, C., 2012. Incremental

feedback learning methods for voice recognition based

on DTW. In Modelling, Identification & Control

(ICMIC), 2012 Proceedings of International

Conference on (pp. 1011-1016). IEEE.

Engel, Y., Etzion, O., Feldman, Z., 2012. A basic model

for proactive event-driven computing. In 6th ACM

Conf. on Distributed Event-Based Systems, pp. 107-

118, ACM.

Ertürk, S., 2002. Real-time digital image stabilization

using Kalman filters. Real-Time Imaging, 8(4), 317-

328.

Kalman, R. E., 1960. A new approach to linear filtering

and prediction problems. Journal of Fluids

Engineering, 82(1), 35-45.

Kandepu, R., Foss, B., & Imsland, L. (2008). Applying the

unscented Kalman filter for nonlinear state estimation.

Journal of Process Control, 18(7), 753-768.

Lee, J. H., Lee, K. S., 2007. Iterative learning control

applied to batch processes: An overview. Control

Engineering Practice, 15(10), 1306-1318.

Lewis, F. L., Vrabie, D., & Vamvoudakis, K. G. (2012).

Reinforcement learning and feedback control: Using

natural decision methods to design optimal adaptive

controllers. Control Systems, IEEE, 32(6), 76-105.

Lourakis, M. I., 2005. A brief description of the

Levenberg-Marquardt algorithm implemented by

levmar.Foundation of Research and Technology,4,1-6.

Montgomery, D. C., Peck, E. A., Vining, G. G., 2012.

Introduction to linear regression analysis (Vol. 821).

John Wiley & Sons.

Sai Kiran, P. V. R., Vijayaramkumar, S., Vijayakumar, P.

S., Varakhedi, V., Upendranath, V., 2013. Application

of Kalman Filter to prognostic method for estimating

the RUL of a bridge rectifier. In Emerging Trends in

Communication, Control, Signal Processing &

Computing Applications (C2SPCA), 2013

International Conference on (pp. 1-9). IEEE.

Tang, Y., Wang, Z., Fang, J. A., 2011. Feedback learning

particle swarm optimization. Applied Soft Computing,

11(8), 4713-4725.

Vohnout, K. D., 2003. Curve fitting and evaluation.

Mathematical Modeling for System Analysis in

Agricultural Research

, 140-178.

Willmott, C. J., & Matsuura, K. (2005). Advantages of the

mean absolute error (MAE) over the root mean square

error (RMSE) in assessing average model

performance. Climate research, 30(1), 79.

Won, S. H. P., Melek, W. W., Golnaraghi, F. (2010). A

Kalman/particle filter-based position and orientation

estimation method using a position sensor/inertial

measurement unit hybrid system. Industrial

Electronics, IEEE Transactions on, 57(5), 1787-1798.

Yunfeng, L., 2013. The improved Kalman filter algorithm

based on curve fitting. In Information Management,

Innovation Management and Industrial Engineering

(ICIII), 2013 6th International Conference on (Vol. 1,

pp. 341-343). IEEE.

Continuous Improvement of Proactive Event-driven Decision Making through Sensor-Enabled Feedback (SEF)

173