Comparison of Fuzzy Extent Analysis Technique and its Extensions with

Original Eigen Vector Approach

Faran Ahmed and Kemal Kilic

Faculty of Engineering and Natural Sciences, Sabanci University, Universite Cd. No:27, Istanbul, Turkey

Keywords:

Fuzzy AHP, Fuzzy Extent Analysis, Eigen Vector Approach.

Abstract:

Fuzzy set theory has been extensively incorporated in the original Analytical Hierarchical Process (AHP) with

an aim to better represent human judgments in comparison matrices. One of the most popular technique in

the domain of Fuzzy AHP is Fuzzy Extent Analysis method which utilizes the concept of extent analysis

combined with degree of possibility to calculate weights from fuzzy comparison matrices. In original AHP,

where the comparison matrices are composed of crisp numbers, Satty proposed that Eigen Vector of these

comparison matrices estimate the required weights. In this research we perform a comparison analysis of

these two approaches based on a data set of matrices with varying level of inconsistency. Furthermore, for

the case of FEA, in addition to degree of possibility, we use centroid defuzziﬁcation and defuzziﬁcation by

using the mid number of triangular fuzzy number to rank the ﬁnal weights calculated from fuzzy comparison

matrices.

1 INTRODUCTION

Analytical Hierarchy Process (AHP) proposed by

(Saaty, 1980) is a methodology for structuring, mea-

surement and synthesis (Forman and Gass, 2001)

which utilizes pairwise comparisons to derive ratio

scales indicating the preferences of the decision mak-

ers among different alternatives and associated crite-

ria. These comparisons are recorded in a comparison

matrix and processed to determine the corresponding

weights of the given criterion as well as available al-

ternatives. The normalized weighted sum provides a

weight associated with each available alternatives and

thus help decision maker to choose the best decision.

In the literature, two different scales are used to

record pairwise comparisons i.e. scale based on crisp

numbers (scale of 1-9) and scale based on fuzzy num-

bers. The original method uses the scale of 1-9

in which decision maker preferences of weak, nor-

mal and strong are represented by some number in

the given scale and recorded in comparison matri-

ces. Afterwards, weights are calculated from well-

deﬁned mathematical structure of consistent matrices

and their associated eigenvectors ability to generate

true or approximate weights (Saaty, 1980).

However, this approach has found some criti-

cism on the premises that crisp numbers disregards

the vagueness of human language thus implying that

vague linguistic variables (i.e., weak, strong, etc.)

cannot be represented with a ratio scale based on crisp

numbers and may lead to wrong decisions in the de-

cision analysis process (Tsaur et al., 2002).

Fuzzy set theory introduced by (Zadeh, 1965)

has been used frequently in the literature to repre-

sent vagueness of human thought. It represents the

belongingness of an object to a set by means of

membership functions which ranges from zero to one

and has found many applications over the past many

years. Some of the ﬁelds which utilize fuzzy sets in-

clude health care (Kilic et al., 2004), system modeling

(Uncu et al., 2004; Uncu et al., 2003), supplier selec-

tion (Kahraman et al., 2003), control theory (Takagi

and Sugeno, 1985), capital investment (Tang et al.,

2005) etc.

Fuzzy numbers are introduced as part of fuzzy set

theory, which takes the form of a set of real numbers

with a convex and continuous membership function of

bounded support. These numbers can be used to accu-

rately represent linguistic scales incorporating vague-

ness and uncertainties of human mind. Fuzzy AHP is

simply an extension of the original AHP with human

preferences recorded in the form of fuzzy numbers

and hence the resulting comparison matrix formed is

also composed of fuzzy numbers. However, to ex-

tract weights from these fuzzy comparison matrices

require additional treatment as the arithmetic opera-

tions of fuzzy numbers is different from crisp num-

bers. To address this issue, various algorithms have

174

Ahmed, F. and Kilic, K.

Comparison of Fuzzy Extent Analysis Technique and its Extensions with Original Eigen Vector Approach.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 2, pages 174-179

ISBN: 978-989-758-187-8

been proposed over the years with an aim to process

these fuzzy comparison matrix and extract weights.

Some of the most popular algorithms are given by

(Van Laarhoven and Pedrycz, 1983; Boender et al.,

1989; Buckley, 1985; Deng, 1999). Readers are re-

ferred to (B

ozkan et al., 2004) and (Ataei et al.,

2012) for a comprehensive review of literature on

FAHP algorithms and its applications.

Among these FAHP algorithms, Fuzzy Extent

Analysis (FEA) method (Chang, 1996) is the most

frequently used FAHP algorithm (Ding et al., 2008).

It utilizes the concept of extent analysis combined

with degree of possibility to calculate weights from

fuzzy comparison matrices. However, this method

has been criticized (Wang et al., 2006) mainly due to

the way fuzzy numbers are compared using degree of

possibility. Over the last ﬁve years around hundred

research articles have been published on how to com-

pare fuzzy numbers which shows that there is no gen-

eral consensus on a single method to rank and order

fuzzy numbers (Zh

u, 2014). Therefore, in our anal-

ysis in addition to the original method of degree of

possibility, we will also use Centroid Defuzziﬁcation

(Ross, 1995) and defuzziﬁcation by simply using the

mid number of the triangular fuzzy number.

Rest of the paper is organized as follows. In Sec-

tion 2, a brief overview of fuzzy arithmetic and FEA

method will be provided. In section 3 the set up used

for the experimental analysis will be discussed. Later

in section 4, the results of the experimental analysis

will be presented. Paper will be ﬁnalized with some

concluding remarks as well as future research direc-

tions in section 5.

2 FUZZY EXTENT ANALYSIS

As discussed before, one of the major challenges

faced in AHP is to employ a weighing scale which

accurately represents expert opinions in the form

of comparison ratios while taking into account the

inherent vagueness of human thought. Note that

this vagueness is neither random nor stochastic

(Ataei et al., 2012) and fuzzy numbers are helpful in

capturing this imprecision. The construction of fuzzy

numbers are such that it represents the linguistic

variables with a set of possible values each having its

own membership degree and thus aids in capturing

this vagueness. There are many different types of

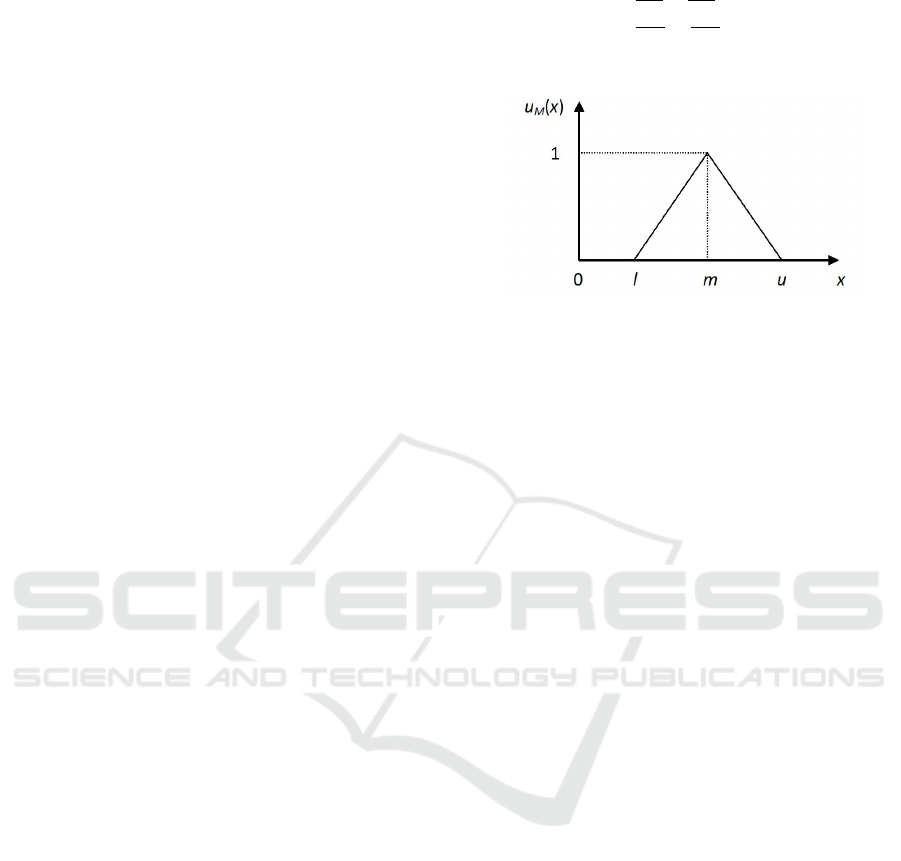
fuzzy numbers, however in this paper we will use

a triangular fuzzy number which is represented

through [l m u] and membership function µ

deﬁned

as follows and graphically illustrated in Figure 1;

(x) =











m−l

−

m−l

, x ∈ [l m]

m−u

−

m−u

, x ∈ [m u]

0, otherwise

(1)

Figure 1: Membership function of Triangular Fuzzy Num-

ber.

Let (l

) and (l

) then the basic fuzzy

arithmetic operations are summarized as follows;

• Addition:

) ⊕ (l

) = (l

+ l

+ m

+ u

)

• Multiplication:

)  (l

) = (l

)

• Scalar Multiplication:

(λ λ λ) (l

) = (λ.l

λ.m

λ.u

)

• Inverse:

)

−1

≈ (1/u

1/m

1/l

)

Fuzzy Extent Analysis (FEA) proposed by

(Chang, 1996) is one of the most popular technique in

the literature to calculate weights from fuzzy compar-

ison matrices. In the original Extent Analysis method,

provided we have X = {x

,···, x

} as an object set

and G = {g

,· ··, g

} as a goal set, then for each

object, extent analysis for each goal g

is performed.

Applying this theory in fuzzy comparison matrix, one

can calculate the value of fuzzy synthetic extent with

respect to the i

object as follows;

∑

j=1

⊗

∑

i=1

∑

j=1

−1

(2)

Where

∑

j=1

∑

j=1

∑

j=1

∑

j=1

(3)

In the original AHP, while using the scale of 1-9,

we can calculate the ﬁnal weights through the pro-

cess explained above. However, for the case where

fuzzy triangular numbers are employed in the judg-

ment scale, the result would be a fuzzy triangular

weight value as indicated in Equation 3.

As opposed to the straight forward ordering of

crisp numbers, ordering of the fuzzy numbers are not

Comparison of Fuzzy Extent Analysis Technique and its Extensions with Original Eigen Vector Approach

175

that simple. In fact, over the last couple of years

many articles have been published discussing this is-

sue and as of today there is no widely accepted tech-

nique (Zh

u, 2014) to rank and order fuzzy numbers.

In the FEA technique proposed by (Chang, 1996), a

method known as degree of possibility is proposed for

ordering as well as defuzzifying weights calculated

from Equation 3

In this approach, a pair wise comparison is carried

out for every fuzzy weight with other fuzzy weights

and the corresponding degree of possibility of being

greater than other fuzzy weights is determined. The

minimum of these possibilities is used as the overall

score for each criterion i. That is to say by applying

the comparison of the fuzzy numbers, the degree of

possibility is obtained for each pair wise comparison

as follows:

V (M

≥ M

) = hgt(M

∩ M

) = µ

(d) =











1, if m

≥ m

0, if l

≥ u

−u

)−(m

−l

)

, otherwise.

The same is illustrated in the Figure 2.

Figure 2: Degree of possibility.

Note that, degree of possibility for a convex fuzzy

number to be greater than k convex fuzzy numbers is

given by;

V (M ≥ M

,· ··, M

) = V [(M ≥ M

) and

(M ≥ M

),· ··, (M ≥ M

)]

= minV (M ≥ M

), i = 1, 2,· · ·, k

Assuming that w

= minV (M

≥ M

) then weight vec-

tor is given by

= w

,· ··, w

Normalizing the above weights gives us the ﬁnal pri-

ority vector w

,· ··, w

Subsequent research on this methodology has pro-

posed some modiﬁcations. for example, (Wang et al.,

2006) in its review of the normalization processes in

fuzzy systems proposed that row sums should be nor-

malized by Equation 4 in order to calculate fuzzy syn-

thetic extent values. This modiﬁcation will also be

part of our analysis.

∑

j=1

i j

∑

j=1

i j

∑

k=1,k6=i

∑

j=1

k j

∑

j=1

i j

∑

k=1

∑

j=1

k j

∑

j=1

i j

∑

j=1

i j

∑

k=1,k6=i

∑

j=1

k j

(4)

Therefore, our experimental analysis will include in

total following ﬁve techniques;

• FEA with degree of possibility (Original Method)

• FEA with degree of possibility including modiﬁ-

cation to normalization (Wang et al., 2006)

• FEA with Centroid Defuzziﬁcation (Ross, 1995)

• FEA with defuzziﬁcation using mid number of the

triangular fuzzy number

• Original eigen vector method (Saaty, 1980)

3 RESEARCH METHODOLOGY

Three major control parameters are employed in the

experimental analysis to evaluate the performance of

the techniques discussed in the paper. These param-

eters include level of fuzziness (α), inconsistency of

the decision maker (β), and size of the comparison

matrices (n). By varying the levels of these control

parameters, we generate a set of matrices on which

we apply the above mentioned techniques. Note that

even though there exist some algorithms in the lit-

erature (Golany and Kress, 1993) which provides a

methodology to generate comparison matrices with

various levels of consistency levels, however these

technique are limited only for original AHP and thus

cannot be replicated for comparison matrices consist-

ing of fuzzy numbers. Therefore, in this research a

novel framework is proposed through which random

fuzzy comparison matrices can be generated for vari-

ous control parameters as required by the experimen-

tal set up.

This algorithm is step by step explained as fol-

lows;

Step 1: Assuming we have n criterion, we ran-

domly generate crisp weights w

,· ··, w

and nor-

malize them.

Step 2: Through these weights we can generate a

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

176

perfectly consistent comparison matrix as follows

W =







·· · w







Step 3: Once the comparison matrix is generated,

each element of the matrix is converted into a trian-

gular fuzzy number [l

] with a fuzziﬁcation pa-

rameter α such that l

= w

− α, m

= w

and

= w

+ α.

Step 4: As stated before, in reality human judg-

ments are rarely consistent and thus comparison ma-

trices formed through these judgments are also not

consistent. Therefore, we introduce different levels

of inconsistency in the matrices through the incon-

sistency parameter β. Depending on this parameter,

an interval [a b] is generated for each l

of the tri-

angular fuzzy number such that a = l

− l

(β) and

b = l

+ l

(β). Same procedure is followed to create

inconsistency intervals for m

and u

. Afterwards, a

number is randomly selected from each one of these

intervals and is correspondingly assigned as the lower,

modal and upper value of the triangular fuzzy num-

ber i:e., [l m u]. However, once inconsistency param-

eter is increased, there is a possibility that the inter-

val [a b] generated for each element of the triangu-

lar fuzzy number intersects and the numbers are ran-

domly chosen in such a way that they violates the con-

dition l < m < u. We address this issue as follows;

Whenever the inconsistency intervals intersect, they

are shrunk in such a way that for each lower value of

the triangular fuzzy number, the right endpoint of the

interval is readjusted such that it is the mid point of

the right end point of the interval of lower value and

the left end point of the interval generated for modu-

lar number. Similarly, both end points of the inconsis-

tency interval of modular number are readjusted and

the left endpoint of the inconsistency interval of up-

per number is readjusted. Numbers randomly chosen

from these intervals will always satisfy the condition

of l < m < u. This part of the algorithm is graphically

explained below for clarity.

Figure 3: Interval formation.

Previous comparative analysis of methodologies

in the original AHP shows that level of inconsistency

and size of the matrix are two important criteria which

directly affects the performance of a certain tech-

nique. In fuzzy AHP, the weighing scale is composed

of fuzzy numbers and thus we add a third performance

evaluation criteria which is level of fuzziness. There-

fore, the aim of our analysis will be to not only in-

vestigate performance measure of each algorithm in

general but also change in performance as we change

these three parameters.

4 RESULTS AND DISCUSSIONS

The framework of our experimental analysis includes

three variables α, β and n. For the fuzziﬁcation pa-

rameter (α) three fuzziﬁcation levels are used (0.05,

0.1 and 0.15) and decision analysts can set the fuzzi-

ﬁcation level himself and conduct FAHP accordingly

as this parameter is not inherent to the problem. The

inconsistency parameter (β) indicates to the level of

inconsistency of the decision maker. For this analy-

sis we used ﬁve different levels for the inconsistency

parameter (0, 0.5, 1, 1.5 and 2). In addition, four dif-

ferent matrix sizes were considered (3, 7, 11 and 15).

Matrices having dimension 3 × 3 can be regarded as

the representative of a small sized problems while ma-

trices of dimensions 7 × 7 and 11 × 11 are represen-

tatives for medium sized problems and 15 × 15 size

matrix can be considered for larger cases.

Therefore, our experimental analysis consists of

60 different experimental conditions and for each con-

dition 10 replications are created randomly. In to-

tal the data set consists of six hundred matrices with

varying parameters of fuzziﬁcation, inconsistency and

size of the matrix. The error terms are calculated as

the root mean squared difference between the result-

ing weights calculated from the 5 different techniques

discussed in this paper and the initial weights used to

construct comparison matrices.

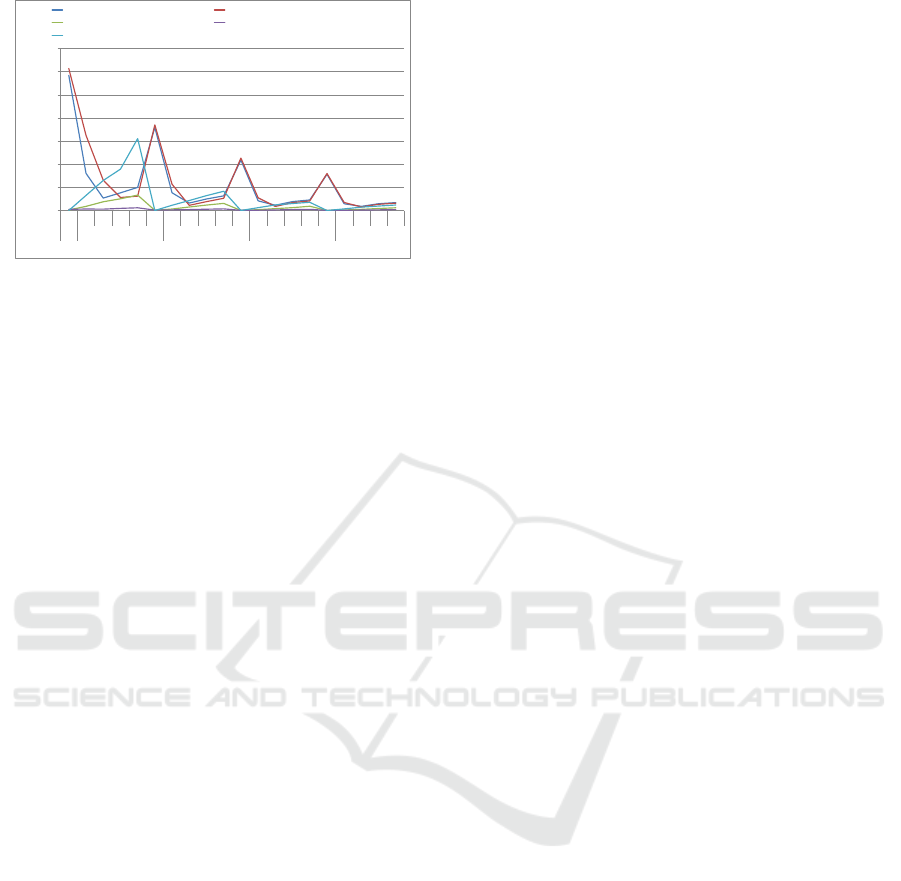
Through this experimental study, we can conclude

that utilizing just the mid number of a triangular

fuzzy weight can give us more accurate results (Fig-

ure 4). While the original method of degree of possi-

bility as well as the Eigen Vector approach along with

FEA method with other defuzziﬁcation techniques

performed inferior compared to using mid number of

the triangular fuzzy number.

Figure 4 shows that increase in size of the matrix

has a signiﬁcant effect on the performance of all the

algorithms. However, this improved performance is

due to the fact that as we increase the size of the ma-

trix, the values of the starting normalized weights are

Comparison of Fuzzy Extent Analysis Technique and its Extensions with Original Eigen Vector Approach

177

0.000

0.050

0.100

0.150

0.200

0.250

0.300

0.350

Beta 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 1.5 2.0 0.0 0.5 1.0 1.5

n 3 7 11 15

Error

Experimental Parameters

Original FEA Wang Normalization Modification

FEA with Centroid Defuzzification FEA while utilising only Mid Number

Eigen Vector Approach using Crisp Matrix

Figure 4: Experimental Analysis.

decreased and hence the ﬁnal error term is also low

which depicts improvement in performance. There-

fore, this improved performance cannot be associated

with any of the FAHP algorithm.

As we increase the inconsistency factor, perfor-

mance of most of the algorithms is decreased except

for original FEA method and FEA method with mod-

iﬁed normalization for which performance increases

as we increase the inconsistency. However, this in-

crease in performance is not enough and even at high

inconsistency levels, FEA with defuzziﬁcation using

mid number is the best performing algorithm.

5 CONCLUSIONS

In this paper, we introduced a novel experimental

analysis framework through which performance of

various FAHP technique can be analyzed. The analy-

sis revealed that the FEA method with defuzziﬁcation

using mid number outperformed the other techniques

in almost all experimental conditions.

Review of the existing literature on FAHP reveal

that there are many different algorithms proposed in

this domain. However, there is no throughout analysis

of these techniques which measure their performance

for different experimental conditions. Such a com-

parison would be invaluable for the researchers and

the practitioners of the ﬁeld since it will hint which

technique might be more suitable for the problem that

they are facing.

In future we plan to conduct similar performance

analysis for other FAHP algorithms and through ex-

perimental analysis such as this, we plan to inves-

tigate differences between conventional AHP tech-

niques with Fuzzy AHP techniques.

REFERENCES

Ataei, M., Mikaeil, R., Hoseinie, S. H., and Hosseini, S. M.

(2012). Fuzzy analytical hierarchy process approach

for ranking the sawability of carbonate rock. Inter-

national Journal of Rock Mechanics and Mining Sci-

ences, 50:83–93.

Boender, C., De Graan, J., and Lootsma, F. (1989). Multi-

criteria decision analysis with fuzzy pairwise compar-

isons. Fuzzy sets and Systems, 29(2):133–143.

Buckley, J. J. (1985). Fuzzy hierarchical analysis. Fuzzy

sets and systems, 17(3):233–247.

ozkan, G., Kahraman, C., and Ruan, D. (2004). A

fuzzy multi-criteria decision approach for software

development strategy selection. International Journal

of General Systems, 33(2-3):259–280.

Chang, D.-Y. (1996). Applications of the extent analysis

method on fuzzy ahp. European journal of opera-

tional research, 95(3):649–655.

Deng, H. (1999). Multicriteria analysis with fuzzy pair-

wise comparison. International Journal of Approxi-

mate Reasoning, 21(3):215–231.

Ding, Y., Yuan, Z., and Li, Y. (2008). Performance evalua-

tion model for transportation corridor based on fuzzy-

ahp approach. In Fuzzy Systems and Knowledge Dis-

covery, 2008. FSKD’08. Fifth International Confer-

ence on, volume 3, pages 608–612. IEEE.

Forman, E. H. and Gass, S. I. (2001). The analytic hi-

erarchy process-an exposition. Operations research,

49(4):469–486.

Golany, B. and Kress, M. (1993). A multicriteria evalua-

tion of methods for obtaining weights from ratio-scale

matrices. European Journal of Operational Research,

69(2):210–220.

Kahraman, C., Cebeci, U., and Ulukan, Z. (2003). Multi-

criteria supplier selection using fuzzy ahp. Logistics

information management, 16(6):382–394.

Kilic, K., Sproule, B. A., T

urksen, I. B., and Naranjo, C. A.

(2004). Pharmacokinetic application of fuzzy struc-

ture identiﬁcation and reasoning. Information Sci-

ences, 162(2):121–137.

Ross, T. J. (1995). Fuzzy Logic With Engineering Applica-

tions. Mcgraw-Hill College, ﬁrst edition edition.

Saaty, T. L. (1980). The Analytic Hierarchy Process: Plan-

ning, Priority Setting, Resource Allocation (Decision

Making Series). Mcgraw-Hill (Tx).

Takagi, T. and Sugeno, M. (1985). Fuzzy identiﬁcation

of systems and its applications to modeling and con-

trol. Systems, Man and Cybernetics, IEEE Transac-

tions on, (1):116–132.

Tang, Y.-C., Beynon, M. J., et al. (2005). Application

and development of a fuzzy analytic hierarchy pro-

cess within a capital investment study. Journal of Eco-

nomics and Management, 1(2):207–230.

Tsaur, S.-H., Chang, T.-Y., and Yen, C.-H. (2002). The

evaluation of airline service quality by fuzzy mcdm.

Tourism management, 23(2):107–115.

Uncu, O., Kilic, K., and Turksen, I. (2004). A new fuzzy

inference approach based on mamdani inference us-

ing discrete type 2 fuzzy sets. In Systems, Man and

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

178

Cybernetics, 2004 IEEE International Conference on,

volume 3, pages 2272–2277. IEEE.

Uncu, O., Turksen, I., and Kilic, K. (2003). Localm-fsm: A

new fuzzy system modeling approach using a two-step

fuzzy inference mechanism based on local fuzziness

level. In Proceedings of international fuzzy systems

association world congress, pages 191–194.

Van Laarhoven, P. and Pedrycz, W. (1983). A fuzzy exten-

sion of saaty’s priority theory. Fuzzy sets and Systems,

11(1):199–227.

Wang, Y.-M., Elhag, T., and Hua, Z. (2006). A modi-

ﬁed fuzzy logarithmic least squares method for fuzzy

analytic hierarchy process. Fuzzy Sets and Systems,

157(23):3055–3071.

Zadeh, L. (1965). Fuzzy sets. Information and Control,

8(3):338 – 353.

u, K. (2014). Fuzzy analytic hierarchy process: Fallacy

of the popular methods. European Journal of Opera-

tional Research, 236(1):209–217.

Comparison of Fuzzy Extent Analysis Technique and its Extensions with Original Eigen Vector Approach

179