Automated Segmentation of the Walkable Area from Aerial Images for

Evacuation Simulation

Fabian Schenk, Matthias R

uther and Horst Bischof

Institute for Computer Graphics and Vision, Graz University of Technology, Graz, Austria

Keywords:

Aerial Images, Walkable Area, Seeded Region Growing, Evacuation Maps, Accessibility.

Abstract:

Computer-aided evacuation simulation is a very import preliminary step when planning safety measures for

major public events. We propose a novel, efﬁcient and fast method to extract the walkable area from high-

resolution aerial images for the purpose of evacuation simulation. In contrast to previous work, where the

authors only extracted streets and roads or worked on indoor scenarios, we present an approach to accurately

segment the walkable area of large outdoor areas. For this task we use a sophisticated seeded region growing

(SRG) algorithm incorporating the information of digital surface models, true-orthophotos and inclination

maps calculated from aerial images. Further, we introduce a new annotation and evaluation scheme especially

designed for assessing the segmentation quality of evacuation maps. An extensive qualitative and quantitative

evaluation, where we study various combinations of SRG methods and parameter settings by the example of

different real-world scenarios, shows the feasibility of our approach.

1 INTRODUCTION

Millions of people visit sports competitions, concerts

and religious celebrations every year and with the ever

growing population the number is not likely to de-

crease. There is a large variety of possible emergen-

cies (natural disasters, ﬁre, terrorist attacks, bomb-

ings) with most of them requiring a full or partial

evacuation of the event area. Adequate safety mea-

sures are required to prevent crowd disasters like the

ones at the Love Parade 2010 (Duisburg, Germany)

(Krausz and Bauckhage, 2012) and the Water Festi-

val 2010 (Phnom Penh, Cambodia) (Hsu and Burkle,

2012).

To assure the safety of events, evacuation simula-

tion is an important preliminary step in the planning

stage, but is normally a tedious and time-consuming

task due to the complex layout of large event sites.

For computer-aided evacuation simulation and

planning for outdoor events, digital maps are re-

quired. A computer can then perform a wide vari-

ety of simulations on the given topology using differ-

ent hazards, escape routes and human properties like

walking speed or age.

The technology for recording aerial images has

been around for some time, but in recent years high-

resolution cameras have improved the accuracy sig-

niﬁcantly and small unmanned aerial vehicles (UAV)

can perform on-demand recordings of certain areas.

In previous work on outdoor evacuation simulations,

(Taubenb

ock et al., 2009; L

ammel et al., 2010) only

extracted streets and roads, but did not achieve very

high accuracy. It is not enough to simply segment

a certain height level, roads or just ﬂat areas because

humans can walk on different surfaces (slopes, stairs).

If measurements are wrong or blocking structures are

missing in the digital map, a simulation cannot be per-

formed accurately. To our knowledge, we are ﬁrst to

address the difﬁcult challenge of automatically seg-

menting the walkable area (WA) of large outdoor ar-

eas. This is a complex segmentation problem com-

prising the following challenges:

• Getting measurements correctly into the map

• Providing accurate contours for buildings and

blocking structures (walls, food stands, tents,...)

• Segmenting potential emergency exits (roads,...)

In this work, we present a novel, efﬁcient and easy-to-

use approach to generate highly accurate digital maps

of the WA from high-resolution aerial images. Our

approach generalizes very well to various scenarios

and cities and by adapting the parameters for slopes

and stairs we can also incorporate the special needs

of handicapped people (wheelchair users, elderly per-

sons). These maps can then be used for evacuation

planning and simulation (see Fig. 1). Further, we in-

Schenk, F., Rüther, M. and Bischof, H.

Automated Segmentation of the Walkable Area from Aerial Images for Evacuation Simulation.

In Proceedings of the 2nd International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2016), pages 125-135

ISBN: 978-989-758-188-5

125

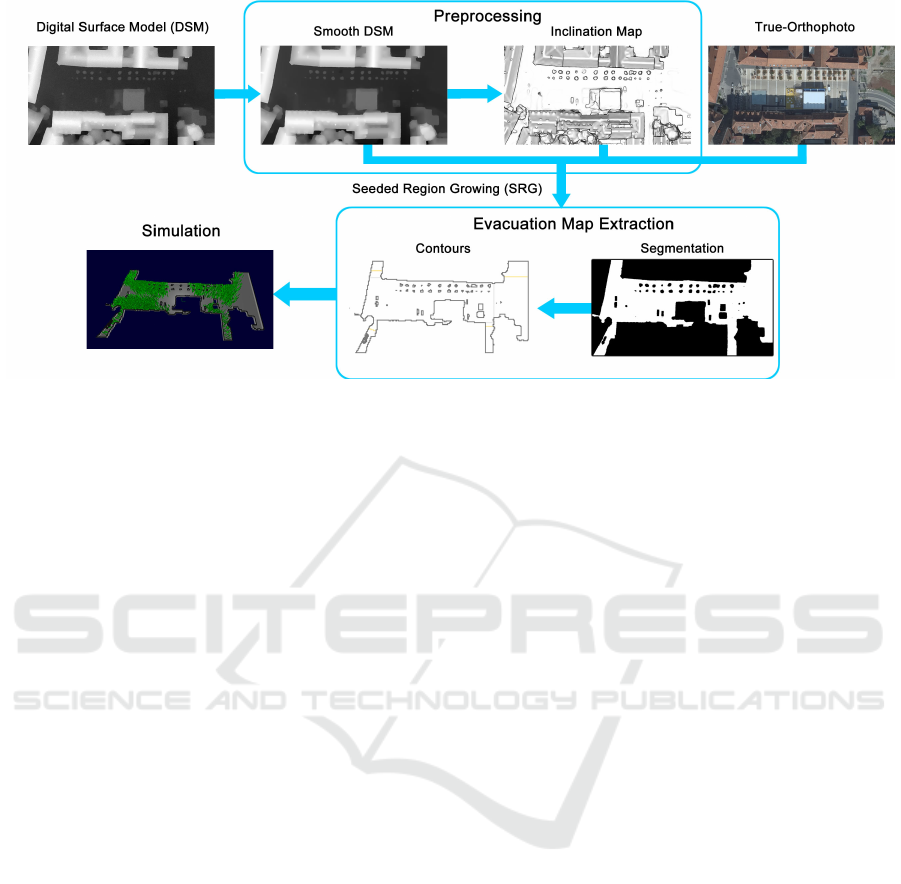
Figure 1: We use a sophisticated seeded region growing (SRG) algorithm to segment the walkable area (WA) incorporating

information from the DSM, true-orthophoto and orientation map. From this segmentation, the contours can be extracted and

used in most common evacuation simulation programs.

troduce a new annotation scheme to assess the quality

of the extracted maps with regard to evacuation simu-

lation. Additionally, aerial images give us the oppor-

tunity to acquire data shortly before the actual event

and to include structures like stages, food stands and

tents into our map. To our knowledge, we are the ﬁrst

to address the difﬁcult challenge of getting an accu-

rate digital map of the WA for evacuation planning

in outdoor environments using high-resolution aerial

images.

The paper is organized as follows. Section 2 de-

scribes related work on evacuation simulation and

street segmentation and its limitations. In Section 3,

we describe the input data, the necessary preprocess-

ing steps and ﬁnally our method to segment the WA.

An exhaustive qualitative and quantitative evaluation

of our different SRG algorithms and important param-

eters is shown in Section 4. Section 5 concludes the

paper and gives some ideas about future work on this

topic. In the Appendix, we will show an evacuation

simulation using our extracted digital maps.

2 RELATED WORK

Evacuation simulation is an active research area

and many different software tools have been devel-

oped, which can be classiﬁed as microscopic (Galea,

2002; Kl

upfel, 2006; Tsai et al., 2011) and macro-

scopic (Schneider and K

onnecke, 2001). All tools

require a digital map for evacuation simulation and

most of them support CAD (computer-aided drafting)

models. Previous work can be divided into indoor and

outdoor scenarios.

Indoor Scenarios. For these scenarios usually

CAD and sometimes even 3D models are provided

by architects and they have been extensively studied

in recent years. (Johnson, 2008) performed an evacu-

ation simulation to improve security and safety of the

2012 Olympic venues, while (Shi et al., 2012) studied

different evacuation scenarios for the very crowded

metro stations in Tokyo, Japan. An indoor ﬁre simula-

tion model was presented in (Tang and Ren, 2012) and

(Tsai et al., 2011) evaluated the evacuation strategies

for the International Terminal at Los Angeles Airport.

Outdoor Scenarios. The investigation of evac-

uation strategies for tsunami incidents is an impor-

tant research ﬁeld. In this context, (Mas et al., 2013)

proposed an evacuation model with a tsunami sim-

ulation for casualty estimation for the urban area of

La Punta, Peru. Evacuation analysis at city-scale

by the example of Padang, Indonesia for the case

of a tsunami incident was performed in (Taubenb

ock

et al., 2009; L

ammel et al., 2010). They achieved

building level accuracy, by extracting semantic labels

from four band satellite images.With their city-wide

analysis they do not achieve very high accuracy and

for planning public events only small areas of a city

like squares or parks are of particular interest.

Road and street segmentation from aerial images

acquired by satellites or UAVs is also a well re-

searched topic (Hu et al., 2007; Zhou et al., 2015;

Dal Poz et al., 2012; Lin and Saripalli, 2012). Even

though these approaches give us an idea of the WA,

humans can access more than just roads and streets

and for evacuation planning a more sophisticated

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

126

segmentation is needed. OpenStreetMap provides

geospatial data for certain urban areas, but it is very

not accurate, often outdated and does not include the

special layout of major events.

Land-use classiﬁcation from aerial images has

been presented in (Cheriyadat, 2014; Huth et al.,

2012), while (Han et al., 2015) try to ﬁnd objects and

their respective bounding boxes. These methods are

well suited for land-use study of whole cities or even

larger regions but lack the necessary accuracy for WA

analysis, where the contours of blocking structures

like buildings are essential. Further, due to the lim-

ited number of labels, unknown classes are regularly

un- or misclassiﬁed in the ﬁnal result, e.g. cars as

streets, bushes or small trees as grass or ﬁeld.

(Kl

upfel, 2006) performed crowd simulations for

large outdoor events by the examples of the World

Youth Day 2005 in Cologne and an egress (non-

emergency) from a football stadium but mainly fo-

cused on evacuation details (reaction time, walking

speed).

3 EVACUATION MAP

EXTRACTION

The main challenge is to get an accurate digital map of

the WA from high-resolution aerial images (see Fig.

1). From these images we can calculate the corre-

sponding digital surface models (DSMs) and then we

use edge-preserving smoothing to facilitate the subse-

quent calculation of the inclination map (see Section

3.1).

One downside of the very high resolution is the

large amount of data and processing a whole city can

take from hours to days, depending on the available

computational power. Thus, we perform our segmen-

tation in a region of interest (ROI). Within this ROI

the user then has to choose a point manually. Start-

ing from this point a seeded region growing (SRG)

(Adams and Bischof, 1994) algorithm segments the

WA (see Section 3.2). The result is a binary segmen-

tation of the WA, which can be exported to most com-

mon evacuation simulation program (see Section 3.3).

3.1 Aerial Image Input Data and

Preprocessing

The acquisition of the aerial images and calculation

of the DSMs and true-orthophotos are not part of our

approach but will be brieﬂy explained. Aerial im-

ages are typically recorded with three (RGB) or four

channels (+ near infrared) by UAVs like drones or

smaller airplanes because of the higher spatial reso-

lution compared to satellites. UAVs follow a certain

pattern when taking images of an area to get mul-

tiple, overlapping views of all the structures. Then

the high-resolution aerial images are used for aerial

triangulation, which is also known as Structure for

Motion, to get accurate photo alignments from im-

age measurements only (Irschara et al., 2012). Match-

ing points between the recorded images are calculated

using Scale Invariant Feature Transform (SIFT) with

Lowe distance ratio (Lowe, 2004) and then used in a

sparse bundle adjustment (Triggs et al., 2000) to esti-

mate all camera poses.

A dense height map for each image is estimated

with a multi-view reconstruction approach similar to

the one presented in (Rumpler et al., 2013; Irschara

et al., 2012). The basic idea is that the actual height

value of a pixel can be found by comparing two over-

lapping images from different views. A plane sweep

approach (Collins, 1996) then shifts one image in a

certain direction, while the other one stays ﬁxed and

calculates a matching cost between these two, result-

ing in a 3D cost volume. In (Rumpler et al., 2013),

they use a winner-takes-all method on the cost vol-

ume and always choose the cheapest matching cost

for each pixel as the correct height. Alternatively, an

optimizer on the cost volume followed by multi-depth

ﬁltering can be used to get the correct height values.

The next step is generating a DSM I, which rep-

resents the height information of Earth’s surface in-

cluding all objects (buildings, trees, cars,...). From

the overlapping height maps calculated in the previ-

ous step we get multiple proposals for the height of a

pixel. For each pixel the most likely height value from

all the proposals is found and incorporated into the

DSM. The ﬁnal height resolution of the DSM is usu-

ally much higher than that of the overlapping height

maps.

The DSM is only a 2.5D model because the aerial

images are recorded from above, where only part of

the surface is visible. Recording what is beneath is

not possible (e.g., a tunnel under a mountain or a river

under a bridge) and therefore only the top surface of

a structure is present in the DSM.

By back-projecting the point from the DSM into

the camera and coloring the pixel accordingly a

true-orthophoto with a uniform scale (like an ordi-

nary map) can be generated and used for measur-

ing distances. The applications of DSMs and true-

orthophotos are widespread and include infrastructure

planning, 3D building reconstruction, city modeling

and simulations for natural disaster management. As

input for our algorithm we use the DSM and the cor-

responding true-orthophoto (see Fig. 2).

Automated Segmentation of the Walkable Area from Aerial Images for Evacuation Simulation

127

Figure 2: For the SRG segmentation we use a true-

orthophoto, a DSM and an inclination map. In the DSM

model, height is represented as intensity values (higher is

brighter).Calculating the inclination map directly from the

DSM shows a stair-casing effect (depicted as ORIG), which

is greatly reduced when computed from a smooth DSM

(shown as ROF). Images are contrast-enhanced for visual-

ization purposes.

We are not only interested in ﬂat areas but also in

ramps with a moderately steep slope and stairs, which

have a larger difference in height (around 16-20 cm).

To get an idea about the inclination of a surface we

calculate the surface normal representation from the

DSM.

Calculating the surface normals directly from the

DSM computed from the aerial images leads to ar-

tifacts due to the plane-sweep approach (Collins,

1996). We address this problem by using a smooth-

ing algorithm, which smooths the DSM I while keep-

ing the edges intact. Edge information is crucial be-

cause we want to keep accurate contours of build-

ings and other structures. The difference between cal-

culating this representation on the smooth and non-

smooth DSM can be seen in Figure 2 (ORIG vs ROF).

For our particular problem we choose the model in-

troduced by Rudin, Osher and Fatemi (ROF)(Rudin

et al., 1992):

min







Ω

|∇I

|dx +

Ω

− I)







, (1)

where the ﬁrst part is the regularization term, the sec-

ond the data ﬁdelity term and I

a convex, continuous

function. We want to reconstruct an image I

, which

is smooth but also similar to the original input im-

age I. In order to get a smooth I

, the regularization

term reduces the differences within I

by penalizing

the L1-norm of the gradients. The data ﬁdelity in-

duces similarity by punishing differences between I

and I with a quadratic norm.

The weighting term λ serves as a trade-off be-

tween data ﬁdelity and regularization. A higher λ

gives more emphasize to the data ﬁdelity term, lead-

ing to I

being more similar to the original I, while a

lower λ results in a very smooth I

. To solve this con-

vex optimization problem, a primal-dual optimization

algorithm (Chambolle and Pock, 2011) is used. Af-

ter this step, the results look smoother and are more

suitable for our approach (see Fig. 2, ROF).

The DSM only has one channel (height informa-

tion) but for the calculation of the surface normal

representation we need vectors with 3D coordinates.

Therefore, we generate a 3D representation

of I

where

(x,y) is given as

(x,y) = (x · s

,y · s

(x,y)), (2)

with s

and s

representing the spatial resolution in x-

and y-direction. Typically, we can assume s

= s

The basic idea for the surface normal calculation

is to compute the two tangential vectors

and

at a

point I

(x,y). An easy way to compute

and

is to

simply calculate the vectors from the 4-neighborhood

of the pixel I

(x,y) (see Fig. 3 (a)). We deﬁne

and

as:

(x − 1, y) −

(x + 1, y),

(x,y − 1) −

(x,y + 1).

We achieve fast computation and minimal memory

access with integral images as described in (Holz

et al., 2012).

For the pixel

(x,y), the surface normal vector~n

is then given as:

~n =

. (3)

For the next steps the inclination of the slope is im-

portant, which is the angle α between a view vector

~v and the surface normal vector ~n. α is given by the

deﬁnition of the dot product as:

cos(α) =

~v ·~n

|~v||~n|

. (4)

In our DSMs the camera typically has a top-down

view on the scene, thus we assume a view vector

~v = (0, 0,1). Thus, only the normalized z-component

of the surface normal vector ~n is used. A ﬂat sur-

face has an angle α = 0

◦

, thus cos(α) = 1. The 4-

neighborhood is used for the calculation of the incli-

nation, which results in an angle between the view

vector~v and ~n at edges (see Fig. 3(c))

Alternatively, one could compute a similar map by

using an edge weighting term e

−β|∇I

, where I

is the

smooth DSM model and β is a constant.

3.2 Segmentation of the Walkable Area

(WA)

The main and most crucial part in our approach is the

extraction of the WA. For an accurate simulation it

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

128

Figure 3: (a) and (b) are the two different pixel neighbor-

hoods (red) around the center pixel p

(cyan) considered

during the SRG algorithm. Case I is the 4-neighborhood

1−4

), used for growing over a slope or color difference.

Case II shows a larger neighborhood (p

5−8

) for growing

over stairs, which is necessary because of the surface nor-

mal orientation at edges depicted in (c).

is not enough to just segment a certain height level

because the whole WA (including slopes and stairs) is

interesting. This is a complex search problem because

accessibility highly depends on the topology. An area

might be inaccessible from one side due to a large

height difference but by using stairs or ramps on an-

other side it might become accessible. As a result we

want to have a binary segmentation, where all points

accessible by humans from the chosen starting point

are labeled 1 and the rest 0. We use a seeded region

growing (SRG) approach (Adams and Bischof, 1994),

which starts from a manually chosen seed point and

adds adjacent pixels to the segmentation if they fulﬁll

certain conditions (see Fig. 3). These pixels in turn

become the next seed points. This method is espe-

cially feasible for our problem because it can model

walking directions very well and we can easily incor-

porate different segmentation conditions for various

input data. We utilize all the available information by

using the DSM, the true-orthophoto and the inclina-

tion map as depicted in Figure 1.

With our approach we want to segment the walk-

able area including slopes and stairs. Starting from a

center pixel p

we have the two different cases pre-

sented in Figure 3 (a,b).

Case I In this case we check the pixels in the 4-

neighborhood (see Fig. 3(a)). We calculate the height

difference ∆h between a pixel p

and p

from the

DSM I

and add it if it is smaller than a threshold

value T

slope

. The true-orthophoto gives us additional

color information and we assume that in most cases

an accessible area with the same color does not sud-

denly become inaccessible. Thus we allow a slightly

greater height difference ∆h of 2 · ∆T

slope

when the

color difference ∆c is below a threshold T

color

. We

use I

instead of the inclination map because of the

clearer edges (see Fig. 3(c)).

Case II Stairs usually have a higher height dif-

ference ∆h but are still walkable by humans. To in-

clude such a concept in our algorithm we allow grow-

ing over a greater height difference (∆h ≤ T

stair

) if the

Figure 4: (a) is an artiﬁcially generated DSM with two ad-

jacent ramps and the seed point at the top left corner. (b)

shows the segmentation when not taking the height differ-

ence into account, while (c) is the correct segmentation with

barriers. The possible walking directions are depicted as red

arrows.

orientation is nearly horizontal/ﬂat (cos(α) ≥ 1 − ε

We have to check the neighborhood (x ± 3,y) and

(x,y ± 3) because the surface normal vectors are not

pointing upwards at edges (see Fig. 3(b,c)). If a pixel

fulﬁlls the criteria, we also add the pixels between

it and p

(depicted in gray) to the segmentation.

We can divide our SRG approach into the three

different parts SRG

, SRG

and SRG

, depending

on the segmentation criteria:

• SRG

: ∆h ≤ T

slope

• SRG

: ∆h ≤ 2 · T

slope

, ∆c ≤ T

color

• SRG

: ∆h ≤ T

stair

, cos(α

),cos(α

) ≥ 1 − ε

with cos(α

) and cos(α

) the orientation at the cen-

ter pixel p

and the one to be added p

. ε

and T

color

are constants, while T

slope

and T

stair

can be adapted

according to the age and mobility of the expected

people at the event. One would probably choose a

very low T

slope

and T

stair

for elderly people and for

wheelchair users T

stair

= 0. In Section 4.3, we will

thoroughly evaluate the usefulness of the different

parts and their combinations.

Slopes, and stairs both introduce the same kind of

problem. When structures of different height levels

are next to each other (no pixels between them) then

a complete segmentation would lead to a whole area

being segmented, even though it is not possible to go

from one height level to the other (see Fig. 4,(a)).

Usually, height information cannot be used in the

simulation programs, thus we put a barrier with width

of one pixel between the structures if their height dif-

ference ∆h > T

stair

. Figure 4(b,c) depicts the segmen-

tations and possible walking directions (red arrows)

with and without barrier, demonstrating the feasibil-

ity of this approach. The result is a complete, binary

segmentation of the WA including ramps and stairs.

Different digital maps of the WA extracted with our

method and the corresponding ground truth will be

presented in Section 4.3.

3.3 Exporting the CAD Model

Normally, evacuation simulation tools cannot directly

use a binary segmentation but require a computer-

aided drafting (CAD) model. For the CAD model

Automated Segmentation of the Walkable Area from Aerial Images for Evacuation Simulation

129

only the outer boundaries and the contours of disturb-

ing structures on the inside are of particular interest.

We extract the boundaries and then use them to gen-

erate the CAD model for most common simulation

tools. In Appendix 5 we show how we can utilize our

binary segmentation in the evacuation simulation tool

PedGo (Kl

upfel, 2006).

4 EXPERIMENTS AND RESULTS

In this section, we propose a novel annotation scheme

for assessing the quality of extracted evacuation maps

(see Sec. 4.1). With an extensive evaluation of the

different SRG methods presented in Section 3.2 on

real-world scenarios, we then show the feasibility of

our approach. In the last part, we study different pa-

rameter settings for T

stair

, λ and T

slope

and analyze

their inﬂuence on the segmentation.

4.1 Experimental Setup

For evaluation of computer vision methods the results

are usually compared to known and more accurate ref-

erences, which are commonly referred to as ground

truth (GT). Getting any kind of GT data for aerial im-

ages is very difﬁcult and to our knowledge no ground

truth data is available for the special case of evacua-

tion maps. Therefore, a computer vision expert manu-

ally annotated the WA based on the true-orthophotos.

Accurate manual segmentation is also challenging be-

cause the true-orthophotos are calculated from mul-

tiple recordings and often exact borders are hard to

determine.

For the evaluation of our SRG algorithms, we

choose four outdoor scenarios from various cities

and with different spatial resolutions. We use the

Dice coefﬁcient (DC) (Dice, 1945) and the Jaccard

similarity (JS, also known as Tannimoto Coefﬁcient)

(Jaccard, 1908) to compare our segmentation SEG

to the GT. |SEG| and |GT | denote the sum of

segmented pixels.

Dice Coefﬁcient (DC)

The DC is a measure for comparing 2D region

overlap with a range from [0, 1] and is deﬁned as:

DC =

2|SEG ∩ GT |

|SEG| + |GT |

(5)

Jaccard Similarity (JS)

The JS is very similar to the DC and ranges from

[0,1] but is usually lower. It is deﬁned as:

JS =

|SEG ∩ GT |

|SEG ∪ GT |

(6)

The DC and JS are good indicators for the overall

segmentation quality but do not give us a measure-

ment for usefulness of the extracted evacuation map.

Further, the segmented areas are quite large (> 1MP)

and missing small but important structures hardly

affects the overall score.

Evacuation Map Annotation

To assess the quality of extracted evacuation maps,

we propose a new annotation scheme with two types

of labels:

• Potential evacuation routes GT

• Structures that must not be segmented GT

These additional GT annotations can then be com-

pared to the segmentation. We deﬁne two scores S

in the range [0,1] to assess the segmentation qual-

ity of potential evacuation routes and blocking struc-

tures. They are deﬁned as:

|SEG ∩ GT

|GT

, (7)

and

= 1 −

|SEG ∩ GT

|GT

, (8)

with GT

as the annotated potential evacuation routes,

the blocking structures and SEG the segmenta-

tion result. These two values must always be evalu-

ated jointly because S

= 100% if the whole image is

segmented, while S

= 100% if nothing is segmented.

Examples for such annotations can be seen in Figure 5

(c, f, i, l) with GT in white, GT

in red and GT

green.

All the computations were performed on an Intel

i7-4790 (3,6 GHz x 8) with 32 GB of memory run-

ning Ubuntu Linux 14.04. The denoising and SRG

algorithms are completely implemented in C++ using

OpenCV 3.0.0 to allow fast computations. For a typ-

ical 15 MP image, denoising is by far the most com-

putationally expensive operation (around 2 minutes),

while segmentation works a lot faster (< 1 second).

4.2 Aerial Image Data

Real-world scenarios are very challenging because

the algorithm has to deal with vegetation, different re-

gional building styles, cars and other obstacles. The

performance of our method mainly depends on the

quality of the DSMs and true-orthophotos, which are

usually subject to noise and reconstruction artifacts.

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

130

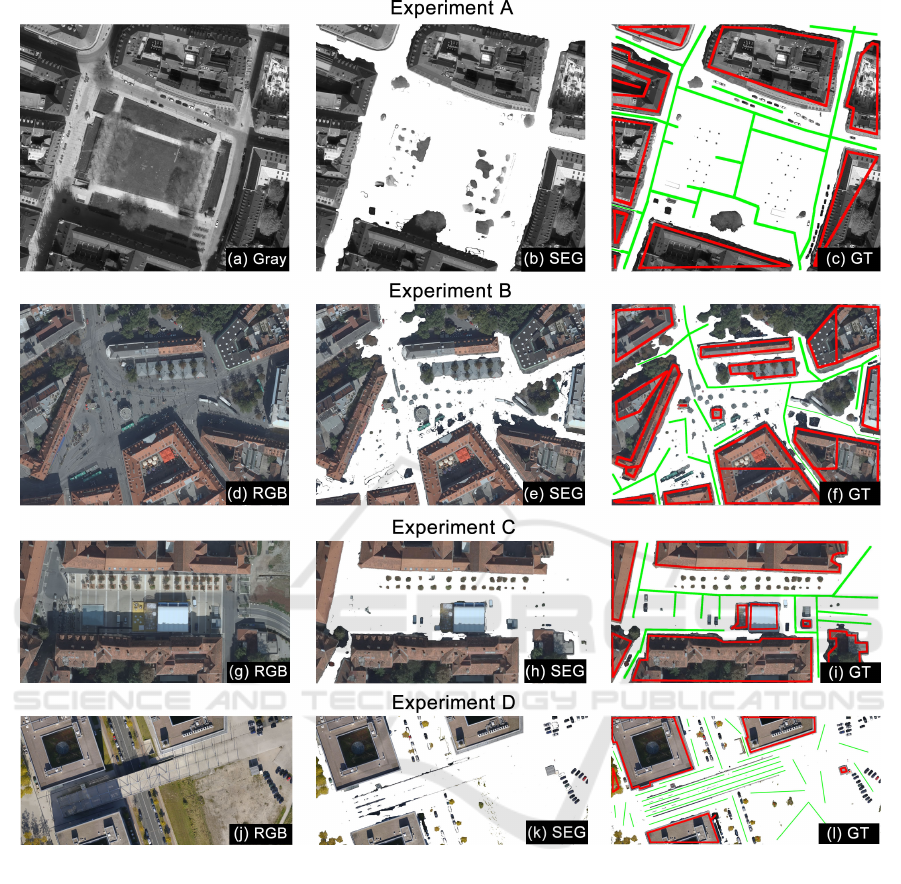
Figure 5: Experiment A, Marienhof (Munich, Germany), Experiment B, Jakominiplatz (Graz, Austria), Experiment C,

Karmeliterplatz (Graz, Austria), Experiment D, Bridge (Hannover, Germany). First column: true-orthophoto; second col-

umn: overlay with our segmentation (SEG); third column: overlay with the GT (including the G

and G

In all the real-world experiments, the GT is compared

to the automatically generated results from the algo-

rithm. We choose four sites from three different cities

(Exp. A-D).

Experiment A is the Marienhof, which is a big

park with space for a lot of people and many adjacent

streets (see Fig. 5(a)). In this recording only gray-

scale true-orthophotos were available.

Experiment B is the Jakominiplatz, which has a

very difﬁcult setup due to the many bus stops, buses,

trams and street lamps (see Fig. 5 (d)).

Experiment C is the Karmeliterplatz, where an

event took place at the moment of recording (see Fig.

5 (g)). A large tent with a stage in front is present.

Experiment D shows a bridge over a small road

next to the Expo Plaza in Hannover, Germany (see

Fig. 5 (j)). This is the only drone recording and

therefore has a much higher spatial resolution. The

setup is especially interesting because it includes

stairs, slopes, cars, buildings and different height lev-

els (bridge, road).

The spatial resolution of Experiment A-C is s

= 10 cm, while in Experiment D it is s

= s

= 3

cm.

Automated Segmentation of the Walkable Area from Aerial Images for Evacuation Simulation

131

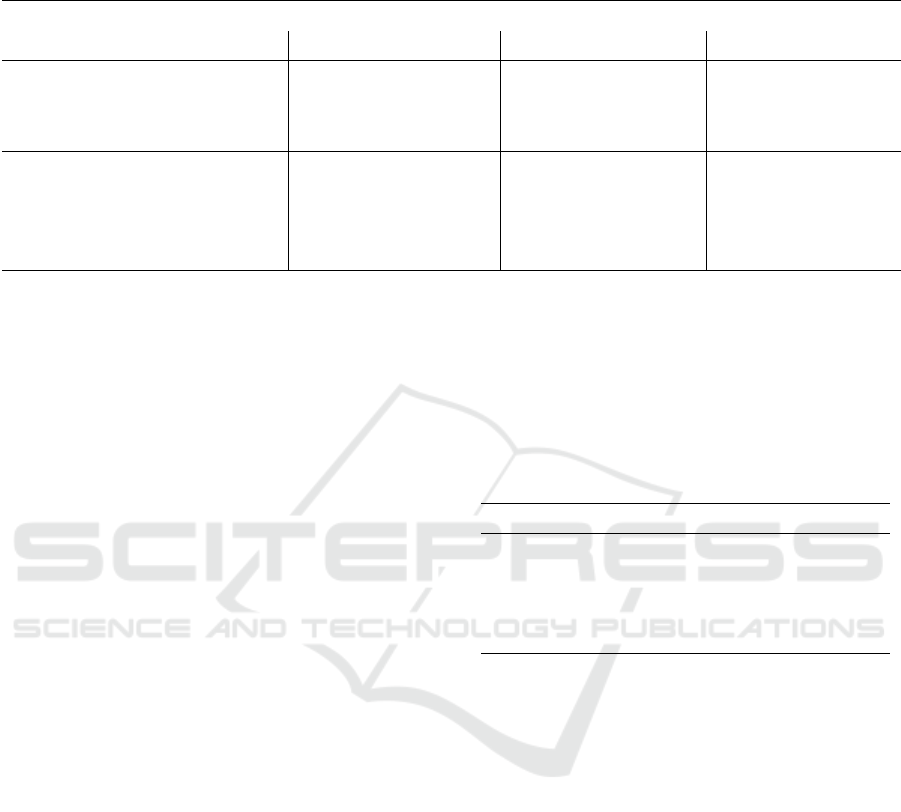
Table 1: The segmentation results of the four experiments with different SRG methods (best scores are depicted in bold).

The Dice coefﬁcient (DC), the Jaccard similarity (JS), the segmentation score for potential evacuation routes S

. Only results

where no blocking structures were segmented are shown (S

= 100 %).

SRG Experiment A Experiment B Experiment C Experiment D

[%] DC JS S

DC JS S

SL 95.74 91.83 94.72 90.52 82.69 93.28 95.70 91.76 92.22 97.51 95.14 99.88

ST 92.40 85.87 93.30 83.53 71.72 87.96 90.70 82.99 91.19 96.26 92.79 97.15

C 1.68 0.85 2.21 29.17 17.07 20.41 18.78 10.36 13.54 1.28 0.64 0.00

SL,ST 95.84 92.01 94.72 90.67 82.93 93.29 95.70 91.76 92.22 98.24 96.54 99.90

SL,C 95.13 90.72 94.56 91.83 84.89 96.02 97.88 95.85 99.38 98.10 96.27 99.93

ST,C 95.26 90.95 94.20 91.61 84.52 96.20 95.78 91.89 98.76 97.17 94.50 98.16

SL,ST,C 96.04 92.39 94.92 91.83 84.90 96.02 97.88 95.85 99.38 98.07 96.21 99.88

4.3 Results and Discussion

In this section, we present an extensive quantitative

and qualitative evaluation of the segmentation re-

sults for Experiment A-D, followed by a discussion,

where we also investigate various parameter settings

for T

stair

, λ and T

slope

. For the evaluation, we study

the different SRG methods presented in Section 3.2

and their combinations. Table 1 shows the DC, JS

and S

as percentages for different SRG methods and

their combinations. We assure a fair comparison by

optimizing the parameters T

slope

(up to a maximum of

35 % of the spatial resolution s

x,y

) and λ (up to a value

of 500) for each SRG method and their combinations.

Further, T

stair

was set to the realistic values 10 and 20

cm, T

color

was set to ±3 for each channel (R,G,B) and

= cos(10

◦

). For Experiment A only gray-scale

true-orthophotos were available, thus we simply used

the one intensity channel for each of the three color

channels (R,G,B). In our evaluation we only included

results, where all the blocking structures were not seg-

mented (S

= 100%). The settings for T

stair

, λ and

slope

for each experiment are presented in Table 2

and their choice will be discussed later.

Table 1 shows that the worst scores were achieved

by SRG

, which cannot handle color changes (i.e.,

shadows) and usually only segments an area sur-

rounding the seed point. SRG

performs far bet-

ter but can only segment areas, which are either ﬂat

or stairs. SRG

slope

shows high scores but is in gen-

eral outperformed by combinations of different SRG

methods. Overall, the combination of the three SRG

methods SRG

, SRG

and SRG

yields very good

results and performs quite well in all the test-cases.

Therefore, we used this combination and the optimal

parameters in Table 2 to generate the qualitative re-

sults. Figure 5 shows the results of Experiment A-D.

First, we show the original gray-scale and color true-

orthophoto (gray/RGB), then an overlay with our seg-

mentation (SEG) and ﬁnally another overlay with the

GT segmentation including the annotations of poten-

tial evacuation routes GT

(green) and blocking struc-

tures GT

(red).

Table 2: Optimal settings for T

stair

, λ,T

slope

and the spatial

resolution s

x,y

for Experiment A-D.

stair

[cm] T

slope

[cm] λ s

x,y

[cm]

Exp. A 20 3.5 4 10

Exp. B 10 3.5 24 10

Exp. C 10 3.0 78 10

Exp. D 10 1.0 24 3

With our automated evacuation map extraction al-

gorithm we achieve very good segmentation scores of

over 90 % in all the real-world experiments. Com-

pared to a manually annotated GT our approach seg-

ments a similar area and almost all potential evacua-

tion routes.

In Experiment A we get promising results, de-

spite the gray-scale true-orthophoto. All the main ex-

its from the square were segmented correctly, while

three narrow streets were left out. During DSM gen-

eration the estimation of the height of narrow streets

is difﬁcult because their ground levels are only visible

in the few aerial images taken directly above the them.

Thus, the surrounding buildings greatly inﬂuence the

calculation and the ground level appears higher than it

actually is. A similar problem occurs in Experiment

B, where the street on the top left corner is mostly

covered by trees.

Experiment C contains a square with a stage and

a tent, which were both correctly left out of the seg-

mentation. An interesting part is the narrow street at

the left bottom, where the DSM is not very good, but

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

132

using the SRG

approach, we manage to overcome

this small obstacle and correctly segment most of the

area. This is also the reason for the difference in S

between the combinations involving SEG

color

and the

ones without.

The spatial resolution in Experiment D is by

far the best and we are even able to leave most of

the cars out of the segmentation, which is quite

difﬁcult with a higher resolution of around 10 cm

(like in Experiment A). The limiting factors in

the real-world scenarios are the quality and spatial

resolution of the DSMs and true-orthophotos because

we calculate the segmentation from these inputs,

meaning our results are only as good as the input data.

The choice of T

stair

, λ and T

slope

Our segmentation results depend not only on the

quality of the input data, but also on the right parame-

ter settings. Table 2 shows different choices for T

stair

λ and T

slope

for Experiment A-D (optimal settings in

bold). In our experiments, we found that the value of

stair

is not critical, thus we focus only on the choices

for λ and T

slope

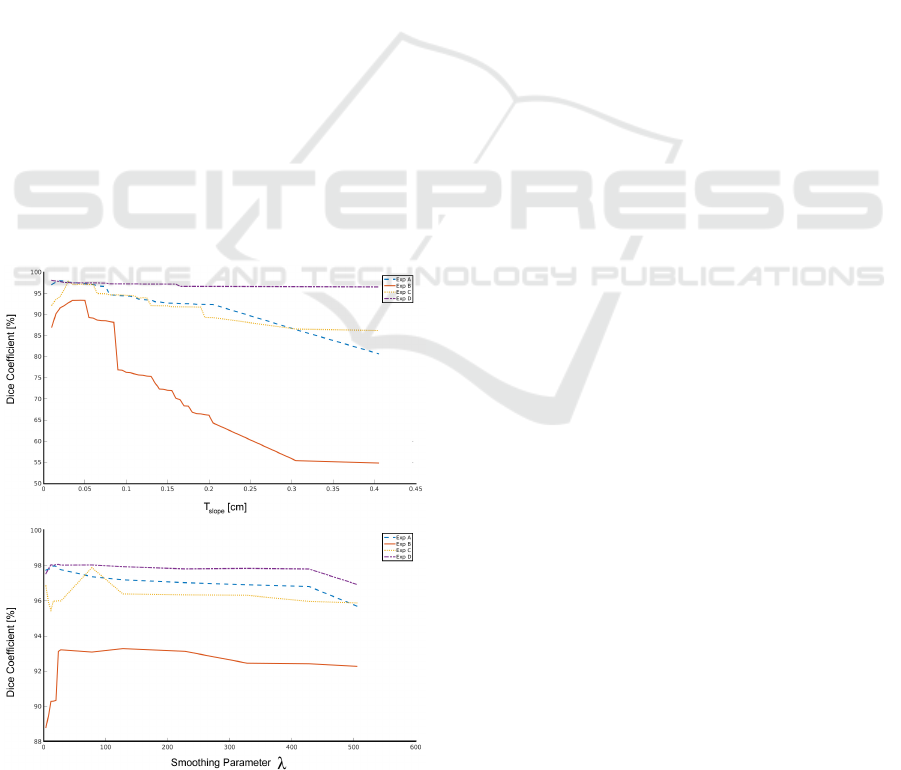
Figure 6 depicts the evaluation of the DC [%] for

Experiment A-D for T

slope

= [0.005,0.5] cm (top)

and λ = [4, 500] (bottom). The step-sizes are very

small in the beginning and widen when the values get

higher. For the evaluation of λ we set T

slope

to the op-

timal value calculated in Section 4.3 and vice versa.

Figure 6: Two plots showing the DC [%] for different val-

ues of T

slope

(top) and λ (bottom). Especially the choice of

slope

is very important for the DC.

slope

is in general limited by the accessibility and a

decent choice is usually around an inclination of 35

%, which would mean T

slope

= 3.5 for a spatial reso-

lution of s

= s

= 10 cm. Higher values can easily

lead to an over-segmentation and the WA would in-

clude inaccessible areas in that case.

A very small λ gives more emphasize to the

smoothing term and we even smooth over edges,

which can lead to an over-segmentation, while a

higher λ reduces the smoothing effect. We found that

values 10 < λ < 150 are in general good choices.

5 CONCLUSION AND OUTLOOK

In this paper, we presented a novel, efﬁcient and easy-

to-use approach to create digital maps for simula-

tion of outdoor evacuation scenarios. Using DSMs

and true-orthophotos computed from high-resolution

aerial images, we got a very accurate segmentation

of the WA in outdoor environments. We also showed

that a combination of different SRG approaches is in-

deed feasible. From the segmentation a CAD model

can be generated, which can then be used in most

common evacuation simulation tools. Additionally,

we introduced a new annotation scheme to assess the

quality of the extracted evacuation maps.

Despite the promising results of our approach,

there is still room for improvement. Extending the

SRG algorithm to also segment narrow streets and

evaluating our method by the example of an actual

event are potential topics for future work.

ACKNOWLEDGEMENTS

This work was ﬁnanced by the KIRAS program (no

840858, AIRPLAN) under supervision of the Aus-

trian Research Promotion Agency (FFG) and in co-

operation with the Austrian Ministry for Trafﬁc, In-

novation and Technology (BMVIT).

REFERENCES

Adams, R. and Bischof, L. (1994). Seeded region growing.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 16(6):641–647.

Chambolle, A. and Pock, T. (2011). A ﬁrst-order primal-

dual algorithm for convex problems with applications

to imaging. Journal of Mathematical Imaging and Vi-

sion, 40(1):120–145.

Cheriyadat, A. M. (2014). Unsupervised feature learning

for aerial scene classiﬁcation. IEEE Transactions on

Geoscience and Remote Sensing, 52(1):439–451.

Automated Segmentation of the Walkable Area from Aerial Images for Evacuation Simulation

133

Collins, R. T. (1996). A space-sweep approach to true

multi-image matching. In Computer Vision and Pat-

tern Recognition, pages 358–363. IEEE.

Dal Poz, A. P., Gallis, R. A., da Silva, J. F., and Martins,

E. F. (2012). Object-space road extraction in rural ar-

eas using stereoscopic aerial images. Geoscience and

Remote Sensing Letters, IEEE, 9(4):654–658.

Dice, L. R. (1945). Measures of the amount of ecologic

association between species. Ecology, 26(3):297–302.

Galea, E. R. (2002). Simulating evacuation and circulation

in planes, trains, buildings and ships using the exo-

dus software. Pedestrian and Evacuation Dynamics.

Springer, pages 203–225.

Han, J., Zhang, D., Cheng, G., Guo, L., and Ren, J. (2015).

Object detection in optical remote sensing images

based on weakly supervised learning and high-level

feature learning. Transactions on Geoscience and Re-

mote Sensing, 53(6):3325–3337.

Holz, D., Holzer, S., Rusu, R. B., and Behnke, S. (2012).

Real-time plane segmentation using rgb-d cameras. In

RoboCup 2011: Robot Soccer World Cup XV, pages

306–317. Springer.

Hsu, E. B. and Burkle, F. M. (2012). Cambodian bon om

touk stampede highlights preventable tragedy. Pre-

hospital and disaster medicine, 27(05):481–482.

Hu, J., Razdan, A., Femiani, J. C., Cui, M., and Wonka, P.

(2007). Road network extraction and intersection de-

tection from aerial images by tracking road footprints.

IEEE Transactions on Geoscience and Remote Sens-

ing, 45(12):4144–4157.

Huth, J., Kuenzer, C., Wehrmann, T., Gebhardt, S., Tuan,

V. Q., and Dech, S. (2012). Land cover and land use

classiﬁcation with twopac: Towards automated pro-

cessing for pixel-and object-based image classiﬁca-

tion. Remote Sensing, 4(9):2530–2553.

Irschara, A., Rumpler, M., Meixner, P., Pock, T., and

Bischof, H. (2012). Efﬁcient and globally optimal

multi view dense matching for aerial images. ISPRS

annals of photogrammetry, remote sensing and spatial

information sciences, 1:227–232.

Jaccard, P. (1908). Nouvelles recherches sur la distribution

ﬂorale.

Johnson, C. W. (2008). Using evacuation simulations

for contingency planning to enhance the security and

safety of the 2012 olympic venues. Safety science,

46(2):302–322.

upfel, H. (2006). The simulation of crowd dynamics at

very large events. Trafﬁc and Granular Flow’05, 5.

Krausz, B. and Bauckhage, C. (2012). Loveparade 2010:

Automatic video analysis of a crowd disaster. Com-

puter Vision and Image Understanding, 116(3):307–

319.

ammel, G., Grether, D., and Nagel, K. (2010). The rep-

resentation and implementation of time-dependent in-

undation in large-scale microscopic evacuation simu-

lations. Transportation Research Part C: Emerging

Technologies, 18(1):84–98.

Lin, Y. and Saripalli, S. (2012). Road detection and tracking

from aerial desert imagery. Journal of Intelligent &

Robotic Systems, 65(1-4):345–359.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2):91–110.

Mas, E., Adriano, B., and Koshimura, S. (2013). An inte-

grated simulation of tsunami hazard and human evac-

uation in la punta, peru. Journal of Disaster Research,

8(2):285–295.

Rudin, L., Osher, S., and Fatemi, E. (1992). Nonlinear total

variation based noise removal algorithms. Physica D:

Nonlinear Phenomena, 60(1):259–268.

Rumpler, M., Wendel, A., and Bischof, H. (2013). Prob-

abilistic range image integration for dsm and true-

orthophoto generation. In Image Analysis, pages 533–

544. Springer.

Schneider, V. and K

onnecke, R. (2001). Simulating evacu-

ation processes with aseri. Pedestrian and Evacuation

Dynamics, pages 301–313.

Shi, C., Zhong, M., Nong, X., He, L., Shi, J., and Feng,

G. (2012). Modeling and safety strategy of passenger

evacuation in a metro station in china. Safety Science,

50(5):1319–1332.

Tang, F. and Ren, A. (2012). Gis-based 3d evacuation sim-

ulation for indoor ﬁre. Building and Environment,

49:193–202.

Taubenb

ock, H., Post, J., Kieﬂ, R., Roth, A., Ismail, F. A.,

Strunz, G., and Dech, S. (2009). Risk and vulnera-

bility assessment to tsunami hazard using very high

resolution satellite data: The case study of padang, in-

donesia. EARSeL eProceedings, 8(1):53–63.

Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgib-

bon, A. W. (2000). Bundle adjustmenta modern syn-

thesis. In Vision Algorithms: Theory and Practice,

pages 298–372. Springer.

Tsai, J., Fridman, N., Bowring, E., Brown, M., Epstein,

S., Kaminka, G., Marsella, S., Ogden, A., Rika, I.,

Sheel, A., et al. (2011). Escapes: evacuation simula-

tion with children, authorities, parents, emotions, and

social comparison. pages 457–464. AAMAS.

Zhou, H., Kong, H., Wei, L., Creighton, D., and Nahavandi,

S. (2015). Efﬁcient road detection and tracking for

unmanned aerial vehicle. IEEE Transactions on Intel-

ligent Transportation Systems, 16(1):297–309.

APPENDIX

In the Appendix, we show a typical evacuation sim-

ulation scenario where our generated digital map can

be used. We use the map of the Marienhof (Munich,

Germany) generated in Experiment A and utilize the

software tool PedGo (Kl

upfel, 2006) mentioned in

Section 1. The software package comprises three dif-

ferent programs:

• PedEd - Used for editing the map, placing persons

and marking the exits

• PedGo - The simulation program, where various

scenarios can be simulated

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

134

• PedView - A 3D visualization of the previously

calculated simulations

The ﬁrst step is always loading the map into the

editor PedEd and placing the exits (see Fig. 7, left).

They are usually at the end of the streets leading away

from the central area. After that, persons (or agents)

can be put onto the map and corrections of the map

can be made. The whole process usually takes less

than three minutes. The next step is starting the sim-

ulation tool (PedGo) and loading the project. To get

an estimate of the average evacuation time, multiple

simulations should be performed (see Fig. 7, left).

With PedView we can view simulation ﬁles gen-

erated with PedGo in full 3D (see Fig. 8).

Figure 7: With PedEd the extracted CAD model can be

edited and then various simulations can be performed with

PedGo.

Figure 8: PedView can present the simulations calculated

with PedGo in 3D.

Automated Segmentation of the Walkable Area from Aerial Images for Evacuation Simulation

135