SJClust: Towards a Framework for Integrating

Similarity Join Algorithms and Clustering

Leonardo Andrade Ribeiro

, Alfredo Cuzzocrea

Karen Aline Alves Bezerra

and Ben Hur Bahia do Nascimento

Instituto de Inform

atica, Universidade Federal de Goi

as, Goi

ania, Brazil

University of Trieste and ICAR-CNR, Trieste, Italy

Departamento de Ci

encia da Computac¸

ao, Universidade Federal de Lavras, Lavras, Brazil

Keywords:

Data Integration, Data Cleaning, Duplicate Identiﬁcation, Set Similarity Joins, Clustering.

Abstract:

A critical task in data cleaning and integration is the identiﬁcation of duplicate records representing the same

real-world entity. A popular approach to duplicate identiﬁcation employs similarity join to ﬁnd pairs of similar

records followed by a clustering algorithm to group together records that refer to the same entity. However,

the clustering algorithm is strictly used as a post-processing step, which slows down the overall performance

and only produces results at the end of the whole process. In this paper, we propose SjClust, a framework to

integrate similarity join and clustering into a single operation. Our approach allows to smoothly accommo-

dating a variety of cluster representation and merging strategies into set similarity join algorithms, while fully

leveraging state-of-the-art optimization techniques.

1 INTRODUCTION

The presence of multiple records representing the

same real-world entity plagues practically every large

database. Such records are often referred to as fuzzy

duplicates (duplicates, for short), because they might

not be exact copies of one another. Duplicates arise

due to a variety of reasons, such as typographical er-

rors and misspellings during data entry, different nam-

ing conventions, and as a result of the integration of

data sources storing overlapping information.

Duplicates degrade the quality of the data deliv-

ered to application programs, thereby leading to a

myriad of problems. Some examples are mislead-

ing data mining models owing to erroneously inﬂated

statistics, inability of correlating information related

to a same entity, and unnecessarily repeated opera-

tions, e.g., mailing, billing, and leasing of equipment.

Duplicate identiﬁcation is thus of crucial importance

in data cleaning and integration.

Duplicate identiﬁcation is computationally very

expensive and, therefore, typically done ofﬂine. How-

ever, there exist important application scenarios that

demand (near) real-time identiﬁcation of duplicates.

Prominent examples are data exploration (Idreos

et al., 2015), where new knowledge has to be efﬁ-

ciently extracted from databases without a clear def-

inition of the information need, and virtual data inte-

gration (Doan et al., 2012), where the integrated data

is not materialized and duplicates in the query result

assembled from multiple data sources have to be iden-

tiﬁed — and eliminated — on-the-ﬂy. Such scenarios

have fueled the desire to integrate duplicate identiﬁ-

cation with processing of complex queries (Altwaijry

et al., 2015) or even as a general-purpose physical op-

erator within a DBMS (Chaudhuri et al., 2006).

An approach to realize the above endeavor is to

employ similarity join in concert with a clustering al-

gorithm (Hassanzadeh et al., 2009). Speciﬁcally, sim-

ilarity join is used to ﬁnd all pairs of records whose

similarity is not less than a speciﬁed threshold; the

similarity between two records is determined by a

similarity function. In a post-processing step, the

clustering algorithm groups together records using the

similarity join results as input.

For data of string type, set similarity join is an ap-

pealing choice for composing a duplicate identiﬁca-

tion operator. Set similarity join views its operands as

sets — strings can be easily mapped to sets. The cor-

responding similarity function assesses the similarity

between two sets in terms of their overlap and a rich

variety of similarity notions can be expressed in this

way (Chaudhuri et al., 2006). Furthermore, a num-

ber of optimization techniques have been proposed

Ribeiro, L., Cuzzocrea, A., Bezerra, K. and Nascimento, B.

SJClust: Towards a Framework for Integrating Similarity Join Algorithms and Clustering.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 1, pages 75-80

ISBN: 978-989-758-187-8

over the years (Sarawagi and Kirpal, 2004; Chaud-

huri et al., 2006; Bayardo et al., 2007; Xiao et al.,

2008; Ribeiro and H

arder, 2011) yielding highly efﬁ-

cient and scalable algorithms.

The strategy of using a clustering algorithm

strictly for post-processing the results of set similar-

ity join has two serious drawbacks, however. First,

given a group of n, sufﬁciently similar, duplicates, the

set similarity join performs





similarity calculations

to return the same number of set pairs. While this

is the expected behavior considering a similarity join

in isolation, it also means that repeated computations

are being performed over identical subsets. Even

worse, we may have to perform much more additional

similarity calculations between non-duplicates: low

threshold values are typically required for clustering

algorithms to produce accurate results (Hassanzadeh

et al., 2009). Unfortunately, existing ﬁltering tech-

niques are not effective at low threshold values and,

thus, there is an explosion of the number of the com-

parison at such values. Second, the clustering is a

blocking operator in our context, i.e., it has to con-

sume all the similarity join output before producing

any cluster of duplicates as result element. This fact is

particularly undesirable when duplicate identiﬁcation

is part of more complex data processing logic, possi-

bly even with human interaction, because it prevents

pipelined execution.

In this paper, we present SJClust, a framework

to integrate set similarity join and clustering into a

single operation, which addresses the above issues.

The main idea behind our framework is to repre-

sent groups of similar sets by a cluster representative,

which is incrementally updated during the set simi-

larity join processing. Besides effectively reducing

the number similarity calculations needed to produce

a cluster of n sets to O (n), we are able to fully lever-

age state-of-the-art optimization techniques at high

threshold values, while still performing well at low

threshold values where such techniques are less ef-

fective. Moreover, we exploit set size information to

identify when no new set can be added to a cluster;

therefore, we can then immediately output this clus-

ter and, thus, avoid the blocking behavior. On the

other hand, improving performance of clustering al-

gorithms is critical for next-generation big data man-

agement and analytics applications (e.g., (Cuzzocrea

et al., 2013b; Cuzzocrea, 2013; Cuzzocrea et al.,

2013a)).

Furthermore, there exists a plethora of clustering

algorithms suitable for duplicate identiﬁcation and no

single algorithm is overall the best across all scenar-

ios (Hassanzadeh et al., 2009). Thus, versatility in

supporting a variety of clustering methods is essen-

tial. Our framework smoothly accommodates various

cluster representation and merging strategies, thereby

yielding different clustering methods for each combi-

nation thereof.

2 BASIC CONCEPTS AND

DEFINITIONS

In this section, we present important concepts and

deﬁnitions related to set similarity joins before

present important optmization techniques.

We map strings to sets of tokens using the popular

concept of q-grams, i.e., sub-strings of length q ob-

tained by “sliding” a window over the characters of

an input string v. We (conceptually) extend v by pre-

ﬁxing and sufﬁxing it with q −1 occurrences of a spe-

cial character “$” not appearing in any string. Thus,

all characters of v participate in exact q q-grams. For

example, the string “token” can be mapped to the set

of 2-gram tokens {$t, to, ok, ke, en, n$ }. As the re-

sult can be a multi-set, we simply append the symbol

of a sequential ordinal number to each occurrence of

a token to convert multi-sets into sets, e.g, the multi-

set {a,b,b} is converted to {a◦1, b◦1, b◦2}. In the

following, we assume that all strings in the database

have already been mapped to sets.

We associate a weight with each token to obtain

weighted sets. A widely adopted weighting scheme

is the Inverse Document Frequency (IDF), which as-

sociates a weight idf (tk) to a token tk as follows:

idf (tk)=ln (1 + N/df (tk)), where df (tk) is the doc-

ument frequency, i.e., the number of strings a token

tk appears in a database of N strings. The intuition

behind using IDF is that rare tokens are more dis-

criminative and thus more important for similarity as-

sessment. We obtain unweighted sets by associating

the value 1 to each token. The weight of a set r, de-

noted by w (r), is given by the weight summation of

its tokens, i.e., w(r) =

∑

tk∈r

w(tk); note that we have

w(r) =

for unweighted sets.

We consider the general class of set similarity

functions. Given two sets r and s, a set similarity

function sim (r, s) returns a value in [0,1] to represent

their similarity; larger value indicates that r and s have

higher similarity. Popular set similarity functions are

deﬁned as follows.

Deﬁnition 1 (Set Similarity Functions). Let r and s

be two sets. We have:

• Jaccard similarity: J (r,s) =

w(r∩s)

w(r∪s)

• Dice similarity: D (r,s) =

2·w(r∩s)

w(r)+w(s)

• Cosine similarity: C (r, s) =

w(r∩s)

√

w(r)·w(s)

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

We now formally deﬁne the set similarity join op-

eration.

Deﬁnition 2 (Set Similarity Join). Given two set col-

lections R and S , a set similarity function sim, and

a threshold τ, the set similarity join between R and

S returns all scored set pairs h(r, s),τ0i s.t. (r, s) ∈

R ×S and sim (r, s) = τ0 ≥ τ.

In this paper, we focus on self-join, i.e., R = S;

we discuss the extension for binary inputs in Section

4. For brevity, we use henceforth the term similarity

function (join) to mean set similarity function (join).

Further, we focus on the Jaccard similarity and the

IDF weighting scheme, i.e., unless stated otherwise,

sim(r,s) and w (tk) denotes J (r,s) and idf (tk), re-

spectively.

Example 1. Consider the sets r and s below

x = {A,B,C, D,E}

y = {A, B,D, E,F}

and the following token-IDF association table:

tk A B C D E F

idf (tk) 1.5 2.5 2 3.5 0.5 2

We have w (r) = w (s) = 10 and w (r ∩s) = 8; thus

sim(r,s) =

10+10−8

≈ 0.66.

3 OPTIMIZATION TECHNIQUES

In this section, we describe a general set similar-

ity join algorithm, which provides the basis for our

framework.

Similarity functions can be equivalently repre-

sented in terms of an overlap bound (Chaudhuri et al.,

2006). Formally, the overlap bound between two sets

r and s, denoted by O (r, s), is a function that maps

a threshold τ and the set weights to a real value, s.t.

sim(r,s) ≥ τ iff w (r ∩s) ≥ O (r,s)

. The similarity

join can then be reduced to the problem of identify-

ing all pairs r and s whose overlap is not less than

O(r,s). For the Jaccard similarity, we have O(r, s) =

1+τ

·(w (r) + w (s)).

Further, similar sets have, in general, roughly sim-

ilar weights. We can derive bounds for immedi-

ate pruning of candidate pairs whose weights dif-

fer enough. Formally, the weight bounds of r, de-

noted by min (r) and max (r), are functions that map

τ and w (r) to a real value s.t. ∀s, if sim (r,s) ≥ τ,

then min(r) ≤ w (s) ≤ max (r) (Sarawagi and Kirpal,

2004). Thus, given a set r, we can safely ignore all

For ease of notation, the parameter τ is omitted.

other sets whose weights do not fall within the in-

terval [min(r) ,max (r)]. For the Jaccard similarity,

we [min (r), max (r)] =

τ ·w (r) ,

w(r)

. We refer the

reader to (Schneider et al., 2015) for deﬁnitions of

overlap and weight bounds of several other similarity

functions, including Dice and Cosine.

We can prune a large share of the compari-

son space by exploiting the preﬁx ﬁltering principle

(Sarawagi and Kirpal, 2004; Chaudhuri et al., 2006).

Preﬁxes allow selecting or discarding candidate pairs

by examining only a fraction of the original sets. We

ﬁrst ﬁx a global order O on the universe U from

which all tokens in the sets considered are drawn. A

set r

⊆ r is a preﬁx of r if r

contains the ﬁrst

to-

kens of r. Further, pref

(r) is the shortest preﬁx of r,

the weights of whose tokens add up to more than β.

The preﬁx ﬁltering principle is deﬁned as follows.

Deﬁnition 3 (Preﬁx Filtering Principle (Chaudhuri

et al., 2006)). Let r and s be two sets. If w(r ∩s) ≥α,

then pref

(r) ∩pref

(r) 6= ∅, where β

= w(r) −α

and β

= w (s) −α, respectively.

We can identify all candidate matches of a given

set r using the preﬁx pref

(r), where β = w (r) −

min(r). We denote this preﬁx simply by pref (r). It

is possible to derive smaller preﬁxes for r, and thus

obtain more pruning power, when we have informa-

tion about the set weight of the candidate sets, i.e., if

w(s) ≥ w (r) (Bayardo et al., 2007) or w (s) > w (r)

(Ribeiro and H

arder, 2011). Note that preﬁx overlap

is a condition necessary, but not sufﬁcient to satisfy

the original overlap constraint: an additional veriﬁca-

tion must be performed on the candidate pairs.

Further, the number of candidates can be signif-

icantly reduced by using the inverse document fre-

quency ordering, O

id f

, as global token order to obtain

sets ordered by decreasing IDF weight

. The idea is

to minimize the number of sets agreeing on preﬁx el-

ements and, in turn, candidate pairs by shifting lower

frequency tokens to the preﬁx positions.

Example 2. Consider the sets r and s in Example 1

and τ = 0.6. We have O (r,s) = 7.5; [min (r), max (r)]

and [min (s), max (s)] are both [6, 16.7]. By ordering

r and s according to O

id f

and the IDF weights in Ex-

ample 1, we obtain:

x = [D,B,C, A,E]

y = [D, B,F,A,E].

We have pref (r) = pref (s) = [D].

A secondary ordering is used to break ties consistently

(e.g., the lexicographic ordering). Also, note that an equiv-

alent ordering is the document frequency ordering, which

can be used to obtain unweighted sets ordered by increas-

ing token frequency in the collection.

SJClust: Towards a Framework for Integrating Similarity Join Algorithms and Clustering

4 THE SIMILARITY JOIN

ALGORITHM

In this section, we provide the details on the similarity

join algorithm.

Similarity join algorithms based on inverted lists

are effective in exploiting the previous optimizations

(Sarawagi and Kirpal, 2004; Bayardo et al., 2007;

Xiao et al., 2008; Ribeiro and H

arder, 2011). Most

of such algorithms have a common high-level struc-

ture following a ﬁlter-and-reﬁne approach.

Algorithm 1 formalizes the steps of a similarity

join algorith. The algorithm receives as input a set

collection sorted in increasing order of set weights,

where each set is sorted according to O

id f

. An in-

verted list I

stores all sets containing a token t in their

preﬁx. The input collection R is scanned and, for each

probe set r, its preﬁx tokens are used to ﬁnd candidate

sets in the corresponding inverted lists (lines 4–10);

this is the candidate generation phase, where the map

M is used to associate candidates to its accumulated

overlap score os (line 3). Each candidate s is dynam-

ically removed from the inverted list if its weight is

less than min (r) (lines 6–7). Further ﬁlters, e.g., ﬁlter

based on overlap bound, are used to check whether s

can be a true match for r, and then the overlap score

is accumulated, or not, and s can be safely ignored in

the following processing (lines 8–10). In the veriﬁca-

tion phase, r and its matching candidates are checked

against the similarity predicate and those pairs sat-

isfying the predicate are added to the result set. To

this end, the Verify procedure (not shown) employs

a merge-join-based algorithm exploiting token order

and the overlap bound to deﬁne break conditions (line

11). Finally, in the indexing phase, a pointer to set r

is appended to each inverted list I

associated with its

preﬁx tokens (lines 12 and 13).

Algorithm 1 is actually a self-join. Its extension

to binary joins is trivial: we ﬁrst index the smaller

collection and then go through the larger collection

to identify matching pairs. For simplicity, several ﬁl-

tering strategies such positional ﬁltering (Xiao et al.,

2008) and min-preﬁxes (Ribeiro and H

arder, 2011),

as well as inverted list reduction techniques (Bayardo

et al., 2007; Ribeiro and H

arder, 2011) were omit-

ted. Nevertheless, these optimizations are based on

bounds and preﬁxes and, therefore, our discussion in

the following remains valid.

5 THE SJClust FRAMEWORK

We now present SJClust, a general framework to in-

tegrate clustering methods into similarity joins algo-

Algorithm 1: Similarity join algorithm.

Input: A set collection R sorted in increasing order

of the set weight; each set is sorted according

to O

id f

; a threshold τ

Output: A set S containing all pairs (r, s) s.t.

Sim(r,s) ≥ τ

1 I

,...I

← ∅, S ← ∅

2 foreach r ∈R do

3 M ← empty map from set id to overlap score (os)

4 foreach t ∈ pref (r) do // can. gen. phase

5 foreach s ∈ I

6 if w(s) < min (r)

7 Remove s from I

8 if ﬁlter (r, s, M (s))

9 M (s) .os ←−∞ // invalidate s

10 else M (s) .os = M (s) .os + w (t)

11 S ←S ∪Verify (r,M,τ) // verif. phase

12 foreach t ∈ pref (r) do // index. phase

13 I

← I

∪{r}

14 return S

Figure 1: Cluster representation.

rithms. The goals of our framework are threefold: 1)

ﬂexibility and extensibility to accommodate different

clustering methods; 2) efﬁciency by fully leveraging

existing optimization techniques and by reducing the

number of similarity computations to form clusters;

3) non-blocking behavior by producing results before

having consumed all the input.

The backbone of SJClust is the similarity join al-

gorithm presented in the previous section. In partic-

ular, SJClust operates over the same input of sorted

sets, without requiring any pre-processing, and has

the three execution phases present in Algorithm 1,

namely, candidate generation, veriﬁcation, and index-

ing phases. Nevertheless, there are, of course, major

differences.

First and foremost, the main objects are now clus-

ter of sets, or simply clusters. Figure 1 illustrates

strategy adopted for cluster representation. The inter-

nal representation contains a list of its set element’s

ids, an (optional) auxiliary structure, and the cluster’s

complete representation, a set containing all tokens

from all set elements. The cluster export its external

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

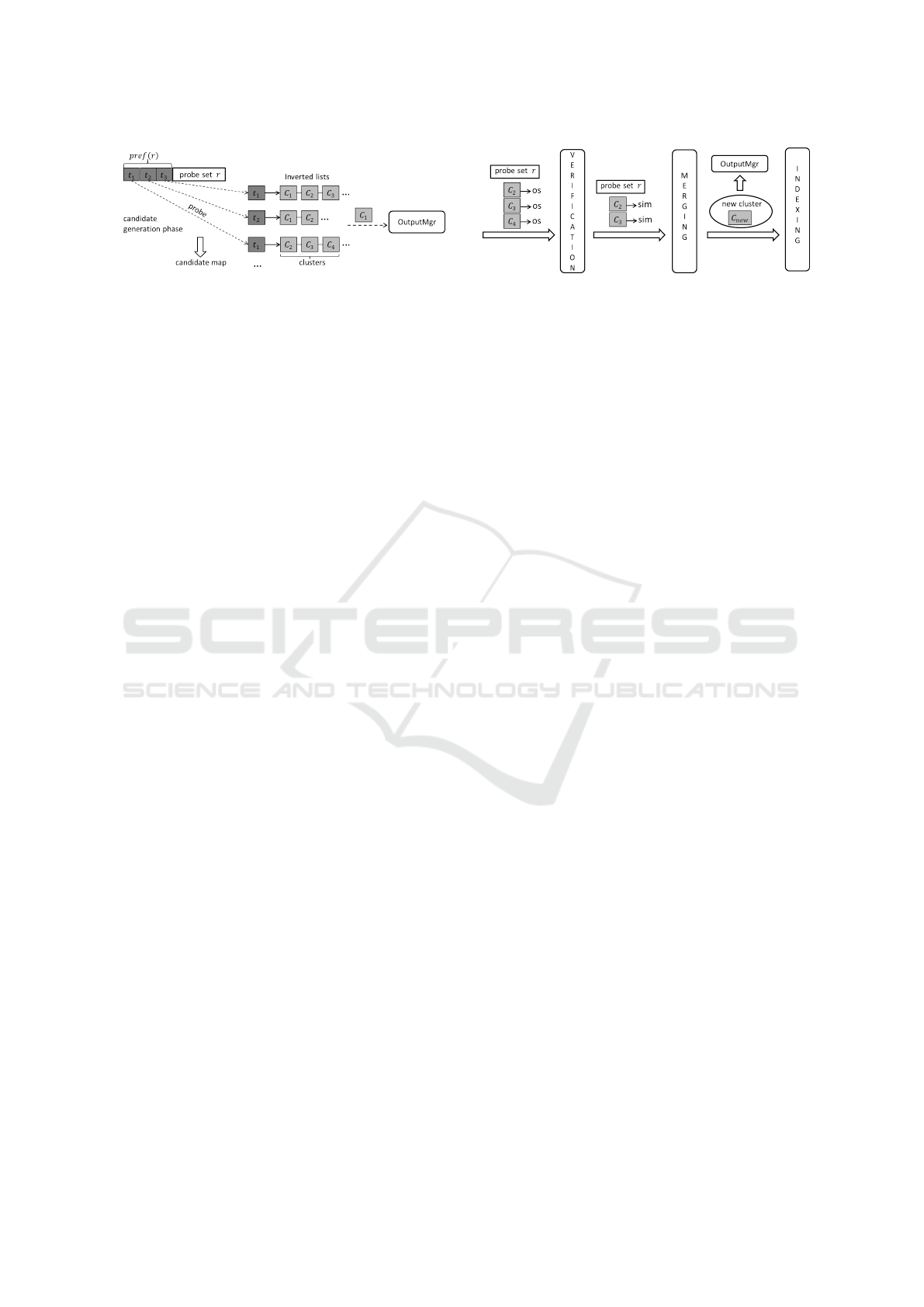
(a) Candidate generation. (b) SJClust course of evaluation.

Figure 2: SJClust framemork components.

representation as the so-called cluster representative

(or simply representative), which is fully comparable

to input sets. Similarity evaluations are always per-

formed on the representatives, either between a probe

set and a cluster or between two clusters. In the fol-

lowing, we use the term cluster and representative

interchangeably whenever the distinction is unimpor-

tant for the discussion.

Figure 2 depicts more details on the SJClust

framework. In the candidate generation phase, preﬁx

tokens of the current probe set are used to ﬁnd clus-

ter candidates in the inverted lists (Figure 2(a)). Also,

there is a merging phase between veriﬁcation and in-

dexing phases (Figure 2(b)). The veriﬁcation phase

reduces the number of candidates by removing false

positives, i.e., clusters whose similarity to the probe

set is less than the speciﬁed threshold. In the merging

phase, a new cluster is generated from the probing

set and the clusters that passed through the veriﬁca-

tion are considered for merging with it according to a

merging strategy. In the indexing phase, references to

the newly generated cluster are stored in the inverted

lists associated with its preﬁx tokens. Finally, there

is the so-called Output Manager, which is responsi-

ble for maintaining references to all clusters —a ref-

erence to a cluster is added to the Output Manager

right after its generation in the merging phase (Figure

2(b)). Further, the Output Manager sends a cluster to

the output as soon as it is identiﬁed that no new prob-

ing set can be similar to this cluster. Clusters in such

situation can be found in the inverted lists during the

candidate generation (Figure 2(a)) as well as identi-

ﬁed using the weight of the probe set (not shown in

Figure 2).

The aforementioned goals of SJClust are met as

follows: ﬂexibility and extensibility are provided by

different combinations of cluster representation and

merging strategies, which can be independently and

transparently plugged into the main algorithm; efﬁ-

ciency is obtained by the general strategy to cluster

representation and indexing; and non-blocking behav-

ior is ensured by the Output Manager.

6 RELATED WORK

The duplicate identiﬁcation problem has a long his-

tory of investigation conducted by several research

communities spanning databases, machine learning,

and statistics, frequently under different names, in-

cluding record linkage, deduplication, and near-

duplicate identiﬁcation (Koudas et al., 2006; Elma-

garmid et al., 2007). Over the last years, there is

growing interest in realizing duplicate identiﬁcation

on-the-ﬂy. In (Altwaijry et al., 2013), a query-driven

approach is proposed to reduce the number of clean-

ing steps in simple selections queries over dirty data.

The same authors presented a framework to answer

complex Select-Project-Join queries (Altwaijry et al.,

2015). Our work is complementary to these proposals

as our framework can be encapsulated into physical

operators to compose query evaluation plans.

There is long line of research on (exact) set sim-

ilarity joins (Sarawagi and Kirpal, 2004; Chaudhuri

et al., 2006; Bayardo et al., 2007; Xiao et al., 2008;

Ribeiro and H

arder, 2009; Ribeiro and H

arder, 2011;

Wang et al., 2012). Aspects most relevant to our work

have already been discussed at length in Section 2.

To the best of our knowledge, integration of cluster-

ing into set similarity joins has not been investigated

in previous work.

In (Mazeika and B

ohlen, 2006), the authors em-

ploy the concept of proximity graph to cluster strings

without requiring a predeﬁned threshold value. The

algorithm to automatically detected cluster borders

was improved later in (Kazimianec and Augsten,

2011). However, it is not clear how to leverage state-

of-the-art set similarity joins in these approaches to

improve efﬁciency and deal with large datasets.

In (Hassanzadeh et al., 2009), a large number of

clustering algorithms are evaluated in the context of

duplicate identiﬁcation. These algorithms use simi-

larity join to produce their input, but can start only

after the execution of the similarity join.

SJClust: Towards a Framework for Integrating Similarity Join Algorithms and Clustering

7 CONCLUSIONS AND FUTURE

WORK

In this paper, we presented SJClust, a framework to

integrate clustering into set similarity join algorithms.

Our framework provides ﬂexibility and extensibility

to accommodate different clustering methods, while

fully leveraging existing optimization techniques and

avoiding undesirable blocking behavior.

Future work is mainly oriented towards enriching

our framework with advanced features such as un-

certain data management (e.g., (Leung et al., 2013)),

adaptiveness (e.g., (Cannataro et al., 2002)), and exe-

cution time prediction (e.g, (Sidney et al., 2015)).

ACKNOWLEDGEMENTS

This research was partially supported by the Brazilian

agencies CNPq and CAPES.

REFERENCES

Altwaijry, H., Kalashnikov, D. V., and Mehrotra, S. (2013).

Query-driven approach to entity resolution. PVLDB,

6(14):1846–1857.

Altwaijry, H., Mehrotra, S., and Kalashnikov, D. V. (2015).

Query: A framework for integrating entity resolution

with query processing. PVLDB, 9(3):120–131.

Bayardo, R. J., Ma, Y., and Srikant, R. (2007). Scaling up

all pairs similarity search. In Proc. of the 16th Intl.

Conf. on World Wide Web, pages 131–140.

Cannataro, M., Cuzzocrea, A., Mastroianni, C., Ortale, R.,

and Pugliese, A. (2002). Modeling adaptive hyperme-

dia with an object-oriented approach and xml. Second

International Workshop on Web Dynamics.

Chaudhuri, S., Ganti, V., and Kaushik, R. (2006). A prim-

itive operator for similarity joins in data cleaning. In

Proc. of the 22nd Intl. Conf. on Data Engineering,

page 5.

Cuzzocrea, A. (2013). Analytics over big data: Explor-

ing the convergence of datawarehousing, OLAP and

data-intensive cloud infrastructures. In 37th Annual

IEEE Computer Software and Applications Confer-

ence, COMPSAC 2013, Kyoto, Japan, July 22-26,

2013, pages 481–483.

Cuzzocrea, A., Bellatreche, L., and Song, I. (2013a). Data

warehousing and OLAP over big data: current chal-

lenges and future research directions. In Proceedings

of the sixteenth international workshop on Data ware-

housing and OLAP, DOLAP 2013, San Francisco, CA,

USA, October 28, 2013, pages 67–70.

Cuzzocrea, A., Sacc

a, D., and Ullman, J. D. (2013b).

Big data: a research agenda. In 17th International

Database Engineering & Applications Symposium,

IDEAS ’13, Barcelona, Spain - October 09 - 11, 2013,

pages 198–203.

Doan, A., Halevy, A. Y., and Ives, Z. G. (2012). Principles

of Data Integration. Morgan Kaufmann.

Elmagarmid, A. K., Ipeirotis, P. G., and Verykios, V. S.

(2007). Duplicate record detection: A survey. TKDE,

19(1):1–16.

Hassanzadeh, O., Chiang, F., Miller, R. J., and Lee, H. C.

(2009). Framework for evaluating clustering algo-

rithms in duplicate detection. PVLDB, 2(1):1282–

1293.

Idreos, S., Papaemmanouil, O., and Chaudhuri, S. (2015).

Overview of data exploration techniques. In Proc. of

the SIGMOD Conference, pages 277–281.

Kazimianec, M. and Augsten, N. (2011). Pg-skip: Proxim-

ity graph based clustering of long strings. In Proc. of

the DASFAA Conference, pages 31–46.

Koudas, N., Sarawagi, S., and Srivastava, D. (2006). Record

linkage: Similarity measures and algorithms. In Proc.

of the SIGMOD Conference, pages 802–803.

Leung, C. K., Cuzzocrea, A., and Jiang, F. (2013).

Discovering frequent patterns from uncertain data

streams with time-fading and landmark models. T.

Large-Scale Data- and Knowledge-Centered Systems,

8:174–196.

Mazeika, A. and B

ohlen, M. H. (2006). Cleansing databases

of misspelled proper nouns. In Proc. of the First Int’l

VLDB Workshop on Clean Databases.

Ribeiro, L. and H

arder, T. (2009). Efﬁcient set similarity

joins using min-preﬁxes. In Proc. of ADBIS Confer-

ence, pages 88–102.

Ribeiro, L. A. and H

arder, T. (2011). Generalizing preﬁx

ﬁltering to improve set similarity joins. Information

Systems, 36(1):62–78.

Sarawagi, S. and Kirpal, A. (2004). Efﬁcient set joins on

similarity predicates. In Proc. of the SIGMOD Con-

ference, pages 743–754.

Schneider, N. C., Ribeiro, L. A., de Souza In

acio, A.,

Wagner, H. M., and von Wangenheim, A. (2015).

Simdatamapper: An architectural pattern to integrate

declarative similarity matching into database applica-

tions. In Proc. of the SBBD Conference, pages 967–

972.

Sidney, C. F., Mendes, D. S., Ribeiro, L. A., and H

arder,

T. (2015). Performance prediction for set similarity

joins. In Proc. of the the ACM Symposium on Applied

Computing, pages 967–972.

Wang, J., Li, G., and Feng, J. (2012). Can we beat the

preﬁx ﬁltering?: an adaptive framework for similarity

join and search. In Proc. of the SIGMOD Conference,

pages 85–96.

Xiao, C., Wang, W., Lin, X., and Yu, J. X. (2008). Efﬁcient

similarity joins for near duplicate detection. In Proc.

of the 17th Intl. Conf. on World Wide Web, pages 131–

140.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems