
Efficient Self-similarity Range Wide-joins Fostering Near-duplicate
Image Detection in Emergency Scenarios
Luiz Olmes Carvalho, Lucio F. D. Santos, Willian D. Oliveira, Agma J. M. Traina, Caetano Traina Jr.
Institute of Mathematics and Computer Sciences, University of S
˜
ao Paulo, S
˜
ao Paulo, Brazil
Keywords:
Similarity Search, Similarity Join, Query Operators, Wide-join, Near-duplicate Detection.
Abstract:
Crowdsourcing information is being increasingly employed to improve and support decision making in emer-
gency situations. However, the gathered records quickly become too similar among themselves and handling
several similar reports does not add valuable knowledge to assist the helping personnel at the control center
in their decision making tasks. The usual approaches to detect and handle the so-called near-duplicate data
rely on costly twofold processing. Aimed at reducing the cost and also improving the ability of duplication
detection, we developed a framework model based on the similarity wide-join database operator. We extended
the wide-join definition empowering it to surpass its restrictions and accomplish the near-duplicate task too.
In this paper, we also provide an efficient algorithm based on pivots that speeds up the entire process, which
enables retrieving the top similar elements in a single-pass processing. Experiments using real datasets show
that our framework is up to three orders of magnitude faster than the competing techniques in the literature,
whereas also improving the quality of the result in about 35 percent.
1 INTRODUCTION
Emergency situations can threaten life, environment
and properties. Thus, a great effort are being made
to develop systems aimed at reducing injuries and fi-
nancial losses in crises situations. Existing solutions
employ ultraviolet, infrared sensors and surveillance
cameras (Chino et al., 2015). The problem of using
sensors is that they need to be installed near to the
prospected emergency places, and forecasting all the
possible crisis situations in a particular region is not
feasible.
On the other hand, surveillance cameras can pro-
vide visual information of wider spaces. When asso-
ciated the increasing popularity of smartphones with
good quality cameras and other mobile devices, they
may lead to better solutions to map crisis scenarios
and allow speeding up planning emergency actions to
reduce losses. Seizing the opportunity to take such in-
formation into accont, the Rescuer
1
Project is devel-
oping an emergency-response system to assist Crisis
Control Committees during a crisis situation. It pro-
vides tools that allow witnesses, victims and the res-
cue staff to gather emergency information based on
1
Rescuer: Reliable and Smart Crowdsourcing
Solution for Emergency and Crisis Management -
<http://www.rescuer-project.org>
images and videos sent from the incident place using
a mobile crowdsourcing framework.
Crowdsourcing data can provide a large amount
of information about the emergency scenario, but it
often leads to a large amount of records very simi-
lar among themselves too. For instance, let us con-
sider the occurrence of an event such as a building
on fire or a serious incident in an industrial plant. As
the eyewitnesses register the event with their smart-
phones many and repeatedly times, several pictures
become copies almost identical to others. In the im-
age retrieval context, the images too similar to each
other with only smooth variations imposed by the
devices or the capture conditions (resolution, illumi-
nation, cropping, rotation, framing) are called near-
duplicates (Li et al., 2015; Yao et al., 2015).
For instance, Fig. 1 depicts a 9 days-long fire oc-
curred in an industrial plant at Santos, Brazil, in April
2015. As shown in Fig. 1, eyewitnesses e
1
, e
2
and
e
3
took photos from the same perspective of the burn-
ing industrial plant, whereas e
4
, e
5
and e
6
took photos
from another side of the scenario and the same hap-
pened to eyewitness e
7
, e
8
, e
9
and e
10
. Too much
similar images from the same perspectives (near-
duplicates) may not improve the decision making sup-
port. In this example, each image subset {img
1
, img
2
,
img
3
}, {img
4
, img
5
, img
6
}, {img
7
, img
8
, img
9
} and
Carvalho, L., Santos, L., Oliveira, W., Traina, A. and Jr., C.
Efficient Self-similarity Range Wide-joins Fostering Near-duplicate Image Detection in Emergency Scenarios.
In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 1, pages 81-91
ISBN: 978-989-758-187-8
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
81

{img
10
} forms near-duplicates. Thus, it is more use-
ful to remove the near-duplicates, fostering more di-
versified results, which present a holistic vision about
the incident, such as using only the subset {img
1
,
img
6
, img
8
, img
10
}.
Figure 1: An example of taking photos of an emergency
scenario (industrial plant on fire).
On the other hand, sometimes it is interesting to
retrieve and return the near-duplicate elements. In
the aforestated example (Fig. 1), law enforcement of-
ficers and investigators may be interested on the near-
duplicate images. Although the near-duplicate ele-
ments may be not useful for non-expert people, those
professionals usually see things differently and are
trained to recognize small details among the images
that can contribute to the investigation.
Near-duplicate image detection has attracted con-
siderable attention in multimedia and database com-
munities (Xiao et al., 2011; Wang et al., 2012; Li
et al., 2015; Yao et al., 2015). However, to the best
of our knowledge, the near-duplicate detection is yet
an open problem, with no consolidated technique able
to accomplish such task in terms of both efficiency
and efficacy. Most of the approaches to detect near-
duplicate images rely on executing a twofold process-
ing, described as follows:
1. Building: the first phase aims at retrieving a candi-
date set of near-duplicate elements. It can use ev-
ery individual image in the dataset as a similarity
query center to retrieve the images most similar to
each one (Xiao et al., 2011), or employ clustering-
based techniques (Li et al., 2015).
2. Improvement: the second phase processes the can-
didate set and refines it removing false positives.
The main differences among the distinct meth-
ods are in this phase. Most of them sacrifices the
computational efficiency to enhance the result ef-
ficacy.
Considering the scenario depicted in Fig. 1, it is
reasonable to consider that a crowdsourcing frame-
work can be “flooded” with a large amount of images.
In that case, employing a twofold technique may take
too much time to generate the first perspective about
the incident scene and, when it is achieved, the situa-
tion may already be changed.
As a possible solution, recent approaches (Xiao
et al., 2011; Carvalho et al., 2015) consider us-
ing well-known searching operators from both the
database and information retrieval areas, namely sim-
ilarity joins and wide-joins, to detect near-duplicate
elements. Similarity joins (Silva et al., 2013) obtain
pairs of elements similar among themselves, assum-
ing each pair corresponds to the near-duplicate candi-
dates obtained by the building phase. However, those
retrieval operators were applied only to detect near-
duplicate elements in data represented by strings, as in
(Xiao et al., 2011), but they were not explored in other
domains such as images. In their turn, wide-joins
(Carvalho et al., 2015) are designed to retrieve the
overall most similar pairs, leading to an inherent com-
bination of building and improvement phases in their
processing. However, wide-joins process two distinct
sets, while near-duplicate detection must combine a
set with itself.
Although employing the join-based techniques
may improve the performance, they require comput-
ing the similarity among all possible pairs of image
received. As the amount of elements is usually large,
the situation becomes similar to the first alternative.
Therefore, both alternatives present drawbacks when
applied to emergency control systems.
To detect near-duplicate images for emergency
scenarios efficiently, this paper introduces a frame-
work based on the similarity range wide-join database
operator. We extended the operator definition to en-
able processing a single relation, thus we enlarged its
usability as a unary self wide-join operator. Moreover,
we devised an optimized algorithm based on pivots
to speed up processing similarity wide-join, prioritiz-
ing early result generation, as required by emergency-
based support systems, with no need of further im-
provement steps. Experiments performed on two real
datasets show that our proposal is at least two orders
of magnitude faster than existing techniques, whereas
always returning a high-quality answer.
The remainder of this paper is organized as fol-
lows: Section 2 describes the main concepts and re-
lated work. Section 3 introduces our framework to
detect near-duplicate images, the definition and algo-
rithms for the self wide-join. Section 4 presents ex-
perimental evaluation of our technique and discusses
the main results. Finally, Section 5 summarizes the
main achievements and outlines future steps.
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
82

2 BACKGROUND
This Section overviews the main concepts and the
related work to ours regarding to the image rep-
resentation (Section 2.1), near-duplicates object de-
tection (Section 2.2) and the evaluation of similar-
ity queries, including the types similarity joins (Sec-
tion 2.3). Also, the main symbols employed along the
paper are summarized in Table 1.
2.1 Feature Extraction and Image
Representation
Aiming at enabling retrieval by content and hence
the near-duplicate detection, images are compared ac-
cording to a similarity measure. To evaluate the sim-
ilarity, images are represented by an n-dimensional
array of numerical values, called feature vector, that
describes their content. The features are numerical
measurements of visual properties.
The algorithms responsible for processing images
and obtaining their features are known as feature ex-
tractors methods. For each data domain there are
specific features to be considered and, in the case of
images, the off-the-shelf extractors capture features
based on colors (e.g. histograms), texture (e.g. Har-
alick features) and/or shape (e.g. Zernike Moments)
(Sonka et al., 2014).
The evaluation of the similarity measure between
two feature vectors is performed by a metric. For-
mally, given a feature vector space D (the data do-
main), a distance function d : D ×D 7→ R
+
is called a
metric on D if, for all x,y,z ∈ D, there holds:
• d(x,y) ≥ 0 (non-negativity)
• d(x,y) = 0 ⇒ x = y (identity of indiscernibles)
• d(x,y) = d(y,x) (symmetry)
• d(x,y) ≤ d(x,z)+ d(z,y) (triangle inequality)
The pair
h
D,d
i
is called metric space (Searc
´
oid,
2007). The metric space is the mathematical model
that enables to perform similarity queries, and hence
to detect the near-duplicate elements.
2.2 Near-duplicate Detection
Several techniques for near-duplicate detection rely
on the Bag-of-Visual Words (BoVW) model (Li et al.,
2015; Yao et al., 2015). That model represents the
features as visual words and the image representation
consists of counting the words to create an histogram.
However, BoVW reliability for duplicate detection is
small, as it does not capture the spatial relationship
existing among the extracted features.
Aimed at surpassing this drawback, studies like
(Yao et al., 2015) combined the spatial information
with the BoVW local descriptors. However, local de-
scriptors yet generate feature vectors of varying di-
mensionality, which is troublesome to represent in
metric spaces, requiring high-costly metrics.
Other approaches considered to spot near-
duplicates are hash functions and the Locality Sen-
sitive Hashing (LSH) (Bangay and Lv, 2012; Wang
et al., 2012). Whereas hash functions fail on rep-
resenting information for similarity retrieval, once
small differences in images leads to distinct hash rep-
resentations, the LSH circumvents this problem by
retrieving approximate result sets. In the same line,
weighted min-Hash functions improve the image rep-
resentation, but once they are usually based on bag-
of-words, they may present the same drawbacks of
the other technique (Chum et al., 2008). Unlike those
techniques, we are interested in accurate answers.
Still worth to mention is the “Adaptive Cluster
with k-means” technique (ACMe) (Li et al., 2015). It
applies clustering algorithms to group near-duplicate
images in a twofold process. First it clusters the
dataset using the k-means algorithm. Subsequently,
the coherences of the obtained clusters are checked
to determine the need of recursively processing each
cluster. The result is then refined using local descrip-
tors. This is a highly expensive technique that re-
quires for the Improvement phase. Moreover, as the
k-means algorithm is sensitive to outliers, our intu-
ition is that better quality result might be achieved
replacing it with the k-medoids algorithm. Surpass-
ing the existing drawbacks in algorithms that have an
improvement phase, our proposal extends similarity
joins to speed up the detection of near duplicates with-
out post-processing the image database.
2.3 Similarity Join
Similarity joins are database operators that combine
the tuples of two relations T
1
and T
2
so that each
retrieved pair
h
t
1
∈ T
1
,t
2
∈ T
2
i
satisfies a similarity
predicate θ
s
. The similarity conditions most em-
ployed in similarity joins generate the similarity range
join and the k-nearest neighbor join (Silva et al.,
2013).
Assume that each relation has an attribute S
1
⊆ T
1
and S
2
⊆ T
2
, both sampled from the same metric
space
h
D,d
i
. Given a maximum similarity threshold
ξ, the similarity range join retrieves the pairs
h
t
1
,t
2
i
,
t
1
∈ T
1
and t
2
∈ T
2
, such that d(t
1
[S
1
],t
2
[S
2
]) ≤ ξ.
Given an integer value k ≥ 1, the k-nearest neighbor
join retrieves k ∗ |T
1
| tuples
h
t
1
,t
2
i
such that t
2
is one
Efficient Self-similarity Range Wide-joins Fostering Near-duplicate Image Detection in Emergency Scenarios
83

Table 1: Symbols.
SYMBOL MEANING
ξ similarity limiar
D data domain
d distance function / metric
F feature extractor method
f feature value
img an image
k, κ,m,n integer values
S,S
1
,S
2
attributes subject to a metric
T,T
1
,T
2
relations
t,t
1
,t
2
,t
i
,t
j
tuples
t[S] the value of attribute S in tuple t
v feature vector
of the k most similar attributes to each t
1
(Carvalho
et al., 2015).
A third type of similarity join is often described
in the database literature (Silva et al., 2013): the k-
distance join. It retrieves the k pairs
h
t
1
,t
2
i
having the
most similar values t
1
[S
1
] and t
2
[S
2
]. This operator is
an instance of the similarity wide-join (Carvalho et al.,
2015). Wide-joins retrieve the most similar pairs in
general, sorting the tuple internally, allowing its pro-
cessing to comply with the relational theory and exe-
cuted efficiently.
Similarity joins can be used to perform several
tasks, including near-duplicate detection. For this last
purpose, however, similarity joins have been explored
only in string-based data represented as tokens, using
metrics such as the Edit or Hamming distance, as in
(Xiao et al., 2011). Our proposal considers other do-
mains but string data and employs more general met-
rics, such as the Minkowski (L
p
) family over image
domains. Likewise, similarity wide-joins have been
restricted used to operate on two distinct relations,
loosing optimization opportunities that exists when
processing elements lying in the same set.
3 NEAR-DUPLICATE
DETECTION
Detecting near-duplicates on multimedia repositories
plays an important role in presenting a more use-
ful result, as returning images too much similar not
only poses a negative impact on the retrieval time, but
generally it also reduces the users’ browsing experi-
ence. Imposing users to interactively analyze near-
duplicates until obtaining the desired result is annoy-
ing, and requires a lot of time that would be more
wisely employed specially when handling emergency
Figure 2: The architecture of the framework for near-
duplicate detection.
scenarios. Following, we present a novel framework
to detect near-duplicates (Section 3.1) and an ex-
tension of the similarity wide-join definition, which
greatly reduces such drawbacks (Section 3.2). Last
but not least, Section 3.3 presents the basic approach
to implement our proposed wide-join extension and
also devises an optimized version based on pivots to
achieve an efficient computation.
3.1 The Framework Architecture
The proposed framework is composed of two mod-
ules, organized according to Figure 2. The Fea-
ture Extractor module processes images such as a
content-based image retrieval system, representing
them as n-dimensional arrays. Formally, the Fea-
ture Extractor module receives an image repository
C =
{
img
1
,.. .,img
m
}
with m images, and extracts the
visual features v
i
= F(img
i
) of each image img
i
∈ C.
Each v
i
is a feature vector
h
f
1
,.. ., f
n
i
, where n is the
number of features extracted by the feature extractor
method F. The features depend on the kind of vi-
sual aspect considered, e.g., color, shape, texture, etc,
as discussed in Section 2.1. Its result is m Feature
Vectors stored into the S attribute in relation T such
that T[S] =
{
v
1
,.. .,v
m
}
, and the corresponding im-
ages are stored as another attribute in T.
The second module – Near Duplicate Detection –
is the core module of our framework. It can perform
either a Similarity Join-based or a Clustering-based
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
84

near-duplicate detection. Both compare the feature
vectors according to a distance function. The detec-
tion based on similarity join executes our specialized
similarity join operator (described in Section 3.2) on
T, employing two user-defined parameters that allows
tuning the comparison to follow the user’s perception
of how pairs of images can be considered as near-
duplicates. The Cluster-based detection processes T
executing one of the defined clustering techniques:
the Adaptive Cluster with k-means (ACMe - Section
2) or our Adaptive Cluster with k-medoids variation
(ACMd - Section 4). The framework returns the re-
sulting pairs of images that each algorithm detects as
near-duplicates, allowing comparing the considered
techniques. Thus, our proposal allows users either
removing, preserving or return the near-duplicate ac-
cording to the interest of users.
3.2 Self Similarity Wide-joins
The similarity joins operators, such as the range join
and the k-nearest neighbor join, present shortcomings
when employed to query databases. Both of them re-
turn result sets whose cardinality is often too high,
which leads to many more pairs of elements than
users really need or expect. Hence, that large result
set usually includes pairs truly similar, as well as pairs
holding a low or even questionable degree of similar-
ity. Therefore, to fulfill the near-duplicate task, the
result of a similarity join must be further processed in
order to exclude the pairs whose the similarity mea-
sure is doubtful.
Moreover, the k-nearest neighbor join is also trou-
blesome because it does not assure an equivalent sim-
ilarity among the k-th nearest pairs from distinct el-
ements. Thus, given two vectors v
i
= t
i
[S] and v
j
=
t
j
[S], the distances ξ
i
and ξ
j
from v
i
to its k-nearest
neighbor, let v
ik
, and from v
j
to its k-nearest neigh-
bor, let v
jk
, are completely uncorrelated. In this way,
for any given k ≥ 1, a pair
h
v
i
,v
ik
i
may be a near-
duplicate whereas the pair
v
j
,v
jk
may not. Hence,
looking at the range ξ variation in the k-neighbors be-
comes the main focus of our investigation.
Our proposal is that the resulting pairs of a sim-
ilarity range join must have the similarity between
their component elements evaluated and subsequently
ranked so that the top-ranked ones correspond to the
near-duplicate elements. Such kind of processing can
be efficiently achieved by extending the similarity
join operator called range wide-join (Section 2).
Wide-joins are intended to compute the similarity
join between two relations and retain only the global
most similar elements. The near-duplicate detection
requires combining a set with itself, but wide-joins do
not comply with such processing once the most sim-
ilar pairs will include combinations of each element
with itself, distorting the result.
For this purpose, we employ a tailored version of
the wide join operator, namely self range wide-join,
that atomically performs (i) the similarity evaluation
over the same set or relation and (ii) the retrieval of
the most similar elements in general. Those two op-
erations intrinsically coupled as a single operator en-
able retrieving the element pairs considered as near-
duplicates in a single-pass, avoiding further process-
ing of refinement phase.
Formally, let D be a data domain, d : D × D 7→
R
+
be a metric over D, T be a relation, S ⊆ T be an
attribute subject to d with values sampled from D, ξ
be a maximum similarity threshold and κ be an upper
bound integer value. The self similarity range wide-
join is given by Definition 1.
Definition 1 (The Self similarity range wide-join).
The self similarity range wide-join no
(S,ξ,κ)
T is a
similarity range join where both left and right input
relations T
1
and T
2
are the same relation T, and it re-
turns at most κ pairs
h
t
1
,t
2
i
|t
1
,t
2
∈ T such that t
1
6= t
2
,
d(t
1
[S
1
],t
2
[S
2
]) ≤ ξ and the returned pairs are the κ
closest to each other. The self range wide-join is ex-
pressed in relational algebra according to (1).
no
(S,ξ,κ)
T ≡
π
{
T
1
,T
2
}
σ
(ord≤κ)
π
{
T
1
,T
2
,F (d(t
1
[S
1
],t
2
[S
2
]))→ord
}
ρ
(S/S
1
)
(T/T
1
)
d(t
1
[S
1
],t
2
[S
2
])≤ξ
on ρ
(S/S
2
)
(T/T
2
)
(1)
The self similarity range wide-join is a unary op-
erator (it takes one relation) that internally performs a
range join, sorts the intermediate result by the dissim-
ilarity among the tuples and returns the top-κ pairs
t
i
,t
j
of most similar elements in T. In (1), F is
a database aggregate function that receives the dis-
tances between the attributes t
1
[S
1
] and t
2
[S
2
] and
projects the ordinal classification of those dissimilar-
ity values into an attribute ord that exists only during
the operator execution. Further, that transient attribute
is used to select the most similar pairs and discarded.
Following (1), the self similarity range join relies
on the maximum limiar ξ in order to filter the candi-
date pairs to compose the answer. This operation is
related to the building processing phase, where two
images a and b are possible near-duplicates iff the
dissimilarity between them is at most the threshold
ξ, that is, d(a, b) ≤ ξ.
The inner similarity join may be influenced by the
data distribution. Each attribute S
1
of the pairs
h
t
1
,t
2
i
Efficient Self-similarity Range Wide-joins Fostering Near-duplicate Image Detection in Emergency Scenarios
85

Algorithm 1: NLWJ(T,ξ, κ).
1 Q ← ∅;
2 for i ← 1 to |T| −1 do
3 for j ← i + 1 to |T| do
4 dist ← d(t
i
[S],t
j
[S]);
5 if dist ≤ ξ then
6 if |Q| ≤ κ then
7 Q ← Q ∪{
t
i
,t
j
,dist
};
8 else
9 Let q ∈ Q be the high-priority
element;
10 if dist < d(q[S
1
],q[S
2
]) then
11 Q ← Q −{q};
12 Q ← Q ∪{
t
i
,t
j
,dist
};
13 return Q;
can be combined with varying quantities of values in
S
2
. Thus, the inner join in (1) retrieves pairs in a large
range of distances, but only the smaller distances truly
correspond to near-duplicate elements. The greater
the distance among S
1
and S
2
, the smaller the confi-
dence that the pair is a near-duplicate.
Sorting the self-similarity of the pairs is related to
the improvement phase of a near-duplicate process.
As it is performed internally by the wide-join, no fur-
ther processing is required. In addition, that step also
solves a frequent issue existing in traditional similar-
ity joins: how to define ξ. Once the self range wide-
join sorts the pairs and filters just the closest, the ξ
parameter can be overestimated without adversely af-
fecting the quality of the final answer. Moreover, it
improves both the query answer quality and the per-
formance of the self similarity range wide-join oper-
ator, as it was confirmed by the experiments reported
in Section 4.
3.3 Algorithmic Issues
Self similarity range wide-joins can be implemented
more efficiently than the sequence expressed in (1),
following a strategy based on a nested-loop (Nested-
Loop Wide-Join - NLWJ), as depicted in Algorithm 1.
Usually, the traditional range wide-join performs n
2
distance computations, where n = |T|. However, our
self version of the algorithm (steps 2 and 3) requires
only half of that amount because, as the join condition
is a metric, it meets the symmetry property. There-
fore, a first improvement is that it is necessary to com-
pute the distances d(t
i
[S],t
j
[S]) and d(t
j
[S],t
i
[S]) only
once, resulting in n(n − 1)/2 distance calculations.
Following, the κ most similar pairs qualifying as
near-duplicates (steps 5-6) are added into a priority
𝑑 𝑝
2
, 𝑠
𝑞
+ 𝜉
𝜉
𝑠
𝑞
𝑑 𝑝
1
, 𝑠
𝑞
− 𝜉
𝑝
1
𝑝
2
Qualifying region
𝑑 𝑝
1
, 𝑠
𝑞
+ 𝜉
𝑑 𝑝
2
, 𝑠
𝑞
− 𝜉
𝑠
1
𝑠
2
Figure 3: Pivot-based strategy to prune the search space.
queue Q (step 7). The priority parameter is the sim-
ilarity distance: a greater distance corresponds to a
higher priority for removal. After κ pairs were ob-
tained, the current pair
t
i
,t
j
replaces the higher pri-
ority element (q - step 9) whenever it is more similar
than q, as tested in step 10. Thus, the second im-
provement is truncating the sorting operation, as F
in (1) can be incrementally performed by the prior-
ity queue, which avoids the cost of sorting the total
whole amount of pairs or overflowing memory with
too many elements. When the procedure finishes, the
priority queue Q already contains the near-duplicate
images.
Finally, we designed a third improvement to com-
pute self-similarity range wide-joins. The trick here is
based on the triangle inequality property of a metric
(Section 2), using pivot elements in order to prune the
in-list search space and further reduce the number of
distance computations.
For an arbitrary and small number p n of pivots
chosen among the available element in the database,
we first compute the distance between each element
t
i
[S] to each one of the p pivots. In such manner, each
element in the database is filtered by their distances
to each pivot. Notice that, until this step, only p ∗ n
distance computations were performed.
The next step performs the similarity join. Each
element s
q
is compared to each elements s
i
, and when
they are closer than the similarity threshold ξ, the pair
is part of the answer. To prune comparisons, it is first
verified if s
i
is within the qualifying area of s
q
regard-
ing to each pivot, assuring that for each pivot p
i
the
conditions defined in (2) and (3) simultaneously hold.
d(p
i
,s
i
) ≥ d(p
i
,s
q
) − ξ (2)
d(p
i
,s
i
) ≤ d(p
i
,s
q
) + ξ (3)
For instance, element s
2
in Fig. 3 satisfies conditions
(2) and (3) with respect to the pivot p
1
, i.e., s
2
is
within the hyper-ring delimited by the pivot p
1
. How-
ever, when analyzed in relation to the pivot p
2
, s
2
does not satisfy (3), thus it is guaranteed that s
2
is out-
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
86

side the intersection area among the two hyper-rings.
Therefore, the comparison of s
q
with s
2
is pruned.
Still considering Fig. 3, notice that the element s
1
holds conditions (2) and (3) with respect to both piv-
ots and should be compared to s
q
. In this case, al-
though s
1
is within the qualifying area defined by the
two pivots, it is not within the range area of s
q
, which
can be verified with just one distance computation.
For those elements within the qualifying area, the
number of additional distance computations is based
on the data distribution and cannot be predicted be-
forehand. However, the worst and highly improvable
situation occurs when the n elements in the database
lie within the qualifying area. In this case, it is neces-
sary to perform, for each element s
q
, n distance com-
putations, which leads to a total of np + n(n − 1)/2
calculations. Similar to the nested-loop case, due to
the symmetry property of the metric (Section 2), at
most a half of all the distance computations are re-
quired.
Nevertheless, it is very uncommon and easy to
avoid to have all the dataset in the qualifying area.
In Fig. 3, notice that making p = 3, thus putting a
third pivot next to the element s
2
, would substantially
reduce the qualifying area, restricting it to almost the
coverage region of s
q
.
The opposite situation occurs when no element
qualifies. In that case, there is no distance computa-
tion. In average, the number of distance computations
can be estimated as the arithmetic mean among the
best and worst cases, which leads the required num-
ber of distance calculations to be significantly less
than n(n − 1 + 2p)/4 distance computations, already
including the n ∗ p pivot-elements performed calcula-
tions.
Similarity wide-join based on pivots (WJ-P) can
be implemented in external memory following the
block-nested loop approach introduced in Algo-
rithm 2. Similar to Algorithm 1, the WJ-P implemen-
tation also relies on a priority queue Q (step 1) in or-
der to achieve the sorting step of similarity wide-joins.
In step 2, p pivots are chosen at random. Heuristics
on how the pivots should be chosen are out of scope in
this paper. Steps 3-6 iterate over the blocks where the
tuples are stored. The nested-loop of steps 8 and 12 it-
erates over the elements inside the blocks. In order to
avoid combining a element with itself ensuring a self
similarity join, the condition in step 10 increments the
start position of the inner loop.
For each pivot picked in step 2, Equations (2) and
(3) must hold (step 13). Notice that the distance be-
tween the elements and the pivots can be precomputed
and stored when reading the elements in the loops of
steps 8-12. Step 13 means that the analyzed tuple (t
y
)
Algorithm 2: WJ-P(T,ξ, κ).
1 Q ← ∅;
2 Choose p pivots at random in T;
3 for i ← 1 to number of blocks of T do
4 for j ← i +1 to number of blocks of T do
5 load block i to memory;
6 load block j to memory;
7 x ← 1;
8 while x < number of elements in block i
do
9 y ← x;
10 if i = j then
11 y ← y +1;
12 while y < number of elements in
block j do
13 if expressions (2) and (3) hold
∀ pivot p then
14 dist ← d(t
x
[S],t
y
[S]);
15 if dist ≤ ξ then
16 if |Q| ≤ κ then
17 Q ← Q ∪
{
hh
t
x
,t
y
i
,dist
i
};
18 else
19 Let q ∈ Q be the
high-priority
element;
20 if dist <
d(q[S
1
],q[S
2
])
then
21 Q ← Q −{q};
22 Q ← Q ∪
{
hh
t
x
,t
y
i
,dist
i
};
23 return Q;
is within the qualifying hyper-ring defined by the piv-
ots. The pertinence of t
y
to the region convered by t
x
is
then checked in step 14-15, where an additional dis-
tance computation was performed. The steps 15-22
are similar to those presented in Algorithm 1, where
κ elements are selected so the algorithm checks for
possible replacements of the most similar pairs.
4 EXPERIMENTS
This section reports on experiments using our frame-
work for near-duplicate image detection. The goal
is to evaluate the proposed self range wide-join tech-
Efficient Self-similarity Range Wide-joins Fostering Near-duplicate Image Detection in Emergency Scenarios
87
0
0.01
0.02
0.03
0.04
0.05
WJ-P NLWJ ACMe ACMd
2
4
6
8
10
12
14
Time (s)
(a) Runtime
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Precision
Recall
WJ-P
ACMe
ACMd
(b) Precision × Recall
Figure 4: Performance and quality analysis: the Fire dataset.
nique in terms of both the computational performance
and the answer quality, targeting prioritizing those as-
pects as required for an emergency monitoring sys-
tem.
4.1 Experiment Setup
We describe the results performed on a real dataset
- Fire - composed of 272 images of fire incidents.
Those images were obtained from an emergency situ-
ation simulation, held in an Industrial Complex. The
dataset was previously labeled by domain experts and
25 distinct incident scenes were recognized. The im-
ages were submitted to the Color Layout (Kasutani
and Yamada, 2001) extractor, which generated 16 fea-
tures. The L
2
(Euclidean) metric was employed to
evaluate the vector distances.
We compared our improved pivot-based self range
wide-join (WJ-P, Algorithm 2) using 5 pivots with
three other techniques. The first is the similarity wide-
join with a nested-loop approach (NLWJ), that is the
self version of the baseline found in the literature
(Carvalho et al., 2015). The second method is the
Adaptive Cluster with k-means (ACMe - Section 2)
(Li et al., 2015). Also, once k-means is sensitive to
outliers and often computes “means” that do not cor-
respond to real dataset images, we generated a third
method that is an ACMe variant replacing k-means
with the k-medoids algorithm, calling it ACMd, in or-
der to better analyze the answer quality. When neces-
sary, the parameter ξ was set to retrieve about 1% of
the total number of possible pairs.
The experiments were executed in a computer
with an Intel
R
Core
TM
i7-4770 processor, running at
3.4 GHz, with 16 GB of RAM under Ubuntu 14.04.
All evaluated methods were implemented in C++.
Each technique was evaluated with respect to both the
total running time (Section 4.2) and the answer qual-
ity (Section 4.3), as follows.
4.2 Performance Experiment
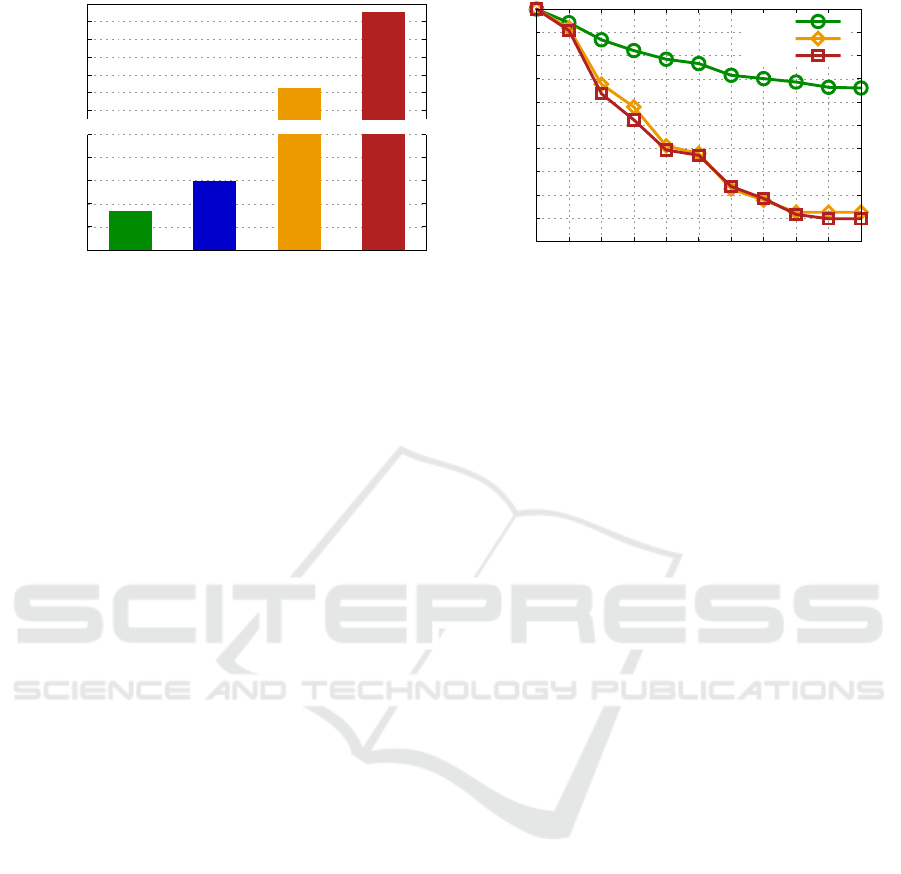
Fig. 4(a) presents the total running time of the four
approaches evaluated. The reported time corresponds
just to the execution of the Near Duplicate Detec-
tion Module, as feature extraction was performed only
once to provide data to the four methods. In this ex-
periment, WJ-P was 44.45% faster than NLWJ. Also,
both techniques based on self wide-join were 2 orders
of magnitude faster than ACMe and 3 orders of mag-
nitude faster than ACMd, whereas returning a high
quality result set.
Such behavior occurs due to the fact that ACMe
and ACMd cluster the dataset and recursively redis-
tribute the elements following a hierarchical approach
for the improvement phase, until the coherence of
each cluster does not exceed a maximum value, com-
puted during the process. In addition, to achieve
the result, an improvement phase is usually required,
which contributes to increase the computational cost
of those approaches. Distinctly, the WJ-P performs
a single pass computation that embodies the build-
ing and the improvement phases into an atomic, op-
timized operation.
Both ACMe and ACMd require a parameter k to
execute their core clustering algorithms, the k-means
and k-medoids, respectively. Nevertheless, they re-
turned a number of clusters greater than k, because
the clusters obtained in the building phase are sub-
divided according to their coherence values. Those
techniques achieved the better results when k is set to
values between 20 and 30. Unlike, the WJ-P method
was able to achieve the result without the need of sev-
eral executions in order to find out the better parame-
ter adjustments.
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
88

Figure 5: Near-duplicates obtained by the three evaluated methods for the query center shown.
4.3 Answer Quality Evaluation
To analyze the answer quality, we evaluated how ac-
curate is the result returned by the proposed frame-
work. In order to enable fair comparisons among the
distinct algorithms, we computed Precision and Re-
call (P × R) curves. Evaluating P × R is a common
technique used for information retrieval evaluation.
Precision is defined as the rate of the number of rele-
vant elements retrieved by the number of retrieved el-
ements. Recall is given as the rate between the num-
ber of relevant elements retrieved by the number of
relevant elements in the database. In P × R plots, the
closer a curve to the top, the better the corresponding
method.
Fig. 4(b) shows the P × R curves achieved by the
three approaches. In this experiment, we did not con-
sider the NLWJ approach because its result is the
same also produced by the WJ-P and therefore both
curves are identical, only varying their runtime. Our
self range wide-join based on pivots achieved the
larger precision for every recall amount. It was, in av-
erage, 35.14% more precise than ACMe and 36.78%
than ACMd. After retrieving all relevant images in the
dataset (recall of 100%), WJ-P consistently obtained
66.00% of precision in the result, whereas the com-
petitor techniques achieved a maximum precision of
12.50%.
In order to show the obtained gain of preci-
sion, Fig. 5 samples the images considered as near-
duplicates by the three techniques. Again, NLWJ is
omitted once it computes the same result of the WJ-P,
but the former is slower than the latter. For an im-
age randomly chosen as query center (Fig. 5(a) - the
10th image with label 13), Fig. 5(b) shows the near-
duplicates retrieved by WJ-P. As it can be seen, they
have the same label and are in fact related to the query,
recognizing even images with zoom and rotations.
Figs. 5(c) and 5(d) show the clusters obtained by
the ACMe and ACMd, respectively. Both are the clus-
ters where the query image (Fig. 5(a)) was allocated
As it can be noted, both methods retrieved false pos-
itives, where the existence of false positives con-
tributed to decrease the precision of ACMe and
ACMd. Although ACMe theoretically leads to worse
clusters than ACMd, as the means are not real im-
ages whereas the medoids are, the precision differ-
ence among both was in average only 1.63% (see
Fig. 4(b)).
The superior quality of the answer of WJ-P when
compared to the cluster-based methods shown in
Fig. 4(b) is explained by the fact that the clusters
are generated based on centroids or medoids seeds,
and the remaining elements are allocated according to
their distances to the seeds. The cluster elements are
analyzed only in relation to the seeds, ignoring the re-
lationship among themselves. This fact leads to some
images that are distinct among them but considered
similar to their seed, as represented in Figs. 5(c) and
5(d). In its turn, the self wide-join method establishes
a “pairing relationship” among the elements, avoiding
such drawback and increasing the answer quality, as
also observed in Fig. 5(b).
Notice that Fig. 5 shows the images spoted as
near-duplicates by each of the three techniques. Ac-
cording to the user interest, those near-duplicates can
be either removed from the final answer of the frame-
work so as to provide a more informative result set, or
returned, allowing to analyze similar occurrences.
4.4 Scalability Analysis
The Fire dataset contains real images from an emer-
gence scenario from the Rescuer Project, but it con-
tains few images. So, we evaluated the scalability of
our technique employing the Aloi dataset
2
. It con-
tains images of 1,000 objects rotated from 0
o
to 360
o
in steps of 5
o
(72 images per object, which we assume
to be near-duplicates) giving a total of 72,000 distinct
images. The Color Moment extractor (Stricker and
2
<http://aloi.science.uva.nl> Access: Sept. 11, 2015.
Efficient Self-similarity Range Wide-joins Fostering Near-duplicate Image Detection in Emergency Scenarios
89

0
500
1000
1500
2000
2500
3000
3500
1K 10K 20K 30K 40K 50K
50000
100000
150000
200000
250000
300000
350000
400000
Time (s)
Cardinality
0.426
1.295
WJ-P
NLWJ
ACMe
ACMd
(a) Runtime
0
2000
4000
6000
8000
10000
12000
14000
1K 10K 20K 30K 40K 50K
# Distance computations (x 10
5
)
Cardinality
1.560
4.995
WJ-P
NLWJ
(b) Distance computations
Figure 6: Scalability analysis: Aloi dataset.
Orengo, 1995) generates 144 features, which were
compared using the L
2
metric.
For the scalability evaluation, we shuffled the
Aloi images and varied the cardinality of the sub-
mitted data in several executions of our framework.
Fig. 6(a) depicts the total runtime of each algorithm.
The pivot-based self range wide-join (WJ-P) was
in average 49.58% faster than NLWJ. Also, it was
96.25% faster than ACMe and 99.59% than ACMd,
that is, it was correspondingly 2 and 3 orders of mag-
nitude faster. For example, for a cardinality of 10,000
objects, WJ-P execution took 1.16 minutes and NLWJ
took 2.20 minutes, while ACMe took 1.18 hours and
AMCd took 6.61 hours.
Finally, Figure 6(b) compares both the similarity
wide-join techniques (NLWJ and WJ-P) with respect
to the number of distance computations performed to
achieve the result. The pivot-based self range wide-
join (WJ-P) executed at least 44.69% less distance
calculations than NLWJ for a cardinality of 40K, but
the greatest reduction of distance computations was
observed for a cardinality of 1K, where WJ-P per-
formed 68.75% less calculations. Nevertheless, it is
important to highlight that both techniques obtained
the same final result, but WJ-P was able to save com-
putational resources in its processing.
Fig. 6 shows that as the cardinality increases, the
cluster-based methods need to process more elements
in the building phase. However, the coherence value
is not used in this phase, so the next one (refinement
phase) requires more iterations to subdivide the clus-
ters and ensure that coherence is maintained. Dis-
tinctly, the wide-join perform a one-pass strategy. The
increased cardinality turns the process more costlier,
but in a less pronounced way as compared to the
cluster-based ones. Moreover, to avoid performing
distance calculations among every pair as occurs in
NLWJ, the WJ-P prunes the number of comparisons,
which also reduces the running time.
4.5 Experiment Highlights
In a general way, there are three main reasons explain-
ing why the introduced self similarity range wide-join
technique overcomes its correlates:
• Single-pass computation: usually, the near-
duplicate detection is divided into two phases.
The wide-join operator surpass the requirement
for a refinement phase. As aforestated, such one-
pass execution allowed to reduce the cost of the
entire process in 2 orders of magnitude.
• Efficient prune technique: a prune technique
based on pivots enables the proposed WJ-P algo-
rithm to perform a reduced amount of element-
to-element comparisons. The pivots delimit small
regions of the space to be analyzed, allowing to
discard several elements that surely will not com-
pose the answer. Also, such strategy reduced the
number of distance computations in about 44% in
relation to the traditional nested-loop approach.
• Similarity relationship between elements: unlike
the cluster methods, that computes the proximity
of an element to a group, the self wide-join oper-
ator establishes a similarity relationship between
each distinct pair of elements. It avoids the diver-
sity found in two elements lying in opposite sides
of a cluster, which increased the answer quality in
about 35% in relation to the existing approaches.
5 CONCLUSIONS
In this paper we presented a framework model to
detect near-duplicates using the similarity wide-join
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
90

database operator as its core. We introduced the self
range wide-join operator: an improved version of the
wide-join that enables computing similarity by com-
bining a relation to itself. We optimized the wide-
join algorithm to scan the search space relying on
pivots and using metric space properties to prune ele-
ments, which enabled achieving a large performance
gain when compared to the existing solutions.
The experiments were executed using two real
datasets. They showed that our proposed wide-join-
based framework is able not only to improve the near-
duplicate detection performance by at least 2 and up
to 3 orders of magnitude, but also to improve the qual-
ity of the results when compared to the previous tech-
niques.
The introduced technique is general enough to be
applied over any dataset in a metric space, but we fo-
cused its application for an emergency-based appli-
cation. When handling an emergency scenario, it is
common that the eyewitnesses capture a large amount
of photos and videos about the incident. Existing
monitoring systems can benefit from those crowd-
sourcing information, aiming at improving decision
making support. However, as the information in-
creases, its elements tend to become too similar, so
it is crucial to provide efficient techniques to properly
handle near-duplicates.
As future work, we are exploring data distribution
statistics and selectivity estimations for join operators
in order to provide accurate definitions of the param-
eters required by the self-similarity range wide-join.
We also intend to combine the images with their as-
sociated meta-data in order to further improve both
the precision and the performance of near-duplicate
detection.
ACKNOWLEDGEMENTS
The authors are grateful to FAPESP, CNPQ, CAPES
and Rescuer (EU FP7-614154 / CNPQ 490084/2013-
3) for their financial support.
REFERENCES
Bangay, S. and Lv, O. (2012). Evaluating locality sensitive
hashing for matching partial image patches in a social
media setting. Journal of Multimedia, 1(9):14–24.
Carvalho, L. O., Santos, L. F. D., Oliveira, W. D., Traina, A.
J. M., and Traina Jr., C. (2015). Similarity joins and
beyond: an extended set of operators with order. In
Proc. 8th Int. Conf. on Similarity Search and Applica-
tions, pages 29–41.
Chino, D. Y. T., Avalhais, L. P. S., Rodrigues Jr., J. F., and
Traina, A. J. M. (2015). Bowfire: detection of fire
in still images by integrating pixel color and texture
analysis. In Proc. 28th Conf. on Graphics, Patterns
and Images, pages 1–8.
Chum, O., Philbin, J., and Zisserman, A. (2008). Near du-
plicate image detection: min-hash and tf-idf weight-
ing. In British Machine Vision Conference, pages 1–
10.
Kasutani, E. and Yamada, A. (2001). The mpeg-7 color
layout descriptor: a compact image feature descrip-
tion for high-speed image/video segment retrieval. In
Proc. 8th Int. Conf. on Image Processing, pages 674–
677.
Li, J., Qian, X., Li, Q., Zhao, Y., Wang, L., and Tang, Y. Y.
(2015). Mining near-duplicate image groups. Multi-
media Tools and Applications, 74(2):655–669.
Searc
´
oid, M.
´
O. (2007). Metric spaces. Springer.
Silva, Y. N., Aref, W. G., Larson, P.-A., Pearson, S., and
Ali, M. H. (2013). Similarity queries: their concep-
tual evaluation, transformations, and processing. The
VLDB Journal, 22(3):395–420.
Sonka, M., Hlavac, V., and Boyle, R. (2014). Image
Processing, Analysis, and Machine Vision. Cengage
Learning.
Stricker, M. and Orengo, M. (1995). Similarity of color
images. In Proc. 3rd Conf. on Storage and Retrieval
for Image and Video Databases, pages 381–392.
Wang, X.-J., Zhang, L., and Ma, W.-Y. (2012). Duplicate
search based image annotation using web-scale data.
Proc. of the IEEE, 100(9):2705–2721.
Xiao, C., Wang, W., Lin, X., Yu, J. X., and Wang, G. (2011).
Efficient similarity joins for near-duplicate detection.
ACM Transactions on Database Systems, 36(3):15:1–
15:41.
Yao, J., Yang, B., and Zhu, Q. (2015). Near-duplicate image
retrieval based on contextual descriptor. IEEE Signal
Processing Letters, 22(9):1404–1408.
Efficient Self-similarity Range Wide-joins Fostering Near-duplicate Image Detection in Emergency Scenarios
91
