Validation of Loop Parallelization and Loop Vectorization

Transformations

Sudakshina Dutta, Dipankar Sarkar, Arvind Rawat and Kulwant Singh

Indian Institute of Technology Kharagpur, Kharagpur, India

Keywords:

Loop Parallelization, Loop Vectorization, Dependence Graph, Conﬂict Access, Validation.

Abstract:

Loop parallelization and loop vectorization of array-intensive programs are two common transformations ap-

plied by parallelizing compilers to convert a sequential program into a parallel program. Validation of such

transformations carried out by untrusted compilers are extremely useful. This paper proposes a novel algo-

rithm for construction of the dependence graph of the generated parallel programs. The transformations are

then validated by checking equivalence of the dependence graphs of the original sequential program and the

parallel program using a standard and fairly general algorithm reported elsewhere in the literature. The above

equivalence checker still works even when the above parallelizing transformations are preceded by various

enabling transformations except for loop collapsing which changes the dimensions of the arrays. To address

the issue, the present work expands the scope of the checker to handle this special case by informing it of

the correspondence between the index spaces of the corresponding arrays in the sequential and the parallel

programs. The augmented algorithm is able to validate a large class of static afﬁne programs. The proposed

methods are implemented and tested against a set of available benchmark programs which are parallelized

by the polyhedral auto-parallelizer LooPo and the auto-vectorizer Scout. During experiments, a bug of the

compiler LooPo on loop parallelization has been detected.

1 INTRODUCTION

Parallelization and vectorization of loops in a sequen-

tial program are two of the most important transfor-

mations performed by parallelizing compilers. There

is a growing need to verify the correctness of the par-

allelizing transformations as they become more rel-

evant in the prevalent high performance computing

systems. In this paper, we propose a novel method to

generate dependence graphs (DGs) that can be used to

verify the equivalence of the original sequential pro-

gram and the parallelized program. A DG captures

data dependences among array elements in the pro-

gram. Equivalence checking can be performed on the

dependence graph abstractions of the sequential and

the parallel programs.

A DG oriented equivalence checking mechanism

for sequential programs reported in (Verdoolaege

et al., 2012) is sophisticated enough to handle many

loop transformations with recurrences. The method,

however, cannot be applied for validating paralleliz-

ing transformations because their DG construction

mechanism does not apply directly to the transformed

parallel programs. In the present work, we propose

a method of constructing DGs of loop parallelized or

vectorized programs. Like the method described in

(Verdoolaege et al., 2012), our method incorporates

dependence analysis so that the pre-processing steps

to convert an input sequential program and its loop-

parallelized version to the dynamic single assignment

(DSA) forms can be avoided; this is achieved using

an independently devised data-ﬂow analysis method

similar to that proposed in (Collard and Griebl, 1997).

In the example program of Fig. 1(a), loop skewing fol-

lowed by loop interchange are applied to get the par-

allel program of Fig. 1(b) and the proposed method is

able to construct DGs of this program where wait −

signal synchronization statements are not present in

the body of the parallel loop.

In our experimental results section, we have gen-

erated the parallel programs using the parallelizing

compiler LooPo (Griebl and Lengauer, 1996) on the

sequential programs available with the compiler and

PolyBench (version 3.2) (Pouchet, 2012) benchmark

programs. In the process of translation validation,

we have detected a bug of the parallelizing compiler

LooPo.

Vectorization is a compiler transformation that

Dutta, S., Sarkar, D., Rawat, A. and Singh, K.

Validation of Loop Parallelization and Loop Vectorization Transformations.

In Proceedings of the 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering (ENASE 2016), pages 195-202

ISBN: 978-989-758-189-2

195

(a) (b)

output D[100]

do i = 1, n

do j = 1, n

: A[i][ j] = 5

end do

do i = 2, n − 1

do j = 2, n −1

: D[i][ j] = A[i][ j]

: A[i][ j] = (A[i −1][ j]

+A[i][ j − 1] +A[i + 1][ j]

+A[i][ j + 1])

end do

output D[100]

do i = 1, n

do j = 1, n

: A[i][ j] = 5

end do

min(n − 1, j − 2)

: A[i][ j − i] = (A[i − 1][j −i]

parallel do i = max(2, j − n +1),

do j = 4, n +n − 2

+A[i][ j − 1 −i] + A[i + 1][ j −i]

+A[i][ j + 1 −i])

: D[i][ j − i] = A[i][ j − i]

end parallel do

end do

Figure 1: (a) Source code, (b) Loop parallelized version

of the source code where loop skewing followed by loop

interchange transformations are applied prior to loop paral-

lelization.

transforms loops to vector operations. We propose a

method to construct the DG for a vectorized program.

In this method, the vectorized code (e.g., Fig. 2(b)) is

ﬁrst converted to its loop parallelized version (e.g.,

Fig. 2(c)) and then its DG is constructed to estab-

lish equivalence with the sequential program (e.g.,

Fig. 2(a)). In the experimental result section we gen-

(a)

(b)

T’

(c)

do i = 1, N

: A[i] = B[i]

: C[i] = A[i] + B[i]

: E[i] = C[i + 1]

end do

: A[1:N] = B[1:N]

: E[1 : N] = C[2 : N +1]

: C[1:N] = A[1:N] + B[1:N]

parallel do i = 1, N

1,1

: T mp1[i] = B[i]

end parallel do

parallel do i = 1, N

1,2

: A[i] = T mp1[i]

end parallel do

parallel do i = 1, N

2,1

: T mp2[i] = C[i +1]

end parallel do

parallel do i = 1, N

2,2

: E[i] = T mp2[i]

end parallel do

parallel do i = 1, N

3,1

: T mp3[i] = A[i] + B[i]

end parallel do

parallel do i = 1, N

3,2

: C[i] = T mp3[i]

end parallel do

Figure 2: (a) Sequential code snippet (S), (b) transformed

vectorized code (T), (c) corresponding parallelized code

erated vectorized programs using a conﬁgurable auto-

vectorizer Scout(Krzikalla et al., 2011) which applies

various enabling transformations such as, loop distri-

bution, loop unrolling, loop collapsing, etc., before

applying vectorization. Among the enabling transfor-

mations, loop collapsing cannot be handled by the ex-

isting equivalence checking method. Consider the ex-

ample of Fig. 3. The dimensions of the output arrays

of the source program S is 2 and the same for the loop

parallelized version of the vectorized program T

is 1.

Here the method of (Verdoolaege et al., 2012) used

to establish equivalence fails. We resolve this with a

(a)

(b)

(c)

T’

do i = 1, 5

do j = 1, 5

: A[i][ j] = B[i][ j]

+C[i j]

end do

+C[i][ j]

: A[1 : 25] = B[1 : 25]

+C[1 : 25]

: A[i j] = B[i j]

parallel do i j = 1, 25

end parallel do

Figure 3: (a) Sequential code snippet (S), (b) corresponding

vectorized code after aplication of loop collapsing enabling

transformation (T ), (c) transformed loop parallelized code

novel solution in section 4.1.7. The contributions of

the paper are summarized as follows.

• DG construction methods for loop parallelized

programs are proposed.

• DG construction methods for vectorized programs

are proposed. In the ﬁrst step, the vectorized pro-

gram is transformed to loop parallelized program;

• The scope of the existing equivalence checking

method has been broadened for validating loop

collapsing followed by loop vectorization trans-

formations.

• All of the above are experimentally supported in

the current paper. During the experimental work,

a bug of the parallelizing compiler LooPo has

been detected.

The paper is organized as follows. Section 2 focuses

on the related work and section 3 describes the class

of programs that can be analyzed using our method.

Section 4 describes the proposed method using for-

mal model as well as illustrative examples. Section 5

presents the experimental results and we conclude in

section 6.

2 RELATED WORK AND

MOTIVATION

Three kinds of parallelisms namely, instruction-level,

thread-level and process-level parallelisms are gener-

ally applied on sequential scalar-handling programs.

The methods of (Karfa et al., 2008), (Kundu et al.,

2010) can be applied for instruction-level paralleliz-

ing transormation and that of (Bandyopadhyay et al.,

2012) for validating thread-level parallelization tech-

niques. None of the above methods, however, applies

to validation of array-intensive programs.

Loop parallelization and loop vectorization are

two most commonly used parallelizing transforma-

tions applied primarily on array-intensive sequen-

tial programs as such programs handle more data-

intensive computations than those carried out by

ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering

196

scalar-handling programs. In loop parallelization

transformations, which fall under thread-level paral-

lelization techniques, the iterations of a loop are parti-

tioned as threads which concurrently execute on a set

of processors to achieve the data computation of the

loop. To the best of our knowledge, the reported liter-

ature has not addressed the problem of validating par-

allelization or vectorization for array-handling pro-

grams. However, some methods for checking equiv-

alence between two sequential array-handling pro-

grams are reported in (Shashidhar et al., 2005), (Ver-

doolaege et al., 2012); for all of them, the equivalence

is checked using DG based abstractions of the pro-

grams.

The authors of (Krinke, 1998) describe threaded

program dependence graphs (tPDGs) for represent-

ing control and data dependences for concurrent pro-

grams. The available literature (Collard and Griebl,

1997) provides a method for dataﬂow analysis of

array-handling parallel programs. The current work

uses a method similar to the method of dataﬂow anal-

ysis for array data structures of data-parallel programs

to construct the DGs for loop parallelized programs.

More precisely, the method of computing maxima i.e.,

ﬁnding the exact source of values for each uses of the

program is independently devised (in the method of

costruction of DG for a given CAG in section 4.1.5)

and the proposed method is used to construct DGs for

parallel programs.

3 CLASS OF INPUT PROGRAMS

The algorithm to generate a dependence graph han-

dles programs with the following properties:

1. Subscripts in arrays and expressions in the bounds

of f or-loops are all piecewise afﬁne in the iterator

variables of the enclosing f or-loop.

2. There are no pointer references in the program.

3. The control ﬂow of the program does not depend

on input data i.e., the program has static control

ﬂow. Alternatively, control dependencies have

been converted to data dependencies (Allen et al.,

1983).

It may be noted that none of the above properties are

too restrictive but are common in the literature.

4 PROPOSED APPROACH

In general, two programs are said to be equivalent to

each other if they generate the same outputs given the

same inputs.

To understand the method of construction of DGs

for loop parallelized and vectorized programs, we will

begin by looking into a brief overview of the vocabu-

lary used in the remainder of the section followed by

a detailed description of the proposed method of con-

struction of DGs of loop parallelized and vectorized

programs and enhancement of the equivalence check-

ing method.

4.1 Deﬁnitions and Methods

4.1.1 Deﬁnition: Access and Access Instances

An access refers to read and write accesses of the

statements present in the program. It depicts the

type (i.e., read or write) of the access and the set

of memory locations it refers to in the program. If

the access α is a read access, then the set of write

accesses which write on some or all of the memory

locations as α are kept in a ﬁeld called S

. This ﬁeld

is later used for dataﬂow analysis. The accesses are

instantiated by the surrounding loops in the program.

4.1.2 Deﬁnition: Conﬂict Access and Conﬂict

Access Instance

Two accesses α

occurring in statement s

and α

oc-

curring in statement s

are conﬂict accesses if the fol-

lowing three conditions hold simultaneously: (1) both

accesses refer to the same array, (2) type of α

or α

or both are write accesses, and (3) they refer to all or

some of the same memory locations. The conﬂict ac-

cess instances corresponding to α

and α

are repre-

sented as (α

(i), α

)), where both α

(i) and α

)

of i −th and i

−th iterations of the loops, respectively

refer to the same array element(s).

4.1.3 Deﬁnition: Conﬂict Access Graph (CAG)

A conﬂict access graph or CAG of a program P is a

directed graph C

= (A, E

) where A is the set of ver-

tices and E

is the set of directed edges. The set A

comprises the accesses in P. The edges in E

asso-

ciate the conﬂict accesses; their directions capture the

dependence between them. In general, for a conﬂict

access pair (α

, α

), for some of their instances, the

dependence may be from α

to α

and for the remain-

ing instances, the dependence may be from α

to α

;

hence an instance-wise analysis is needed.

Two conﬂict accesses α

and α

belonging to the

vertex set A are connected by an undirected edge if

the order of execution is yet to be determined and

connected by a directed edge hα

(

i), α

)i (hα

(ii) if α

(i) (α

)) executes after α

) (α

(i)).

Validation of Loop Parallelization and Loop Vectorization Transformations

197

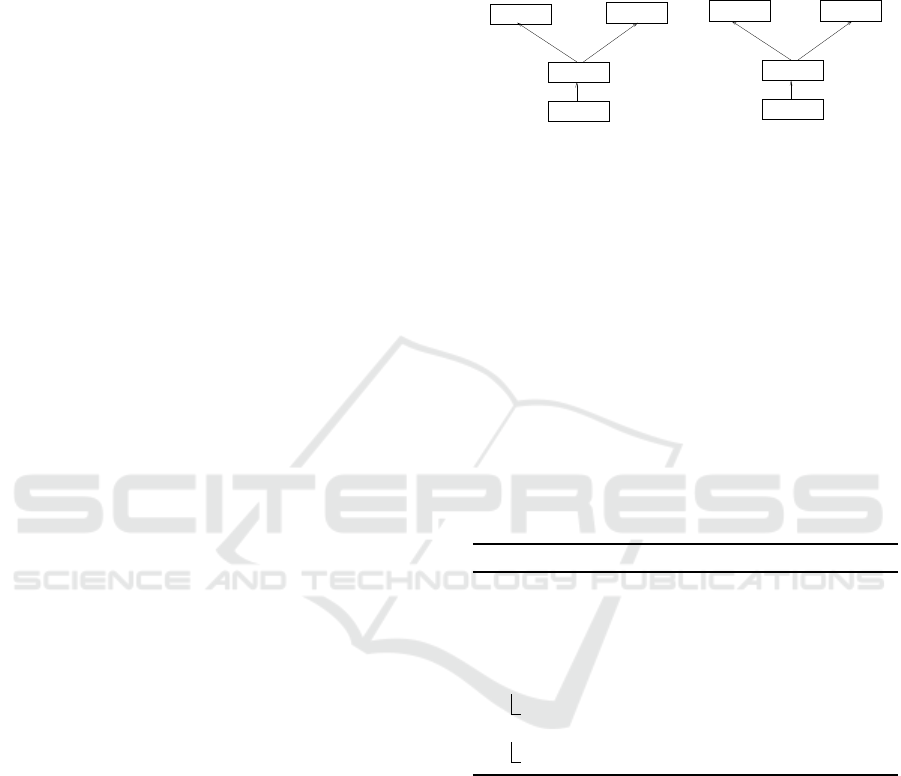
Equivalently, an edge hα

, α

i (hα

, α

i) is drawn

and a mapping M

hα

,α

hα

,α

), deﬁning the ex-

act access instance-wise dependence of α

on α

(α

on α

) is provided. E

is the set of all such conﬂict

edges in C

. A conﬂict edge can be a RAW (read after

write), WAR (write after read) or WAW (write after

write) edge depending on the type of α

and α

Example 1. [Conﬂict Access] In statement s

Fig. 1(a), let the two read accesses “A[i - 1][j]” and

“A[i][j - 1]” be denoted as α

2,1

, α

2,2

, respectively

(where the ﬁrst sufﬁx refers to the statement num-

ber and the second sufﬁx refers to the two read ac-

cesses from left to right); the write access “A[i][j]” be

denoted as α

2,l

where the second sufﬁx l stands for

the left hand side (lhs) of the assignment operation

’=’ in the statement. The other accesses are similarly

interpreted in Fig. 1(a). For example in Fig. 1(a),

the access instances α

2,l

(2, 2), α

2,1

(3, 2) conﬂict as

they access the same memory location A[2][2]. For all

the conﬂict access instances (α

2,l

(i − 1, j), α

2,1

(i, j)),

3 ≤ i ≤ n−1, 2 ≤ j ≤ n−1, of the members of the pair

(α

2,l

, α

2,1

), since α

2,1

(i, j)  α

2,l

(i−1, j), we say that

there is a RAW dependence of α

2,1

on α

2,l

which is

depicted by the edge hα

2,1

(i, j), α

2,l

(i−1, j)i, 3 ≤ i ≤

(n − 1), 2 ≤ j ≤ (n − 1). Similarly the dependences

among the other conﬂict accesses of Fig. 1(b) are de-

termined.

4.1.4 Deﬁnition: Dependence Graph (DG)

A dependence graph is a connected labeled directed

graph G = hV, E, I, V

i with vertices V and directed

edges E, each v ∈ V involves a single arithmetic op-

eration f and each e ∈ E captures the dependences

from a vertex to another vertex (or more precisely,

their operations). There is a set of vertices V

⊂ V

corresponding to an output arrays (or output opera-

tions) and a set I ⊂ V of vertices corresponding to

input arrays (or input operations).

A vertex v in V is represented by a 3-tuple

hl, f , Di, where f is the operation associated with v,

l is the line number of the program where f occurs,

and D is a set of integers depicting the iteration do-

main of l.

An edge e is represented by a 3-tuple

hs(e), t(e), M

i, where s(e)(t(e)) is the source

(target) vertex of e; the third member M

is a map-

ping from some subset of elements of s(e) to that of

t(e). It is to be noted that the DG only represents

RAW dependences of operations.

Example 2. [DG of Programs in Fig. 3(a),

Fig. 3(b)] Fig. 4(a) and Fig. 4(b) show the DGs

corresponding to the programs in Fig. 3(a) and

Fig. 3(c), respectively. In Fig. 4(a), v

represents the

output vertex and v

, v

the input vertices. The vertex

represents the addition operation performed in the

statement s

and the domain D

of v

is [1 : 5][1 : 5].

The edge hv

, v

i represents the RAW dependence of

the output array A on the statement s

In, B

[1, 5][1, 5]

Out : A

, +

, C

[1, 5][1, 5]

In, B

Out : A

, +

, C

[1, 25]

[1, 25][1, 25]

(i, j) → v

(i, j)|1 ≤ i ≤ 5∧ 1 ≤ j ≤ 5}

(i, j) → v

(i, j)|1 ≤ i ≤ 5∧ 1 ≤ j ≤ 5}

(i j) → v

(i j)|1 ≤ i j ≤ 25}

(i j) → v

(i, j)|1 ≤ i j ≤ 25}

(i j) → v

(i j)|1 ≤ i j ≤ 25}

(i, j) → v

(i, j)|1 ≤ i ≤ 5∧ 1 ≤ j ≤ 5}

Figure 4: (a) DG of the sequential program of Fig. 3(a), (b)

DG of the vectorized program of Fig. 3(c).

4.1.5 Methods: DG Construction for Loop

Parallelized Programs

The present section describes the DG construction

method for loop parallelized programs.

High Level Method to Construct DG for a Given

Parallel Program

The DG construction procedure for a parallel

program P is outlined in Algorithm 1. It

ﬁrst obtains the CAG for P using the procedure

ConstructCon f lictAccessGraph. In the next step,

it is processed to obtain the DG by a call to

ConstructDGFromCAG.

Algorithm 1: ConstructDGParallelProgram (P).

Input: The parallel program P

Output: The dependence graph for the program P

1 Let S be the set of statements of P; Let Z be the set of

output array of P;

2 hC

, f lagi ← ConstructCon f lictAccessGraph (S);

3 if f lag == ”undirectedEdge” then

4 report (”non-determinate program”) and return;

5 else

6 ConstructDG (Z, S, C

);

Method to Construct CAG for a Given Parallel

Program

The method for construction of the CAG takes the set

of statements of the sequential or parallel program as

input and constructs the CAG containing all the ac-

cesses and the directed edges connecting the conﬂict

accesses. For sequential programs and for the parallel

programs, the direction of a conﬂict edge between two

conﬂict accesses is determined by observing their ex-

ecution order. Method to Construct DG for a Given

CAG

For a sequential program, the order of every pair of

conﬂict access instances can be determined and it is

represented by directed conﬂict edges. If the con-

ﬂict access instances are present in different parallel

ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering

198

threads, then the order can only be determined in pres-

ence of wait − signal synchronization statements. In

the present cotext, wait −signal statements are absent

in the parallel program; hence, the order of execution

of presence of conﬂict accesses in different threads

(if any) cannot be determined and it is represented by

undirected conﬂict edge depicting “non-determinate”

program. The ﬁeld ﬂag in algorithm 1 indicates that.

The following rule is used to decide whether the

two conﬂict accesses α

(i) and α

) occur in paral-

lel threads or not: suppose, α

(i) and α

) are the

conﬂict access instances of the transformed parallel

program. Let i = (i

, i

, ···, i

−1

, i

, ···, i

···, i

) and i

= (i

, i

, ···, i

−1

, i

+ m, i

, ···,

, ·· ·, i

); thus, k

is the outermost loop index where

they differ. The accesses occur in the same therad if

and only if the k

-loop is not parallelized.

Returning to Fig. 1(b), for example, consider the

access instances of one of the four pairs (α

2,l

( j, i),

2,1

( j + 1, i + 1)), 4 ≤ j + 1 ≤ n + n - 2, max(2, j -

n + 1) ≤ i + 1 ≤ min(n - 1, j - 2). The iterator vec-

tors ﬁrst differ in the outer loop iterator values and

the outer loop is not parallelized. Hence, the con-

ﬂict access instances are performed sequentially and

the direction of the conﬂict edge is ascertained to be

hα

2,1

( j + 1, i + 1), α

2,l

( j, i)i. Similarly, the direction

of the rest of the pairs, where α

2,l

is one of the ac-

cesses, are ascertained.

If the parallel program is not a “non-determinate”

program, then algorithm 1 proceeds to construct the

DG. For each of the output arrays, a DG vertex v is

installed ﬁrst in the dependence graph. To construct

the DG of the parallel program, three types of RAW

dependence edges are installed — 1) output array ver-

tex to the vertex depicting operation which computes

the values of the array, 2) the vertex depicting opera-

tion to the vertex depicting input array if the array is

one of the operands to the operation, 3) the vertex de-

picting operation to the vertex depicting the same or

other operation which computes the values for the for-

mer. The ﬁrst type of edges represent the dependence

of the output array elements on the corresponding el-

ements of the operations which compute the values

of the array. The second type of edges represent the

dependence of some operation on the corresponding

elements of the input array. The last type of edges

are borrowed from the CAG of the program. To do

that, the S

ﬁeld of each of the read access α is sorted

based on WAW conﬂict edges of the CAG; this is done

to ﬁnd the last write operation on the memory location

referred in the corresponding read access. The edges

are installed for each such read access occurring in an

argument position of an operation to the vertex cor-

responding to the operation which is used to compute

the values of the last write access on the same memory

location. This in short depicts our dataﬂow analysis

technique used to construct the DGs.

4.1.6 Method: DG Construction for Vectorized

Programs

The process of construction of the parallelized version

from a vectorized code T is as follows. For every

vector instruction s

of T , a piece of loop parallelized

code segment is generated in T

. More precisely, for

a vector statement s

in T , two statements s

1,1

and

1,2

, enclosed in two different parallel do loops, are

generated in T

. If the write access of s

in T is

a[l

: h

], say, then the iteration domains of both

the parallel do loops are generated as l

≤ i ≤ h

where i is the iterator variable of the parallel do loop.

The generated statement s

1,1

is an assignment of the

computation performed on the rhs of the statement

in T to the elements of a temporary array, T mp

say, and the other statement s

1,2

in T

is the assign-

ment statement of the elements of the array T mp to

the corresponding elements of the array occurring in

the lhs of s

in T . Consider any read access α

, j

b[l

, j

: h

, j

] in the rhs of s

; then the corresponding

access is assumed as b[i + l

, j

− l

] in s

1,1

, where

i is the thread designators for both the parallel loops

introduced in the parallelized version T

of the vec-

torized program T . The two statements of the gen-

erated loop parallelized code segment are executed in

two different loops as all the computation in rhs of

the vectorized statement are executed ﬁrst and they

are assigned to the vector register in parallel fashion

in the next step as per semantics of vectorization.

Example 3. (contd). For example, statement s

of Fig. 2(b) is converted to the statements s

2,1

and

2,2

of Fig. 2(c). Here the iteration domains of both

the parallel do loops are [l

= 1, h

= N]. The

only read access on the rhs of s

is transformed to

C[i + l

− l

] i.e., C[i + 1] of the statement s

2,1

4.1.7 Method: Vectorization in Presence of

Enabling Transformations

Loop collapsing (Padua and Wolfe, 1986) is one of

the enabling transformations which enables the pro-

cess of parallelization; it transforms a two-nested loop

into a single loop, which is used to increase the effec-

tive vector length for vector machines. For example,

for validating vectorization transformation, the vec-

torized code T is converted to its loop parallelized

version T

given in Fig.3. (Note that we have avoided

the usage of temprary array while generating the loop

Validation of Loop Parallelization and Loop Vectorization Transformations

199

parallelized version of Fig. 3(c) from the vectorized

version Fig. 3(b) to avoid distraction from the main

issue.) However, the existing equivalence checking

technique fails right at the begining to establish equiv-

alence between S and T

as the dimensionalities of

two input arrays and those of two output arrays mis-

match in S and T

4.1.8 Method: Overview of the Existing

Equivalence Checking Method

The method of checking equivalence of (Verdoolaege

et al., 2012) of two programs takes two DGs as in-

puts. It starts by pairing up the output array vertices

of the two DGs and associating with the pair a goal

want

which asserts that each element of the output ar-

ray is computed identically in both the programs. The

process of establishing equivalence is carried out by a

goal reduction process and it is captured by construct-

ing a tree, called equivalence tree (ET). To start with,

the root node r associates the only output nodes of the

DGs with their entire domains captured in R

want

. A

node n = hv

, v

i is made to have a child node c = hv

i along the DG-edges hv

, v

i and hv

, v

i; R

want

is now propagated (reduced) to R

want

which captures

the equality of values of the instances of the functions

associated with v

and v

; the instances and the corre-

sponding subdomains are derived using the mappings

associated with the edges hv

, v

i and hv

, v

i. If the

child creation process leads to a leaf node l with R

want

depicting the goal of proving the equalities of the cor-

responding elements of the input arrays, then the goal

is ascertained to have been met by synthesizing an-

other predicate R

lost

0. Non-empty R

lost

have to

be synthesized at a leaf node when the non-identical

elements of the input arrays are referred. Non-empty

lost

predicates are then propagated back to the root

capturing the parts of the output arrays for which the

equality remains unproved.

Validation of Vectorization Preceded by Enabling

Transformations

The following example underlines the fact that for

validation of such transformations, the equivalence

checking module requires as inputs the correspon-

dence of the respective output array index spaces and

that of the input array index spaces which are assumed

to be equivalent in both the programs. For a given cor-

respondence of the output array index spaces, if the

given correspondence of the input array index spaces

is entailed by the predicate R

want

at the leaf nodes,

then R

lost

in these leaf nodes are not generated; Oth-

erwise R

lost

is generated.

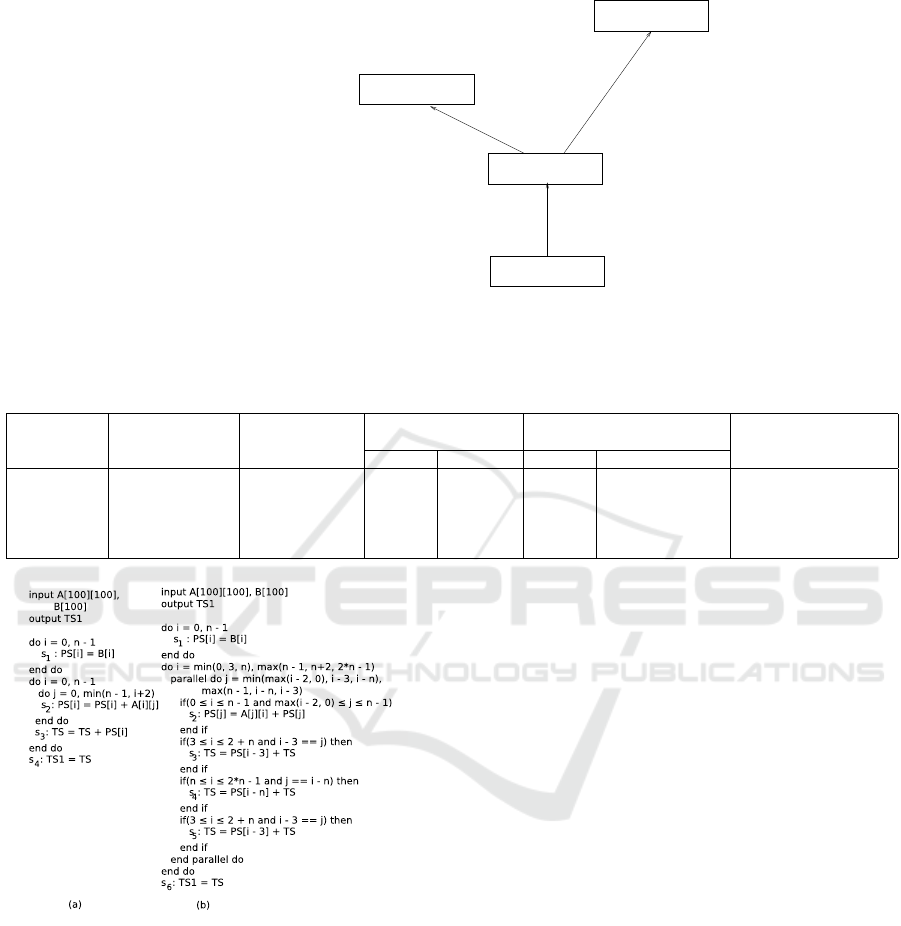
Example 4. [Enhanced Equivalence Check for

Loop Collapsing Followed by Vectorization Fol-

lowed by Loop Parallelization]. In Fig. 4, the DGs

corresponding to the sequential and the parallel pro-

grams of Fig. 3 are shown. The ET of the DGs is

drawn in Fig. 5. Let the correspondence of the out-

put arrays be provided to the equivalence checker as

A[i][ j] is equivalent to A[i j] where i j = (i − 1) ∗ 5 + j,

1 ≤ i ≤ 5 and 1 ≤ j ≤ 5; similarly, let the correspon-

dence of the input arrays be provided to the equiva-

lence checker as B[i][ j] is equivalent to B[i j] where

i j = (i − 1) ∗ 5 + j, 1 ≤ i ≤ 5 and 1 ≤ j ≤ 5. So the

proof goal at the root node n

of the ET in Fig. 5 be-

comes R

want

= {(i, j) ↔ i j | 1 ≤ i ≤ 5 ∧ 1 ≤ j ≤ 5

∧ 1 ≤ i j ≤ 25 ∧ i j = (i − 1) ∗ 5 + j}, it is eventually

reduced at n

to R

want

= {(i, j) ↔ i j | 1 ≤ i ≤ 5 ∧

1 ≤ j ≤ 5 ∧ 1 ≤ i j ≤ 25 ∧ i j = (i − 1) ∗ 5 + j} which

conforms with the correspondence of the input arrays

provided as input to the equivalence checking mod-

ule. Hence, R

lost

0. Similar situation happens for

ET-node n

also.

5 EXPERIMENTAL RESULTS

The DG construction method described in this paper

has been implemented in C and run on a 1.80-GHz

Intel



Core

i3 processor with 4-GB RAM for 5

benchmarks shown in Table 1.

The sequence of transformations applied for a spe-

ciﬁc benchmark is listed in the 3

column. The lines

of codes in both source and transformed programs are

provided in the 4

and 5

columns, respectively. The

DG construction times of the source and the trans-

formed programs (in seconds) are listed in the 6

and

the 7

columns. The 8

column records the time

taken by the equivalence checking module reported

in (Verdoolaege et al., 2012) when fed with the DGs

of the source and the transformed programs produced

by our modules. The ﬁrst 2 benchmarks are taken

from the benchmark suite available with a paralleliz-

ing compiler LooPo and they have been parallelized

with this compiler. The last 3 benchmarks are taken

from an available polyhedral benchmark suite Poly-

Bench; they have been parallelized with the LooPo

compiler.

In the 1

benchmark, as shown in Fig. 6, loop

skewing, interchange and parallelization transforma-

tions have been applied on the source program to gen-

erate the transformed program. The source program

computes

n−1

∑

i=0

B[i] +

n−2

∑

i=0

i+1

∑

j=0

A[i][ j] +

n−1

∑

i=n−3

n−1

∑

j=0

A[i][ j].

In this example, the target code does not produce the

same result as the source code. It may be noted that

in both the source and the transformed programs, the

output variable T S1 gets the same value as the vari-

able T S. In the transformed code, if (3 ≤ i ≤ n + 2)

ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering

200

↔ v

want

= {(i, j) ↔ i j|1 ≤ i ≤ 5 ∧1 ≤ j ≤ 5 ∧ 1 ≤ i j ≤ 25 ∧ i j = 5(i − 1)+ j}

want

= {(i, j) ↔ i j|1 ≤ i ≤ 5 ∧1 ≤ j ≤ 5 ∧ 1 ≤ i j ≤ 25 ∧ i j = 5(i − 1)+ j}

want

= {(i, j) ↔ i j|1 ≤ i ≤ 5 ∧1 ≤ j ≤ 5 ∧ 1 ≤ i j ≤ 25 ∧ i j = 5(i − 1)+ j}

↔ v

want

= {(i, j) ↔ i j|1 ≤ i ≤ 5 ∧1 ≤ j ≤ 5 ∧ 1 ≤ i j ≤ 25 ∧ i j = 5(i − 1)+ j}

Figure 5: ET of the DGs of Fig. 4.

Table 1: Experiments of Validation of Loop Parallelization preceded by Enabling Transformations. Col. 2 - Applied transfor-

mation for the test case (1 - loop parallelization, 2 - loop interchange, 3 - loop fusion, 4 - loop skewing).

Serial

Number (1)

Cases (2)

Transformation

Applied (3)

Lines of codes DG Construction Time (Sec)

Equivalence Checking

Time (Sec) (8)

Src (4) Trans (5) Src (6) Trans (7)

1 adder 4, 3, 2, 1 13 20 0.221 0.255 0.004

2 matmul − imper 2,1 17 17 0.157 0.155 0.004

3 2mm 4, 3, 2, 1 17 14 0.234 0.221 0.004

4 atax 4, 2, 1 20 19 0.245 0.248 0.005

5 covariance 3, 1 30 24 0.286 0.297 0.008

Figure 6: (a) The source code adder.c, (b) The non-

equivalent target code where loop skewing, interchange and

parallelization are applied generated by LooPo.

and (i −3 == j) hold, then the variable T S is updated

twice — ﬁrst in statements s

and then in statement s

Also, if (3 ≤ i ≤ n+2) and (n ≤ i ≤ 2n−1) hold, then

T S can be updated in statements s

, s

and s

depend-

ing on the values of j. However, in the source code,

for any values of i, TS can be updated only once. This

bug is detected by the equivalence checker although

the parallelizing compiler LooPo generated the paral-

lel code without reporting any error.

Table 2 records the results obtained for vectorization

validation of 4 benchmarks and one example program

borrowed from literature. The benchmark programs

are vectorized by a conﬁgurable source-to-source auto

- vectorization tool Scout. Scout provides the means

to vectorize loops using SIMD instructions at source

level. It uses a conﬁguration ﬁle to deﬁne the tar-

get SIMD architecture and it contains essential infor-

mation such as, vector size etc. We have used con-

ﬁguration ﬁles to deﬁne the vector instructions for

Intel



AVX architecture.

The meanings of columns of table 2 are the same as

the meanings of columns of table 1. The ﬁrst 4 ex-

amples are taken from the benchmark suite available

with the auto - vectorizing compiler Scout; they have

been converted automatically into the corresponding

parallelized versions using the method described in

this work and the DGs are subsequently generated

by the method proposed for loop parallelized pro-

grams. The 5

testcase has been taken from (Padua

and Wolfe, 1986) and loop collapsing is applied man-

ually to generate the transformed code.

6 CONCLUSION

In the present work, we have described a validation

method for loop parallelization and loop vectoriza-

tion which are the most commonly applicable par-

Validation of Loop Parallelization and Loop Vectorization Transformations

201

Table 2: Experiments of Validation of Loop Vectorization preceded by Enabling Transformations. Col. 3 - Applied transfor-

mations for the test case (1 - loop vectorization, 2 - loop collapsing, 3 - loop distribution, 4 - loop unrolling).

Serial

Number (1)

Cases (2)

Transformation

Applied (3)

Lines of codes DG Construction Time (Sec)

Equivalence Checking

Time (Sec) (8)

Src (4) Trans (5) Src (6) Trans (7)

1 alias regression 2 3, 1 15 22 0.223 0.245 0.004

2 alias regression 3,1 14 22 0.147 0.125 0.004

3 const expr 3, 1 15 20 0.101 0.114 0.036

4 conditional expr 3, 1 13 26 0.102 0.125 0.035

5 loop collapsing 3, 2, 1 18 21 0.115 0.145 0.005

allelizing transformations by parallelizing compilers.

Our experimental section indicates encouraging re-

sults for some non-trivial benchmarks for both the

transformations. The present work can be extended

in future along the following directions: 1. validation

of other parallelizing transformations such as soft-

ware pipelining applied by parallelizing compilers, 2.

localizing faulty application of enabling transforma-

tions when more than one of them are applied.

ACKNOWLEDGEMENT

We sincerely thank Dr. Debarshi Kumar Sanyal for

helping us communicating this paper.

REFERENCES

Allen, J. R., Kennedy, K., Porterﬁeld, C., and Warren, J.

(1983). Conversion of control dependence to data de-

pendence. In Proceedings of the 10th ACM SIGACT-

SIGPLAN Symposium on Principles of Programming

Languages, POPL ’83, pages 177–189, New York,

NY, USA. ACM.

Bandyopadhyay, S., Banerjee, K., Sarkar, D., and Mandal,

C. (2012). Translation validation for PRES+ mod-

els of parallel behaviours via an FSMD equivalence

checker. In Progress in VLSI Design and Test - 16th

International Symposium, VDAT 2012, Shibpur, India,

July 1-4, 2012. Proceedings, pages 69–78.

Collard, J.-F. and Griebl, M. (1997). Array dataﬂow analy-

sis for explicitly parallel programs. Parallel Process-

ing Letters, 07(02):117–131.

Griebl, M. and Lengauer, C. (1996). The loop parallelizer

loopo. In Proceedings of Sixth Workshop on Compil-

ers for Parallel Computers, volume 21 of Konferen-

zen des Forschungszentrums Jlich, pages 311–320.

Forschungszentrum.

Karfa, C., Sarkar, D., Mandal, C., and Kumar, P. (2008). An

equivalence-checking method for scheduling veriﬁca-

tion in high-level synthesis. Computer-Aided Design

of Integrated Circuits and Systems, IEEE Transactions

on, 27(3):556–569.

Krinke, J. (1998). Static slicing of threaded programs. In

Proceedings of the 1998 ACM SIGPLAN-SIGSOFT

Workshop on Program Analysis for Software Tools

and Engineering, PASTE ’98, pages 35–42, New

York, NY, USA. ACM.

Krzikalla, O., Feldhoff, K., Mller-Pfefferkorn, R., and

Nagel, W. E. (2011). Scout: A source-to-source trans-

formator for simd-optimizations. In Alexander, M.,

D’Ambra, P., Belloum, A., Bosilca, G., Cannataro,

M., Danelutto, M., Martino, B. D., Gerndt, M., Jean-

not, E., Namyst, R., Roman, J., Scott, S. L., Traff,

J. L., Valle, G., and Weidendorfer, J., editors, Euro-

Par Workshops (2), volume 7156 of Lecture Notes in

Computer Science, pages 137–145. Springer.

Kundu, S., Lerner, S., and Gupta, R. K. (2010). Transla-

tion validation of high-level synthesis. IEEE Trans. on

CAD of Integrated Circuits and Systems, 29(4):566–

579.

Padua, D. A. and Wolfe, M. J. (1986). Advanced compiler

optimizations for supercomputers. Commun. ACM,

29(12):1184–1201.

Pouchet, L. (2012). Polybench: The polyhedral bench-

mark suite. http://www-roc.inria.fr/pouchet/software/

polybench/download/.

Shashidhar, K. C., Bruynooghe, M., Catthoor, F., and

Janssens, G. (2005). Functional equivalence check-

ing for veriﬁcation of algebraic transformations on

array-intensive source code. In Proceedings of De-

sign, Automation and Test in Europe, 2005. Proceed-

ings, pages 1310–1315 Vol. 2.

Verdoolaege, S., Janssens, G., and Bruynooghe, M. (2012).

Equivalence checking of static afﬁne programs using

widening to handle recurrences. ACM Trans. Pro-

gram. Lang. Syst., 34(3):11:1–11:35.

ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering

202