
Matrix Multinomial Systems with Finite Syntax
Rudolf Hanel
Section for Science of Complex Systems, Medical University of Vienna, Spitalgasse 23, 1090 Vienna, Austria
Keywords:
Complex Processes, Decidability, Phase-space Growth, Oslo Sand-pile Model.
Abstract:
Typically, describing complex processes and the sequences of events they generate requires both statistical and
structural information. Statistical information alone does not suffice when intrinsic constraints allow a process
to produce well-formed sequences of events but not others. Typically, processes become history dependent;
the multiplicity of well-formed sequences with identical histogram and derived concepts, entropy for instance,
start to depend on the structure, the grammar, of the underlying process. We demonstrate that for a sufficiently
well behaved class of complex processes, it is possible to derive an exact criterion for deciding whether a
sequence of arbitrary length is well formed or not. The approach is based on representing events by matrices
and sequences of events by products of respective matrices. Formally such processes have a multinomial
structure only that the elements are not numbers, but matrices. We demonstrate the approach by applying it
to enumerate the well known Oslo sand-pile model, resulting in an elegant formula for the number of stable
attractor states for Oslo sand-piles of arbitrary size.
1 INTRODUCTION
Several disciplines, such as statistical physics of non-
equilibrium systems, the theory of formal languages
and grammars, information theory and algorithmic
complexity all deal with, or are applied to mod-
eling complex phenomena (from chemical- to eco-
systems). For real world applications complex typi-
cally means driven dissipative systems with strongly
interacting and diverse components, but also roughly
corresponds to Kolmogorov’s way of measuring com-
plexity in terms of the amount of information we
have to provide to specify a process. In this sense
of conveying information about a class of processes
the complexity of Classical Mechanics, for instance,
is likely to be lower than the one of Molecular Biol-
ogy.
Overlaps between disciplines, for instance,
emerge as interrelations between thermodynamic
computation costs and algorithmic complexity of a
process (Zurek, 1989), or in the ways chemistry
can be modeled with formal theories of languages
and grammars (Fontana, 1991); conveying the same
fundamental observation. Purely statistical informa-
tion does not suffice to characterize complex pro-
cesses, (Miller & Chomsky, 1963). For examples
where structural information determines which pat-
tern a process follows or conversely, which pattern
a process avoids also compare (Corominas-Murtra,
2015; Bandt and Pompe, 2002). Recently it also has
been demonstrated that the functional form of en-
tropy and divergence, notions deriving from multi-
plicities and probabilities of sequences with respect
to a so called macro-states (i.e. the histogram of a
sample) depend on the underlying processes class as
well (Hanel, 2014; Hanel, 2015). In (Hanel, 2015) we
have derived the entropy and divergence of multistate
P
´
olya urn processes (P
´
olya, 1930). Here we develop
the same philosophy by considering the decision algo-
rithm that distinguishes well formed from ill formed
sequences of a well behaved class of processes that
can be represented as directed multi-graphs. This al-
gorithm forms the key ingredient for exactly deter-
mining the multiplicities (and thus the entropy) of
processes subject to intrinsic constraints, determining
whether a particular sequence is well formed or not.
We usually understand complex processes as se-
quences of events or actions that follow each other
according to particular generative rules describing the
intrinsic constraints. This is why we have invented
notebooks, calenders, and appointment schedules, to
organize our daily actions and events into mutually
compatible sequences. Such rules may regulate how
deterministic or probabilistic a process behaves. We
may think of distinct events as words (letters) a in a
lexicon (alphabet) A and sequences of words, i.e. sen-
tences λ = (λ
1
,··· , λ
N
), with each λ
n
∈ A. Event suc-
cession rules can be interpreted as syntactic rules that
26
Hanel, R.
Matrix Multinomial Systems with Finite Syntax.
In Proceedings of the 1st International Conference on Complex Information Systems (COMPLEXIS 2016), pages 26-31
ISBN: 978-989-758-181-6
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tell us which sentences are well-formed and which
sentences are not. If there are no constraints on how
different actions can follow each other, then any se-
quence of events is possible and (for finite numbers
of possible actions) the sequences of actions follows
a multinomial statistics. This in turn allows one to
predict the most likely distribution function of ob-
served events by minimizing the Kullback-Leibler di-
vergence (Kullback and Leibler, 1951; Hanel, 2014).
Alternatively one can maximize Shannon entropy,
(Shannon, 1948), under constraining conditions im-
plemented by so called cross-entropy terms (Hanel,
2014; Hanel, 2015). Entropy emerges asymptotically,
as the logarithm of the multiplicity of a given se-
quence divided by the effective number of degrees of
freedom, which in the multinomial case is the number
of observations N. Since in the purely multinomial
case all permutation of a sequence are well formed
and have identical probabilities, the multiplicity of
such sequences is given by the multinomial factor.
To sketch how Shannon entropy and Kullback-Leibler
divergence depend on the multinomial statistics of
the underlying process we may consider a Bernoulli
process the states i = 1,··· ,W with prior probabili-
ties q = (q
1
,··· , q
W
). We note that 1 = (
∑
i
q
i
)
N
=
∑
|k|
1
=N
N
k
∏
i
q
k
i
i
, where k = (k
1
,··· , k
W
) is the his-
togram of the process after N observations, i.e. k
i
is
the number of occurrences of state i. In particular the
probability P(k|q) = M(k)G(k|q) of the histogram k
factorizes into the probability to find a sequence with
histogram k given by G(k|q) =
∏
i
q
k
i
i
and the mul-
tiplicity of such sequences given by the multinomial
coefficient, M(k) =
N
k
. It follows that Shannon en-
tropy asymptotically (for large N) is given by H(p) =
−
∑
i
p
i
log p
i
=
1
N
logM(k), where p = k/N, are the
relative frequencies of observing states i. Similarly
−
1
N
logG(k|q) = −
∑
p
i
logq
i
is the cross entropy, and
D
KL
(p||q) =
∑
i
p
i
(log p
i
− log q
i
) = −
1
N
logP(k|q) is
the Kullback-Leibler divergence. Maximum entropy
estimates therefore correspond to the so called max-
imum configuration, the most likely histogram of a
process after N observations. If generative rules con-
strain sequences, the rules of a regular grammar for
instance, then the number of sequences with identi-
cal histograms becomes smaller than the multinomial
factor, directly affecting the functional form of en-
tropy (the scaled logarithm of multiplicity) and diver-
gence, (Hanel, 2014; Hanel, 2015).
If we think of networks (e.g. the streets of Lon-
don), consisting of nodes and sets of links connecting
those nodes. A walk on such a network can be in-
terpreted as a process composing elementary actions
symbolized by links i → j from a node i to another
node j. Typically, not all actions can be freely com-
posed. We can only compose those actions where the
end-node j of one link i → j is the starting-node of
another link j → k. If one moves from one place,
X, in town to another, Y, then the next move has
to start in Y. In different processes of even higher
complexity, language for instance, well formed se-
quences of states may follow different rules of suc-
cession that may become more complicated than the
simple groupoid induced by an underlying network
topology. In order to develop the information the-
ory of such processes we need an appropriate gener-
alization of the multinomial coefficient counting only
well-formed sequences. In other words, the syntactic
rules governing a complex process become important
for correctly counting the numbers of well-formed se-
quences of length N. We note, that beneath the statis-
tical description of a system we again require a struc-
tural one that allows us to identify well formed or typ-
ical sequences. The efforts required to identify a par-
ticular process, or at least the class a process belongs
to, can not be avoided, reminding us of the non exis-
tence of a free lunch (Wolpert and Macready, 1995).
In the following we show that if a process pos-
sesses a description in terms of a directed multi-graph,
i.e. if the process can be understood with a finite num-
ber of states for sequences of arbitrary length (regu-
lar grammars, finite automatons), then enough of the
multinomial structure of the process is preserved, to
implement decision rules into a matrix representation
of words a ∈ A, which automatically takes care of
the syntactic rules. - We will demonstrate the power
of the methodology in an example, providing an ele-
gant way for counting the number of stable attractor
states that exist in the Oslo sandpile model, (Corral,
2004), depending on the size of the basis of the Oslo-
sandpile.
2 FINITE STATE TRANSITION
SYSTEMS
Let σ
0
be the initial state of a process before we
sample the first step. Let A be the lexicon, each
word in the lexicon representing a possible event. Let
λ = (λ
1
,··· , λ
N
) be a sequence of events λ
n
∈ A. Any
sequence λ can either be well formed or not. Those
sequences that are not well-formed again have to be
distinguished into two sub-classes. The first class
contains transient sequences that are not well formed
at length N but are part of a well formed sequence, i.e.
there exists a λ
0
with length N
0
> N such that λ
0
n
= λ
n
for all n = 1,· · · ,N and λ
0
is well formed. What re-
mains are sequences that are not well formed and do
not form the beginning of a longer well formed se-
Matrix Multinomial Systems with Finite Syntax
27

quence. We call those sequences void.
We assume that non-void sequences of events
λ
n
∈ A describe how the process evolves along a fi-
nite number of W possible states σ
i
with i ∈ I ≡
{1,··· ,W }. We will identify σ
i
≡ i. We also as-
sume that those events are sufficient to encode the
succession rules of sequences of arbitrary length, such
that any non-void sequence λ is associated with a se-
quence of abstract states x = (x
1
,··· , x
N
), with x
n
∈ I,
such that x
1
= λ
1
σ
0
and for n > 1, x
n
= λ
n
x
n−1
.
We order those states such that sequences ending in
i = 1, · · · ,W
α
are well formed. Sequences that end in
states i = W
α
+ 1,··· ,W
α
+ W
β
, are transient states.
If a process is stopped in a transient state, then the re-
sulting sequence is non-void but also not well-formed.
A sequence becomes void if at some point n ≤ N the
transformation a = λ
n
can not be applied to the state
x
n
. We capture this by considering an additional null-
state
/
0 such that
/
0 = λ
n
x
n−1
. We point out that in this
way the syntax of such systems gets encoded by the
way words a ∈ A transform states i = 1,··· ,W , σ
0
,
and
/
0, defined by the maps a : {σ
0
} → I ∪ {
/
0} and
a : I → I ∪ {
/
0}, under the constraint a
/
0 =
/
0 for all
a ∈ A.
This formal set-up corresponds to constructing a
multi-graph with the states σ
i
as nodes and the letters
of the alphabet a corresponding to sets of links on the
graph (compare Fig. 1). The transitions correspond-
ing to the alphabet can be easily encoded in matrix no-
tation. States get represented by (W + 1) × 1 vectors.
The components of the vectors σ
i
, i = 0, 1, · · · ,W are
given by (σ
i
)
j
= δ
i j
, where δ
i j
is the Kronecker delta
with δ
i j
= 1 for i = j and δ
i j
= 0 otherwise. The zero-
state
/
0 is the (W + 1) ×1 vector consisting only of ze-
ros. A word a ∈ A is a non zero (W + 1) × (W + 1)
matrix with (i) a
i j
∈ {0,1}, (ii) a
0i
= 0, for all i =
0,1,··· ,W , (iii)
∑
W
i=0
a
i j
≤ 1.
Property (i) guarantees that σ
0
, only appears as
the initial state of the process but never in a sequence
of states x. Property (iii) guarantees that a ∈ A only
moves around the non zero component of the σ
i
vec-
tor from index i to another index j of the state σ
j
=
aσ
i
. Moreover, for those j where
∑
W
i=0
a
i j
= 0 it fol-
lows that
/
0 = aσ
j
.
Once one has encoded the syntactical rules of a
suitable process into a matrix representation of trans-
formations a ∈ A on the index-set I = {0,1,··· ,W }
it becomes very simple to count the number of well
formed sequences. For this we define the matrix
¯
A =
∑
a∈A
a, (1)
which can be interpreted as the adjacency matrix of
the transition multi-graph. By taking the matrix
¯
A
to the N’th power we compute the sum over the ma-
trix products of all possible sequences of transforma-
tions of length N that can be formed with transfor-
mations a ∈ A. The well formed sequences of length
N however will be in a final state 1 ≤ x
N
≤ W
α
. As
a consequence the number of well-formed sequences
of length N can be easily computed:
Ω
A
(N) = π
α
¯
A
N
σ
0
, (2)
where π
α
is the 1 × (W + 1) vector with (π
α
)
0
= 0,
(π
α
)
i
= 1 for i = 1, · · · ,W
α
, and (π
α
)
j
= 0 for j > W
α
.
This works since
¯
A
N
is the sum over all possi-
ble sequences over all sequences λ ∈ A
N
. For ex-
ample consider the three word lexicon A = {a, b, c},
with
¯
A = a + b + c (compare Fig. 1). All sequences
of length 2 can be represented by
¯
A
2
= aa + ab +
ac + ba + bb + bc + ca + cb + cc. But only the se-
quences ac, cc, and bc are well formed it follows that
¯
A
2
σ
0
= (ac + bc + cc)σ
0
, and only well formed se-
quences contribute to the Ω(2).
We point out that it is also possible to obtain more
detailed statistics. For instance one can determine the
number of times well-formed sequences of length N
contain a certain word a ∈ A, or how many times well
formed sequences pass through state i. This can be
done by embedding the matrices a ∈ A into larger ma-
trices which also implement a counting mechanism
that, in a first step, allows us to compute cumulative
visiting distributions; for instance the number of times
well-formed sequences with length N
0
≤ N visit state
i. By computing such cumulative distributions of se-
quences of length 1 to N then allows us to compute
the visiting distributions for sequences of particular
length N from the cumulative distributions. However,
considering the scope of this paper, we will present
a detailed description of this counting methodology
and a study of the corresponding multiplicities of se-
quences, i.e. entropies, elsewhere.
3 EXAMPLE: THE STABLE
ATTRACTOR STATES OF THE
OSLO-MODEL
The Oslo sandpile model has one dimension. The
model will serve as a simple example for a driven,
dissipative system. At the basis the Oslo sand-pile
has N grains of sand. At the right side next to site
N the pile is supported by a wall. To the left of site
1 there is a rim such that grains toppling from site 1
over the rim are removed from the pile. Whenever the
pile is in a stable configuration the pile gets loaded by
dropping a grain on site N. At each site n = 1, · · · , N
the pile has a hight h(n). If h(n) − h(n − 1) > 2 the
COMPLEXIS 2016 - 1st International Conference on Complex Information Systems
28
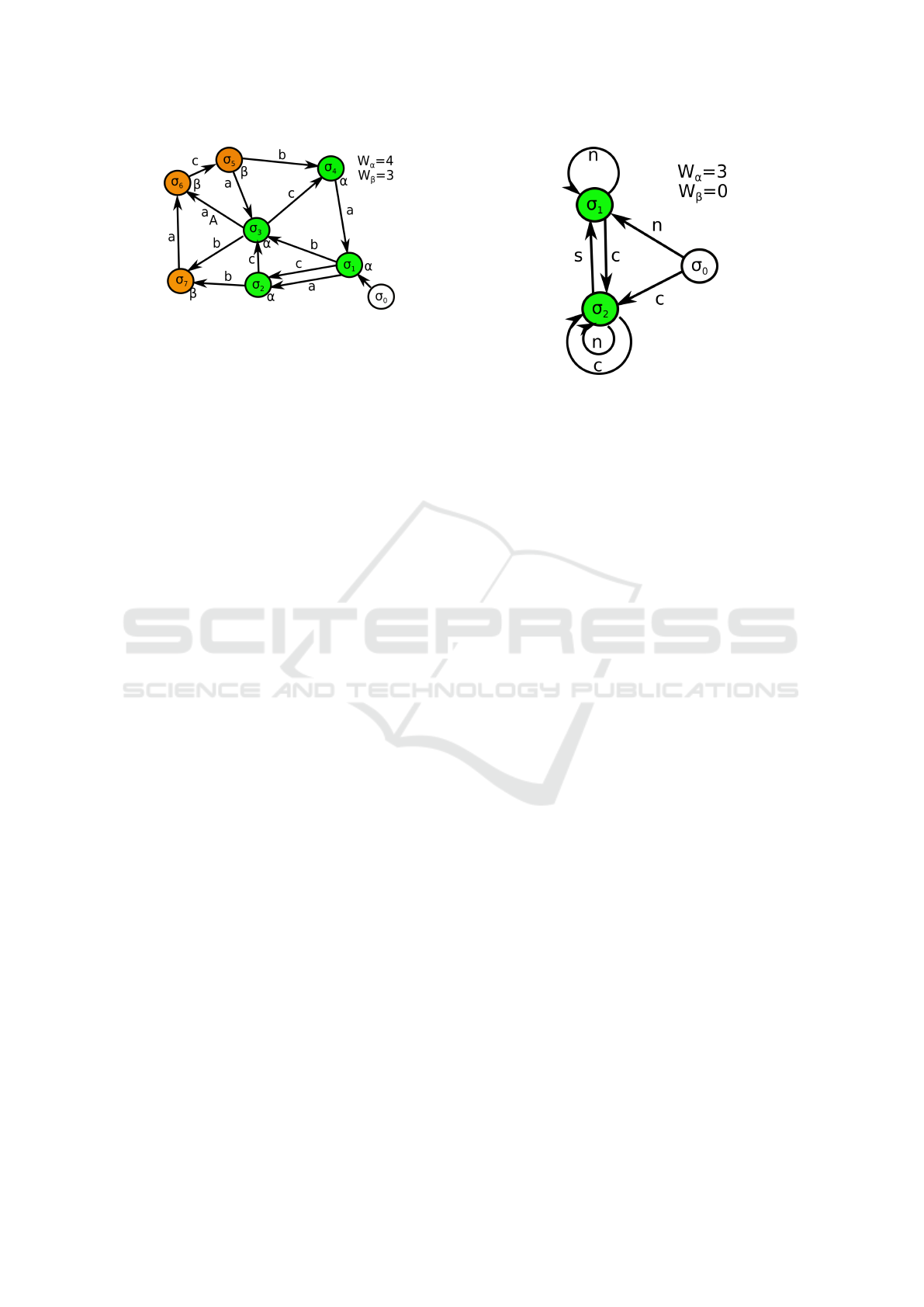
Figure 1: Example system over the alphabet A = {a,b,c}
with σ
0
being the initial state, σ
1
-σ
4
are α-states, i.e. se-
quences ending in those states are well formed, while σ
5
-
σ
7
are transient β-states. For instance the only well formed
sequences of length 2 are ac, cc, and bc. aa is void. ab
is non-void but not well-formed. However, ab is the be-
ginning of a longer, well formed sequence abaca. Between
σ
1
and σ
2
there exist two distinct links (multi-graph), one
belonging to a and the other to c.
pile is instable at this point and one grain topples
from site n to site n − 1 (the rim can be thought of
as site n = 0 with h(0) = 0). If h(n) − h(n − 1) = 2
site n is stable with some probability p and instable
with probability 1 − p, in which case also one grain
of sand topples from site n to site n − 1. In case
0 ≤ h(n) − h(n − 1) ≤ 1, site n is stable. After the
pile gets loaded, it is left to relax until it ends up in
a stable configuration. This means, we can write any
stable attractor configuration of the pile as a sequence
of λ = (λ
1
,··· , λ
N
) consisting of three possible words
s (sink), n (neutral), and c (critical), i.e. A = {s,n,c}.
If λ
n
= s corresponds to h(n)−h(n−1) = 0, λ
n
= n to
h(n)−h(n−1) = 1, and λ
n
= c to h(n)−h(n−1) = 2.
Not all sequences in
¯
A
N
are allowed. Well formed
sequences follow particular syntactical rules that fol-
low from the sandpile dynamics. Those syntactic
rules of the Oslo sandpile model have been analyzed
in (Corral, 2004) and can be summarized as follows:
• (R1) Starting from site 1, the first word in the se-
quence λ that is not n, cannot be s.
• (R2) After the occurrence of word s, the first word
in the symbol string λ that is not n, cannot be a s.
These two rules completely characterizes all well-
formed stable attractor states of the Oslo sand-pile
model. All we have to do is to construct an adequate
matrix representation of the lexicon A. Two states σ
1
and σ
2
suffice.
The following maps encode the syntactic rules:
/
0 = sσ
0
follows from R1; σ
1
= nσ
0
is the state re-
quired for opening a sequence with the neutral n;
σ
2
= cσ
0
if the sequence starts with a critical c. Fur-
ther,
/
0 = sσ
1
follows either from R1 or R2, depending
on whether σ
1
is a result of pumped n’s, or by a c that
compensates for a previous occurrence of a sink s. It
Figure 2: Cartoon of the structure of attractor states of the
Oslo sandpile model with the alphabet A = {s,n,c}. All se-
quences that can be formed by walks on the transition graph
are well formed, all other sequences are void.
is not difficult to realize that the transitions σ
1
= nσ
1
,
σ
2
= cσ
1
; σ
1
= sσ
2
, σ
2
= nσ
2
, and σ
2
= cσ
2
com-
plete the transition graph, consistent with R1 and R2
(compare Fig 2). As a consequences, W = W
α
= 2,
and the unique matrix representation of the words s,
n, and c is given by:
s =
0 0 0
0 0 1
0 0 0
,
n =
0 0 0
1 1 0
0 0 1
,
c =
0 0 0
0 0 0
1 1 1
.
(3)
Using Eq. (2) tells us that
Ω
A
(N) = (0,1,1)
0 0 0
1 1 1
1 1 2
N
1
0
0
. (4)
This allows us to compute the num-
ber of well-formed sequences: Ω
A
(N) =
2,5,13,34,89,233,610,1597,···; which exactly
reproduces the number of well-formed sequence as
computed in (Corral, 2004) by other mathematical
means.
4 DISCUSSION
Since logarithmically scaled multiplicities of well
formed sequences of events, consistently provide us
with the functional form of entropy required in maxi-
mum entropy principles (Hanel, 2014), multiplicities
of possible sequences need to be determined for dif-
ferent processes classes. We analyzed how this can be
Matrix Multinomial Systems with Finite Syntax
29

done for processes following simple generative rules
(regular grammar). The distribution of sequences
generated by such systems again follow distributions
with a multinomial structure, only that the elements
are not mere numbers (e.g. the prior probabilities
defining a Bernoulli process), but matrices describing
how a local action, the emission of a word, changes
the state of a system and the possibilities to continue
the sequence. The matrix representation automati-
cally provides us with a decision criterion that distin-
guishes void, transient, and well-formed sequences.
The aggregate representation of the system is a multi
graph with links between nodes representing abstract
states. The links are labeled with words of the lexicon
such that every out-link of a node of the multi-graph
has a distinct label. As a consequence of the decision
criterion, it becomes possible to determine how often
a system can be found in a particular state or emits a
particular event in well-formed sequences of arbitrary
length; and as a further consequence determine the
entropy (reduced Boltzmann entropy, logarithmically
scaled multiplicities) of a process. A more extensive
analysis of such entropies goes beyond the scope of
the paper and will be given elsewhere.
While the mathematic machinery that comes into
play here is well known (e.g. from dealing with fi-
nite automata), the matrix-multinomial structure of
the underlying multi-graph emerges naturally from
the need to determine multiplicities in the considered
class of processes. Other classes of processes require
different mathematical means, e.g. P
´
olya urn pro-
cesses (Hanel, 2015). We may also note that sim-
ilarly to using prior probabilities to bias events in
Bernoulli processes with multinomial statistics we
may (in principle) also consider matrices representing
words to carry weights for the various possible transi-
tions on the multi-graph, completing the analogy with
Bernoulli processes with simple multinomial statis-
tics. We also note that it is possible to consider sys-
tems with potentially infinitely many states. Natural
processes frequently explore the possible states they
can attain as they evolve (heaps law). This means that
matrix representations of words will need to use larger
matrices as the sample size N increases. Such adap-
tive representations only hold up to a maximal sample
size and become inaccurate for larger samples.
We have started the analysis from considering the
words in the lexicon as maps between abstract states,
and the composition of events follows simple compo-
sition rules (groupoid) characterized by the emergent
multi-graph. We might ask if groupoids can be uti-
lized to characterize complex processes, their multi-
plicities, and histogram probabilities, and derived no-
tions of entropy and divergence in general.
5 CONCLUSIONS
In complex processes both statistical and structural
information become necessary for fully describing
processes (reminding us of the non-existence of a
free lunch in analyzing and reconstructing processes).
The simplest random processes, Bernoulli process,
are associated with multinomial probability distribu-
tions of samples, and multiplicities, which correspond
to Kullback-Leibler divergence and Shannon entropy.
For complex processes the notions of divergence and
entropy can take different functional forms. As a con-
sequence, it becomes necessary to determine multi-
plicities in complex processes in order to determine
the process specific notions of entropy and divergence
consistently. For systems with an aggregate descrip-
tion as directed multi-graphs, exact decision criteria
exist that allow us to identify well formed sequences
of the process, which in principle also allows us to ef-
ficiently compute the associated entropy of such pro-
cesses. We have demonstrated in the example of Us-
ing the Oslo sandpile model as an example we demon-
strated that the attractor states of this simple model of
a driven dissipative system can be fully characterize
along the presented lines.
We acknowledge fruitful discussion with B.
Corominas-Murtra.
REFERENCES
Bandt C. and Pompe B. (2002), Permutation Entropy: A
Natural Complexity Measure for Time Series, Phys.
Rev. Lett. 88 174102.
Corominas-Murtra B., Hanel R., and Thurner S. (2015),
Understanding scaling through history-dependent
processes with collapsing sample space, Proc. Nat.
Acad. Sci. USA 112 5348-5353.
Corral A. (2004), Calculation of the transition matrix and of
the occupation probabilities for the states of the Oslo
sandpile model, Phys. Rev. E 69 026107;
Fontana W. (1991), Algorithmic Chemistry, In Artificial
Life II, SFI studies in the Sciences of Complexity
(Eds.: Langton, C.G.; Taylor C.; Farmer, D.; Ras-
mussen, S.) Addison-Wesley 1991; 159–209.
Hanel R., Thurner S., and Gell-Mann M. (2014), How
multiplicity of random processes determines entropy:
derivation of the maximum entropy principle for com-
plex systems, Proc. Nat. Acad. Sci. USA 111 6905–
6910.
Hanel R., Corominas-Murtra B., and Thurner S. (2015),
Analytical computation of frequency distribu-
tions of path-dependent processes by means of
a non-multinomial maximum entropy approach,
arXiv:1511.00414.
COMPLEXIS 2016 - 1st International Conference on Complex Information Systems
30

Miller G.A. and Chomsky N. (1963) Finitary models of lan-
guage users, In Handbook of Mathematical Psychol-
ogy (Ed.: D. Luce) John Wiley & Sons, 419–491.
Shannon C.E. (1948), A Mathematical Theory of Commu-
nication, Bell Syst. Tech. J. 27 379-423, 623-656.
Kullback S. and Leibler R.A. (1951), On information and
sufficiency, Ann. Math. Stat. 22 79-86.
P
´
olya G. (1930), Sur quelques points de la th
´
eorie des prob-
abilit
´
es, Ann. Inst. Henri Poincare 1 117–161.
Wolpert, D.H. and Macready W.G. (1996), No free lunch
theorems for search, Technical Report, SFI-TR-95-
02-010, Santa Fe Institute.
Zurek W. H. (1989), Thermodynamic cost of computation,
algorithmic complexity, and the information metric,
Nature 341 119–124.
Matrix Multinomial Systems with Finite Syntax
31
