Modeling Embedded Interpersonal and Multiagent Coordination

Michael J. Richardson

, Rachel W. Kallen

, Patrick Nalepka

, Steven J. Harrison

, Maurice Lamb

Anthony Chemero

, Elliot Saltzman

and R. C. Schmidt

Center for Cognition, Action and Perception, University of Cincinnati, Cincinnati, OH, U.S.A.

School of Health, Physical Education and Recreation, University of Nebraska Omaha, Omaha, NE, U.S.A.

Department of Physical Therapy and Athletic Training, Sargent College of Health and Rehabilitation Sciences,

Boston University, Boston, MA, U.S.A.

Department of Psychology, College of the Holy Cross, Worcester, MA, U.S.A.

Keywords: Multiagent Systems, Social Coordination, Task Dynamics, Complex Systems, Self-organization.

Abstract: Interpersonal or multiagent coordination is a common part of everyday human activity. Identifying the

dynamic processes that shape and constrain the complex, time-evolving patterns of multiagent behavioral

coordination often requires the development of dynamical models to test hypotheses and motivate future

research questions. Here we review a task dynamic framework for modeling multiagent behavior and

illustrate the application of this framework using two examples. With an emphasis on synergistic self-

organization, we demonstrate how the behavioral coordination that characterizes many social activities

emerges naturally from the physical, informational, and biomechanical constraints and couplings that exist

between two or more environmentally embedded and mutually responsive individuals.

1 INTRODUCTION

Many of the everyday movements and actions that

individuals perform are accomplished in a social

setting and are coordinated with the actions of other

individuals. Such behavioral activity is sometimes

deliberate and conscious, like when two people are

moving a large piece of furniture together, or

spontaneous and automatic, such as when two

people avoid bumping into one another when

walking on a busy sidewalk. It can involve the

synchronous coordination of rhythmic movements,

such as when individuals synchronize their legs

movements while walking and talking, or the

asynchronous coordination of complementary or

discrete actions, such as when loading a dishwasher

together. Finally, multiagent coordination tasks often

involve a nested structure of sub-actions, with the

varied sequencing of these actions making up the

complex syntax of everyday social activity.

The varied complexity of social and multiagent

coordination, however, belies the seemingly

effortless and robust manner with which human (and

many animal) agents are able to perform these

activities. Indeed, two or more human agents can

often spontaneously coordinate their movements and

actions in highly novel task contexts with little to no

prior experience or learning. This apparent context

insensitivity has led many researchers to focus on

trying to identify the invariant set of internal

(mental) neurocognitive and perceptual-motor

mechanisms that might support effective multiagent

coordination across a wide range of task goals and

situations (Graf, et al., 2009; Newman-Norland et

al., 2007; Vesper et al., 2010). It is becoming

increasingly clear, however, that that the CNS

cannot “do it all”, and that there is more to social

action and coordinated multiagent activity than

simply neurocognitive processes alone (Coey et al.,

2012; Eiler et al., 2013; Knoblich, et al., 2011;

Schmidt et al., 2011). This is particularly true for

complex multiagent tasks that require individuals to

continuously adapt their behavior to each other and

to a dynamic task environment, where adopting a

purely neurocognitive approach requires increasing

appeals to ever higher levels of ungrounded,

representational complexity, as well as unsustainable

levels of executive control (Chemero, 2009; Schmidt

et al., 1990; 2011).

So what other processes or mechanisms might

Richardson, M., Kallen, R., Nalepka, P., Harrison, S., Lamb, M., Chemero, A., Saltzman, E. and Schmidt, R.

Modeling Embedded Interpersonal and Multiagent Coordination.

In Proceedings of the 1st International Conference on Complex Information Systems (COMPLEXIS 2016), pages 155-164

ISBN: 978-989-758-181-6

155

operate to shape and constrain the complex time-

evolving patterns of behavioral coordination that

characterize everyday interpersonal or multiagent

activity? Here, we propose that many of the stable

patterns of interpersonal and multiagent coordination

that occur during social activity lawfully emerge

from the physical and informational constraints and

couplings that exist between two or more

environmentally embedded and mutually responsive

individuals (Marsh et al., 2009; Richardson and

Kallen, 2015; Schmidt et al., 1990; Schmidt et al.,

2011). Of particular relevance here is the resultant

implication that context dependent multiagent

coordination can be understood and modeled as a

coupled nonlinear dynamical system. Accordingly,

the aim of the current paper is to provide a general

overview of how one can employ coupled nonlinear

dynamical models to capture and explain the robust,

time-evolving structure of Embedded Multi-Agent

Dynamics (EMAD). Drawing heavily on the task

(Saltzman and Kelso, 1987) and behavioral dynamic

(Warren, 2006) approaches to human behavior, we

first briefly define a conceptual framework for

modeling EMAD. We then offer paradigmatic

examples illustrating how this framework can be

employed to formalize low-dimensional, coupled,

nonlinear differential equation models of

coordinated interpersonal and multiagent behavior.

2 MODELING FRAMEWORK

Consistent with more general nonlinear dynamics

and complex systems approaches to human behavior

(for reviews see e.g., Kelso, 1995; Richardson et al.,

2014; Thelen and Smith, 1994; Warren, 2006), and

building on the dynamical interpersonal coordination

research of Schmidt and colleagues (e.g., Schmidt et

al, 1990; Schmidt and O’Brien, 1997; Schmidt and

Turvey, 1994), the framework for modeling EMAD

detailed here emphasizes self-organization and

contextual emergence. Accordingly, the stable

organization of multiagent behavior is not captured

by means of a centralized control structure or

neurocognitive mechanism, but rather is modeled as

an emergent, a posteriori consequence of the

distributed interaction of physical processes,

informational and neurological couplings, and

contextual constraint. Accordingly, stable patterns of

behavioral coordination correspond to functional

(re)organizations of a multiagent-environment

system (e.g., limbs, movements of different actors,

objects within a social task environment), one that is

temporarily constrained to act as a single coherent

unit or synergy, formed and destroyed in response to

changing task goals and perceived action

possibilities (Riley, et al., 2011).

More formally, environmentally embedded

interpersonal or multiagent coordination emerges

from the activity of two or more agents, A

(where i

= 1, 2, … n agents) in a changing task environment,

E, via the detection of information, I, and the

reciprocal and mutually constraining modulation of

behavioral action and environmental events by the

physical forces, F, exerted in the environment by the

agents or by other environmental objects or surfaces

(or by both).

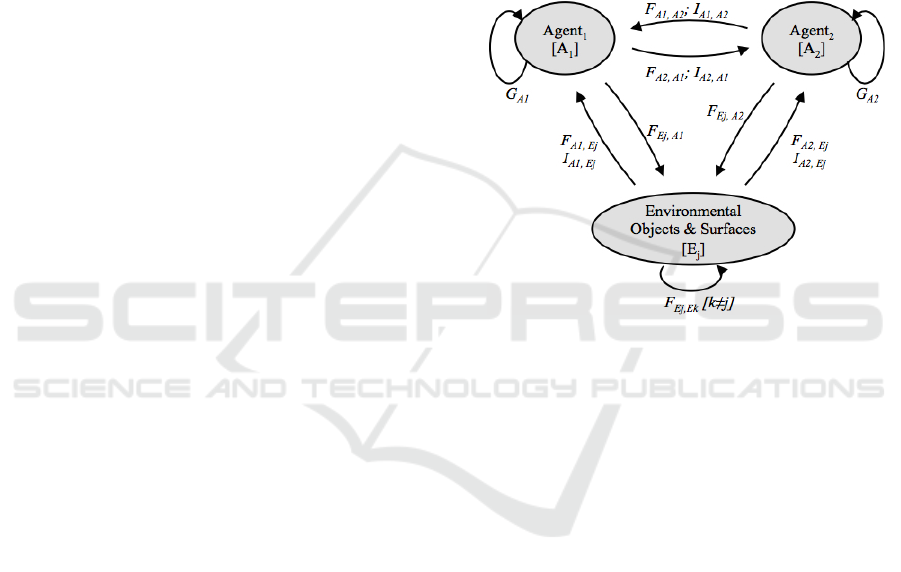
Figure 1: Illustration of a task dynamic framework for

modeling Embedded Multi-agent Dynamics (EMAD). See

text for details.

A two-agent (interpersonal) illustration of this

multiagent-environment modeling framework is

illustrated as a system graph in Fig. 1. Here, each

agent, i, and task relevant environmental objects and

surfaces, j, are represented as nodes, with the

different nodes linked via mechanical forces, F, and

information, I. Note that an agent’s behavior is also

a function, G, of intrinsic dynamical or self-

referential processes. Similarly, environmental

objects or surfaces can also be influenced via

physical, F, object-object and object-surface

interactions.

This graph representation defines the “bottom-

up-all-the-way-down” nature of EMAD, where the

general aim of modeling such behavior is to

formalize the simplest set of functional relations that

give rise to observed macroscopic behavioral order.

Different task systems will of course entail different

graphs, each needing to be formalized into a specific

system of dynamical equations. This is best achieved

by defining a functional description of the

multiagent task dynamics in terms of an abstract task

space. Similar to the intrapersonal task dynamic

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

156

formalism of Saltzman and Kelso (1987), this

includes appropriately defining (i) the task goal in

terms of the relevant terminal objective, (ii) the

minimal number of task dimensions (i.e., relevant

task axes or variables), which correspond to the

active degrees-of-freedom of the task’s end-effector,

and (iii) the appropriate task dynamics (equations of

motion) for each task dimension; equations that

should qualitatively capture the movement or action

trajectories that are afforded along each task axis of

the terminal objective.

Admittedly, defining the relevant task

dimensions and appropriate equations of motion for

a specific multiagent task is not always easy and can

require an extensive amount of empirical research

and theorizing, not to mention a considerable

amount of trial-and-error. It is with this mind that we

have chosen to review a range of simple, yet

ubiquitous joint-action tasks and behaviors in order

to best illustrate this modeling process and how task

dynamic models (specifically with respect to

differential equation models) can be formulated to

capture and understand the interactive and self-

organizing processes that determine coordinated

multiagent behavior.

3 RHYTHMIC COLLISION

AVOIDANCE

As a first example of how to model the task

dynamics of goal directed multiagent coordination,

we consider the interpersonal rhythmic collision

avoidance task investigated by Richardson et al.,

(2015). For this task, pairs of naive participants were

instructed to continuously move a visual, computer

cursor (a small red dot) back and forth between

different sets of square target locations, positioned at

diagonally opposite corners of a 50” computer

monitor. Each participant in a pair stood facing their

own computer monitor, which displayed the real-

time motion of the participant’s own cursor, as well

as the motion of their co-participant’s cursor.

Participants controlled their respective computer

cursor using a motion-tracking sensor (see Fig. 2

top). One participant was instructed to continuously

move their cursor between the bottom-left and top-

right targets while the other participant was

instructed to continuously move their cursor

between the bottom-right and top-left targets. Most

importantly, participants were instructed to produce

these continuous cursor motions without colliding

into one another.

In this task, participant pairs were faced with a

conflict between the natural tendency to synchronize

straight-line movement trajectories between the

targets and the fact that such synchronization would

result in a collision. Thus, the research question

being investigated was what stable pattern(s) of

movement coordination would emerge to ensure task

success?

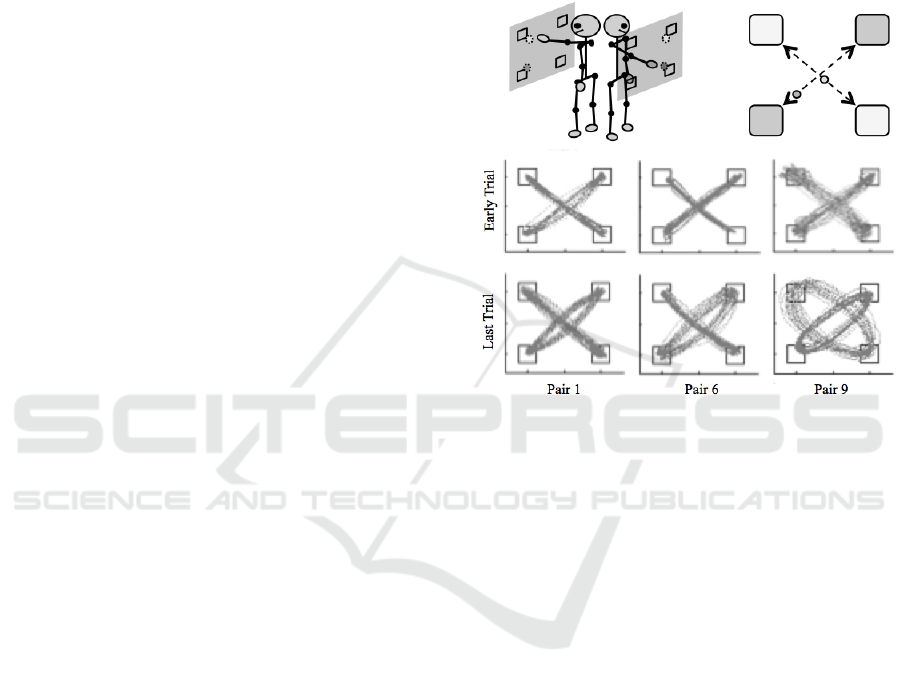
Figure 2: Illustration of the experimental setup (top left)

and task display (top right) employed in the Richardson et

al (2015) collision avoidance task. (bottom) Prototypical

examples of the movement trajectories exhibited by pairs.

Although pairs initially tried to adopt relatively

straight line trajectories between the target locations,

the results revealed that greater than 90% of pairs

quickly converged (by the 3

or 4

trial) onto a

stable task solution that involved complementary

task roles, with one participant adopting a more

straight-line trajectory between targets and the other

participant adopting a more elliptical trajectory

between targets (see Fig. 2, bottom). Moreover, the

participant who adopted the more elliptical

trajectory consistently lagged behind the participant

who adopted the more straight-line trajectory by an

average of approximately 10° to 30°. Richardson et

al., (2015) hypothesized that these complementary

behavioral dynamics were the result of a functional

asymmetry in the repulsive coupling that prevented

collisions, one that not only resulted in an inter-

participant asymmetry in the ellipticality of the

movement trajectories, but also simultaneously

allowed participants to synchronize their between

target movements at a phase lag (further increasing

the margin of safety). Of particular relevance to our

discussion here, is that Richardson et al. were able to

Modeling Embedded Interpersonal and Multiagent Coordination

157

test this hypothesis by developing a task dynamic

model of the interpersonal collision avoidance task.

Figure 3: (a) Illustration of the abstract task space axis for

the collision avoidance model developed by Richardson, et

al., (2015). (b) The task space orientated in the target goal

space for a pair of coupled individuals. See text for more

details.

Motived by the same task dynamic framework

described above, Richardson, et al., (2015)

developed this model by defining the terminal

objective of each actor’s task goal to be a rhythmic

motion of the end-effector (i.e., stimulus/end-

effector/hand, modeled as a point mass) between

two targets within a planar (two-dimensional) task

space (see Fig. 3a). In this task space, the x-axis

corresponded to the axis of instructed direction of

oscillation, and was provided with limit cycle

(oscillatory) dynamics. The orthogonal task axis, y,

corresponded to deviations away from the x-axis.

Given that an actor must minimize these deviations

with respect to achieving the instructed task goal,

Richardson et al. defined the y-axis with simple

point-attractor (damped mass-spring) dynamics.

Assuming a point mass of 1 (for simplicity), the

functional defined task space was then specified as:





−







+













+











+







+







(1a)

for actor 1 and





−







+











+











+







+







(1b)

for actor 2. Here, 



and 



, 



,



and



,



and





correspond to the position, velocity and

acceleration of each actor’s end effector (i.e.,

hand/cursor) along each task axis, respectively. b

and b

are the damping coefficients for axis x

and y

respectively, k

and k

are stiffness coefficients for

axis x

and y

, respectively, and (













 ) is the van

der Pol function for axis x

To capture the natural entrainment observed

between co-actors, Richardson and colleagues then

added an attractive coupling function to each

system, similar to what is typically employed for

modeling generalized rhythmic (inphase)

coordination. That is, they added the diffusive

coupling functions





(



−



)

(2a)

and





(



−



)

(2b)

to the equations that define each actor’s instructed

axes of motion, which resulted in the system





−







+













+







=



(



−



)





+







+











−







+











+







=



(



−



)





+









+









(3)

It is important to note at this point that Eq. (3)

provides an idealized model of inphase interpersonal

rhythmic coordination and can be adapted to model

the inphase coordination of any two end effectors or

point masses (e.g., finger tips; hands, feet, actors)

irrespective of the angular orientation of the

instructed motion axis. Moreover, other behavioral

patterns, such as antiphase coordination and the

bistable nature of rhythmic coordination performed

in the same direction/plane of motion can also be

captured using alternative coupling functions, e.g.,

as previously identified by Haken et al., (1985) (also

see e.g., Dumas et al., 2014; Kelso, 1995; Schmidt

and Richardson, 2008)

Based on the behavior of participants at the

beginning of the experiment (see Fig. 2),

Richardson, et al. (2015) began with the assumption

that pairs were initially constrained by the dynamics

of Eq. (3). The question then became what minimal

changes in the structure of Eq. (3) were required to

produce behavior qualitatively similar to that

produced by pairs by the end of the experiment?

Given that the task instructions were to ‘avoid

bumping or colliding into each other’, the simplest

modification was to add a repelling coupling force

that acted on each participant’s end-effector to

ensure they were repelled from each other. This was

accomplished using the repeller functions





(



+



)

|







(4a)





(



−



)

|







(4b)

for the primary task axes, x

and x

respectively, and





(



−



)

|







(4c)





(



+



)

|







(4d)

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

158

for the secondary task axes, y

and y

respectively.

In short, these repeller functions push the two

participants’ end-effectors away from each other, at

a strength determined by the parameters, γ

, and

inter-cursor distance, i.e., the exponential terms in

Eq. 4 mean that larger (smaller) distances between

the participants’ cursors result in weaker (stronger)

repelling forces (see Richardson et al., 2015 for

more details about how these coupling functions

were derived). Essentially, if γ

in participant-i’s (x,

y) system is set to zero, the effect of the repeller

coupling is null and a straight-line trajectory will be

created that is aligned along the participant’s limit-

cycle axis. However, if γ

is set to a value greater

than zero, the repeller coupling adds a force along

both task-axes of participant-i, resulting not only in

greater ellipticality (due to forces added along the

point-attractor task axis), but also in a phase lag

relative to participant-j when γ

is greater than γ

(due

to forces added along the limit-cycle task axis).

The complete task dynamic model derived by

Richardson et al., (2015) can therefore be written as







−







+













+







=



(



−



)–



(





+



)



|











+







+







=



(



−



)

|











−







+











+



=



(



−



)

+



(





−



)



|













+







+







=−



(



+



)

|







(5)

Importantly, this system was not only able to

successfully capture the stable asymmetric task

solution adopted by participants—namely,

asymmetric movement trajectories and phase-lagged

rhythmic synchronization—but it could also capture

the different types of successful and unsuccessful

movement solutions adopted by participants pairs

throughout the course of the experiment.

Essentially, there are three qualitative types of

movement trajectories that can be generated from

Eq. (5). These are displayed in Fig. 4 and depend on

the magnitudes of γ

and γ

and the degree that γ

≠

. First, if γ

= γ

= 0, then no motion is created

along 



or 



(i.e. 



= 



= 0), which makes the

behavior of Eq. (5) equivalent to the behavior of Eq.

(3). This corresponds to straight-line inphase

coordination (Fig. 4 left) and as noted previously

was what most participants in the Richardson et al

study spontaneously produced at the beginning of

the experiment—albeit to the detriment of success,

in that such behavior leads to collisions.

The second qualitative type of movement

trajectories exhibited by Eq. (5) occur when γ

≠ γ

As can be seen from an inspection of the right panel

of Fig. 4, when γ

≠ γ

an asymmetry in the between

target movement trajectories emerges, as well as a

phase lag between the more elliptical and the more

straight-line trajectory. This behavioral pattern is

similar to the successful task solution adopted by

pairs in the Richardson et al. study and is consistent

with the hypothesis that participants adopted an

asymmetric relation in coupling in order to avoid

collisions and simultaneously synchronize their

between target movements.

Figure 4: Examples of the three qualitative types of

movement trajectories that can be produced by the

Richardson et al., (2015) collision avoidance model, Eq.

(5), for various settings of the parameters of γ

and γ

(see

text for more details).

Lastly, if γ

= γ

> 0, then equivalent motion

patterns are created along 



and 



resulting in

elliptical trajectories that are symmetric across

participants and synchronized with zero phase lag

between the participants’ limit cycle axes.

Interestingly, this third situation also results in a

stable collision avoidance solution, especially for γ

= γ

>> 0, but one that does not include a phase lag

between the limit-cycle axes and, hence, has a lower

‘margin of safety’ than the asymmetric solution

adopted by participants for the second qualitative

type of movement pattern described above.

The third type of task solution was observed in a

follow-up study (Eiler et al., 2015), in which the

participants were not penalized for collisions. Under

these conditions, participant pairs also produced

movements with less ellipticality. That is, pairs

produced a more symmetrical pattern of elliptical

inphase coordination with a smaller degree of

ellipticality than when collisions were penalized.

Given Eq. (5), this suggests that decreasing the cost

of failure not only weakened the repulsive coupling

between participants, but also resulted in pairs

employing similar magnitudes of repulsive

avoidance (i.e., γ

≈ γ

> 0).

Most recently, Eiler et al., (2015) have also

demonstrated how Eq. (5) can predict the types of

patterns exhibited between pairs of individuals

walking or running back and forth between target

Modeling Embedded Interpersonal and Multiagent Coordination

159

locations in a real 3-dimensional space. Specifically,

Eiler et al., instructed pairs of participants to walk or

run at a comfortable pace back and forth between

sets of target landmarks positioned in a cross-type

arrangement (see Fig. 5, left). The distance between

the participants’ target landmarks were also

manipulated, with the landmarks positioned either 3

meters or 5 meters apart. Of particular significance,

was that the 2 (speed: walk vs. run) by 2 (distance: 3

vs. 5 m) within subjects design employed in this

study essentially mapped onto different

“chances/severity” of collision conditions, with

walking between targets positioned 5 m apart having

the lowest chance/severity of collision and running

between targets positioned 3 m apart having the

highest chance/severity of collision.

Figure 5: (left) experimental setup for the walking and

running collision avoidance task investigated by Eiler et

al., (2015). (right) Example movement trajectories for the

different target distance and pace conditions explored.

Figure 6: Experimental setup (top) and birds-eye view of

game field (bottom) for the sheepdog game investigated

by Nalepka et al., (2015).

As expected, the degree to which pairs adopted

synchronous straight line or elliptical movement

trajectories between the target locations, as well as

the symmetry of the co-actors movement

trajectories, was a function of these chance/severity

of collision manipulations (see Figure 5, right)—

patterns that could be captured by Eq. (5) by

modulating limit-cycle axis frequency (i.e., k

and

) and the magnitude and symmetry of the

repulsive coupling parameters γ

4 MULTIAGENT HERDING

As a second example of how task dynamic modeling

can be employed to understand EMAD, we consider

the multiagent sheepdog herding game recently

investigated by Nalepka et al., (2015). This game

required pairs of naïve participants to work together

to contain groups of 3, 5, or 7 virtual sheep (i.e.

small, ‘wool’-covered balls) within a central target

region of a virtual field presented on a large tabletop

display (see Fig. 6). The sheep’s’ movements were

governed by random Brownian motion dynamics

and were repelled away from virtual dogs (a blue or

red colored box) that the participants’ controlled in

real-time using hand-held motion tracking sensors.

Specifically, the participants held the sensors in their

hands on top of the colored boxes (dogs) projected

on the tabletop display, essentially making their

hand the “sheepdog”.

Initially all participants pairs adopted a kind of

search and recover strategy, in which each individual

would move toward and corral the furthest sheep from

the center of the game field on their side

However, when a pair’s search and recover

performance improved to the point where they could

consistently and effectively corral the sheep into the

target region in the center of the game field, most

pairs spontaneously transitioned to a coupled

oscillator containment strategy, in which the

participants synchronously moved back and forth in

a semicircular inphase or antiphase manner around

the target containment region—establishing a kind

of “spatiotemporal” wall around the sheep. The two

modes of behavior are illustrated in Figure 7.

Given that nearly all participant pairs

spontaneously adopted the search and recover

strategy at the very beginning of the

experiment(participants could not talk during the

experiment) and then, over the course of repeated

performance, also discovered the coupled oscillatory

containment strategy, Nalepka, et al., concluded that

both behavioral modes were entailed by the

constraints, goals and inter-agent couplings that

defined the multiagent sheep herding game.

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

160

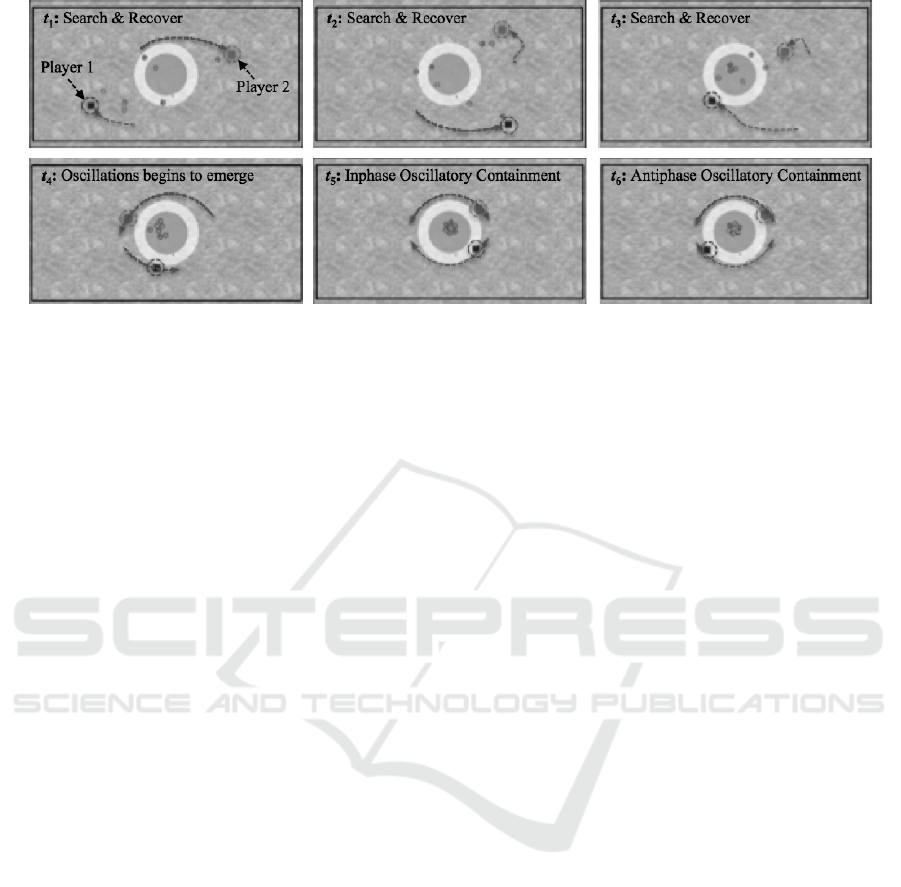
Figure 7: Time lapsed (t1…t6) illustrations of the two behavioral modes exhibited by pairs in the sheepdog herding game.

Dashed arrows indicate movement direction. Dashed circles highlight participant (sheepdog) position of the table, moving

from sheep to sheep in an attempt to get all of the sheep within the central target area and then keep them there.

In other words, the behavioral modes adopted (and

discovered) by participants were both stabilities of

the games task dynamics. Furthermore, finding that

the stable patterns of synchronized oscillatory

containment were consistent with the stabilities of

intra- and interpersonal rhythmic coordination (e.g.,

Haken et al., 1985; Kelso, 1995; Schmidt et al.,

1990; Schmidt et al., 1998; Richardson et al.,

2007)——namely, stable inphase and antiphase

behavior was observed, with inphase coordination

occurring more frequently and more stably than

antiphase coordination—also led Nalepka and

colleagues to conclude that the underlying

dynamical system should entail a corresponding

coupled oscillator process.

In support of these conclusions, Nalepka, et al.

have been developing a simple task dynamic model

of the sheepdog game that not only captures (i) both

behavioral modes within the same system of

equations of motion and (ii) the prototypical

dynamics of interpersonal rhythmic coordination

(i.e., coupled oscillators), but also (iii) the possibility

for a spontaneous transition between the two

behavioral modes as a function of a sheep-distance

dependent Hopf bifurcation (here we present a

preliminary version of the model that has been

developed to date). As illustrated in Fig. 8, the

preliminary model (still to be completely validated)

captures the terminal objective of a participants’

behavior with respect to the center of containment

region within the ξ

and ξ

game space. Here, x

the oscillatory perimeter path of each participant i’s

hand, where i = 1 or 2, with respect to half (π-

radians) of the target containment region of success

closest to the participant’s side of the game space. y

corresponds to the radial distance of each participant

from the center of the game space and θ

is the radial

angle of each participant from the center of the game

space defined with respect to the ξ

polar axis on

each participants side of the table (i.e., +ξ

for

participant 1 and -ξ

for participant 2). Thus, each

participant’s perimeter path, x

, is centered on the

participants radial (y

, θ

) position within the (ξ

, ξ

)

game space.

To be consistent with the previous research

modeling the dynamics of rhythmic arm and hand

movements (Kay et al., 1987), and rhythmic

interlimb and interpersonal coordination (Haken, et

al., 1985; Schmidt and Richardson, 2008), the

topology of the x

perimeter path movement was

defined using a set of coupled hybrid nonlinear

oscillators of the form





+







+









+













+









(





−



)

(



−

(





−



)



)





+







+









+











+







(





−



)

(



−

(





−



)



)

(6)

with the positive/negative (excitatory/inhibitory)

damping parameters 



and 



, scaled as a function

of sheep distance using the equation





=



(

,()



−

,

−



)

(7)

For Eq. 6, 



and 



, 



 and 



 , 



 and 



 correspond

to the position, velocity and acceleration of each

agent’s hand along the 



path, 





defines the

stiffness or frequency of movement along the

corresponding 



path, and the functions (









) and

(













) corresponding to Rayleigh and van der Pol

escapements terms, respectively. The coupling

function to the right of the equals sign in each

equation is the same as that previously derived by

Haken et al., (1985), and defines both inphase (0°)

and antiphase (180°) relative phase relationships as

the stable coordination modes between the two

Modeling Embedded Interpersonal and Multiagent Coordination

161

oscillators (when 



and 



< 0), whose relative

strength is defined by the parameters A and B.

Figure 8: Illustration of the task space employed for the

sheep-herding model which captures player i’s (where i =

1 or 2) sheepdog location at any time within the ξ

and ξ

planar game space in polar coordinates (y

, θ

), with y

corresponding to the radial distance of player i from the

center of the ξ

and ξ

planar game space and θ

corresponding to player i's radial angle (± 90°) from the ξ

game space axis on their side of the game field. x

is the

oscillatory perimeter path of each participant i’s sheepdog

with respect to half (π-radians) of the target containment

region of success closest to the participant’s side of the

game space, such that each participant’s perimeter path, x

is centered on the participants radial (y

, θ

) position within

the (ξ

, ξ

) game space (see text for more details).

Central to the switch between the search and

recover and oscillatory containment modes of

behavior is the Hopf bifurcation that occurs for each

oscillator system, 



, when 



is decreased from a

positive to a negative value. That is, when 



> 0, 



behavior is that of a nonlinear damped mass spring

with a stable fixed-point solution. However, when 



< 0, 



behavior is that of a nonlinear limit cycle

oscillator.

As defined in Eq. (7), the value of 



at any

instance in time, (t), is a differential function of the

distance, 

,()

, of the furthest sheep on participant

i’s side of the game space with respect to a

maximum safe containment distance, 

,

and a

fixed rate of change parameter 



. Accordingly,

when the distance, 

,()

, of the sheep furthest

from the center of the game space on participant i's

side of the game space is outside participant i's

maximum safe containment distance,

,

, 



> 0

and behavior along the 



corresponds to that of a

nonlinear mass damped spring. Conversely, when

the distance, 

,()

, of the sheep furthest from the

center of the game space on participant i's side of the

game space is inside participant i's maximum safe

containment distance,

,

, 



< 0 and behavior

along the 



corresponds to that of a nonlinear limit

cycle oscillator.

A participant’s radial distance, 



, was defined as





+







+







−(

,()

+

,

) = 0

(8)

with the radial orientation 



defined by







+









+







−

,

(



)



,

=0

(9)

Here, 



and 



, and 





and 





correspond to the

velocity and acceleration of participant i’s radial

distance and radial orientation from the center of the

game space, respectively. 

,()

is again the

distance of the furthest sheep on participant i’s side

of the game space and 

,()

is the angle of the

furthest sheep on participant i’s side of the game

space relative to corresponding ξ

polar game space

axis. 

,

is a fixed parameter the sets minimum

preferred distance that a participant likes to approach

a sheep, and 



and 



scale the force (rate) at which

participant i minimizes the difference between the

radial distance and radial angle of their sheepdog

and the radial distance and angle of the furthest

sheep from the center of the game space on their

side of the game field, respectively. Finally, 

,

a Heaviside parameter defined as





=

0, 

,()



,

1, 

,()



,

(10)

which results in the stable fixed point solution



,

=0, when all of the sheep on participant i’s

side of the game space are within the participant’s

maximum safe containment distance,

,

. Thus,

when all of the sheep on participant i’s side of the

game space are within the region of containment, the

radial orientation 



approaches zero for participant i

and their corresponding 



path is centered about ξ

Collectively, the task dynamic model of the (bi-

agent) sheepherding game can be written as follows,

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

162





+







+







−(

,()

+

,

) = 0







+









+







−

,

(



)



,

=0





+







 +









+













+









(





−



)

(

−

(





−



)



)





=



(

,

(



)



−

,

−



)





=

0, 

,()



,

1, 

,()



,





+







+







−(

,()

+

,

) = 0







+









+







−

,

(



)



,

=0





+







 +









+











+







(





−



)

(

−

(





−



)



)





=



(

,()



−

,

−



)





=

0, 

,()



,

1, 

,()



,

(11

)

Importantly, not only does this model effectively

capture the bimodal behavior exhibited by pairs in

the experimental study, but it is also resistant to

perturbations in the sheep movement and location

and is able to spontaneously transition between the

search and recover and oscillatory containment

behavioral modes via a sheep distance dependent

Hopf bifurcation process. Videos presenting

example demonstrations and simulations of the

model, as well as a real participant behavior can be

viewed at: http://www.emadynamics.org/bi-agent-

sheep-herding-game/.

5 CONCLUSION

Our aim here was to provide a brief overview of

how EMAD can be modeled and understood using a

task dynamic framework. It is important to

appreciate that the goal of dynamical modeling is

not to perfectly simulate the exact trajectory or end

state of system behavior, but to shed light on the

structural relations and self-organizing processes

that give rise to effective and robust behavior.

Indeed, the power of a task dynamical model rests

on its ability to validate hypotheses, generate

testable predictions, and motivate future research

questions. It is in this way that developing self-

organized task dynamic models have the potential to

uncover the fundamental processes that shape and

constrain human behavior in general.

ACKNOWLEDGEMENTS

The research was supported by National Institutes of

Health, R01GM105045.

REFERENCES

Chemero, A., 2009. Radical embodied cognitive science.

Boston, MA: MIT Press.

Coey, C., Varlet, M., Richardson, M. J., 2012.

Coordination dynamics in a socially situated nervous

system. Frontiers in human neuroscience. 6, 164.

Dumas, G., de Guzman, G. C., Tognoli, E., Kelso, J. S.,

2014. The human dynamic clamp as a paradigm for

social interaction. Proceedings of the National

Academy of Sciences, 111(35), E3726-E3734.

Eiler, B., Coey, C. A., Ariyabuddhiphongs, K., Kallen, R.

W., Harrison, S. J., Saltzman, E., Schmidt, R. C.,

Richardson, M. J., 2015. Poster presented at the 5th

Joint Action Meeting, Budapest, Hungary, July 2015.

Eiler, B., Kallen, R. W., Harrison, S. J., Saltzman, E.,

Schmidt, R. C., Richardson, M. J., 2015. Behavioral

Dynamics of a Collision Avoidance Task: How

Asymmetry Stabilizes Performance. In Noelle, D. C.,

Dale, R., Warlaumont, A. S., Yoshimi, J., Matlock, T.,

Jennings, C. D., & Maglio, P. P. (Eds.) Proceedings of

the 37th Annual Meeting of the Cognitive Science

Society. Austin, TX: Cognitive Science Society.

Eiler, B., Kallen, R. W., Harrison, S. J., Richardson, M. J.,

2013. Origins of Order in Joint Activity and Social

Behavior. Ecological Psychology, 25, 316–326.

Graf, M., Schütz-Bosbach, S., Prinz, W., 2009. Motor

Involvement in Action and Object Perception

Similarity and Complementarity. In G. Semin, & G.

EchterhoV (Eds), Grounding sociality: Neurons,

minds, and culture. NY: Psychology Press.

Haken, H., Kelso, J. A. S., Bunz, H., 1985. A theoretical

model of phase transitions in human hand movements.

Biological Cybernetics, 51, 347-356.

Kay, B. A., Kelso, J. A., Saltzman, E. L., Schöner, G.

(1987). Space–time behavior of single and bimanual

rhythmical movements: Data and limit cycle model.

Journal of Experimental Psychology: Human

Perception and Performance, 13(2), 178.

Kelso, J. A. S., 1995. Dynamic patterns. Cambridge, MA:

MIT Press.

Knoblich, G., Butterfill, S., Sebanz, N.,

2011. Psychological research on joint action: theory

and data. In B. Ross (Ed.), The Psychology of

Learning and Motivation, 54 (pp. 59-101), Burlington:

Academic Press.

Marsh, K. L., Richardson, M. J., Schmidt, R. C., 2009.

Social connection through joint action and

interpersonal coordination. Topics in Cognitive

Science, 1, 320-339.

Nalepka, P., Riehm, C., Mansour, C. B., Chemero, A.,

Richardson, M. J., 2015. Investigating Strategy

Discovery and Coordination in a Novel Virtual Sheep

Modeling Embedded Interpersonal and Multiagent Coordination

163

Herding Game among Dyads. In Noelle, D. C., Dale,

R., Warlaumont, A. S., Yoshimi, J., Matlock, T.,

Jennings, C. D., Maglio, P. P. (Eds.) Proceedings of

the 37th Annual Meeting of the Cognitive Science

Society. Austin, TX: Cognitive Science Society.

Newman-Norlund RD, Noordzij, ML, Meulenbroek,

R.G.J, Bekkering H., 2007. Exploring the brain basis

of joint action: Co-ordination of actions, goals and

intentions. Social Neuroscience, 2, 48-65.

Richardson, M. J. Dale R., Marsh, K. L., 2014. Complex

Dynamical Systems in Social and Personality

Psychology: Theory, Modeling and Analysis. In H. T.

Reis, and C. M. Judd. (Eds.). Handbook of Research

Methods in Social and Personality Psychology, 2

Edition. New York, NY: Cambridge University Press.

Richardson, M. J., Kallen, R. W., 2015. Symmetry-

Breaking and the Contextual Emergence of Human

Multiagent Coordination and Social Activity. In E.

Dzhafarov, S. Jordan, R. Zhang, and V. Cervantes

(Eds.). Contextuality from Quantum Physics to

Psychology. (pp. 229-286). World Scientific.

Richardson, M. J., Harrison, S. J., Kallen, R. W., Walton,

A., Eiler, B., Schmidt, R. C., 2015. Self-Organized

Complementary Coordination: Dynamics of an

Interpersonal Collision-Avoidance Task. Journal of

Experimental Psychology: Human Perception and

Performance.

Richardson, M. J., Marsh, K. L., Isenhower, R., Goodman,

J., Schmidt, R. C., 2007. Rocking together: Dynamics

of intentional and unintentional interpersonal

coordination. Human Movement Science, 26, 867-891.

Riley, M. A., Richardson, M. J., Shockley, K. Ramenzoni,

V. C., 2011. Interpersonal Synergies. Frontiers in

Psychology, 2, 1-7.

Saltzman, E. L., Kelso, J. A. S. (1987). Skilled actions: A

task dynamic approach. Psychological Review, 94, 84–

106.

Schmidt, R. C., Bienvenu, M., Fitzpatrick, P. A.,

Amazeen, P. G., 1998. A comparison of within- and

between-person coordination: Coordination

breakdowns and coupling strength. Journal of

Experimental Psychology: Human Perception and

Performance, 24, 884-900.

Schmidt, R. C., Carello, C., Turvey, M. T., 1990. Phase

transitions and critical fluctuations in the visual

coordination of rhythmic movements between people.

Journal of Experimental Psychology: Human

Perception and Performance, 16, 227-247.

Schmidt, R. C., Fitzpatrick, P., Caron, R., Mergeche, J.,

2011. Understanding social motor

coordination. Human Movement Science, 30, 834-845.

Schmidt, R. C., O'Brien, B., 1997. Evaluating the

dynamics of unintended interpersonal coordination.

Ecological Psychology, 9, 189-206.

Schmidt, R. C., Richardson, M. J., 2008. Dynamics of

Interpersonal Coordination. In A. Fuchs & V. Jirsa

(Eds.). Coordination: Neural, Behavioral and Social

Dynamics. (pp. 281-308). Heidelberg: Springer-

Verlag.

Schmidt, R. C., Turvey, M. T., 1994. Phase-entrainment

dynamics of visually coupled rhythmic movements.

Biological Cybernetics, 70, 369-376.

Vesper, C., Butterfill, S., Knoblich, G., Sebanz, N.,

2010. A minimal architecture for joint action. Neural

Networks, 23, 998-1003.

Warren, W. H. (2006). The Dynamics of Perception and

Action. Psychological Review, 113, 358–389.

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

164