
Finding Most Frequent Path based on Stratified Urban Roads
Enquan Ge, Jian Xu, Ming Xu, Ning Zheng, Weige Wang and Xinyu Zhang
School of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou, China
Keywords:
Path Query, Upgrade Points, Road Levels, Trajectory Data, Stratified Urban Roads.
Abstract:
The path query based on big trajectory data has become a promising research direction due to the rapid de-
velopment of the Internet. Previous studies mainly focus on searching paths in full road network and ignore
the importance of stratified urban roads. It is observed that higher-level roads gather more trajectory points
which means most drivers prefer the high-level road. In this paper, we study a new path query to find the
most frequent path (MFP) based on road levels in large-scale historical trajectory data. We refer to this query
as most frequent path based on road levels (RLMFP). Intuitively, selecting roads which are in line with local
custom and choosing high-level roads such as high-way are people’s two common sense notions. Our query
not only satisfies aforementioned sense, but also has two advantages in algorithm implementation. First, the
road hierarchy can speed up the path query. Next, the trajectory data can find more reasonable upgrade points
(e.g., path query based on road levels need to find the intersection between low-level roads and high-level
roads). Experiments show the effectiveness and the efficiency of our method.
1 INTRODUCTION
With the increasing amount of available information
in Internet, our society has entered a new period of
information technology. In our daily life, the number
of Global Positioning System (GPS) and devices with
wireless interactive system such as mobile phones,
navigation systems and emergency communications
are increasing quickly. These Location-Based Ser-
vices (LBS) have become increasingly popular. The
demand for such services is also rising, especially
the requirements of recommended route. Specifically,
given a source S, a destination D and a map, a recom-
mended route system is able to find a path from S to
D in a map.
In recent years, a large number of mobile devices
and navigation devices also surge to generate trajec-
tory data, so more and more people begin to focus on
the study of path query with historical trajectory. His-
torical trajectory data can represent the users’driving
habits which are very significant for the path query.
For example, when tourists arrive in an unfamiliar
place and get lost, what they want to do is to ask
a local person rather than use navigation equipment.
Though this path is not the fastest one or the shortest
one, it is the most suitable in a combination of time,
length and road conditions (Su et al., 2014). Thus if a
path query system returns a route based on historical
trajectory data, it also imply the local drivers’ path se-
lection habits. This is the first requirement that a nav-
igation system must meet. Researchers (Luo et al.,
2013)(Chen et al., 2011) have provided methods to
solve it. Another requirement is that users wish to
pass through fewer junctions and drive on better roads
(e.g., freeway or highway). Figure 1 is a partial road
network of Beijing. The set of purple points are the
real trajectory data of taxi drivers, we get the trajec-
tories from (Yuan et al., 2011). This is a sample of
T-Drive trajectory data that contains one-week trajec-
tories of 10,357 taxis. Some of them are presented
on the map of Beijing in Figure 1. We can see that
more drivers prefer higher level roads. Note that there
are less intersections and traffic lights on higher level
roads. Besides, when drivers use a navigation equip-
ment which provides a path with many intersections
and lanes, it is easy for them to take a wrong way or
miss intersections they need to turn. Previous meth-
ods generally search a path on the whole map. There-
fore, they may be insensitive to road levels and could
not meet the second requirement. Note if an algorithm
is searching based on the full map and the map con-
tains a huge number of intersections and roads, the
conventional methods would spend a large amount of
search time.
We study a novel method named most frequent
path based on road levels (RLMFP). Most frequent
paths (MFP) (Luo et al., 2013) use trajectories to rec-
ommend path. Different from other algorithms, the
Ge, E., Xu, J., Xu, M., Zheng, N., Wang, W. and Zhang, X.
Finding Most Frequent Path based on Stratified Urban Roads.
In Proceedings of the 2nd International Conference on Geographical Information Systems Theor y, Applications and Management (GISTAM 2016), pages 51-60
ISBN: 978-989-758-188-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
51
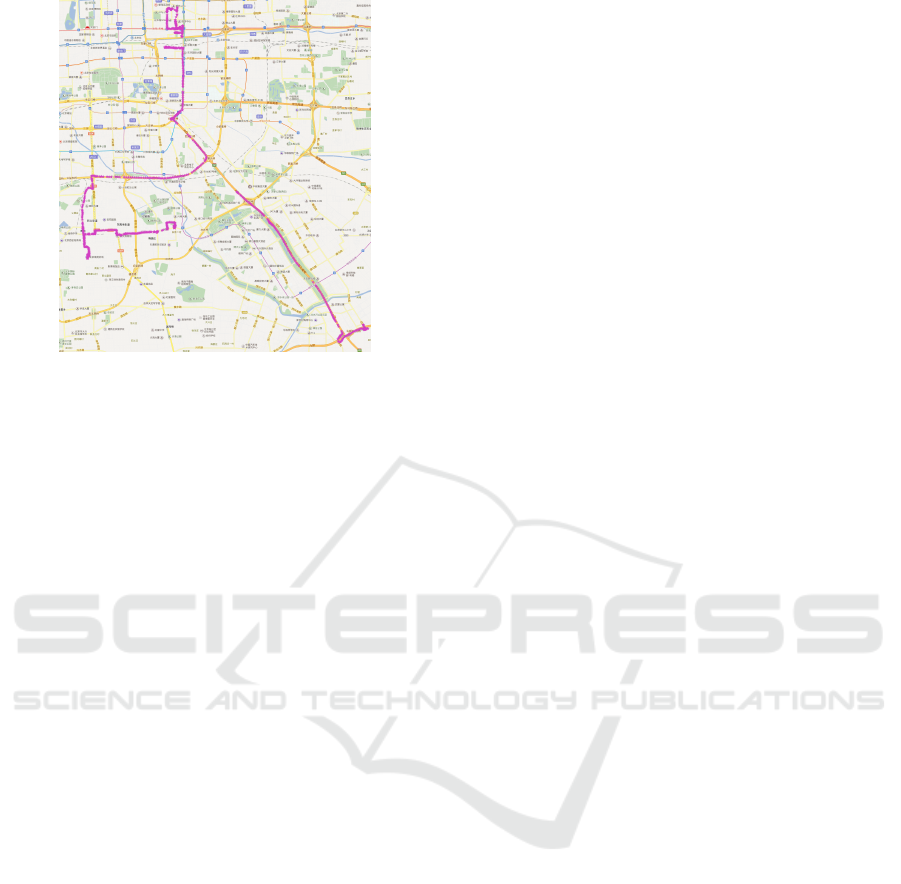
Figure 1: Partial map of Beijing.
weight of an edge in MFP is defined as counting
the number of the trajectories passing through this
edge. This weight of a map is named as edge fre-
quently. And the weight of a path is a sequence ob-
tained by sorting all the edge weights of P in non-
decreasing order. For example, there are five edges
in P and their weights are (5,3,6,4,7). So the weight
of this path is (3,4,5,6,7). Similarly, another path P
0
is (2,6,7,8,9,11). P is better than P
0
in MFP because
3(the first weight of P) is bigger than 2(the first weight
of P). It can well meet the first requirement of users
for the path finding. This method of judging a bet-
ter path is used by RLMFP. Here road level means
the level of a road in a city. Many cities have their
own plan and make roads into several levels accord-
ing to their states, roles and traffic function. For in-
stance, roads of China and Unites States are classified
into 4 levels, and those of European Union are clas-
sified even into 13 levels. The roads of each level
have different functions and properties. For example,
the function of highways is to connect multiple large
regions and the properties of highways define the de-
sign speed (60-80km / h), the number of one-way road
(≥4) and the width of total road (40-70m). In this pa-
per we use the nature road levels to speed up the path
searching and select high-level road segment to meet
the second demand.
In brief, our algorithm first associate level proper-
ties to the vertexes and edges of road networks , then
judges the area where the start point (end point) lies
in and then determines the highest level of road net-
work and the upgrade points (i.e., the points connect-
ing edges in different levels). After that it uses MFP
to find all sub-paths in the area. At last, we combine
all sub-paths and chooses the best one. As shown in
Figure 3, A1,A2,A3 and A4 are the upgrade points of
S in area(2 − 3). Similarly to S, D1 and D2 are the
upgrade points of D. The rough(thin) edges represent
high(low) level roads. Firstly, we get the S.area and
D.area. Here is area(2 − 3) and area(5 − 2). Then
an index named FG(section 6) is used to find a set of
best upgrade points from area(2 − 3) to area(5 − 2).
Assuming A3,A4 and D1 is selected. Then we use
MFP to compute the paths from A to A3,A4 , D to D1
in low level road networks and A3,A4 to D1 in high
level road. Then we combine these sub-paths. There
are two paths which are P1(A → A3 → D1 → D) and
P2(A → A4 → D1 → D). And finally, we select the
better paths with Definition 2.11. The details of algo-
rithm is given in following paragraphs.
So MFP algorithm considering road levels is fea-
sible, effective and evidence-based. But existing hier-
archical algorithm often layers for the convenience of
calculation ignoring the delamination characteristics
owned by the road itself. In this paper, aside from the
function of building a new road network, the trajec-
tory data is also used to determine the upgrade points.
We also construct an index of all upgrade points. This
can not only help correct direction, but also speed up
the algorithm.
Above all, our method is justified in reality and
validated in algorithm. The contributions of this paper
are the following.
• We propose a novel path query named most fre-
quent path based on road levels (RLMFP).
• We present a hierarchical algorithm to solve
RLMFP problem.
• We present an algorithm to build the index struc-
ture of upgrade points (FG).
• We develop a new hierarchical algorithm to solve
RLMFP problem using the index structure of up-
grade points (RLMFPT).
The rest of this paper is organized as follows.
First, we briefly introduce a four-step framework to
solve the RLMFP problem in the context of very large
trajectory data sets (Section 2). Second, we provide
an algorithm to build a weighted road networks (Sec-
tion 3). Third, we explain area division (Section 4).
Fourth, we present a hierarchical algorithm to solve
RLMFP (Section 5). Fifth, we propose a method to
build the index structure of upgrade points. Sixth, we
develop a new hierarchical algorithm to solve PLMFP
utilizing the index structure of upgrade points (Sec-
tion 6). Then we present the experimental results
(Section 7). Next, we review the related work. We
conclude the paper in (Section 8).
GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management
52

Table 1: Summary of Notations.
Notation Description
G,P,Y road network, path, trajectory
V ,E set of vertex(points), set of edge(roads)
G(i),V (i),E(i) i–level of G,V,E
X path or trajectory
X.s/X.d starting/ending vertex of X
X[i] the i–th element of X
T set of trajectory
F(u,v) frequency of edge (u,v)
F(P) frequency of path P
int(q) set of q–level upgrade vertices
NG new graph with trajectory data
FG an index for upgrade points set
S.area(q) the area for point S in q–level graph
P(area)/area(P) the area for point P
Area[i] the i–th area of graph
2 THE RLMFP PROBLEM
2.1 Problem Formulation
In previous section, two key requirements for path
query are provided from the users.
Property 2.1 (Local Drivers Path Selection). Select-
ing roads which are in line with local custom.
Property 2.2 (Better Roads). The roads with less in-
tersections and high-level road.
We have showed that the path from trajectory data
can meet Property 2.1 and the algorithm based on
road levels can satisfy Property 2.2. The definition of
RLMFP should satisfy the above 2 key requirements.
Here follows the formal definition. For clarity, the
main notations used in the rest of this paper are sum-
marized in Table 1.
Definition 2.1 (Road Network). A road network is a
directed graph G = (V,E) where V represents the set
of road intersections and E represents the set of road
segments.
Figure 1 presents a partial road network of Bei-
jing.
Definition 2.2 (Path). Given G, path P is a set of con-
sequent roads E
Q
= {(x
1
,x
2
),(x
2
,x
3
),.. ., (x
k−1
,
x
k
)} and intersections V
Q
= (x
1
,x
2
,.. ., x
k
) from x
1
to
x
k
. P is a subgraph of G and the x
i
are all distinct.
P.s, P.e, and P[i] are used to denote the source ver-
tex x
1
, the ending vertex x
k
, and the i-th vertex x
i
,
respectively. In addition, P is often represented by
P.s → P.e or P(x
1
→ x
2
→ ·· · → x
k
) in short, where
P.s (or P.e) represent x
1
(or x
k
).
Definition 2.3 (Trajectory). Given G, a trajectory Y
is a sequence ((y
1
,t
1
),(y
2
,t
2
),.. ., (y
k
,t
k
)) such that
there exists a path y
1
→ y
2
→ ··· → y
k
on G and t
i
is
a time stamp indicating the time when Y passes y
i
.
Similar to path, Y.s, Y.e, and Y [i] are used to de-
note the source vertex y
1
, the ending vertex y
k
, and
the i–th vertex y
i
, respectively. In addition, Y is often
represented by Y.s → Y.e in short, where Y.s(or Y.e)
represent x
1
(or x
k
) or Y (x
1
→ x
2
→ · ·· → x
k
). We
denote T as the set of Y .
Definition 2.4 (Edge Frequency). Given G, T , and
an edge (u,v) ∈ G, the edge frequency F(u,v) is the
number of the trajectories containing (u,v).
Definition 2.5 (Trajectory Network). A road network
is a directed graph G = (V,E) where V represents the
set of road intersections, E represents the set of road
segments. We use W to represent the set of the weight
of each edge. In this paper, W is a set of the edge
frequency.
Definition 2.6 (Edge Level). Given a road network
G = (V,E), the level of an edge e is denoted as
e.level(i) according to the existing road network,
where i is the level of the road.
As shown in Figure 1, the yellow edges represent
the highest level edges and each level of them is 1
written as e.level(1).
Definition 2.7 (Vertex Level). The level of a vertex v
denoted v.level, is defined as the highest level of all
edges to v. Vertex v is also written as v.level(i) when
the level of a vertex i is known.
As shown in Figure 1, the level of yellow edges is
e.level(1) and the level of buff edges is e.level(2). If
one vertex v is the intersection of the yellow edge and
the buff edge, the level of v takes the highest of edges
and here is v.level(1).
Definition 2.8 (Upgrade Vertex). A vertex v is an up-
grade vertex when the edges it connects are not in the
same level. The set of upgrade vertices in same level
is denoted as int(q) where q is the level.
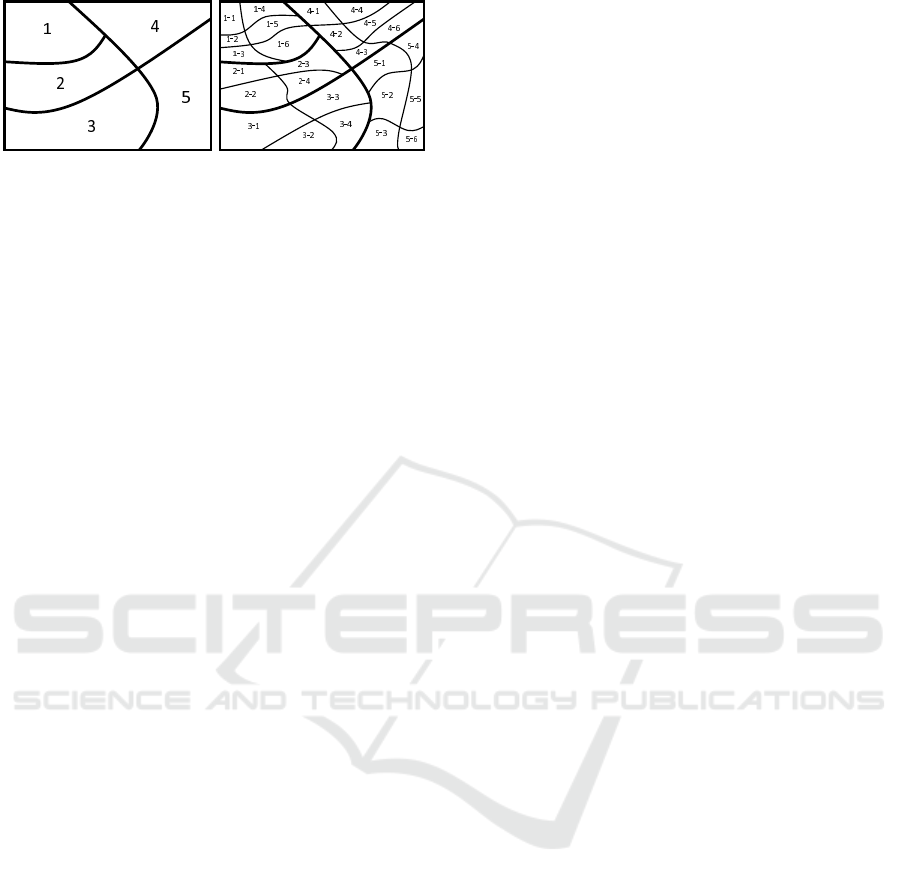
As shown in Figure 3, A1 connected a 3-level edge
and a 2-level edge, so A1 is an upgrade vertex. If we
want to find the path from S to D, then the upgrade
vertices A1,A2,A3,A4 belong to S.int(1).
Definition 2.9 (Layered Graph). Layered graph
G(i) = (V (i), E(i)) is a subgraph of G, to ∀e(or v) ∈
E(i)(or V (i)), e.level(or v.level) ≤ i.
As shown in Figure 2, G(2)is a road network G,
this is because the lowest level of G(2) is 2,so G(2)
contains all vertices and edges. Thus G(2) is G and
G(1), G(2) represents the graph of level 1 and level 2.
Definition 2.10 (Area). Given a graph G(i) =
(V (i),E(i)) ,dividing the G(i + 1) into several sub-
graph through E(i). Each area Area( j) is one
Finding Most Frequent Path based on Stratified Urban Roads
53

area of G(i + 1) where j ∈ (1,2, .. ., k). ∀e ∈
Area( j),e.level ≥ i +1.
As shown in Figure 2, G(1) using its edges to cut
G(2) into five areas. For any area, the level of its
edges is no smaller than 2.
Definition 2.11 (More-frequent-than Relation).
Given two path frequencies F(P) = ( f
1
,.. ., f
m
)
and F(P
0
) = ( f
0
1
,.. ., f
0
n
) w.r.t. the same trajectory
network, F(P) is more-frequent-than F(P), denoted
as F(P) F(P), if one of the following statements
holds:
• F(P) is a prefix of F(P
0
);
• there exists a q ∈ 1,. .. ,min(m, n) such that 1) f
i
=
f
i
for all i ∈ 1,... ,q −1, if q > 1, and 2) f
q
> f
0
q
.
Particularly, F(P) is strictly-more-frequent-than
F(P
0
), denoted as F(P) > F(P
0
), if F(P) F(P
0
) and
F(P) 6= F(P
0
).
Problem Statement: Given a graph G, trajectory
set T, source S and a destination D, the recommended
route system searches MFP based on road levels from
S to D.
2.2 Solution Overview
Most frequent path based on road levels has four
steps. It is shown in Algorithm 1. First, a large num-
ber of trajectory data should be matched to the road
network so as to construct a new road network where
the weight is edge frequency. Then we divide the
graph into different areas according to the natural road
levels. Next the trajectory data T and the stratified
graph G∗ are employed to build index FG (section 6).
Finally, we use the algorithm to search the RLMFP
and return the P.
The first step of this algorithm is to build G∗,
which means make the trajectory data match the road
network. GPS data is a sequence of vertices made by
users, therefore the path depending on the trajectory
can reflect the choice of users. After building a new
graph, some methods (Luo et al., 2013)(Chen et al.,
2011) compute the path on whole road network di-
rectly. Though there are different ways in various al-
gorithms, each of them should scan the full road net-
work. Hence stratification is introduced in this paper.
In step 2, G is divided into areas by road levels. For
example, the first level road network G(1) is the high-
est. Then we utilize the edge of first level to divide
G into areas where any edge of areas is lower than
1. The existing algorithm (Bast et al., 2006) must tra-
verse all upgrade vertices in the area. Here we em-
ploy the trajectory data to reduce the number of up-
graded vertices. After that, the areas, road levels and
upgrades vertices are determined according to detect
which area the start vertex and end vertex lie in. Fi-
nally, we can perform the RLMFP.
Algorithm 1: Five steps for the RLMFP query.
Require:
G: road network; T : trajectory data set; S: start point;
D: end point;
Ensure:
the RLMFP;
1: build a new road network G∗ w.r.t. T ;
2: divide G into areas w.r.t. road levels;
3: build an index FG w.r.t T and stratified graph in 2;
4: find the RLMFP P from S to D;
5: return P;
3 CONSTRUCT WEIGHTED
ROAD NETWORK
In this section, we construct a weighted road network.
According to the Definition 2.5, the weight of an edge
is different in algorithms. The existing algorithms ad-
dress the weight with Euclidean distance (Bellman,
1958)(Dijkstra, 1959), network distance and speed.
In this paper the weight of one road segment is de-
termined by the times that users passed. It is obvious
that the path based on Euclidean distance means the
nearest path and the path based on speed means the
fastest path. However, in fact, some drivers may avoid
aforementioned paths due to their experience, for ex-
ample, when in a strange place, users prefer to believe
the local people rather than the navigation system (Su
et al., 2014).
Algorithm 2: Build weighted road network.
Require:
G: road network; T : trajectory data set;
Ensure:
G∗: new road network;
1: G∗ ← NG[V G][V G] matrix with all entries zeros;
2: for each Y in T do
3: match Y to G ;
4: get a path P corresponds Y in G ;
5: for each edge e in P do
6: search e in G∗;
7: NG.edge.weight + + ;
8: return NG;
The idea is to find path depending on the history
trajectory data of the local residents. It is because the
local person drives in their familiar areas and trajec-
tory data record their driving habits. So the first step is
to build a trajectory network. It is shown in Algorithm
GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management
54
(a) G(1) = E(1) (b) G(1) = E(1) ∪ E(2)
Figure 2: Experiments of similarity, path points and query
time in three algorithms.
2. First of all, we set the weight of each edge 0(line
1). Then we scan each trajectory and match them to
G(line 2-3). Note that there will be a corresponding
path produced(line 4). Next each edge section of the
path are selected from NG and add 1 to the weight of
them. We repeat the last steps until all the trajectory
have been processed.
4 AREA DIVISION
Due to the idea based on stratification, after the com-
pletion of constructing the new road network G∗, G∗
needs to be divided into areas. Though road levels
are used in previous researches, most of them do this
for the convenience of the calculation. In fact, roads
themselves have level property and they are produced
by the traffic conditions, living areas, working areas,
etc. As shown in Figure 2, G(2) is a layered network.
Assuming that we divide road network into 2 lev-
els in Figure 2. According to the function of different
roads, the roads can be divided into first-level roads
E(1)(e.g. highway, freeway)and second-level roads
E(2)(e.g. city roads). In this way, G∗ can be ex-
tracted into a two-level structure of network. Here
G(1) = E(1), G(2) = E(1) ∪ E(2). Those nodes lo-
cated in the same position of different-level graphs
and connect to edges in different levels become the
upgrade vertices, which ensure the conversion of the
roads between the different layers.
After the road stratification, low-level road net-
works should be divided into some smaller areas ac-
cording to the level of the road network. In area-
partition process, the high-level graph is cut by its
edges and the areas from it are the ones of next graphs.
We adopt a flood-filling algorithm (Gonzalez et al.,
2007) to divide the graphs. Firstly, get a random ver-
tex whose level is lower than the cutting edges. Then
apply Breadth-First-Traversal(BFS) to the point. Note
that if BFS encounters a vertex whose level equals to
the level of cutting edges, the vertex would not be-
come traversed one but would be an upgrade point of
this area. We refer to the set of upgrade points as
int(q) in their area, where q is the level of their area.
Process is repeated until there is no traversed point.
As shown in Figure 2, G(1) is dividing into several
areas which named 1,2 etc. according to its edges.
Here every area is the area of G(2) and its edge-level
is 2, its vertex-level is no lower than 2. Each area is
named as (high-level)-(low-level). For example, the
area which name is 1 − 2 represents that it belongs
to area − 1 of G(1) and area − 2 of G(2). This ap-
proach not only addresses the index direction and de-
cides which level of network should be selected, but
also helps build the structure of indexing in every two
areas.
5 STRATIFICATION
ALGORITHM
In this section, we explain a stratification algorithm to
find path from start point to end point. We refer to
this query as most frequent path based on road lev-
els (RLMFP). First, assuming that the start point S
and end point D are in different regions of the L
i
and
L
j
. If S and D are in different levels, we judge higher
level and upgrade the area of lower level to higher
level graph until they are in the same level. Then we
judge whether they are in same area. If not, we repeat
this work till they are in same level and area. In this
way, the highest level road network for S and D is de-
termined. Next the vertices and graphs are upgraded
according to the highest level road network for S and
D. The algorithm is shown in Algorithm 3.
Initially, the algorithm traverses S and D in map
to determine which areas they are in (line1-2). Then
it addresses the highest level network they are both
in and use level record the highest level (line 3-5). If
q == level which means their level is the highest, it
can directly calculate the best path through the MFP
in their common area and the path is saved by P.max
(line 6-8). Otherwise, every path is computed from
S (or D) to S.int(q)(or D.int(q))(line9-12) and level
minus 1. This is one process of upgrading points. Af-
ter the first upgrading, if S and D are still in different
levels, continue to upgrade S and D in the same way.
Here we should compute every SP(the most frequent
path) from points in S.int(q + 1) to points in S.int(q)
till q equals level(line 13-17). At last, a set of paths
P can be gotten by connecting each sub-path from S
to D and P.max can be return through calculating the
final weight of each path in P.
Assuming there are n vertices and m edges in a
network with 2 levels of roads. Each time the average
number of vertices of all the MFP to end is k. The area
including most points has i upgrade points, n
0
vertices
Finding Most Frequent Path based on Stratified Urban Roads
55

Algorithm 3: Stratification algorithm.
Require:
G∗: road network(including q levels, road levels is
E(1), E(2), ..., E(q), etc.); S: start point; D: end point;
Ensure:
the path RLMFP;
1: search S and D in G∗;
2: get S.area(q)and D.area(q);
3: level,oldq ← q;
4: while S.area(level)! = D.area(level) do
5: level ← level −1;
6: if q == level then
7: get SP(S − D) in E(q);
8: P.max ← P(S, D);
9: else
10: get every SP(S,S.int(q)) in E(q);
11: get every SP(D,D.int(q)) in E(q);
12: q ← q − 1;
13: while q > level do
14: get every SP(S.int(q + 1),S.int(q))inE(q);
15: get every SP(D.int(q + 1),D.int(q))inE(q);
16: q ← q − 1;
17: get every SP(S.int(q),D.int(q)) in E(q);
18: for each SP(1) ∈ SP(S, S.int(oldq)),...,SP(k) ∈
SP(D,D.int(oldq)) do
19: P ←
∑
k
i=1
SP(i);
20: get P.max from all P;
21: return P.max;
and m
0
edges at most. Each time the average num-
ber of vertices of all the MFP to end is k
0
. In the first
layer, there are n
00
points, m
00
edges. Each time the
average number of vertices of all the MFP to end is
k
00
. If we take MFP algorithm directly, the time com-
plexity is O(kmn). If we adopt a stratification algo-
rithm in this section, the time complexity of travers-
ing each upgrade of S(or D) in S.area(2) is O(k
0
n
0
m
0
),
the time complexity of the second layer is 2O(k
0
n
0
m
0
).
In the second layer, we should compute S(or D) to
every upgrade points in S.area(1), so the time com-
plexity of the second layer is 2iO(k
0
n
0
m
0
). Similarly,
the time complexity of the first layer is O(k
00
n
00
m
00
).
Finally, the road sections should be connected to a
whole path. Here the path combines with three road
sections and go through two upgrade points, so the
number of paths is i
2
and its time complexity of se-
lecting best paths is O(i
2
). Therefore the whole time
complexity is 2iO(k
0
n
0
m
0
) + O(
00
n
00
m
00
) + O(i
2
). Due
to property (k
0
n
0
m
0
,k
00
n
00
m
00
knm), it’s easy to con-
cluded that the time complexity of RLMFP is much
smaller than MFP. But there may be a situation that
is unsatisfied. If there are too many upgrade vertices
with respect to the points in area are too many, they
would affect the performance of the entire algorithm
and i will affect the time complexity of this work.
Figure 3: Upgrade points.
6 HIERARCHICAL
OPTIMIZATION ALGORITHM
As shown in last section, RLMFP is more efficient
than the MFP, but the number of upgrade points will
affect the time complexity. Worse still, due to the
global optimum road hierarchical algorithm, most of
the upgrade points being traversed are inappropriate.
As shown in Figure 3, A1, A2, A3 and A4 are the up-
grades of S in area(2 − 3). In stratification algorithm,
we need to scan all paths from S to upgrade vertices.
But it is obvious that, people would choose the A3 or
A4 rather than A1 or A2. But the RLMFP in section 5
may upgrade road network through A1 or A2 because
MFP has no sense of direction. So the stratification
algorithm has considered all paths, but there may be a
deviation for the best one and the number of upgrade
points has an impact on the time complexity.
In order to solve the problem, this paper provides
a hierarchical optimization algorithm RLMFPT, the
last T means terminal. As we know, the weight of
edge is based on trajectory, so we can simplify the al-
gorithm by selecting upgrade points according to tra-
jectory data.
The algorithm first establishes an index table
to each of the two regions by storing a series
of upgrade points of different levels. We re-
fer to this index as FG. The storage structure is
(p
1
, p
1
.nub),(p
2
, p
2
.nub),.. ., (p
n
, p
n
.nub). Here p
n
means the id of vertex, p
n
.num means the number of
being selected between the two areas. As shown in
Figure 3, if there is a trajectory from S to D and its re-
spect path pass the upgrade point A3, we plus 1 to the
A3.num in the index of area(2 − 3) and area(5 − 2).
We repeat it until all the trajectory is handled. The
algorithm is shown in Algorithm 4.
Firstly we construct an index structure and mark
all memory locations empty (line 1). The algo-
rithm then traverses all tracks and identifies the ar-
eas of starting point and destination point to deter-
mine where to store in the index (line 2-3). Next,
GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management
56

Algorithm 4: Build area index structure.
Require:
G: road network; T : trajectory data set;
Ensure:
FG: Area index structure
1: set all FG(area(G∗)∗ area(G∗)) with null;
2: for each Y in T do
3: get Y.s(area) and Y.d(area);
4: match Y to G ;
5: get a path P corresponds Y in G ;
6: for each point p in P do
7: if point p ∈ int then
8: push p to FG(area(Y.s))(area(Y.d));
9: area(Y.s)(Y.d).p.nub + +;
10: return FG;
each trajectory is matched to the network for obtain-
ing the appropriate paths (line 4-5). Finally, the al-
gorithm traverses every vertex on the path and judges
whether it is the upgraded one. If it is true, this point
will be stored in the position corresponding to the in-
dex construction. Assuming that the number of tra-
jectory data is |Y |, the number of points in the path
which each track corresponds to is |P|. The com-
plexity of the algorithm is O(|Y P|), space complexity
|area(G∗)|
2
.
Algorithm 5: Optimal Stratification algorithm.
Require:
G∗: road network(including q levels, road levels is
E(1), E(2), ..., E(q), etc.); S: start point; D: end point;
FG: Area index structure;
Ensure:
the path RLMFPT;
1: search S and D in G∗;
2: get S.area(q)and D.area(q);
3: get FG(area(S)(D));
4: level,oldq ← q;
5: while S.area(level)! = D.area(level) do
6: level ← level −1;
7: if q == level then
8: get SP(S − D) in E(q);
9: P.max ← P(S, D);
10: else
11: get all S.int and D.int from FG(area(S)(D))
12: get every SP(S,S.int(q)) in E(q);
13: get every SP(D,D.int(q)) in E(q);
14: q ← q − 1;
15: while q > level do
16: get every SP(S.int(q + 1),S.int(q))inE(q);
17: get every SP(D.int(q + 1),D.int(q))inE(q);
18: q ← q − 1;
19: get every SP(S.int(q),D.int(q)) in E(q);
20: for each SP(1) ∈ SP(S, S.int(oldq)),...,SP(k) ∈
SP(D,D.int(oldq)) do
21: P ←
∑
k
i=1
SP(i);
22: get P.max from all P;
23: return P.max;
Different from the RLMFP, for the same condi-
tion, the algorithm determines the areas of start point
and end point and then determines the set of upgrade
vertices in FG. If upgrade vertices is in top 5 after
sorting their number, they are the upgrade ones of this
area. For example, FG(2 −3)(5 −2) has 100 upgrade
points(A1 − A100). We sort the number of points,
including A1.num, A2.num,..., A100.num. Then the
vertices in top 5 are selected as the upgrade ones.
The Algorithm 5 is similar to Algorithm 3. The
difference is getting the index in FG (line 3) and us-
ing the int(q) in FG(area(S)(D)) replace the int(q) in
area(line 11). The remaining part of the idea is same
as Algorithm 3.
Assuming the same condition of Algorithm 3, the
number of upgrade points is i
0
. And we have proved
that i
0
is among 5 to 10. The time complexity is
2iO(k
0
n
0
m
0
)+ O(k
00
n
00
m
00
)+ O(i
02
). Since i
0
is smaller
than i, thus the complexity is smaller than that of Al-
gorithm 3. In addition, because i
0
is a defined low
value, it will not affect the time complexity. For ex-
ample, suppose each steps ratio of upgrade points is
cut to 30%, O(i
02
) is only 9% of O(i
2
). So the im-
proved results to Algorithm 3 is obvious.
7 EXPERIMENT
In this section we conduct experiment to compare
RLMFP, RLMFPT wiht MFP. In order to show ad-
vantages of RLMFPT, we design four experiments
for these three algorithms. Similarity is designed to
prove that RLMFPT has the advantages of MFP and
RLMFP, which means it satisfies Property 2.1. There
are more high-level roads in RLMFPT as a result of
natural hierarchical policy. A comparison of path
points is also done to prove that RLMFPT satisfies
Property 2.2. In addition, we compare the query time
of three algorithms to show the high query speed of
RLFMPT. At last, feasibility of RLMFPT is displayed
through the memory size of different algorithms.
In order to ensure the correctness and fairness of
the experiments, the trajectories is under the same
conditions. So We obtain trajectory data using the
famous Network-based Generator of Moving Objects
by Tomas Brinkhoff(Brinkhoff, 2002), which is a well
known system of generating trajectory data. In addi-
tion, the maps are Oldenburg and San Joaquin. The
smaller map Oldenburg has 6105 nodes and 7035
edges. The bigger map is San Joaquin with 18496
nodes and 24123 edges. In each map, we divide roads
into 2 levels. All the experiments are conducted on a
PC with an Intel CPU of 3.20GHz and 4GB memory.
Finding Most Frequent Path based on Stratified Urban Roads
57
(a) Similarity(OLD). (b) Similarity(SAN). (c) Path points(OLD).
(d) Path points(SAN). (e) Query time(OLD). (f) Query time(SAN).
Figure 4: Experiments of similarity, path points and query time in three algorithms.
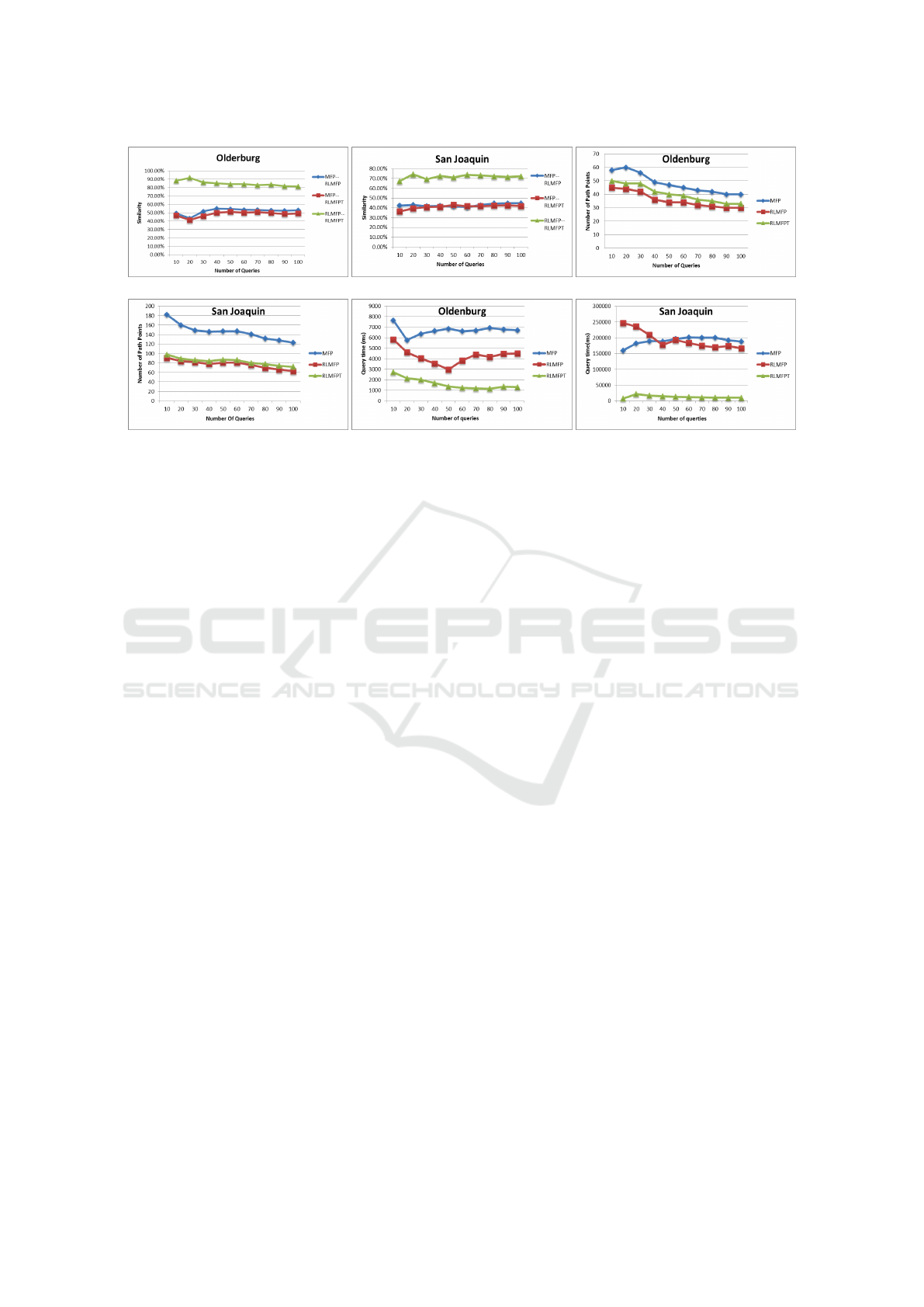
7.1 Similarity
To evaluate the similarity of three path queries (MFP,
RLMFP and RLMFPT), we compare the results of
them through counting different quantities of the
same starting point and destination point path queries.
Due to the different sizes of the two maps, we pro-
duce 70000 and 510000 trajectories by traffic simula-
tor as the data set for each of them. Then we set the
weights and build index FG for each graph with above
data set. Next we apply 10 to 100 path queries from
the same start point to the same end point for every
algorithm.
We use the ratio of the number of same edges in
two paths and the total number of edges in path which
is being com-pared. As shown in Figure 4(a) and Fig-
ure 4(b), there are about 40% of similarity between
MFP, RLMFP and RLMFPT, which indicates that the
similarity is relatively high. The difference is because
both RLMFP and RLMFPT traverse a high level map
when they get upgrade points, do not adapt MFP all
time. Because of the same principles and the high
similarity, it is shown that both RLMFP and RLMFPT
have the advantage of MFP and can satisfy the first
demand of users. In addition, comparing RLMFP
with RLMFPT, there is high similarity between them.
Thus, RLMFPT (RLMFP with FG) has the advan-
tages of RLMFP.
7.2 Path Points
In this experiment, to evaluate the less number of
path points of RLMFP and RLMFPT, we compare the
results of them through counting different quantities
of the same starting point and destination point path
queries. The conditions are set up the same as 7.1.
As shown in Figure 4(c) and 4(d), with the in-
creasing number of queries, the number of points in
algorithms (RLMFP and RLMFPT) remains stable
between 30 and 35 in Figure 4(c) or 60 and 80 in Fig-
ure 4(d). The points of MFP gradually reduce with
the growing queries, but they are 50% more than that
of RLMFP or RLMFPT in Figure 4(d). It shows that
RLMFP and RLMFPT select less path points than
MFP, which satisfies the second demand of users.
7.3 Query Time
Algorithm proposed in this paper enjoy faster query
speed. Therefore, in this experiment, we compare
the results of the query time of three algorithms
(MFP, RLMFP, RLMFPT) through counting different
quantities of the same starting point and destination
point path queries to evaluate the less query time of
RLMFPT. The conditions are set up the same as 7.1.
As shown in Figure 4(e), with the increasing num-
ber of queries, the query time of MFP remains stable
at 7000ms. To the end point that have large number
of upgrade points, query time has ups and downs, be-
cause too many upgrade points would lead to a lot
of stitching path and affect the query time. Thus the
number of upgrade is an uncertain factor. But the
query time in 4(e) is still better than MFP. Besides,
because of the small number of upgrade points (less
than 9), the factor of that in RLMFP will not affect
RLMFPT. Therefore, the query time of RLMFPT still
remains at a relatively low state.
In large map San Joaquin shown in Figure 4(f),
as the number of queries increased, the query time of
MFP is decreasing and that of RLMFP is increasing.
GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management
58

Figure 5: Memory size.
After stabilized,the query time of RLMFP is higher
than that of MFP. The reason is that the scale of up-
grade points is constantly increasing with the bigger
map, which affects the query time directly. In addi-
tion, the query time of RLMFPT still remains at a
short level. This is because the number of upgrade
points does not affect RLMFPT. Thus in San Joaquin
map, RLMFPT reflects the stable and short advan-
tages and also shows the advantages of FG.
7.4 Memory Size
In this experiment, we compare the results of the
memory size of common graph, stratified-graph and
FG by counting two maps to evaluate the acceptable
small extra memory size of RLMFPT.
As shown in Figure 5, regardless of the size of
maps, the memory size of stratified-graph is twice as
common graph. Besides, the memory size of FG is
similar to stratified graph and also twice as common
graph. Therefore, the memory size of RLMFPT is
about four times as common graph. In reality, such
additional storage is acceptable either on the client or
the server.
8 RELATED WORK
The best path algorithms have been studied for many
years. The most classic work is the shortest path algo-
rithm in the graph theory. (Dijkstra, 1959)(Bellman,
1958) propose two shortest path algorithms. These
algorithms have been studied for more than 50 years.
On the basis of these algorithms, the later researchers
develop some improved methods. (Pohl, 1971) pro-
poses bidirectional Dijkstra’s algorithm to improve
the efficiency of the algorithm. New approaches (Hart
et al., 1968) for fastest path finding are proposed aim-
ing at using heuristic information to reduce the time
complexity. In addition, if the weight on each edge
represents travel time, shortest path finding becomes
fastest path finding. (Kanoulas et al., 2006) raises
an idea that speed is changing in different time pe-
riods. He estimates the optimal departure time and
the shortest time depending on the property of each
edge. (Ding et al., 2008) also makes a way to find
the fastest path under large graph. Due to the chang-
ing information in some roads, it may lead to update
whole road network so as to cause a huge waste of
resources. (Shang et al., 2010) uses two tree of prun-
ing map to solve the problems of update roads, which
effectively improves the memory utilization. Con-
sidering that clients may make too many requests in
the same period of time and lead to network con-
gestion, (Leong et al., 2014) broadcasts packets of
speed-changing weight. Then the client only accepts
needed data packets and compute paths in local. Dif-
ferent from shortest/fastest path querying, we study
the problem of finding the most frequent path. Thus
their methods for determining the better path are dif-
ferent and shortest/fastest path are not suitable for this
problem.
Finding a path utilizing the hierarchical road net-
work is another related work. (Geisberger et al., 2008)
offers CH algorithm, which first orders all points and
compute this order to simplify the network gradually.
After pretreatment, it queries a path following the or-
der. Similar to (Geisberger et al., 2008), there are
many other methods through pretreating data such as
(Bast et al., 2006). (Bast et al., 2006) divides the
graph into many areas. When a point comes out from
the area, it should pass the access points. He prepro-
cesses all shortest paths between every pair areas for
optimization. But such approach has a defect that pre-
treatment time is too long. So (Akiba et al., 2013)
presents a large map of the road network under the
pruning techniques, resulting in great reducing of the
processing time. (Jing et al., 1996) proposes a hier-
archical road network to simplify algorithm. Though
these algorithms are searching a path according the
hierarchical idea, they are not focus on finding a path
based on stratified urban roads.
Querying a path based on trajectory data is the
most closely related work to this paper. Some
approaches (Gonzalez et al., 2007)(Yuan et al.,
2011)(Yuan et al., 2010)for fastest path finding are
proposed aiming at using user-generated GPS trajec-
tories to estimate the distribution of travel time on a
given road network. (Chen et al., 2011) recommends
a route by mining route preferences of the past visi-
tors. Specially, this method constructs a graph only
through trajectory clustering. He defines the possi-
bility of next point from query point to destination
point as the weight of graph. However, the method
may contain infrequent sub-path. (Luo et al., 2013)
proposes TPMFP to improve MPR. She utilizes edge
frequency as weight of graph. In addition, edge fre-
quency is computed in time of period, so the path do
not contain infrequent sub-path. (Su et al., 2014) is
Finding Most Frequent Path based on Stratified Urban Roads
59

the first one who put local drivers advices into query
system. These methods are based on trajectories, but
they will lead to a high responding time due to search-
ing a path on a whole road network. In addition, a
path based on trajectories which favors the high-level
roads are ignored by these methods. They are there-
fore not a good method to find a way based on trajec-
tory data.
9 CONCLUSION
In this paper, we propose two algorithms RLMFP and
RLMFPT (RLMFP with FG) to solve the problem
of path query. We observe two common sense no-
tions, which are selecting roads in line with local cus-
toms and choosing high-level roads such as highway.
Moreover, we study a four-step framework to solve
the problem. The first step is to set the weight to the
common graph with trajectory graph. The second step
is to divide graph into several areas. The third step is
to build an index named FG to speed up the query and
find more reasonable upgrade points. The last step is
to use RLMFPT to compute the paths. The experi-
ment results demonstrate the efficiency, the effective-
ness and the stability of our index FG and algorithm
RLMFPT. The memory size of RLMFPT is also ac-
ceptable for customers or providers. In the future, we
will extend our solution on real networks and recom-
mand custum made route via allowing drivers to select
preferable upgrade points.
ACKNOWLEDGEMENTS
This work is supported by the National Natural Sci-
ence Foundation of China (No. 61572165) and
the State Key Program of Zhejiang Province Nat-
ural Science Foundation of China under Grant No.
LZ15F020003.
REFERENCES
Akiba, T., Iwata, Y., and Yoshida, Y. (2013). Fast exact
shortest-path distance queries on large networks by
pruned landmark labeling. In Proceedings of the 2013
ACM SIGMOD International Conference on Manage-
ment of Data, pages 349–360.
Bast, H., Funke, S., Matijevic, D., Demetrescu, C., Gold-
berg, A., and Johnson, D. (2006). Transit: Ultrafast
shortest-path queries with linear-time preprocessing.
9th DIMACS Implementation Challenge — Shortest
Path / Demetrescu, Camil ; Goldberg, Andrew ; John-
son, David, (2006):175–192.
Bellman, R. (1958). On a routing problem. Quarterly Appl
Math, 16:87–90.
Brinkhoff, T. (2002). A framework for generating network-
based moving objects. Geoinformatica, 6(2):153–180.
Chen, Z., Shen, H.T., and Zhou,X.(2011). Discovering pop-
ular routes from trajectories. Icde,6791(9):900–911
Dijkstra, E.W.(1959), A note on two problems in connexion
with graphs. Numerische Mathematik,1(1):269–271
Ding, B., Yu, J. X., and Qin, L. (2008). Finding time-
dependent shortest paths over large graphs. Proc Edbt,
pages 205–216.
Geisberger, R., Sanders, P., Schultes, D., and Delling, D.
(2008). Contraction Hierarchies: Faster and Sim-
pler Hierarchical Routing in Road Networks. Springer
Berlin Heidelberg.
Gonzalez, H., Han, J., Li, X., Myslinska, M., and Sondag,
J. P. (2007). Adaptive fastest path computation on a
road network: A traffic mining approach. In In Proc.
2007 Int. Conf. on Very Large Data Bases (VLDB07,
pages 794–805.
Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A formal
basis for the heuristic determination of minimum cost
paths. Systems Science & Cybernetics IEEE Transac-
tions on, 4(2):100–107.
Jing, N., Huang, Y. W., and Rundensteiner, E. A. (1996).
Hierarchical optimization of optimal path finding for
transportation applications. In In Proc of Acm Con-
ference on Information & Knowledge Management,
pages 261–268.
Kanoulas, E., Du, Y., Xia, T., and Zhang, D. (2006). Finding
fastest paths on a road network with speed patterns.
In In Proc. Int. Conf. on Data Engineering (ICDE06,
pages 10–10.
Leong, H. U., Zhao, H. J., Man, L. Y., Li, Y., and Gong,
Z. (2014). Towards online shortest path computation.
IEEE Transactions on Knowledge & Data Engineer-
ing, 26(4):1012–1025.
Luo, W., Tan, H., Chen, L., and Ni, L. M. (2013). Finding
time period-based most frequent path in big trajectory
data. In Proceedings of the 2013 ACM SIGMOD Inter-
national Conference on Management of Data, pages
713–724.
Pohl, I. (1971). Bi-directional search. Machine Intelli-
genceC, 6:1359–1364.
Shang, S., Deng, K., and Zheng, K. (2010). Efficient best
path monitoring in road networks for instant local traf-
fic information. In Conferences in Research and Prac-
tice in Information Technology Series, pages 47–56.
Su, H., Zheng, K., Huang, J., Jeung, H., Chen, L., and
Zhou, X. (2014). Crowdplanner: A crowd-based route
recommendation system. In 2014 IEEE 30th Inter-
national Conference on Data Engineering (ICDE),
pages 1144–1155.
Yuan, J., Zheng, Y., Xie, X., and Sun, G. (2011). Driv-
ing with knowledge from the physical world. Kdd,
pages316–324.
Yuan, J., Zheng, Y., Zhang, C., Xie, W., Xie, X., Sun,
G., and Huang, Y. (2010) T-drive: driving directions
based on taxi trajectories. In Proceedings of the 18th
SIGSPATIAL International conf. on advances in geo-
graphic information systems, pages 99–108 ACM.
GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management
60
