Ontology Matching based on Multi-Aspect Consensus Clustering of

Communities

André Ippolito and Jorge Rady de Almeida Júnior

Computer and Digital Systems Department, Polytechnic School of University of São Paulo,

Avenida Professor Luciano Gualberto, n.º 158, São Paulo, Brazil

Keywords: Ontology Matching, Aspect, Consensus Clustering, Bayesian Cluster Ensembles, Community Detection.

Abstract: With the increase in the number of existing ontologies, ontology integration becomes a challenging task. A

fundamental step in ontology integration is ontology matching, which is the process of finding

correspondences between elements of different ontologies. For large-scale ontology matching, some authors

developed a divide-and-conquer strategy, which partitions ontologies, clusters similar partitions and restricts

the matching process to ontology elements of similar partitions. Works related to this strategy considered only

a single ontology aspect for clustering. In this paper, we proposed a solution for ontology matching based on

Bayesian Cluster Ensembles (BCE) of multiple aspects of ontology partitions. We partition ontologies

applying Community Detection techniques. We believe that BCE of multiple aspects of ontology partitions

can provide an ontology clustering that is more precise than the clustering of a single aspect. This can result

in a more precise matching.

1 INTRODUCTION

In the World Wide Web (WWW), developers create

web pages with information that humans can

interpret. Nevertheless, the underlying meaning of the

information is not sufficiently explicit to be machine-

interpretable. In order to overcome this difficulty, the

World Wide Web Consortium (W3C) is developing

technologies related to the Semantic Web, an

extension of the WWW, in which information

semantics of a domain becomes explicit with the use

of ontologies. Ontologies are formal specifications

about a knowledge domain, with logical descriptions

about real-world entities, which enable the inference

of rules. The Linked Open Data (LOD) Project

specifies the best practices in the publication of

ontologies. Recent statistics (Schmachtenberg, Bizer

and Paulheim, 2014) indicate an increase in the

number of published ontologies in the LOD Cloud,

related to a wide range of domains, e.g. Government,

Life Sciences, User-generated Content, Media and

Social Web.

With the progressive number of existing

ontologies, developed with different patterns, thus

increasing heterogeneity, ontology integration

becomes challenging. Ontology integration is

necessary when enterprises need to do a merge or an

acquisition, for example, because they have to

integrate their heterogeneous ontologies into a single

one. Ontology matching is the first step before

merging the ontologies and is the process of finding

correspondent elements in different ontologies. The

set of correspondences is the ontology alignment.

Euzenat and Shvaiko (2013) highlight a divide-and-

conquer strategy for large-scale ontology matching.

Given two ontologies, this strategy fragments both

ontologies in partitions and clusters similar partitions

of the two ontologies. The final step is the matching

process, which compares only the elements of the two

ontologies that belong to the same cluster. According

to Euzenat and Shvaiko (2013), the goal of this

strategy is to improve the matching efficiency,

avoiding the comparison of all ontology elements.

Algergawy, Massmann and Rahm (2011) and

Moawed et al. (2015) developed clustering-based

solutions for ontology matching. To cluster ontology

partitions, these authors considered the

terminological content (terms of labels and

annotations) of ontology elements of the partitions

and applied document clustering techniques.

However, these works did not explore other ontology

aspects, e.g. instance-based aspect, in the clustering

phase, which can help to increase the number of

correct clusters and correct matching

correspondences.

Ippolito, A. and Júnior, J.

Ontology Matching based on Multi-Aspect Consensus Clustering of Communities.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 2, pages 321-326

ISBN: 978-989-758-187-8

321

In this work, we propose a solution for ontology

matching that initially partitions two ontologies using

Community Detection techniques (Fortunato, 2010).

In the sequence, we consider three different aspects

of the ontology partitions: terminological content,

topological features and instance-based aspect, also

known as extensional aspect. For each aspect, we

apply Independent Component Analysis (ICA)

(Honkela, Hyvärinen and Väyrynen, 2010) for

dimensionality reduction. ICA is a technique inspired

in the problem of blind signal separation that applies

linear transformations on data to obtain statistically

independent components, reducing data to its most

relevant features. After applying ICA, we cluster

ontology partitions according to each aspect,

considered separately, and find a consensus clustering

applying Bayesian Cluster Ensembles (BCE) (Wang,

Shan and Banerjee, 2011). Finally, we match classes

and properties of ontology partitions that belong to

the same consensual cluster.

This paper has the following structure: in section

2, we explain BCE; in section 3, we review the related

works; in section 4, we explain our methods; in

section 5, we outline the expected results. Since this

work is an ongoing project, we plan to present its

results and conclusions in future publications.

2 BAYESIAN CLUSTER

ENSEMBLES

Cluster Ensembles techniques combine clustering

solutions (base clusterings), obtained by different

algorithms, into a consensual clustering, which

captures different assumptions of the algorithms,

making the solution more accurate and more robust

(Wang, Shan and Banerjee, 2011).

In BCE, given n data points to be clustered, Wang,

Shan and Banerjee (2011) assume that each data point

participates in all consensual clusters, in different

proportions, given by probabilities. BCE is based on

a probabilistic generative process, which considers

that the consensual clusters generate the base

clusterings. Figure 1 illustrates the generative process

of BCE. Matrix B represents the base clusterings and

matrix C refers to the consensual clusters. In matrix

B, the lines represent seven data points, given by x

= 1,…,7). There are three base clusterings, given by

, which are the columns of B. The entries of B are

the base clusterings’ labels. In the generative process,

these labels are drawn from probabilistic distributions

related to the consensual clusters (matrix C). The

labels of the base clusterings follow discrete

distributions.

In the example of figure 1, let us consider that λ

for x

was generated by the consensual cluster 2.

Then, according to column 1 and line 2 of C, we have

a probability of 0.1 that x

is in cluster 1. Following

the same discrete distribution, the probability that x

is in cluster 2 is 0.1 and the probability of x

being in

cluster 3 is 0.8. Given that 0.8 is the highest

probability for λ

(column 1 of C), considering the

two consensual clusters, we conclude that the

consensual cluster 2 generated x

and that x

has label

The goal of BCE is to infer the consensus

clustering with Bayesian Inference, such that the base

clusterings are the observed data. As figure 1 shows,

the inference process of BCE follows the inverse

direction of the generative process. BCE infers the

degree of membership Ɵ of each data point to the

consensual clusters and infers the consensual label z

assigned to the data points, considering α and β as

probabilistic parameters of the model. Wang, Shan

and Banerjee (2011) made an experiment with

scientific datasets to compare BCE to other Cluster

Ensembles techniques and clustering algorithms, e.g.

Hypergraph Partitioning Algorithm and K-means.

Wang, Shan and Banerjee (2011) measured the

clustering accuracy, considering the number of data

points correctly assigned to a cluster, based on a gold

standard. BCE outperformed the other techniques and

algorithms in most of the cases.

3 RELATED WORKS

Algergawy, Massmann and Rahm (2011) and

Moawed et al. (2015) used the Vector Space Model

(VSM) (Manning, Raghavan and Schütze, 2009) and

clustered ontology partitions solely based on their

terminological content, not considering different

aspects that partitions have. Considering multiple

aspects for clustering can help finding additional

correct clusters, which can increase the number of

similar ontology elements grouped in the same

cluster, helping to improve the precision of the

matching results.

Ferrara et al. (2015) found a consensus clustering

based on the co-occurrence of ontology elements in

the same cluster in different clustering solutions.

Ferrara et al. (2015) did not apply BCE, which can

provide more accurate clustering results than other

Cluster Ensembles techniques (Wang, Shan and

Banerjee, 2011). This accuracy can improve the

ontology clustering result, influencing on the

ontology alignment by increasing its precision.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

322

Figure 1: Bayesian Cluster Ensembles.

Moawed et al. (2015) applied Latent Semantic

Analysis (LSA) (Landauer, Foltz and Laham, 1998)

for dimensionality reduction. However, according to

Honkela, Hyvärinen and Väyrynen (2010), ICA was

able to reveal more relevant features in document

collections than LSA. We intend to extend the results

of ICA to ontologies, by finding more relevant terms

also in ontology partitions.

Thus, we propose a solution that applies BCE and

ICA with the goal of bridging the gaps of the related

works.

4 METHODS

Our proposed solution (figure 2) has four steps:

community detection to partition the ontologies into

communities; community clustering based on

multiple aspects; consensus clustering of multiple

aspects with BCE; matching ontology elements of

consensual clusters.

4.1 Community Detection to Partition

the Ontologies into Communities

In the first step, we take two different ontologies O

and O’ for matching and consider each ontology

structure as a graph, using one of the approaches of

Coskun et al. (2011): subjects and objects of each

ontology correspond to nodes and predicates

correspond to edges. We partition each of the

ontology graphs into communities applying the

Community Detection algorithms that had the most

accurate clustering results in the study of Coskun et

al. (2011): Random Walks, Fast Greedy Algorithm

and Potts Model (Fortunato, 2010).

We evaluate the community structure obtained by

each of the algorithms using the modularity function

(Fortunato, 2010). Modularity measures the

difference between a community structure and the

structure of a random graph, i.e. a graph with edges

placed at random. The higher the modularity, the

better the community structure is. For each ontology

graph, we choose the set of communities given by the

algorithm that provides the highest modularity. Let e

be the fraction of ends of edges that belong to the

same community i. Let b

be the fraction of edges

whose ends belong to different communities. The

modularity Q is:

Q =

∑

iii

- b

)

(1)

4.2 Community Clustering based on

Multiple Aspects

In the second step, we consider each ontology

community according to three different aspects:

terminological, topological and extensional. For each

aspect, we first model the ontology communities

according to their features, calculate distances

between communities and then cluster the

communities based on their distances.

4.2.1 Model and Distances for the

Terminological Aspect

For the terminological aspect, we extract terms of

labels and annotations of ontology elements of each

community, considering a community as a document.

Then we apply removal of stop words, stemming,

tokenization and use the VSM for modelling the

Ontology Matching based on Multi-Aspect Consensus Clustering of Communities

323

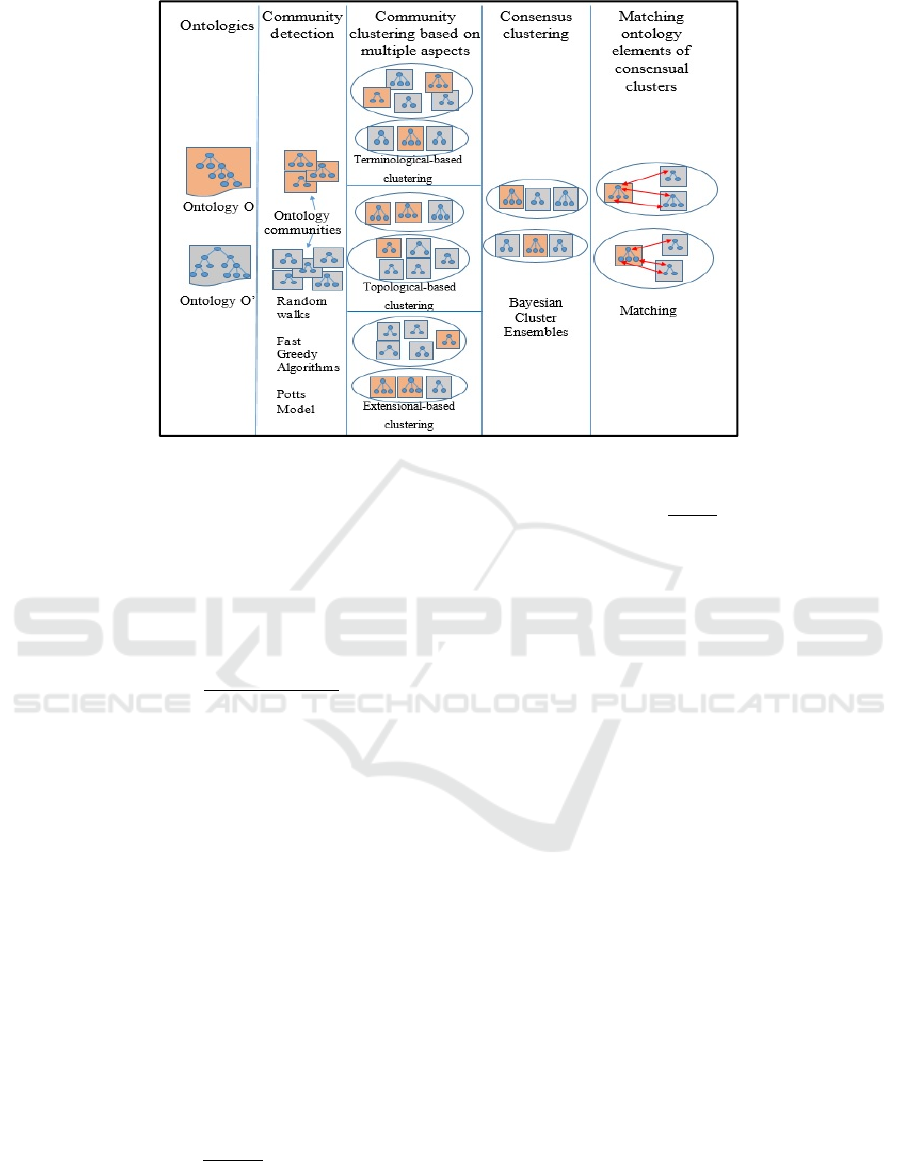
Figure 2: Overview of the proposed solution.

communities. We apply ICA for dimensionality

reduction and obtain the distances that are the input

for the clustering algorithms using the cosine distance

(Manning, Raghavan and Schütze, 2009). Let c1 and

c2 be two ontology communities and v









and

v









be its vectors representations in the VSM. The

cosine distance CD between c1 and c2 is:



c1,c2



=1-









.v 

















|

v 







|

(2)

4.2.2 Model and Distances for the

Topological Aspect

For the topological aspect, we represent the topology

of each community based on three features (Albert

and Barabási, 2002): global clustering coefficient,

average path length and the exponent of the power

law. We calculate the distances based on these

features, applying the Euclidean distance (Manning,

Raghavan and Schütze, 2009).

Let k

be the number of edges connecting a given

node i to its neighbours and let E

be the number of

edges between the neighbours of i. The local

clustering coefficient of i, denoted by LCC

, is given

by (3). The global clustering coefficient GCC of a

community is the average of the LCC

of the nodes of

the community.

LCC

(

-1)

(3)

Given a community with N nodes and K edges,

the average path length L is:

L =

ln (N)

(

)

(4)

Given a random node i of a graph, the probability

P(k) of i having k edges is given by the power law as

in (5), where γ is the exponent of the power law:

P(k) = k

(5)

Let c1 and c2 be two communities with d features,

whose values are given by c1

and c2

respectively,

with z = 1,…,d. The Euclidean Distance ED is:

ED(c1,c2) = (

∑

|c1

- c2

)

1/2

(6)

4.2.3 Model and Distances for the

Extensional Aspect

For the extensional aspect, we model each

community considering each of its distinct concepts

as a different dimension whose value is the number of

its instances. We use ICA for dimensionality

reduction and apply an extension of the distance

developed by Hu et al. (2006) to calculate distances

between ontology communities.

Hu et al. (2006) developed a distance for

ontologies based on the Kullback-Leibler distance.

Hu et al. (2006) defined a probability based on the

distance ∆(C

), which is a distance between a concept

and an ideal concept C

that instantiates infinite

objects. Hu et al. (2006) calculate a concept

restriction as the inverse of the number of its instances

and use the difference between concept restrictions to

calculate distances between concepts. Given ∆(C

)

and ∆(C

), with j≠k, Hu et al. (2006) formulated an

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

324

equation for the probability P(C

P(C

) =

1 - ∆(C

)

∑

(1 -

∆(C

))

(7)

Considering P(C

), Hu et al. (2006) defined the

distance ΔJ between two ontologies O and O’, with

concepts C

and C’

respectively:

ΔJ

∑





log

P(C

)

P(C'

)

∑





log

P(C'

)

P(C

)

(8)

For the distances, we also ponder the common

instances of a pair of .ontology communities. Let cmi

be the number of common instances of two ontology

communities and let ti be the total number of

instances of the two communities. The distance ΔI

based on the common instances is given by (9) and

we apply the average of (8) and (9) to obtain the

distance between two given communities of different

ontologies.

ΔI =1-

cmi

(9)

4.2.4 Community Clustering of each Aspect

For each aspect, we consider its respective distances

between pairs of ontology communities. Based on the

distances, we apply the following clustering

algorithms: Single-link, Complete-link, Unweighted

Pair Group Method with Arithmetic Mean, Ward’s

Method, Divisive Analysis, Partitioning Around

Medoids, Expectation Maximization and K-Means.

Thus, we have eight clustering results for each aspect

and we choose the best clustering result, such that we

have only one clustering result for each aspect.

4.2.5 Selection of the Clustering Result of

Each Aspect

For each aspect, we compare the eight clustering

results based on the silhouette width (Rousseeuw,

1987), which is a measure that considers the

separation between different clusters and the degree

of compactness of a cluster. Let a

be the average

distance between an element i and all the elements of

the same cluster of i and let b

be the average distance

between element i and the elements of the nearest

cluster. The silhouette width S is given by (10). For

each aspect, we select the clustering result with the

highest silhouette width. These selected clustering

results are the input for the next step.

S =

-a

max

(

)

(10)

4.3 BCE of Multiple Aspects

In the third step, we take the selected clustering result

of each aspect and apply BCE to find a consensus

clustering. The selected clustering results are the

observed data, based on which we infer the consensus

clustering using BCE.

4.4 Matching between Ontology

Elements of Consensual Clusters

In the fourth step, we apply matching techniques to

the ontology classes and properties of ontology

communities of the same consensual cluster. We plan

to use syntactic, structural and semantic techniques,

comparing the matching results to a benchmark,

publicly available on the web or provided by experts.

Given an alignment A and a benchmark result B, we

evaluate the matching result with regard to recall (R),

precision (P) and F-measure (F) (Euzenat and

Shvaiko, 2013):

R(A,B) =

|B∩A|

|B|

(11)

P(A,B) =

|B∩A|

|A|

(12)

F(A,B) =

2PR

P + R

(13)

5 EXPECTED RESULTS

According to Wang, Shan and Banerjee (2011), BCE

provided a more accurate clustering than the

clustering obtained by other algorithms applied

separately. We believe that we can extend these

results to ontologies, with BCE of multiple ontology

aspects providing a more precise ontology clustering

than the clustering of each ontology aspect. In our

comparative evaluation, we plan to apply the

silhouette width to compare the ontology clustering

result of BCE with the clustering results of each

ontology aspect.

A more precise ontology clustering of BCE can

imply in more ontology elements grouped together

that are similar, which can result in a more precise

matching. We plan to compare the matching metrics

(recall, precision and F-measure) that result from the

use of BCE with the matching metrics that result from

the clustering of each aspect.

Since BCE finds a consensus among different

clustering solutions, BCE tends to find fewer clusters

Ontology Matching based on Multi-Aspect Consensus Clustering of Communities

325

than the sum of clusters of all clustering solutions. In

the divide-and-conquer strategy, less clusters imply in

less comparisons during the matching process. We

plan to compare the number of matching comparisons

that results from the use of BCE with the number of

comparisons that results from the union of clusters of

all aspects.

To illustrate the potential contributions of our

approach, let us consider two ontologies, O and O’,

and two ontology communities, co and co’, taken

from O and O’ respectively. Let us also consider that

co has a concept C labelled “Creator” and that co’ has

a concept C’ with the label “Author”. C and C’ are

semantically correspondent concepts. Communities

co and co’ have common instances and approximate

exponents of the power law.

Clustering the terminological aspect tend not to

cluster co and co’, because labels’ strings of C and C’

are not similar. Nevertheless, the extensional and the

topological similarities of co and co’ contribute to

group co and co’ together. The reduced distances

between co and co’, due to their similarities, increase

the silhouette width. Grouping co with co’ implies in

grouping concepts C and C’, thus helping to increase

the matching metrics.

Let us also consider that the community clustering

based on the three aspects results in ten clusters and

that BCE finds five consensual clusters. Then, we

match the elements of five clusters instead of ten

clusters, contributing to reduce the number of

comparisons in the matching process.

REFERENCES

Albert, R., Barabási, A., 2002. Statistical Mechanics of

Complex Networks. In Reviews of Modern Physics 74,

47. arXiv:cond-mat/0106096.

Algergawy, A., Massmann, S., Rahm, E., 2011. A

Clustering-Based Approach for Large-Scale Ontology

Matching. In Advances in Databases and Information

Systems, vol. 6909, pp. 415-428.

Coskun, G., Rothe, M., Teymourian, K., Paschke, A., 2011.

Applying Community Detection Algorithms on

Ontologies for Identifying Concept Groups. In

WOMO’11, 5

International Workshop on Modular

Ontologies. IOS Press.

Euzenat, J., Shvaiko, P., 2013. Ontology Matching.

Springer, 2

edition.

Ferrara, A., Genta, L., Montanelli, S., Castano, S., 2015.

Dimensional Clustering of Linked Data: Techniques

and Applications. In Transactions on Large-Scale Data

and Knowledge-Centered Systems XIX, pp. 55-86.

Fortunato, S., 2010. Community Detection in Graphs. In

Physics Reports 486 (3), pp. 75-174.

Honkela, T., Hyvärinen, A., Väyrynen, J. J., 2010.

WordICA - Emergence of Linguistic Representations

for Words by Independent Component Analysis. In

Natural Language Engineering (16), pp. 277–308.

Hu, B., Kalfoglou, Y., Alani, H., Dupplaw, D., Lewis, P.,

Shadbolt, N., 2006. Semantic Metrics. In: EKAW’06.

International Conference on Knowledge

Engineering and Knowledge Management. Springer.

Landauer, T. K., Foltz, P.W., Laham, D., 1998. Introduction

to Latent Semantic Analysis. In Discourse Processes

(25), pp. 259-284.

Manning, C. D., Raghavan, P., Schütze, H., 2009. An

Introduction to Information Retrieval. Cambridge

Press.

Moawed, S. Algergawy, A., Sarhan, A., Eldosouky, A.,

Saake, G., 2015. Improving Clustering-Based Schema

Matching Using Latent Semantic Indexing. In

Transactions on Large-Scale Data and Knowledge-

Centered Systems XV, pp. 102-123.

Rousseeuw, P. J., 1987. Silhouettes: a Graphical Aid to the

Interpretation and Validation of Cluster Analysis. In

Journal of Computational and Applied Mathematics,

vol. 20, pp.53-65.

Schmachtenberg, M., Bizer, C., Paulheim, H., 2014. State

of the LOD Cloud 2014. University of Mannheim.

Wang, H., Shan, H., Banerjee, A., 2011. Bayesian Cluster

Ensembles. In Statistical Analysis and Data Mining:

The ASA Data Science Journal, vol. 4, pp. 54-70. Wiley

Periodicals.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

326