Key based Reducer Placement for Data Analytics across Data Centers

Considering Bi-level Resource Provision in Cloud Computing

Jiangtao Zhang

1,2

, Lingmin Zhang

1,3

, Hejiao Huang

1,3

, Zeo L. Jiang

1,4

and Xuan Wang

1,4,∗

School of Computer Science and Technology, Harbin Institute of Technology, Shenzhen Graduate School,

518055, Shenzhen, China

Public Service Platform of Mobile Internet Application Security Industry, 518057, Shenzhen, China

Shenzhen Key Laboratory of Internet of Information Collaboration, 518055, Shenzhen, China

Shenzhen Applied Technology Engineering, Laboratory for Internet Multimedia Application, 518055, Shenzhen, China

Keywords:

Reducer Placement, Resource Provision, Hadoop Across Data Centers, Distributed Cloud.

Abstract:

Due to the distribution characteristic of the data source, such as astronomy and sales, or the legal prohibition,

it is not always practical to store the world-wide data in only one data center (DC). Hadoop is a commonly

accepted framework for big data analytics. But it can only deal with data within one DC. The distribution

of data necessitates the study of Hadoop across DCs. In this situation, though we can place mapper in the

local DCs, where to place reducers is a great challenge, since each reducer almost needs to process all map

output across all involved DCs. Aiming to reduce costs, a key based scheme is proposed which can respect

the locality principle of traditional Hadoop as much as possible while realizing deployment of reducers with

lower cost. Considering both data center level and server level resource provision, a bi-level programming

is used to formalize the problem and it is solved by a tailored two level group genetic algorithm (TLGGA).

Extensive simulations demonstrate the effectiveness of TLGGA. It can outperform both the baseline and the

state-of-the-art mechanisms by 49% and 40%, respectively.

1 INTRODUCTION

Distributed cloud consists of multiple geo-distributed

data centers (DCs) which are connected by dedicated

high-speed links or expensive long distance links. It

provides abundant computation and storage capac-

ity and has been widely adopted to support vari-

ous services, especially for data intensive applica-

tions (Schadt et al., 2010). Because these data have

sheer size and even come from disparate geographical

locations, it is impractical to move such heavy geo-

spanned data together and store all data in one DC.

Not to mention the fact that in some countries, such as

the EU, the data security laws require some data must

be stored locally. Generally,data can be stored in DCs

closer to data generating sources to facilitate the more

frequent local data analysis with smaller access de-

lay. For example, the US census data are collected

and stored by each state (Jayalath et al., 2014). The

huge remote sensing data are stored in geo-distributed

data centers (Zhang et al., 2014). Although these data

are managed regionally, they also aim to be processed

*Corresponding author. Tel.: +86 755 26033789

collaboratively for a common purpose (Jayalath et al.,

2014) (Zhang et al., 2014). How to process such

distributed data has arrested extensive attentions of

scholars (Jayalath et al., 2014) (He et al., 2012) (Wang

et al., 2013) and practitioners.

Hadoop, the open source version of MapReduce,

which has been widely used in big data analytics,

does not support data analysis across DCs in the

current versions (Apache, ) (White, 2010). In re-

cent years, several MapReduce-like frameworks, such

as G-Hadoop (Wang et al., 2013) and G-MR (Jay-

alath et al., 2014) (we use G-frameworks to repre-

sent them), have been proposed to process distributed

data across DCs. Both G-frameworks try to inherit

the legacy of current MapReduce. They respect data

locality principle and prefer to map data locally (we

use italic format to indicate the general MapReduce

terminologies). But the great differences introduced

by multiple DCs have led to new challenges to be

addressed. The main differences include determina-

tion of reducers locations, the intermediate data copy

and storage. Detailed information please refer to sec-

tion 2.1.

Zhang, J., Zhang, L., Huang, H., Jiang, Z. and Wang, X.

Key based Reducer Placement for Data Analytics across Data Centers Considering Bi-level Resource Provision in Cloud Computing.

DOI: 10.5220/0005894202430254

In Proceedings of the International Conference on Internet of Things and Big Data (IoTBD 2016), pages 243-254

ISBN: 978-989-758-183-0

243

To process data across DCs, a cloud service

provider (CSP) should ﬁrst select DCs and then the

hosted servers to place the reducer Java virtual ma-

chines (VMs, Fig. 1). In the single-DC scenario, ba-

...

1 432 5 876

DC 3

Servers

High

Level:

level

Low

Level:

Server

level

DC 1

DC 2

DC n

Flattened network topology

Figure 1: Reducer placement for distributed data analysis

considering both DC and server level resource provision in

distributed cloud.

sically, the network within one DC is a ﬂattened two

level topology (White, 2010) (Bard, ). Servers or

physical machines (PMs) in each rack have a top-of-

rack switch. Top-of-rack switches are connected by

off-rack switches. The maximum number of hops is

2. Considering that the intermediate mapper results

are dispersed across the racks and each reducer almost

needs to reduce the outputs of all mappers, MapRe-

duce does not sedulously select the location of reduc-

ers (White, 2010) (Bard, ).

In the multi-DC scenario, the map output is stored

locally in each DC. The scheme that reduces the data

in each DC and then aggregates the intermediate re-

sults may change the ﬁnal result (e.g., to calculate

the global commodities sales proportion) or inefﬁ-

cient (Tudoran, 2014). So the universal case is to

move all the intermediate data to DC where the re-

ducer locates. Generally, in each DC, the intermedi-

ate output partitioned to a reducer has different size.

The intuitive method is to place reducer in the DC

where more intermediate data partitioned to it are

stored. But it is required to know the data volume in

advance. Fortunately, MapReduce has provided sam-

plers which can be used to sample a subset of key

space produced by mapper to approximate the dis-

tribution of keys, further to estimate the data volume

partitioned to one reducer. This scheme has been rec-

ommended by the deﬁnitive Hadoop guide in chap-

ter 8 (White, 2010) and used by other work (Jayalath

et al., 2014). The analysis result of data used for sam-

pling can be reused later. The huge volume data trans-

fer across long distance links will incur great costs, in-

crease job delay and even deteriorate the availability.

Moreover, the price of computation resource of PMs

in different DCs varies widely (Amazon, ). Placing

more reducers in the expensive DC will lead to more

costs. The locations of reducers have a big inﬂuence

on costs and services.

Because the data transfer across DCs will take

more time, the G-framework supposes a dedicated

component to copy data from one DC to the target

DC where the reducer locates. The copied data should

be stored in the target DC in the whole reduce phase.

This leads to additional storage costs. Similar to the

computation resources, each DC differs in the pric-

ing of storage (Amazon, ). Large volume data should

avoid being stored in expensive DC.

To make the maximum proﬁt, CSP strives to cut

costs as much as possible. In addition to the afore-

mentioned bandwidth costs consumed by data trans-

fer and PM costs (includes computation and stor-

age) which contribute about 60% to the costs of a

DC (Greenberg et al., 2008), another key contribution

is power. Power draw accounts for 15% not includ-

ing cooling and power distribution (Greenberg et al.,

2008). CSP can further cut power costs by exploiting

various electricity prices of distributed DCs (EIA, )

when placing reducers.

Each reducer can be assigned to a slot equipped

with a same determined computation and memory

resources in Hadoop 1.0. To improve the resource

efﬁciency, capture the heterogeneous capability of

PMs and match the volume of data to be pro-

cessed, Hadoop 2.0 (YARN) has permitted to conﬁg-

ure the CPU and memory of VMs of map and reduce

tasks (Lublinsky et al., 2013). Inside each DC, VM of

different size can be consolidated so that fewer PMs

are used and more power is saved.

Focusing on the distributed data analytics, this pa-

per tries to place reducer VMs costs efﬁciently across

the involved DCs. The main contributions are as fol-

lows:

1. We propose a key based scheme to determine the

location of reducers and optimize data transfer.

This method can further indicate the conﬁguration

of reducers based on the data volume partitioned

to it. It is applicable to all data no matter data are

associative (Section 2.2) or not.

2. Considering the costs of data transfer and storage,

computation and power, we formulate the prob-

lem as a 0-1 integer linear bi-level programming.

3. A novel uniﬁed algorithm, two level grouping ge-

netic algorithm (TLGGA) is tailored. It can real-

ize the selection of DC and server simultaneously

at the lest costs.

4. Extensive simulation demonstrates TLGGA out-

performs the traditional Hadoop 49% and the

state-of-the-art algorithm (G-MR) 40%.

The remainder of the paper is organized as fol-

lows. In section 2, background information and re-

IoTBD 2016 - International Conference on Internet of Things and Big Data

244

lated work are introduced. Section 3 formulates the

problem. Section 4 presents a novel genetic algorithm

(GA). It is evaluated in section 5 and concluded in

section 6 with some future works.

2 BACKGROUND AND RELATED

WORK

2.1 MapReduce and MapReduce Across

Data Centers

2.1.1 MapReduce

Generally, MapReduce is backed up by Hadoop dis-

tributed ﬁle system (HDFS). In HDFS, data are di-

vided into equal size data blocks (default value: 64M)

which distribute across the ﬂattened network. Each

data split consists of one (normally) or more data

blocks and is processed by one mapper in the fash-

ion of key-value pair (< key

,val

>). MapReduce

includes two phases: map phase and reduce phase.

The number of mappers is determined by the number

of MapReduce job input: data splits. Normally, it is

the same as that of the blocks. The number of reduc-

ers needs to be conﬁgured. It is suggested to be 2/3

of the number of mappers (Tannir, 2014). Mappers

and reducers all run in independent VMs. Mapper re-

spects data locality principle, i.e., prefers colocating

with the input split data to decrease data copying and

speed up the job. If it is impossible (e.g., computation

resources are not enough in the PM where the split lo-

cates), the computation nodes in the same rack will be

tried, and then the nodes in other racks. The interme-

diate map output, list(< key

,val

>), is stored in the

local disk.

Then, by default, the intermediate data are par-

titioned to each reducer by hashing key

space. Al-

though, a reducer is tried to be placed in a node where

the intermediate data are stored, since each reducer

almost need to process the outputs of all mappers, it

does not have the advantage of data locality in despite

of the slight differences between intra-rack and inter-

rack data copying. Essentially, a random scheme is

used to place the reducer. All the intermediate data to

be reduced should be copied to where the reducer lo-

cates for further process. At last, the reducer outputs

the ﬁnal results list(< key

,val

>) and writes them

to HDFS.

2.1.2 MapReduce Across Data Centers

G-hadoop (Wang et al., 2013) and G-MR (Jayalath

et al., 2014) are two extensions of MapReduce. Both

of them aim to process data intensive service across

DCs. Although they differ in some ways, they

have similar architectures. Comparing to MapReduce

within one DC, a HigherJobTracker is introduced to

coordinate data and determine the locations of map-

pers and reducers across all involved DCs. Job-

Tracker in each DC is responsible for the execution

of the tasks assigned to the DC. Generally, the map

input is bigger than its output, moving map input is

not an ideal way. Mappers are still placed in each

DC according to data locality principle and the map

phase in each DC is just the same as the scenario of

one DC. The intermediate data are stored locally in

Gfarm (Wang et al., 2013) or HDFS (Jayalath et al.,

2014). Since reducer will process almost all output of

all mappers, it necessitates data copying across DCs.

Once the location of one reducer is determined, Job-

Tracker will use a dedicated component, CopyMan-

ager, to copy data for reducing. The copied data is

stored either in a shared SAN (Wang et al., 2013),

or DHFS/S3 (Jayalath et al., 2014). Since SAN/S3

is independent from cluster, so wherever the reducer

is, the intra-DC network occupied is the same. If the

map output is stored in HDFS, it is similar to Hadoop

in terms of the distribution of data across nodes within

DC though Hadoop stores output in local disk. Now

the original Hadoop scheme (Wang et al., 2013) or

other advanced one (Jayalath et al., 2014) can be used

to place reducers. In total, the MapReduce across data

centers introduces many differences, such as deter-

mination of reducers locations, the intermediate data

copy and storage.

2.2 Existing Work in Distributed Data

Intensive Services

Within one DC, The authors of (Tudoran et al., 2012)

propose an iterative reduce scheme for reduce inten-

sive services. It uses a reduce tree to get the last re-

sult. The assumption is that the input data are associa-

tive, i.e., the iterative and hierarchical reduce will not

change the ﬁnal result. Fast completion time of sets

of MapReduce is pursued by authors of (Chang et al.,

2011). Various off-line and online approximation al-

gorithms are proposed to decrease the job completion

time. Energy is explored for MapReduce by decreas-

ing the servers used (Maheshwari et al., 2012). The

MapReduce jobs are scheduled considering workload

in each server. The server which utilization is un-

der a threshold can be turned off so that power is

saved. Different from physical resources, thermal

aware scheduling schemes are presented in (Kulka-

rni, ). The temperature distribution is optimized so

that cooling costs are minimized. Approximation al-

Key based Reducer Placement for Data Analytics across Data Centers Considering Bi-level Resource Provision in Cloud Computing

245

gorithms are presented in (Kuo et al., 2014): a 3-

approximate algorithm followed by a 2-approximate

algorithm at a higher computing costs. Both papers

limit data nodes and computation nodes in the same

DC. Furthermore, they only consider bandwidth costs

optimization.

In DC network, the authors of (Zeng et al., 2014)

propose a centralized algorithm to distribute latency

sensitive contents and the application servers de-

pended on gradient search. Multi-party data inten-

sive services are proposed by using a multi-phase ant

colony scheme (Wang and Shen, 2014) where the ser-

vice may use a large amount of data sets. Ant colony

is also used to ﬁnd the optimum of costs and execu-

tion time of a composite service (Wang et al., 2015).

Performance fairness is studied in (Xu and Li, 2012).

A subgradient based distributed solution is presented

to guarantee that users at disadvantage locations can

also enjoy proper performance. Latency is optimized

by a distributed scheme based on alternating direction

method of multipliers. The only work which consid-

ers both DCs and servers level is (Yao et al., 2014).

The authors propose a two-time-scale Lyapunov op-

timization algorithm to select DCs and servers to re-

duce power costs. It is argued that it is ﬁt for delay

tolerant workloads, such as MapReduce. But in all

these papers, no concrete map and reduce phase are

detailed. It is due to that MapReduce concerned in

the work does not support data analytics across DCs.

MapReduce across DCs are explored in pa-

per (Wang et al., 2013) (Zhang et al., 2014) (Jay-

alath et al., 2014). G-Hadoop (Wang et al., 2013)

can embrace any scheme to place reducer, though it

uses the traditional scheme by default. It randomly

places reducers in involved DCs. All intermediate

data partitioned to one reducer are then copied to the

DC where the reducer locates. This scheme does not

consider the distribution mode of intermediate data

and reducers. In the subsequent work (Zhang et al.,

2014), scheduling strategies are studies to process re-

mote sensing data across DCs. Hypergraph integrated

with task tree is used to lessen the inter-DC data trans-

fer and select the key workﬂow path so that optimize

the task completion time. Comparatively, G-MR (Jay-

alath et al., 2014) uses an advanced scheme by deﬁn-

ing a single directional weighted graph to depict the

data placement and transfer path. All input data in

each DC should be partitioned to equal size partitions.

The nodes of the graph are the combination of parti-

tions in different DCs before map or reduce phase and

the edge is the transfer path from one node to another.

Weight of the node is the cost to maintain the node,

while weight of the edge is the cost to copy data. Ob-

viously, there are m

nodes where m is the number of

partitions of data in each DC and n is the number of

DCs, and therefore a even bigger number of paths. If

arbitrary partition is allowed there will be a nodes and

paths catastrophe. To reduce the size of the graph, the

authors make several limits, for example, partitions

must be equal in size, data transfer only be allowed if

the number of DCs can be reduced and exchange of

data between two DC is not allowed. But these limits

lead to some unproﬁtable consequences and deterio-

rate the optimality.

3 PROBLEM FORMULATION

Suppose the distributed data are stored in K DCs. In

each DC k (k = 1,...,K), there are J

PMs. The total

number of PMs in all DCs is J, i.e.,

∑

k=1

= J. Map-

per works according to data locality principle and the

map output is stored locally. I is the conﬁgured num-

ber of reducers. Based on the sampling result, the data

in DC k hashed to reducer V

is d

. The cost aware re-

ducer placement problem can be summarized as, plac-

ing I reducers which aims to reduce all the intermedi-

ate data on J PMs distributed in K DCs, so as to min-

imize the overall costs at both DC and server level,

including power, server and network. The problem is

modeled as a 0-1 integer linear bi-level programming

(ILBLP).

3.1 Low Level Objective and

Constraints

Low level is server level. It aims to select PMs in DC

to host the reducers assigned to this DC by the higher

level, i.e., DC level, as illustrated in Fig. 1). Sup-

pose the number of reducers assigned to DC k is I

∑

k=1

= I. Reducer V

requires H kinds of resources

,...,V

, such as CPU, memory and disk storage,

etc. P

denotes PM j in DC k. It possesses H kinds

of resources P

,...,P

. Speciﬁcally, we designate

the ﬁrst dimension resource as CPU (P

and V

) for

ease of notation. The low level can only decide the

host PM for each reducer. The decision variable is de-

noted by a boolean variable x

. x

indicates whether

is assigned to P

. It equals 1 if V

is assigned to P

and 0 otherwise. The other variable controlled by low

level is y

which denote whether to activate PM P

. It

equals 1 if P

is active and 0 otherwise.

For each DC k, the low level programming is writ-

ten as:

min

y,x

f(y,x) =

∑

j=1

∑

h=1

(LLP)

IoTBD 2016 - International Conference on Internet of Things and Big Data

246

s.t.

∑

i=1

≤ P

h = 1,··· ,H, j = 1,··· ,J

(1)

≥ (

∑

i=1

)/I

j = 1,··· , J

(2)

∈ {0,1} j = 1,··· ,J

(3)

∑

j=1

= 1 i = 1,··· ,I

(4)

∈ {0,1} i = 1,··· ,I

, j = 1, · · · , J

. (5)

The objective function is the resource costs of PM

used inside each DC k where c

is the price for re-

source h. Constraint (1) indicates that in each PM, the

resource capacity should be respected. Constraint (2)

states a PM is viewed as active if it hosts at least one

VM. Constraint (4) implies a VM can only be placed

in one PM.

3.2 High Level Objectives and

Constraints

High level focuses on choosing reducers and assign-

ing them to a certain DC. It optimizes the overall

power costs, inter-DC bandwidth costs and PM nodes

costs. Binary variable z

indicates whether assign re-

ducer i to DC k. If it is true then z

= 1 and 0 other-

wise.

Power Costs. CSP can leverage the geo-diverse

electricity price of geo-distributed DCs involved in

the MapReduce job to optimize the power costs. Sup-

pose the electricity price of D

is e

. Let a is the coef-

ﬁcient to reﬂect the relation between power and CPU

load. p

is the power consumption of P

in idle or

standby state. Because power grows largely positive

proportional to CPU utilization (Fan et al., 2007), we

use an afﬁne function of CPU load (

∑

∈P

) to esti-

mate power costs. To make the power consumed and

physical resource costs comparable, we follow the

way of (Greenberg et al., 2008). All the one time pur-

chased physical resource costs is amortized in a rea-

sonable lifetime. So all the physical resource prices

in the formulation are the amortized ones. Implicitly,

in the formulation, we only balance the costs in the

amortized period. The power costs of all the reducers

are

(z,y,x) =

∑

k=1

∑

j=1

∑

∈P

+ p

). (6)

The former half of F

(z,y,x) represents power costs

caused by workload and the latter half is power in

idle or standby state.

PM Nodes Costs. PM nodes costs is determined

by server level in each DC. It is modeled the same as

f(y,x). The total PM nodes costs in K DCs cared by

high level is

(z,y,x) =

∑

k=1

∑

j=1

∑

h=1

. (7)

Inter-DC Bandwidth Costs. Let t

is the data

transmission price from D

to D

derived form the

bandwidth price of cloud service providers. t

. t

= 0, if j = k. d

is the data volume in

witch has been partitioned to reducer i. Once

reducer i is assigned to D

(that means z

= 1),

all data, i.e.,

∑

j=1

data should be moved to D

for reducing and incur cost

∑

j=1

(

∑

i=1

. So

for K DCs, the total inter-DC bandwidth costs are

∑

k=1

∑

j=1

(

∑

i=1

. The inter-DC bandwidth

costs are

(z) =

∑

k=1

∑

j=1

(

∑

i=1

. (8)

Intermediate Data Storage Costs. Let s

is the

storage price in DC k, then storing all the intermediate

data in target DC needs cost

(z) =

∑

k=1

∑

j=1

(

∑

i=1

. (9)

The high level optimization can be summarized as

a 0-1 linear integer programming HLP:

min

z,y,x

F(z,y,x) = (6) + (8) + (7) + (9) (HLP)

∑

i=1

≥ (

∑

j=1

)/J

k = 1,··· ,K (10)

∑

k=1

= 1 i = 1,··· ,I (11)

∈ {0,1} i = 1,··· ,I,k = 1,··· ,K (12)

∈ {0,1} j = 1,··· ,J

,k = 1,··· ,K (13)

where x and y are the solutions of the low level pro-

gramming.

In the high level constraints, (10) indicates that,

once there is one active PM in D

, then must be a

reducer which is assigned to DC k. Every reducer

should be assigned to a certain DC so that all the con-

ﬁgured I reducers are used in the job. It is reﬂected in

(11).

Bi-level programming is proved to be strong NP-

hard (Bard, 1991). GA has been demonstrated as

a very efﬁcient scheme to address bi-level program-

ming (Zhang et al., 2016b) (Sun et al., 2008). We

resort to GA to solve it.

Key based Reducer Placement for Data Analytics across Data Centers Considering Bi-level Resource Provision in Cloud Computing

247

4 ALGORITHM

The framework of GA is same. After encoding of the

problem, crossover and mutation operations are ap-

plied to the encoded populations until the stopping

condition is satisﬁed. Then the result is decoded to

the solutions of the problem to be addressed. The

encoding and decoding scheme, operations should be

customized for speciﬁc problems.

4.1 Encoding and Decoding Scheme

The encoding scheme should reﬂect the structure and

information of the problem to be optimized in the

genes of a chromosome. Considering that we should

try to keep the VMs in a DC with the lowest power

price, the lowest resource price and the most data to

be processed, we adopt the encoding scheme of multi-

level group GA (MLGGA) (Moghaddam et al., 2014).

It is illustrated in Fig. 2.

Reducers:

EBADCFAF:yxxyxzxz:yxz

Encoding:

PMs

DCs

Figure 2: Grouping encoding.

Suppose I reducers should be assigned to PMs in

K DCs. Each candidate PM (DC) is numbered and

given a serial number (SN). The encoding comprises

three parts. The ﬁrst one lists the SNs of PMs in which

VMs are placed. The second one lists the SNs of DCs

to which PMs belong. The third one is the lineup of

SNs of DCs in the second part after deleting the re-

peated ones. The three parts are isolated by a colon.

Suppose PMs A ∼ F, x = A,B,C, y = D, E,z = F

where “=” means that the right PMs belonging to the

left DC. Fig. 2 encoding the placement of 8 reducers.

The decoding is self-evident.

4.2 Initial Population Generation

We try to equip each initial population with a pretty

good gene, so that it can be inherited by the off-

springs. MLGGA only aims to reduce the number

of servers and DCs used. In our problem, the fewest

servers and DCs cannot ensure the optimality of the

solution. So we propose new initial population gener-

ation schemes.

It is assumed readers are familiar with GA, otherwise please

refer (Zhang et al., 2016a) for details.

To save power and take full use of all the PM

nodes resources dedicated for reduce tasks, we mod-

ify the ﬁrst ﬁt decreasing algorithm (denoted as

MFFD). Some notions are introduced ﬁrst. The ca-

pacity of an empty PM P

is deﬁned as

∑

h=1

i.e., the sum of all the resources dimensions of P

The normalized weight for dimension h is ω

1/(max

j,k

). Or

∑

h=1

if there exists one VM

in this PM, where r

is the h-dimension residue ca-

pacity of P

. The reason is that in computer, if any

dimension is used up, then the PM cannot support any

more VMs. DC capacity is deﬁned as the sum of the

capacity of all PMs in the DC. Capacity request of

VMV

is similar to the upper deﬁnition except that P

is replaced by V

. Sort all VMs-yet-to-be-assigned

according to their capacity. Then assign the biggest

VM to the active PM with the smallest residue capac-

ity. If the PM can accommodate the VM then the VM

is places in this PM. Otherwise, try the next active PM

until the VM can be placed or a new PM is activated.

This process is repeated until all VMs are assigned in

this DC. MFFD can optimize the objective of the low

level programming. It is also used for local optimiza-

tion to speed up the convergence.

Some genes embrace the power costs F

, the least

power costs VM placement algorithm (LPC) is pro-

posed in Algorithm 1.

Algorithm 1: Least power costs VM placement algorithm

(LPC).

1: Input: V: VMs set, DC: K Candidate DCs where the

input data are stored

2: Output: VM placement solution encoding X

3: Sort DCs according to e

. Sort VMs-yet-to-be-

assigned according to their capacity

4: A cheaper DC and a bigger VM are selected with

higher probability. The selected VM is placed in this

DC by leveraging MFFD. This process is repeated until

all VMs are placed

5: Encoding the solution as X according to section 4.1

In Algorithm 1, we can replace the sorting crite-

rion e

with resource price c

(deﬁned as the sum of

unit resources prices: c

∑

h=1

). Then we have

another method which strives to place the biggest

VMs in the DC with the cheapest PM nodes resource.

We denote it as LeastNodeCost (LNC). LNC aims to

optimize F

For F

, we use a simple heuristic to place reducers.

A reducer is assigned to a DC with more data to be

reduced by it. If there are two same DCs, any one

is randomly selected. This scheme aims to incur the

least data transfer (LDT).

LPC, LNC and LDT will be invoked x times, re-

IoTBD 2016 - International Conference on Internet of Things and Big Data

248

spectively, to produce 3 ∗ x initial feasible solutions.

This scheme can produce a rather large scale initial

populationand the three groups of population embody

a relatively good placement for the three factors of the

high level objective, respectively. Thus, the parents

are endowed with some optimal properties. In the lat-

ter crossover and mutation, though the initial solution

maybe will be replaced by a new one, the size of the

initial population remained at least 3 ∗ x so that the

GA can converge faster.

4.3 Crossover Operator

The mechanism of the crossover operator in MLGGA

is adopted. But to optimize nodes costs and power

simultaneously, we use MFFD to replace the classic

FFD used in MLGGA.

The crossover tries to inherit the property of the

parent and preserve the VMs in the inserted group

(PM or DC) unchanged. It will delete the different

resident VMs in the same group in the target chro-

mosome ﬁrst and keep the common VMs. For exam-

ple, if there are two chromosomes, P

: EBADCFAF :

yxxyxzxz : |y|xz where DC y contains VM 1 and VM 4,

while P

is: afcdeabd : XZXYYXXY : |X|ZY where

DC Y contains VM 4 and VM 5. Herein we use the

same alphabet with different case represents the same

PM or DC. Therefore, y and Y represent the same

DC. | means crossover point. For target chromosome

, when crossover operates, X will be replaced by y.

Now there are two same DC y and Y in the offspring

of P

. So VMs in y should be deleted so that VMs

in Y are preserved unchanged, i.e., VM 5 in y will be

reassigned by FFD and VM 4 is kept.

Once a DC has the most intermediate data for one

reducer, the lowest power and resource prices, then

the three initial population generation schemes tend to

place the reducer in the same DC. In the crossover op-

eration, this kind of reducers will be remained. Other

reducers will be changed to different DC to seek the

smallest overall costs.

4.4 Mutation Operator

The mutation happens in the third part, i.e., DC level,

thus leads to reduction of DCs. Considering that data

transfer has most effect on costs and consumes more

time in the MapReduce work. We give a higher prob-

ability to mutate the DC with less data. All the VMs

in the mutated DC should be placed to the target DC

with MFFD.

4.5 The Uniﬁed Genetic Algorithm:

TLGGA

The uniﬁed GA algorithm, two level grouping GA

(TLGGA) is depicted in Algorithm 2. Local opti-

mization is used to speed up the convergence by ap-

plying MFFD.

Algorithm 2: The uniﬁed genetic algorithm (TLGGA).

1: Generate x initial population by LPC, LNC and LDT,

respectively. Denotes these 3∗x population as C

2: while (Stopping condition is not satisﬁed) do

3: Crossover. Random select one individual from C

and denote as X

, and another different X

. Apply-

ing crossover to X

with a probability to produce

two offspring Y, Z until X

traverse C

4: Mutation. Applying mutation with a probability to all

Y,Z to produce Y

′

5: Local optimization. Applying MFFD to Y, Z

6: Update of C . For each X in C ,

If F(Y

′

) ≤ F(X), then X = Y

′

If F(Z

′

) ≤ F(X), then X = Z

′

The size of C is kept not less than 3∗ x

7: The X in C with the least objective value is the solu-

tion

8: end while

4.6 Algorithm Execution in

G-framework

After a small part of data in each DC, such as 5% per-

cent, is mapped, the HigherJoberTracker can sample

the outputs in each DC. The approximate key distri-

bution is obtained and the data volume for each key is

estimated. The conﬁguration of reducers that matches

the input size can further be predicated so that no re-

duce task takes more time and thus decrease the job

delay. Now HigherJobTracker can use the conﬁgu-

ration information to select the location of reducers

by invoking TLGGA. At the same time, the other ini-

tial data can be mapped. Once the location is deter-

mined, the later output of mappers will be continu-

ously copied to the target DC according to keys.

5 SIMULATION

5.1 Evaluation Test Bed

Since there are normally a dozen of DCs for the

commercial cloud service providers (e.g., at least

11 DCs for Amazon (Amazon, ) and 13 DCs for

Google (google, )), we randomly select seven DCs

in Amazon regions to store the data. Each region is

numbered and the number indicates the sequence of

Key based Reducer Placement for Data Analytics across Data Centers Considering Bi-level Resource Provision in Cloud Computing

249

DC to be added. Table 1 gives the sequence number,

where “H”, “M” and “C” indicates “Hour”, “Month”

and “Cents”, respectively.

In each DC, the number of PMs follows U(30−

50) and the type is uniformly selected from the four

PM classes. The conﬁguration of PM is borrowed

from IBM System x M5 server and System x3300

M4 server. We adopt four kinds of EC2 conﬁgu-

rations of Amazon m3-serials (for consistency with

PM, GiB is replaced by GB) as the resource require-

ments of VMs. M3-serials are designed for gen-

eral purpose and are representative. According to

VMWare (VMware, ), the number of logical cores in

each PM is equal to or at most the twice of that num-

ber of the physical cores. The number of vCPUs of

VMs in the PM cannot exceed the logical cores of the

PM. So we suppose there is a one-to-one relation be-

tween vCPU and physical core. The details are listed

in table 2.

Suppose there are 900 data blocks stored in DCs

and each block is 128 MB. 900 mappers are used to

process the data. After sampling the map outputs

from all involved DCs, the key space is 1000. In

each DC, the input data volume of each key follows

U(0− 0.1) GB. We follow the guidance of (Tannir,

2014) to conﬁgure 600 reducers. Each key is hashed

to a certain reducer to process. The reduce output is

set as 1% of the reduce input (we call it the ratio of

reduce output). Assume that each medium VM can

process 2.5 GB data per hour. Other VM with multi-

ple relation conﬁguration can process the same multi-

ple data in the same duration. Hence the time needed

can be estimated by VM type and data volume.

The price of resources are illustrated in table 1.

We try to use the public data of Amazon to keep the

price consistent. Considering the multiple relations

of conﬁguration of PMs and requirement of VMs, we

only list the price of the medium class. The price of

other class also follows the multiple relations. For

example, xLarge VM with 4 vCPUs requires 4 times

higher price than that of the medium size one. Storage

price is from S3. Table 1 gives the price of medium

VM and storage prices in different regions. We derive

the price of data transfer from Amazon Import/Export

service and transferring each GB needs 0.0243$. The

electricity price pool is from the data of July, 2014 of

EIA (EIA, ). Each simulated DC is equipped with a

random price selected from the pool. We adopt the

idle or standby power consumption p

as 60% of the

peak power (Fan et al., 2007).

The initial solution size of TLGGA is 3 ∗ x and

x = 15. The crossover probability is 0.6 and the mu-

tation probability is 0.3. All numerical experiments

stop after 10 thousand iterations (It is observed that

the algorithm converges after about one thousand it-

erations as illustrated in Fig. 3.).

Basicly, G-Hadoop is a direct extension of tradi-

tional Hadoop. We use G-Hadoop with the random

placement scheme of reducers as the baseline (de-

noted as GHadoop in the later simulation). All Map-

pers follow data locality principle, i.e., each mapper

locates in the same DC where the data it will process

are stored. This leads to that the mapper results are

distributed in multiple DCs. To reduce the map out-

put, we select the DC which total costs (the sum of

∼ F

) is minimum and then move all map output to

the selected DC to reduce. In the selection, the VM

is placed using MFFD just as TLGGA does and each

DC is compared straight forward. The state-of-the-art

of MapReduce across DCs is G-MR (Jayalath et al.,

2014). In the realization of G-MR, the initial partition

size is set as 20 percent of the total input size as rec-

ommended in (Jayalath et al., 2014). Note that both

GHadoop and G-MR will store the reduce result in

only one DC. While TLGGA may distribute reduce

output among DCs. To compare the cost of TLGGA

and other two algorithms, we straight forward select

the DC to move all reduce result to it with the mini-

mum costs after execution of TLGGA.

5.2 Simulation Results

5.2.1 The Convergence of TLGGA

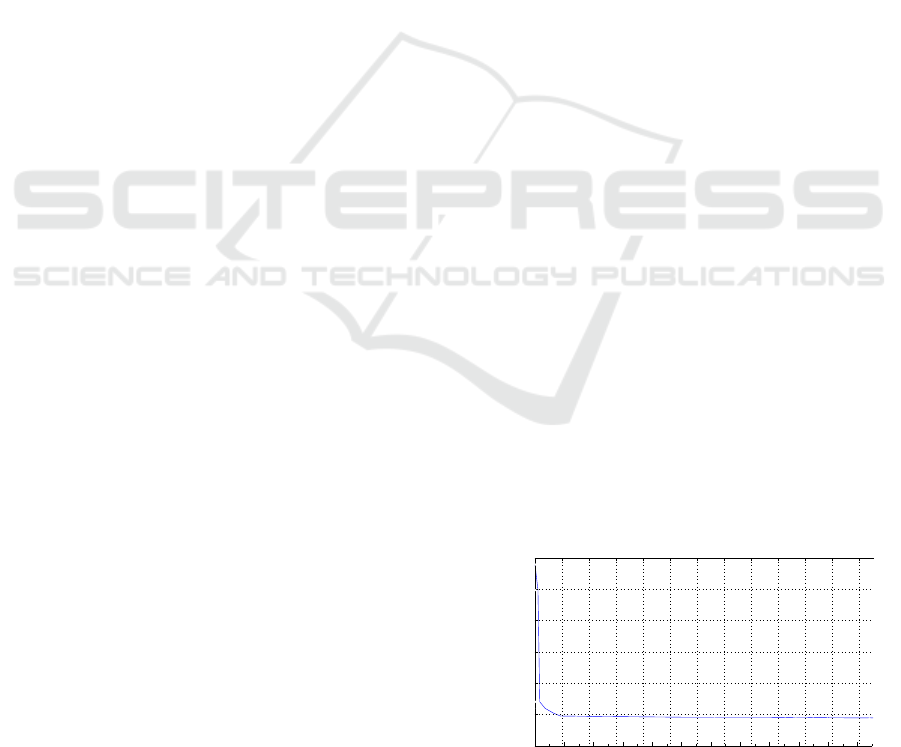
Fig. 3 demonstrates the convergence of TLGGA when

there are 4 DCs (DC 1 ∼ DC 4). In the simulation,

it is found that in the ﬁrst 200 iterations (consists of

the crossover of all population, the mutation and local

optimization), the objective value decreases fast and

the curve is very steep. Then in the later 800 itera-

tions, it starts to level off. After about one thousand

iterations, the objective function value decreases very

slowly though it takes more time. We can obtain a

rather good solution within about 2 seconds.

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 1,00001,1000

500

1000

1500

2000

2500

3000

3500

Iterations

Cost ($)

0 2 4 6 8 10 12 14 16 18 20 22 24

500

1000

1500

2000

2500

3000

3500

Execution time (Sec.)

Figure 3: Convergence of TLGGA for 4 DCs.

IoTBD 2016 - International Conference on Internet of Things and Big Data

250

Table 1: Sequence number and resources prices of data centers in different regions.

Data centers California Frankfurt Singapore Sao Paulo Oregon Ireland Sydney

Sequence Number 1 2 3 4 5 6 7

medium PM ($/H) 0.408 0.400 0.498 0.48 0.368 0.38 0.472

medium VM ($/H) 0.077 0.075 0.098 0.095 0.067 0.073 0.093

Storage ($/GB/M) 0.033 0.0324 0.03 0.0408 0.03 0.03 0.033

Electricity (C/KW/H) 11.91 9.49 15.47 14.37 8.77 8.90 15.47

Table 2: PMs resource conﬁgurations and VMs resource requirements.

PM Cores Memory VM vCPUs Memory

medium 4 32 medium 1 3.75

large 8 64 large 2 7.5

xlarge 24 192 xlarge 4 15

2xlarge 32 256 2xlarge 8 30

5.2.2 Scalability Evaluation

To evaluate the sensitivity of the three algorithms on

the number of DCs, we add 1 DC according to the

sequence number every time. The cost is depicted in

Fig. 3 where the number of DCs increases from 2 to

It is observed that the intuitive GHadoop incurs

the highest cost. G-MR comes next and TLGGA is

the most cost effective mechanism. This is due to that

after map locally, GHadoop will select a DC and then

copy all the map output to it to reduce. For G-MR,

since it partitions data in one DC into several parts,

this enables it to ﬁnd lower cost with a rather ﬁne

grained management. But because the size of the par-

tition is ﬁxed, it cannot differentiate keys and cannot

take into their distribution characteristics. Thus it still

incurs most cost than TLGGA. TLGGA estimates the

key space and the input of each key. This facilitates

TLGGA to place the reducer in the DC where most

data hashed to it are stored and avoid more data trans-

fer costs. Together with the other resources, i.e., PM,

storage and electricity price, it seeks the cheapest so-

lution and saves more costs than GHadoop and G-MR

by about 49% and 40%, respectively.

With the number of DCs increasing, the costs of

765432

1000

1250

1500

1750

2000

Number of DCs

Cost ($)

TLGGA

G−MR

GHadoop

Figure 4: Cost when the number of DCs increases.

all algorithms begin to increase. This illuminates that

if data are distributed among more DCs, it will cause

more cost in the Hadoop framework. It is beneﬁcial

to cost saving if the number of DCs is limited to a

reasonable scale.

Note that after DC 5 (Oregon) is added, the costs

of all algorithms show a slight decrease. This is due to

that all resources prices of this DC are relatively lower

than those of the former 4 DCs. This DC provides

a better candidate and all the algorithms prefer this

newly added one.

Ideally, it is desired that the algorithm is as slight

as possible. We record the execution time in table 3.

When the number of DCs is not more than 3, G-MR

and GHadoop exhibit the similar efﬁciency. When it

increases continually, the execution time of GHadoop

grows slowly. But the time cost of G-MR increases

with an exponential speed. The large directed graph

leads to this situation and G-MR is not suitable for

large scale application. The quality of solution of

TLGGA comes at the cost of time. It takes more time

than GHadoop and G-MR when the number of DCs is

not bigger than 5. But its time cost grows slowly with

DCs. Moreover, as discussed before, we can obtain a

rather good solution within a much shorter duration.

5.2.3 Effect of Key Distribution

In a cloud, perhaps the key distribution is uneven. We

use “uneven” to indicate that the number of keys at

different DCs differs greatly. It will have great effect

on costs in Hadoop across DCs. Herein we get the

number of keys uniformly from 1000∼2000 for the

seven DCs (i.e., 1281, 1993, 1614, 1147, 1700, 1064

and 1522). The cost is demonstrated in Fig. 5 and the

cost changes are depicted in Fig. 6.

In total, the cost tendency is just similar to that of

Fig. 4. But when there are only 2 DCs, G-MR even

Key based Reducer Placement for Data Analytics across Data Centers Considering Bi-level Resource Provision in Cloud Computing

251

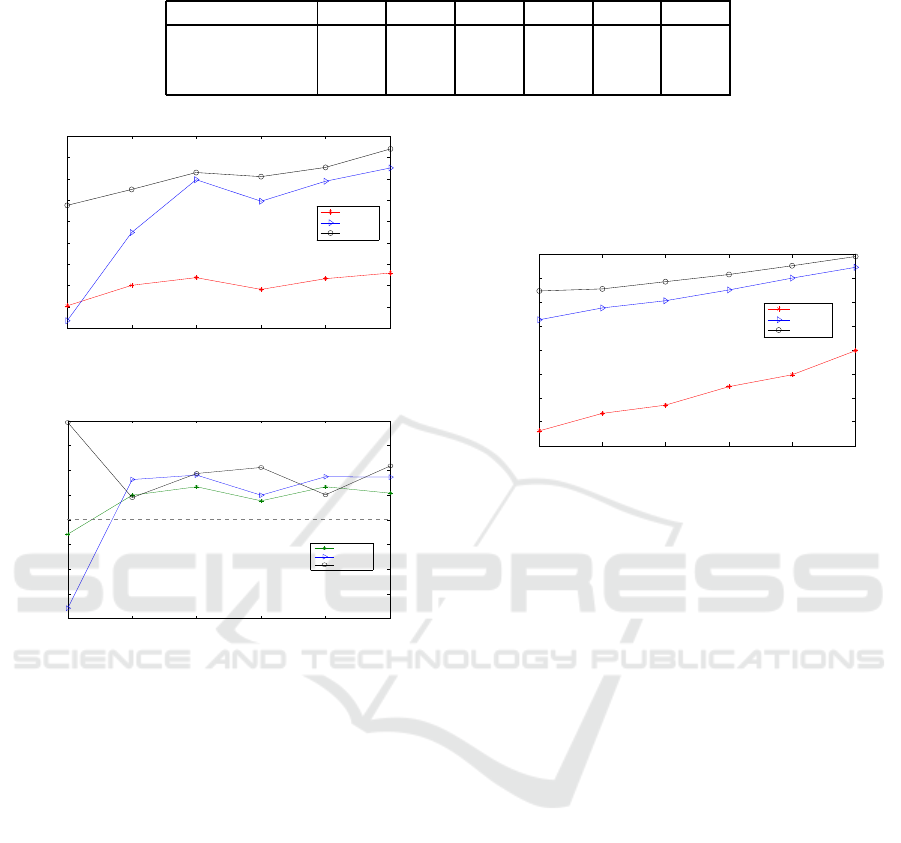
Table 3: Execution time of algorithms (times are in seconds).

Number of DCs 2 3 4 5 6 7

TLGGA 19.71 20.35 21.73 22.31 22.70 23.55

GHadoop 0.17 0.19 0.28 0.44 0.58 0.62

G-MR 0.04 0.17 1.88 12.34 48.60 246.7

765432

600

800

1000

1200

1400

1600

1800

2000

2200

2400

Number of DCs

Cost ($)

TLGGA

G−MR

GHadoop

Figure 5: Cost with the number of DC increasing when the

key is uneven.

765432

−400

−300

−200

−100

100

200

300

400

Number of DCs

Cost changes ($)

TLGGA

G−MR

GHadoop

Figure 6: Cost changes with the number of DC increasing

when the key is uneven.

outperforms TLGGA. This is because that there are

most keys in the relatively cheaper DC 2 (Frankfurt),

G-MR prefers moving more data from DC 1 to DC 2.

But TLGGA will move data across 2 DCs according

to the distribution of keys and thus offsets the proﬁt of

the more granular management.

The changes demonstrate an interesting phe-

nomenon. When there are 2 DCs, the uneven distri-

bution of keys makes the costs of G-MR and TLGGA

decrease. But GHadoop cannot make use of the un-

even property to save its costs. In summary, costs of

TLGGA increase least and G-MR takes the second.

GHadoop ﬂuctuates without regularity.

Because the ﬁnal reduce output should be aggre-

gated to one DC, we change the reduce output ratio.

Fig. 7 demonstrates the effect. It is observed that GH-

daoop is almost not sensitive to the reduce output.

This lies in that it reduces data only after all input

is transferring to one DC. G-MR is more sensitive to

reduce output since it will reduce part data and then

aggregates. TLGGA is most sensitive to it because it

only moves the reduce output. But generally, costs of

TLGGA are still much smaller than those of the other

two algorithms. Note that the reduce output is rather

small generally, TLGGA is suitable for data process

across DCs.

0.5 0.75 1 1.25 1.5 1.75

600

800

1000

1200

1400

1600

1800

2000

2200

Ratio of reduce output (%)

Cost ($)

TLGGA

G−MR

GHadoop

Figure 7: Cost when the ratio of reduce output changes.

6 CONCLUSION AND FUTURE

DIRECTIONS

This paper explores the reducer placement for

Hadoop across data centers. Aiming to save costs and

respect the locality principle of tradition Hadoop as

much as possible, the problem is formalized as a bi-

level programming which can capture both DC level

and server level resources. A new scheme to place re-

ducers based on the key distribution is proposed. The

scheme tries to place the reducer in the DC where the

data hashed to it have the largestvolume together with

optimal resources costs. A two level group genetic al-

gorithm (TLGGA) is tailored to facilitate the scheme.

Speciﬁc initial population methods are presented ac-

companied with a local optimization tactic. Extensive

simulations revealed the effectiveness of TLGGA. It

outperforms both the baseline method, i.e., traditional

Hadoop, and also the state-of-the-art, G-MR.

Due to data across DCs, latency is also a factor

which should be considered in Hadoop across data

center (Chang et al., 2011). In addition to the long dis-

tance between DCs, many factors may increase the la-

tency, such as ﬁle size, job failures, etc. We try to op-

timize latency while keeping low costs and compare

the performance by utilizing the OSM model (Chang

and Wills, 2015) which can capture all the factors.

Another issue worthy of study for data analytics

across DCs is security (Chang and Ramachandran,

IoTBD 2016 - International Conference on Internet of Things and Big Data

252

2016) and disaster recovery (Chang, 2015). Inside

one DC, the job can be completed within one VPN

and is in a trust network. Job across DCs may span

public network and it would absolutely have to be

over one VPN. A framework integrated with some

major security technologies, such as ﬁrewall, iden-

tity management and encryption has been proposed

for business cloud (Chang et al., 2015) (Chang and

Ramachandran, 2016). Focusing on GHadoop, the

authors of (Zhao et al., 2014) explores the framework

for big data computing across data centers. All these

works can be coordinated with the G-framework to

reﬁne the architecture.

ACKNOWLEDGEMENTS

This work was ﬁnancially supported by National

High Technology Research and Development

Program of China (No. 2015AA016008), Na-

tional Science and Technology Major Project (No.

JC201104210032A), National Natural Science

Foundation of China (No. 11371004, 61402136),

Natural Science Foundation of Guangdong Province,

China (No. 2014A030313697), International Ex-

change and Cooperation Foundation of Shenzhen

City, China (No. GJHZ20140422173959303),

Shenzhen Strategic Emerging Industries Pro-

gram (No.ZDSY20120613125016389), Shen-

zhen Overseas High Level Talent Innova-

tion and Entrepreneurship Special Funds (No.

KQCX20150326141251370), Shenzhen Applied

Technology Engineering Laboratory for Internet

Multimedia Application of Shenzhen Development

and Reform Commission (No. [2012]720), Public

Service Platform of Mobile Internet Application

Security Industry of Shenzhen Development and

Reform Commission (No. [2012]900).

REFERENCES

Amazon. Amazonproduct. http://aws.amazon.com/.

Apache. hadoop. http://hadoop.apache.org/.

Bard, H. understanding-hadoop-clusters-and-the-network.

http://bradhedlund.com/2011/09/10/

understanding-hadoop-clusters-and-the-network/.

Bard, J. (1991). Some properties of the bilevel program-

ming problem. Journal of optimization theory and

applications, 68(2):371–378.

Chang, H., Kodialam, M., Kompella, R., Lakshman, T.,

Lee, M., and Mukherjee, S. (2011). Scheduling in

mapreduce-like systems for fast completion time. In

INFOCOM, 2011 Proceedings IEEE, pages 3074–

3082.

Chang, V. (2015). Towards a big data system disaster recov-

ery in a private cloud. Ad Hoc Networks, 35:65–82.

Chang, V., Kuo, Y. H., and Ramachandran, M. (2015).

Cloud computing adoption frameworka security

framework for business clouds. Future Generation

Computer Systems, 57:2441.

Chang, V. and Ramachandran, M. (2016). Towards achiev-

ing data security with the cloud computing adoption

framework. IEEE Transactions on Services Comput-

ing, pages 1–1.

Chang, V. and Wills, G. (2015). A model to compare cloud

and non-cloud storage of big data. Future Generation

Computer Systems.

EIA. Usapowerprice. http://www.eia.gov/state/data.cfm?

sid=CT.

Fan, X., Weber, W.-D., and Barroso, L. A. (2007).

Power provisioning for a warehouse-sized computer.

SIGARCH Comput. Archit. News, 35(2):13–23.

google. Google data centers locations. http://www.google.

com/about/datacenters/inside/locations/index.html.

Greenberg, A., Hamilton, J., Maltz, D. A., and Patel, P.

(2008). The cost of a cloud: research problems in data

center networks. ACM SIGCOMM Computer Com-

munication Review, 39(1):68–73.

He, C., Weitzel, D., Swanson, D., and Lu, Y. (2012). Hog:

Distributed hadoop mapreduce on the grid. In High

Performance Computing, Networking, Storage and

Analysis (SCC), 2012 SC Companion:, pages 1276–

1283. IEEE.

Jayalath, C., Stephen, J., and Eugster, P. (2014). From

the cloud to the atmosphere: Running mapreduce

across data centers. Computers, IEEE Transactions

on, 63(1):74–87.

Kulkarni, S. Cooling hadoop: Temperature aware sched-

ulers in data centers.

Kuo, J.-J., Yang, H.-H., and Tsai, M.-J. (2014). Optimal ap-

proximation algorithm of virtual machine placement

for data latency minimization in cloud systems. In IN-

FOCOM, 2014 Proceedings IEEE, pages 1303–1311.

IEEE.

Lublinsky, B., Smith, K. T., and Yakubovich, A. (2013).

Professional Hadoop solutions. John Wiley & Sons,

Inc.

Maheshwari, N., Nanduri, R., and Varma, V. (2012). Dy-

namic energy efﬁcient data placement and cluster re-

conﬁguration algorithm for mapreduce framework.

Future Generation Computer Systems, 28(1):119127.

Moghaddam, F. F., Moghaddam, R. F., and Cheriet, M.

(2014). Carbon-aware distributed cloud: multi-level

grouping genetic algorithm. Cluster Computing,

pages 1–15.

Schadt, E. E., Linderman, M. D., Sorenson, J., Lee, L., and

Nolan, G. P. (2010). Computational solutions to large-

scale data management and analysis. Nature Reviews

Genetics, 11(9):647–657.

Sun, H., Gao, Z., and Wu, J. (2008). A bi-level program-

ming model and solution algorithm for the location of

logistics distribution centers. Applied Mathematical

Modelling, 32(4):610 – 616.

Tannir, K. (2014). Optimizing Hadoop for MapReduce.

Packt Publishing Ltd.

Key based Reducer Placement for Data Analytics across Data Centers Considering Bi-level Resource Provision in Cloud Computing

253

Tudoran, R. (2014). High-Performance Big Data Man-

agement Across Cloud Data Centers. Theses, ENS

Rennes.

Tudoran, R., Costan, A., and Antoniu, G. (2012). Mapiter-

ativereduce: a framework for reduction-intensive data

processing on azure clouds. In Proceedings of third

international workshop on MapReduce and its Appli-

cations Date, pages 9–16.

VMware. vcpu. http://pubs.vmware.com/vsphere-50/

index.jsp#com.vmware.vsphere.vm

admin.doc 50/

GUID-13AD347E-3B77-4A67-B3F4-

4AC2230E4509.html.

Wang, L. and Shen, J. (2014). Multi-phase ant colony

system for multi-party data-intensive service provi-

sion. Services Computing, IEEE Transactions on,

PP(99):1–1.

Wang, L., Shen, J., and Luo, J. (2015). Facilitating an ant

colony algorithm for multi-objective data-intensive

service provision. Journal of Computer & System Sci-

ences, 81(4):734–746.

Wang, L., Tao, J., Ranjan, R., Marten, H., Streit, A.,

Chen, J., and Chen, D. (2013). G-hadoop: Mapre-

duce across distributed data centers for data-intensive

computing. Future Generation Computer Systems,

29(3):739–750.

White, T. (2010). Hadoop: The Deﬁnitive Guide. 2nd Edi-

tion. O’Reilly Media, Inc.

Xu, H. and Li, B. (2012). A general and practical datacen-

ter selection framework for cloud services. In Cloud

Computing (CLOUD), 2012 IEEE 5th International

Conference on, pages 9–16. IEEE.

Yao, Y., Huang, L., Sharma, A., Golubchik, L., and Neely,

M. (2014). Power cost reduction in distributed data

centers: A two-time-scale approach for delay tolerant

workloads. IEEE Transactions on Parallel and Dis-

tributed Systems, 25(1):200–211.

Zeng, L., Veeravalli, B., and Wei, Q. (2014). Space4time:

Optimization latency-sensitive content service in

cloud. Journal of Network and Computer Applica-

tions, 41:358–368.

Zhang, J., Huang, H., and Wang, X. (2016a). Resource

provision algorithms in cloud computing: A survey.

Journal of Network and Computer Applications,pages

1–1

Zhang, J., Zhang, L., Huang, H., Wang, X., Gu, C., and He,

Z. (2016b). A uniﬁed algorithm for virtual desktops

placement in distributed cloud computing. Mathemat-

ical Problems in Engineering, 2016:1 – 15.

Zhang, W., Wang, L., Ma, Y., and Liu, D. (2014). Design

and implementation of task scheduling strategies for

massive remote sensing data processing across mul-

tiple data centers. Software Practice & Experience,

44(7):873–886.

Zhao, J., Wang, L., Tao, J., Chen, J., Sun, W., Ranjan,

R., Kołodziej, J., Streit, A., and Georgakopoulos, D.

(2014). A security framework in g-hadoop for big

data computing across distributed cloud data centres.

Journal of Computer and System Sciences,80(5):994–

1007.

IoTBD 2016 - International Conference on Internet of Things and Big Data

254