
A Fuzzy System to Automatically Evaluate and Improve Fairness of
Multiple-Choice Questions (MCQs) based Exams
Ibrahim A. Hameed
Department of Automation Engineering (AIR), Faculty of Engineering and Natural Sciences,
Norwegian University of Science and Technology (NTNU), Larsgårdsvegen 2, 6009 Ålesund, Norway
Keywords: Automatic Assessment, Academic Assessment, Students’ Achievement, Efficient and Effective Assessment,
Question Importance, Question Complexity, Artificial Intelligence in Education.
Abstract: Examination is one of the common assessment methods to assess the level of knowledge of students.
Assessment methods probably have a greater influence on how and what students learn than any other
factor. Assessment is used to discriminate not only between different students but also between different
levels of thinking. Due to the increasing trends in class sizes and limited resources for teaching, the need
arises for exploring other assessment methods. Multiple-Choice Questions (MCQs) have been highlighted
as the main way of coping with the large group teaching, ease of use, testing large number of students on a
wide range of course material, in a short time and with low grading costs. MCQs have been criticised for
encouraging surface learning and its unfairness. MCQs have a variety of scoring options; the most widely
used method is to compute the score by only focusing on the responses that the student made. In this case,
the number of correct responses is counted, the number of incorrect answers is counted and a final score is
reported as either the number of the correct answers or the number of correct answers minus the number of
incorrect answers. The disadvantages of this approach are that other dimensions such as importance and
complexity of questions are not considered, and in addition, it cannot discriminate between students with
equal total score. In this paper, a method to automatically evaluate MCQs considering importance and
complexity of each question and providing a fairer way to discriminating between students with equal total
scores is presented.
1 INTRODUCTION
Assessment is defined as ‘the multi-dimensional
process’ in which learning is appraised and feedback
is used to improve teaching (Angelo and Cross,
1993). Assessment methods have a greatest
influence on how and what students learn than any
other factors. Students are usually preoccupied with
what constitutes the assessment in their chosen field
and therefore assessment usually drives student
learning. Assessment determines student approaches
to learning (Boud, 1988). Assessment method sends
messages to students to define and priorities what is
important to learn and ultimately how they spend
their time leaning it. Assessment can be used to, as
far as possible, create positive incentives for
teachers to teach well, and for students to study well
(Wiliam, 2011). However, despite its importance,
‘assessment remains the aspect of the curriculum
teaching and learning practices that is least
amenable to change’ (Scarino, 2013). Despite the
challenges of making changes to assessment, there
has been a need for ‘change’ due to the increasing
trends in class sizes and limited resources for
teaching (Donnelly, 2014).
MCQs based examinations are utilised as a result
primarily of limited resources, and are used in the
majority of cases to address the need to assess a
large class of students in a short time (Donnelly,
2014). MCQs are popular for evaluating medical
students given the logistical advantages of being
able to test large numbers of candidates with
minimal human intervention, their ease of use, low
grading cost and testing efficiency comprise the sole
rational for their continued use (McCoubrie, 2004).
Due to the weakness and the criticism that MCQs
cannot assess the foundational knowledge or core
concepts and encourage superficial learning
(Pamplett and Farnill, 1995), MCQs would not be
the ideal form of assessment for lecturers if
476
Hameed I.
A Fuzzy System to Automatically Evaluate and Improve Fairness of Multiple-Choice Questions (MCQs) based Exams.
DOI: 10.5220/0005897204760481
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016), pages 476-481
ISBN: 978-989-758-179-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

resources and time allowed (Donnelly, 2014). MCQs
based exams are reliable only because they are time-
efficient (McCoubrie, 2004). Brady (2005)
suggested when deciding on assessments, lectures
are carrying out an ethical activity, and that they
must be confident and justified in the assessment
that they are have chosen.
MCQs based exams have a variety of scoring
options. The most widely used method is to compute
the score by only focusing on the responses that the
student made. In this case, the number of correct
responses is counted, the number of incorrect
answers is counted and a final score is reported as
either the number of the correct answers or the
number of correct answers minus the number of
incorrect answers. The practicality of MCQs is to
evaluate large groups of students in short time and it
might be difficult or time consuming to set different
grades for each question. Another aspect is the so-
called ‘assessment by ambush’ where the choice of
questions is determined by the desire to discriminate
as clearly as possible between high and low
achievers (Brown, 1992). This may lead to
omissions of questions on essential or fundamental
parts of the curriculum because they are ‘too easy’
and insufficiently discriminatory which may drive
examiners to skip over potentially important topics
(McCoubrie, 2004). This might lead to an
assessment approach that is unable to discriminate
between students with equal total scores. A student
who answered a set of more significant questions to
the curriculum and more complex questions that
might require more time and thinking may be
rewarded a score equal to that of another student
who answered a set of less significant and easy
questions (Hameed, 2010; 2011).
Importance is based on how much a question is
essential for the curriculum. Difficulty of a question
is based upon the amount of effort needed to answer
a question, solve a question, or complete task. Such
questions, problems, or tasks are defined as easy or
hard and are determined by how many people can
answer the question, address the problem, or
accomplish the task correctly or successfully.
Complexity, on the other hand, defined as easy and
hard and relates to the kind of thinking, action, and
knowledge needed in order to answer a question,
solve a problem, or complete a task and how many
ways are there to do this. Complex questions,
problems, and tasks are often challenge and engage
students to demonstrate thinking (Francis, 2014).
Fair assessment should not just consider plain grades
but should also consider the aforementioned
dimensions as well (Saleh and Kim, 2009; Hameed,
2011). Improving the fairness of MCQ is an
increasingly important strategic concept to improve
the validity of their use (McCoubrie, 2004) and to
ensure that all students receive fair grading so as not
to limit students’ present and future opportunities
(Saleh and Kim, 2009; Hameed, 2011).
In this paper, a fuzzy system based evaluation
approach for MCQs based exams considering
importance, complexity, and difficulty of each
question is proposed. The main purpose is to provide
a fairer way to discriminate between students with
equal total scores and to reflect the aforementioned
dimensions for fairer evaluation. The paper is
organized as follows: the proposed evaluation
system is presented in Section 2. In Section 3, an
example and results are presented. Concluding
remarks and future work are presented in Section 4.
2 EVALUATION SYSTEM
DESIGN
The proposed evaluation system will consist of some
modules as follows:
2.1 Difficulty Ratio
For other forms of written exams, difficulty ratio of
a question can be calculated as a function of the
accuracy rate a student has achieved and the time
used to answer a question (i.e., answer-time) (Saleh
and Kim, 2009). So if a student has obtained a
higher accuracy rate in less time, it means that the
question is easy, and vice versa. In case of MCQs
based exam where answers are either true or false, a
student will get either the full mark of the question
or nothing at all (Omari, 2013). Therefore and for
the sake of simplicity, difficulty in this paper will be
defined as ‘the percentage of the number of students
who answered the question correctly’. Difficulty
ration or coefficient can be calculated using the
formula:
D
i
= 1 - T
i
/N (1)
where D
i
is the difficulty ratio or coefficient of
question i, T
i
is number of students who answered
question i correctly, and N is the total number of
students who answered the question or attended the
exam. As an example, assume that (4) students from
(10) answered the first question correctly, so the
difficulty coefficient for this question is given by (1-
4/10) = 0.6. Since the difficulty coefficient is a ratio,
so its value is between zero and one, and when the
coefficient of difficulty is zero or close to zero it is a
A Fuzzy System to Automatically Evaluate and Improve Fairness of Multiple-Choice Questions (MCQs) based Exams
477
sign that the question is very easy, and if its value is
1 or close then that means that the question is very
difficult. This means that the difficulty factor of a
question is inversely proportional to its easiness. It is
recommended that the difficulty value to be in the
range of 0.50 to 0.75. Exam designers are
recommend to put some easy questions at the
beginning of the exam to encourage students, but
some hard questions that determine strong students
are posted at the end of the exam.
2.2 Score Adjustment
In this paper and as a proof of concept (PoC) to
realize the proposed approach, only difficulty will be
used in evaluation to adjust students’ grades. The
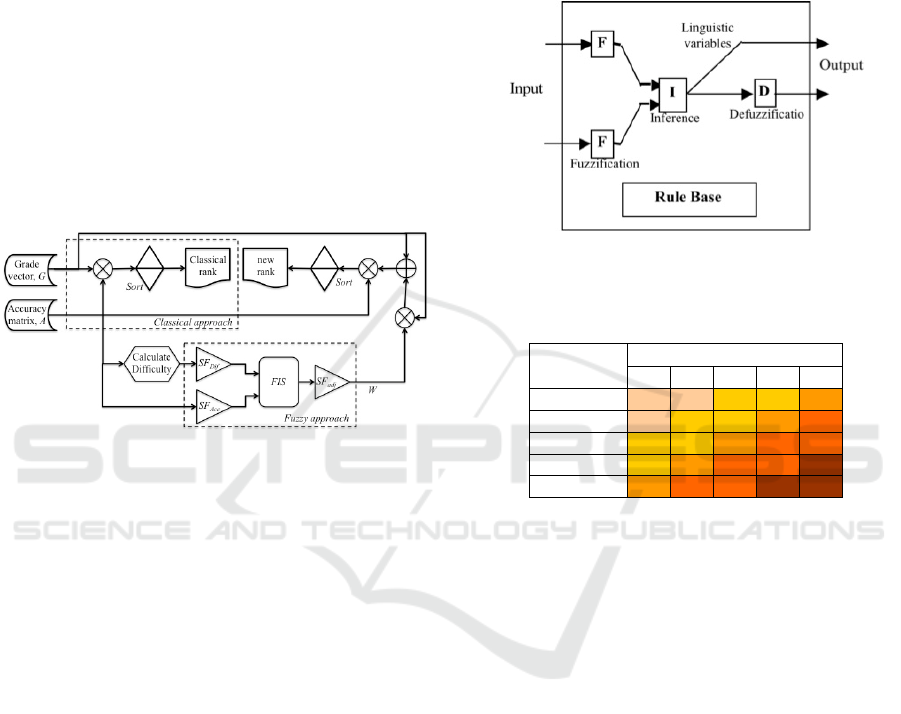
developed approach is shown in Figure 1.
Figure 1: Schematic diagram of the proposed evaluation
system.
Assume that there are n students laid to an exam
of m questions. Here, the accuracy rate matrix,
A=[a
ij
] is of m×n dimensions, where a
ij
denotes the
accuracy rate of student j on question i. In case of
written form exams, a
ij
∈[0, 1] and in case of
true/false MCQs based exams, a
ij
∈{0, 1}. G
T
denotes the transpose of G, where G is of m×1
dimension, G= [g
i
], g
i
∈[1, 100], denotes the
assigned maximum score to question i, where:
g
i
i=1
m
∑
= 100
(2)
Classical ranking approach relies merely on
accuracy rate of each student in his/her exam
questions and therefore it can be considered as a
quantitative approach that is unable to differentiate
between students with equal total scores and cannot
reflect other dimensions such as importance,
complexity, and difficulty of each question. The
classical ranking is then obtained as:
S=
G
T
A
(3)
The fuzzy evaluation system, on the other hand,
incorporates difficulty of each question and
produces a new grading vector, W, as it is shown in
Figure 1. Inputs to the system, on the left hand side
of the figure, are the difficulty vector calculated in
Section 2.1, and the accuracy rate matrix, A, given
by exam results. A Mamdani type fuzzy inference
system (FIS) with two scalable inputs and one
output is used, as it is shown in Figure 2.
Figure 2: Mamdani FIS to map difficulty and accuracy
into adjustment (Saleh and Kim, 2009).
Table 1: Fuzzy rule base to infer Adjustment.
Accuracy
Difficulty
1 2 3 4 5
1 1 1 2 2 3
2 1 2 2 3 4
3 2 2 3 4 4
4 2 3 4 4 5
5 3 4 4 5 5
Mamdani's fuzzy inference method is the most
commonly seen fuzzy. Mamdani's method was
among the first control systems built using fuzzy set
theory. It was proposed in 1975 as an attempt to
control a steam engine and boiler combination by
synthesizing a set of linguistic control rules obtained
from experienced human operators methodology
(Mamdani and Assilian, 1975). Mamdani's effort
was based on Zadeh's 1973 paper on fuzzy
algorithms for complex systems and decision
processes (Zadeh, 1973). The proposed FIS maps a
two-to-one fuzzy relation by inference through a
given rule base, shown in Table 1 where 1, 2, 3, 4
and 5 stands for the five linguistic labels of the fuzzy
sets shown in Figure 3; low, more or less low,
medium, more or less high and high, respectively.
In this paper, five Gaussian membership
functions (GMFs) with fixed mean and variable
variance or standard deviation are used to fuzzify
each input into a linguistic variable with a degree of
membership. Variable variance value is used to
reflect the degree of uncertainty chosen by the
domain expert or examiner to reflect his/her degree
of uncertainty in the grades assigned to each
question. The FIS has two input scale factors and
CSEDU 2016 - 8th International Conference on Computer Supported Education
478

one output scale factor; difficulty scale factor, SF
Dif
,
accuracy scale factor, SF
Acc
, and adjustment scale
factor, SF
Adj
. Input scale factors are chosen in a
manner to emulate the degree of importance of each
input. In this paper, SFs are chosen to be unity to
consider the equal influence of each input on the
output. In total 25 fuzzy rules, shown in Table 1, are
used to infer adjustment in terms of accuracy and
difficulty. As an example:
IF Accuracy is low (1) AND Difficulty is medium
(3) THEN Adjustment is more or less low (2).
Figure 3: Five Gaussian Mfs with σ = 0.2; low, more or
less low, medium, more or less high, and high.
The surface view of the fuzzy relation to infer
adjustment in terms of difficulty and accuracy is
shown in Figure 4.
Figure 4: Input/output mapping to infer adjustment.
3 RESULTS
In this Section, an example is tailored to test the
proposed MCQs based fuzzy evaluation system.
3.1 Example
Assume that we have n students laid to an exam of m
questions where n=10 and m=5. The accuracy rate
matrix, A, and the grade vector, G, are given as
follows:
A =
1011001000
0000100011
0111011011
1100100110
1001110111
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
G
T
= 10 15 20 25 30
⎡
⎣
⎤
⎦
.
3.2 Classical Grading Approach
The classical ranking is obtained using Equation (3)
as follows:
S= G
T
A
= [90
9
70
5
65
10
65
1
60
4
55
8
50
6
45
2
30
7
30
3
]
From which we can find that student number 9
has got 90 and therefore he/she has occupied the first
rank. Student number 5 has got 70 and therefore
he/she occupies the second place, etc. Classical
ranking method relies only on accuracy rate of each
student and therefore there are four students with
equal total final scores. As an example, both
students 1 and 10 occupy the 3
rd
and 4
th
highest
ranks with an equal total score of 65 while students
3 and 7 occupy the last 9
th
and 10
th
ranks with an
equal total final score of 30. Students 1 and 10 have
correctly solved two different sets of questions;
student 1 has solved the set
{q
1
, q
4
, q
5
} while
student 10 has solved the set {
q
2
, q
3
, q
5
}, while
students 3 and 7 have correctly solved the same set
of questions, i.e.,
{q
1
, q
3
}. From results, it is obvious
that this approach is unable to differentiate between
students with equal total final grades even though
they have solved different sets of questions with
different difficulty ratios.
3.3 Fuzzy Grading Approach
In this approach, the difficulty ratio of the exam
questions is first calculated using Equation (1) to be:
D
T
= 0.6 0.7 0.3 0.5 0.3
⎡
⎣
⎤
⎦
The difficulty ratio is recommended to be in the
range of 0.50 to 0.75 and exam should start with
easy questions (i.e., less difficulty ratio) to
encourage students (Omari, 2013). Sorting questions
according to its difficulty ratio gives
q
2
>>q
1
>>q
4
>>q
3
=q
5
. The average grade of each
question is then obtained as:
A Fuzzy System to Automatically Evaluate and Improve Fairness of Multiple-Choice Questions (MCQs) based Exams
479

A
T
= aij
i=1
n
∑
∀ j = 1:m,
= 0.4 0.3 0.7 0.5 0.7
⎡
⎣
⎤
⎦
.
The difficulty ratio and the average grade of
each question are then fuzzified using the five
Gaussian MFs shown in Figure 3 and used to infer
adjustment, W, though the rule base given in Table 1
to be:
W = 0.29 0.30 0.30 0.29 0.30
⎡
⎣
⎤
⎦
where w
i
is the adjustment factor (%) required for
modifying the grade of question i in order to
compensate for its difficulty. As a result, the
adjusted grade vector is slightly modified to be:
G
Fuz
T
= 9.9 15.1 20.1 24.8 30.1
⎡
⎣
⎤
⎦
.
The modified grade vector is then used to
recalculate the final grades and the new ranks of
each student using Equation (3) as follows:
S
Fuz
= G
Fuz
T
A
= [90.1
9
70.0
5
65.3
10
64.9
1
60.1
4
55.0
8
50.2
6
44.9
2
30.0
7
30.0
3
]
By comparing the original grade vector, G, and
G
fuz
, it becomes obvious that the grades are slightly
changed. This change could be increased or
decreased further by tuning the scale factors SF
Acc
,
SF
Dif
, and/or SF
Adj
in a manner to reflect the
effectiveness and importance of each variable. The
modified grades did not make any dramatic changes
in students’ final grades, however, it provided
distinct ranking especially of students with equal
final grades. Students 1 and 10 in the classical
grading approach have obtained equal final score of
65 and therefore occupied the same ranking order
but with the new fuzzy approach, where difficulty is
considered, the final score of student 10 has slightly
increased and that of student 1 has slightly decreased
so student number 10 now clearly occupies the
highest 3
rd
rank while student 1 occupies the 4
th
highest rank. The proposed approach can provide
distinct ranks and consider other qualitative
dimension in the evaluation process such as
complexity and importance. In this paper, difficulty
ratio has been calculated using formula (1),
however, it could be obtained directly from the
domain expert or examiner .
4 CONCLUSIONS
In this paper, a fuzzy based evaluation approach for
MCQs based exams is presented. The proposed
system can automatically grade students considering
difficulty of each question. It can discriminate
between students of equal final total grades and
hence can provide fairer grading in a manner that
foster motivation and learning. Other qualitative
dimensions such as complexity and importance can
also be considered. The proposed system can be
used or can be extended to various areas of decision
support system. As a future work, complexity and
importance will be considered and the real exam
data will be used to validate it. The evaluation
systems proposed in this paper have been
implemented using the Fuzzy Logic Toolbox™ for
building a fuzzy inference system from
MathWorks™ (Fuzzy Logic Toolbox, 2016).
REFERENCES
Angelo, T.A., Cross, K.P., 1993. Classroom assessment
techniques: A handbook for college teachers. San
Francisco: Jossey-Bass, 2nd edition.
Boud, D., 1988. Developing student autonomy in learning
(2nd ed). London: Kogan Page.
Brady, A.M., 2005. Assessment of learning with multiple-
choice questions. Nurse Education in Practice, 5, 238-
242.
Brown, S., 1992. Trends in assessment, in: R. Harden, I.
Hart & H. Mulholland (Eds) Approaches to the
Assessment of Clinical Competence, Vol. 1 (Dundee,
Centre for Medical Education), pp. 3–8.
Donnelly, C., 2014. The use of case based multiple choice
questions for assessing large group teaching:
implications on student’s learning. Irish Journal of
Academic Practice, 3(1), Art. 12, 1-15.
Francis, E.M., 2014. Teaching higher order thinking and
depth of knowledge. Retrieved in Feb. 7
th
2016 from
http://maverikeducation.blogspot.com/2014/03/difficul
ty-vs-complexity-whats.html.
Fuzzy Logic Toolbox™ 2.2.7, 2016, retrieved from
http://www.mathworks.com/products/fuzzylogic/ in
February 6
th
2016 (license no. 914603).
Hameed, I.A., 2011. Using Gaussian membership
functions for improving the reliability and robustness
of students' evaluation systems. Expert systems with
Applications, 38(6), 7135-7142.
Hameed, I.A., Sørensen, C.G., 2010. Fuzzy Systems in
Education: A More Reliable System for Student
Evaluation, Fuzzy Systems, Azar A. T. (Ed.), ISBN:
978-953-7619-92-3, INTECH, Croatia.
Mamdani, E.H., Assilian, S., 1975. An experiment in
linguistic synthesis with a fuzzy logic
controller. International Journal of Man-Machine
Studies, 7(1), 1-13.
McCoubrie, P., 2004. Improving the fairness of multiple-
choice questions: a literature review. Medical Teacher,
Vol. 26, No. 8, 2004, pp. 709–712.
Omari, A., 2013. An Evaluation and Assessment System
for Online MCQ's Exams. International Journal of
CSEDU 2016 - 8th International Conference on Computer Supported Education
480

Electronics and Electrical Engineering, 1(3), 219-222,
doi: 10.12720/ijeee.1.3.219-222.
Pamplett, R., Farnill, D., 1995. Effect of anxiety on
performance in multiple choice examination. Medical
Education, 29, 298-302.
Saleh, I., Kim, S.-I., 2009. A fuzzy system for evaluating
students’ learning achievement. Expert systems with
Applications, 36(3), 6236-6243.
Scarino, A., 2013. Language assessment literacy as self-
awareness: Understanding the role of interpretation in
assessment and in teacher learning. Language Testing,
30(3), 309-327.
Wiliam, D., 2011. Bryggan mellan undervisning och
lärande (The bridge between teaching and learning).
Lärarförbundets Förlag, Pedagogiska Magasinet, 113-
120 (its English version is retrieved from
http://www.dylanwiliam.org/Dylan_Wiliams_website/
Papers_files/Pedagogiska%20magasinet%20article.do
cx in 29 December 2015).
Zadeh, L.A., 1973. Outline of a new approach to the
analysis of complex systems and decision processes.
IEEE Transactions on Systems, Man, and Cybernetics,
3(1), 28-44.
A Fuzzy System to Automatically Evaluate and Improve Fairness of Multiple-Choice Questions (MCQs) based Exams
481
