What Should We Add to Syntax-oriented Generation of Random

Expressions to Meet Pedagogical Needs?

Rein Prank

Institute of Computer Science, University of Tartu, Liivi Str 2, Tartu, Estonia

Keywords: Exercise Environments, Algebraic Expressions, Random Generation, Propositional Logic.

Abstract: The paper looks for an exercise environment where the teacher program would enable to fix parameters of

random generation so that the generated tasks have desired pedagogical properties. In particular, it should be

possible to prescribe qualitative content and size of the solution and its parts, opportunities to make certain

errors, probabilities of different decisions to be made by the student. We analyse two existing environments

for algebraic exercises in Propositional Logic and identify what additional options are necessary and what

computational engines or precomputed resources could produce the desired properties.

1 INTRODUCTION

Random generation of expressions has become a

widely used technique in Computer-Aided Learning

of Mathematics. There are many websites and pro-

grams, which enable students to solve randomly

generated drill tasks on virtually all technical topics

of Basic School. Teachers use random generation of

individualized tasks to ensure that students complete

their independent work and tests without plagiarism.

They often prefer random homework and test tasks

even if they require different amount of work from

different students. The importance of random gener-

ation will increase with the development of MOOC

(Massive Open Online Courses) by the universities.

Exercise software often contains teacher tools for

compiling homework and test task sets. The teacher

can usually design a task chain by selecting for each

task the task type and by entering ‘difficulty level’

or the values of generation parameters. Quite often

the optional parameters describe mainly the syntac-

tic properties of generated expressions and do not

enable specification of tasks with desired properties

of solutions. In this case the teacher can implement

his/her pedagogical ideas only partially or has to use

fixed tasks that are the same for all students.

This paper analyses random generation options

of two environments that are implemented and used

at our institute for algebraic exercises in Proposi-

tional Logic. Both environments use quite typical

syntax-oriented formula generation algorithms

where the main teacher-defined parameters are the

number of variables and numbers of each of the

logical operators. We identify what solution-oriented

generation parameters are necessary to add to such

generators and what computational engines or pre-

computed resources could produce the desired prop-

erties of tasks.

Section 2 of this paper describes related work. In

Section 3 we attempt to present a list of typical ped-

agogical requirements for a random generation algo-

rithm and for a set of teacher-definable generation

parameters. Section 4 introduces our software for

computerized propositional exercises. Sections 5 and

6 analyze random generation in our truth-table and

formula manipulation environments in the frame-

work of the requirements introduced in Section 3.

Section 7 contains a summary.

2 RELATED WORKS

There are many websites that offer students a possi-

bility to solve randomly generated tasks belonging to

virtually all task types in Basic School algebra.

Many such sites give teachers the possibility to

compile worksheets consisting of tasks of one or

more task types. For example, a web search with the

phrase ‘random generation algebra’ gave us seven

quite universal websites (beginning with Coolmath

in References). The website of IXL.com lists hun-

dreds of task types but offers no difficulty levels or

482

Prank, R.

What Should We Add to Syntax-oriented Generation of Random Expressions to Meet Pedagogical Needs?.

In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 1, pages 482-487

ISBN: 978-989-758-179-3

specification of more detailed properties of expres-

sions within the types. The website of Mathmix.com

does not contain nearly as many types but the ex-

pression generation can be driven by a number of

parameters (Figure 1).

Figure 1: Task generation parameters for two-step linear

equations in Mathmix.com.

Available websites demonstrate the features

that are currently available for students and teachers,

the pedagogical and computational level of applica-

tions. It is clear that none of the websites enable the

teacher to compile task chains which contain all the

cases that are covered by exercises in textbooks. The

menus simply do not contain enough options and

usually the generated expressions contain only 2-4

operations (fractions, monomials etc).

Another relevant tool is Wolfram Problem

Generator (Wolfram). It generates problems, checks

answers, provides hints and displays step by step

solutions for a small number of most relevant task

types. The tasks have three difficulty levels, with the

advanced tasks having much more complex expres-

sions than the aforementioned websites.

Several authors have created syntactical tools

that can be used for random generation of expres-

sions from predefined operators and functions. Ex-

amples include: RANDPOLY (Wright,1994),

Matlab Expression Generator, Math Expression

Generator (see References).

There are only a few published papers about the

use of random generation of expressions with peda-

gogical objectives. The best-known are the papers

on major systems of Computer Aided Assessment.

These systems are designed for task creators who are

able to use some more powerful language for de-

scription of desired expressions. AIM is a well-

known test system that uses computer algebra.

N. Strickland states in (Strickland, 2002): “Current-

ly all AIM questions are written using a kind of

mark-up language incorporating elements of Maple

code and elements of LaTeX”. STACK, a more

recent system, allows describing random generation

of expressions based on templates with variable

coefficients and expressions for generation of each

coefficient (Sangwin, 2006). Similar features of the

ActiveMath system are described in (Mavrikis and

Gonzales, 2004). In these systems pedagogical con-

siderations are not so much concern of generating

mechanism but concern of people who create the

templates. The same is true for Basic Logic Tutor

ORGANON (Dostalova and Lang, 2011) where the

authors state "Therefore the database is not filled up

by concrete exercises but by PATTERNS". Unfortu-

nately the authors do not demonstrate the spectrum

of exercises derived from one pattern.

T-algebra is an interactive exercise environ-

ment for Basic School Algebra (Prank et al, 2007).

A system of task types and difficulty levels and the

functioning of random generation at each level can

be observed when trying to compose task files with

the T-algebra teacher program (T-algebra).

A series of papers on random generation of

tasks in different topics has been published by a

group of researchers supported by Microsoft where

S. Gulwani seems to be the key person. The paper

(Andersen, Gulwani and Popovic, 2013) traces the

use of operations in standard solutions of tasks. The

received traces are used for comparison of problems,

analysis and synthesis of problem sets.

3 DESIRED FEATURES OF A

GENERATION ALGORITHM

AND TEACHER CONTROL

Many task types in our package for Mathematical

Logic (Prank, 1991) and all the 60+ task types in T-

algebra (Prank et al, 2007) contain random genera-

tion of exercises. We have had many discussions

with university colleagues and school teachers about

their expectations in that regard. We now try to for-

mulate general requirements for random generation

of initial expressions of tasks. Requirements A and

B describe mainly the features of generation algo-

rithm while C-F indicate what should be possible to

specify by selection of generation parameters.

 A. Sufficient variety of generated expressions.

The set of possible initial expressions should

cover initial expressions of usual textbook exer-

cises.

 B. Exception of cases that are forbidden for

particular task type or are trivial.

 C. Sufficiently precise specification of qualita-

tive content of student’s work. In case of our

propositional exercises it should specify:

─ what operations are performed by filling

the truth-table,

What Should We Add to Syntax-oriented Generation of Random Expressions to Meet Pedagogical Needs?

483

─ what patterns are to be used for finding the

formula corresponding to given column of

values,

─ what conversion rules are necessary for

formula transformation.

 D. Specification of opportunities to make cer-

tain errors/inappropriate steps.

 E. Specification of solution size (amount of

student’s work):

─ general size,

─ size of particular parts of the solution

(stages of solution algorithm).

 F. Equal or teacher-definable probabilities of

positive and negative answers about tautologi-

city, equivalence etc.

Requirement A is satisfied practically by any

usual (string- or tree-based) syntax-oriented genera-

tion algorithm if the allowed number of variables

and length of generated expressions is not too small.

In our course the only task types where some ini-

tial formulas are forbidden are conversions to nor-

mal form where tautologically false/true initial ex-

pressions do not have disjunctive/conjunctive NF.

Our random generator takes the task type into ac-

count and does not generate forbidden initial formu-

las. The generators also do not generate formulas

where an operation is to be performed between two

copies of the same variable. We discuss type-

specific trivial cases and requirements C-F in the

context of concrete environment and task types.

4 OUR SOFTWARE FOR

PROPOSITIONAL LOGIC

The content of the two following sections is based

on our experience with the design, implementation

and use of exercise environments for truth-table and

formula manipulation exercises. In 1987-1993 we

computerized ten 90-minute exercise labs together

with homework and tests. The computerized exer-

cise labs were introduced in our third-semester

course Introduction to Mathematical Logic, begin-

ning from 1991 (Prank, 1991).

Having been created many years ago, the soft-

ware has required upgrades in task types, user inter-

face, hint facilities, security, support for teacher’s

work, web access, etc. The programs have been re-

implemented as Bachelor and Master projects. How-

ever, even implementation of the minimum neces-

sary mechanisms of the exercise environments usu-

ally exceeded the normal size of a thesis. Next round

in our work will be implementation of desired new

features. In the next two Sections of the paper we

describe what can be added to our existing computa-

tional tools and random generation schemes to

achieve sufficient meeting of didactical needs.

5 TRUTH-TABLE EXERCISES

Our truth-table environment contains the following

exercise types:

1) Filling the truth-table,

2) Checking of tautology,

3) Checking of satisfiability,

4) Checking of equivalence of two formulas,

5) Checking whether the first formula implies

the second,

6) Construction of formula having a given re-

sulting truth-column.

The solution dialogs of tasks of types 2-5 begin

with filling the rows of the table until it is possible to

justify the decision (positive or negative).

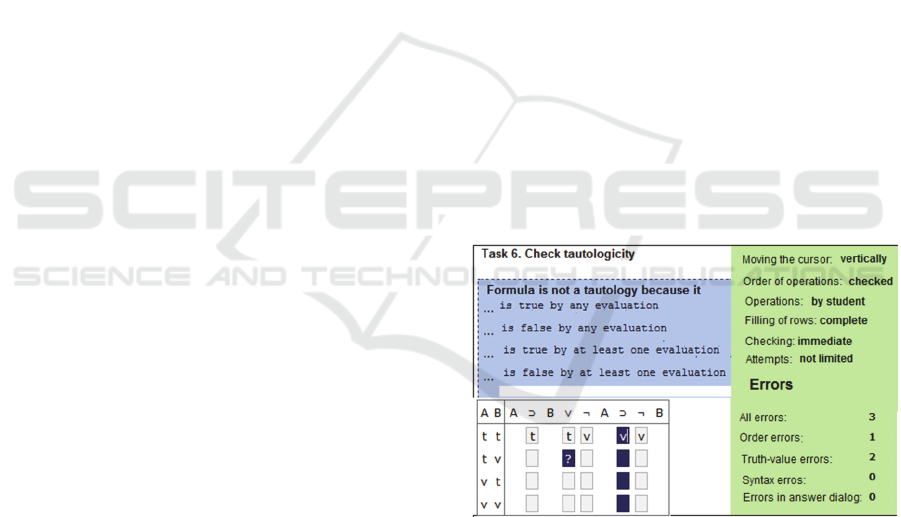
Figure 2 depicts the solution window for tautol-

ogy checking (original Estonian texts have been

replaced with English). The student has filled one

row and switched to answer dialog because the

truth-value on this row was  (false). The student

should now select from the menu the reason why the

formula is not a tautology.

Figure 2: Solution window for tautology checking task.

For formula construction tasks the program dis-

plays the required column of truth-values. When the

student enters the formula, the program automatical-

ly calculates its truth-table. In case of a wrong an-

swer the student should correct the formula.

For random generation the teacher program ena-

bles to specify the number of variables, the numbers

of each of the propositional connectives



, &,⋁, ⊃

,~and the percentage of truth-values true in the

column of values (0-25, 26-50, 51-75, 76-100 or

unspecified). For example, initial formula of Figure

CSEDU 2016 - 8th International Conference on Computer Supported Education

484

2 can be received when the teacher selects 2 varia-

bles, 1 disjunction, 2 implications and 2 negations.

Consider now our pedagogical aims for different

task types and expression generation principles that

allow implementing them. Our task sets contain for

each exercise type some tasks with fixed formulas.

The fixed tasks of types 2-5 contain classical exam-

ples and counterexamples of formulas with and

without corresponding properties, and a collection of

the main propositional equivalencies to be proved

using a truth-table. In type 6 there are some fixed

tasks that guide the student to recognize patterns of

all binary connectives and their negations and a

series of tasks that directs the student to discover the

possibility to build the formula with given truth-

values in disjunctive normal form (before introduc-

tion of NF in lectures). However, to ensure inde-

pendent work of students in every task type, we

include tasks with randomly generated formulas.

Propositional connectives are completely new

material for the students. Weaker students need a

considerable amount of training, with the program

checking the truth-values and the order of opera-

tions. The available generating parameters allow

adjusting the content of tasks and corresponding

error opportunities (requirements C-D) by specifying

the connectives in the formula. The amount of work

(req. E) is sufficiently well determined by the num-

ber of variables and total number of connectives.

The same is true for task types 2-5 where filling the

table constitutes the bulk of the work and remaining

part of the content is defined by the task type.

For checking of tautology, satisfiability etc it

would be desirable to have nearly equal probabilities

of positive and negative answers (requirement F).

Our current control of parameters does not enable

this. Currently we generate formulas with 76-100

percents of values true for tautology and 0-25 per-

cents of true for satisfiability checking but in prac-

tice we only get a few tautological and a few non-

satisfiable formulas. The generator could work in

two stages, first choosing the answer (tautology/not)

and then generating formulas until the suitable truth-

column is received.

With our current generation control options, we

generate for equivalence checking two formulas

with the lowest or highest percentage of true. For

inference checking we generate first a formula with

0-25 percent of true and second a formula with max-

imum number of true. This produces quite a satisfac-

tory distribution of results for inference but not for

equivalence. It is clear that the formulas for types 4-

5 should actually be generated together, choosing

first the answer true/false and then iterating the gen

eration.

Consider now the tasks on construction of a for-

mula for a given column of truth-values. After pre-

senting and practicing the above-described ideas of

pattern recognition and normal form we assign a

series of randomly generated tasks with three varia-

bles and 3-6 values true. The student is asked to find

a formula of ‘reasonable’ length. Having 3-6 values

true guarantees that the normal forms are longer

than the ‘reasonable’ formula.

Note here that our current task parameters do not

enable to set an upper limit for the length of the

formula (in terms of the number of connectives or

symbols). This feature can easily be added but it

should be used carefully. The task of finding the

formula is quite difficult for weaker students and

there should remain some opportunity to get partial

credit for the long answer in DNF.

In our obligatory exercises we do not require that

the shortest formula for given truth-values should be

found. This task is too difficult. However, we have

assigned such tasks for bonus points outside of com-

puterized environment. Could we generate reasona-

ble shortest formula tasks randomly? It proves to be

easier than expected. The usual breadth-first algo-

rithm produces the shortest formulas (containing all

connectives or a specified subset of them) for three-

variable columns very quickly and for four-variable

columns within seconds (on a standard laptop or

desktop computer). In the latter case we can also use

pre-computed files with 64K formulas. This allows

generation of training series with a growing length

of optimal formulas, tasks with equal complexity for

tests, tasks with maximum complexity, etc.

Knowledge about the shortest formula can also be

used for elimination of trivial cases (like tftftftf) by

generating the truth-columns for standard tasks.

6 FORMULA MANIPULATION

EXERCISES

Our environment for algebraic manipulation imple-

ments the following exercise types for propositional

formulas:

1) Three task types on expression of formula using

, &, ,∨, , ⊃,

2) Conversion to disjunctive/conjunctive normal

form (DNF/CNF),

3) Conversion to full disjunctive/conjunctive nor-

mal form (FDNF/FCNF),

4) Moving negations inside/outside,

5) Free conversion (the program checks only

What Should We Add to Syntax-oriented Generation of Random Expressions to Meet Pedagogical Needs?

485

equivalence at each step).

While working with our program, the student en-

ters the solution step by step. Each conversion step

is entered in two substeps. At the first substep the

student marks a subformula to be changed. For the

second substep the program has two different work-

ing modes. In Input mode the student enters a sub-

formula that replaces the marked part. In Rule mode

the student selects a conversion rule from the menu

and the program applies it. Figure 3 shows the solu-

tion window in Rule mode. The student has elimi-

nated biconditional and implications and intends

now to move negation inside (it could be better to

begin with the outermost negation).

Figure 3: Solution window of Formula Manipulation Envi-

ronment in Rule mode. The student has performed three

solution steps and marked a subformula for the fourth step.

Our exercise labs in Elements of Discrete Math-

ematics contain exercises of types 1 and conversion

to full disjunctive normal form.

The teacher program allows specification of the

number of variables and the numbers of proposition-

al connectives for random generation of a formula.

Consider now our type-specific pedagogical aims

and corresponding ideas for task generation.

In the first task types on expression of formulas

using given connectives the solution algorithm is

trivial: eliminate the undesired connectives one by

one. The qualitative content of tasks and error op-

portunities mean then: what equivalencies (conver-

sion rules) are necessary in the tasks. Requirements

C and D are satisfied because the teacher can

(roughly speaking) specify the left side of the con-

version rule by placing the corresponding connective

in the initial formula and the right side by specifying

the task type (what connectives are allowed in the

result).

Concerning requirement E we see that the size of

solution can be very directly specified by connec-

tives in the initial and target formula. Every conjunc-

tion, disjunction and implication can be eliminated

in one step. Biconditional requires 2-4 steps depend-

ing on binary target connective. Additional steps for

simplification of the result (mainly related to nega-

tions) are considerably easier and do not have great

impact.

There is yet one issue that affects the difficulty

of generated tasks (both on expression through given

connectives and DNF). The conversion rules for

elimination of biconditional multiply the arguments

of biconditional into two copies and make the for-

mula longer. For example, ~ ≡ & ∨ &.

This impact is small if the arguments of bicondition-

al are only variables or their negations, and is much

larger if the arguments are complex formulas (see

Fig. 3). It means that the amount and complexity of

work on tasks to be solved by different students has

a random component. For elimination of this ran-

domness it could be desirable to add a generation

parameter that defines the size(s) of arguments of

biconditional or at least have some lower bound (for

example, at least one argument/both arguments

should contain a binary connective).

Consider now FDNF exercises. We present in

our lectures the following version (Palm and Prank,

2004) of the usual algorithm for conversion of a

formula to FDNF :

1) Eliminate implications and biconditionals from

the formula;

2) Move negations inside;

3) Use distributive law to expand the conjunctions

of disjunctions;

4) Exclude contradictory conjunctions and redun-

dant copies of literals;

5) Add missing variables to conjunctions;

6) Order variables alphabetically, exclude redun-

dant copies of conjunctions.

Requirements C-E mean in FDNF exercises

mainly control over the numbers of steps to be made

at stages 1-6 of the algorithm. The teacher program

enables to generate formulas with the desired num-

ber of implications and biconditionals for stage 1.

We can also get a high probability of nontrivial stage

2, generating formulas with 3-4 negations. Using

existing generating parameters, we have limited

control over stages 3-6. The use of reverse engineer-

ing does not show much promise. The 6-stage algo-

rithm is too long for this. What can be added?

There is a quite simple opportunity for regulation

of sizes of stages 5-6 and partially of stages 3-4. The

number of necessary steps in these stages depends,

to a great extent, on the number of members in full

DNF. It means that the control over the number of

truth-values true would improve the situation with

CSEDU 2016 - 8th International Conference on Computer Supported Education

486

regard to requirements C-E.

More promising seems to be to generate the ini-

tial formulas and pick out those that meet our peda-

gogical needs. For this we need an Automated Solv-

er. How far are we from it? Our student program of

2013 already contains a solution engine that is used

for giving hints for next step (what to mark and how

to replace the marked part). It even creates full solu-

tions but does not make them available outside. On

the other hand, the student program saves in the

solution file the whole student solution together with

conversion rules used at each step (in case of Rule

mode). This means that, combining these two mech-

anisms, we would not have to program any new

engines for solving the task and checking what stag-

es of the algorithm are active. Our experience with

random generation for school algebra program T-

algebra shows that it is also possible to solve the

computation speed problems.

7 SUMMARY

In Sections 5 and 6 we found several possibilities for

giving the teacher better control over the properties

of generated tasks:

1. The teacher can specify precisely the acceptable

numbers of values true for generated formulas.

2. The program first randomly chooses the desired

answer (tautology/not, etc) and then generates

the corresponding formula(s).

3. The program is able to find the shortest formula

with a given column of values (using a corre-

sponding program module or a precomputed list

of formulas).

4. The teacher can specify the sizes of arguments

of biconditionals in generated formulas.

5. The program computes the solution stages of

generated normal form tasks, finds their sizes

and chooses appropriate formulas.

Addition of features 1-4 to our programs can be

implemented in a Bachelor thesis. Addition of fea-

ture 5 could result in a strong Master thesis. In fact,

our program already contains an algorithm for find-

ing the solution but it is necessary to experiment and

find sufficiently quick ways of generation.

ACKNOWLEDGEMENTS

Current study is supported by Study IT in

Estonia programme.

REFERENCES

Andersen, E., Gulwani, S., Popovic, Z., 2013. A Trace-

based Framework for Analyzing and Synthesizing

Educational Progressions. In CHI '13, Proceedings of

the SIGCHI Conference on Human Factors in Compu-

ting Systems, pp. 773-882. ACM.

Dostálova, L., Lang, J., 2011. ORGANON: Learning

Manament System for Basic Logic Courses. In Black-

burn, P. et al (eds.) TICTTL 2011. LNAI 6680, pp. 46-

53.

Mavrikis, M., Gonzalez, A. P., 2004. Mathematical Inter-

active Exercise Generation from Static Documents.

Electronic Notes in Theoretical Computer Science, 93,

183-201.

Palm, R., Prank, R., 2004. Sissejuhatus matemaatilisse

loogikasse. University of Tartu.

Prank, R., 1991. Using Computerised Exercises on

Mathematical Logic, In Informatik und Schule 1991.

Informatik-Fachberichte 292, pp. 34-38, Springer.

Prank, R., Issakova, M., Lepp, D., Tonisson, E., Vaiksaar,

V., 2007. Integrating Rule-based and Input-based

Approaches for Better Error Diagnosis in Expression

Manipulation Tasks. In Li, S., Wang, D., Zhang, J.

(eds). Symbolic Computation and Education. pp. 174-

191, World Scientific.

Sangwin, C.J., Grove, M., 2006. STACK: addressing the

needs of the neglected learners. In Seppälä, M.,

Xambo, S, Caprotti, O. (eds.). WebALT 2006

Proceedings, pp. 81-96. http://web.mat.bham.ac.uk/

C.J.Sangwin/Publications/2006WebAlt.pdf.

Strickland, N., 2002. Alice Interactive Mathematics.

MSOR Connections, 2(1), 27-30. http://

ltsn.mathstore.ac.uk/newsletter/feb2002/pdf/aim.pdf.

Wright, F.J.: RANDPOLY: A Random Polynomial

Generator. (1994) http://www.reduce-algebra.com/

docs/randpoly.pdf.

Coolmath Algebra, http://coolmath.com/algebra/

index.html.

Dynamically Created Math Worksheets, http://www.math-

aids.com/

HomeSchoolmath, http://www.homeschoolmath.net/

worksheets/

IXL Maths, http://eu.ixl.com/math/

Math.com Algebra Worksheet Generator, http://

www.math.com/students/worksheet/algebra_sp.htm.

Math Mix, http://www.mathmix.com/worksheets/Algebra/

StudyMaths.co.uk, http://studymaths.co.uk/workoutMenu.

php?type=algebra.

Wolfram Problem Generator, http://www.wolframalpha.com/

problem-generator/

Matlab Expression Generator, http://m2matlabdb.ma.

tum.de/download.jsp?MC_ID=9&MP_ID=118.

Math Expression Generator, http://www.softwareriviera.

com/indexMathExpressionGenerator.php.

T-algebra, http://math.ut.ee/T-algebra/

What Should We Add to Syntax-oriented Generation of Random Expressions to Meet Pedagogical Needs?

487