An Enhanced Block Notation for Discrimination Network Optimisation

Christoph Terwelp, Karl-Heinz Krempels and Fabian Ohler

Information Systems, RWTH Aachen University, Aachen, Germany

Keywords:

Rule-based Systems, Discrimination Networks.

Abstract:

Because of their ability to efﬁciently store, access, and process data, Database Management Systems (DBMSs)

and Rule-based Systems (RBSs) are used in many information systems as information processing units. A ba-

sic function of a RBS and a function of many DBMSs is to match conditions on the available data. To improve

performance, intermediate results are stored in Discrimination Networks (DNs). The resulting memory con-

sumption and runtime cost depend on the structure of the DN. A lot of research has been done in the area of

optimising DNs. In this paper, we focus on re-using network parts considering multiple rule conditions and

exploiting the characteristics of equivalences. Hence, we present an approach incorporating the potential of

both concepts as an enhancement to previous work.

1 INTRODUCTION

Because of their ability to efﬁciently store, access,

and process data, Database Management Systems

(DBMSs) and Rule-based Systems (RBSs) are used

in many information systems as information process-

ing units (Brownston et al., 1985; Forgy, 1981). A ba-

sic function of a RBS and a function of many DBMSs

is to match conditions on the available data. Check-

ing all data repeatedly every time some data changes

performs badly. It is possible to improve performance

by saving intermediate results in memory introduc-

ing the method of dynamic programming. A com-

mon example for this approach is the Discrimination

Network (DN). Different DN optimization techniques

are discussed in (Forgy, 1982), (Miranker, 1987), and

(Hanson and Hasan, 1993). These approaches only

address optimisations limited to single rules. Fur-

ther improvement is possible by optimising the full

rule set of a RBS. By exploiting the characteris-

tics of equivalences, additional performance improve-

ments are possible. In this paper, we will introduce

an approach extending (Ohler and Terwelp, 2015) and

(Ohler et al., 2016) incorporating the potential of both

concepts.

This paper is organized as follows: In Section 2,

we introduce DNs and in Section 3, we explain the

concept of re-using network parts for different rules.

Section 4 describes the potential of binding variables

in rule conditions. In Section 5, we discuss the arising

problems in the ﬁeld of node sharing. Existing work

in the area of DN and query optimisation are pre-

sented in Section 6. The identiﬁed problems are then

addressed in Section 7 by introducing an advanced

version of the block notation. Section 8 comprises

the conclusion and gives an outlook on future work.

2 DISCRIMINATION NETWORKS

Rules in RBSs and DBMSs both comprise a condi-

tion and actions. The actions of a rule must only be

executed, if the data in the system matches the con-

dition of the rule. DNs are an efﬁcient method of

identifying rules to be executed employing dynamic

programming trading memory consumption for run-

time improvements. Rule conditions are split into

their atomic (w. r. t. conjunction) sub-conditions. In

the following, such sub-conditions are called ﬁlters.

DNs apply these ﬁlters successively joining only

the required data. Intermediate results are saved to

be reused in case of data changes. Each ﬁlter is rep-

resented by a node in the DN. Additionally, every

node has a memory, at least one input, and one out-

put. The memory of a node contains the data received

via its inputs matching its ﬁlter. The output is used

by successor nodes to access the memory and receive

notiﬁcations about memory changes. Data changes

are propagated through the network along the edges.

The atomic data unit travelling through a DN is called

fact. Changed data reaching a node is joined with the

data saved in nodes connected to all other inputs of the

node. So only the memories of affected nodes have to

268

Terwelp, C., Krempels, K-H. and Ohler, F.

An Enhanced Block Notation for Discrimination Network Optimisation.

In Proceedings of the 12th International Conference on Web Information Systems and Technologies (WEBIST 2016) - Volume 2, pages 268-273

ISBN: 978-989-758-186-1

be adjusted. Each rule condition is represented by a

terminal node collecting all data matching the com-

plete rule condition.

data input nodes serve as entry points for speciﬁc

types of data into the DN. They are represented

as diamond shaped nodes.

ﬁlter nodes join the data from all their inputs and

check if the results match their ﬁlters. They are

represented as inverted triangle shaped nodes.

terminal nodes collect all data matching the condi-

tions of the corresponding rules. They are repre-

sented as triangle shaped nodes. The action part

of a rule should be executed for each data set in

its terminal node.

3 NODE SHARING

The construction of a DN that exploits the structure

of the rules and the facts to be expected in the sys-

tem is critical for the resulting runtime and memory

consumption of the RBS. To avoid unnecessary re-

evaluations of partial results, an optimal network con-

struction algorithm has to identify common subsets of

rule conditions. In the corresponding DN, these com-

mon subsets may be able to use the output of the same

network nodes. This is called node sharing and was

already described in (Brant et al., 1991).

Despite the fact, that there is a lot of potential

to save runtime and memory costs, current DN con-

struction algorithms mostly work rule by rule (cf. Sec-

tion 6). This way it will not always be possible to ex-

ploit node sharing to its full extent, e. g., if the nodes

were constructed in a way, that the network is (lo-

cally) optimal for the single rule it was constructed

for, but prevents node-sharing w. r. t. further rules and

might therefore thwart ﬁnding the (globally) optimal

DN for all rules in case sharing the nodes would have

reduced costs (cf. example 3.1).

Example 3.1. Assume there are two ﬁlters: ﬁlter f

uses facts of type a and b, ﬁlter f

uses facts of type b

and c. Furthermore, there are two rules: rule r

using

and rule r

using f

and f

. Then ﬁlter f

is used

in both rules and we can construct a DN where both

rules use the same node to apply f

to the input (see

Figure 1).

If we were to construct rule r

ﬁrst and would have

decided to construct the node f

as an input for f

sharing f

with r

afterwards would have been im-

possible, since the output of the node for f

is also

already ﬁltered by f

It is therefore advisable to construct the DN taking

into account the set of rules as a whole.





























Figure 1: Simple node sharing example network.

4 EQUIVALENCE CLASSES

The common rule description languages resemble

the Domain Relational Calculus (DRC) such that

variable symbols that appear multiple times (e. g.,

within different relations or comparable constructs)

implicitly cause that the condition is only true

if the values of all symbol occurrences are the

same. Considering the following condition in DRC

{

a, b,c | X(a, b) ∧ Y (a, c) ∧ a > 20

}

one may choose

whether the test a > 20 is applied to the data of X or

Y (or both). The occurrences of a variable symbol in

locations where the variables can be bound to values

are collected in what we will from now on call equiv-

alence classes. The resulting freedom in choosing an

element of the equivalence class for ﬁlters can be con-

sidered within DN construction algorithms. Addition-

ally, a minimal set of tests to ensure the equality of all

elements of an equivalence class can be chosen freely.

5 CHALLENGES

Since node sharing is beneﬁcial in most situations,

DN construction algorithms should be presented the

necessary data to maximise the potential savings in

runtime cost and memory consumption. This section

will present the challenges associated with generating

these information.

Sadly, identifying common subsets of rule condi-

tions isn’t sufﬁcient to make use of node sharing in

network construction. This can be seen by extending

An Enhanced Block Notation for Discrimination Network Optimisation

269

the previous example.

Example 5.1. Assume there is an additional third rule

using only the ﬁlter f

. Now f

is part of r

and r

while f

is part of r

and r

. Despite the fact that

there are two non-trivial rule condition subsets, we

can’t share both ﬁlters between the three rules in an

intuitive way. The rule r

requires a network that ap-

plies the ﬁlters f

and f

successively. Yet, the rule

) needs the output of a node applying nothing

but f

( f

), meaning the corresponding nodes receive

unﬁltered input. Thus, we need two nodes for the two

ﬁlters side by side at be beginning of the network and

some additional node to satisfy the chained applica-

tion of the two ﬁlters. There are three result networks

still applying node sharing to some extent: We can ei-

ther share f

and duplicate f

, share f

and duplicate

, or re-use both nodes for r

by introducing an ad-

ditional node that selects only those pairs of facts that

contain identical b-typed facts in both inputs.

Formalising the phenomenon just observed, we say

that two ﬁlters are in conﬂict if they use the same

facts. Since in (Ohler and Terwelp, 2015) it has been

shown that the runtime costs of the third network in

example 5.1 are always higher than those of the other

two networks, we will not consider such networks

here. The decision which of the two remaining net-

works performs better depends on the data to be ex-

pected.

Furthermore, there may be situations where node

sharing is not beneﬁcial. For example, two rules shar-

ing a ﬁlter that all facts pass should not share that ﬁlter

if they have other (more selective) ﬁlters that could be

applied to the data ﬁrst. Sharing the ﬁlter would re-

quire to apply that ﬁlter ﬁrst resulting in a high main-

tenance cost for the corresponding node. Applying

the ﬁlter last could lead to very low maintenance costs

as very few facts reach the node such that even the

twofold costs are lower than the costs in the sharing

situation. Detecting these situations requires informa-

tion about e. g., ﬁlter selectivities, but can continue to

improve the quality of the resulting network.

Finally, integrating the degree of freedom intro-

duced by the equivalence classes as mentioned in Sec-

tion 4 into the network construction is a further aspect

considered here.

6 STATE OF THE ART

There are several DN construction algorithms creat-

ing different types of networks such as Rete (Forgy,

1982), TREAT (Miranker, 1987), and Gator (Hanson

et al., 2002). Yet, they all consider the rules one after

another so that the degree of sharing network parts is

governed mainly by the order in which the rules are

considered and the order of the ﬁlters within the rule

conditions. Moreover, the optimisation potential in-

troduced by the equivalence classes is neglected and

all variables are assumed to be bound or are bound in

a preliminary consideration.

An approach for query optimisation for in-

memory DRC database systems is presented in

(Whang and Krishnamurthy, 1990). They exploit the

concept of equivalence classes, but only consider left-

deep join plans and look at each query on its own

without evaluating node-sharing.

In (Aouiche et al., 2006), the authors apply a data-

mining technique to decide which views to materi-

alise during the processing of a set of queries in a rela-

tional database system. Here, several queries are con-

sidered together and grouped by a similarity heuristic.

Columns relevant for materialisation are identiﬁed by

a cost function and re-used as much as possible to pre-

vent repeated evaluations. In doing so, the ﬁlters to be

applied are reduced to the ones relevant to all queries

involved. Thereby, they do not identify the problem

of conﬂicts as such and decisions are made based on

columns to be materialised instead of ﬁlters as done

here.

A ﬁrst version of the block notation was presented

in (Ohler and Terwelp, 2015), which was a rather sim-

ple approach not yet considering equivalence classes,

existentials and predicates occurring more than once

per rule among other aspects. It was further developed

and evaluated in (Ohler et al., 2016). The new version

integrates the gaps mentioned before, but still suffers

from some shortcomings. Predicates occurring multi-

ple times per rule could not be fully exploited for shar-

ing and some situations, in which sharing would be

possible, could not be taken advantage of since all oc-

currences of an equivalence class within a block were

restricted in the same way.

7 APPROACH

Previously, we referred to different types of facts,

which we will now call templates. A template resem-

bles a class and its ﬁelds are called slots. All facts are

instances of templates. More speciﬁcally, we will use

the term fact binding to be able to distinguish between

several facts of the same template. Every fact in the

resulting fact tuple of a rule condition corresponds to

a fact binding and vice versa. Equivalence classes

as introduced in Section 4 contain fact bindings, slot

bindings (bindings to a slot of a fact binding), con-

stants, and functional expressions (i. e. ?x+?y). A ﬁl-

ter comprises a predicate (the test to be executed) and

WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies

270

the equivalence classes to be used as parameters.

Existential parts of a condition have to be pro-

cessed in a special way. If an equivalence class con-

tains bindings originating from two different scopes,

it is split into two classes containing the correspond-

ing elements. Additionally, equivalence classes in

child scopes know of their corresponding equivalence

class in parent scopes. New scopes are created by ex-

istentials, which can also be nested. Filters appearing

within existential parts can then be divided into three

categories:

1. ﬁlters using only equivalence classes belonging to

the current scope

2. ﬁlters using only equivalence classes belonging to

parent scopes

3. ﬁlters using equivalence classes belonging to the

current and parent scopes

The ﬁlters of the ﬁrst two categories can be processed

separately and have to be applied to the data prior to

those of the third category. When applying the ﬁlters

of the third category, the corresponding join merges

the regular data with the existential data and imple-

ments the existential semantics. In a pre-processing

step, all ﬁlters of the third category are merged into

one ﬁlter, which we call the ﬁnal ﬁlter of an existential

condition part. It also contains the tests for equality

of equivalence classes contained in the surrounding

as well as in the existential scope. The parameters of

this predicate are marked according to whether they

are regular, existential or negated existential ones. As

a consequence, existential condition parts can be inte-

grated into the concepts to be presented.

We will now introduce a directed graph containing

different types of nodes for different concepts repre-

sented. For this, we use the following example ex-

plaining the key parts.

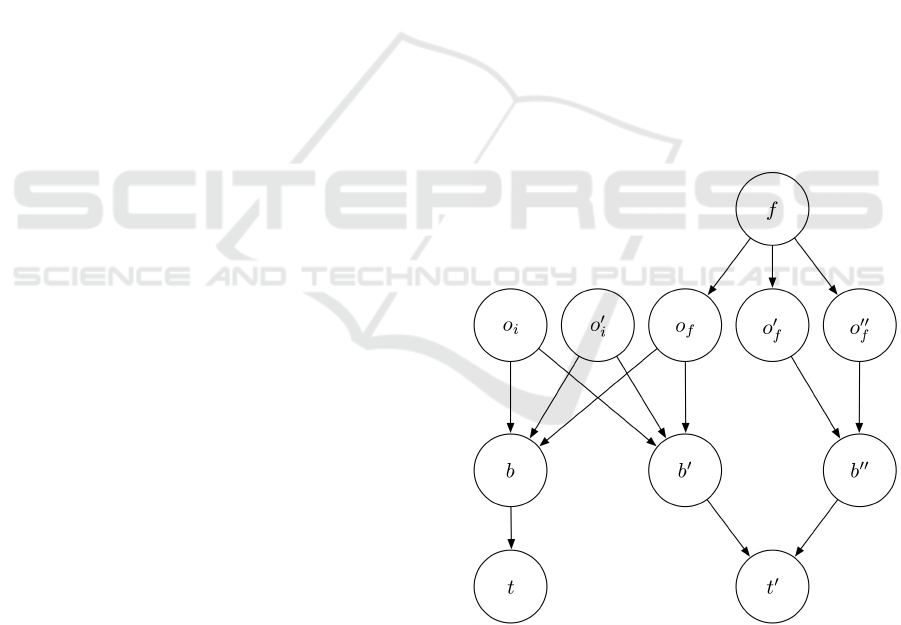
Example 7.1. Consider the following rule condition

with two template instances (i. e. facts) and a ﬁlter

with three arguments:

(t (s ?x))

(t’ (s’ ?x) (s’’ ?y))

(test (f ?x ?y ?y))

In the so called assignment graph, we create a node

for every ﬁlter ( f ) and every template instance (t and

). We let F denote the set of ﬁlter nodes and T de-

note the set of template instance nodes. As the rule

contains three slot bindings, we create three corre-

sponding nodes b for t::s, b

for t’::s’, and b

for

t’::s’’. These nodes are gathered in the set of fact

and slot bindings B

. The variable ?x can be bound to

t::s and t’::s’, so the corresponding equivalence

class contains those two slot bindings. For every ele-

ment of an equivalence class, we create a correspond-

ing node in the assignment graph gathered in the set

of implicit equivalence class occurrence (more on

that later). Thus, for the equivalence class corre-

sponding to ?x, there are the two nodes o

for t::s,

and o

for t’::s. Since the variable ?y can only be

bound to t’::s’’ and the corresponding equivalence

class only contains one element, we omit the creation

of a corresponding node as for all trivial equivalence

classes. Finally, we create a node for every parameter

of a ﬁlter (o

, o

and o

). These nodes are gathered

in the set O

of equivalence class occurrences within

ﬁlters.

Figure 2 shows the assignment graph with the cor-

responding directed edges. One can identify four lay-

ers the way the graph is depicted. The top layer con-

tains the ﬁlters (F). Below, there are the equivalence

class occurrences (O). Every ﬁlter is connected to its

occurrences via edges. The third layer contains the

bindings (B). The occurrences are connected to the

bindings contained in the corresponding equivalence

classes via edges. In the bottom layer the template

instances are contained (T ) and connected to the cor-

responding bindings in the third layer via edges.

Figure 2: Assignment graph example.

The four layers already described i. e. the corre-

sponding sets of nodes form the node set V = F

∪ O

∪

∪ T of the assignment graph G = (V, E). The set of

occurrences O = O

∪ O

additionally contains

the set O

of occurrences within functional expres-

sions and the set of bindings B = B

∪ B

addi-

tionally contains the set B

of constant bindings and

An Enhanced Block Notation for Discrimination Network Optimisation

271

the set B

of functional expression bindings. Note

that constants occurring in multiple rules are mapped

to one node per rule they are contained in. O

contains

one node per equivalence class element.

The set of edges E = E

∪ E

of the as-

signment graph comprise the edges E

from the ﬁlters

f ∈ F to the corresponding occurrences in O

⊂ O

the edges E

to the template instances t ∈ T origi-

nating from the corresponding slot and fact bindings

in B

⊂ B

, and the edges E

from the occurrences

⊂ O of an equivalence class Q to its bindings

⊂ B.

Every rule is represented in the graph by at least

one connected component of the assignment graph.

Thus there are no edges between rules.

A non-empty subset Z ⊂ E(G) of the edges of the

assignment graph G is called a block row if the fol-

lowing conditions are fulﬁlled:

• If an edge adjacent to a ﬁlter is in Z, all edges in

G adjacent to that ﬁlter have to be in Z.

• The edge to a non-implicit occurrence is in Z iff at

least one edge from that occurrence to a binding

is in Z.

• The edge from a fact or slot binding to the corre-

sponding template instance is in Z iff at least one

edge from an occurrence to a binding of this tem-

plate instance is in Z.

• If an edge from an occurrence to a functional ex-

pression binding is in Z, all edges originating from

that binding have to be in Z.

• If an edge from a functional expression binding is

in Z, at least one edge to that binding has to be in

• An edge from an implicit occurrence to its corre-

sponding binding is in Z iff at least one other edge

to that binding is in Z.

• If the edges (o, b), (o, b

), and (o

, b) for occur-

rences o, o

and bindings b, b

are in Z, then (o

, b

)

has to be in Z.

• For all occurrences in functional expressions with

adjacent edges in Z, it holds that there are paths in

Z from these occurrences to slot, fact, or constant

bindings.

• If an existential edge ( f , o) adjacent to a ﬁlter f is

in Z, the connected component originating from

removing all existential edges adjacent to f that

contains o has to be a subset of Z.

Two block rows are compatible iff both block rows

are disjoint and no edge in the one block row is adja-

cent to an edge in the other block row.

A non-empty subset S ⊂ E(G) of the edges of the

assignment graph G is called a block column if the

following conditions are fulﬁlled:

• All edges in S are pairwise non-adjacent

• For the set of start or target nodes V

of the edges

in S one of the following conditions holds:

– V

contains ﬁlters only and they all apply the

same predicate having the same parameters

marked as (negated) existential

– V

only contains implicit occurrences

– V

only contains non-implicit occurrences rep-

resenting the same position in the list of param-

eters of a ﬁlter or functional expression.

– V

only contains bindings to the same constant.

– V

only contains bindings to slots of the same

name. The equality of the template is assured

via the compatibility of block columns (see be-

low).

– V

only contains fact bindings.

– V

only contains bindings to functional expres-

sions and they all use the same function.

– V

only contains template instances (facts) of

the same template.

• If all start nodes of the edges in S are implicit oc-

currences, either all or none of the edges lead to

the corresponding binding.

Two different block columns S and S

are compat-

ible iff at most one pair of the sets of start and target

nodes of S and the sets of start and target nodes of S

are identical and all others are disjoint.

We also refer to the number of the elements of a

block column as the height of the block column.

A set of pairwise compatible block rows Z

together with a set of pairwise compatible block

columns S is called a block iff the set of all edges

of the block rows is identical to the set of all edges

of the block columns and the amount of block rows

corresponds to the height of the block columns.

A block with more than one row represents the

possibility of sharing its included ﬁlters. So only one

row of the block has to be implemented in the DN

and can be reused for the implementation of the other

rows. Implicit occurrences allow sharing of implicit

equalities represented by equivalence classes.

Two blocks X = (Z, S), Y = (Z

, S

) are in conﬂict

iff none of the following conditions are satisﬁed:

• T ∩ T

0 with T and T

being the template in-

stances of the blocks X and Y , respectively.

• ∀Q ∈ Q ∃R ∈ R : R ⊂ Q for Q , R ∈ {S , S

} as

well as Q , R ∈ {Z, Z

} with Q 6= R in both cases.

WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies

272

A block set free of conﬂicts between blocks is use-

ful to prevent conﬂicts between ﬁlters.

We say that a set of blocks is complete, if every

node of the assignment graph is contained in at least

one block, none of the blocks contains all elements of

another block partitioned the same way, and no block

can be extended further.

Constructing the DN for a complete, conﬂict-free

block set can be done by materialising the ﬁlters in the

blocks starting with the blocks containing the fewest

columns. Within the set of blocks containing an equal

number of columns the order is arbitrary, since none

of these blocks can be the input of another block in

that set (otherwise they would “overlap” and would

have been in conﬂict). A more detailed explanation

of how to construct the network (part) for a block in-

cluding considerations about the optimisation poten-

tial and what to keep in mind w. r. t. ﬁlters with exis-

tential parameters is given in (Ohler et al., 2016).

The construction order is relevant only if blocks

contain the same nodes. Since the block set is

conﬂict-free and complete, if one block overlaps with

another block, the columns of one of the blocks are a

subset of the columns of the other block. As the one

with fewer columns is constructed ﬁrst, its output can

be used to construct the larger (w. r. t. column count)

block.

8 CONCLUSION & OUTLOOK

We presented a concept for an optimisation of DNs

for RBSs considering node-sharing and integrating

the degree of freedom emerging from being able

to choose between elements that are supposed to

be equal. This block concept is able to formalise

the problems of node-sharing, i. e. which network

parts would compete against each other. Equivalence

classes were integrated into the block concept to allow

for a free choice of which element to use for which

ﬁlter and of how to check the equality among the ele-

ments efﬁciently, e. g., using a minimal spanning tree.

Based on the notation presented, we are currently

developing optimisation algorithms considering sev-

eral rules at once. The output of such an algorithm

should be a conﬂict-free set of blocks, where no block

can be extended and no block contains all elements

of another block partitioned the same way. An opti-

mising DN construction algorithm can then use this

information to decide, whether node-sharing is bene-

ﬁcial in terms of runtime cost and memory consump-

tion w. r. t. the data to be expected. Developing such

an algorithm with acceptable runtime costs – despite

the fact that it has to look at a set of rules instead of a

single one – is pending.

ACKNOWLEDGEMENTS

This work was funded by German Federal Ministry

of Economic Affairs and Energy for project Mobility

Broker (01ME12136).

REFERENCES

Aouiche, K., Jouve, P.-E., and Darmont, J. (2006).

Clustering-based materialized view selection in data

warehouses. In Manolopoulos, Y., Pokorný, J., and

Sellis, T. K., editors, Advances in Databases and In-

formation Systems, volume 4152 of Lecture Notes in

Computer Science, pages 81–95. Springer Berlin Hei-

delberg.

Brant, D. A., Grose, T., Lofaso, B., and Miranker, D. P.

(1991). Effects of database size on rule system perfor-

mance: Five case studies. In Lohman, G. M., Ser-

nadas, A., and Camps, R., editors, Proceedings of

the 17th International Conference on Very Large Data

Bases, pages 287–296.

Brownston, L., Farrell, R., Kant, E., and Martin, N. (1985).

Programming expert systems in OPS5. Addison-

Wesley Pub. Co., Inc., Reading, MA.

Forgy, C. L. (1981). OPS5 User’s Manual. Tech. Report

CMU-CS-81-135. Carnegie-Mellon Univ. Pittsburgh

Dept. Of Computer Science.

Forgy, C. L. (1982). Rete: A fast algorithm for the many

pattern/many object pattern match problem. Artiﬁcial

Intelligence, 19(1):17–37.

Hanson, E. N., Bodagala, S., and Chadaga, U. (2002). Trig-

ger condition testing and view maintenance using op-

timized discrimination networks. IEEE Transactions

on Knowledge and Data Engineering, 14(2):261–280.

Hanson, E. N. and Hasan, M. S. (1993). Gator : An Op-

timized Discrimination Network for Active Database

Rule Condition Testing. Tech. Report TR93-036, Univ.

of Florida, pages 1–27.

Miranker, D. P. (1987). TREAT: A Better Match Algorithm

for AI Production Systems; Long Version. Technical

report, Austin, TX, USA.

Ohler, F., Krempels, K.-H., and Terwelp, C. (2016). Ran-

domised optimisation of discrimination networks con-

sidering node-sharing. Manuscript submitted for pub-

lication.

Ohler, F. and Terwelp, C. (2015). A notation for discrim-

ination network analysis. In Proceedings of the 11th

International Conference on Web Information Systems

and Technologies, pages 566–570.

Whang, K.-Y. and Krishnamurthy, R. (1990). Query opti-

mization in a memory-resident domain relational cal-

culus database system.

An Enhanced Block Notation for Discrimination Network Optimisation

273