Unveiling Political Opinion Structures with a Web-experiment

Pietro Gravino

, Saverio Caminiti

, Alina Sˆırbu

, Francesca Tria

, Vito D. P. Servedio

2,4

and Vittorio Loreto

1,4

Institute for Scientiﬁc Interchange Foundation, Via Alassio 11/c, 10126, Turin, Italy

Institute for Complex Systems (ISC-CNR), Via dei Taurini 19, 00185 Roma, Italy

University of Bologna, Dept. of Computer Science and Engineering, Bologna, Italy

Sapienza University of Rome, Physics Dept., P.le Aldo Moro 2, 00185 Roma, Italy

Keywords:

Opinion Dynamics, Web-experiment, Politics.

Abstract:

The dynamics of political votes has been widely studied, both for its practical interest and as a paradigm of

the dynamics of mass opinions and collective phenomena, where theoretical predictions can be easily tested.

However, the vote outcome is often inﬂuenced by many factors beyond the bare opinion on the candidate,

and in most cases it is bound to a single preference. The voter perception of the political space is still to be

elucidated. We here propose a web experiment (laPENSOcos`ı) where we explicitly investigate participants’

opinions on political entities (parties, coalitions, individual candidates) of the Italian political scene. As a main

result, we show that the political perception follows a Weber-Fechner-like law, i.e., when ranking political

entities according to the user expressed preferences, the perceived distance of the user from a given entity

scales as the logarithm of this rank.

1 INTRODUCTION

In the United States hundreds of millions of

dollars are yearly spent for presidential cam-

paigns (Buchanan, 2004), but the very mechanisms

through which public opinion can be succesfully in-

ﬂuenced are not fully understood. Politics is a uni-

versal topic of conversation. People express opin-

ions, try to convince their interlocutors, build them-

selves their believes under the inﬂuence of a variety

of factors, with different degrees of rationality (Za-

ller, 1992; Bartels, 2010; Kahneman, 2011; Ben-

dor et al., 2011; Antonakis and Dalgas, 2009). In-

formation from mass media and political campaigns

strongly inﬂuence the debate, and often in an impre-

dictable way (Berelson et al., 1954; Buchanan, 2004).

More at the core of the question, people perception

of politics and political subjects follows laws that are

largely to be uncovered. Due to the practical as well

as theoretical interest in the understanding of politi-

cal opinion dynamics, available data have been stud-

ied seeking for universals (Chatterjee et al., 2013) and

experiments have been proposed aiming to highlight

different mechanisms inﬂuencing voters opinions on

candidates (Todorov et al., 2005). Also, models of

opinion dynamics inspired from statistical physics,

which analyse the mechanics of opinion formation,

have been proposed recently (Sirbu et al., 2013b;

Castellano et al., 2009; Sirbu et al., 2013a). How-

ever, comprehensive and focused databases of politi-

cal opinions are lacking. While in fact political elec-

tions outcomes constitute precious databases to inves-

tigate voters behavior (Borghesi and Bouchaud, 2010;

Hummel and Rothschild, 2013), the real opinion of

voters may be hidden by many different factors, as

for instance tactical voting (Arajo et al., 2010) and

limitations imposed by the election rules. Moreover,

the electoral system usually allows the expression of

a single positive vote per elective assembly, so that

individuals are called to compress all their interpreta-

tion of the political landscape in a single preference.

Most importantly, voters are bound to express positive

votes, so that only approval and not disappointment

can be directly expressed. For all these reasons, elec-

tions outcomes only partially represent voter opinions

and the study of the political perception of citizens has

to rely on different kinds of data.

Here we propose an experiment aiming at over-

coming these limitations, providing a more complete

picture of the political perception and allowing in this

way a quantitative analysis of the complex structure

of individuals opinions. In particular, following a

Gravino, P., Caminiti, S., Sîrbu, A., Tria, F., Servedio, V. and Loreto, V.

Unveiling Political Opinion Structures with a Web-experiment.

In Proceedings of the 1st International Conference on Complex Information Systems (COMPLEXIS 2016), pages 39-47

ISBN: 978-989-758-181-6

general trend emerged in the last few years, where

web-games are adopted as interesting laboratory to

run experiments in the social sciences (Howe, 2006;

Lazer and et al., 2009; Salganik and Watts, 2009; Suri

and Watts, 2011), we propose a web experiment in

which people are directly called to express their opin-

ions on political subjects. The data gathered with the

laPENSOcos`ı experiment reﬂect the general negative

sentiment the italian population has towards its polit-

ical class. More interestingly, we found that opinions

follow a distribution compatible with an exponential

distribution, with a negative coefﬁcient whose abso-

lute value decreases with the level of optimism, but

that remains almost constant across different politi-

cal orientations. This result strongly recalls a well

known law linking stimuli and perception, i.e., the

Weber-Fechner law. This law has been observed in

several situations involving physical perceptions, e.g.

light brightness (Hecht, 1924) or noise intensity, and

also in other less tangible contexts, e.g. numerical

cognition (Dehaene, 2003; Nieder and Miller, 2003)

and more recently in the subjective perception of the

quality of a service (Reichl et al., 2010; Egger et al.,

2012). The presence of a Weber-Fechner-like law in

political perception is a novel aspect. This ﬁnding

could foster other experiments in this direction and

can have a profound impact on the way models of

opinion dynamics are constructed.

2 RESULTS

2.1 The Experiment

In the last few years the Web has been progressively

acquiring the status of an infrastructure for social

computing that allows researchers to coordinate the

cognitive abilities of users in online communities, and

to suggest how to steer the collective action towards

predeﬁned goals (Howe, 2006; Suri and Watts, 2011;

Salganik and Watts, 2009; Fischer and et al., 2012;

Gravino et al., 2011). Web games prove to be partic-

ularly fruitful whenever the peculiar human computa-

tion abilities are crucially required for research pur-

poses (von Ahn and Dabbish, 2004; von Ahn, 2006;

Schawinski and et al., 2010; Cooper and et al., 2010;

Khatib and et. al, 2011). The laPENSOcos`ı experi-

ment takes advantage of the Experimental Tribe

plat-

form for web-based experiments and social computa-

tion (Caminiti et al., 2013; Cicali et al., 2011).

In the laPENSOcos`ı

experiment, people were

freely available at http://www.xtribe.eu

still available at http://www.lapensocosi.it

called to express their opinion on political subjects,

including single candidates, parties and coalitions.

Opinions are expressed by means of a real number

in the interval [−1,1], negative numbers expressing

disapproval. Subjects were randomly presented from

a pool composed by the 160 most famous italian

politicians, parties and coalitions. Data were gath-

ered from middle of January 2013 to the early days of

March 2013, exploiting the italian political elections

that took place on 24-25th February 2013. We here

present results on 39154 opinions expressed by 1038

users, corresponding to the data gathered in the last

version of our experiment (refer to the Section 3 for

details). People were free to assign to each of the ran-

domly presented political subject a vote in the inter-

val [−1,1]. The actual normalization of the interval

is arbitrary and does not affect generality, while its

extension over a range of both negative and positive

values allows people to express both disapproval and

approval in a straightforward way. A possibility to

abstain is also given, together with a direct link to the

wikipedia page describing the politician or the party

under evaluation, in the case it would be unknown to

the user. As an additional information, the user can

also leave an explicit comment on the political entity

they are called to judge. A snapshot of the game is

given in Fig. 1, while for a detailed description we

refer to the Method section.

2.2 Outcomes

A ﬁrst portrait of the perception of the political world

can be drawn by measuring the distribution of the

opinions in the whole dataset, referred to any polit-

ical subject and expressed by any user.

This distribution is reported in Fig. 2, showing the

average opinion on any political entities being signif-

icantly negative (the mean value of the distribution

being −0.472). This simply corresponds to the gen-

eral negative perception of politics. The distribution

shows peaks at the extremes (value −1 and +1) and

of the center (the zero value) of the interval, with the

highest peaks at the extremes. The peaks can be eas-

ily explained as due in part to a natural tendency of

extremization, and to the visually attractive effect of

extremes and natural numbers, and more in particular

as an effect of the visualization of the voting interval.

More interestingly, the distribution between the peaks

seems to follow an exponential law, decreasing when

the opinion value is growing.

This behavior reminds of a general property of

perception, the Weber-Fechner law, which states that

the perception is proportional to the logarithm of the

stimuli. In our context, for each user we can rank the

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

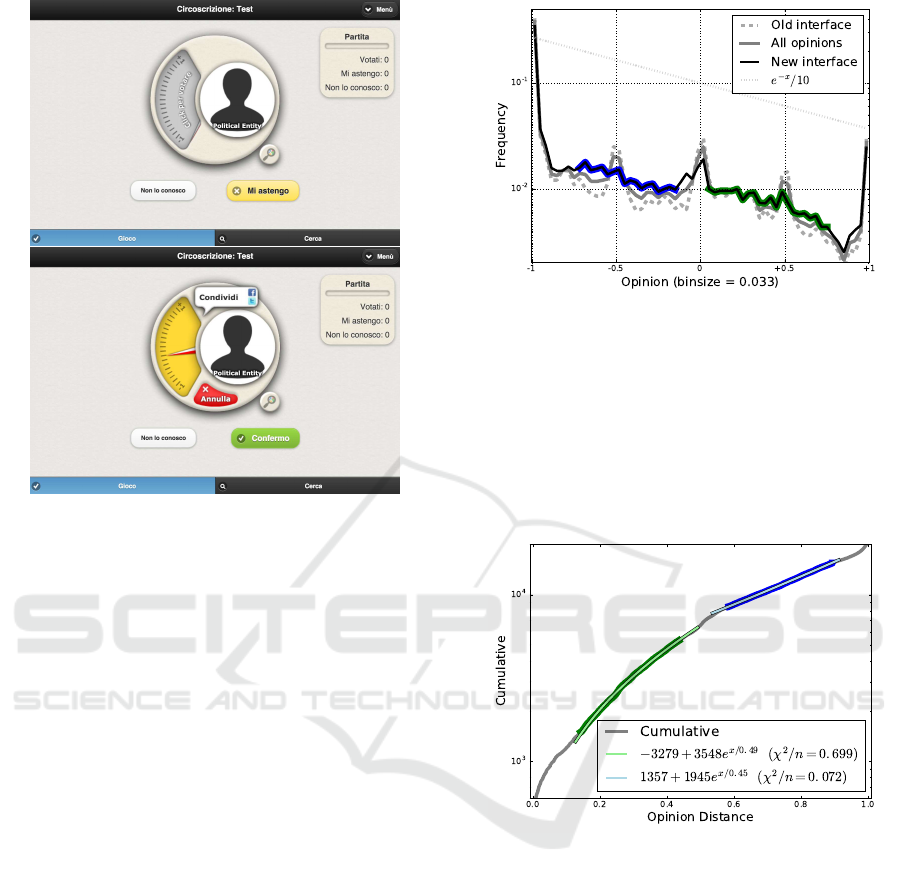
Figure 1: Two screenshots of the last version of the inter-

face, before (top) and after (bottom) the interaction. Users

were prompted with a photo of a politician or a party logo

and were asked to use the scale on the left to express their

opinions.

political subjects according to the appreciation they

expressed on them, from the most esteemed to the

most unappreciated. We can thus interpret the posi-

tion in this rank as a sort of distance between the user

and the given political subject. This allows to directly

interpret the exponential form of the opinion distribu-

tion in terms of the Weber-Fechner law.

We can deﬁne this opinion “distance” as x

(1 − o)/2, where o is the opinion expressed by the

user in [−1, +1]. To support the hypothesis of the ex-

ponential, we performed a ﬁt on the areas of interest

(blue and green part of the curve in Fig. 2). In order

to have a less noisy curve we converted opinions in

distances and used the cumulative distribution repre-

sented in Fig. 3.

To perform a χ

test we estimated the error for

the cumulative distribution as the 1%. The results

are strongly supporting the compatibility with an

exponential-like law.

In order to more deeply investigate this phe-

nomenon, we looked at the robustness of the opinion

distribution against political orientation of the users

and against their optimistic or pessimistic attitude, as

signalled by the average of the individual opinion dis-

tribution (refer to Section 3 section for more details).

Results are reported in Figures 4 and 5 respectively,

showing how the form of the distribution remains sta-

Figure 2: The histogram of the opinions expressed by users

in semilog scale. In black, the histogram relative to data

gathered with the last version of the interface. We high-

lighted in blue and in green the exponential-like parts, that

appear linear in semilog scale. A simple exponential is re-

ported as a reference. Also, it is reported the histogram of

the dataset obtained with the old interface (gray, dashed)

and the histogram of the whole dataset (gray). With the old

interface, peaks at -0.5 and +0.5 emerged as a consequence

of major ticks in the scale where users expressed their opin-

ions.

Figure 3: The gray curve represents the cumulative distribu-

tion of opinions in the distance space. In green and in blue

the area of interest already highlighted in Fig. 2. In light

green and in light blue we reported the exponential ﬁts. In

the legend we can see the results of the χ

test. Relative

errors have been estimated to be ∼ 1%.

ble against subsampling of the population. Interest-

ingly, when subsampling the population according to

the individual level of optimism, the exponent of the

exponential law appears to be directly related to the

degree of optimism, its absolute value increasing with

optimism.

We note that the distributions considered so far

are aggregated distributions of many users, while the

Weber-Fechner law refers to the perception of each

individual. It is thus important to show that the aggre-

gate distribution well reﬂects an individual property.

This point is addressed in Section 3, where we report

Unveiling Political Opinion Structures with a Web-experiment

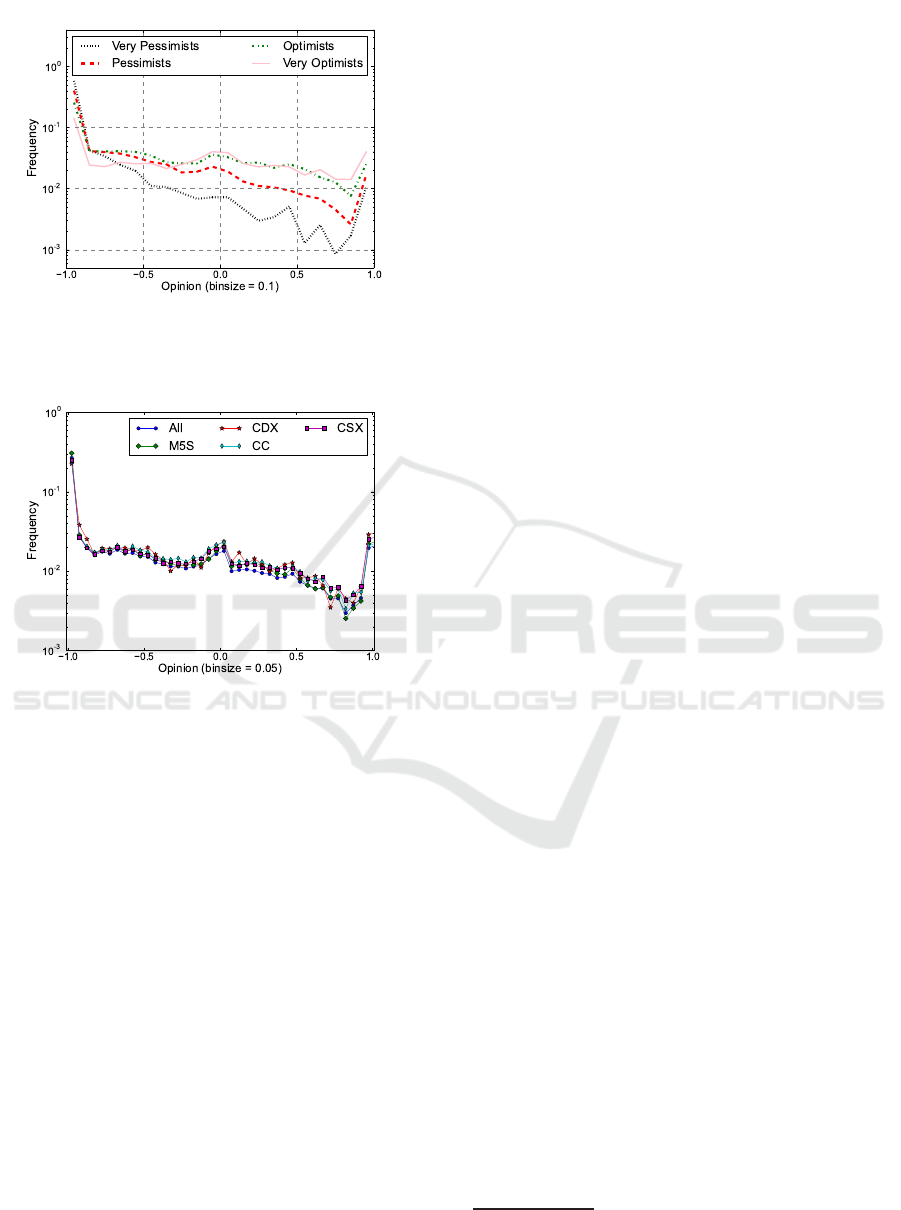
Figure 4: Histograms of the opinions for 4 subsets of users,

divided according to their level of “optimism”, i.e. the user

average opinion.

Figure 5: The histogram of the opinions weighted consid-

ering 4 different “points of view” relative to the 4 poles of

Italian politics. Each histogram is calculated by weighting

each user opinion with the user average opinion distance

from the entity of the given pole.

that both individual and collective opinion structures,

reported in Fig. 8, show some slight differences that

disappear if we disaggregate the set depending on the

level of optimism of the user. In other words, if we

consider groups of users with the same level of opti-

mism, the individual opinion distribution is fairly sim-

ilar to the collective one. Finally, we built a graph

representation of the political space. Each time a user

provides opinions about two or more entities, they are

actually deﬁning a distance amongst them. By aver-

aging the distances provided between all the pairs of

entities we created a graph in which nodes are the en-

tities and the weight of links are the inverse of these

distances. The result is reported in Fig. 6 (we tried

several spacial disposition algorithms ﬁnding similar

results). Colors represent different coalitions and the

relative clustering spontaneously emerge as a natural

consequence of the spacial disposition according to

links weight. This network representation points out

the distance between traditional left-wing and right-

wing parties, and the middle position of center mod-

erate parties. Furthermore, the perception of the novel

political force (at the time of the elections consid-

ered) “Movimento 5 Stelle” is accurately reproduced

and perceived as new and different from all the oth-

ers. Fig. 6 reproduce the actual overview of the Ital-

ian political landscape. The accuracy in the portrait is

a very interesting result stemming from a completely

bottom-up elaborated representation.

3 Methods

3.1 laPENSOcos

Experimental Tribe (XTribe in short)

, is a general

purpose platform to help researchers to realize web

games/experiments with a very small coding over-

head. We released the laPENSOcos`ı

experiment

hosted on the XTribe portal in the middle of January

2013. In the default mode (named “Modalit`a Gioco”,

Game Mode, GM in the following), subjects were

presented randomly 20 political entities to be rated

from a pool composed by the 160 most famous ital-

ian politicians and all existing parties. Users could

also check the list of candidates (in List Mode, LM)

or use a search engine. We focused on the dataset ob-

tained in GM because in LM users tended to evaluate

their preferred entities. Aiming at a representation of

the political space, the random sampling obtained in

game mode represents a more effective choice. The

experiment exploited the hot topic of political elec-

tions in Italy at the end of February 2013 (24-25th

February 2013). At the early days of March 2013 the

experiment gathered in Game Mode 81,508 opinions

expressed by 1,727 users, on our pool of 160 political

subjects. In Fig. 7 we reported the daily number of

opinions, users and sessions of play.

For the analysis presented in this paper (except

the gray dashed curve in Fig. 2), we considered only

data gathered with this last version of the interface.

This interface has been introduced at the beginning

of February 2013 and 39,154 opinions were gathered

thanks to 1,038 users. Data obtained with the pre-

vious interface were discarded because the interface

introduced an optical bias: in the opinion scale, major

ticks at -0.5 and +0.5 attracted the attention so that the

opinion distribution, reported in Fig. 2, shows peaks

at -0.5 and +0.5.

http://www.xtribe.eu

http://www.lapensocosi.it

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

Figure 6: The graph of italian political entities immediately before February 2013 political elections. Nodes are coloured

according to the coalition: red for left-wing coalition, blue for right-wing coalition, purple for center coalition and yellow for

Movimento 5 Stelle (M5S), a novel formation not belonging to a coalition. The color clustering spontaneously emerges by

imposing distances between entities obtained by averaging those deﬁned by users opinion.

3.2 Reliability of the Data

The data gathered with the experiment correctly re-

produce the italian political scene, in terms of rela-

tions between political subjects, as visible in Figure

6. The accuracy of the reproduction is an indirect val-

idation of the dataset, since the aim was to measure

the political opinion structure and not the forecasting

of the elections outcome.

3.3 Recruitment

In order to make the experience possibly viral, we im-

plemented some social sharing functionalities, allow-

ing users to publish their opinion on Facebook and

Twitter, advertising the experiment. Furthermore, to

improve the user experience enjoyability, the request

for opinions has been formulated in the shape of a

“personality test”: after each session of evaluation

(which consisted in 20 evaluation rounds) the user re-

ceived a proﬁle describing them. According to the

average value of opinion in the session the user was

classiﬁed as an optimist (high average) or a pessimist

(low average). Also, depending on the value of the

standard deviation of session opinions, the user was

labeled as an extremist (high standard deviation) or a

moderate (low standard deviation). The result of the

test was sharable on Facebook or Twitter, in order to

attract other to discover their proﬁle.

3.4 Optimists and Pessimists

We divided the population in 4 parts according to

users average opinion: the quarter with the highest av-

erages has been considered “very optimist”, the quar-

ter with the highest average above the remaining has

been considered “optimist”, and so on. Then we cal-

culated the opinion distribution for the 4 subpopula-

tion. The result is shown in Fig. 4. It appears clearly

how the whole structure is coherent with an exponen-

tial law: the only thing changing seems to be the coef-

ﬁcient of the exponential regression. This highlights

the importance of the exponential law and also points

out that the exponent can be considered a measure of

the “structural optimism” about political perception.

In fact, differently from the optimism deﬁned as the

simple average of the opinions of a given user, the ex-

ponent gives us more information. Obviously, from

an higher exponent follows an higher average but also

a different opinion structure, with deep consequences

in terms of resolution in the comprehension of polit-

ical entities relations, as we will see in the following

sections.

3.5 Political Points of View

As anticipated in Section 2, we tested also the dis-

tribution stability against differences in the political

point of view of the considered population. The ital-

ian political forces scheme can be divided in four

main political factions: the center-right coalition (will

be indicated as CDX); the center coalition (CC); the

center-left coalition (CSX); the Movimento 5 Stelle

party (M5S). Since in this case there is no clear dis-

tinction we managed to deﬁne, for each user, an ag-

gregated opinion (agg. op. in the following) about

each one of these poles. These opinions have been

used to weight all other opinions while recalculating

the opinion distribution. In other words, to get the

opinion distribution of the CDX supporter we used

Unveiling Political Opinion Structures with a Web-experiment

Figure 7: The daily number of opinions, users and session

of play.

the agg. op. about CDX of each user to weight his/her

opinions, so that, for example, if a user had a CDX

agg. op. = +1 then his/her opinions were considered

normally while if CDX agg. op. = −1 then his/her

opinions were not considered at all. The result of this

analysis are the four front weighted distributions that

are reported in Fig. 5. It is clearly visible how all the

distributions are fairly compatible. This graph sug-

gests that the opinion distribution we measured and

showed in Fig. 2 is a quite robust feature. Again, in

Fig. 5 we can ﬁnd the exponential shape (with some

noise due to the reduction of the statistics, conse-

quence of the weighting procedure). Furthermore, the

opinion structure of different voters tends to be simi-

lar even if the political point of view is different (and

even opposite). This interestingly points out a sort of

universality in the perception of the political space.

3.6 Individual vs Collective Opinions

Structure

The opinion distribution shown in Fig. 2, which is one

of the focal points of this paper, is calculated by ag-

gregating all users opinions. It is a collective measure,

but since we want to infer the properties at the individ-

ual level, we had to show that individual and collec-

tive distribution are compatible. To this purpose we

calculated a new distribution of opinions, by rescal-

ing by +1 and by normalizing to 1. In other words,

the new opinions o

′

is deﬁned as follows:

′

o+ 1

∑

user

(o+ 1)

(1)

where the sum runs on the other opinions of the same

user. This novel set of opinions has been compared

with a syntetic set representing the collective opin-

ion distribution. For each user, we generated a syn-

tetic user with the same number of opinions randomly

Figure 8: The distribution of opinions rescaled and normal-

ized by user, for real users and for a syntetic set of users.

Differences reﬂect the difference in the opinion structure

between single user and the collective result.

picked from the whole set of opinions, in order to de-

stroy correlations. The histrograms of the real and

syntetic opinions is reported in Fig. 8. The distribu-

tion seems quite similar but some differences emerge.

To those differences we performed the two sample

Kolmogorv-Smirnov test, for 100 random sampling,

ﬁnding p-value= 0.065±0.078which gives a quanti-

tative measure of the differencebetween the collective

and individual distribution. This points out that the

global aggregation is imperfect to represent individ-

ual behaviour. Some level of disaggregation should

be introduced. We already reported about the impor-

tance of the optimism level so we used this parame-

ter to disaggregate. We divided the population in two

sets, according to the user level of optimism. Thus we

performedagain the same analysis on the two separate

sets. The KS test showed a more high p-value in both

cases: 0.096 ± 0.072 and 0.289 ± 0.119. From these

analysis we can state that individual behaviour can be

in ﬁrst approximation represented by the collective

behaviour but disaggregating by optimism level im-

proves strongly the compatibility between the single

user opinion structure and the global one.

3.7 The Emergence of Weber-Fechner

Law

3.7.1 The Opinion Space

In this paragraph, we shall provide the interpretation

of the exponential law observed in Fig. 2. In order to

understand the implication of the exponentials, let us

try to reformulate our problem. To simplify, we will

consider a bounded space, an opinion space, whose

distribution follows just an exponential law. In the

opinion space, each user can place political subjects

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

according to their perception. Our experiment asks

for opinions between −1 and +1 but we can also

translate these opinions in some sort of distance per-

ceived by the user. In this framework, entities near

+1 can be considered as perceived near the user while

those entities near −1 can be considered as far from

the user, according to his perception. We can thus say

that users assign to each entity a coordinate in this per-

ceptual space, that we will call x

(i) (as we already

did in Section 2, for entity i). Without loss of general-

ity, we shift and normalize the range of the perceptual

space to the interval [0,+1], whereas 0 corresponds to

opinion +1 and 1 corresponds to opinion −1. The ex-

ponential law we measured in Fig. 3 represents, in this

framework, the density of the political subject in the

perceptual space. We can then express the perceived

density as an exponential with a proper normalization

in the following way:

) =

− 1

(2)

where λ is a characteristic parameter of the user (or of

the subset of similar users considered). As we saw in

Fig. 4, this parameter is probably linked to the “op-

timism”. What we described so far is a matter of

perception. The situation is similar to what happens

with our “normal” senses (sight, hearing, touch, etc).

For the ﬁve senses, we can measure their efﬁciency

in mapping reality by knowing how a certain stimu-

lus (or a distribution of stimuli) is translated in our

perception (or in a distribution of perceptions).

In the present case, we measured the perceived

distribution, but what about the stimuli distribution?

We measured the perceived density distribution of a

set of political entities, but how were they distributed

originally? And in what kind of space?

3.7.2 The Rank Space

It is not just a matter of stimuli distribution. If the

sensing process we are considering is a sort of map-

ping, what exactly are we mapping in the opinion

space? From what kind of space the mapping starts?

So far we considered the evaluation process as a sort

of positioning of the entity in the opinion space. Po-

sitioning may also be considered a second order pro-

cess with respect to a ranking process. It sounds rea-

sonable to assume that users have their own personal

rank of the political subjects. In this rank, we can con-

sider the ﬁrst as the nearest to the user, and the last as

the farthest. While telling their opinion, the user is

basically translating a rank into a position. Thus, we

can deﬁne a rank space in which entity are placed,

sorted by their rank. By deﬁnition of rank, entities are

simply distributed uniformly, in a discrete sense (one

in each rank position). Even if the rank space discrete

by deﬁnition, in order to analyze the mapping, we will

consider it as a continuous space, in which x

(i) will

refer to the rank position of the entity i. The bound

of the rank will be 1 and the number of entities N

As we said, we consider the density as a continuous

uniform density distribution deﬁned as follows:

) =

(3)

3.7.3 Mapping and Resolving Power

Now that we have both the perceived and the original

distribution we can ﬁnd the transformation by impos-

ing that:

)dx

= ρ

)dx

(4)

This condition is equivalent to require that the trans-

formation from x

to x

is essentially a bijection, i.e.

to each point x

there is one and only one correspond-

ing point x

. This assumption is quite reasonable for

a perceptive mapping. In Eq. 4, by substituting Eq. 2

and Eq. 3, we get:

− 1

= N

− 1

(5)

and by integrating we obtain:

λN

− 1

(6)

= λlog

− 1

λN

∝ logx

(7)

Eq. 7 tells us how the rank space is transformed in

the opinion space, i.e. according to a logarithmic law.

This law appears similar to others perception map-

ping law, such that observed for spatial disposition for

natural numbers. To investigate the efﬁciency of the

mapping, let us consider Eq. 5. If we substitute Eq. 7

we get:

(8)

which describes how the perception becomes less ef-

ﬁcient when x

is growing. In other words, differ-

ences are perceived smaller and smaller as we go far

from the user. Hence it is more difﬁcult to distinguish

among different but far (from the user) entities. Eq. 8

and Eq. 7 strongly recall a well-known law linking

stimuli and perception: the Weber-Fechner law. The

Unveiling Political Opinion Structures with a Web-experiment

presence of a Weber-Fechner-like law in political per-

ception is a novel aspect. The emergence of this sort

of “Political Myopia” can have a profound impact on

the way models of opinion dynamics are constructed.

To complete, let us calculate the resolving power. By

considering dx

as a ﬁxed parameter ∆x

, we can also

ﬁnd an expression for the opinion space, deﬁning the

resolving power needed to notice a difference ∆x

a function of x

RP(x

|∆x

;λ;N

) =

∆x

log

− 1

λN

. (9)

4 CONCLUSIONS AND

PERSPECTIVES

The laPENSOcos`ı web-experiment aimed to measure

the political opinion structure. By exploiting the hot

topic of Italian political elections of February 2013,

this web application gathered opinions of more than

one thousand users in few weeks. Participants were

asked to express their opinion about political entities

on a continuous scale between [−1,+1], in order to

overcome limitations of usual vote procedure. The

resulting dataset gave us precious insights about how

political entities are distributed in the opinion space.

With a novel bottom-up approach, we managed to re-

produce the relation between italian political entities,

represented by the graph in Fig. 6, in a very accu-

rate way. We also measured the distribution of the

opinions, reported in Fig. 2, unfolding how politi-

cal entities perceptions are distributed. This distri-

bution reﬂected the main feature of the political sce-

nario in Italy in the early 2013: a general negative

feeling and a strong contrast between political play-

ers, leading to a negative opinion average and peaks

at the extremes. Another interesting feature of the dis-

tribution is an exponential-like shape, which recalls a

known law linking stimuli and perception, the Weber-

Fechner law. The exponential shape has been proved

to appear also by disaggregating and resampling the

dataset, thus seemed to be quite robust, like a sort of

universal law of political perception. Obviously more

experimental conﬁrmations are needed to improve the

robustness of these conclusions. We plan to repeat

the experiment at the next political elections in Italy

and also abroad, in order to check if the exponential-

like opinion distribution shows traits of universality

irrespective of nationality. This can be easily done,

because of the experimental procedure adopted. In

fact, the laPENSOcos`ı web-experiment exploited the

services of the Experimental Tribe platform, a so-

cial computation platform designed to help the im-

plementation of web-experiments. Beside the inves-

tigation of the opinions distribution, new experiments

can also deal with the opinion structure in a dynamical

way, by monitoring a population opinion distribution

over time. This kind of experiments could provide di-

rect informationabout opinion dynamics and precious

hints in the design of new models to analyze political

opinion dynamics.

ACKNOWLEDGEMENTS

We acknowledge support from the KREYON project

funded by the Templeton Foundation under contract

n. 51663. VDPS acknowledges the EU FP7 Grant

611272 (project GROWTHCOM) and the CNR PNR

Project “CRISIS Lab” for ﬁnancial support.

REFERENCES

Antonakis, J. and Dalgas, O. (2009). Predicting elections:

Child’s play! Science, 323(5918):1183.

Arajo, N., Andrade, J. J., and Herrmann, H. (2010). Tactical

voting in plurality elections. PLoS ONE, 5(9):e12446.

Bartels, L. (2010). The study of electoral behavior. The

Oxford Handbook of American Elections and Political

Behavior, pages 239–261.

Bendor, J., Diermeier, D., Siegel, D. A., and Ting, M. M.

(2011). A behavioral theory of elections. Princeton

University Press.

Berelson, B., Lazarsfeld, P., and McPhee, W. (1954). Vot-

ing: A study of opinion formation in a presidential

campaign. University of Chicago Press.

Borghesi, C. and Bouchaud, J.-P. (2010). Spatial corre-

lations in vote statistics: a diffusive ﬁeld model for

decision-making. The European Physical Journal B,

75(3):395–404.

Buchanan, M. (2004). How strategists design the perfect

candidate. Science, 306(5697):799–800.

Caminiti, S., Cicali, C., Gravino, P., Loreto, V., Serve-

dio, V. D., Sirbu, A., and Tria, F. (2013). Xtribe: a

web-based social computation platform. In Cloud and

Green Computing (CGC), 2013 Third International

Conference on, pages 397–403. IEEE.

Castellano, C., Fortunato, S., and Loreto, V. (2009). Statis-

tical physics of social dynamics. Reviews of modern

physics, 81(2):591.

Chatterjee, A., Mitrovi/’c, M., and Fortunato, S. (2013).

Universality in voting behavior: an empirical analy-

sis. Scientiﬁc Reports, 3.

Cicali, C., Tria, F., Servedio, V. D., Gravino, P., Loreto, V.,

Warglien, M., and Paolacci, G. (2011). Experimen-

tal tribe: a general platform for web-gaming and so-

cial computation. Proceedings of the NIPS Workshop

on Computational Social Science and the Wisdom of

Crowds.

COMPLEXIS 2016 - 1st International Conference on Complex Information Systems

Cooper, S. and et al. (2010). Predicting protein struc-

tures with a multiplayer online game. Nature,

466(7307):756–760.

Dehaene, S. (2003). The neural basis of the weber–fechner

law: a logarithmic mental number line. Trends in cog-

nitive sciences, 7(4):145–147.

Egger, S., Reichl, P., Hosfeld, T., and Schatz, R. (2012).

”time is bandwidth”? narrowing the gap between

subjective time perception and quality of experience.

In Communications (ICC), 2012 IEEE International

Conference on, pages 1325–1330. IEEE.

Fischer, D. and et al. (2012). Planet Hunters: The First Two

Planet Candidates Identiﬁed by the Public using the

Kepler Public Archive Data. Monthly Notices of the

Royal Astronomical Society, 419:2900–2911.

Gravino, P., Servedio, V. D. P., Barrat, A., and Loreto,

V. (2011). Complex structures and semantics in free

word association. Advances in Complex Systems.

Hecht, S. (1924). The visual discrimination of intensity and

the weber-fechner law. The Journal of General Phys-

iology, 7(2):235–267.

Howe, J. (2006). The rise of crowdsourcing. Wired, 14(06).

Hummel, P. and Rothschild, D. (2013). Fundamental

models for forecasting elections. ResearchDMR.

com/HummelRothschild

FundamentalModel.

Kahneman, D. (2011). Thinking, fast and slow. Macmillan.

Khatib, F. and et. al (2011). Crystal structure of a

monomeric retroviral protease solved by protein fold-

ing game players. Nat Struct Mol Biol, 18:1175–1177.

Lazer, D. and et al. (2009). Social science: Computational

social science. Science, 323(5915):721–723.

Nieder, A. and Miller, E. K. (2003). Coding of cogni-

tive magnitude: Compressed scaling of numerical in-

formation in the primate prefrontal cortex. Neuron,

37(1):149–157.

Reichl, P., Egger, S., Schatz, R., and D’Alconzo, A. (2010).

The logarithmic nature of qoe and the role of the

weber-fechner law in qoe assessment. In Communica-

tions (ICC), 2010 IEEE International Conference on,

pages 1–5. IEEE.

Salganik, M. J. and Watts, D. J. (2009). Web-Based Ex-

periments for the Study of Collective Social Dynam-

ics in Cultural Markets. Topics in Cognitive Science,

1(3):439–468.

Schawinski, K. and et al. (2010). The Sudden Death of the

Nearest Quasar. The Astrophysical Journal Letters,

724(1):L30.

Sirbu, A., Loreto, V., Servedio, V. D., and Tria, F.

(2013a). Cohesion, consensus and extreme informa-

tion in opinion dynamics. Advances in Complex Sys-

tems, 16(06):1350035.

Sirbu, A., Loreto, V., Servedio, V. D., and Tria, F. (2013b).

Opinion dynamics with disagreement and modulated

information. Journal of Statistical Physics, 151(1-

2):218–237.

Suri, S. and Watts, D. J. (2011). Cooperation and contagion

in web-based, networked public goods experiments.

PLoS ONE, 6(3):e16836.

Todorov, A., Mandisodza, A. N., Goren, A., and Hall, C. C.

(2005). Inferences of competence from faces predict

election outcomes. Science, 308(5728):1623–1626.

von Ahn, L. (2006). Games with a purpose. Computer,

39(6):92–94.

von Ahn, L. and Dabbish, L. (2004). Labeling images with

a computer game. In CHI ’04: Proceedings of the

SIGCHI conference on Human factors in computing

systems, pages 319–326, New York, NY, USA. ACM.

Zaller, J. (1992). The nature and origins of mass opinion.

Cambridge university press.

Unveiling Political Opinion Structures with a Web-experiment