Internet of Things for Flexible Manufacturing Systems` Diagnosis

Calin Ciufudean and Corneliu Buzduga

Stefan cel Mare University, 13 University, Suceava, Romania

Keywords: Internet of Things, Flexible Manufacturing System, Discrete Event Model, Memory Buffer, Markov Chain.

Abstract: This paper deals with an actual topic concerning the diagnosis of Internet of Things (IoT) controlled flexible

manufacturing systems (FMS). We focus on models realized with Markov chains of FMS with stochastic and

not equal throughput rates. Discrete-event models assume that FMS is decomposed, and we study the

following events: an Internet server fails, an Internet server is repaired, an Internet server memory buffer fills

up, an Internet server memory buffer empties. The IoT diagnosis is performed with by calculating the time to

absorption in Markov model of the IoT controlled FMS. Future development of IoT diagnosis of FMS are

also discussed in this work.

1 INTRODUCTION

In this work, we assume that a flexible manufacturing

system controlled and monitored by Internet of

Things (IoT) is similar to a discrete event system

(DES) and we model it in a discrete stochastic space.

Absorbing states of Markov chain models display

a steady-state i.e., the absorbing state attended after

time T; therefore, only transient analysis displays the

system performance. Our approach deals with an IoT

controlled system which displays in time a trajectory

modelled with a Markov chain

0} t {x(t); ≥

with state

space

...} 1, {0, S =

and space generator W. Let i, j ∈S

and, we have (Viswandham, 1992), (Kemeny, 1960):

i} j/ x(0) P{x(t) (t) p

===

(1)

(t)] [p A(t)

(2)

The following equations describe the behavior of

the above mentioned Markov chain (Buzacott, 1993),

(Narahari, 1994), (Ciufudean, 2008), (Viswandham,

1994):

W A(t) [A(t)]

⋅=

(3)

A(t) W *[A(t)]

⋅=

(4)

Where A(0) = I. For matrix components we have:

)t(pw (t) p . w (t)][p

kjijijij

∑

⋅+=

(5)

∑

⋅+=

kjikijiiij

)t(pw (t) p . w (t)][p

(6)

The solution is:

e A(t)

⋅

(7)

()

∑

∞

⋅

(8)

The state probabilities

...] (t),p (t),[p Y(t)

where

S jj},=P{x(t) = (t)p

∈

, are given by the

following equation:

W. Y(t) Y(t)] [

(9)

The solution is:

e . Y(0) Y(t)

⋅

(10)

i} X(0)j/ P{X(t) (t)p

===

(11)

For t > 0, and T the time to reach the absorbing state,

we obtain:

n)}+m , ... 1,+(m P{X(t) = t}> P{T ∉

(12)

Where m

≥

0, n > 0, we have (m+1) states, and the

next states are absorbing ones.

()

∑

jm,0

tp - 1 t} P{T

(13)

468

Ciufudean, C. and Buzduga, C.

Internet of Things for Flexible Manufacturing Systems‘ Diagnosis.

In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 468-471

ISBN: 978-989-758-184-7

 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

Then time interval T may be displayed by:

()

∑

jm,0T

tp (t)F

(14)

Where

(t)p

m0,

is given by equation (3) (Ciufudean,

2008), (Viswandham, 1994), (Dallery, 1992).

2 THE MODEL FOR IOT

DIAGNOSIS OF FMS

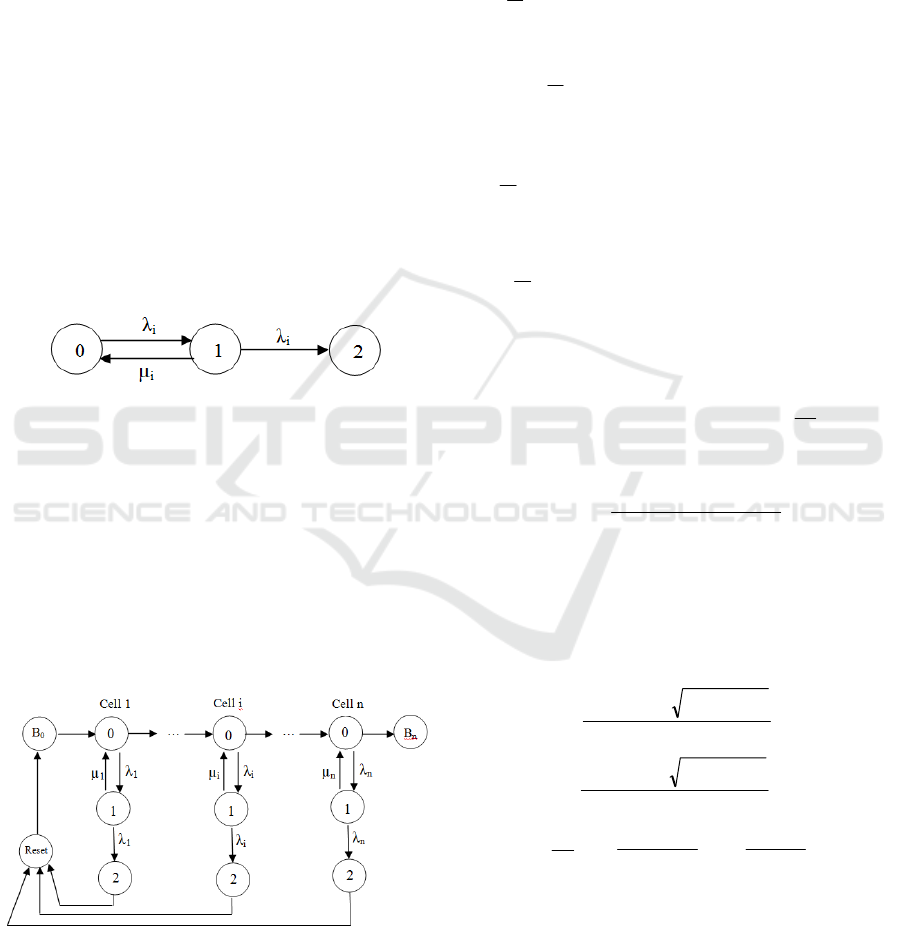
The basic cell of the IoT system diagnosis of a FMS

consists of a computer e.g. server connected to

Internet, S

with memory buffer and its downstream

machine from the FMS. In figure 1 we depicted the

Markov chain model of the one of the n identical cells

of our model for IoT control and diagnosis of a FMS,

where n represents the number of servers necessary to

control the FMS (Ciufudean, 2008).

Figure 1: The basic model of Markov chain for IoT

diagnosis.

The meaning of the cell depicted in figure 1 is that

the server S

is in state 0 when there is no information

to process, and there is the transfer of the information

to/from machines of FMS. In state 1, we process

information, and a deadlock occurs in state 2.

Information bits transfer rate is

and the servers

processing rate of information bits is

. The Markov

chain model for IoT diagnosis of FMS is depicted in

figure 2.

Figure 2: Markov chain model for IoT diagnosis of FMS.

Here T is the time elapses until deadlock occurs,

and deadlock is a probability

(t).p (t)Da

02T

In order

to determine

(t)p

we will use the generator W of

the above depicted Markov chain:

()

⎥

⎦

⎤

⎢

⎣

⎡

λμ+λ−μ

λλ−

000

iiii

(15)

From equation (6) we have the probability

:(t)p

(t)

p .

w (t)

p .

w (t)

p .

w)t(

++=

(16)

But we also have w

= 0, and therefore:

)t(

⋅λ+⋅λ−=

(17)

Similar, for

(t)p

we have:

(t)

p .

w (t)

p .

w (t)

p .

w)t(

++=

(18)

And

1 (t)p

, and therefore:

)t(

()t(

)t(

λ+⋅μ+λ−⋅μ−=

(19)

Where

(s)p

is the Laplace transform of :(t)p

()

12i02i02

pp (s)sp λ+λ−=

(20)

()

12ii02i12

pp (s)sp

⋅μ+λ−μ= +

(21)

Equations (20) and (21) determine:

()

[]

iii

2ss

(s)p

s λ+μ+λ+

(22)

And equations (22) have as solution the

probability

(t)p

eC eB A (t)p

-bt-at

⋅+⋅+=

(23)

Where, a, b, A, B, C are [2, 3]:

iii

2 μλ+μ

+μ+λ

(24)

iii

2 μλ+μ

−μ+λ

(25)

;

()

abab

a2b

−

;

()

abb

−

(26)

3 THE EVENTS OF MEMORY

BUFFERS

For components manufactured in FMS, the transition

from one event to next event depends on current state

Internet of Things for Flexible Manufacturing Systems‘ Diagnosis

469

and on the generator W of the FMS. So, we may say

that in a FMS controlled by IoT deadlocks have

mainly two possibilities of diagnosis: a blocked

server empties its memory or information less (e.g.

empty server) commands its downstream machine.

Therefore the events dynamic is determined by

information which flow both way from S

to the

downstream machine. We consider a FMS controlled

by servers S

i-1

, S

and S

i+1

, and the memory buffers B

and B

We assume that an event occurs at time t and let

TA be the apparent time of the next event. We have:

is the information processing speed (bits-

unit/time-unit) of server S

, i = 1, ... , n.

⎪

⎩

⎪

⎨

⎧

repairunderis

Sif0,

functionalis

Sserverif1,

t)S(i,

⎪

⎩

⎪

⎨

⎧

stateotherwise1,

fullis

Bbufferif2,

emptyis

Bbufferif,0

t)B(j,

⎩

⎨

⎧

otherwise0,

ttimeatemptiesBif1,

BEj(t)

(t) Time necessary to store information in B

(t) Time necessary to deliver information from B

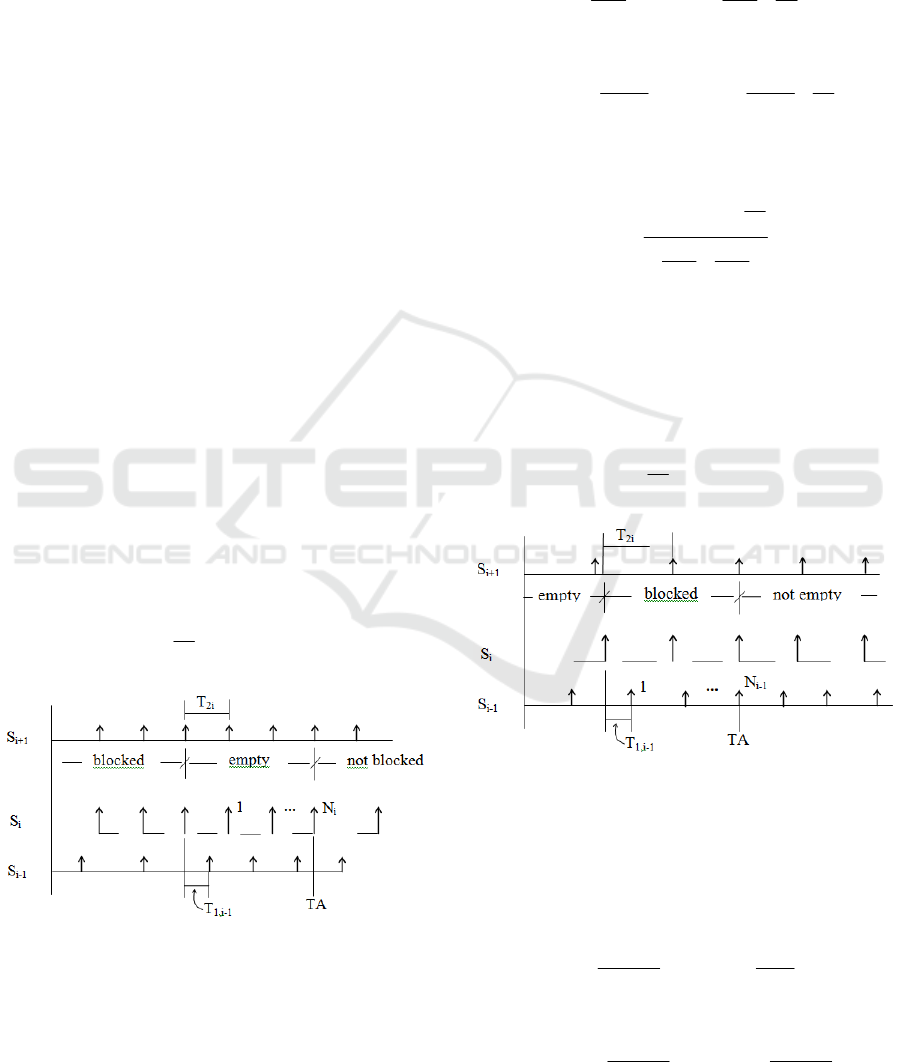
We have the following scenarios:

First scenario: server S

i+1

is faster than S

i-1

. This is

modeled in figure 3 and we have (Ciufudean, 2008),

(Viswandham, 1994), (Dallery, 1992):

)() T (T

1i1i

1-i1,21

−+

μ>μ∩

(27)

Figure 3: Dynamic of servers when S

i+1

is faster than S

i-1

In figure 3 and 4 we depicted with continuous line

server data processing and with arrows we depicted

data flow (Ciufudean, 2008), (Viswandham, 1994),

(Dallery, 1992). Intervals blank mark the idle

processing time due to blockage/repair of servers.

Memory buffer B

empties from full memory. The end

of processing time of the (N

+1) bits on server S

greater than the time when memory B

empties. The

dual case is for the first N

bits. Therefore we have

(Martinelli, 2001):

T t

i1i

1-i 1,

++<

−+

(28)

and

i1i

1-i 1,

T t

T t TA

−

++≥

−

++=

−+

(29)

For B

equations (27) and (28) estimate the bits to

next event:

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

−

−−

+−

−

1i1i

1i,1i2

Int 1 N

(30)

Another scenario studied here is dual to first discuss:

server M

i-1

process data faster than server S

i+1

and the

empty server S

fills its memory buffer B

(Di

Benedetto, 2001), (Harrell, 2014), (Dolin, 2015),

(Storey, 2014). After that, server S

i-1

processes N

i-1

bits, and blockage is modeled in figure 4.

()

1i1i

1-i 1, 2i

T T

+−

μ>μ∩

⎟

⎠

⎞

⎜

⎝

⎛

(31)

Figure 4: Dynamic of servers when S

i-1

is faster than S

i+1

Figure 4 shows that arrival time of 1)(N

+ bits

at buffer B

i-1

is less than the processing time of server

. The dual case holds for the first N

i-1

bits

(Vermesan, 2014), (Ciufudean, 2009), (Ciufudean,

2007), (Ciufudean, 2006). Therefore we have:

1-i 1,

T t

−

++>

−

(32)

and

1-i 1,

T t

T t TA

−

++≤

−

++=

(33)

MoMa-GreenSys 2016 - Special Session on Modelling Practical Paradigms of Green Manufacturing Systems

470

Similar with the first scenario, for B

i-1

we estimate

the next event:

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

−

−−

−+

−

1i1i

i21i,1

1-i

Int 1 N

(34)

Equations (29) and (33) allow us to avoid the

above mentioned scenarios of deadlocks by fairly

dimensioning the buffers, and taking into

consideration flow rate of bits until next event: T

in relation (29) and, respectively, T

1,i-1

= p

relation (33); where p

is given by relation (23)

(Ciufudean, 2008), (Ciufudean, 2007).

As we proved in this paper the failure/blocking of

servers can be avoided, if the buffer size is bigger than

the critical size (e.g. the size determined with

equations (30), (33), (34). The necessary and

sufficient condition is to have an average time to

repair a server smaller than the average time to fill the

memory of server.

4 CONCLUSIONS

A model for IoT diagnosis of a FMS diagnosis has

been proposed in this paper. The model may be

obtained with our discrete-event approach or using

heuristic models.

A discrete-event system formulation and FMS

controlled by IoT connected by processing cells and

fast determines an accurate diagnosis at an increased

speed and costless. We observe that if the

deadlock/repair time is known and the duration of

diagnosis estimation is less than it, then transient

analysis is more appropriate than the steady state

analysis.

Further development of this approach should

focus on intelligent flexible manufacturing systems

modeled with Markov chains which have self-

recovery algorithms from deadlock situations.

REFERENCES

Viswandham, N., Narahari, J., 1992. Performance

Modeling of Automated Manufacturing System

Englewood Cliffs, NJ: Prentice Hall.

Kemeny, J., Snell, W., 1960.

Finite Markov Chains, Van

Nostrand.

Buzacott, J., A., Shantikumar, J., G., 1993.

Stochastic

Models of Manufacturing System

, Englewood Cliffs,

NJ: Prentice Hall.

Narahari, J., Viswandham, N., 1994. Transient Analysis of

Manufacturing System Performance,

IEEE Trans on

Rob and Autom., vol. 10

, no. 2.

Ciufudean, C., Satco, B., 2008. Algebraic formalism for

modelling the deadlock in flexible manufacturing

systems,

Jurnal of Applied Mathematics, vol.1, no.3,

pp. 157-165.

Viswandham, N., Ram, R., 1994. Composite performance-

dependability analysis of cellular manufacturing

systems,

IEEE on Rob and Autom., vol. 10, no. 2.

Dallery, J., Gershwin, S., B., 1992. Manufacturing flow line

systems: A review of models and analytical results,

Technical Report 91-002,

Laboratory for

Manufacturing and Productivity, MIT

Martinelli, F., Shu, C., Perkins, J.R. 2001. On the

Optimality of Myopic Productions Controls for Single-

Server Continuous-Flow Manufacturing Systems,

IEEE Trans. Autom. Contr., vol.46, no.8, pp.1269-

1273, 200.

Di Benedetto, M., D., Vintecentelli, A., S., Villa, T., 2001.

Model Matching for Finite State Machines,

IEEE

Trans. Autom. Contr., vol.46

, no.11, pp.1726-1743.

Harrell, C., 2014, The Internet of Things and Control

System Architecture, http://blog.aac.advantech.com/th

e-internet-of-things-and-control-system-architecture.

Dolin, R., 2015, Building an IoT for industrial control: Part

1 – What is Industrial IoT? ,http://www.embedded.com

/design/real-world-applications/4426952/Building an

IoT for industrial control. Part 1 What is Industrial IoT?

Storey, H., Bullotta, R., Drolet, D. 2014, The industrial

internet of things ,http://www.controleng.com/industry

-news/single-article/the-industrial-internet-of-things/c9

8837a0efec387df9fc14c2de0a3b2f.ht,.

Vermesan, O., Friess, P., (Eds.), 2014. Internet of Things –

From Research and Innovation to Market Deployment,

River Publishers, Aalborg, Denmark.

Ciufudean, C., Filote, C., 2009. Safety discrete event

models for Holonic cyclic manufacturing systems in

Holonic and Multi-Agent Systems for Manufacturing,

pp. 225-233,

Springer Berlin Heidelberg.

Ciufudean, C., Filote, C., Amarandei, D., 2007. Measuring

the Performance of Distributed Systems with Discrete

Event Formalisms,

Proc. of The 2nd Seminar for

Advanced Industrial Control Applications

, SAICA,

Madrid, Spain.

Ciufudean, C., Graur, A., Filote, C., Turcu, C., Popa, V.,

2006. Diagnosis of complex systems using ant colony

decision petri nets, Availability, Reliability and

Security.

ARES 2006. The First International

Conference on, Vienna, Austria.

Ciufudean, C., Satco, B., Filote, C., 2007. Reliability

Markov chains for security data transmitter analysis,

Availability, Reliability and Security.

ARES 2007. The

Second International Conference on, pp. 886-894.

Internet of Things for Flexible Manufacturing Systems‘ Diagnosis

471