
Fuzzy Clustering based Approach for Ontology Alignment
Rihab Idoudi
1,2
, Karim Saheb Ettabaa
2
, Kamel Hamrouni
1
and Basel Solaiman
2
1
Université Tunis ElManar, Ecole Nationale d'Ingénieurs de Tunis, Tunis, 1200, Tunisia
2
Laboratoire ITI, Telecom Bretagne, Brest, 29238, France
Keywords: Fuzzy C-Medoid, Ontology Aligning, Semantic Similarity, Similarity Measures.
Abstract: Recently, several ontologies have been proposed for real life domains, where these propositions are large and
voluminous due to the complexity of the domain. Consequently, Ontology Aligning has been attracting a great
deal of interest in order to establish interoperability between heterogeneous applications. Although, this
research has been addressed, most of existing approaches do not well capture suitable correspondences when
the size and structure vary vastly across ontologies. Addressing this issue, we propose in this paper a fuzzy
clustering based alignment approach which consists on improving the ontological structure organization. The
basic idea is to perform the fuzzy clustering technique over the ontology’s concepts in order to create clusters
of similar concepts with estimation of medoids and membership degrees. The uncertainty is due to the fact
that a concept has multiple attributes so to be assigned to different classes simultaneously. Then, the
ontologies are aligned based on the generated fuzzy clusters with the use of different similarity techniques to
discover correspondences between conceptual entities.
1 INTRODUCTION
As the study on data engineering actively progresses,
knowledge management constitutes, nowadays, a
primordial problematic, where the challenge relies on
resolving the knowledge capitalization problem by
improving knowledge merge and share. In this
context, ontologies are introduced as a potential mean
for conventional knowledge modeling for any given
complex domain (Idoudi et al., 2014). In practice,
several ontologies within the same domain are
developed independently by different communities.
Consequently, to date, the popularity of ontologies is
rapidly rising, and the amount of available ontologies
remains increasing. Thus, in case of knowledge
sharing, it is crucial to establish interoperability
between those ontologies to handle the semantic
heterogeneity problem (Hamdi and Safar, 2009).
Several ontology engineering processes are assuming
this task, mainly the ontology alignment. This area of
research has resulted in numerous studies (Fernández
et al., 2012); (Shvaiko and Euzenat, 2005); (Qiu and
Liu, 2014). Nevertheless, most of those approaches
fail spectacularly to capture adequate
correspondences when dealing with large ontologies
of extremely different levels of granularities (Duan et
al., 2011). This is due to the size and monolithic
nature of these large ontologies. In this paper, we
direct our attention to explore ways of ontology
aligning. We therefore propose and evaluate a new,
more efficient, fuzzy clustering-based approach. The
main objective of adopting the fuzzy clustering is that
it contributes to optimal organization of the
ontological structure and it ensures that all the
resulting clusters are concise enough to avoid any loss
of information. The alignment process is based on
three main steps; first the candidate ontology is
clustered into concise clusters with estimation of
medoids to the different generated clusters. Thus, we
propose a semantic distance for clustering analyze.
Second, clusters of both ontologies are aligned by
means of their medoids using the semantic similarity
to determine similar clusters. Once the pairs of similar
clusters are retained, the third step consists on
aligning the correspondent entities. Although,
several clustering based alignment methods have
been proposed, our approach is characterized the use
of fuzzy clustering to avoid information loss when
ontologies clustering. Moreover, our method uses the
medoid notion to determine similar blocks, contrarily
to exisitng method which consist on parsing the
whole cluster’s entities to conclude similar ones. The
rest of the paper is organized as follows: in the next
section, we introduce some related works. In Section
3, we propose our algorithm for ontology fuzzy
clustering. In Section 4, we present an alignment
method. In Section 5, we show some initial
594
Idoudi, R., Ettabaa, K., Hamrouni, K. and Solaiman, B.
Fuzzy Clustering based Approach for Ontology Alignment.
In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 1, pages 594-599
ISBN: 978-989-758-187-8
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

experimental results to demonstrate the efficiency of
the method.
2 RELATED WORK
Thus, in order to perform ontology alignment process,
several researchers have been interested to perform
clustering techniques over ontologies. In (Algergawy
et al., 2011), the author proposed a clustering approach
based on structural nodes similarity. Therefore, each
cluster of the source ontology has to be aligned with
only one subset of the target ontology. In (Seddiquia
and Aono, 2009), the approach starts by anchoring, a
pair of “look-alike” neighbors concepts to be aligned.
The method outputs a set of alignments between
concepts within semantically similar subsets. The
authors in (Hu et al., 2006) address the problem of
aligning large class hierarchies by introducing a
partition-based block approach. The process is based
on predefined anchors and uses structural and
linguistic similarities to partition class hierarchies into
small blocks. The COMA++ system presented in
(Massmann et al., 2011) consists on partitioning large
ontologies by using relatively simple heuristic rules. It
starts by transforming ontologies into graphs. Then,
clustering algorithm is applied to partition the graphs
into disjoint clusters. To determine similar clusters, the
aligning process uses limited information about the
cluster, which results in less alignment quality. In (Hu
et al., 2008), starting from small clusters, Falcon-AO
system merges progressively clusters together. The
alignment process, exploits the whole cluster
information to determine clusters pairs having higher
proximity. This proximity is based on anchors. The
more these clusters share anchors, the more similar
they are. A structural clustering method based on
network analysis was proposed in (Schlicht and
Stuckenschmidt, 2008). The latter produces, in a
consuming time, an important number of too small
modules (which may affect the concept’s overall
context). Authors in (Wang et al., 2011) use two types
of reduction anchors to align ontologies. In order to
predict ignorable similarity calculations, positive
reduction anchors use the concept hierarchy while
negative reduction anchors use locality of matching.
3 ONTOLOGY FUZZY
CLUSTERING
In this section, we present our method for ontology
fuzzy clustering using the FCMdd algorithm over
ontology concepts. The use of fuzzy clustering is
justified by the fact that a concept has multiple
attributes so to be assigned to different classes
simultaneously. Second, the use of fuzzy clustering
may significantly reduce the loss of information while
concept’s clustering.
3.1 The FCMdd Algorithm
FCMdd clustering technique represents a variant of
the FCM technique applied over relational data.
Likewise, the FCMdd allows computing membership
degrees of concepts to different clusters as well as
medoids which represent the representative data of
the clusters. These fuzzy clusters groups semantically
close concepts, where the membership to each cluster
is not deterministic but rather ranges in the unit
interval [0, 1]. It is worth to note that we are interested
only in this work to concepts
, while
relationships
are used to determine similarity
in the clustering task. FCMdd is an iterative algorithm
which tends to minimize this objective function:
(1)
Let = {
} be a set of ontology concepts
where is the number of nodes in ontology,
denotes the semantic distance between two
concepts of X. The set V= {
} represents a
subset of with cardinality (number of clusters); it
represents the medoids set of the clusters,
is the
membership degree of element
to
cluster
is the fuzziness
parameter of the resulting clusters where.
The membership degree is defined as well
(2)
Specifically, each cluster will be represented by a
medoid. The latter represents the concept that has the
minimal average distance with respect to the others.
Formally the medoid of cluster C,
where
:
(
)
(3)
The medoids designate the concepts minimizing
the distance to the other members of the cluster e.g in
the alignment step; those prototypes may intentionally
speed-up the task of searching closest clusters. Finally,
Fuzzy Clustering based Approach for Ontology Alignment
595
a specific similarity measure for concepts is needed.
The latter is presented in the next section.
3.2 New Semantic Distance
Intuitively, we assume that two concepts are
particularly closer while the distance between them is
minimal; to estimate the distance, we consider the
relational context of a concept. The idea is to define
for each concept a relational context that reveals the
entities to which the concept is related in the
ontology. The context must hold the knowledge to
express the circumstances of a concept, its role in the
ontology and its use cases. For this, we consider both
kinds of relationship: First, the subsumption relation
that gives information about concepts subsumed by
the concept of interest or the concept that subsume it.
Second, we consider the object property relation
which reveals the connected concepts. Given the set
of concepts in ontology, the set of relations
including the subsumption and object property
relations, the relational context of a concept
is
given by:
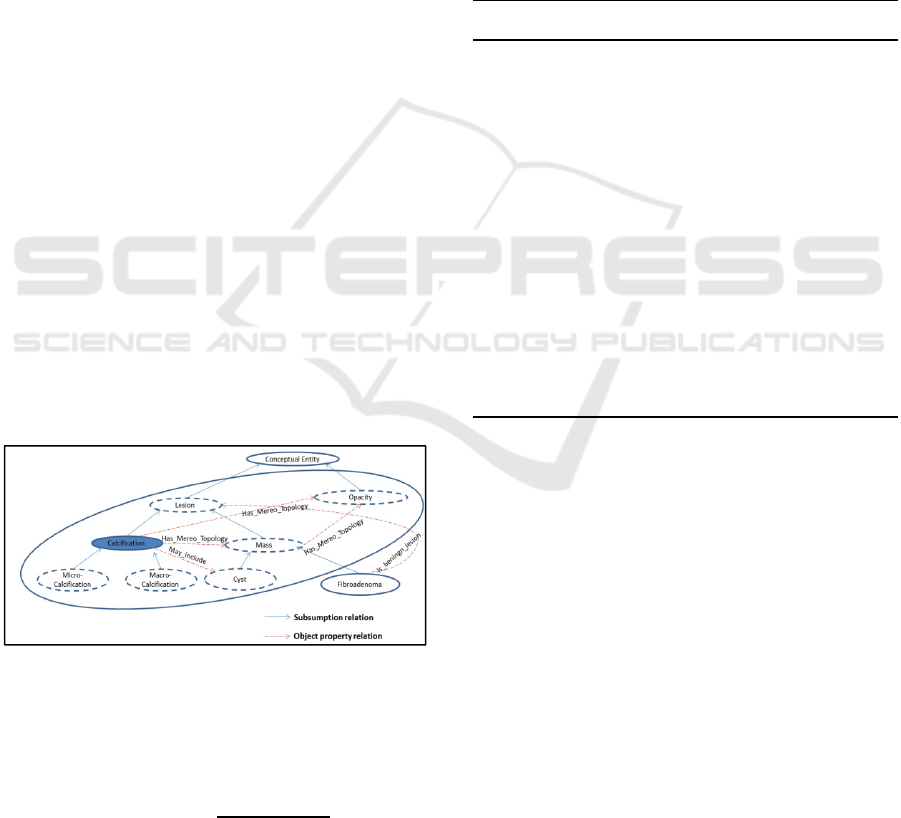
Figure1 gives an example of the relational context
of the concept ‘Calcification’ in the mammographic
ontology, where we can see that it is related according
to subsumption relation with {Micocalcification,
Maco-calcification, Lesion} and according to object-
property relation with {Cyst, Mass, Opacity}, then, we
can define the relational context of the concept
‘Calcification’ as {Calcification, Mico-calcification,
Macocalcification, Lesion, Cyst, Mass, Opacity}.
Figure 1: Relational context of the concept 'Calcification'.
Given two concepts
and
, the
distance
based on relational context between
them is given as well:
(4)
Represents the number of
common elements between the contexts of
and
.
3.3 The Fuzzy Clustering Algorithm
Algorithm 1 illustrates the FCMdd based ontology
clustering based algorithm. The inputs of the
algorithm are m: the fuzziness parameter, c: the
number of clusters (determined by application
requirement.) as well as the membership degrees and
medoids set initialisation. The output of the algorithm
is a set of clusters with correspondant medoids and
the membership degrees of the concepts to the
different clusters. It is worth to note, that the use of
medoids is particularly important for a more flexible
representation of clusters. Moreover, it helps to speed
up the task of determining similar clusters between
candidate ontologies.
4 CLUSTERS ALIGNMENT
In this section, we present our approach for clusters
alignment. The input of the algorithm is the set of
clusters correspondent to the source and target
ontologies to be aligned. The idea is to compare both
sets of clusters using the predefined medoids since
these prototypes give a sketch of the clusters content.
Thus matching medoids is helpful for users to
understand the correspondences between clusters.
The comparison is based on the use of semantic
similarity. For each source cluster, we compute the
semantic similarity of its medoid with the target
medoids. The most similar medoids are retained to
compare their respective clusters’s entities in the next
step. The semantic similarity computation uses an
external resource to compute the similarity value. In
this method, we have used the WordNet thesaurus
Algorithm 1: FCMdd based Ontology Clustering.
:
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
596

which groups words (nouns, verbs, adjectives) into
sets of synonyms called synsets. The latte contains all
the terms denoting a concept. They are linked by
semantic relationship such as generalization or
specialization relationship. The similarity between
two synsets A and B of the two concepts
is
computed as well:
=
(5)
Once we have determined the couples of clusters
deemed to be similar. We move from supervising
predefined matched class pairs to their correspondent
entities. At this step, we assume that as long as two
medoids of source and target clusters are semantically
close, their respective clusters have to be aligned. It is
then carried to fully align elements inside retained
similar clusters with the use different similarity
measures such as the syntactic similarity and the
structural similarity. The syntactic similarity
technique is computed over labels characterizing the
couples of entities to be compared. For this, we have
used a similarity based Edit-distance which consists
on comparing two strings and computing the number
of required edits (insertions, deletions and
substitutions) of characters to transform one word
into another. The syntactic similarity equation of two
concepts
is shown in (6), where
is the
Edit-distance:
(6)
This structural similarity measure relies on the
intuition that the elements of two distinct models are
similar when their adjacent elements are similar. It is
necessary to check if the concept under consideration
is surrounded (descendants and generalizing) by
similar concepts in the target ontology.
(7)
Where
denotes the descendants and
generalizing of the concept
in the ontology
,
and
refers to the descendants and
generalizing of the concept
in the ontology
.
Finally the two kinds of similarity techniques
between cluster’s entities computed above are
aggregated to determine the global similarity value
(8)
5 EXPERIMENTAL RESULTS
In this section, we present some initial experimental
results in order to evaluate the performance of the
proposed method. We conduct a set of experiments
applied on real world mammographic ontologies.
-‘Breast Cancer Grading Ontology (BCGO)’
(Bulzan, s.d.): The BCGO ontology has been
developed in 2009; it contains 541 classes, 56
properties and 164 individuals. It is designed to be
application oriented ontology and addresses the
problem of semantic gap between high-level semantic
concepts and the characteristics of the low-level
image.
-‘Mammo ontology’ (Toujilov, 2012): The Gimi
mammography ontology has been developed in 2012;
it contains 692 classes and 135 properties, it is used
to describe the richness and complexity of the domain
and has been implemented with OWL 2, where the
goal is to be integrated into a learning tool to compare
the reviews of trainees with the expert annotations.
First, we proceed to compare the semantic
distance with respect of an existing one called the
structural proximity proposed in (Hu et al., 2008) and
has been extensively used for ontology clustering
such as (Ngo, 2012) and (Tu et al., 2005,) which is:
)
(9)
Where
is the common superclass of
,
and depth
gets the depth of
in the original class
hierarchy.
For the clustering evaluation, we have used the
cluster validity measures: Partition coefficient (PC)
and Partition Entropy (PE). The PC indicates the
average relative total of membership sharing among
pairs of fuzzy subsets (Wanga and Zhang, 2007),
where a high PC score designates a better
partitioning. PC is computed as well:
(10)
The PE reveals the repartition of entities within
the clusters (Jafar and Sivakumar, 2014), where a low
score of PE indicates a better quality of partitioning.
PE=
(11)
The algorithm is implemented using Java
language, with setting parameters as well: m = 2 and
the number of clusters (not the same for all clusters).
The algorithm converges when the centroids become
stable. The histograms drawn in Figure 2 present the
evaluation results of both distance metrics, where we
notice that the algorithm reported good results for the
relational context distance; where it generates for
each data set maximum PC and minimum PE. We
notice that, by
using the structural proximity based
Fuzzy Clustering based Approach for Ontology Alignment
597

distance classes with weak depth tend to have low
membership to different classes. Moreover,
we
find
that, in most cases, medoids designate the classes
with increased depths, which may lead to
insignificant representative data, or the latter have to
be as representative and general as possible among
data in a cluster.
Figure 2: Evaluation of the proposed semantic distance.
To evaluate the alignment quality, we make a
comparison between the alignments generated from
our method and the ones generated from FALCON-
AO (Ningsheng et al., 2005) and S-Match
(Giunchiglia et al., s.d.). These systems are open
source and available on the net. To this end, we adopt
3 standard known metrics widely used in data mining
field: Precision, Recall and F-measure. We assume
that designates the set of correspondences
discovered between ontological entities by the
proposed tool. is the set of reference
correspondences found by the domain expert. These
metrics are defined as follows:
-: which represents the proportion of
true positives among all matching elements found by
the method. This allows qualifying the relevance of
the alignment method:
P=
indicates the proportion of true positives
among all matching elements in the reference
alignment. This measure quantifies the cover of the
alignment method: R=
represents the harmonic mean
between precision and recall. It compares the
performance of methods by means of single measure:
Figure 3: Alignment methods comparaison.
The Falcon-AO is a method that is based on
partitioning the ontologies into crisp clusters before
aligning the blocks. As regarding the S-Match tool,
it is based on non-partitioning strategy; but it uses
structural as well as element-based similarity
techniques for correspondences discovering. The
results in Figure 3 indicate that our fuzzy clustering-
based method achieves a slight improvement in
alignment quality as compared to the other existing
tools. The reduced search space performs good
precision by reducing the total of false positives
number. Although the Falcon-AO system adopts
ontology partitioning technique to reduce the
complexity of the alignment problem, the proposed
method is more efficient. This is due to benefit of the
use of fuzzy clustering which increases the chance of
finding correct alignments. As first observation, the
use of fuzzy clustering has positively influenced the
alignment quality. This confirms that:
-The use of clustering technique may reduce
noticeably the scalability problem by reducing the
search space.
-Assigning a concept to several clusters
simultaneously increases the chance of discovering
more correct alignments.
6 CONCLUSION AND FUTURE
WORK
In this paper, we propose a fuzzy clustering alignment
method. The main contributions of this paper are as
follows:
-We present a fuzzy clustering method which
consists on partitioning the ontology into fuzzy
clusters where a concept may belong to several
clusters simultaneously. To this end, we have
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
Falcon-AO
Our method
SMATCH
Falcon-AO
Our method
SMATCH
Falcon-AO
Our method
SMATCH
precision recall F-measure
ICEIS 2016 - 18th International Conference on Enterprise Information Systems
598

proposed a new semantic distance for clustering
analyze.
-We introduce an approach to aligning clusters
based on the predefined medoids. The latter may
facilitate the knowledge base visualization, as well as
speed up the task of matched clusters pairs.
-We proceed to align similar clusters’ entities
with the use of multiple similarity techniques.
As the next step, we are planning to ameliorate the
system efficiency in terms of precision and recall, we
are looking as well to perform experiments over large
ontologies so to be able to participate in benchmark
OAEI.
REFERENCES
Algergawy, S. Massmann & E. Rahm, 2011. A Clustering-
Based Approach For Large-Scale Ontology Matching.
Advances In Databases And Information Systems,
January.Pp. 415-428.
Bulzan, S.D. Bioportal. [En Ligne]
Available At: Http://Bioportal.Bioontolgy.Org/Ontolo
gies/Bcgo [Accès Le 26 June 2009].
Bulzan, Bioportal. [En Ligne]
Available At: Http://Bioportal.Bioontology.Org/Ontol
ogies/Bcgo [Accès Le 26 June 2009].
Duan, Fokoue, A., K.Srinivas & B.Byrne, 2011. A
Clustering-Based Approach To Ontology Alignment.
The Semantic Web–Iswc Springer, Pp. 146-161.
Fernández, J.Velasco, I.J.Marsa-Maestre & M.Lopez-
Carmona, 2012. Fuzzyalign: A Fuzzy Method For
Ontology Alignment.. Keod 2012 – Proceedings Of The
International Conference On Knowledge Engineering
And Ontology Development, Pp. 98-107.
Giunchiglia, Autayeu, A. & Pane, J., S.D. S-Match: An
Open Source Framework For Matching Lightweight
Ontologies.. Semantic Web, 3(3), Pp. 307-317.
Hamdi, F. & Safar, B., 2009. Partitionnement D’ontologies
Pour Le Passage A L’échelle Des Techniques
D’alignement. 9eme Journées Francophones
Extraction Et Gestion Des Connaissances.
Hu, W., Qu, Y. & Cheng, G., 2008. Matching Large
Ontologies: A Divide-And-Conquerapproach. Data
And Knowledge Engineering, Volume 67, Pp. 140-160.
Hu, W., Zhao, Y. & Y.Qu, 2006. Partition-Based Block
Matching Of Large Class Hierarchies. Proceedings Of
The First Asian Conference On The Semantic Web, P.
72–83.
Idoudi, R., Ettabaa, K. S., Hamrouni, K. & Solaiman, B.,
2014. An Evidence Based Approach For Multipe
Similarity Measures Combining For Ontology
Aligning. 1st Ieee International Conference On Image
Processing Applications And Systems Conference
(Ipas), November.
Jafar, O. M. & Sivakumar, R., 2014. Hybrid Fuzzy Data
Clustering Algorithm Using Different Distance
Metrics: A Comparative Study. International Journal
Of Soft Computing And Engineering (Ijsce), January,
3(6), Pp. 241-248.
Massmann, S. Et Al., 2011. Evolution Of The Coma Match
System. Ontology Matching, June.Volume 49.
Ngo, D., 2012. Enhancing Ontology Matching By Using
Machine Learning, Graph Matching And Information
Retrieval Techniques, Montpellier: Université
Montpellier Ii.
Ningsheng, Cheng, W. & Q.Yuzhong, 2005. Falcon-Ao:
Aligning Ontologies With Falcon. K-Cap Workshop On
Integrating Ontologies, Pp. 85-91.
Qiu & Liu, Y., 2014. An Effective Approach To Fuzzy
Ontologies Alignment. International Journal Of
Database Theory And Application, 7(3), Pp. 73-82.
Schlicht, A. & Stuckenschmidt, H., 2008. A Flexible
Partitioning Tool For Large Ontologies. Ieee/Wic/Acm
International Conference On Web Intelligence, Wi,
December.P. 482–488..
Seddiquia, M. & Aono, M., 2009. An Efficient And
Scalable Algorithm For Segmented Alignment Of
Ontologies Of Arbitrary Size. Web Semantics, 7(4), Pp.
344-356.
Shvaiko & Euzenat, J., 2005. Survey Of Schema-Based
Matching Approaches. Journal On Data Semantics Iv,
Pp. 146-171.
Toujilov, P., 2012. Mammographic Knowledge
Representation In Description Logic. Springer, August
.Pp. 158-169.
Tu, K. Et Al., 2005,. Towards Imaging Large-Scale
Ontologies For Quick Understanding And Analysis.
Proceedings Of The 4th International Semantic Web
Conference, Lncs, Volume 3729, P. 702–715.
Wanga & Zhang, 2007. On Fuzzy Cluster Validity Indices.
Fuzzy Sets And Systems, 14 March, 158(19), P. 2095–
2117.
Wang, Zhou & B.Xu, 2011. Matching Large Ontologies
Based On Reduction Anchors. Proceedings Of The
Twenty-Second International Joint Conference On,
Volume 3, P. 2343–2348.
Fuzzy Clustering based Approach for Ontology Alignment
599
