
An Energy-aware Scheduling Algorithm in DVFS-enabled Networked
Data Centers
Mohammad Shojafar
1
, Claudia Canali
1
, Riccardo Lancellotti
1
and Saeid Abolfazli
2
1
Department of Engineering ”Enzo Ferrari”, University of Modena and Reggio Emilia, Modena, Italy
2
YTL Communications, Xchanging Malaysia, Kuala Lumpur, Malaysia
Keywords:
Virtualized Networked Data Centers, Optimization, Dynamic Voltage Frequency Scaling, Resource provi-
sioning, Energy-efficiency.
Abstract:
In this paper, we propose an adaptive online energy-aware scheduling algorithm by exploiting the reconfig-
uration capability of a Virtualized Networked Data Centers (VNetDCs) processing large amount of data in
parallel. To achieve energy efficiency in such intensive computing scenarios, a joint balanced provisioning
and scaling of the networking-plus-computing resources is required. We propose a scheduler that manages
both the incoming workload and the VNetDC infrastructure to minimize the communication-plus-computing
energy dissipated by processing incoming traffic under hard real-time constraints on the per-job computing-
plus-communication delays. Specifically, our scheduler can distribute the workload among multiple virtual
machines (VMs) and can tune the processor frequencies and the network bandwidth. The energy model used
in our scheduler is rather sophisticated and takes into account also the internal/external frequency switching
energy costs. Our experiments demonstrate that the proposed scheduler guarantees high quality of service to
the users respecting the service level agreements. Furthermore, it attains minimum energy consumptions under
two real-world operating conditions: a discrete and finite number of CPU frequencies and not negligible VMs
reconfiguration costs. Our results confirm that the overall energy savings of data center can be significantly
higher with respect to the existing solutions.
1 INTRODUCTION
Energy-saving computing through Virtualized Net-
worked Data Centers (VNetDCs) is an emerging
paradigm that aims at performing the adaptive en-
ergy management of virtualized computing plat-
forms (Baliga et al., 2011; Canali and Lancellotti,
2016). The goal is to provide high quality Internet ser-
vices to large populations of clients, while minimiz-
ing the overall computing-plus-networking energy
consumption (Cugola and Margara, 2012; Mishra
et al., 2012; Baliga et al., 2011). Nowadays, the
energy cost of the communication infrastructure for
current data centers may represent a significant frac-
tion of the overall system due to the presence of
switches, routers, load balancers and other network
devices (Azodolmolky et al., 2013; Warneke and Kao,
2011). In our scenario we consider a VNetDC that re-
ceives as input a set of computationally-intensive jobs
and operates on such input data. An example of this
type of applications is cloud based data processing
based on a map-reduce paradigm. In this scenario,
we define the quality of service (QoS) requirements
as a threshold on the per-job execution time. To sup-
port this type of Service Level Agreement (SLA) the
VNetDC must be able to quickly adapt its resource
allocation to the current (a priori unpredictable) size
of the incoming traffic. A final requirement for our
data center is to minimize energy consumption, an as-
pect that is receiving a growing amount of interest in
the scientific literature (Chase et al., 2001; Herbert
and Marculescu, 2007; Canali and Lancellotti, 2014).
New energy-aware CPU technologies, such as the Dy-
namic Voltage and Frequency Scaling (DVFS) (Her-
bert and Marculescu, 2007), are rapidly being adopted
for data center energy provisioning. The paradigm
of cloud computing relying on virtualization is an-
other characteristic we should take into account in our
system. Several approaches (i.e., (Urgaonkar et al.,
2010; Mathew et al., 2012; Wang et al., 2014; Corde-
schi et al., 2013) highlighted these concepts within
the energy management. Specifically, authors in (Ur-
gaonkar et al., 2010) considered optimal resource al-
location and power management in VNetDCs with
heterogeneous applications; however, they do not take
into account re-configuration and network costs. Au-
Shojafar, M., Canali, C., Lancellotti, R. and Abolfazli, S.
An Energy-aware Scheduling Algorithm in DVFS-enabled Networked Data Centers.
In Proceedings of the 6th International Conference on Cloud Computing and Services Science (CLOSER 2016) - Volume 2, pages 387-397
ISBN: 978-989-758-182-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
387

thors in (Mathew et al., 2012) proposed a new method
to reduce the energy consumption of large Internet-
scale distributed systems by modeling the problem
into offline algorithm and an online algorithm to ex-
tract energy savings both at the level of local load bal-
ancing within a data center and global load balanc-
ing across data centers. The drawback of this method
is that it cannot manage the spikes and valleys of in-
coming workloads, and does not to control the inter-
nal/external switch of the server frequencies. The au-
thors of (Wang et al., 2014) introduce an algorithm to
minimize the number of switches that will be used and
to balance network traffics and handle the data center
energy. This mathematical approach can be applied
in large-scale data centers, but it is unable to manage
the tear-and-wear of the server, the workload fluctu-
ations and does not consider inter-costs for reconfig-
uration among various discrete ranges of frequencies.
Finally, the works in (Cordeschi et al., 2013; Corde-
schi et al., 2014; Shojafar et al., 2015) concentrate
on the computing-plus-communication energy con-
sumed for the several components of the VNetDCs
and try to manage the entire energy of data centers
respecting the considered SLAs, but did not empha-
size the internal switching costs occurring at the VMs
level. In particular, the work in (Shojafar et al., 2015)
is based on a simplified approach for the computation
of the communication costs, that does not consider
the Shannon-Hartley model; moreover, the results are
compared with a limited number of state-of-the-art al-
ternatives. In this paper, we propose a new approach
to minimize energy consumption in computing, com-
munication and reconfiguration costs in a scenario of
parallel data processing based on cloud computing,
while satisfying SLAs that are expressed as the max-
imum time to process a job (including computation
and communication times).
A qualifying contribution of our research is that
we consider an energy objective model that is a non-
convex function. Hence, we propose a mathemati-
cal approach to change non-convexity into convexity.
Additional features of our approach are its scalabil-
ity, easy implementation, and independence of work-
load scheduling from the reconfiguration costs. The
remainder of this paper is organized as follows. Af-
ter presenting the system model in Section 2, the
approach and the mathematical proofs which cover
computation-plus-communication objective functions
and the optimization problem constraints are intro-
duced in Section 3. Numerical results are presented
in Section 4. Finally, Section 5 summarizes the main
results and outlines future research directions.
2 SYSTEM MODEL
The considered VNetDC is modeled as multiple virtu-
alized processing units interconnected by a single-hop
virtual network and managed by a central controller.
Each processing unit executes the currently assigned
task using its own local virtualized storage and com-
puting resources. When a request for a new job is sub-
mitted to the VNetDC, the central resource controller
dynamically performs both admission control and al-
location of the available virtual resources (Almeida
et al., 2010) as in Fig. 1.
We recall that the model for a VNetDC adopted
in this paper follows the emerging trends for
communication-plus-computing system architecture.
A VNetDC is composed by multiple reconfigurable
VMs, that are interconnected by a throughput-limited
switched Virtual Local Area Network (VLAN). We
assume a star-topology VLAN where, in order to
guarantee inter-VM communication, the Network
Switch of Fig. 1 acts as a gather/scatter central
node. The operations of both VMs and VLAN
are jointly managed by a Virtual Machine Manager
(VMM), which performs task scheduling by dynami-
cally allocating the available virtual computing-plus-
communication resources to the VMs and Virtual
Links of Fig. 1. A new job is initiated by the ar-
rival of a data of size L
tot
[bit]. Due to the SLA for-
mulation, full processing of each input job must be
completed within assigned and deterministic process-
ing time which spans T seconds. M ≥ 1 is the maxi-
mum number of VMs in the data center. In this paper,
we assume that the VMs deployed over a server can
change their share of server resources according to the
model described in (Daniel Gmach and Cherkasova,
2012), that is widely adopted in private cloud envi-
ronments. This model tends to face conditions of high
computational demand by means of few large VMs
instead of many small VMs. For the sake of this
research, we adopt a simplified model where a sin-
gle VM is deployed over each server and uses all the
available resources for that server. At any given time,
the physical server CPU operates at a frequency f
i
(chosen within a pre-defined set of frequencies avail-
able from the DVFS technology). A VM on server i is
capable to process F(i) bits per second as in (Corde-
schi et al., 2013), where the processing rate F(i) of
VM i is linearly proportional to the CPU frequency
f (i). An extension of the model to consider more
VMs on each physical server is left as an open issue
to be addressed in future works.
TEEC 2016 - Special Session on Tools for an Energy Efficient Cloud
388
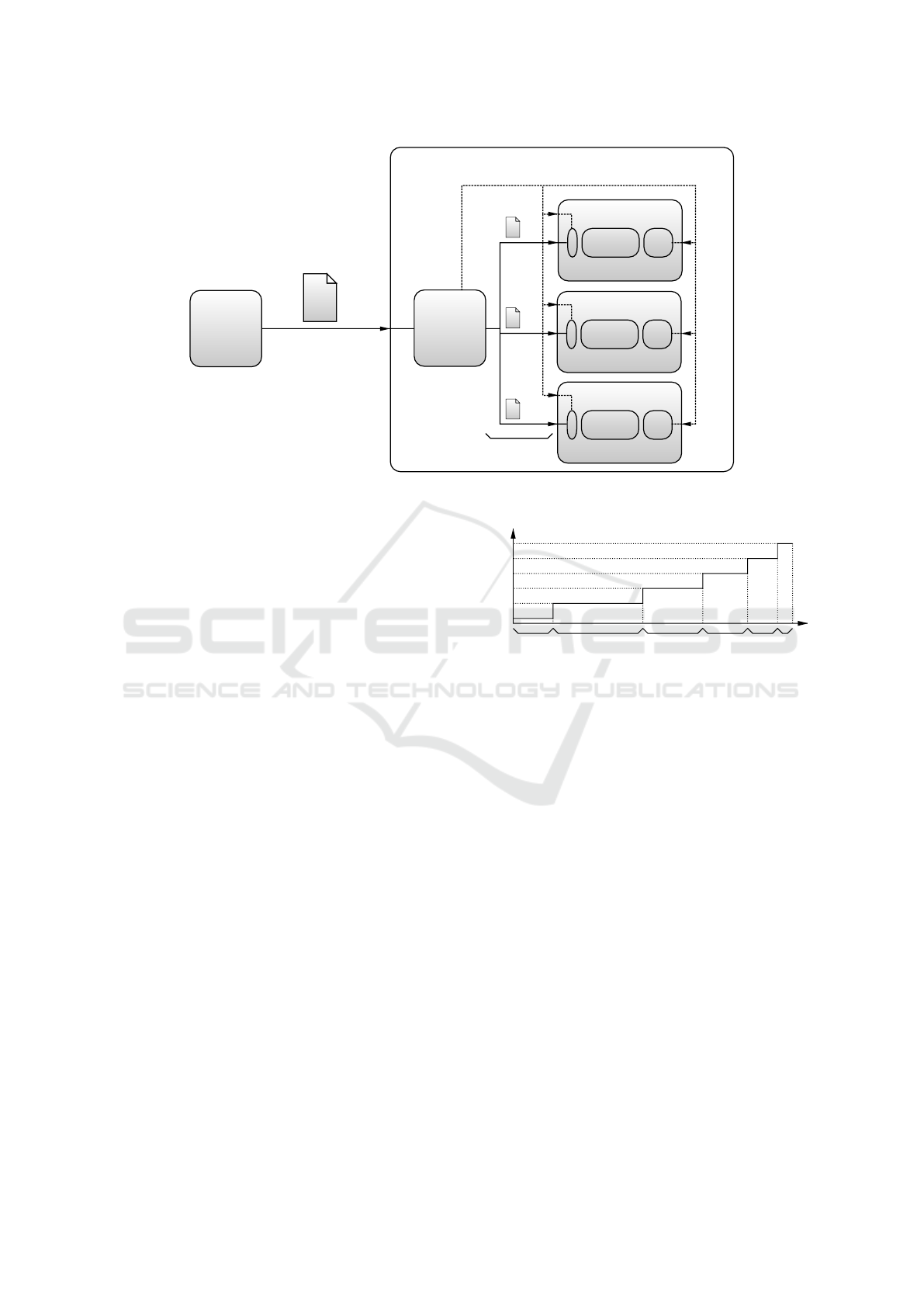
Server 1
Job
VM 1
VNIC DVFS
Server i
VM i
VNIC DVFS
Server M
VM M
VNIC DVFS
CPU frequency
Data transmission rate
Network
switch
&
VMM
VNetDC
Clients
Configuration
info
VLAN
Figure 1: The considered VNetDC architecture.
2.1 Computational Cost
The adopted model for the computing energy is based
on the CPU energy curve and VM states (we recall
that each physical server hosts only one VM). DVFS
is applied by the hosting physical servers to stretch the
processing times of the tasks and reduce the energy
consumptions by decreasing the CPU frequencies of
the active VMs. For this purpose, each server can
be operated at multiple voltages which operate dif-
ferent CPU frequencies (Azodolmolky et al., 2013).
Q is the number of CPU frequencies allowed for each
VM (plus an idle state). The set of the allowed fre-
quencies is f (i) ∈
f
j
(i)
, with i ∈ {1,...,M}, j ∈
{0,1,...,Q}, where f
j
(i) is the j − th discrete fre-
quency of VM i, with j = 0 representing the idle state.
Furthermore, we define t
j
(i) as the time where i-th
VM operates at frequency f
j
(i). Fig. 2 illustrates an
example for Q = 5.
According to (Qian et al., 2013), the dynamic
power consumption P of the hosting CPU grows with
the third power of the CPU frequency. So we can de-
fine the energy consumption of the generic VM i as:
ε
CPU
(i) ,
Q
∑
j=0
AC
e f f
f
j
(i)
3
t
j
(i), [Joule],∀i = {1, . .. ,M},
(1)
2.2 Frequency Reconfiguration Cost
For the CPU frequency reconfiguration (switching)
cost, we need to consider two costs: internal switch-
ing cost and external switching cost. The first one
f
0
=f
idle
f
1
f
2
f
3
f
4
f
5
=f
Q
f
j
(i)
t
0
(i) t
1
(i) t
2
(i) t
3
(i) t
4
(i) t
5
(i)
Figure 2: The discrete range of frequencies considered for
V M(i).
is the cost of changing the internal-switching among
discrete frequencies of V M(i) from f
j
(i) to f
j+k
(i)
(i.e., k steps movement to reach the next active dis-
crete frequency). The second one is the cost for
external-switching from the final active discrete fre-
quency of VM i at the end of a job to the first active
discrete frequency for the next incoming job of size
L
tot
. Note that the active discrete frequencies are a
subset of the available operating frequencies found
based on their related times-quota variables, which
means that frequency f
j
(i) belongs to the set of active
discrete frequencies if and only if t
j
(i) > 0. Given
the list of active discrete frequencies for each VM for
each job coming into the system, switching from the
current active discrete frequency to another one af-
fects the reconfiguration cost. We start from the first
active discrete frequency ( f
k
(i)), move to the second
one ( f
k+1
(i)) and so on. We define the differences
as ∆ f
k
(i) , f
k+1
(i) − f
k
(i) and the cost is k
e
∆ f
k
(i)
2
,
where k
e
[Joule/(Hz)
2
] is the reconfiguration cost in-
duced by a unit-size frequency switching. Typical val-
ues of k
e
for current DVFS-based virtualized comput-
ing platforms are limited up to few hundreds of µJ per
[MHz]
2
(Cordeschi et al., 2014). If we consider ho-
An Energy-aware Scheduling Algorithm in DVFS-enabled Networked Data Centers
389

mogeneous VMs, the total cost of internal-switching
for all VMs is: k
e
∑
M
i=1
∑
K
k=0
(∆F
k
(i))
2
, where k ∈
{0,1,...,K}. K ≤ Q is the number of active discrete
frequencies for VM i. The external-switching cost is
calculated as multiplication of k
e
with the quadratic
differences between the last active discrete frequency
of i-th VM for the current job and the first active dis-
crete frequency of i-th VM in the next incoming job,
which is named Ext C ost. In a nutshell, the total re-
configuration energy can be written as (2):
M
∑
i=1
ε
Recon f
(i) , k
e
M
∑
i=1
K
∑
k=0
(∆ f
k
(i))
2
+ k
e
M
∑
i=1
Ext Cost
(2)
In the worst case, K = Q + 1 and for external-
switching we need to move Q steps to f
0
(Idle
state). In this case the internal-switching cost is
k
e
M
∑
Q
k=0
(∆F
k
)
2
and the external-switching cost is
k
e
M( f
t
Q
− f
t−1
0
)
2
.
2.3 Communication Cost
We assume that each VM i communicates to the
scheduler through a dedicated (i.e., contention-free)
reliable virtual link, that operates at the transmission
rate of R(i) [bit/s], i = 1,. . ., M and it is equipped with
suitable Virtual Network Interface Cards (VNICs) (as
in Fig. 1). The one-way transmission-plus-switching
operation over the i-th virtual link drains a (vari-
able) power of P
net
(i) = P
T
net
(i)+P
R
net
(i) [Watt], where
P
T
net
(i) is the power consumed by the transmit VNIC
and Switch and P
R
net
(i) is related to VNIC receiving
operations. We assume that the channel power of
transmitting and receiving are the same and can be
calculated according to the Shannon-Hartley expo-
nential formula as
P
net
(i) = ζ
i
2
R(i)/W
i
− 1
+ P
idle
(i), [Watt], (3)
with ζ
i
,
N
0
(i)W
i
g
i
, i = 1, . .. , M, where N
0
(i), [W /Hz],
W
i
[Hz] and g
i
are noise spectral power density, trans-
mission bandwidth and (nonnegative) gain of the i-th
link, respectively. Hence, the corresponding one-way
transmission delay equates: D(i) =
Q
∑
j=1
F
j
(i)t
j
(i)/R(i),
so that the corresponding one-way communication
energy ε
net
(i) is:
ε
net
(i) , P
net
(i)
Q
∑
j=1
F
j
(i)t
j
(i)
R(i)
[Joule]. (4)
2.4 Optimization Problem
The goal is to minimize the overall resulting
communication-plus-computing energy, formally de-
Table 1: Main taxonomy of the paper.
Symbol Meaning/Role
F
j
(i) [bit/s] j-th processing rate of VM(i)
L
tot
[bit] Job size
R(i) [bit/s] Communication rate of the i-th
end-to-end connection
R
t
[bit/s] Aggregate communication rate of the Virtual LAN
T [s] Per-job maximum allowed
computing time
t
j
(i) [s] Computing time of V M(i) working at F
j
(i)
T [s] Per-job maximum allowed
computing-plus-communication time
P
net
(i) [Watt] Power consumed by the i-th
end-to-end connection
P
idle
(i) [Watt] Power consumed by the i-th
end-to-end link connection in the idle mode
ε
tot
[Joule] Total consumed energy
ε
CPU
[Joule] Computing energy
ε
Recon f
[Joule] Reconfiguration energy
ε
net
[Joule] Communication(Network) energy
M Maximum number of available VMs
Q + 1 Number of discrete CPU frequencies
allowed for each VM
PMR Peak-to-Mean Ratio of the offered workload
fined as:
ε
tot
,
M
∑
i=1
ε
CPU
(i) +
M
∑
i=1
ε
Recon f
(i) +
M
∑
i=1
ε
net
(i) [Joule],
(5)
where ε
CPU
(i), ε
Recon f
(i), ε
net
(i) are the computa-
tional cost, the reconfiguration cost, and the commu-
nication cost of V M(i), respectively. Furthermore, we
recall the our problem is subject to the hard constraint
T on the allowed per-job execution time Table 1 sum-
marizes the main notations of in this paper.
3 PROPOSED SOLUTION FOR
THE OPTIMIZATION
PROBLEM
The proposed methodology aims to minimize the to-
tal energy consumption of incoming workload by se-
lecting the best computing resource for job execu-
tion based on current load level and by selecting the
optimal bandwidth to minimize the communication
energy consumption, while considering the content-
based reconfiguration frequencies for each VM. Com-
puting resources are the collection of Physical Ma-
chines (PMs), each comprised of one or more cores,
memory, network interface and local I/O. Specifically,
this functionality aims to tune properly the task sizes,
the communication rates and the processing rates of
the networked VMs. The goal is to minimize (on a
per-job basis) the overall resulting communication-
plus-computing energy, which includes the summa-
tion of ε
CPU
(i), ε
Recon f
(i) and ε
net
(i) for all M VMs
in ε
tot
which are calculated for each VM. Further-
TEEC 2016 - Special Session on Tools for an Energy Efficient Cloud
390

more, the total duration takes to process each incom-
ing workload is bounded to a hard constraint T [s]
which conveys the SLA considered for that workload.
For the solution of the optimization problem, we
find it useful to add an additional parameter, namely
T , that is a threshold for the computation operation
in job processing (without considering network de-
lays). Hence, we split the SLA into two different con-
straints, that are computation time less or equal than
T and network-related time less or equal than T − T .
The resulting Optimization Problem can thus be
expressed as follows:
min
M
∑
i=1
ε
CPU
(i) +
M
∑
i=1
ε
Recon f
(i) + ε
net
(i) (6.1)
s.t.:
M
∑
i=1
Q
∑
j=0
F
j
(i)t
j
(i) = L
tot
, (6.2)
M
∑
i=1
R(i) ≤ R
t
, (6.3)
Q
∑
j=0
t
j
(i) ≤ T, i = 1,. . . , M, (6.4)
Q
∑
j=0
2F
j
(i)t
j
(i)
R(i)
≤ T − T, i = 1,. . .,M, (6.5)
0 ≤ t
j
(i) ≤ T, i = 1,...,M, j = 0,...,Q, (6.6)
0 ≤ R(i) ≤ R
t
, ∀i = 1,...,M. (6.7)
Specifically, equation (6.1) is the objective function
which consists of the sum of three terms which ac-
counts for the computing energy, the reconfiguration
energy cost is the networking energy. The decision
variables of the optimization problem are the t
j
(i) (the
time spent by each VM operating at frequency f
j
and
R(i) is the transmission rate for VM i. Eq. (6.2) is the
(global) constraint which guarantees that the overall
job is decomposed into M parallel tasks. Here, L
tot
is the size of the incoming job that needs to be dis-
tributed over M VMs for computation. Also, the prod-
uct F
j
(i)t
j
(i) is the workload processed for each dis-
crete frequency f
j
which is processed by VM i during
the interval t
j
(i). The bandwidth inequality in (6.3)
ensures that the bandwidth summation of each VM
must be less than the maximum available bandwidth
of the global network. Eq. (6.4) is the constraint on
computation time, while Eq. (6.5) is the constraint on
data exchange time (the two constraints combined ex-
press the SLA) Eq. (6.6) guarantees that the duration
of each computing interval is no negative and less
than T . Finally, the last constraint in (6.7) ensures
that our control parameter R (communicate rate of the
channel) is positive and lower than the maximum net-
work capacity.
The third term of the optimization problem is non-
convex but the rest of the constraints are affine or
convex in their considered range and in closed-form.
However the global problem can still be turned into
an equivalent (possibly, feasible) convex problem, as
pointed out by the following Proposition 1.
Proposition 1. ε
net
can be put in the following form
M
∑
i=1
Q
∑
j=0
2P
net
(i)
F
j
(i)t
j
(i)
R(i)
=
(T − T )
M
∑
i=1
Q
∑
j=0
P
net
(i)
2F
j
(i)t
j
(i)
T − T
.
(7)
Proof: Let R(i)
∗
be the optimal solution of the eq.
(6.1), and let
(8)C ,
(
−−−−−→
F
j
(i)t
j
(i)
∈ (R
+
0
)
M
:
Q
∑
j=0
F
j
(i)t
j
(i)/R(i)
∗
−−−−−→
F
j
(i)t
j
(i)
!
≤
(
T − T )/2,i = {1, . . . , M}, j = {0, . . . , Q};
M
∑
i=1
Q
∑
j=0
R(i)
∗
−−−−−→
F
j
(i)t
j
(i)
≤ R
t
)
,
be the region of nonnegative M-dimensional Eu-
clidean space constituted by all
−−−−−→
F
j
(i)t
j
(i) vectors
meeting the constraints in (6.4) and (6.5). For fea-
sibility and solution of (6.1) we have
i) The communication term in (6.1) is feasible if and
only if the vector
−−−−−→
F
j
(i)t
j
(i) meets the following
condition:
M
∑
i=1
Q
∑
j=0
F
j
(i)t
j
(i) ≤ R
t
(T − T )/2 (9)
ii) The solution of the communication term in eq.
(6.1) is given by the following closed-form ex-
pression:
R(i)
∗
−−−−−→
F
j
(i)t
j
(i)
≡ R(i)
∗
Q
∑
j=0
F
j
(i)t
j
(i)
!
≡
Q
∑
j=0
2F
j
(i)t
j
(i)/(T − T )
!
,i = 1,. . . , M.
(10)
For any assigned
−−−−−→
F
j
(i)t
j
(i), the objective function
in (6.1) is the summation of M(Q + 1) nonnegative
terms, where the i j-th term depends only on R(i) for
all j. Thus, being the objective function in (6.1)
An Energy-aware Scheduling Algorithm in DVFS-enabled Networked Data Centers
391

separable and its minimization may be carried out
component-wise. Since the i j-th term in (6.1) is in-
creasing in R(i) and the constraints in (6.4) and (6.5)
must be met, the i j-th minimum is attained when the
constraints in (6.4) and (6.5) are binding, and this
proves the validity of (9). Finally, the set of rates in
(10) is feasible for the communication cost if and only
if the constraint in (6.5) is met, and this proves the va-
lidity of the feasibility condition in (10).
Moreover, the end-to-end links power cost
Q
∑
j=0
2P
net
(i)(F
j
(i)t
j
(i)/R(i)) is the product of the end-
to-end link formula which is based on Shannon-
Hartley in (3) and is continuous, nonnegative and
nondecreasing for R(i) > 0, ∀i ∈ {1,...,M}, with
the multi-variable coefficient which can be feasible if
only the following equation holds (we use ”→” which
means implies):
Q
∑
j=0
2F
j
(i)t
j
(i)
R(i)
≤ T − T →
Q
∑
j=0
F
j
(i)t
j
(i)
R(i)
!
≤
(T − T )
2
.
(11)
Equation (11) is obtained by manipulating equa-
tion (6.4). To make the optimization problem easier to
solve, we recast the second control variable by rewrit-
ing R(i) based on another control variable (t
j
(i)) as
follows:
Q
∑
j=0
2F
j
(i)t
j
(i)
R(i)
≤ T − T → R(i) ≥
Q
∑
j=0
2F
j
(i)t
j
(i)
T − T
.
(12)
Applying the result of equations (11) and (12) in
the third term of the objective function, we have that
the end-to-end link function ε
net
which is based on
two control variables G(R(i);t
j
(i)) can be re-written
by changing the second control variable R(i) to a
function of other control variable t
j
(i) in eq. (13):
ε
net
(i) = G (R(i);t
j
(i)) , H (t
j
(i)). (13)
The new formula for energy-aware communica-
tion end-to-end link just depends on the summation
of time variables for each VM and the main function
(H (.)) can be written according to the equation (7).
Thus, this proves the third term in (6.1) is convex.
4 PERFORMANCE
COMPARISONS
This section evaluates the simulated performance of
the proposed scheduler for different scenarios and
compares it with the IDEAL no-DVFS techniques
presented in (Mathew et al., 2012), the Standard (or
Real) available DVFS-enabled technique (currently,
one of the methods being used in the DVFS-enabled
data centers) (Kimura et al., 2006), the Lyapunov
method in (Urgaonkar et al., 2010) and the NetDC
approach (Cordeschi et al., 2013). It is worth to note
that the proposed approach can be applied in real data
centers, differently from NetDC that relies on calcu-
lated fractions of real frequency, which cannot be ap-
plied in real environments. Hence, we emphasize that
the considered NetDC (Cordeschi et al., 2013) and
IDEAL no-DVFS techniques (Mathew et al., 2012)
work with the continue ranges of frequencies, which
is unrealistic and not feasible in real scenarios, while
the proposed scheduler could be one of the best viable
solutions in networked data centers.
4.1 Testbed Setup
The simulation is done by using the CVX solver over
Matlab (Grant and Boyd, 2015). We consider three
different scenarios: two synthetic workloads, both in-
cluding multiple VMs and detailed in Table 2 and Ta-
ble 3, and a real-world workload trace. The main dif-
ferences between the two synthetic scenarios are the
corresponding CPU discrete frequencies and the in-
coming workload. In order to account for the effects
of the reconfiguration costs and the time-fluctuations
of the offered workload on the energy performance
of the simulated schedulers, we model the offered
jobs as an independent identically distributed (i.i.d.)
random sequence L
tot
, whose samples are uniformly
distributed over the interval [L
tot
− a,L
tot
+ a], with
L
tot
≡ 8 [Gbit] with a = 2 [Gbit] and L
tot
= {8, 70}
(i.e., PMR = 1.25) (as in (Cordeschi et al., 2014)).
Furthermore, we pose a = 2 [Gbit] with PMR =
1.1428 and L
tot
= 8 in scenario 1 and a = 10 [Gbit]
with PMR = 1.25 and L
tot
= 70 in scenario 2. The
discrete frequency for the first scenario are taken from
Intel Nehalem Quad-core Processor (Kimura et al.,
2006) called F1 = {0.15,1.867,2.133,2.533,2.668}.
The second scenario is based on a power-scalable real
Crusoe cluster with TM-5800 CPU in (Almeida et al.,
2010), e.g., F2 = {0.300,0.533, 0.667, 0.800, 0.933}.
Each simulated point has been numerically evaluated
by averaging over 1000 independent runs.
4.2 Simulation Results
We evaluate the proposed scheduler with the afore-
mentioned scenarios as follows.
4.2.1 First Scenario
In the first scenario, which is based on Table 2 param-
eters, we evaluate the average (per-job) energy con-
TEEC 2016 - Special Session on Tools for an Energy Efficient Cloud
392

Table 2: Default values of the main system parameters for
the first test scenario.
Parameter Value
PE=M [1,...,10]
T
t
7 [s]
T 5 [s]
R
t
100 [Gbit/s]
C
e f f
1 [µF]
k
e
0.05 [Joule/(GHz)
2
]
F F1 [GHz]
Q 5
A 100%
P
idle
(i) 0.5 [Watt]
ζ
i
0.5 [mWatt]
f
max
i
2.668 [GHz]
Table 3: Default values of the main system parameters for
the second test scenario.
Parameter Value
k
e
0.005 [Joule/(GHz)
2
]
Q 5
F F2 [GHz]
L
tot
70 [Mbit]
M {20,30,40}
f
max
i
0.933 [GHz]
sumed by the system for a varying number M of avail-
able VMs, and the variation of k
e
related to the pro-
cessing rate F1, as shown in Fig. 3a. Based on the
synthetic traces of the workload in the first scenario,
the comparison in Fig. 3a confirms that by increas-
ing the VMs the consumed energy decreases, with
a reduction ranging from 80% (case of k
e
= 0.005
with the lower plot) to 85% (case of k
e
= 0.05 with
the upper plot). These results confirm the expecta-
tions (Baliga et al., 2011) that noticeable energy sav-
ings may be achieved by jointly changing the avail-
able computing-plus-communication resources.
Fig. 3b tests the computing-vs-communication en-
ergy trade-off for the first scenario of Table 2 for dif-
ferent values of T . It confirms that small T ’s values
lead to higher per-VM processing rate which leads to
increasing the ε
tot
. While T increases, the proposed
scheduler exploits the processing time in order to de-
crease ε
tot
(i.e., reduction close to 20% in the two up-
per curves of Fig. 3b). On the other hand, extremely
large T values induce high end-to-end communication
rates, which lead to increasing the ε
tot
(see eq. (6.5)).
We perform another experiment in order to eval-
uate the energy reduction due to scaling up/down
of the computing, reconfiguration and communica-
tion rates when the number of VMs increases (i.e.,
2 4 6 8 10
45
50
55
60
65
70
75
M
E
tot
[Joule]
F 1, k
e
= 0.005
F 1, k
e
= 0.05
(a) Impact of E
tot
by reconfiguration parameter
2 3 4 5 6
20
30
40
50
60
T [s]
E
tot
[Joule]
M = 10
E
CP U
, ζ
i
= 0.2
E
tot
, ζ
i
= 0.5
E
tot
, ζ
i
= 0.2
(b) Computing-vs.- Communication tradeoff
Figure 3: E
tot
of the proposed method in the first test
scenario, for various k
e
(Fig. 3a) and for various T and ζ
(Fig. 3b).
we process the results for the one time implemen-
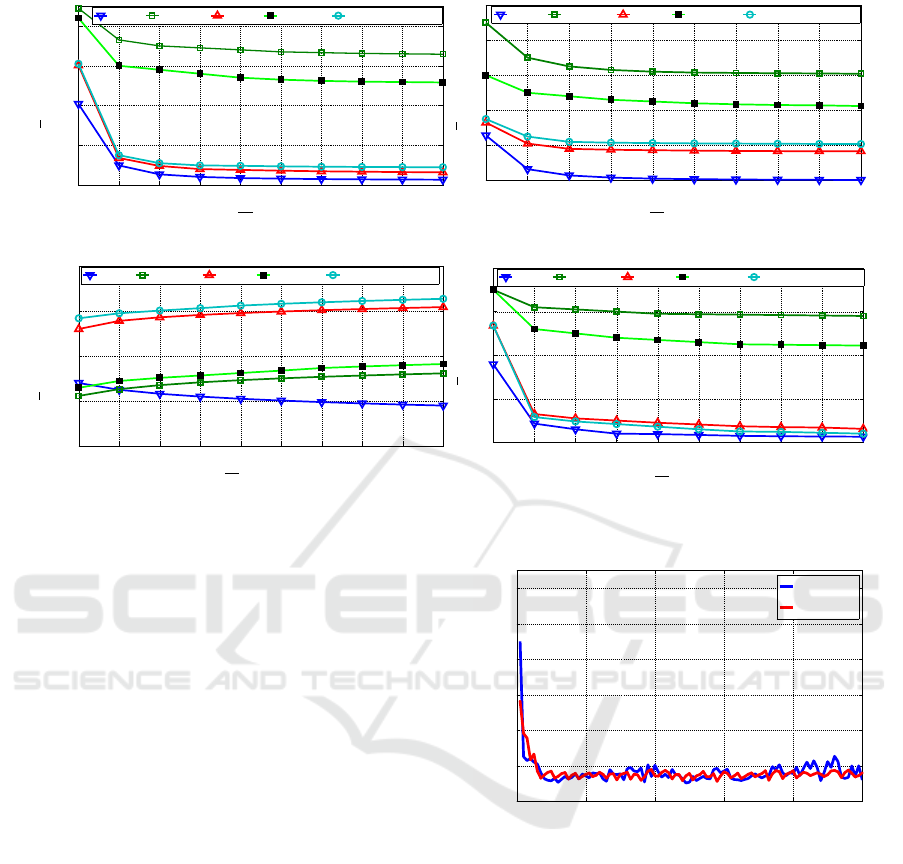
tation over 10 VMs). In detail, Fig. 4 presents
the average over 1000 offered jobs of the total en-
ergy ε
tot
, Computation energy ε
CPU
, reconfigura-
tion energy ε
Recon f
, and communication energy ε
net
for our approach, IDEAL, Standard, Lyapunov-based
method in (Urgaonkar et al., 2010) and a recent work
done in this area in (Cordeschi et al., 2013), in sub-
figures 4a, 4b, 4c, 4d, respectively. Specifically,
Fig. 4a points out that the average total cost for all ap-
proaches decreases by increasing the number of VMs
because a lower fraction of L
tot
is assigned to each
VM (i.e., F
j
(i)t
j
(i)), and the needed frequency to pro-
cess the data within the allowed time decreases, with
a major gain in terms of energy. In Fig. 4a, the aver-
age energy-saving of the proposed method is approx-
imately 50% and 60% compared to Lyapunov-based
and Standard schedulers, respectively. Furthermore,
in Fig. 4b we observe that an increase of the number
of VMs over M = 2 has a reduced effect on the cost of
the computing energy. This is due to the system being
able to manage the running time for each active dis-
crete frequency even while M is low (M < 4): with an
An Energy-aware Scheduling Algorithm in DVFS-enabled Networked Data Centers
393
1 2 3 4 5 6 7 8 9 10
0
100
200
300
400
M
E
tot
[Joule]
IDEAL Standard NetDC Lyapunov Proposed Method
(a) E
tot
1 2 3 4 5 6 7 8 9 10
0
20
40
60
80
100
M
E
CP U
[Joule]
IDEAL Standard NetDC Lyapunov Proposed Method
(b) E
CPU
1 2 3 4 5 6 7 8 9 10
10
−6
10
−4
10
−2
10
0
10
2
E
Reconf
[Joule]
M
IDEAL Standard NetDC Lyapunov Proposed Method
(c) E
Recon f
1 2 3 4 5 6 7 8 9 10
0
100
200
300
400
M
E
net
[Joule]
IDEAL Standard NetDC Lyapunov Proposed Method
(d) E
net
Figure 4: Comparison of average energy terms of eq. (6.1) with PMR=1.25 for the considered approaches in the first scenario.
increased number of VMs, the system goes to the Idle
mode or F
0
for most of the time and less or no time is
assigned to the remaining frequencies. Fig. 4c shows
the reconfiguration costs. We recall that our approach
considers two costs (internal-switching and external-
switching) for each V M(i), thus resulting in increased
reconfiguration costs compared to NetDC (Cordeschi
et al., 2013) and Lyapunov-based scheduler in (Ur-
gaonkar et al., 2010), which consider just probabili-
ties of previous and next active discrete frequencies
for each V M(i) (i.e., external-cost of our approach).
Lastly, Fig. 4d points out that the communication
cost of the proposed technique is lower with respect to
the other alternatives and close to IDEAL: according
to the third term of the (6.1), the optimization prob-
lem tries to find the optimum objective variables when
more resources are available. Fig. 4d shows that the
proposed scheduler is about 10%, 50%, 65% better
than NetDC (Cordeschi et al., 2013), Lyapunov (Ur-
gaonkar et al., 2010), and Standard (Kimura et al.,
2006) schedulers, respectively. Indeed, the proposed
scheduler is able to find proper running times of the
active discrete frequencies for each offered job (it
means that
∑
F
j
(i)t
j
(i) is the same for all approaches
and equal to L
tot
). Figure 5 reports the average ex-
ecution time (AET) per each job for the first 100 of-
fered jobs with M = 2 and M = 10 in the first scenario.
Specifically, while the number of jobs increases, the
AET per-job decreases significantly after some slots:
0 20 40 60 80 100
0.2
0.4
0.6
0.8
1
1.2
1.4
Workload
AET [s]
M = 2
M = 10
Figure 5: Average execution time (AET) per-job for the first
100 jobs.
this is due to the proposed scheduler being able to
adapt itself to the incoming traffic using optimization
technique (see (6.1)), with a consequent reduction in
the AET per job.
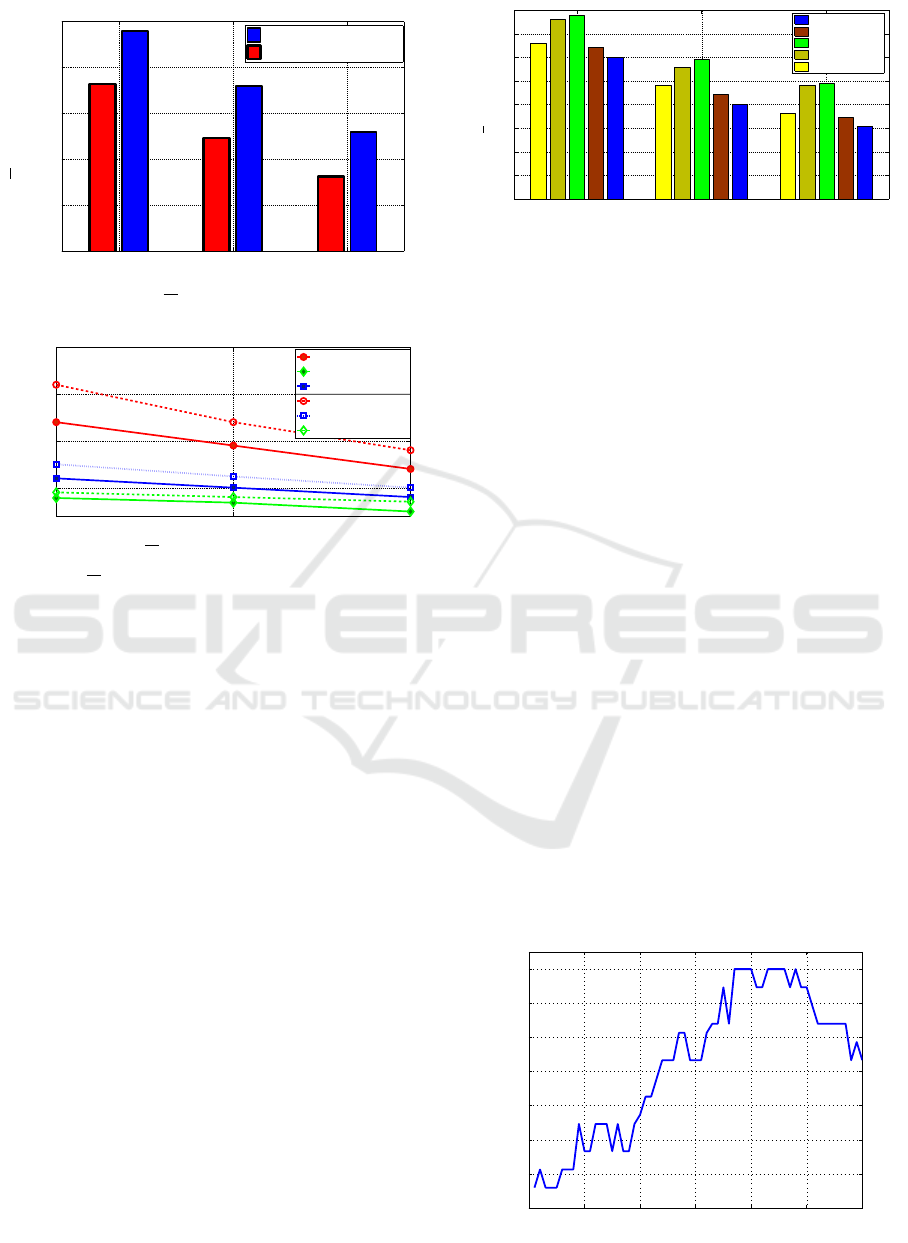
4.2.2 Second Scenario
In the second scenario we evaluate the energy con-
sumption of the proposed scheduler for a high amount
of jobs and VMs. Figs. 6 and 7 present the total
average consumed energy for 20, 30, and 40 VMs
and high volume of incoming jobs. In Fig. 6, we
show the results of a sensitivity analysis carried out
with respect to the parameters T (maximum comput-
ing time), R
t
(maximum network data transfer rate)
TEEC 2016 - Special Session on Tools for an Energy Efficient Cloud
394
20 30 40
300
350
400
450
500
550
M
E
tot
[Joule]
T = 5
R
t
= 10, ζ
i
= 0.5
R
t
= 100, ζ
i
= 0.5
(a) E
tot
-vs.-M-vs.-R
t
20 30 40
500
1000
1500
2000
M
E
tot
R
t
= 100
T = 3, ζ
i
= 0.2
T = 5, ζ
i
= 0.2
T = 4, ζ
i
= 0.2
T = 3, ζ
i
= 0.5
T = 4, ζ
i
= 0.5
T = 5, ζ
i
= 0.5
(b) E
tot
-vs.-M-vs.-T -vs.-ζ
Figure 6: E
tot
of the proposed method for various R
t
(Fig. 6a) and for various T and ζ (Fig. 6b).
and the communication coefficient ζ in order to eval-
uate the energy consumption of the proposed method
while facing various SLA ranges. Fig. 6a shows that,
by fixing T = 5 and ζ = 0.5 and increasing the R
t
data center communication boundary by a factor of
10, the proposed scheduler saves more energy (ap-
proximately 15% with a high number of VMs). This
confirms that the scheduler can save energy depend-
ing on the assigned communication boundary. Then,
we repeat the experiment considering a fixed value of
R
t
= 100 and varying the range for T and ζ. The re-
sults shown in Fig. 6b confirm that the best value for T
is 5. Moreover, we observe that the energy consump-
tion is less sensitive to the choice of the communica-
tion coefficient ζ; anyway, the energy costs is lower
for smaller values of ζ (i.e. ζ = 0.2). Observing
Fig. 7, we note that by increasing the number of VMs
(system with high resources), the energy consump-
tion significantly decreases even increasing the job
volumes. In detail, the energy reduction of proposed
method compared to Standard (Kimura et al., 2006)
and Lyapunov (Urgaonkar et al., 2010) is about 20%
and 15%, respectively, and this saving increases for an
increasing number of VMs. Moreover, it is interesting
to note that the gap between the proposed method and
the NetDC and IDEAL decreases by increasing the
VMs: note that the NetDC (Cordeschi et al., 2013)
20 30 40
0
50
100
150
200
250
300
350
400
M
E
tot
[Joule]
IDEAL
NetDC
Standard
Lyapunov
Proposed Method
Figure 7: Comparison of average energy terms (eq. (6.1)
with PMR=1.25) for the second scenario.
and IDEAL (Mathew et al., 2012) schedulers works
with continues CPU frequencies speed that cannot be
applied in a real environment due to CPU hardware
limitations. We can conclude that our approach works
properly even with high number of VMs.
4.3 Performance Comparisons Under
Real-world Workload Traces
The previous conclusions are confirmed by the nu-
merical results of this subsection, that refers to a real-
world workload trace represented in Fig. 8: this is
the same real-world workload trace considered in (Ur-
gaonkar et al., 2007). We perform preliminary exper-
iments and we found that the best parameter values
for this workload are k
e
= 0.5 [Joule/(MHz)
2
] and
T = 1.2 [s]. Furthermore, in order to maintain the
(numerically evaluated) PMR of the workload trace
of Fig. 8 at 1.526, we assume that each job has a
mean length of 0.533 [Mbit], so that at each slot the
input workload has an intensity of 16 [Mbit/slot]. It
is worth that this workload scenario is characterized
by a higher variance with respect to the previous one
(as testified by the higher PMR). However, even in
this case the average energy reduction of the proposed
scheduler, of NetDC and Lyapunov schedulers with
respect to the Standard alternative is 82%, 85%, and
0 10 20 30 40 50 60
2
4
6
8
10
12
14
16
Slot index
Number of arrivals per slot
Figure 8: Measured workload trace: PMR = 1.526.
An Energy-aware Scheduling Algorithm in DVFS-enabled Networked Data Centers
395

19%, respectively. In particular, the corresponding
average energy saving of the proposed scheduler com-
pared to the Lyapunov alternative is 76%; moreover,
its gap over the IDEAL scheduler remains limited to
30%.
5 CONCLUSION AND FUTURE
RESEARCH DIRECTIONS
The goal of this paper is to provide an adaptive
and online energy-aware resource provisioning and
scheduling of VMs in DVFS-enabled networked data
centers. Also, it is aimed at summarizing key
techniques and mathematical policies that minimize
the data center energy consumption, which is split
into three sub-problems subject to total computing
and communication time’s constraints, while meet-
ing given SLAs. In the process, we identified the
sources of energy consumptions in data centers and
presented a high-level solution to the related sub-
problems. The numerical results highlight that the
proposed approach can guarantee significant average
energy savings over the Standard and Lyapunov alter-
natives. Our proposed scheduler can manage not only
the online workloads, but also the inter-switching
costs among the active discrete frequencies for each
VM. An interesting achievement is that, when com-
munication costs are considered, our method is able
to approach the IDEAL algorithm significantly faster
than Lyapunov, Standard and NetDC models, respec-
tively. Under soft latency constraints, the energy effi-
ciency of the DVFS based systems could be, in prin-
ciple, improved by allowing multiple jobs to be tem-
porarily queued at the middleware layer of the cloud
systems. This paper is just a first effort in a new line
of research. Future extensions of the present work,
currently left as open issues, include: management
of the admission control using split workload estima-
tion, improved data center model that considers more
than one VM per physical server, and introduction of
economic aspects (such as variable VMs cost) in the
optimization problem.
ACKNOWLEDGEMENT
The first three authors acknowledge the support of the
University of Modena and Reggio Emilia through the
project SAMMClouds: Secure and Adaptive Manage-
ment of Multi-Clouds.
REFERENCES
Almeida, J., Almeida, V., Ardagna, D., Cunha,
´
I., Fran-
calanci, C., and Trubian, M. (2010). Joint admis-
sion control and resource allocation in virtualized
servers. Journal of Parallel and Distributed Comput-
ing, 70(4):344–362.
Azodolmolky, S., Wieder, P., and Yahyapour, R. (2013).
Cloud computing networking: challenges and oppor-
tunities for innovations. Communications Magazine,
IEEE, 51(7):54–62.
Baliga, J., Ayre, R. W., Hinton, K., and Tucker, R. (2011).
Green cloud computing: Balancing energy in process-
ing, storage, and transport. Proceedings of the IEEE,
99(1):149–167.
Canali, C. and Lancellotti, R. (2014). Exploiting ensem-
ble techniques for automatic virtual machine cluster-
ing in cloud systems. Automated Software Engineer-
ing, 21(3):319–344.
Canali, C. and Lancellotti, R. (2016). Parameter Tuning
for Scalable Multi-Resource Server Consolidation in
Cloud Systems. Communications Software and Sys-
tems, 11(4):172 – 180.
Chase, J. S., Anderson, D. C., Thakar, P. N., Vahdat, A. M.,
and Doyle, R. P. (2001). Managing energy and server
resources in hosting centers. ACM SIGOPS Operating
Systems Review, 35(5):103–116.
Cordeschi, N., Shojafar, M., Amendola, D., and Baccarelli,
E. (2014). Energy-efficient adaptive networked data-
centers for the qos support of real-time applications.
The Journal of Supercomputing, 71(2):448–478.
Cordeschi, N., Shojafar, M., and Baccarelli, E. (2013).
Energy-saving self-configuring networked data cen-
ters. Computer Networks, 57(17):3479–3491.
Cugola, G. and Margara, A. (2012). Processing flows of
information: From data stream to complex event pro-
cessing. ACM Computing Surveys (CSUR), 44(3):15.
Daniel Gmach, J. R. and Cherkasova, L. (2012). Sell-
ing t-shirts and time shares in the cloud. In Proc. of
12th IEEE/ACM International Symposium on Cluster,
Cloud and Grid Computing, CCGrid 2012, Ottawa,
Canada, May 13-16, 2012, pages 539–546.
Grant, M. and Boyd, S. (2015). Cvx: Matlab software for
disciplined convex programming.
Herbert, S. and Marculescu, D. (2007). Analysis
of dynamic voltage/frequency scaling in chip-
multiprocessors. In ISLPED, pages 38–43.
ACM/IEEE.
Kimura, H., Sato, M., Hotta, Y., Boku, T., and Takahashi, D.
(2006). Emprical study on reducing energy of parallel
programs using slack reclamation by dvfs in a power-
scalable high performance cluster. In IEEE CLUS-
TER’06, pages 1–10. IEEE.
Mathew, V., Sitaraman, R. K., and Shenoy, P. (2012).
Energy-aware load balancing in content delivery net-
works. In INFOCOM, 2012 Proceedings IEEE, pages
954–962. IEEE.
Mishra, A., Jain, R., and Durresi, A. (2012). Cloud com-
puting: networking and communication challenges.
Communications Magazine, IEEE, 50(9):24–25.
TEEC 2016 - Special Session on Tools for an Energy Efficient Cloud
396

Qian, Z., He, Y., Su, C., Wu, Z., Zhu, H., Zhang, T., Zhou,
L., Yu, Y., and Zhang, Z. (2013). Timestream: Reli-
able stream computation in the cloud. In Proceedings
of the 8th ACM European Conference on Computer
Systems, pages 1–14. ACM.
Shojafar, M., Cordeschi, N., Amendola, D., and Baccarelli,
E. (2015). Energy-saving adaptive computing and
traffic engineering for real-time-service data centers.
In Communication Workshop (ICCW), 2015 IEEE In-
ternational Conference on, pages 1800–1806. IEEE.
Urgaonkar, B., Pacifici, G., Shenoy, P., Spreitzer, M., and
Tantawi, A. (2007). Analytic modeling of multitier
internet applications. ACM Transactions on the Web
(TWEB), 1(1):2.
Urgaonkar, R., Kozat, U. C., Igarashi, K., and Neely, M. J.
(2010). Dynamic resource allocation and power man-
agement in virtualized data centers. In NOMS, pages
479–486. IEEE.
Wang, L., Zhang, F., Arjona Aroca, J., Vasilakos, A. V.,
Zheng, K., Hou, C., Li, D., and Liu, Z. (2014).
Greendcn: a general framework for achieving energy
efficiency in data center networks. Selected Areas in
Communications, IEEE Journal on, 32(1):4–15.
Warneke, D. and Kao, O. (2011). Exploiting dynamic re-
source allocation for efficient parallel data processing
in the cloud. Parallel and Distributed Systems, IEEE
Transactions on, 22(6):985–997.
An Energy-aware Scheduling Algorithm in DVFS-enabled Networked Data Centers
397
