
Cloud Services Selection by Load Balancing between Clouds
A Hybrid MCDM/Markov Chain Approach
Ouassila Hioual
1, 2
and Sofiane Mounine Hemam
1, 3
1
Department of Mathematics and Computer Science, Abbès Laghrour University, Khenchela, Algeria
2
LIRE Laboratory of Constantine, Constantine Algeria
3
ICOSI Laboratory of Khenchela, Khenchela, Algeria
Keywords: Cloud Computing, Cloud Service, Service Selection, TOPSIS, Load Balancing, Multi Cloud Computing,
Multi Agents System, MCDA Discrete Time Markov Chain, Contract Net Protocol, CNP.
Abstract: With the rapid growth of cloud computing, a number of service providers have appeared who offer similar
services at various prices and performance levels. So, the increasing number of cloud services has made
service selection a challenging decision-making problem. In a multi cloud environment, we need to find a
service from multiple clouds by taking into account several requirements (user and system ones). In this paper,
we present a cloud service selection model in which we focus on load-balancing across the replicas of services
placed at different clouds, this, by taking into account end-user requirements for the service price.
1 INTRODUCTION
Web Intelligence presents excellent opportunities and
challenges for the research and development of new
generation Web-based information processing
technology, as well as for exploiting business
intelligence. With the rapid growth of the Web,
research and development on WI have received much
attention (Yao et al., 2001). In this optic, Cloud
computing has emerged as a new paradigm which
provides a set of accessible computing resources as
services that can be accessed through the network
from anywhere in the world. The aim of the cloud
computing model is to increase the opportunities for
cloud user by accessing leased infrastructure and
software applications from anywhere anytime
manner (Whaiduzzaman et al, 2014). The NIST
(National Institute of Standards and Technology)
(Mell and Grance, 2011) classifies cloud services in
three models: SaaS (Software as a Service), PaaS
(Platform as a Service) and IaaS (Infrastructure as a
Service). Also, a service provider can use four types
of cloud deployment models: private cloud,
community cloud, public cloud, and hybrid cloud.
The first three deployment models are ordered from
the least to the most dynamic in terms of provisioning
elasticity, and the hybrid cloud is a mix of resources
from two or more of the other models. In this paper,
we will consider services based on the SaaS model.
In a multi cloud environment, a difficult decision
emerges when a customer has to select a Cloud
service because of the growth of public Cloud
offerings. When several, and often conflictive,
criteria should be taken into account to select one
Cloud service from a set of similar services, the
decision becomes more difficult. In such a situation,
however, it is challenging to find an appropriate
service by taking into consideration two criteria: load
balancing between the different clouds and
minimizing the service cost. So, There is a need for a
cloud service selection approach that takes into
account the multitude of available cloud services,
variations in QoS performance (as well as service
cost), and the user's criteria to rank available cloud
services, and then assists in selecting the best and
most advantageous service (
Zia et al, 2013).
In previous work (Hioual and Boufaida, 2011),
we have proposed an agent based architecture for web
services composition. In this regard, we propose a
Cloud service selection solution based on the agent
paradigm, which has proved to be effective for
distributed applications. Also, the selection of
alternatives in the presence of multiple properties or
attributes is referred to as a Multiple Attribute
Decision Making (MADM) problem (
Roy, 1990).
Therefore, it seems natural to use multi-criteria
decision-making methods in order to evaluate a set of
Cloud services alternatives.
Hioual, O. and Hemam, S.
Cloud Services Selection by Load Balancing between Clouds - A Hybrid MCDM/Markov Chain Approach.
In Proceedings of the 12th International Conference on Web Information Systems and Technologies (WEBIST 2016) - Volume 1, pages 289-295
ISBN: 978-989-758-186-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
289

In this paper, we focus on load-balancing across
clouds containing replicas of services. And since
cloud services are payable, we try to minimize, the
most possible, the cost to pay by a Cloud customer.
The literature shows that MCDA techniques are
indeed effective and can be used for cloud service
selection. Also, several works do reveal that TOPSIS
and both outranking methods (ELECTRE and
PROMETHEE) are more suitable for this purpose. If
the number of available services is very large, then
TOPSIS is appropriate because of its computational
simplicity, so we will use this later in order to rank
service alternatives and in order to select the best one.
And, since our system changes dynamically (Cloud
states change dynamically according to service
requests), we will use Discrete Time Markov Chain
(DTMC) that is well established analytical tool for
understanding dynamic systems behavior (Kemeny
and Snell, 1976), and it has been applied to a variety
of practical problems in real-world domains.
The remainder of the paper is structured as
follows: In Section 2 some related works are
presented. In Section 3, first the overall model of the
cloud service selection, in multiple cloud
environments, is presented, and then how this model
can minimize the cost and in the same time how it
balances the load between the different clouds, is
discussed. The paper is concluded and an outlook on
future work is given in Section 4.
2 LITERATURE REVIEW
Making a decision involves that there are alternative
choices to be taken into account and in a such
situation we need to choose the one that best fits with
our goals, objectives, desires, values and so on.
Several researches show that MCDA techniques are
effective and can be used for cloud service selection.
In this regard, several approaches which are based
on MCDM techniques, that assist a user in making a
service selection decision in the Cloud environment,
exist. For instance TOPSIS (Qu and Chen, 2009),
AHP (Zuo et al, 2008), and PROMETHEE (Karim et
al, 2011) were applied for service selection. Chen et
al. In (Qu and Chen, 2009), the authors developed a
general QoS-based service selection method. By
importing the proposed QoS ontology into OWL-S
standards, the proposed method can express Web
service's nonfunctional attributes in a semantic and
extensible way. Web service QoS based selection is
formulated as a multi-criteria decision making
(MCDM) which can be solved by using different
MCDM models to evaluate QoS criteria of the
candidate Web services. The values of quality
parameters of a Web service are normalized to a non-
negative real-valued number where higher normalized
values represent higher levels of service performance.
(Zuo et al., 2008) focused on the problem that how
to select the optimal service among many Web
services which all meet the functional needs,
establishes an index system for Web services products
selection from four aspects, namely the supply side,
the user, product and environment. Based on this, the
authors collected the views of 30 experts by Analytic
Hierarchy Process (AHP) method and calculated the
weight of each index at all levels based on the data
collected from questionnaire survey. In the overall
sample data analysis, the authors put two types of
sample data namely business operation experts and
academics for comparative analysis. The Web
services selection model proposed could provide the
reference to Web services managers when they
selecting Web services, and also contributed to in-
depth research on the adoption of Web services based
information system.
In (Karim et al., 2011), the authors proposed to
use an enhanced PROMETHEE model for QoS-based
web service selection. The first enhancement of
authors was to take into account the QoS
interdependency by using the Analytical Network
Process (ANP) to calculate the weight/priority
associated with each criterion. User's QoS
requirement is not considered in the original
PROMETHEE model. As a consequence, the second
enhancement of authors was to check the outranking
flows of each service with respect to the request in the
ranking step, so that they knew how well a service
satisfies the user requirement.
(Chen et al., 2012) proposed a system that enables
automatic conflict detection between the user's
criteria and enterprise policies in cloud service
selection for enterprises. Their system checks various
conflicts which result from the violation of enterprise
policies and inconsistency in a cloud service user's
requirements. Then, it selects an appropriate service
that satisfies the user's requirements and also
complies with enterprise policies, using constraint
programming. Zia et al. (Rehman et al., 2011).
presented the cloud service selection problem as a
multi-criteria decision making problem by proposing
a mathematical framework for multi-criteria cloud
service selection.
A few numbers of existing approaches, however,
simultaneously consider user requirements (as well as
cost) and load balancing between Clouds. In contrast
to the above research works and discussion, we
approach cloud service selection in a multiple cloud
WIS 2016 - Special Session on New Trends in Web Intelligence and Services
290
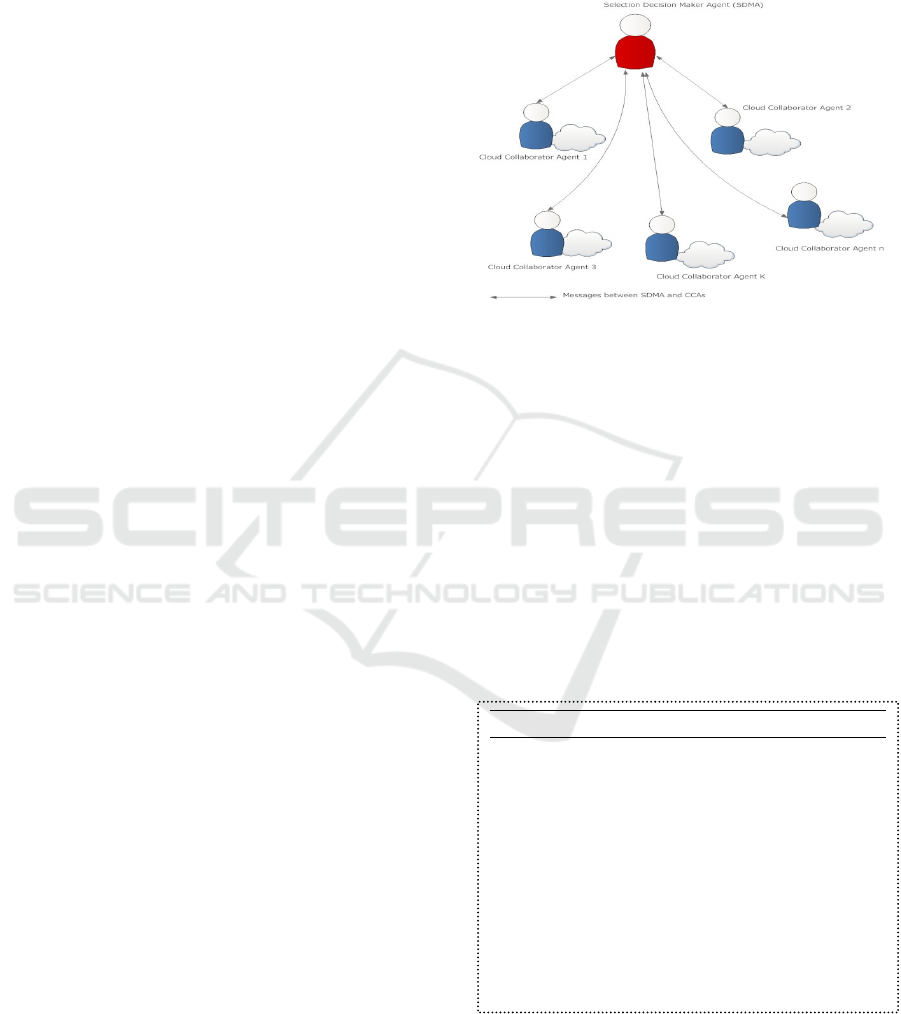
environment by proposing multi agent based
architecture. We assume that each Cloud Collaborator
Agent (CCA) has a complete knowledge of all
services deployed in its Cloud. The Selection
Decision Maker Agent (SDMA) selects the best
service alternative which minimizes both load and
cost.
3 PROPOSED CLOUD SERVICE
SELECTION MODEL
3.1 Load Balancing and Minimizing
Cost: A Bi-criteria Issue
For making the choice between different instances of
the same service, we have considered two criteria,
which are very critical when selecting a cloud service,
which are: the load balancing through clouds and the
minimization of the cost of a service instance. Our
research problem can be considered as a schedule
tasks problem on heterogeneous clouds in order to
minimize both maximum load and maximum service
cost.
3.2 Overview of the Proposed Agent
based Architecture
Our architecture (cf. Fig.1) is an agent based one. The
main agents that compose this architecture are:
- Selection Decision Maker Agent (SDMA)
coordinates and assembles the Cloud Collaborator
Agents (CCA) to execute the required operations.
It also initializes the selection process by sending
to CCAs the call for proposal to be realized.
- A set of Cloud Collaborator Agents (CCAs): each
one controls a specific cloud; it means it has a
global idea of the services provided by this cloud
and also, some interesting information like, for
example, the cost of each provided service and the
number of request incoming to its specific cloud.
3.3 SDMA and CCAs Behaviors
In this work, we use the well-known contract net
protocol (CNP) (Smith, 1981). in order to select a
proper service by balancing load between clouds and
resolving consumer requirements. As it is known, the
rules that define the reaction of agents to events (e.g.,
reception of a call-for-proposals message) define an
agent behavior. For each type of agent that constitutes
our architecture, one or a set of behaviors is defined.
Selection Decision Maker Agent and Cloud
Collaborator Agents interact among each other to
select a persistent Cloud service by adopting a set of
agent behaviors as it will be discussed in the next sub-
sections.
Figure 1: A simplified overview of our architecture.
3.3.1 SDMA Behaviors
A SDMA has a main behavior and a sub behavior.
The first one is derived from the contract net protocol
initiator behavior that submits consumer preferences
to CCAs. The second one is the Result_evaluator
behavior which receives proposals from CCAs, and
then it selects an adequate cloud service according to
two criteria: the load balancing between clouds and
the service cost.
CNP_SDMA_Initiator Behavior
This behavior is shown in Table 1:
Table 1: Initiator behaviour of a SDMA.
We assume that it exist at least one proposal for each
call for proposal.
SDMA_Result_Evaluator Sub-behavior
For making the choice between different instances of
CNP_SDMA_Initiator Behavior
Input: (i) Cloud Consumer request
Output: (i) A single virtualized service
1: Send call_for_proposals(Reqi) to m CCAs
2: nProposals ← BlockReceive(Proposals, timeout)
3: if (nProposals > 0) then
4: Result_evaluator sub behavior
5 Send reject_proposal to(nProposals-1) CCAs
6: Send accept_proposal to one (1) CCA
7: BlockReceive(Reqi.Output)
8: else
9: Treat exception
10:Gather outputs into a single virtualized service
Cloud Services Selection by Load Balancing between Clouds - A Hybrid MCDM/Markov Chain Approach
291

the same cloud service and in addition to consumer
preferences, the SDMA has to consider another
criterion, which is very critical when selecting a
service, that is: the load balancing through clouds. For
this, the SDMA will find a ranking of service
alternatives, it uses TOPSIS method (Technique for
Order Preference by Similarity to Ideal Solution).
The Technique for Order Preference by Similarity
to Ideal Solution (TOPSIS) method, which is initially
proposed by (Hwang and Yoon, 1981), is one of the
well-known multiple criteria decision making
(MCDM) methods. This technique shows preference
for the similarity to an ideal solution, which tries to
select an alternative that is closest to the ideal solution
and simultaneously farthest from the anti-ideal
solution. In this technique, the decision matrix is first
normalized using vector normalization, and the ideal
and anti-ideal solutions are identified within the
normalized decision matrix (Whaiduzzaman et al,
2014). The main steps of TOPSIS are given in the
next section
This SDMA behavior is illustrated in Table 2:
Table 2: Result evaluation behaviour of a SDMA.
NB. We assume that the weights of criteria are as
follow: W
load
=0,9 and Wcost=0,1. It means load
balancing criterion has bigger weight than the cost
service criterion.
TOPSIS steps
Given the positive solution A
*
and the negative
solution A
*
which are calculated as follow:
A
*
={ g
1
*, …, g
j
*,…, g
n
* }
Where g
j
* is the best value for the j
th
criteria of all
the alternatives.
A
*
= {g
1*
, …, g
j*
, …, g
n*
}
Where g
j*
is the worst value for the j
th
criteria of all
the alternatives.
The procedure of TOPSIS can be expressed in a
series of six steps:
Step1. Calculate the normalized decision matrix.
The normalized ratings r
j
(x
i
)
are calculated as:
()
g
x
i
j
()
rx
ji
m
2
(())
g
x
i
j
i1
=
=
Where i = 1,…, m and j = 1,…, n
Step2. Calculate the weighted normalized
decision matrix. The weighted normalized rating
v
j
(x
i
) is calculated as:
V
j
(x
i
) = w
j
r
j
(x
i
) for i = 1,…, m and j = 1,…, n;
Where w
j
is the weight of the j
th
criterion.
Step3. Determine the positive and negative ideal
solutions as follow:
A* = {v
1
*, …, v
j
*,…, v
n
* }
= {(max
i
v
j
(x
i
)/ j∈J1), (min
i
v
j
(x
i
)/ j∈J2)}
A
*
= {v
1*
, …, v
j*
, …, v
n*
}
= {(min
i
v
j
(x
i
)/ j∈J1), (max
i
v
j
(x
i
)/ j∈J2)},
Where J1 is associated with benefit criteria, and J2 is
associated with cost criteria.
NB. In this paper, we focus only on two cost
criteria, we have not benefit criteria.
Step 4. Calculate the separation measures, using
the n dimensional Euclidean distance. The separation
of each alternative from the positive ideal solution,
and with respect from the negative ideal solution, is
given as:
Step5. Calculate the relative closeness to the ideal
solution. The relative closeness of the alternative A
j
with respect to A
*
is defined as:
c (x
i
) = d
*
(x
i
)/ (d*(x
i
)+d
*
(x
i
))
Step6. Rank the preference order. For ranking
alternatives, we use the index c (x
i
), we can rank them
in decreasing order.
3.3.2 CCAs Behaviors
The main behavior of CCAs handles call for
proposals to fulfill requirements coming from
SDMA. Participants’ (CCAs’) proposals contain,
SDMA_Result_evaluator Sub- Behavior
Input: (i) A set of CCAs proposals (a set of
Rinf )
Output: (i) A selected alternative cloud
service
1: Rank service alternatives, provided by
under loaded clouds, by using TOPSIS method
2:Select the alternative service which has the
minimum cost according to load balancing
between clouds
()
=
−=
n
j
v
j
x
i
v
j
x
i
d
1
*
)(
2
)(
*
()
=
−=
n
j
v
j
x
i
v
j
x
i
d
1
*
)(
2
)(
*
WIS 2016 - Special Session on New Trends in Web Intelligence and Services
292

essentially, service alternatives costs, ID providers,
and the load probability of the managed cloud.
Table 3: Participant behaviour of a CCA.
The Prepare and Send Proposal step (line 3 of
CNP_CCA_Participant Behavior) determines the
main functionality of CCAs.
The proposal of a CCA is a set of information
noted Rinformation :
Rinformation=<C_LoadProbability, A list
ranking of (S_alt
x
, ID_provider, C_inf) >
Where:
C_LoadProbability is the actual load
probability of the managed cloud;
S_alt
x
: the X
th
alternative of S / S is the
requested cloud service;
ID_provider: the corresponding provider of
the X
th
alternative of S;
C_inf: contains the cost of a service
alternative.
A list ranking of (S_alt
x
, ID_provider, C_inf) is
ranked in increasing order according to service cost.
To determine the value of C_LoadProbability, we
use Discret Time Markov Chain Model (Kemeny and
Snell, 1976). We assume that the set of state space of
our model is S = {G
i
; O
i
; R
i
}, where:
• G
i
: is the state of the Cloud CL
i
when it is
underloaded i.e. Green State ( Load ≤ λ
2
) (cf.
Figure 2).
• R
i
: is the state of the Cloud CL
i
when it is
overloaded, i.e. Red State( Load ≥ λ
1
). .
• O
i
: is the state of the Cloud CL
i
when it is
between the two G and R states, i.e. Orange
State (λ
2
<
Load < λ
1
)
Each cloud has its Discrete Time Markov chain.
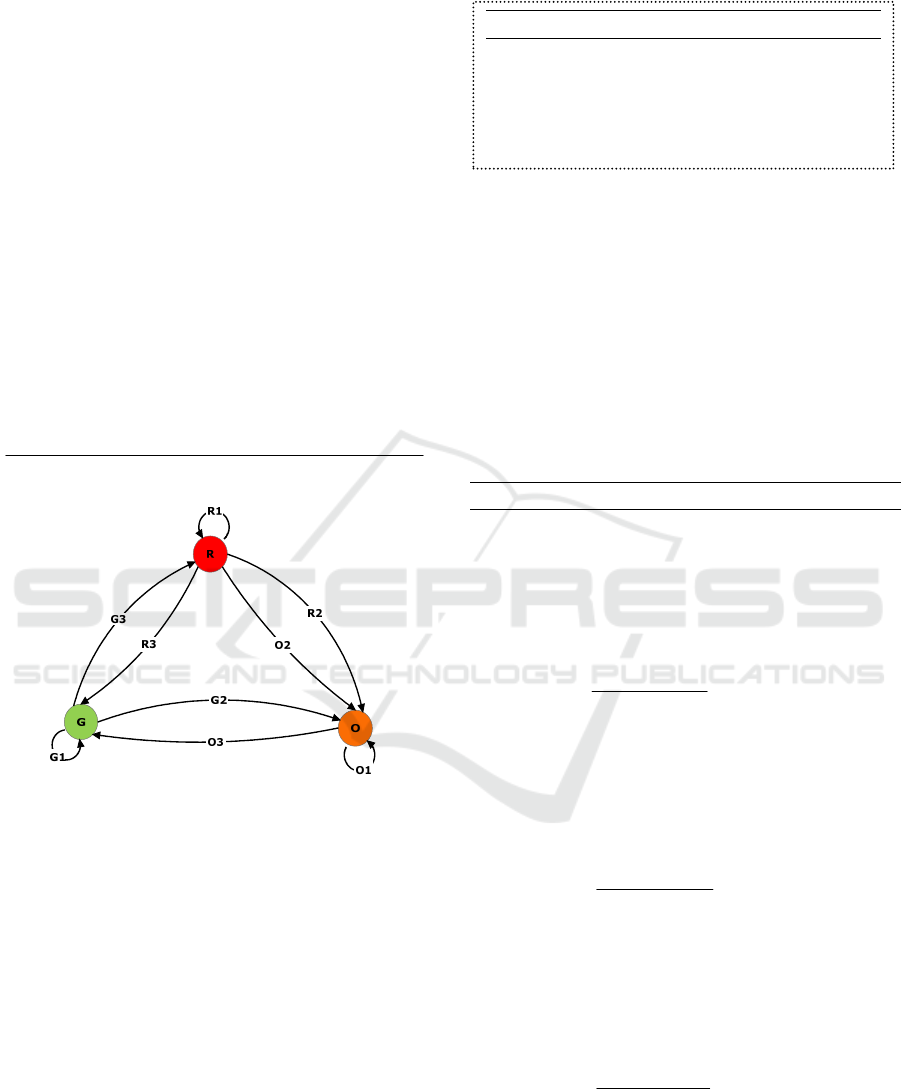
Figure 2: Load states of the cloud.
The state transition probabilities are derived as
follows. Given states S
i
, S
j
, where i, j= 1…3 and (S
i
,
S
j
) ∈ S, p
ij
, is the probability of transitioning for state
S
i
to state S
j
written as S
i
→S
j
.
We can distinguishes between nine (9) kinds of
state transition probabilities, which are (cf. Figure 3):
• G1: is the probability that the cloud still in Green
state
• G2: is the probability that the state cloud
changes from Green to Orange
• G3: is the probability that the state cloud
changes from Green to Red
• O1: is the probability that the cloud still in
Orange state
• O2: is the probability that the state cloud
changes from Orange to Red
• O3: is the probability that the state cloud
changes from Orange to Green
• R1: is the probability that the cloud still in Red
state
• R2: is the probability that the state cloud
changes from Red to Orange
• R3: is the probability that the state cloud
changes from Red to Green
We note that:
= 3..1i
i
G
= 1
= 3..1i
i
O
= 1
= 3..1i
i
R
= 1
These probabilities are used to calculate the
frequency (probability) of states, we have three kinds
of frequency:
•
G
π
: frequency of Green State
•
O
π
: frequency of Orange State
•
R
π
: frequency of Red State
1
λ
2
λ
CNP_CCA_Participant Behavior
Input: (i) call_for_proposals from SDMA
Output: (i) A ranking of CS
i
alternatives or a
Failure message
1: BlockReceive(call_for_proposals(Reqi))
2: if (exist (CS
i
)) then
3: Prepare and Send Proposal
4: Else
5: Send Failure message
6: Start over
Cloud Services Selection by Load Balancing between Clouds - A Hybrid MCDM/Markov Chain Approach
293
The C_LoadProbability represents the frequency
of Green state(
G
π
).
Since all states of our Markov Chain model, are
in the same recurrent class, then, according to Steady-
State Probabilities (Tijms, 2003), the probability to
going from state i to state j in n steps is:
)(nr
ij
=
take the limit as n →∞ we have the equilibrium
equations
G
π
=
321
*** GGG
ROG
πππ
++
O
π
=
321
*** OOO
GRO
πππ
++
R
π
=
321
*** RRR
GOR
πππ
++
R
π
+
O
π
+
G
π
= 1
From these equilibrium equations we conclude that
G
π
is evaluated according the formula (1) below:
)1)(1()]1)(1()1()[1(
)1)(1()1)(1(
211221113221
21122113
−−−+−−−++−−−
−−−+−−−
OORGRRGRRGOO
OORGRROG
Figure 3: Markv Chain Model.
The resulting Transition Probability Matrix
(TPM) is a 3 ×3 stochastic matrix, shown in Figure 4.
Here rows stand for the state the transition originates
from, and columns represent states the transition goes
to. Each cell in a TPM (cf. Figure 4) represents a p
ij
,
where p
ij
= O
i
, R
i
or G
i
and i= 1..3. . As in any
stochastic TPM, the transition values of all columns
in a row must sum to one (1.0).
TPM =
Figure 4: Transition Probability Matrix.
Table 4: How to calculate C_LoadProbability.
CNP_CCA Accept Proposal Behavior
In the case when a CCA receives an accept proposal
from a SMDA, it must update its TPM according to
its state. Here we can distinguishes Three cases:
• The case when the load of the cloud is less than
λ
2
• The case when the load of cloud is more than λ
1
• The case when the load of the cloud is between
λ
1
and λ
2
Table 5: Accept proposal behaviour of a CCA
CNP_CCA Accept Proposal Behavior
Input: Accept Proposal
Output: TPM updated
1: If State Cloud = Green
2: G
1
← G
1*
G
π
3: G
2
← G
2*
O
π
4: G
3
← G
3*
R
π
5: G
i
← , i= 1..3
6: State Cloud ← State of transition of max(G
i
)
7: If State Cloud = Orange
8: O
1
← O
1*
O
π
9: O
2
← O
2*
R
π
10: O
3
← O
3*
G
π
11: O
i
← , i= 1..3
12: State Cloud ← State of transition of max(O
i
)
13: If State Cloud = Red
14: R
1
← R
1*
R
π
15: R
2
← R
2*
O
π
16: R
3
← R
3*
G
π
17: R
i
← , i= 1..3
18: State Cloud ← State of transition of max(R
i
)
The lines 5, 11 and 17 allow to guaranty that =
1, where X∈{G,O,R}
321
321
321
GGG
RRR
OOO
++
321
OOO
O
i
++
321
RRR
R
i
= 3..1i
i
X
++
321
GGG
G
i
−
k
kjik
Pnr )1(
Calculate C_LoadProbability Function
Output: C_LoadProbability
1: Calculate
G
π
according to the formula (1)
2: Return
G
π
WIS 2016 - Special Session on New Trends in Web Intelligence and Services
294

4 CONCLUSION
The cloud service selection problem is a challenging
research issue because of the tremendous growth in
the number of available services, the dynamic
environment and changing user needs. In this paper,
we have presented our proposed model for the
dynamic cloud service selection problem by taking
into account two critical criteria: the load balancing
through the different clouds, and the minimization of
a cloud service cost. We have focused on
demonstrating the effectiveness of adopting agent-
based techniques, MCDA methods and Markov chain
model for Cloud service selection by showing the
desirable property that our agents can autonomously
and successfully deal with changing service
requirements.
To improve our proposed solution, we will
address the problem where the selected service is
overloaded in an unloaded cloud over the other
clouds, this will result response time increasing. Also,
we aim to evaluate our approaches more extensively
through some case studies.
REFERENCES
Chen, C., Yan, S., Zhao, G., Lee, B. S. and Singhal, S.,
2012. A Systematic Framework Enabling Automatic
Conict Detection and Explanation in Cloud Service
Selection for Enterprises, in: IEEE 5th International
Conference on Cloud Computing (CLOUD), IEEE, pp
883-890.
Hioual, O and Boufaida, Z., 2011. An Agent Based
Architecture (Using Planning) for Dynamic and
Semantic Web Services Composition in an EBXML
Context. International Journal of Database
Management Systems (IJDMS), Vol.3, No.1, February
2011.pp 110-131
Hwang, C. and Yoon, K., 1981. Multiple attribute decision
making methods and application. Springer, New York.
Karim, R., Chen, D., and Chi-Hung, C., 2011. An Enhanced
PROMETHEE Model for QoS-Based Web Service
Selection. In Proceedings of the Services Computing
(SCC), 2011 IEEE, pp. 536-543.
Kemeny, J. and Snell, J., 1976. Finite Markov Chains.
Springer, New York.
Mell, P. and Grance, T. 2011. The NIST Definition of
Cloud Computing. National Institute of Standards and
Technology
Qu, L.-l. and Chen, Y., 2009. QoS ontology based efficient
web services selection. In Proceedings of the
Management Science and Engineering, ICMSE, pp. 45-
50.
Rehman, Z., Hussain, F. K., Hussain O. K., 2011. Towards
Multi-criteria Cloud Service Selection, in: Fifth
International Conference on Innovative Mobile and
Internet Services in Ubiquitous Computing (IMIS), pp:
44- 48.
Roy, B., 1990. Readings in multiple criteria decision aid,
chapter The outranking approach and the foundations
of ELECTRE methods. Springer-Verlag.
Smith, R. G., 1981. Correction to the contract net protocol:
high-level communication and control in a distributed
problem solver. IEEE Transactions on Computers, pp:
330, 372.
Tijms H. C., 2003. A first course in stochastic models.
Wiley, New York (N. Y.).
Whaiduzzaman, Md., Gani, A., Badrul, N, Shiraz, M.,
Haque, M.N., and Haque, I.T., 2014. Cloud Service
Selection Using Multicriteria Decision Analysis. The
Scientific World Journal, vol 2014. 10 pages. Hindawi
Publishing Corporation.
Yao, Y. Y., Zhong, N., Liu, J., Ohsuga, S., and Wong,
S.K.M.,2001. Web Intelligence (WI): Research
challenges and trends in the new information age, Web
Intelligence: Research and Development. In
Proceedings of the First Asia-Pacific Conference, WI
2001, LNCS 2198, (Eds.), Springer, pp. 1-17.
Zia, R., Khadeer Hussain, O., Khadeer Hussain, F., 2013.
Parallel Cloud Service Selection and Ranking Based on
QoS History. International Journal of Parallel
Programming. Vol 42 (5), pp: 820-852.
Zuo, M., Wang, S., and Wu, B., 2008. Research on web
services selection model based on AHP. In Proceedings
of the Service Operations and Logistics, and
Informatics, IEEE/SOLI, pp. 2763-2768.
Cloud Services Selection by Load Balancing between Clouds - A Hybrid MCDM/Markov Chain Approach
295
